Subdiffusive Reaction Model of Molecular Species in Liquid Layers: Fractional Reaction-Telegraph Approach
Abstract
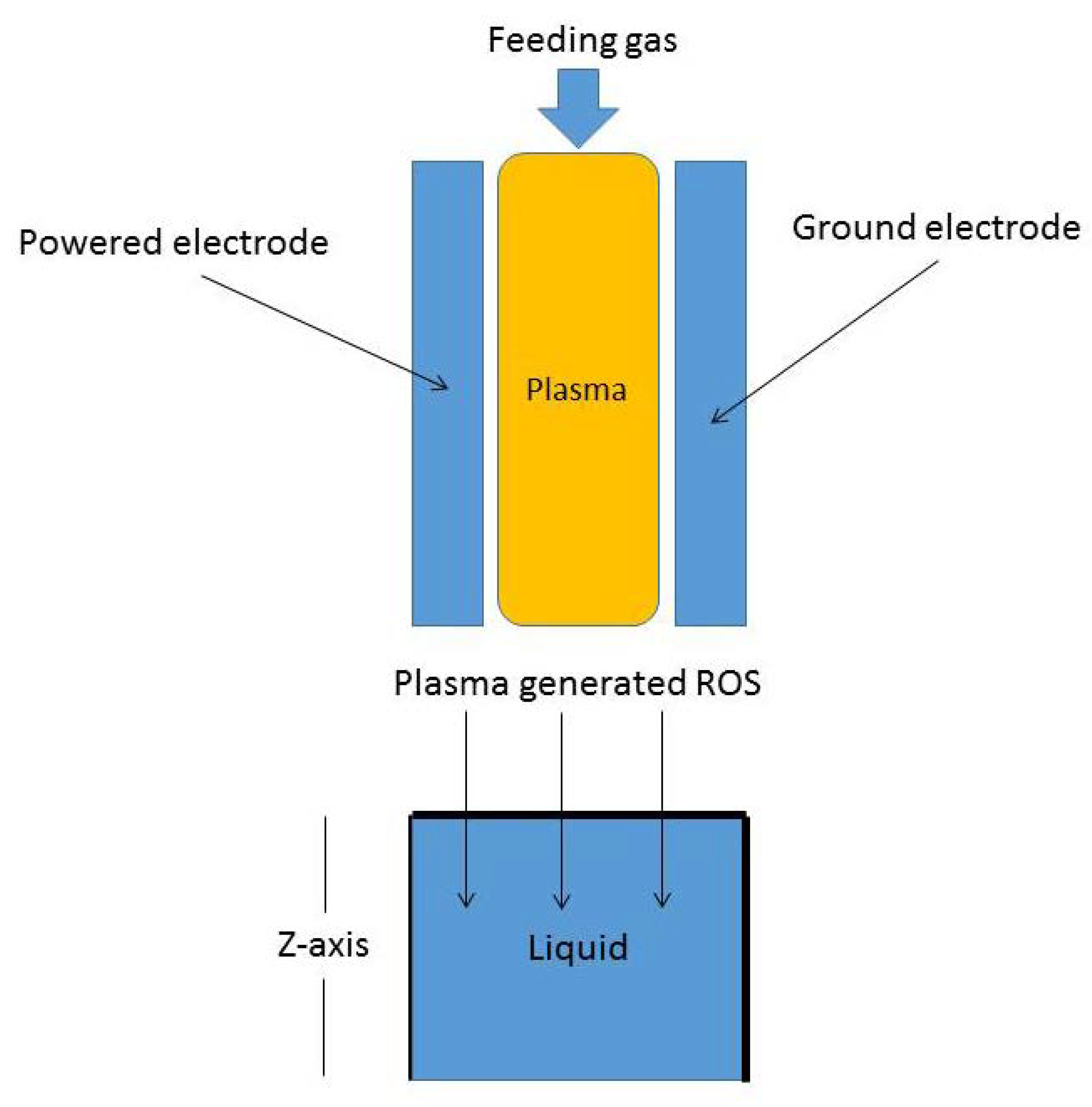
1. Introduction
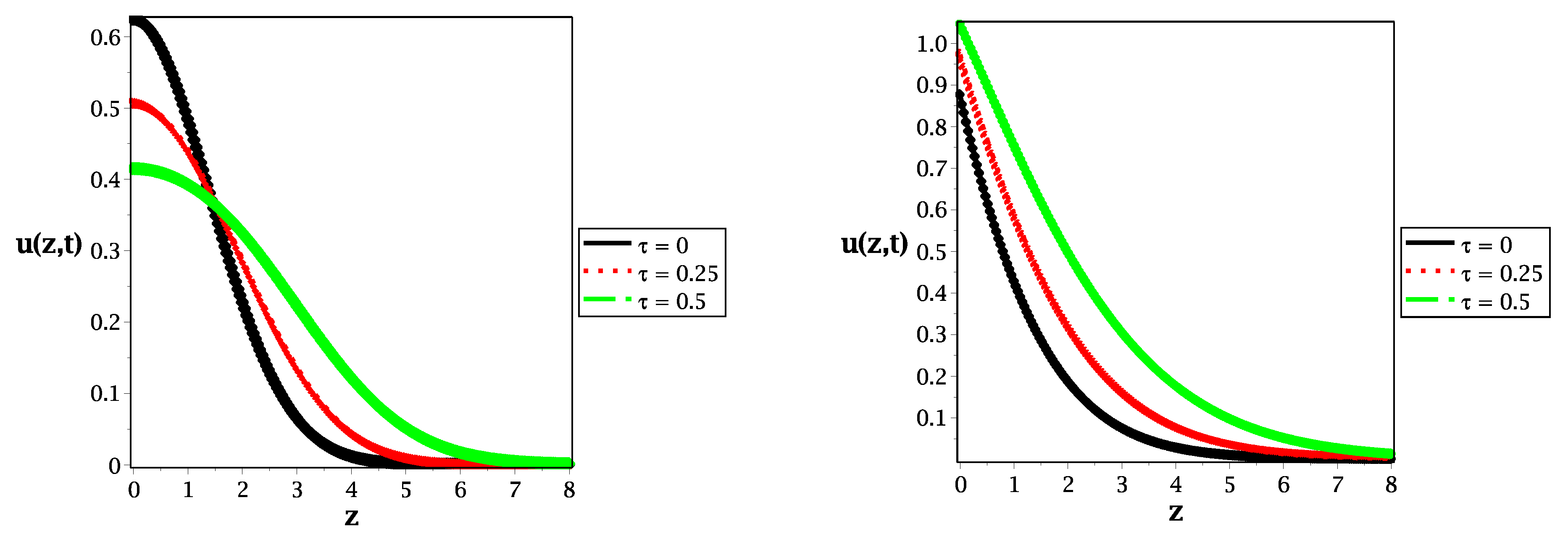
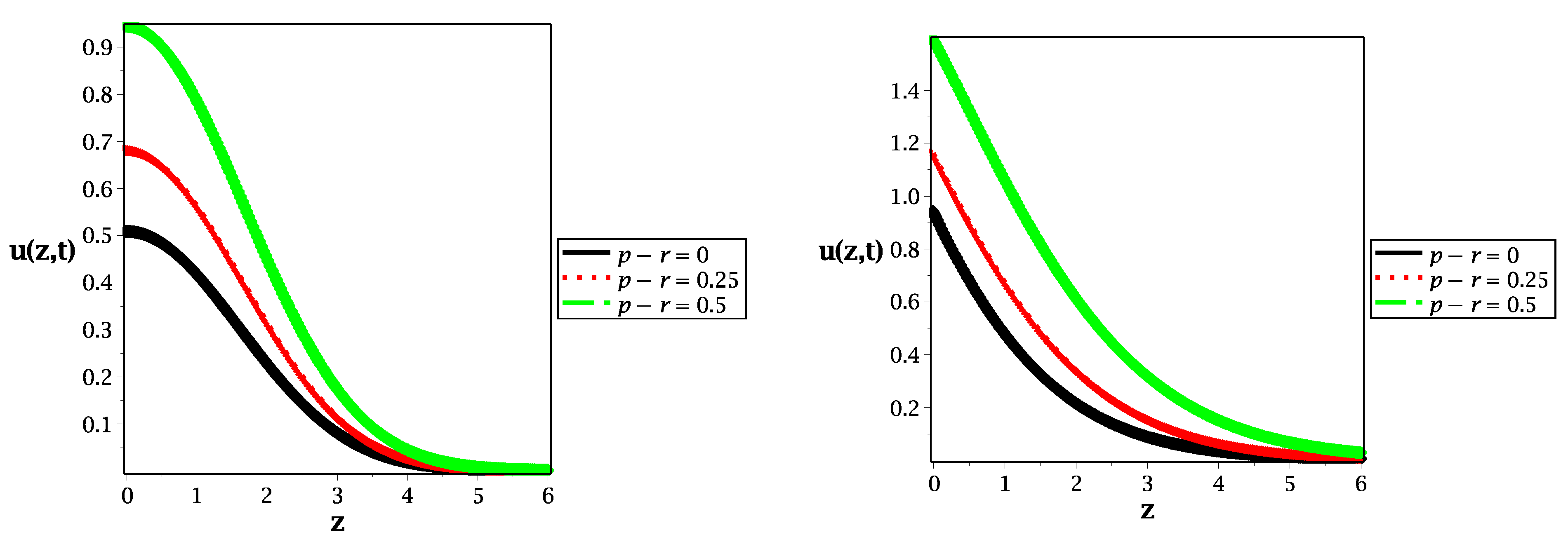
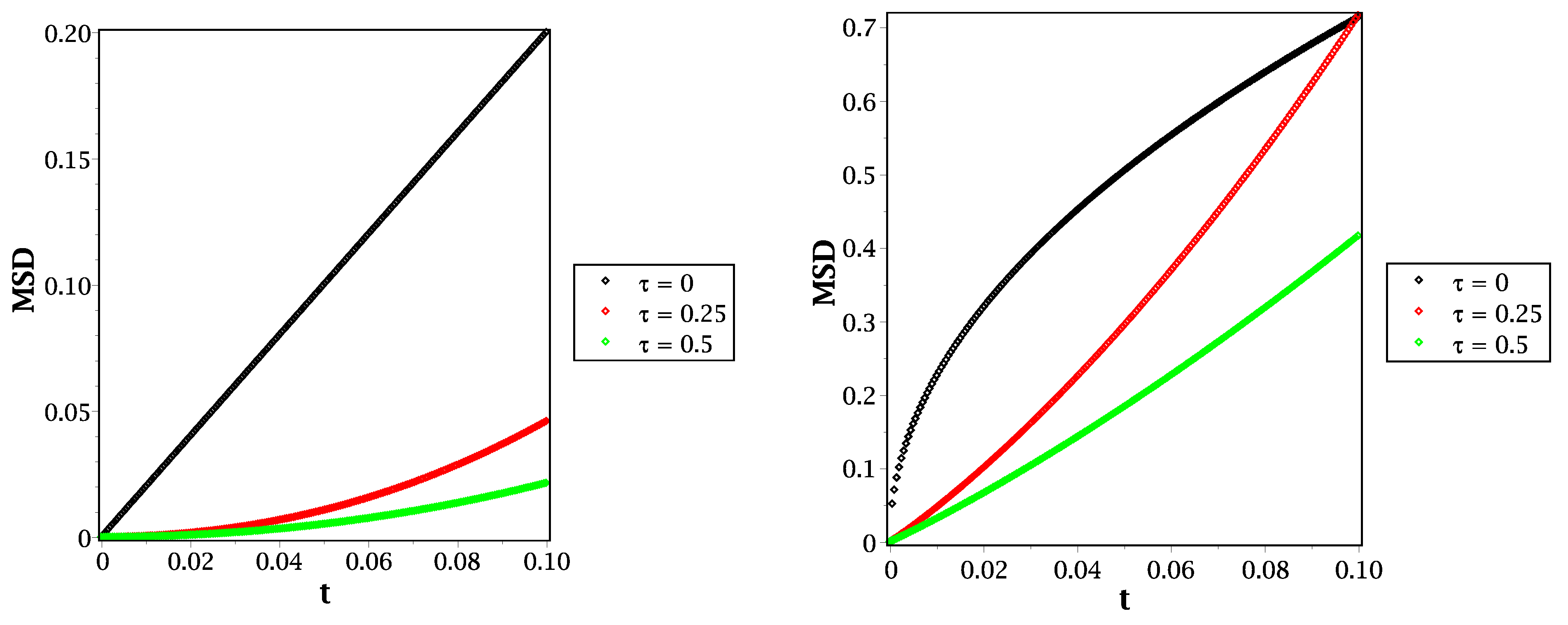
2. Fractional Reaction–Telegraph Model
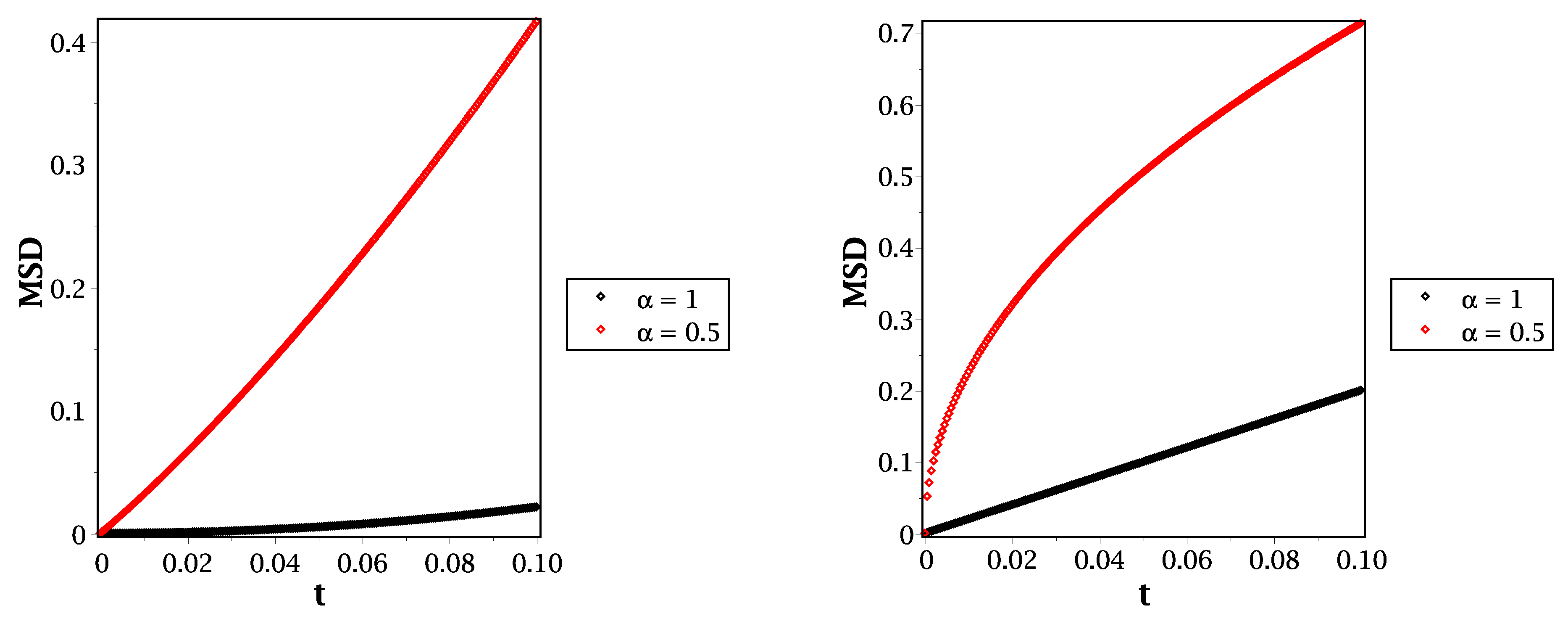
3. Discussion
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Fridman, A. Plasma Chemistry; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Kong, M.G.; Kroesen, G.; Morfill, G.; Nosenko, T.; Shimizu, T.; Van Dijk, J.; Zimmermann, J. Plasma medicine: An introductory review. New J. Phys. 2009, 11, 115012. [Google Scholar] [CrossRef]
- Laroussi, M.; Kong, M.; Morfill, G. Plasma Medicine: Applications of Low-Temperature Gas Plasmas in Medicine and Biology; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Hefny, M.M.; Kairo, A. Experimental Study of Cold Atmospheric Plasma for Plasma Medicine Research and Applications. Ph.D. Thesis, Ruhr-Universität Bochum, Bochum, Germany, 2019. [Google Scholar]
- Fridman, G.; Friedman, G.; Gutsol, A.; Shekhter, A.B.; Vasilets, V.N.; Fridman, A. Applied plasma medicine. Plasma Process. Polym. 2008, 5, 503–533. [Google Scholar] [CrossRef]
- Bekeschus, S.; Wende, K.; Hefny, M.M.; Rödder, K.; Jablonowski, H.; Schmidt, A.; von Woedtke, T.; Weltmann, K.D.; Benedikt, J. Oxygen atoms are critical in rendering THP-1 leukaemia cells susceptible to cold physical plasma-induced apoptosis. Sci. Rep. 2017, 7, 1–12. [Google Scholar] [CrossRef] [PubMed]
- El-Kalliny, A.S.; Abd-Elmaksoud, S.; El-Liethy, M.A.; Abu Hashish, H.M.; Abdel-Wahed, M.S.; Hefny, M.M.; Hamza, I.A. Efficacy of Cold Atmospheric Plasma Treatment on Chemical and Microbial Pollutants in Water. ChemistrySelect 2021, 6, 3409–3416. [Google Scholar] [CrossRef]
- Hefny, M.M.; Pattyn, C.; Lukes, P.; Benedikt, J. Atmospheric plasma generates oxygen atoms as oxidizing species in aqueous solutions. J. Phys. D Appl. Phys. 2016, 49, 404002. [Google Scholar] [CrossRef]
- Benedikt, J.; Hefny, M.M.; Shaw, A.; Buckley, B.R.; Iza, F.; Schäkermann, S.; Bandow, J. The fate of plasma-generated oxygen atoms in aqueous solutions: Non-equilibrium atmospheric pressure plasmas as an efficient source of atomic O (aq). Phys. Chem. Chem. Phys. 2018, 20, 12037–12042. [Google Scholar] [CrossRef]
- Blackert, S.; Haertel, B.; Wende, K.; von Woedtke, T.; Lindequist, U. Influence of non-thermal atmospheric pressure plasma on cellular structures and processes in human keratinocytes (HaCaT). J. Dermatol. Sci. 2013, 70, 173–181. [Google Scholar] [CrossRef]
- Wende, K.; Straßenburg, S.; Haertel, B.; Harms, M.; Holtz, S.; Barton, A.; Masur, K.; von Woedtke, T.; Lindequist, U. Atmospheric pressure plasma jet treatment evokes transient oxidative stress in HaCaT keratinocytes and influences cell physiology. Cell Biol. Int. 2014, 38, 412–425. [Google Scholar] [CrossRef]
- Gorbanev, Y.; O’Connell, D.; Chechik, V. Non-thermal plasma in contact with water: The origin of species. Chem. A Eur. J. 2016, 22, 3496–3505. [Google Scholar] [CrossRef] [PubMed]
- Lukes, P.; Dolezalova, E.; Sisrova, I.; Clupek, M. Aqueous-phase chemistry and bactericidal effects from an air discharge plasma in contact with water: Evidence for the formation of peroxynitrite through a pseudo-second-order post-discharge reaction of H2O2 and HNO2. Plasma Sources Sci. Technol. 2014, 23, 015019. [Google Scholar] [CrossRef]
- Duan, J.; Ma, M.; Yusupov, M.; Cordeiro, R.M.; Lu, X.; Bogaerts, A. The penetration of reactive oxygen and nitrogen species across the stratum corneum. Plasma Process. Polym. 2020, 17, 2000005. [Google Scholar] [CrossRef]
- Yusupov, M.; Razzokov, J.; Cordeiro, R.M.; Bogaerts, A. Transport of reactive oxygen and nitrogen species across aquaporin: A molecular level picture. Oxidative Med. Cell. Longev. 2019, 2019. [Google Scholar] [CrossRef] [PubMed]
- Van der Paal, J.; Hong, S.H.; Yusupov, M.; Gaur, N.; Oh, J.S.; Short, R.D.; Szili, E.J.; Bogaerts, A. How membrane lipids influence plasma delivery of reactive oxygen species into cells and subsequent DNA damage: An experimental and computational study. Phys. Chem. Chem. Phys. 2019, 21, 19327–19341. [Google Scholar] [CrossRef]
- Schneider, S.; Lackmann, J.W.; Ellerweg, D.; Denis, B.; Narberhaus, F.; Bandow, J.E.; Benedikt, J. The role of VUV radiation in the inactivation of bacteria with an atmospheric pressure plasma jet. Plasma Process. Polym. 2012, 9, 561–568. [Google Scholar] [CrossRef]
- Hefny, M.M.; Nečas, D.; Zajíčková, L.; Benedikt, J. The transport and surface reactivity of O atoms during the atmospheric plasma etching of hydrogenated amorphous carbon films. Plasma Sources Sci. Technol. 2019, 28, 035010. [Google Scholar] [CrossRef]
- Sene, N. Fractional model for a class of diffusion-reaction equation represented by the fractional-order derivative. Fractal Fract. 2020, 4, 15. [Google Scholar] [CrossRef]
- Hadeler, K.P. Reaction transport systems in biological modelling. In Mathematics Inspired by Biology; Springer: New York, NY, USA, 1999; pp. 95–150. [Google Scholar]
- Boon, J.P.; Lutsko, J.F.; Lutsko, C. Microscopic approach to nonlinear reaction-diffusion: The case of morphogen gradient formation. Phys. Rev. E 2012, 85, 021126. [Google Scholar] [CrossRef]
- Evans, M.R.; Majumdar, S.N. Diffusion with stochastic resetting. Phys. Rev. Lett. 2011, 106, 160601. [Google Scholar] [CrossRef]
- dos Santos, M.A. Fractional Prabhakar derivative in diffusion equation with non-static stochastic resetting. Physics 2019, 1, 40–58. [Google Scholar] [CrossRef]
- Mendez, V.; Fedotov, S.; Horsthemke, W. Reaction-Transport Systems: Mesoscopic Foundations, Fronts, and Spatial Instabilities; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Alharbi, W.; Petrovskii, S. Critical domain problem for the reaction–telegraph equation model of population dynamics. Mathematics 2018, 6, 59. [Google Scholar] [CrossRef]
- Yusupov, M.; Neyts, E.; Simon, P.; Berdiyorov, G.; Snoeckx, R.; Van Duin, A.; Bogaerts, A. Reactive molecular dynamics simulations of oxygen species in a liquid water layer of interest for plasma medicine. J. Phys. D Appl. Phys. 2013, 47, 025205. [Google Scholar] [CrossRef]
- Dorea, C.C.; Medino, A.V. Anomalous diffusion index for Lévy motions. J. Stat. Phys. 2006, 123, 685–698. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Antonio Faustino dos Santos, M. Comb Model with Non-Static Stochastic Resetting and Anomalous Diffusion. Fractal Fract. 2020, 4, 28. [Google Scholar] [CrossRef]
- Klages, R.; Radons, G.; Sokolov, I.M. Anomalous Transport: Foundations and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Datsko, B.; Kutniv, M.; Włoch, A. Mathematical modelling of pattern formation in activator–inhibitor reaction—Diffusion systems with anomalous diffusion. J. Math. Chem. 2020, 58, 612–631. [Google Scholar] [CrossRef]
- Compte, A.; Metzler, R. The generalized Cattaneo equation for the description of anomalous transport processes. J. Phys. A Math. Gen. 1997, 30, 7277. [Google Scholar] [CrossRef]
- Dos Santos, M.A. Non-Gaussian distributions to random walk in the context of memory kernels. Fractal Fract. 2018, 2, 20. [Google Scholar] [CrossRef]
- Sandev, T.; Tomovski, Ž. Fractional Equations and Models; Springer: New York, NY, USA, 2019. [Google Scholar]
- Lenzi, E.K.; Evangelista, L.R.; Zola, R.S.; Petreska, I.; Sandev, T. Fractional Schrödinger equation and anomalous relaxation: Nonlocal terms and delta potentials. Mod. Phys. Lett. A 2021, 36, 2140004. [Google Scholar] [CrossRef]
- Baleanu, D.; Jassim, H.K. Exact Solution of Two-Dimensional Fractional Partial Differential Equations. Fractal Fract. 2020, 4, 21. [Google Scholar] [CrossRef]
- Tawfik, A.M. On fractional approximations of the Fokker–Planck equation for energetic particle transport. Eur. Phys. J. Plus 2020, 135, 1–19. [Google Scholar] [CrossRef]
- Tawfik, A.M.; Abdou, M.; Gepreel, K.A. An analytical solution of the time-fractional telegraph equation describing neutron transport in a nuclear reactor. Indian J. Phys. 2021, 1–6. [Google Scholar] [CrossRef]
- Klafter, J.; Sokolov, I.M. First Steps in Random Walks: From Tools to Applications; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Chechkin, A.; Gorenflo, R.; Sokolov, I. Retarding subdiffusion and accelerating superdiffusion governed by distributed-order fractional diffusion equations. Phys. Rev. E 2002, 66, 046129. [Google Scholar] [CrossRef] [PubMed]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Huang, F.; Liu, F. The space-time fractional diffusion equation with Caputo derivatives. J. Appl. Math. Comput. 2005, 19, 179. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: Cambridge, MA, USA, 1998; Volume 198. [Google Scholar]
- Zimbardo, G.; Perri, S.; Effenberger, F.; Fichtner, H. Fractional Parker equation for the transport of cosmic rays: Steady-state solutions. Astron. Astrophys. 2017, 607, A7. [Google Scholar] [CrossRef]
- Samko, S.; Kilbas, A.; Marichev, O. Fractional Integrals and Derivatives—The Ory and Appli Cations; Gordon and Breach: Longhorne, PA, USA, 1993. [Google Scholar]
- Górska, K.; Horzela, A.; Lenzi, E.; Pagnini, G.; Sandev, T. Generalized Cattaneo (telegrapher’s) equations in modeling anomalous diffusion phenomena. Phys. Rev. E 2020, 102, 022128. [Google Scholar] [CrossRef]
- Halliwell, B.; Gutteridge, J.M. Free Radicals in Biology and Medicine; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Mainardi, F. Why the Mittag-Leffler function can be considered the Queen function of the Fractional Calculus? Entropy 2020, 22, 1359. [Google Scholar] [CrossRef]
- Wright, E.M. On the coefficients of power series having exponential singularities. J. Lond. Math. Soc. 1933, 1, 71–79. [Google Scholar] [CrossRef]
- Mainardi, F.; Mura, A.; Pagnini, G. The M-Wright function in time-fractional diffusion processes: A tutorial survey. Int. J. Differ. Equations 2010, 2010. [Google Scholar] [CrossRef]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag-Leffler Functions, Related Topics and Applications; Springer: New York, NY, USA, 2014. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tawfik, A.M.; Hefny, M.M. Subdiffusive Reaction Model of Molecular Species in Liquid Layers: Fractional Reaction-Telegraph Approach. Fractal Fract. 2021, 5, 51. https://doi.org/10.3390/fractalfract5020051
Tawfik AM, Hefny MM. Subdiffusive Reaction Model of Molecular Species in Liquid Layers: Fractional Reaction-Telegraph Approach. Fractal and Fractional. 2021; 5(2):51. https://doi.org/10.3390/fractalfract5020051
Chicago/Turabian StyleTawfik, Ashraf M., and Mohamed Mokhtar Hefny. 2021. "Subdiffusive Reaction Model of Molecular Species in Liquid Layers: Fractional Reaction-Telegraph Approach" Fractal and Fractional 5, no. 2: 51. https://doi.org/10.3390/fractalfract5020051
APA StyleTawfik, A. M., & Hefny, M. M. (2021). Subdiffusive Reaction Model of Molecular Species in Liquid Layers: Fractional Reaction-Telegraph Approach. Fractal and Fractional, 5(2), 51. https://doi.org/10.3390/fractalfract5020051





