Continuity Result on the Order of a Nonlinear Fractional Pseudo-Parabolic Equation with Caputo Derivative
Abstract
1. Introduction
2. Preliminaries
2.1. The Mittag-Leffler Function
2.2. Related Notation and Representation of the Solution
3. Stability of a Nonlinear Fractional Pseudo-Parabolic Equation Regarding Fractional-Order of the Time
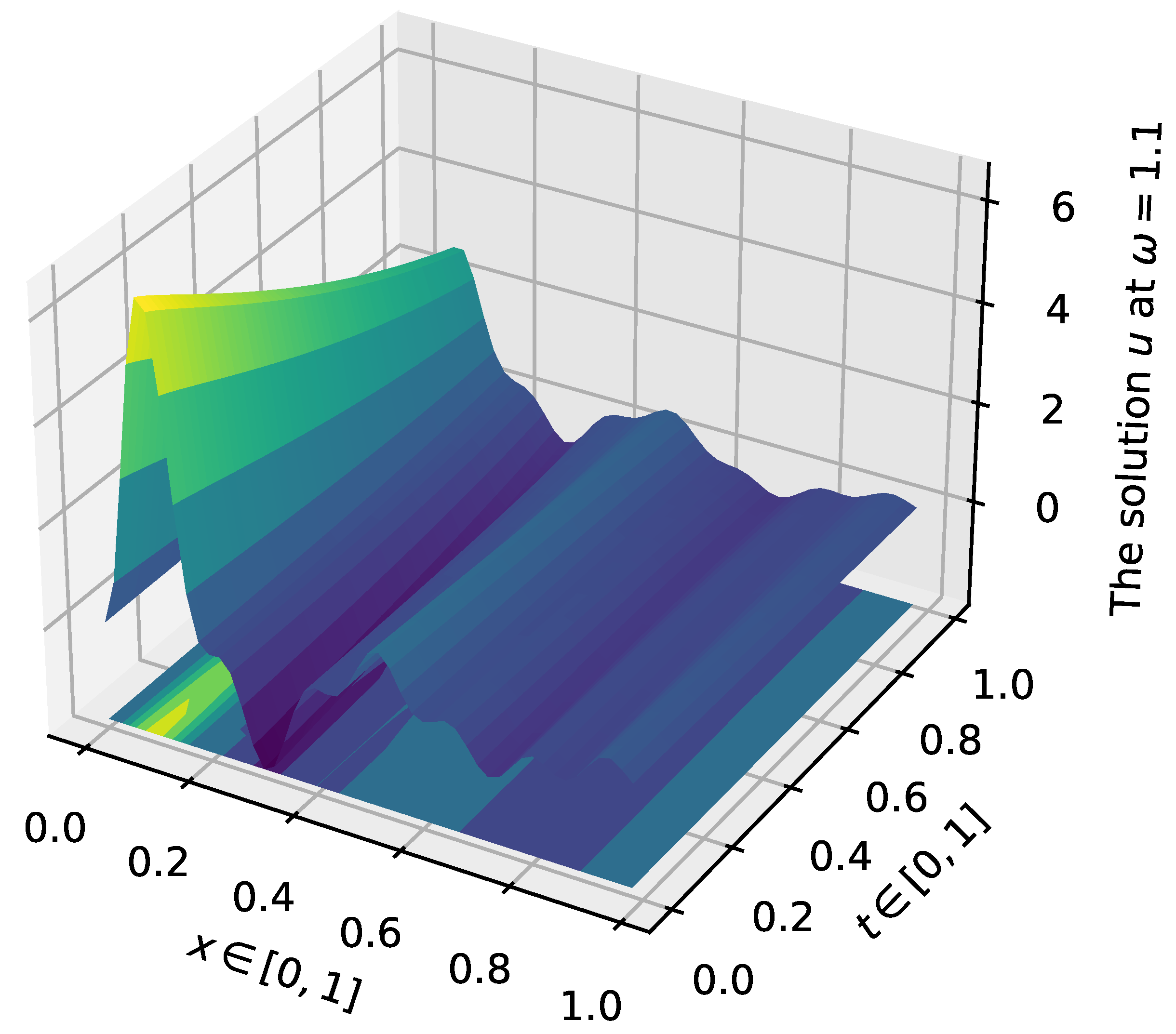
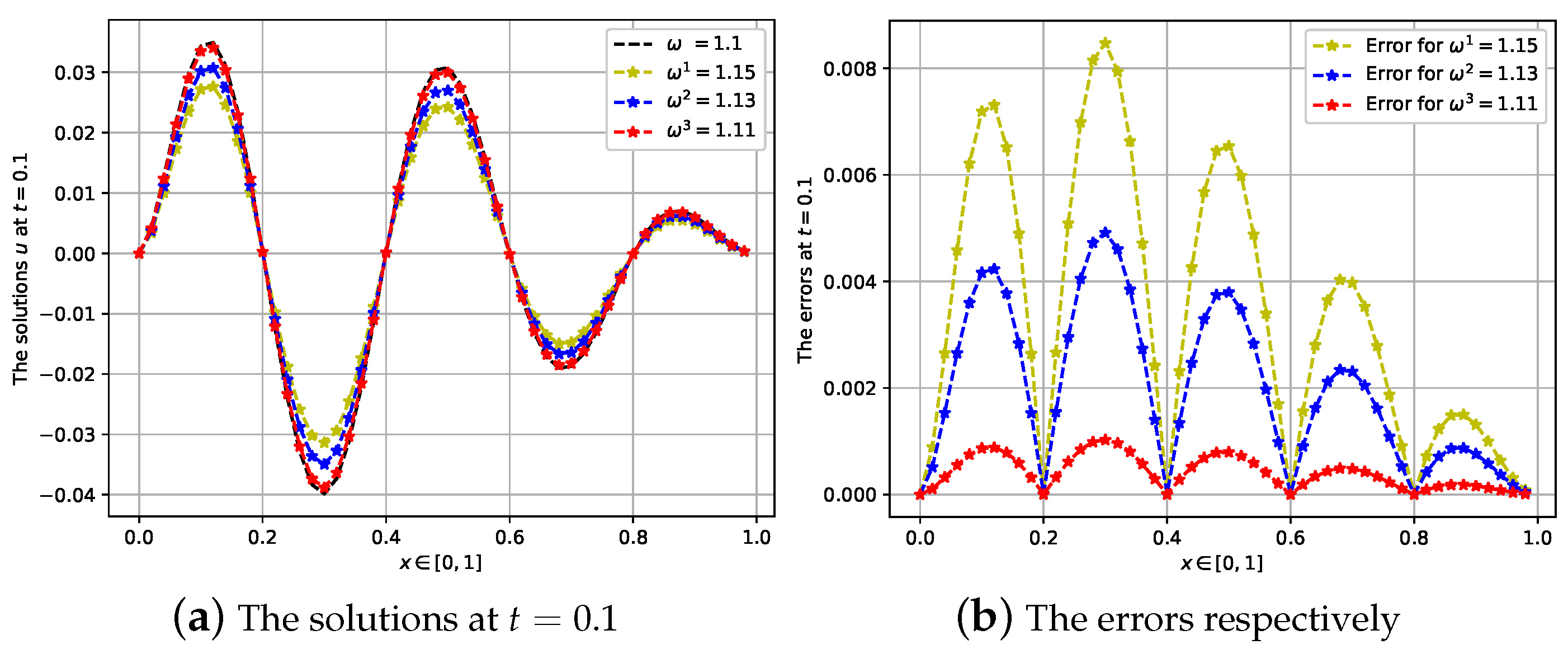
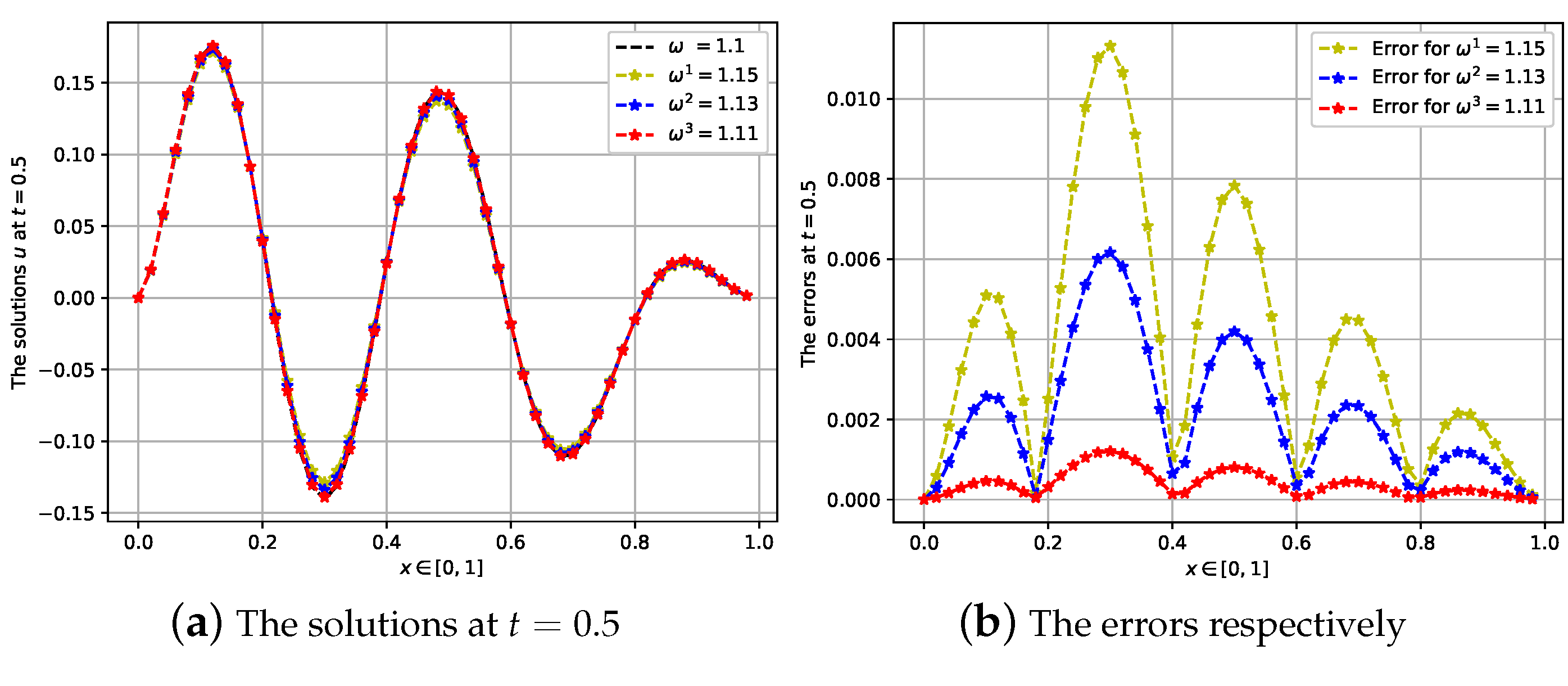
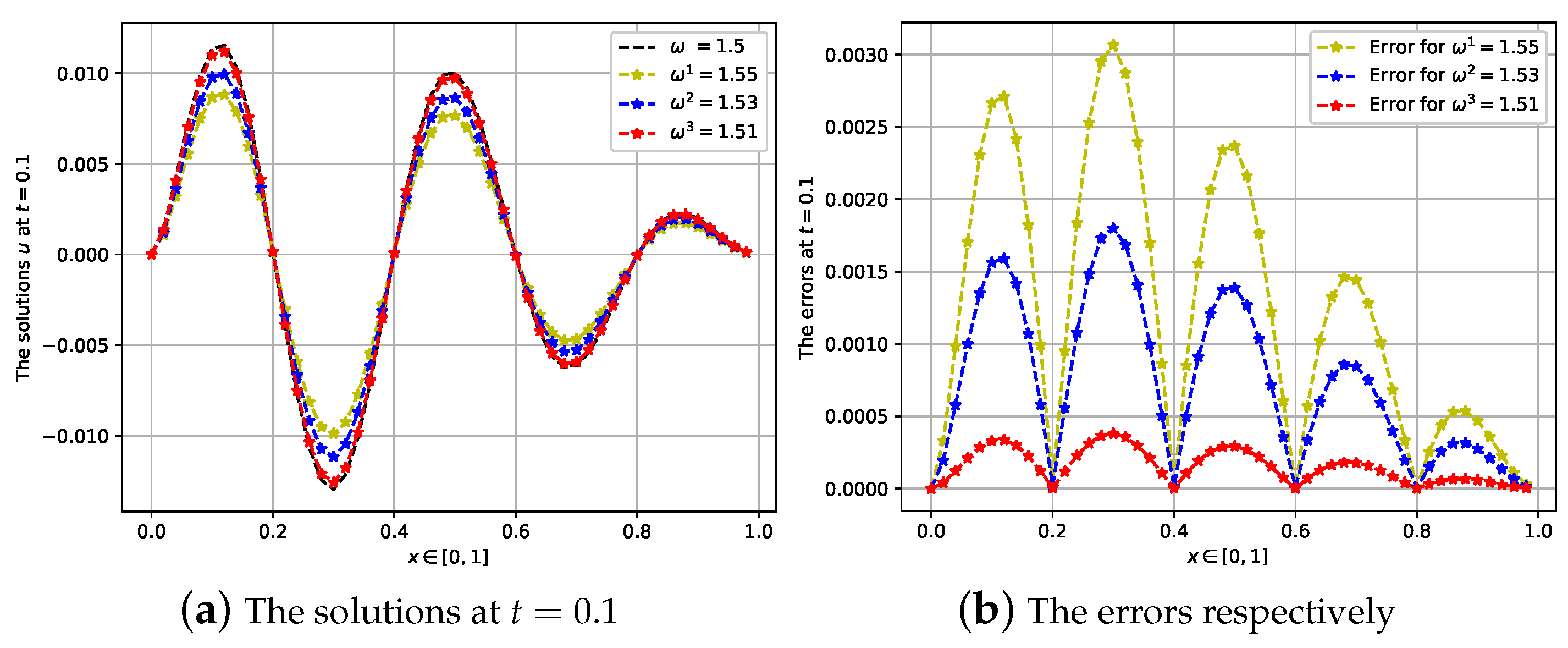
4. Numerical Experiments
4.1. First Case: The Fractional Order Is
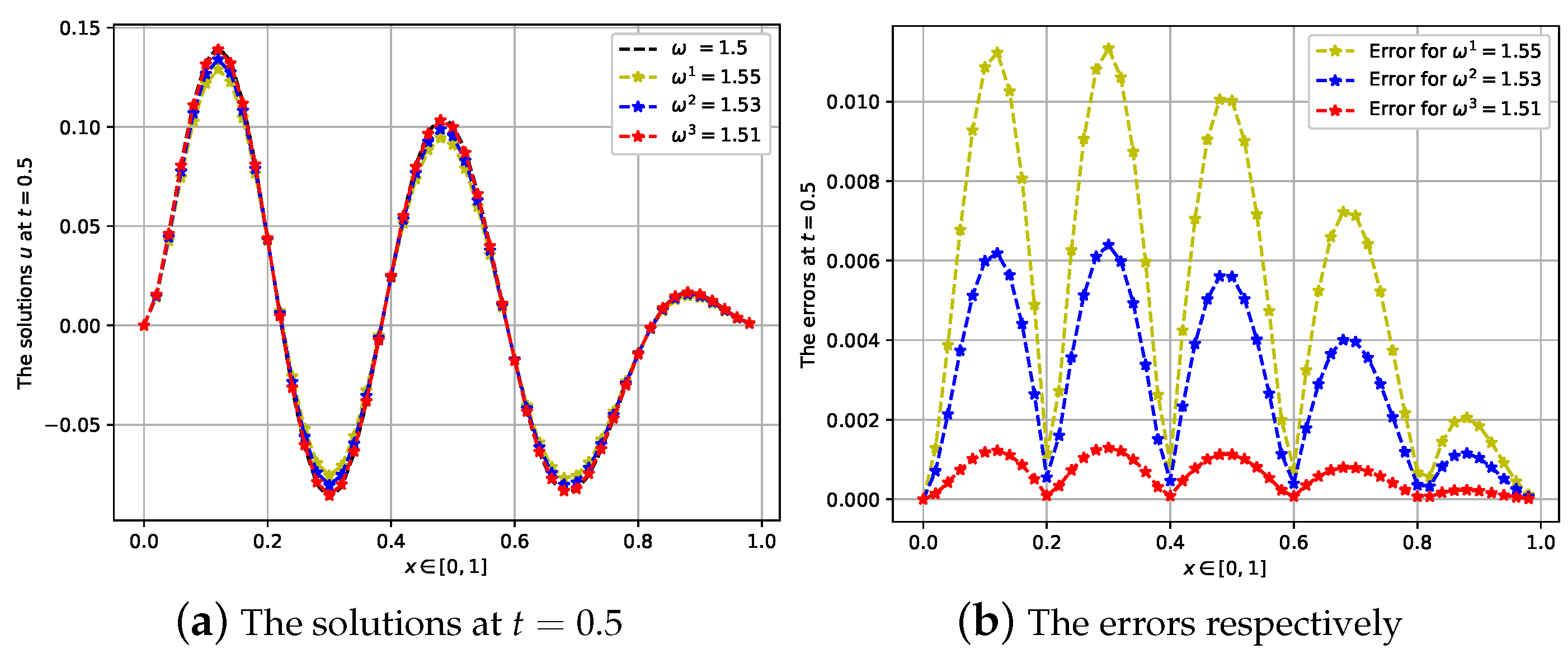
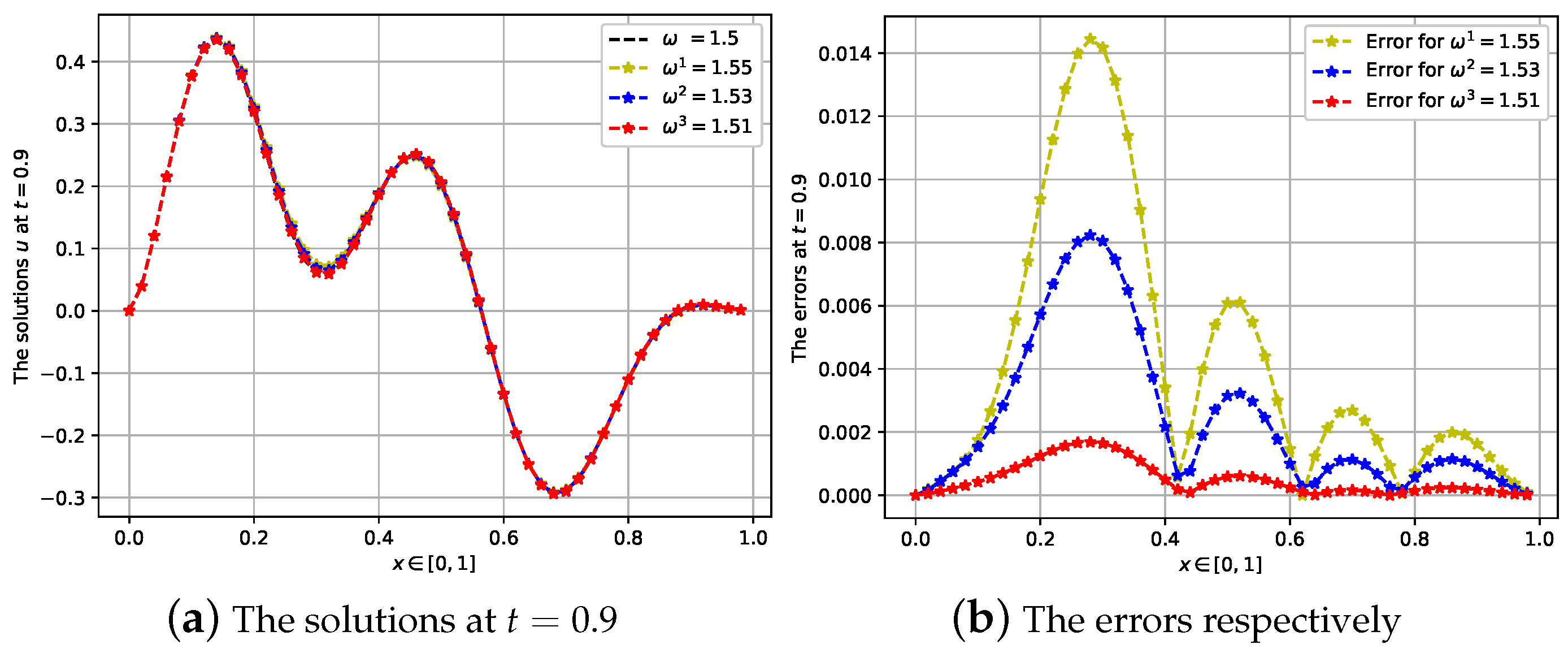
4.2. Second Case: The Fractional Order Is ω = 1.5
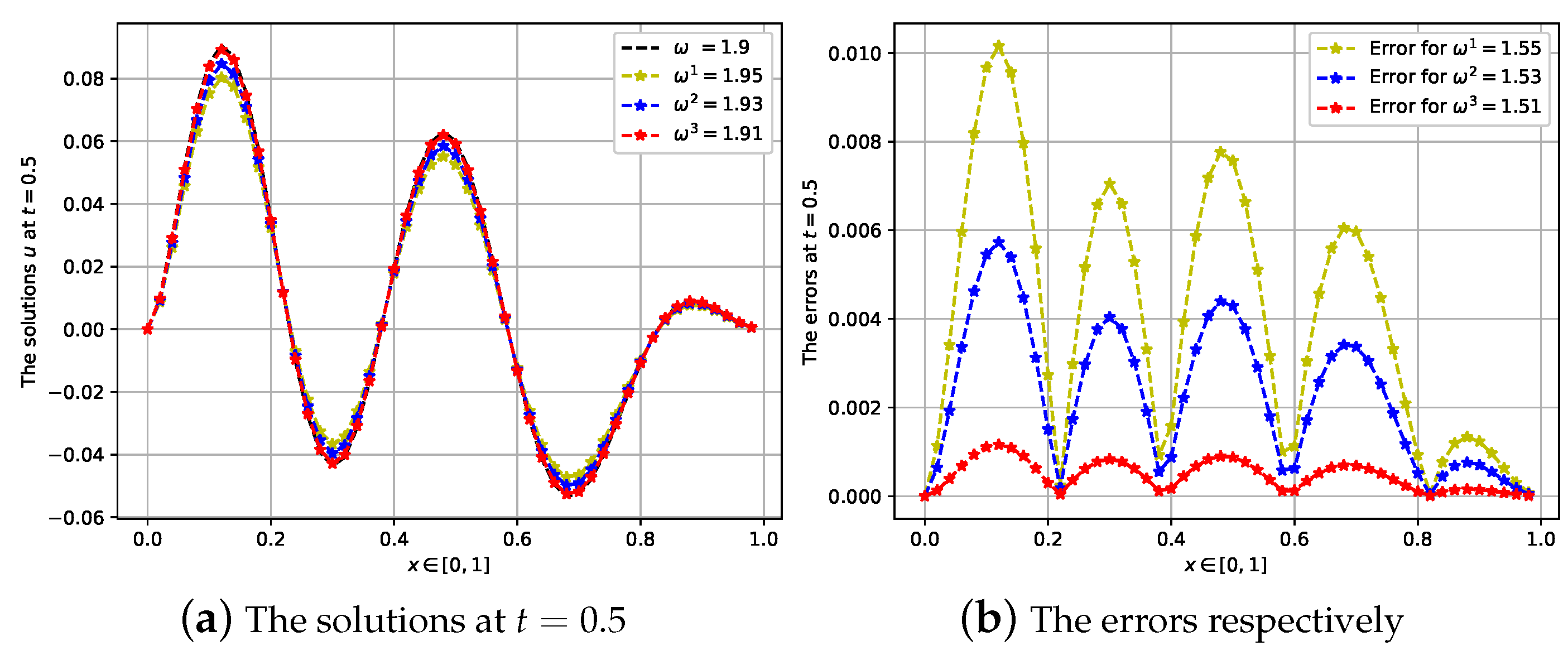
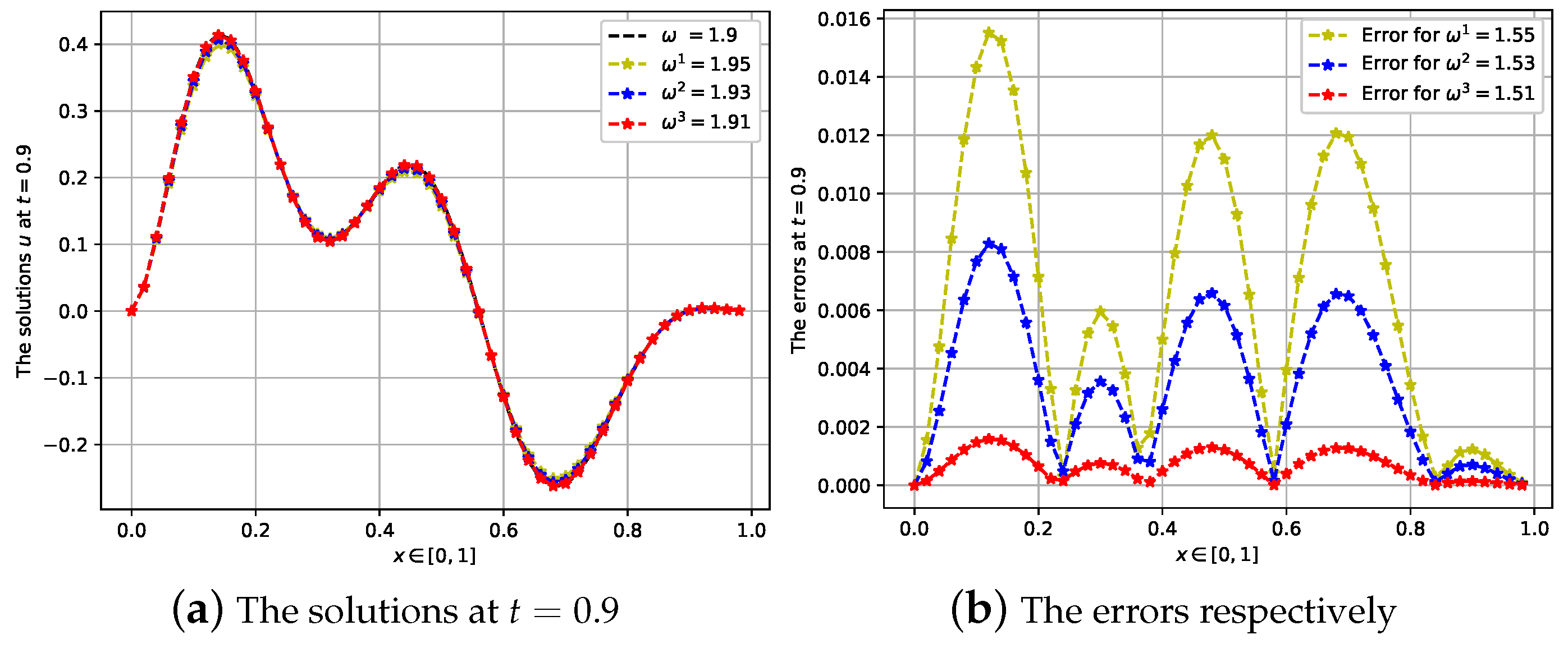
4.3. Third Case: The Fractional Order Is ω = 1.9
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Atangana, A.; Akgül, A.; Owolabi, K.M. Analysis of fractal fractional differential equations. Alex. Eng. J. 2020, 59, 1117–1134. [Google Scholar] [CrossRef]
- Atangana, A.; Hammouch, Z. Fractional calculus with power law: The cradle of our ancestors. Eur. Phys. J. Plus 2019, 134, 429. [Google Scholar] [CrossRef]
- Atangana, A.; Bonyah, E. Fractional stochastic modeling: New approach to capture more heterogeneity. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 013118. [Google Scholar] [CrossRef] [PubMed]
- Atangana, A.A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 18. [Google Scholar] [CrossRef]
- Atangana, A.; Goufo, E.F.D. Cauchy problems with fractal-fractional operators and applications to groundwater dynamics. Fractals 2020. [Google Scholar] [CrossRef]
- Sun, H.G.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y.Q. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic press: Cambridge, MA, USA, 1999. [Google Scholar]
- Abro, K.A.; Atangana, A. Mathematical analysis of memristor through fractal -fractional differential operators: A numerical study. Math. Methods Appl. Sci. 2020, 43, 6378–6395. [Google Scholar] [CrossRef]
- Tuan, N.H.; Baleanu, D.; Thach, T.N.; O’Regan, D.; Can, N.H. Final value problem for nonlinear time fractional reaction-diffusion equation with discrete data. J. Comput. Appl. Math. 2020, 376, 112883. [Google Scholar] [CrossRef]
- Luc, N.H.; Huynh, L.N.; Baleanu, D.; Can, N.H. Identifying the space source term problem for a generalization of the fractional diffusion equation with hyper-Bessel operator. Adv. Differ. Equ. 2020, 261, 23. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Al-Mekhlafi, S.M.; Assiri, T.; Atangana, A. Optimal control for cancer treatment mathematical model using Atangana-Baleanu-Caputo fractional derivative. Adv. Differ. Equ. 2020, 334. [Google Scholar] [CrossRef]
- Tuan, N.H.; Huynh, L.N.; Baleanu, D.; Can, N.H. On a Terminal Value Problem for a Generalization of the Fractional Diffusion Equation with Hyper-Bessel Operator. Math. Methods Appl. Sci. 2020, 43, 2858–2882. [Google Scholar] [CrossRef]
- Kumar, S.; Atangana, A. A numerical study of the nonlinear fractional mathematical model of tumor cells in presence of chemotherapeutic treatment. Int. J. Biomath. 2020, 13, 2050021. [Google Scholar] [CrossRef]
- Kiryakova, V. Generalized Fractional Calculus and Applications; CRC press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Ngoc, T.B.; Baleanu, D.; Duc, L.M.; Tuan, N.H. Regularity results for fractional diffusion equations involving fractional derivative with Mittag-Leffler kernel. Math. Methods Appl. Sci. 2020, 43, 7208–7226. [Google Scholar]
- Ebaid, A.; Cattani, C.; Al Juhani, A.S.; El-Zahar, E.R. A novel exact solution for the fractional Ambartsumian equation. Adv. Differ. Equ. 2021, 2021, 88. [Google Scholar] [CrossRef]
- Heydaria, M.H.; Avazzadehb, Z.; Cattani, C. Taylor’s series expansion method for nonlinear variable-order fractional 2D optimal control problems. Alex. Eng. J. 2020, 59, 4737–4743. [Google Scholar] [CrossRef]
- Mohammad, M.; Cattani, C. A collocation method via the quasi-affine biorthogonal systems for solving weakly singular type of Volterra-Fredholm integral equations. Alex. Eng. J. 2020, 59, 2181–2191. [Google Scholar] [CrossRef]
- Li, L.; Liu, G.J. A generalized definition of Caputo derivatives and its application to fractional ODEs. SIAM J. Math. Anal. 2018, 50, 2867–2900. [Google Scholar] [CrossRef]
- Benjamin, T.B.; Bona, J.L.; Mahony, J.J. Model equations for long waves in nonlinear dispersive systems. Philos. Trans. R. Soc. 1972, 272, 47–78. [Google Scholar]
- Ting, W.T. Certain non-steady flows of second-order fluids. Arch. Ration. Mech. Anal. 1963, 14, 1–26. [Google Scholar] [CrossRef]
- Padron, V. Effect of aggregation on population recovery modeled by a forward-backward pseudo-parabolic equation. Trans. Am. Math. Soc. 2004, 356, 2739–2756. [Google Scholar] [CrossRef]
- Huafei, D.; Yadong, S.; Xiaoxiao, Z. Global well-posedness for a fourth order pseudo-parabolic equation with memory and source terms. Disc. Contin. Dyn. Syst. Ser. B 2016, 21, 781–801. [Google Scholar]
- Sun, F.; Liu, L.; Wu, Y. Global existence and finite time blow-up of solutions for the semi-linear pseudo-parabolic equation with a memory term. Appl. Anal. 2019, 98, 22. [Google Scholar] [CrossRef]
- Ding, H.; Zhou, J. Global existence and blow-up for a mixed pseudo-parabolic p-Laplacian type equation with logarithmic nonlinearity. J. Math. Anal. Appl. 2019, 478, 393–420. [Google Scholar] [CrossRef]
- Jin, L.; Li, L.; Fang, S. The global existence and time-decay for the solutions of the fractional pseudo-parabolic equation. Comput. Math. Appl. 2017, 73, 2221–2232. [Google Scholar] [CrossRef]
- Afshari, H.; Kalantari, S.; Karapinar, E. Solution of fractional differential equations via coupled fixed point. Electron. J. Differ. Equ. 2015, 2015, 1–12. [Google Scholar]
- Karapinar, E.; Fulga, A.; Rashid, M.; Shahid, L.; Aydi, H. Large Contractions on Quasi-Metric Spaces with an Application to Nonlinear Fractional Differential-Equations. Mathematics 2019, 7, 444. [Google Scholar] [CrossRef]
- Karapinar, E.; Abdeljawad, T.; Jarad, F. Applying new fixed point theorems on fractional and ordinary differential equations. Adv. Differ. Equ. 2019, 2019, 421. [Google Scholar] [CrossRef]
- Abdeljawad, A.; Agarwal, R.P.; Karapinar, E.; Kumari, P.S. Solutions of he Nonlinear Integral Equation and Fractional Differential Equation Using the Technique of a Fixed Point with a Numerical Experiment in Extended b-Metric Space. Symmetry 2019, 11, 686. [Google Scholar] [CrossRef]
- Zhu, X.; Li, F.; Li, Y. Global solutions and blow up solutions to a class of pseudo-parabolic equations with nonlocal term. Appl. Math. Comput. 2018, 329, 38–51. [Google Scholar] [CrossRef]
- Cao, Y.; Yin, J.; Wang, C. Cauchy problems of semilinear pseudo-parabolic equations. J. Differ. Equ. 2009, 246, 4568–4590. [Google Scholar] [CrossRef]
- Cao, Y.; Liu, C. Initial boundary value problem for a mixed pseudo- parabolic p-Laplacian type equation with logarithmic nonlinearity. Electron. J. Differ. Equ. 2018, 2018, 1–19. [Google Scholar]
- He, Y.; Gao, H.; Wang, H. Blow-up and decay for a class of pseudo-parabolic p-Laplacian equation with logarithmic nonlinearity. Comput. Math. Appl. 2018, 75, 459–469. [Google Scholar] [CrossRef]
- Lu, Y.; Fei, L. Bounds for blow-up time in a semilinear pseudo-parabolic equation with nonlocal source. J. Inequalities Appl. 2016, 2016, 229. [Google Scholar] [CrossRef][Green Version]
- Sousa, C.V.J.; de Oliveira, C.E. Fractional order pseudo-parabolic partial differential equation: Ulam-Hyers stability. Bull. Braz. Math. Soc. 2019, 50, 481–496. [Google Scholar] [CrossRef]
- Beshtokov, M.K. To boundary-value problems for degenerating pseudo-parabolic equations with Gerasimov-Caputo fractional derivative. Izv. Vyssh. Uchebn. Zaved. Mat. 2018, 10, 3–16. [Google Scholar]
- Beshtokov, M.K. Boundary-value problems for loaded pseudo-parabolic equations of fractional order and difference methods of their solving. Russ. Math. 2019, 63, 1–10. [Google Scholar] [CrossRef]
- Beshtokov, M.K. Boundary value problems for a pseudoparabolic equation with the Caputo fractional derivative. Differ. Equ. 2019, 55, 884–893. [Google Scholar] [CrossRef]
- Dang, D.T.; Nane, E.; Nguyen, D.M.; Tuan, N.H. Continuity of Solutions of a Class of Fractional Equations. Potential Anal. 2018, 49, 423–478. [Google Scholar] [CrossRef]
- Tuan, N.H.; O’Regan, D.; Ngoc, T.B. Continuity with respect to fractional order of the time fractional diffusion-wave equation. Evol. Equ. Control Theory 2020, 9, 773. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives, Theory and Applications; Gordon and Breach Science: Naukai Tekhnika, Minsk, 1987. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Wei, T.; Zhang, Y. The backward problem for a time-fractional diffusion-wave equation in a bounded domain. Comput. Math. Appl. 2018, 75, 3632–3648. [Google Scholar] [CrossRef]
- Sakamoto, K.; Yamamoto, M. Initial value/boundary value problems for fractional diffusion-wave equations and applications to some inverse problems. J. Math. Anal. Appl. 2011, 382, 426–447. [Google Scholar] [CrossRef]
- Kato, T. Perturbation Theory for Linear Operators; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier Science B.V.: Amsterdam, The Netherlands, 2006. [Google Scholar]




| Fractional Order | ||||||
|---|---|---|---|---|---|---|
| 0.17060940 | 21.16% | 0.19486871 | 5.23% | 0.50700111 | 7.41% | |
| 0.09891093 | 12.26% | 0.10425578 | 2.80% | 0.28847739 | 4.22% | |
| 0.02063175 | 2.55% | 0.02002432 | 0.53% | 0.05891203 | 0.86% | |
| Fractional Order | ||||||
|---|---|---|---|---|---|---|
| 0.06218532 | 23.58% | 0.25924582 | 9.55% | 0.20731152 | 2.48% | |
| 0.03645685 | 13.82% | 0.14441751 | 5.32% | 0.11992968 | 1.43% | |
| 0.00769853 | 2.92% | 0.02891043 | 1.06% | 0.02491671 | 0.29% | |
| Fractional Order | ||||||
|---|---|---|---|---|---|---|
| 0.01925768 | 24.99% | 0.20146470 | 12.17% | 0.31121755 | 3.82% | |
| 0.01134916 | 14.72% | 0.11418913 | 6.89% | 0.16942761 | 2.08% | |
| 0.00241016 | 3.12% | 0.02328528 | 1.40% | 0.03311517 | 0.40% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Binh, H.D.; Hoang, L.N.; Baleanu, D.; Van, H.T.K. Continuity Result on the Order of a Nonlinear Fractional Pseudo-Parabolic Equation with Caputo Derivative. Fractal Fract. 2021, 5, 41. https://doi.org/10.3390/fractalfract5020041
Binh HD, Hoang LN, Baleanu D, Van HTK. Continuity Result on the Order of a Nonlinear Fractional Pseudo-Parabolic Equation with Caputo Derivative. Fractal and Fractional. 2021; 5(2):41. https://doi.org/10.3390/fractalfract5020041
Chicago/Turabian StyleBinh, Ho Duy, Luc Nguyen Hoang, Dumitru Baleanu, and Ho Thi Kim Van. 2021. "Continuity Result on the Order of a Nonlinear Fractional Pseudo-Parabolic Equation with Caputo Derivative" Fractal and Fractional 5, no. 2: 41. https://doi.org/10.3390/fractalfract5020041
APA StyleBinh, H. D., Hoang, L. N., Baleanu, D., & Van, H. T. K. (2021). Continuity Result on the Order of a Nonlinear Fractional Pseudo-Parabolic Equation with Caputo Derivative. Fractal and Fractional, 5(2), 41. https://doi.org/10.3390/fractalfract5020041







