An ADI Method for the Numerical Solution of 3D Fractional Reaction-Diffusion Equations

Abstract

A numerical method for solving fractional partial differential equations (fPDEs) of the diffusion and reaction–diffusion type, subject to Dirichlet boundary data, in three dimensions is developed. Such fPDEs may describe fluid flows through porous media better than classical diffusion equations. This is a new, fractional version of the Alternating Direction Implicit (ADI) method, where the source term is balanced, in that its effect is split in the three space directions, and it may be relevant, especially in the case of anisotropy. The method is unconditionally stable, second-order in space, and third-order in time. A strategy is devised in order to improve its speed of convergence by means of an extrapolation method that is coupled to the PageRank algorithm. Some numerical examples are given.

1. Introduction

Diffusive flows, possibly with reaction, play an important role in a number of fields, such as fluid dynamics in porous media and percolation, as well as seepage and groundwater hydraulics; see, e.g., [1,2,3,4]. However, the celebrated Darcy’s law, along with the assumption of continuity of the seepage flow in heterogeneous media and the ensuing diffusion partial differential equation (PDE), is not valid in the general case of real flows. In 1998, J. He [5] proposed a generalized version of the Darcy’s law, containing fractional Riemann–Liouville (RL) derivatives,

$$\mathbf{q}=-\mathbf{K}{\nabla }^{\alpha }p,{\nabla }^{\alpha }:=\left(\frac{{\partial }^{{\alpha }_1}}{\partial x^{{\alpha }_1}},\frac{{\partial }^{{\alpha }_2}}{\partial y^{{\alpha }_2}},\frac{{\partial }^{{\alpha }_3}}{\partial z^{{\alpha }_3}}\right),$$

where $p\equiv p(x,y,z,t)$ is the pressure, $\mathbf{q}=(q_x,q_y,q_z)$ is the fluid velocity, $\mathbf{K}=(K_x,K_y,K_z)$ is the percolation tensor (here assumed to be diagonal), and $\alpha :=({\alpha }_1,{\alpha }_2,{\alpha }_3)$. In this paper, we chose to follow He’s idea in order to model seepage flows in porous media, adopting fractional Riemann–Liouville derivatives, even though several other kinds of fractional derivative exist. The Riemann–Liouville fractional derivative of order $\alpha$ of $F\left(x\right)$ is defined by

$$\frac{d^{\alpha }F\left(x\right)}{d{x}^{\alpha }}:=\frac{1}{\mathrm{\Gamma }(n-\alpha )}\frac{{\mathrm{d}}^n}{\mathrm{d}{x}^n}{\int }_0^x\frac{F\left(\xi \right)}{{(x-\xi )}^{\alpha -n+1}}\mathrm{d}\xi ,$$

(1)

where $n\in \mathbf{N}$ is such that $n-1<\alpha \le n$, see [6], e.g., the literature concerning Fractional Calculus is still rapidly increasing. We only mention [7] for some review on progresses in this field, in particular concerning RL operators, and [8] for reviewing some general basic properties of fractional operators, in particular, RL operators.

Therefore, the more general equation for seepage flow with fractional Riemann–Liouville derivatives that was proposed by J. He [5] reads

$$\begin{array}{cc}{\displaystyle \frac{1}{\nu }\frac{\partial p}{\partial t}}\hfill & =\frac{{\partial }^{{\beta }_1}}{\partial x^{{\beta }_1}}\left(K_x\frac{{\partial }^{{\alpha }_1}p}{\partial x^{{\alpha }_1}}\right)+\frac{{\partial }^{{\beta }_2}}{\partial y^{{\beta }_2}}\left(K_y\frac{{\partial }^{{\alpha }_2}p}{\partial y^{{\alpha }_2}}\right)\hfill \\ {\displaystyle }\hfill & +\frac{{\partial }^{{\beta }_3}}{\partial z^{{\beta }_3}}\left(K_z\frac{{\partial }^{{\alpha }_3}p}{\partial z^{{\alpha }_3}}\right)+f(p;x,y,z,t),(x,y,z)\in \Omega .\hfill \end{array}$$

(2)

Here, $\frac{1}{\nu }$ is the specific storage coefficient (that is assumed to be constant), $f(p;x,y,z,t)$ is a “source” or “sink term”, $\mathrm{\Omega }$ is a given open bounded domain of ${\mathbf{R}}^3$, with piecewise smooth boundary, where the seepage or percolation takes place, t is time, and $0<{\beta }_i<1$, $0<{\alpha }_i\le 1$, with $1<{\beta }_i+{\alpha }_i\le 2$, for $i=1,2,3$, see [2]. In (2), the operator $\frac{{\partial }^{{\alpha }_1}}{\partial x^{{\alpha }_1}}$ denotes the fractional Riemann–Liouville derivative of order ${\alpha }_1$ with respect to x. Note that, when the source term, f, depends on p, the fractional partial differential equation (fPDE) in (2) is a reaction–diffusion, rather than a pure diffusion equation. The boundary and initial conditions

$${p(x,y,z,t)|}_{\partial \mathrm{\Omega }}=\mathrm{\Phi }(x,y,z,t),p(x,y,z,0)=\phi (x,y,z).$$

(3)

are imposed, with $\mathrm{\Phi }$ and $\phi$ being suitable prescribed functions.

In this paper, we consider, rather, fractional diffusions in the nonconservative form,

$$\begin{array}{c}\hfill \frac{\partial p}{\partial t}=K_x\frac{{\partial }^{{\gamma }_1}p}{\partial x^{{\gamma }_1}}+K_y\frac{{\partial }^{{\gamma }_2}p}{\partial y^{{\gamma }_2}}+K_z\frac{{\partial }^{{\gamma }_3}p}{\partial z^{{\gamma }_3}}+f(p;x,y,z,t)\mathrm{in}\mathrm{\Omega }\times (0,T],\end{array}$$

(4)

where all of the space fractional derivatives are of the RL type, defined as in (1), the set $\nu =1$, ${\gamma }_i:={\beta }_i+{\alpha }_i$, for i = 1, 2, 3. Below, we construct a “fractional Alternating Direction Implicit” (fADI) scheme in order to numerically solve such a problem. We will consider such a fractional reaction–diffusion equation with (positive) constant percolation coefficients, $K_x,K_y,K_z$, in (2), with boundary and initial conditions, as above.

Unlike the case of classical (integer order) derivatives, the two model Equations (2) and (4) do not coincide, even when the coefficients $K_x$, $K_y$, and $K_z$ are constants. In fact, it is not true, in general, that, e.g.,

$$\frac{{\partial }^{{\beta }_1}}{\partial x^{{\beta }_1}}\frac{{\partial }^{{\alpha }_1}p}{\partial x^{{\alpha }_1}}u=\frac{{\partial }^{{\beta }_1+{\alpha }_1}}{\partial x^{{\beta }_1+{\alpha }_1}}u.$$

(5)

This is only true under some conditions, for instance, when $u\in C^k$ (i.e., is sufficiently smooth) and ${\alpha }_1,{\beta }_1+{\alpha }_1\in [\ell -1,\ell ]$ for some $\ell \in \mathbf{N}$, $\ell \le k$, see [9]. This restriction on the fractional orders is quite serious, since we expect that $0<{\alpha }_1,{\beta }_1<1$ and $1<{\beta }_1+{\alpha }_1<2$, in order to obtain an anomalous (sub-)diffusion equation. Otherwise, one should just face the fPDE in (2), even when taking out of the derivatives the constants K, and keeping it as it is. There is a name for such fractional equations, which is “sequential fractional differential equations”, see, e.g., ([6], Section 4.2).

Other definitions of fractional derivative exist. One of the most useful in practice has been proven to be Caputo’s definition. The Caputo fractional derivative is given by

$${}_0^C{D}_x^{\alpha }F\left(x\right)\equiv :=\frac{1}{\mathrm{\Gamma }(n-\alpha )}{\int }_0^x\frac{\frac{d^n}{d{x}^n}F\left(\xi \right)}{{(x-\xi )}^{\alpha -n+1}}d\xi ,$$

(6)

where $n-1<\alpha <n$, $n\in \mathbf{N}$. Moreover, the Grünwald–Letnikov fractional derivative is particularly relevant for us, in view of the ensuing numerical treatment. It is defined as [2,6],

$${}_0^{GL}{D}_x^{\alpha }F\left(x\right):=\frac{1}{\mathrm{\Gamma }(-\alpha )}\underset{h\to 0}{lim}\frac{1}{h^{\alpha }}\sum _{i=0}^{\left[\frac{x}{h}\right]}\frac{\mathrm{\Gamma }(i-\alpha )}{\mathrm{\Gamma }(i+1)}F(x-ih),$$

(7)

while the so-called shifted Grünwald–Letnikov derivative is given by

$${}_0^{GLs}{D}_x^{\alpha }F\left(x\right)=:\frac{1}{\mathrm{\Gamma }(-\alpha )}\underset{h\to 0}{lim}\frac{1}{h^{\alpha }}\sum _{i=0}^{\left[\frac{x}{h}\right]+1}\frac{\mathrm{\Gamma }(i-\alpha )}{\mathrm{\Gamma }(i+1)}F(x-(i-1)h),$$

(8)

where $\left[x\right]$ denotes the integer part of x, with h being the step size to be used in the numerical schemes [6], and $\Gamma$ is the Gamma function. The “normalized” Grünwald weights are defined as $g_{\alpha ,i}={(-1)}^i\left(\genfrac{}{}{0pt}{}{\alpha }{i}\right)$. These coefficients will be used in the numerical approximation of the Grünwald–Letnikov fractional discrete operator in (7) or (8); see Section 2.

When applied to smooth functions, for example functions with continuous $(n-1)$th-order derivatives and integrable nth-order derivatives, all of these definitions are known to coincide [6]. Therefore, in this paper, we consider all fractional derivatives appearing in the fPDEs in the sense of Caputo, while the discretizations will be made according to the shifted Grünwald–Letnikov definition.

Given the interest for models that are based on fPDEs and, needless to say, analytic solutions to most fPDEs are usually not available, a number of authors have proposed, over the years, a few numerical methods to solve them, see, e.g., [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]. However, numerical methods that are capable of handling high-dimensional fPDEs seem to be rather few in the existing literature, not to mention their performance. It should be observed that, being the fractional derivatives nonlocal operators, discretizing fPDEs can be expected to be more demanding in terms of memory storage and CPU time, as compared to classical PDEs. All of this calls for devising effective numerical methods in order to solve fPDE problems already in dimension 2 and 3.

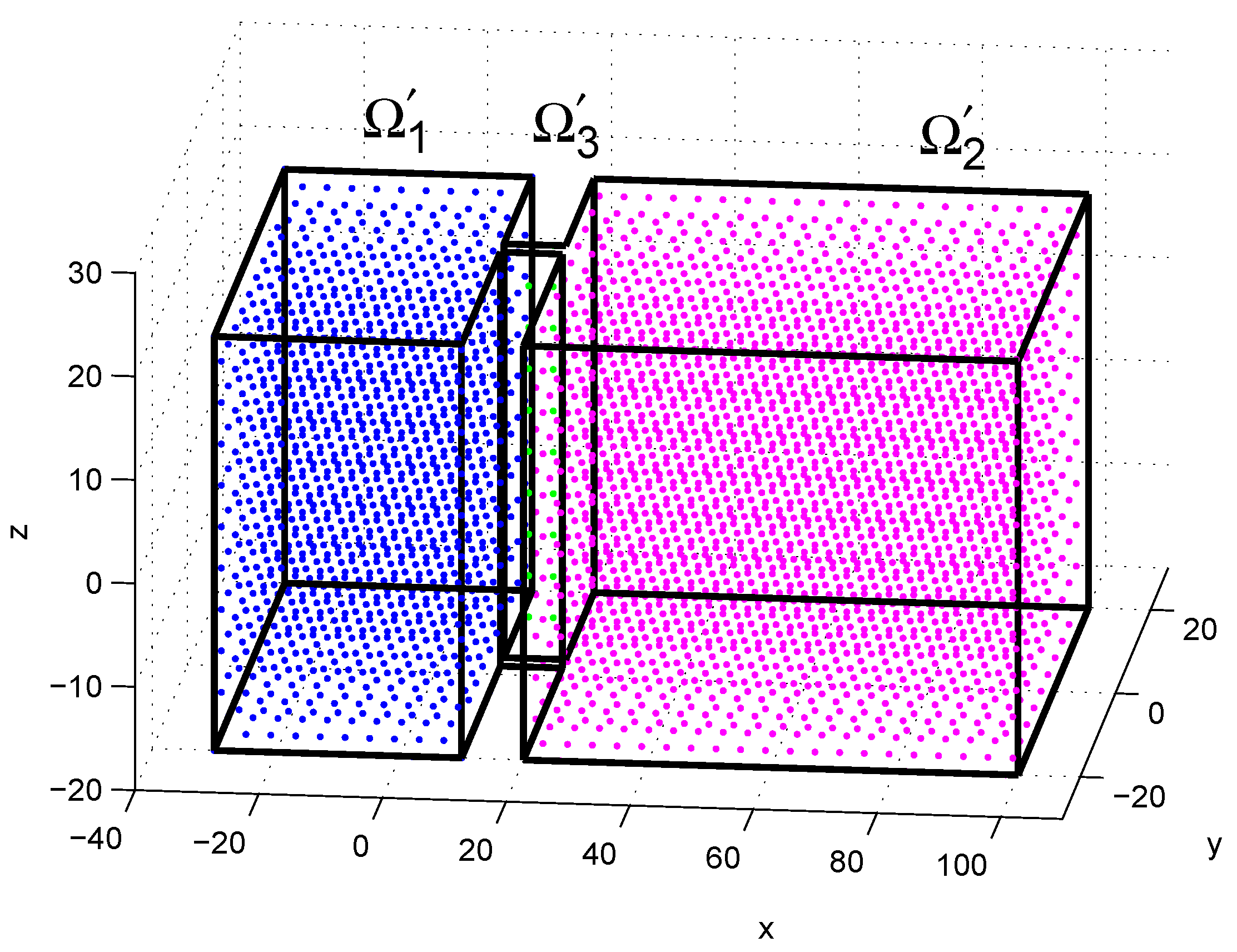
In this paper, we consider the three-dimensional (3D) fractional seepage flow equation in (2), on the bounded domain, $\mathrm{\Omega }:=(0,L_x)\times (0,L_y)\times (0,L_z)$, and the time interval $(0,T]$. Moreover, we assume that such an initial-boundary value problem equation has a unique, sufficiently smooth solution, when the (homogeneous) Dirichlet boundary conditions and initial condition

$${p(x,y,z,t)|}_{\partial \mathrm{\Omega }}=\mathrm{\Phi }(x,y,z),p(x,y,z,0)=\phi (x,y,z),$$

(9)

for some given functions, $\mathrm{\Phi }$ and $\phi$ are imposed.

A new, well “balanced”, fractional version of the Alternating Direction Implicit (ADI) method is introduced, in order to numerically solve 3D diffusion and reaction-diffusion fPDEs. We call our algorithm “balanced”, since it distributes the source term effect in an equal amount among the three equations of the ADI scheme, instead of putting the full source on the right-hand side of the first equation only, see Section 2. This choice seems to be effective, especially when the model presents some degree of anisotropy, and it allows us to increase the space accuracy. 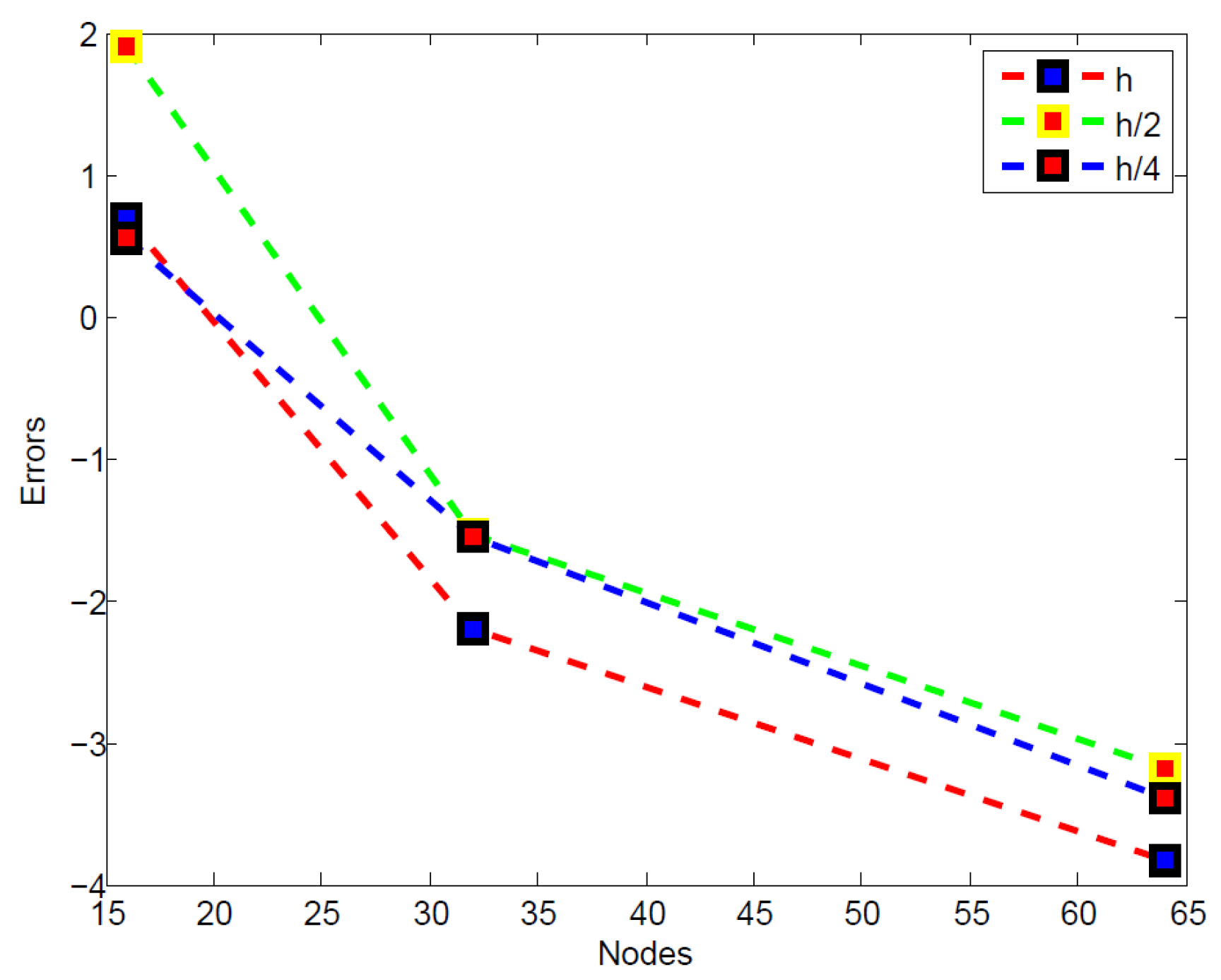In [2], Liu et al. derived a scheme that is accurate to the second order in space, resorting to a Richardson extrapolation, but our balanced scheme turns out to perform better, see Table 12 below.

Our method is shown to be unconditionally stable for every fractional order of space derivatives, second-order accurate in space, and third-order accurate in time. This latter property is established in this paper adopting an extrapolation technique along with an optimization strategy that is realized through Google’s PageRank algorithm. The method followed here to do this for the 3D case is similar to that used for the two-dimensional (2D) case in [29].

Here is the plan of the paper. In Section 2, we formulate a typical problem, and discuss some fractional versions of the ADI (fADI) 3D schemes. In Section 3, we establish the convergence and stability of our algorithm, while, in Section 4, some details regarding optimization and extrapolation are given, and a few numerical examples are presented. Section 5 contains the conclusions of the paper, briefly highlighting its main points.

2. Fractional Diffusion and Seepage Flow in Homogeneous Media

In order to construct our fADI scheme on a bounded domain, we first discretize space and time, as usual, setting $x_i:=i{h}_x$, for $i=0,1,2,\dots ,M_x$, with $h_x:=L_x/M_x$; $y_j:=j{h}_y$, for $j=0,1,2,\dots ,M_y$, with $h_y:=L_y/M_y$; $z_k:=k{h}_z$, for $k=0,1,2,\dots ,M_z$, with $h_z:=L_z/M_z$; and, $t_n:=n\tau$, for $n=0,1,2,\dots ,N$, $\tau :=T/N$. Here, $M_x,M_y,M_z$, and N are positive integers, while $h_x$, $h_y$, $h_z$, and $\tau$ are the space and time step sizes, respectively. The numerical approximation to $p(x_i,y_j,z_k,t_n)$ provided by the scheme at such points will be then denoted by $p_{i,j,k}^n$. Similarly, we write $f_{i,j,k}^n$ in order to denote an approximation of $f(p(x_i,y_j,z_k,t_n);x_i,y_j,z_k,t_n)$ for the source term, $p_{i,j,k}^0={\phi }_{i,j,k}$ for $\phi (x_i,y_j,z_k,0)$, the initial value, and $p_{0,j,k}^n={\mathrm{\Phi }}_1(y_j,z_k,t_n)=0,p_{M_x,j,k}^n={\mathrm{\Phi }}_2(y_j,z_k,t_n)=0$, $p_{i,0,k}^n={\mathrm{\Phi }}_3(x_i,z_k,t_n)=0$, $p_{i,M_y,k}^n={\mathrm{\Phi }}_4(x_i,z_k,t_n)$, $p_{i,j,0}^n={\mathrm{\Phi }}_5(x_i,y_j,t_n)=0$, and $p_{i,j,M_z}^n={\mathrm{\Phi }}_6(x_i,y_j,t_n)$, for the boundary conditions.

We discretize the fPDE, approximating the first-order derivative $\frac{\partial p}{\partial t}$ in (4) by forward finite differences. Assuming that the solution, p, has a first-order continuous space derivative and that its second-order space derivatives are integrable, the operators $\frac{{\partial }^{{\gamma }_1}}{\partial x^{{\gamma }_1}}$, $\frac{{\partial }^{{\gamma }_2}}{\partial y^{{\gamma }_2}}$, and $\frac{{\partial }^{{\gamma }_3}}{\partial z^{{\gamma }_3}}$ in (4) can be discretized while using the shifted fractional Grünwald–Letnikov derivative in (8). Thus, we obtain the implicit finite-difference scheme

$$\begin{array}{cc}{\displaystyle \frac{p_{i,j,k}^{n+1}-p_{i,j,k}^n}{\tau }}\hfill & =\frac{K_x}{h_x^{{\gamma }_1}}\sum _{s=0}^{i+1}{g}_{{\gamma }_1,s}{p}_{i+1-s,j,k}^{n+1}+\frac{K_y}{h_y^{{\gamma }_2}}\sum _{s=0}^{j+1}{g}_{{\gamma }_2,s}{p}_{i,j+1-s,k}^{n+1}\hfill \\ {\displaystyle }\hfill & +\frac{K_z}{h_z^{{\gamma }_3}}\sum _{s=0}^{k+1}{g}_{{\gamma }_3,s}{p}_{i,j,k+1-s}^{n+1}+f_{i,j,k}^{n+1}.\hfill \end{array}$$

(10)

It is known that the fractional discrete operator

$${\delta }_x^{{\gamma }_1}{p}_{i,j,k}^{n+1}:=\frac{1}{h_x^{{\gamma }_1}}\sum _{s=0}^{i+1}{g}_{{\gamma }_1,s}{p}_{i+1,j,k}^{n+1},$$

(11)

provides an $\mathcal{O}\left(h_x\right)$ approximation to the Grünwald–Letnikov shifted fractional derivative of order ${\gamma }_1$ [20]. Similarly, the discrete operators

$${\delta }_y^{{\gamma }_2}{p}_{i,j,k}^{n+1}:=\frac{1}{h_y^{{\gamma }_2}}\sum _{s=0}^{j+1}{g}_{{\gamma }_2,s}{p}_{i,j+1,k}^{n+1},{\delta }_z^{{\gamma }_3}{p}_{i,j,k}^{n+1}:=\frac{1}{h_z^{{\gamma }_3}}\sum _{s=0}^{k+1}{g}_{{\gamma }_3,s}{p}_{i,j,k+1}^{n+1},$$

(12)

provide, respectively, $\mathcal{O}\left(h_y\right)$ and $\mathcal{O}\left(h_z\right)$ approximations to the Grünwald–Letnikov shifted fractional derivatives of order ${\gamma }_2$ and ${\gamma }_3$. Using such operators, the implicit difference scheme in (10) can be rewritten in a more compact form, as

$$(1-K_x\tau {\delta }_x^{{\gamma }_1}-K_y\tau {\delta }_y^{{\gamma }_2}-K_z\tau {\delta }_z^{{\gamma }_3})p_{i,1,k}^{n+1}=p_{i,j,k}^n+\tau f_{i,j,k}^n,$$

(13)

Note that, evaluating $f_{i,j,k}^n$ on the right-hand side at time $t_n$, makes the case simpler when f depends on p, which is when the fPDE is a reaction–diffusion rather than a diffusion equation. In Section 3, we will show that this scheme is characterized by a local truncation error of the order $\mathcal{O}\left(\tau \right)+\mathcal{O}\left(h_x\right)+\mathcal{O}\left(h_y\right)+\mathcal{O}\left(h_z\right)$, and it is unconditionally stable. However, adopting suitable strategies, we have been able to improve such orders, attaining the order $\mathcal{O}\left(\tau \right)+\mathcal{O}\left(h_x^2\right)+\mathcal{O}\left(h_y^2\right)+\mathcal{O}\left(h_z^2\right)$.

Equation (13) (or (10)) yields a linear system of equations satisfied by $p_{i,j,k}^{n+1}$. he corresponding system’s matrix, however, is neither sparse nor band structured, as it happens in the corresponding classical ADI method. This implies that the scheme in (13) requires, at each step, the solution of a large dense linear system of equations. Therefore, we are facing a computationally demanding numerical problem, which calls for constructing suitable efficient numerical schemes, possibly unconditionally stable.

To this purpose, we exploit the idea of the classical ADI method in order to design an implicit difference scheme for each direction, but now in the framework of fractional differential equations. Indeed, we split the computations into three steps, each requiring a reduced computational load. On the first step, we solve the problem in the x-direction, on the second one, we solve it in the y-direction, and in the third one, in the z-direction.

In order to devise such a splitting, we add an extra higher-order term to the left-hand side of (13), so that we are able to factor the operator into three factors,

$$(K_x{K}_y{\tau }^2{\delta }_x^{{\gamma }_1}{\delta }_y^{{\gamma }_2}+K_x{K}_z{\tau }^2{\delta }_x^{{\gamma }_1}{\delta }_z^{{\gamma }_3}$$

$$+K_y{K}_z{\tau }^2{\delta }_y^{{\gamma }_2}{\delta }_z^{{\gamma }_3}-K_x{K}_y{K}_z{\tau }^3{\delta }_x^{{\gamma }_1}{\delta }_y^{{\gamma }_2}{\delta }_z^{{\gamma }_3})p_{i,j,k}^{n+1},$$

(14)

into three factors, without affecting the overall convergence rate, thus obtaining the scheme

$$(1-K_x\tau {\delta }_x^{{\gamma }_1})(1-K_y\tau {\delta }_y^{{\gamma }_2})(1-K_z\tau {\delta }_z^{{\gamma }_3})p_{i,j,k}^{n+1}=p_{i,j,k}^{n+1}+\tau f_{i,j,k}^n.$$

(15)

Now, splitting (15) in the three dimensions, we obtain the unbalanced version of the scheme, which provides the solution at time $t_{n+1}$,

$$\begin{array}{c}(1-K_x\tau {\delta }_x^{{\gamma }_1})p_{i,j,k}^{n+1/3}=p_{i,j,k}^n+\tau f_{i,j,k}^n,\\ \\ (1-K_y\tau {\delta }_y^{{\gamma }_2})p_{i,j,k}^{n+2/3}=p_{i,j,k}^{n+1/3},\\ \\ (1-K_z\tau {\delta }_z^{{\gamma }_3})p_{i,j,k}^{n+1}=p_{i,j,k}^{n+2/3},\end{array}$$

(16)

and turns out to be of the first order in space [2]. However, we can choose to distribute the effect of the source term among the three steps in a more balanced way, obtaining, from (15), the fADI scheme

$$\begin{array}{c}(1-K_x\tau {\delta }_x^{{\gamma }_1})p_{i,j,k}^{n+1/3}=p_{i,j,k}^n+\frac{\tau }{3}{f}_{i,j,k}^n,\\ \\ (1-K_y\tau {\delta }_y^{{\gamma }_2})p_{i,j,k}^{n+2/3}=p_{i,j,k}^{n+1/3}+\frac{\tau }{3}{f}_{i,j,k}^n,\\ \\ (1-K_z\tau {\delta }_z^{{\gamma }_3})p_{i,j,k}^{n+1}=p_{i,j,k}^{n+2/3}+\frac{\tau }{3}{f}_{i,j,k}^n.\end{array}$$

(17)

which also provide the solution at time $t_{n+1}$. As in all classical ADI schemes, the system in (17) is not equivalent to that in (15), but it does within an error that is of order higher that that provided by the scheme.

The algorithm (17) now performs better, as it will be shown in Section 3, below.

The “unbalanced” scheme is accurate to the first order in space and it requires a little shorter computing time, as compared to the better “balanced” scheme. The latter however is accurate to the second order in space, see Theorem 1, below.

The idea of using a more balanced scheme, which equally affects all (the three) directions, results in a better method, which is clearly uneffective when $f\equiv 0$. The algorithm seems to be new, even within the framework of 3D classical (i.e., non-fractional) ADI methods.

Summarizing, the computations are split into three (time) fractional steps, in each of which a one-dimensional equation is solved at time, as follows:

Step 1. Solve the problem in the x-direction (for each fixed pair $(y_j,z_k))$, in order to obtain the intermediate value of the solution, say $p_{i,j,k}^{n+1/3}$, from the first equation in (17).

Step 2. Solve the problem in the y-direction (for each fixed pair $(x_i,z_k))$, in order to obtain the intermediate value $p_{i,j,k}^{n+2/3}$, from the second equation in (17), while using the results that were obtained at Step 1.

Step 3. Solve the problem in the z-direction (for each fixed pair $(x_i,y_j))$, from the third equation in (17), using the results of Step 2.

Taking the boundary values $p_{0,j,k}^{n+1/3}$ and $p_{M_x,j,k}^{n+2/3}$ into account, we can construct the coefficients of the matrix $A:=\left\{a_{s,t}\right\}$ of the linear system in (17): for each fixed $(j,k)$, we have

$$a_{s,t}=\left\{\begin{array}{cc}0,\hfill & t\ge s+2,s=1,2,\dots ,M_x-3,\hfill \\ -K_x\frac{\tau }{h_x^{{\gamma }_1}}{g}_{{\gamma }_1,0},\hfill & t=s+1,s=2,...,M_x-2,\hfill \\ 1-K_x\frac{\tau }{h_x^{{\gamma }_1}}{g}_{{\gamma }_1,1},\hfill & t=s=2,\dots ,M_x-1,\hfill \\ -K_x\frac{\tau }{h_x^{{\gamma }_1}}{g}_{{\gamma }_1,s-t+1},\hfill & t\le s-1,s=2,\dots ,M_x-1.\hfill \end{array}\right.$$

(18)

Subsequently, using the boundary values $p_{i,0,k}^{n+2/3}$ and $p_{i,M_y,k}^{n+2/3}$, we obtain the matrix $B:=\left\{b_{s,t}\right\}$ of the linear system in the second equation of (17). For each fixed $(i,k)$, such a matrix turns out to be similar to A (as given in (18)). Finally, while using the boundary values $p_{i,j,0}^{n+1}$ and $p_{i,j,M_z}^{n+1}$, we obtain the matrix $C:=\left\{c_{s,t}\right\}$ of the linear system in the third equation in (17), which, again, for each fixed $(i,j)$, is similar to A.

Of course, as in the classical ADI Peaceman–Rachford algorithm [30], used to solve “integer-order” (i.e., non-fractional) PDEs, it is necessary to provide certain boundary values to be associated to the diffusion in the x-direction, which is $p_{0,j,k}^{n+1/3}$ and $p_{M_x,j,k}^{n+1/3}$, as well as $p_{i,0,k}^{n+2/3}$ and $p_{i,M_y,k}^{n+2/3}$, associated to the diffusion along y, and similarly for the diffusion along z, when solving the systems with the coefficient matrices A, B, and C. For instance, we need the boundary values $p_{0,j,k}^{n+1/3}$, $p_{M_x,j,k}^{n+1/3}$, which can be obtained from

$$p_{i,j,k}^{n+1/3}=(1-K_y\tau {\delta }_y^{{\gamma }_2})(1-K_z\tau {\delta }_z^{{\gamma }_3})p_{i,j,k}^{n+1},i=0,\dots ,M_x,$$

for $j=1,2,\dots ,M_y-1$, $k=1,2,\dots ,M_z-1$, $n=0,1,\dots ,N-1$, and $p_{i,0,k}^{n+2/3}$, $p_{i,M_y,k}^{n+2/3}$, which can be obtained from

$$p_{i,j,k}^{n+2/3}=(1-K_z\tau {\delta }_z^{{\gamma }_3})p_{i,j,k}^{n+1},i=0,\dots ,M_y,$$

for $i=1,2,\dots ,M_x-1$, $k=1,2,\dots ,M_z-1$, $n=0,1,\dots ,N-1$.

Examining the three matrices A, B, and C, above, it can be seen that, at each time step, it is merely required to solve, for each fixed pair $(j,k)$ (at each x-level), a linear upper triangular system of size $M_x-1$, or, for each fixed pair $(i,k)$ (at each y-level), a linear upper triangular system of size $M_y-1$, or, for each fixed pair $(i,k)$ (at each z-level) a linear upper triangular system of size $M_z-1$.

3. Theoretical Analysis of the 3D fADI Algorithm

As mentioned in Section 2, the fractional discrete operators in (11) and (12) provide an $\mathcal{O}\left(h_x\right)$, $\mathcal{O}\left(h_y\right)$, and $\mathcal{O}\left(h_z\right)$ approximation to the Grünwald–Letnikov shifted fractional derivative of order ${\gamma }_1$, ${\gamma }_2$, and ${\gamma }_3$, respectively, see [20,31].

The “unbalanced” implicit difference scheme (16) is characterized by a local truncation error of order $\mathcal{O}\left(\tau \right)+\mathcal{O}\left(h_x\right)+\mathcal{O}\left(h_y\right)+\mathcal{O}\left(h_z\right)$, and it is unconditionally stable. These facts were established in [32]. Let us now consider our better “balanced” scheme (17). We will prove the following

Theorem 1.

The scheme in (17) is unconditionally stable, third-order accurate in time, and second-order accurate in space, for every choice of the (space) fractional orders, ${\gamma }_i$, $i=1,2,3$.

Proof. 

In [33], the unbalanced scheme in (16) was analyzed and its numerical stability proved. Now consider our balanced scheme in (17). Here, we use the so called “Lubich second-order backward finite difference” [34], which is defined, at time n, in the x-direction, at the point $x_{i+1}$, and for fixed y and z, as

$${}^L{\delta }_x^{{\gamma }_1}p{|}_{x_{i+1}}:=\frac{1}{h_x^{{\gamma }_1}}\sum _c^{}{\omega }_c^{{\gamma }_1}{p}_{i-c,j,k}^n.$$

(19)

Here, $c\in \{-1,0,-1\}$, ${\gamma }_1$ represents the fractional order derivative, and the ${\omega }_c^{{\gamma }_1}$’s are the first three coefficients of the Taylor expansions of the corresponding generating function, say $f_a\left(z\right)$, see [34]. Here, a denotes the order of accuracy and, for $a=2$, such a function is given by

$$f_2^{{\gamma }_1}\left(z\right):={\left(\frac{3}{2}-2z+\frac{1}{2}{z}^2\right)}^{{\gamma }_1}.$$

(20)

The Grünwald–Letnikov definition of the discretized Riemann–Liouville fractional derivative differs from that given by Lubich by an $\mathcal{O}\left(h_x^2\right)$ term, see [34]. Thus, evaluating the fractional Riemann–Liouville derivatives at the point $x_{i+1}$, in order to approximate the space fractional derivative in the sense of Lubich of order ${\gamma }_1$ in the x-direction, we obtain

$${\delta }_x^{{\gamma }_1}p{|}_{x_{i+1}}=\frac{3p_{i+1,j,k}^{n+1/3}-4p_{i,j,k}^{n+1/3}+p_{i-1,j,k}^{n+1/3}}{2{\tau }^{{\gamma }_1}}+\mathcal{O}\left(h_x^2\right),$$

(21)

where $\tau =h_x$. In order to be more general, we could set $\tau :=s{h}_x$, for some $s>0$, but this would not entail any loss of generality because the stability analyis would not affect the location of the roots by this. This holds for each fixed i and $n,j,k$. Using the approximation (21) in (17), we obtain

$$p_{i+1,j,k}^{n+1/3}-K_x\tau \frac{3p_{i+1,j,k}^{n+1/3}-4p_{i,j,k}^{n+1/3}+p_{i-1,j,k}^{n+1/3}}{2{\tau }^{{\gamma }_1}}=p_{i-1,j,k}^n+\frac{\tau }{3}{f}_{i,j,k}^n,$$

(22)

with a truncation error of order $\mathcal{O}\left(h_x^2\right)$. We now approximate the x-space operator applied to $p_{i+1,j,k}^{n+1/3}$ [33] by a second-order Taylor expansion, obtaining

$$1-K_x\tau {\delta }_x^{{\gamma }_1}=L_x+\frac{4}{3}{h}_x{\partial }_x-\frac{4}{9}{h}_x^2{D}_x$$

(23)

where $D_x:={\partial }_{xx}$ and $L_x:=1+\theta h_x{D}_x$, $0<\theta <1$. Subsequently, we can replace the $\mathcal{O}\left(h_x^3\right)$ with the explicit form of $p_{i+1,j,k}^{n+1/3}$ that is given by the extrapolation formula

$$\begin{array}{ccc}\hfill {\tilde{p}}_{i+1,j,k}^{n+1/3}:& =& \frac{147}{2500}{p}_{i+1,j,k}^{n+1/3}-\frac{29409}{100000}{p}_{i+i,j,k}^{n+\ast \ast }-\frac{147}{2500}{p}_{i+1,j,k}^{n+\ast }+\frac{147}{2500}{p}_{i+1,j,k}^n\hfill \\ & =& p_{i+1,j,k}^{n+1/3}+\mathcal{O}\left(h_x^2\right)\hfill \end{array}$$

(24)

(see (29) in Section 4.1 below, and (32) in Section 4.2), where ∗ and $\ast \ast$ represent, respectively, the first and the second intermediate sub-steps between n and $n+1/3$, and $p_{i+1,j,k}^{n+1/3}$ is implicitly defined through (22). We can then insert $L_x$ in (23) ${\tilde{p}}_{i+1,j,k}^{n+1/3}$, obtaining

$$L_x{p}_{i+1,j,k}^{n+1/3}=(1-K_x\tau ){\tilde{p}}_{i+1,j,k}^{n+1/3}-\frac{4}{3}\tau {\partial }_x{\tilde{p}}_{i+1,j,k}^{n+1/3}+\frac{4}{9}{\tau }^2{D}_x{\tilde{p}}_{i+1,j,k}^{n+1/3}.$$

(25)

Subtracting $L_x{\tilde{p}}_{i+1,j,k}^{n+1/3}$ from both sides of (25), we finally obtain

$$\begin{array}{ccc}\hfill L_{x}v& =& -(K_x\tau +\theta h_x{\delta }_x^{{\gamma }_1}){\tilde{p}}_{i+1,j,k}^{n+1/3}-(1+\frac{4}{3}\tau {\partial }_x+\theta h_x{\delta }_x^{{\gamma }_1}){\tilde{p}}_{i+1,j,k}^{n+1/3}\hfill \\ & & -(1+\theta h_x+\frac{4}{9}{\tau }^2){\delta }_x^{{\gamma }_1}{\tilde{p}}_{i+1,j,k}^{n+1/3},\hfill \end{array}$$

(26)

where we set, for short, $v:=p_{i+1,j,k}^{n+1/3}-{\tilde{p}}_{i+1,j,k}^{n+1/3}$, and replaced the classical second order derivative $D_x$ with his fractional version, ${\delta }_x^{{\gamma }_1}$. A von Neumann stability analysis of (26) yields an equation for the amplification factor, $\sigma$,

$$(\theta h_x-K_x\tau ){\sigma }^4{(\sigma -1)}^2=\frac{7}{3}(1+K_x\theta \tau ){\sigma }^3(\sigma -1)-\frac{8}{3}\tau {\sigma }^2(2\sigma -1).$$

(27)

Similar results can be obtained for the y and the z directions. It can be proved that the roots of (27) are in the range $0\le \left|\sigma \right|\le 1$, for every value of $K_x$, $K_y$, $K_z$, $\theta$, $h_x$, and $\tau$ [35]. Consequently, the scheme presented in (26) turns out to be of the second order in space, and unconditionally stable.

The third-order accuracy in time can be established proceeding as in the 2D case worked out in [29]. We stress that such a result follows from the optimization strategy adopted there, in particular, from using the four-steps extrapolation method (see step 3, in Section 4.1 below) coupled with the Page–Rank algorithm. □

4. The Numerical Implementation and Some Examples

In this section, we apply our numerical method in order to solve 3D fractional diffusion as well as reaction-diffusion problems. Examples, including reaction–diffusions, are then given in order to illustrate the performance of the algorithm.

4.1. Some Theoretical Preliminary Considerations

We set up an extrapolation technique to optimize our algorithm, thus attaining an appreciable acceleration. This can be accomplished exploiting the PageRank algorithm, which is widely used by Computer Scientists, but not so much yet in Numerical Analysis.

The Google’s PageRank algorithm [36] makes it possible to index material in Internet, while using the degree of popularity of a given web page, in order to define the position in searching results through the computation of certain optimal coefficients. In this way, this algorithm provides, for instance, an optimization method to make it faster a given web search. This approach will be associated to an extrapolation technique, in order to determine the coefficients that make it optimal. Not only can a considerable amount of CPU time be saved in this way, [10], but this procedure also increases the accuracy of the overall method up to the third order in time, see [29,37]. Let us describe such a technique.

Step 1. Compute first the array $\mathrm{\Psi }={({\psi }_1,{\psi }_2,{\psi }_3,{\psi }_4)}^T$, solving the system

$$\mathrm{\Psi }=\mathbf{v}+d\mathbf{L}\mathrm{\Psi },$$

(28)

of four linear algebraic equations, where d is the so-called damping factor, in general assumed to be around $0.85$ (see [38]; such a numerical value for d was determined by empirical trials), $\mathbf{v}:=(1-d){\left(0,{(N-2)}^{-1},{(N-1)}^{-1},N^{-1}\right)}^T$, N being the dimension of the problem, which, in our case, is equal to 4, and $\mathbf{L}=\left\{{\ell }_{ij}\right\}$ for $i,j=1,\dots ,4$, where $l_{ij}$ are certain nonnegative coefficients, such that, for each j, ${\sum }_{i=1}^N{l}_{i,j}=1$. Note that (28) is an implicit, but linear, equation for $\mathrm{\Psi }$; hence, immediately solvable. An extrapolated solution, depending on $p^n\equiv p_{i,j,k}^n$, is then used to solve the problem. The quantity $p^n$ requires evaluating certain coefficients, which can be obtained by the “PageRank accelerating algorithm” [36]. The previous algebraic system yields the optimal coefficients array $\mathrm{\Psi }$.

Step 2. Compute the solution $p^n$ to a compact difference scheme [28,39,40,41] (see step 3 below), with the four time step sizes $\tau$, $\frac{3}{4}\tau$, $\frac{\tau }{2}$, and $\frac{\tau }{4}$ [40]. This kind of method is usually adopted in order to treat steady convection-diffusion numerical problems on uniform grids [39], rather than time-dependent problems.

Step 3. Evaluate the extrapolated solution, $q^n\left(\tau \right)$, by

$$q^n\left(\tau \right)={\psi }_1{p}^n\left(\tau \right)+{\psi }_2{p}^n\left(\frac{3}{4}\tau \right)+{\psi }_3{p}^n\left(\frac{\tau }{2}\right)+{\psi }_4{p}^n\left(\frac{\tau }{4}\right),$$

(29)

where the dependence of $p^n$ on $\tau$ has been displayed.

4.2. Numerical Examples

In this section, we present a few numerical results in order to support the theoretical analysis developed in the previous sections. In the following, the symbol ${}_a{D}_b^{\alpha }p$ will be used to define the fractional Riemann–Liouville derivative of p of order $\alpha$, in the interval $[a,b]$.

Example 1. Consider the three dimensional fPDE

$$\begin{array}{ccc}\hfill \frac{\partial p}{\partial t}& =& K_{1x}{}_0{D}_x^{\alpha }p+K_{2x}{}_x{D}_2^{\alpha }p+K_{1y}{}_0{D}_y^{\beta }p+K_{2y}{}_y{D}_2^{\beta }p+K_{1z}{}_0{D}_z^{\gamma }p+K_{2z}{}_z{D}_2^{\gamma }p\hfill \\ & & +d_x\frac{\partial p}{\partial x}+d_y\frac{\partial p}{\partial y}+d_z\frac{\partial p}{\partial z}+f(x,y,z,t),\hfill \end{array}$$

(30)

that is a linear diffusion-advection model equation (with ordinary transport and fractional diffusion), on the domain $(x,y,z)\in {[0,2]}^3$, $0<t\le T$, with coefficients

$$\begin{array}{cc}\hfill K_{1x}:=\mathrm{\Gamma }(3-\alpha )x^{\alpha },& K_{2x}=\mathrm{\Gamma }(3-\alpha ){(2-x)}^{\alpha }\\ \hfill K_{1y}:=\mathrm{\Gamma }(3-\beta )y^{\beta },& K_{2y}=\mathrm{\Gamma }(3-\beta ){(2-y)}^{\beta }\\ \hfill K_{1z}:=\mathrm{\Gamma }(3-\gamma )x^{\gamma },& K_{2z}=\mathrm{\Gamma }(3-\gamma ){(2-z)}^{\gamma },\\ \hfill d_x:=\frac{x}{4},& d_y:=\frac{y}{4},d_z:=\frac{z}{4}.\end{array}$$

We define the forcing term

$$\begin{array}{c}\hfill f(x,y,z,t):=-4e^{-t}{x}^2{y}^2{z}^2(x-2)(y-2)(z-2)(3xyz-5x-5y-5z+8)\\ \hfill -\left[l_{\alpha }(x,z,t)+l_{\gamma }(z,x,t)+l_{\alpha }(y,x,t)+l_{\beta }(x,y,t)+l_{\beta }(z,y,t)+l_{\gamma }(y,z,t)\right],\end{array}$$

(31)

where $l_{\delta }(u,v,t):=g(u,t)h_{\delta }\left(v\right)$, being

$$g(u,t):=32e^{-t}{u}^2{(2-u)}^2,$$

and

$$h_{\delta }\left(u\right):=u^2+{(2-u)}^2-\frac{3\left[u^3+{(2-u)}^3\right]}{3-\delta }+\frac{3\left[u^4+{(2-u)}^4\right]}{(3-\delta )(4-\delta )},$$

and impose, furthermore, for all $t>0$, the homogeneous Dirichlet boundary conditions

$$\begin{array}{c}\hfill p(0,y,z,t)=p(x,0,y,t)=p(x,y,0,t)=0,\\ \hfill p(2,y,z,t)=p(x,2,y,t)=p(x,y,2,t)=0,\end{array}$$

as well as the initial condition

$$p(x,y,z,0)=4x^2{(2-x)}^2{y}^2{(2-y)}^2{z}^2{(2-z)}^2.$$

The (exact) analytical solution to Equation (30) under such initial and boundary conditions is known and it is given by

$$p(x,y,z,t)=4x^2{e}^{-t}{(2-x)}^2{y}^2{(2-y)}^2{z}^2{(2-z)}^2,$$

see [42]. All of this can be used in order to validate our 3D algorithm and test its performance. We will then feel confident that it might perform well also when other source terms, that might be encountered in real world problems, enter the model. Below, we will indeed replace the special forcing term in (30) with some other more realistic ones.

From Figure 1, it is rather clear (qualitatively) what is the effect of replacing ordinary derivatives, ($\alpha ,\beta ,\gamma$) = ($2,2,2$), with fractional derivatives, in a given diffusion equation. Here, ($\alpha ,\beta ,\gamma$) = ($1.4,1.5,1.6$), thus accounting for anomalous diffusion. In general, such a modification implies new geometric patterns in the solution, and a possibly anisotropic behavior. These features have been observed, e.g., in certain porous media through which some fluid flows [43,44]. Hereafter, T denotes the final time at which the solution is computed.

In Figure 2, the numerical errors $\parallel q^n-p^n\parallel$ are plotted in the $L^2$ and in the $L^{\infty }$ norms, on a log-scale, where $p^n\equiv p(x_i,y_j,z_k,t_n)$ denotes the exact solution to the fPDE (on the grid points that are defined in Section 2, and $q^n\equiv q^n\left(\tau \right)$ is its approximation that is given by our scheme through Equation (29).

In order to assess the convergence rate when space and time step sizes are refined, we write our approximate solution $q^n$ as $q(h,\tau )$ in order to display its dependence on the space step sizes, $h_x=h_y=h_z=h$ (assumed to be equal), and the time step size, $\tau$. Subsequently, we define, for every $N\in \mathbf{N}$, the time and the space convergence rate, in the two-norm, for a given method of order $m>1$, as

$$r_{time}\left(N\right):={log}_2\left[\frac{\parallel q(h,\frac{h}{N})-p^n{\parallel }_2}{\parallel q(h,\frac{h}{2N})-p^n{\parallel }_2^m}\right],r_{space}\left(N\right):={log}_2\left[\frac{\parallel q(\frac{h}{N},h)-p^n{\parallel }_2}{\parallel q\left(\frac{h}{2N}\right),h{)-p^n\parallel }_2^m}\right].$$

In

Table 1. $L^{\infty }$ and $L^2$ norm errors (in log scale) and convergence rates for Example 1, when the balanced scheme is used, at time $T=1$, for  several values of $(\alpha ,\beta ,\gamma )$, N.

$(\mathit{\alpha },\mathit{\beta },\mathit{\gamma })$	N	$\parallel {\mathit{q}}^{\mathit{n}}-{\mathit{p}}^{\mathit{n}}{\parallel }_{\mathit{\infty }}$	${\mathit{r}}_{\mathit{space}}$	$\parallel {\mathit{q}}^{\mathit{n}}-{\mathit{p}}^{\mathit{n}}{\parallel }_2$	${\mathit{r}}_{\mathit{space}}$	${\mathit{r}}_{\mathit{time}}$
$(1.2,1.2,1.2)$	8	$1.5023\times {10}^{-2}$	$--$	$7.5264\times {10}^{-2}$	$--$	$--$
	16	$2.8925\times {10}^{-3}$	$2.002$	$1.6581\times {10}^{-2}$	$2.015$	$3.009$
	32	$6.8952\times {10}^{-4}$	$2.000$	$5.3265\times {10}^{-3}$	$2.007$	$3.006$
	64	$2.3561\times {10}^{-4}$	$1.996$	$2.3654\times {10}^{-4}$	$1.999$	$3.001$
$(1.4,1.5,1.6)$	8	$2.0253\times {10}^{-2}$	$--$	$3.2564\times {10}^{-2}$	$--$	$--$
	16	$2.9541\times {10}^{-3}$	2.001	$3.1254\times {10}^{-2}$	$2.011$	$3.010$
	32	$7.1254\times {10}^{-4}$	$2.000$	$7.9856\times {10}^{-3}$	$2.007$	$3.005$
	64	$2.5648\times {10}^{-4}$	$1.988$	$2.8930\times {10}^{-2}$	$1.998$	$2.998$
$(1.9,1.9,1.9)$	8	$2.324\times {10}^{-2}$	$--$	$3.5852\times {10}^{-2}$	$--$	$--$
	16	$3.5984\times {10}^{-3}$	$2.005$	$3.9852\times {10}^{-2}$	$2.009$	$3.002$
	32	$7.5214\times {10}^{-4}$	2.002	$7.7815\times {10}^{-3}$	$2.008$	$3.001$
	64	$2.8594\times {10}^{-4}$	1.992	$3.2852\times {10}^{-4}$	$1.989$	$3.000$
$(2.0,2.0,2.0)$	8	$5.2154\times {10}^{-3}$	$--$	$6.7952\times {10}^{-3}$	$--$	$--$
	16	$6.7854\times {10}^{-4}$	$2.001$	$7.1248\times {10}^{-4}$	$2.001$	$3.000$
	32	$5.7453\times {10}^{-5}$	$1.999$	$7.9173\times {10}^{-5}$	$1.998$	$3.000$
	64	$6.7852\times {10}^{-5}$	$2.000$	$7.7945\times {10}^{-5}$	$2.000$	$2.999$

and

Table 2. $L^{\infty }$ and $L^2$ norm errors, and convergence rates for Example 1, when the balanced scheme is used, at time $T=2$, for several values of N.

$(\mathit{\alpha },\mathit{\beta },\mathit{\gamma })$	N	$\parallel {\mathit{q}}^{\mathit{n}}-{\mathit{p}}^{\mathit{n}}{\parallel }_{\mathit{\infty }}$	${\mathit{r}}_{\mathit{space}}$	$\parallel {\mathit{q}}^{\mathit{n}}-{\mathit{p}}^{\mathit{n}}{\parallel }_2$	${\mathit{r}}_{\mathit{space}}$	${\mathit{r}}_{\mathit{time}}$
$(1.4,1.5,1.6)$	8	$8.2654\times {10}^{-3}$	$--$	$9.7452\times {10}^{-3}$	$--$	$--$
	16	$2.6584\times {10}^{-4}$	$2.001$	$2.7852\times {10}^{-3}$	$2.001$	$3.002$
	32	$7.0145\times {10}^{-5}$	$2.000$	$5.3255\times {10}^{-4}$	$1.999$	$3.000$
	64	$1.2420\times {10}^{-5}$	$1.999$	$4.7852\times {10}^{-5}$	$2.000$	$2.999$

, the absolute numerical errors $\parallel q^n-p^n{\parallel }_{\infty }$ and $\parallel q^n-p^n{\parallel }_2$, as well as the corresponding convergence rates that are attained using different space step sizes, are shown. Figure 2 displays the infinity norm and the $L^2$ norm errors for Example 1, when the optimized difference scheme is implemented in (29), at times $T=1$ and $T=2$, for several values of $h_x=h_y=h_z=h=\tau =2/N$, $N=8,16,32,64$, and fixed $\alpha$, $\beta$, and $\gamma$. Here, there is evidence that the numerical errors decrease when increasing N, i.e., decreasing $\tau$. Note that, due to the logarithmic scale, decreased errors correspond to increasing values.

In Figure 3, the discrepancies between the numerical solutions to the classical and the fractional differential equations, obtained by the $ADI$ and the $fADI$ method, respectively, i.e., $\parallel q_{ADI}^n-q_{fADI}^n\parallel$, are plotted in the $L^2$ and the $L^{\infty }$ norms, on a log-scale. This is done in order to appreciate the differences that are visible when one switches from one to the other model. In

Table 3. $L^{\infty }$ and $L^2$ norm discrepancy for Example 1, when the balanced scheme is used, at time $T=1$, for several values of N.

$(\mathit{\alpha },\mathit{\beta },\mathit{\gamma })$	N	$\parallel {\mathit{q}}_{\mathit{fADI}}^{\mathit{n}}-{\mathit{q}}_{\mathit{ADI}}^{\mathit{n}}{\parallel }_{\mathit{\infty }}$	$\parallel {\mathit{q}}_{\mathit{fADI}}^{\mathit{n}}-{\mathit{q}}_{\mathit{ADI}}^{\mathit{n}}{\parallel }_2$
$(1.2,1.2,1.2)$	256	$6.1758\times {10}^{-7}$	$3.8458\times {10}^{-6}$
	512	$2.2548\times {10}^{-7}$	$7.8442\times {10}^{-7}$
$(1.4,1.5,1.6)$	256	$2.8287\times {10}^{-7}$	$1.1205\times {10}^{-6}$
	512	$3.7852\times {10}^{-8}$	$3.7854\times {10}^{-7}$
$(1.9,1.9,1.9)$	256	$1.1582\times {10}^{-7}$	$5.7852\times {10}^{-7}$
	512	$1.7855\times {10}^{-8}$	$5.0023\times {10}^{-7}$
$(2.0,2.0,2.0)$	256	$8.1158\times {10}^{-8}$	$8.7852\times {10}^{-7}$
	512	$1.7852\times {10}^{-8}$	$6.7852\times {10}^{-8}$

and

Table 4. $L^{\infty }$ and $L^2$ norm discrepancy for Example 1, when the balanced scheme is used, at time $T=2$, for several values of N.

$(\mathit{\alpha },\mathit{\beta },\mathit{\gamma })$	N	$\parallel {\mathit{q}}_{\mathit{fADI}}^{\mathit{n}}-{\mathit{q}}_{\mathit{ADI}}^{\mathit{n}}{\parallel }_{\mathit{\infty }}$	$\parallel {\mathit{q}}_{\mathit{fADI}}^{\mathit{n}}-{\mathit{q}}_{\mathit{ADI}}^{\mathit{n}}{\parallel }_2$
$(1.4,1.5,1.6)$	256	$5.7854\times {10}^{-7}$	$1.4002\times {10}^{-8}$
	512	$2.7584\times {10}^{-8}$	$7.7852\times {10}^{-8}$

, such discrepancies, $\parallel q_{ADI}^n-q_{fADI}^n{\parallel }_{\infty }$ and $\parallel q_{ADI}^n-q_{fADI}^n{\parallel }_2$, as well as the corresponding convergence rates, which are achieved using different space step sizes, are shown. Here, again, $q^n\left(\tau \right)$, given by

$$\frac{147}{2500}{p}^n\left(\tau \right)-\frac{29409}{100000}{p}^n\left(\frac{3}{4}\tau \right)-\frac{147}{2500}{p}^n\left(\frac{\tau }{2}\right)+\frac{147}{2500}{p}^n\left(\frac{\tau }{4}\right),$$

(32)

is the extrapolated solution, and $p^n\equiv p_{i,j,k}^n$ satisfies the optimized scheme in (13). Figure 3 shows the convergence rates of the maximum norm and the $L^2$ norm errors for Example 1, when the optimized difference scheme that is presented in (32) is implemented, at times $T=1$, for several values of N, and fixed $\alpha$, $\beta$, and $\gamma$.

Table 5. CPU times in clocks ticks units $\left(CT\right)$ for the unbalanced and the balanced versions of the fADI scheme, $C{T}_{bal}$, and $C{T}_{unbal}$, respectively, required attaining an error of order ${10}^{-5}$, for $h=1/100$ and several values of the fractional orders, $\alpha ,\beta ,\gamma$, and the advection coefficients, $d_x,d_y,d_z$.

$(\mathit{\alpha },\mathit{\beta },\mathit{\gamma })$	$({\mathit{d}}_{\mathit{x}},{\mathit{d}}_{\mathit{y}},{\mathit{d}}_{\mathit{z}})$	${\mathit{CT}}_{\mathit{unbal}}$	${\mathit{CT}}_{\mathit{bal}}$
$(1.8,1.5,1.2)$	$(10,5,1)$	$2.256\times {10}^{-3}$	$8.236\times {10}^{-2}$
$(1.8,1.5,1.3)$	$(8,4,1)$	$4.365\times {10}^{-3}$	$4.255\times {10}^{-2}$
$(1.8,1.6,1.4)$	$(7,3,1)$	$3.256\times {10}^{-2}$	$5.778\times {10}^{-2}$
$(1.8,1.6,1.5)$	$(5,2,1)$	$7.289\times {10}^{-2}$	$2.389\times {10}^{-3}$
$(1.8,1.7,1.6)$	$(3,1,1)$	$6.258\times {10}^{-1}$	$1.756\times {10}^{-3}$
$(1.8,1.7,1.7)$	$(2,1,1)$	$8.236\times {10}^{-1}$	$1.586\times {10}^{-3}$
$(1.8,1.8,1.8)$	$(1,1,1)$	$9.266\times {10}^{-1}$	$1.256\times {10}^{-3}$

shows the CPU times by our algorithm on a Dual Core Pentium with 4GB RAM and with 32bit-MATLAB programs, for different values of fractional orders and advection coefficients $d_x,d_y,d_z$. The CPU time is measured in terms of clocks ticks.

Table 5 and

Table 6. CPU times in clocks ticks units $\left(CT\right)$ for the unbalanced and the balanced versions of the fractional Alternating Direction Implicit (fADI) scheme, $C{T}_{bal}$, and $C{T}_{unbal}$, respectively, required attaing an error of order ${10}^{-5}$, for $N=100$ and several values $h=\frac{1}{\gamma N}$, and of the fractional orders, $\alpha ,\beta ,\gamma$.

$(\mathit{\alpha },\mathit{\beta },\mathit{\gamma })$	h	${\mathit{CT}}_{\mathit{unbal}}$	${\mathit{CT}}_{\mathit{bal}}$
$(1.8,1.5,1.2)$	$0.08$	$5.256\times {10}^{-3}$	$7.256\times {10}^{-2}$
$(1.8,1.5,1.3)$	$0.08$	$6.001\times {10}^{-2}$	$3.856\times {10}^{-2}$
$(1.8,1.6,1.4)$	$0.07$	$7.898\times {10}^{-2}$	$4.258\times {10}^{-2}$
$(1.8,1.6,1.5)$	$0.07$	$8.856\times {10}^{-2}$	$1.759\times {10}^{-2}$
$(1.8,1.7,1.6)$	$0.07$	$4.125\times {10}^{-1}$	$1.896\times {10}^{-2}$
$(1.8,1.7,1.7)$	$0.06$	$7.156\times {10}^{-1}$	$1.325\times {10}^{-3}$
$(1.8,1.8,1.8)$	$0.05$	$8.780\times {10}^{-1}$	$1.126\times {10}^{-3}$

indicate that the our balanced ADI method’s performance is comparable to that proposed in [2], although slightly worse. Recall that our method and that of Liu et al. differ in the strategies that are followed to accelerate them. However, our unbalanced method performs better than that concerning the required CPU times, which are smaller. This is due to the fact that the model problem is anisotropic, behaving rather differently along the direction x than along the other directions. Indeed, all

Table 7. CPU times in clocks ticks units $\left(CT\right)$ for the unbalanced and the balanced versions of the fADI scheme, $C{T}_{bal}$, and $C{T}_{unbal}$, respectively, required attaining an error of order ${10}^{-5}$, for $h=1/100$ and several values of the fractional orders, $\alpha ,\beta ,\gamma$, and the advection coefficients $d_x,d_y,d_z$.

$(\mathit{\alpha },\mathit{\beta },\mathit{\gamma })$	$({\mathit{d}}_{\mathit{x}},{\mathit{d}}_{\mathit{y}},{\mathit{d}}_{\mathit{z}})$	${\mathit{CT}}_{\mathit{unbal}}$	${\mathit{CT}}_{\mathit{bal}}$
$(1.5,1.8,1.2)$	$(5,10,1)$	$7.152\times {10}^{-2}$	$8.256\times {10}^{-2}$
$(1.5,1.8,1.3)$	$(4,8,1)$	$9.856\times {10}^{-2}$	$7.026\times {10}^{-2}$
$(1.6,1.8,1.4)$	$(3,7,1)$	$6.856\times {10}^{-1}$	$5.785\times {10}^{-2}$
$(1.6,1.8,1.5)$	$(2,5,1)$	$7.019\times {10}^{-1}$	$3.256\times {10}^{-3}$
$(1.7,1.8,1.6)$	$(1,3,1)$	$8.786\times {10}^{-1}$	$1.756\times {10}^{-3}$
$(1.7,1.8,1.7)$	$(1,2,1)$	$9.325\times {10}^{-1}$	$1.586\times {10}^{-3}$
$(1.8,1.8,1.8)$	$(1,1,1)$	$1.256$	$1.025\times {10}^{-3}$

,

Table 8. CPU times in clocks ticks units $\left(CT\right)$ for the unbalanced and the balanced versions of the fADI scheme, $C{T}_{bal}$, and $C{T}_{unbal}$, respectively, required attaining an error of order ${10}^{-5}$, for $N=100$ and several values $h=\frac{1}{\gamma N}$, and of the fractional orders, $\alpha ,\beta ,\gamma$.

$(\mathit{\alpha },\mathit{\beta },\mathit{\gamma })$	h	${\mathit{CT}}_{\mathit{unbal}}$	${\mathit{CT}}_{\mathit{bal}}$
$(1.5,1.8,1.2)$	$0.08$	$7.266\times {10}^{-2}$	$5.125\times {10}^{-2}$
$(1.5,1.8,1.3)$	$0.08$	$9.014\times {10}^{-2}$	$4.856\times {10}^{-2}$
$(1.6,1.8,1.4)$	$0.07$	$5.888\times {10}^{-1}$	$2.558\times {10}^{-2}$
$(1.6,1.8,1.5)$	$0.07$	$7.896\times {10}^{-1}$	$1.325\times {10}^{-3}$
$(1.7,1.8,1.6)$	$0.07$	$3.965\times {10}^{-1}$	$1.756\times {10}^{-3}$
$(1.7,1.8,1.7)$	$0.06$	$7.156$	$1.256\times {10}^{-3}$
$(1.8,1.8,1.8)$	$0.05$	$8.780$	$9.254\times {10}^{-4}$

and

Table 9. CPU times in clocks ticks units $\left(CT\right)$ for the unbalanced and the balanced versions of the fADI scheme, $C{T}_{bal}$, and $C{T}_{unbal}$, respectively, required attaining an error of order ${10}^{-5}$, for $h=1/100$, $d_x=d_y=d_z=0$, and several values of the fractional orders, $\alpha ,\beta ,\gamma$.

$(\mathit{\alpha },\mathit{\beta },\mathit{\gamma })$	${\mathit{CT}}_{\mathit{unbal}}$	${\mathit{CT}}_{\mathit{bal}}$
$(1.5,1.5,1.5)$	$8.458$	$7.758\times {10}^{-4}$
$(1.3,1.8,1.3)$	$2.786\times {10}^{-1}$	$7.256\times {10}^{-2}$
$(1.2,1.5,1.2)$	$6.289\times {10}^{-1}$	$2.389\times {10}^{-3}$
$(1.5,1.7,1.5)$	$6.258\times {10}^{-1}$	$1.756\times {10}^{-3}$
$(1.7,1.8,1.7)$	$3.276\times {10}^{-1}$	$5.785\times {10}^{-3}$
$(1.8,1.8,1.8)$	$1.256\times$	$8.785\times {10}^{-4}$

show that when the anisotropic behavior is more pronounced in another direction (others than x), an appropriately balanced method wins over the others.

Example 2. Let us choose, in Equation (30), ($\alpha ,\beta ,\gamma$) = ($1.4,1.5,1.6$), and the (linear) source term $f\left(p\right)=\frac{p}{2}$, instead of the linear source $f(x,y,z,t)$, independent of p, as defined in (31) above. This is a fractional linear reaction–diffusion problem. A forcing term like this often occurs, for instance, in modeling dissolution and precipitation phenomena in porous media [45,46].

In

Table 10. $L^2$ norm discrepancies, and convergence rates for Example 2, when the balanced scheme is used, at time $T=2$, source term $f\left(p\right)=\frac{p}{2}$, $(\alpha ,\beta ,\gamma )$ = $(1.1,1.7,1)$, $h=1/N$, and  several values of N.

N	$\mathit{\tau }$	$\parallel {\mathit{q}}_{\mathit{fADI}}^{\mathit{n}}-{\mathit{q}}_{\mathit{ADI}}^{\mathit{n}}{\parallel }_2$	${\mathit{Rate}}_{\mathit{space}}$	${\mathit{Rate}}_{\mathit{time}}$
16	$h/16$	$8.5825\times {10}^{-4}$	$--$	$--$
32	$h/16$	$3.8501\times {10}^{-4}$	$2.000$	$3.001$
64	$h/16$	$1.7854\times {10}^{-5}$	$2.000$	$3.000$

, we show the numerical results pertaining to this problem, obtained while using the the fADI method for the fPDE with ($\alpha ,\beta ,\gamma$) = ($1.4,1.5,1.6$).

Example 3. Now consider the linear fractional diffusion equation with an impulsive source,

$$\frac{\partial p}{\partial t}=K_x\frac{{\partial }^{\alpha }p}{\partial x^{\alpha }}+K_y\frac{{\partial }^{\beta }p}{\partial y^{\beta }}+K_x\frac{{\partial }^{\gamma }p}{\partial z^{\gamma }}+c\delta (x-x_0,y-y_0,z-z_0,t-t_0),$$

(33)

where $\delta$ is the Dirac delta function, c, $x_0$, $y_0$, $z_0$, and $t_0$ are all positive constants, $(x,y,z)\in \mathrm{\Omega }=(x_1,x_2)\times (y_1,y_2)\times (z_1,z_2)$, $t>0$, and subject to the boundary conditions

$${p(x,y,z,t)|}_{\partial \mathrm{\Omega }}=h(x,y,z,t),(x,y,z)\in \partial \mathrm{\Omega },t\in (0,T],$$

for some $T>0$, and the initial value

$$p(x,y,z,0)=p_0(x,y,z),(x,y,z)\in \overline{\mathrm{\Omega }}.$$

Here, the forcing term mimics the behavior of a seepage flow in a porous medium, which can be either isotropic or even anisotropic in the x, y, and z direction (depending on the coefficients $K_x$, $K_y$, and $K_z$). In view of a numerical treatment of such a problem, we replace the ideally impulsive source with a function that is likely to have a similar behavior, see [47]. Let $\alpha =\beta =\gamma =1.8$ and the domain $\mathrm{\Gamma }={(0,1)}^3$,

$$K_x=0.1\frac{\mathrm{\Gamma }\left(1.4\right)}{\mathrm{\Gamma }\left(3.2\right)},K_y=0.1\frac{\mathrm{\Gamma }\left(1.2\right)}{\mathrm{\Gamma }\left(3\right)},K_z=0.1\frac{\mathrm{\Gamma }\left(1.4\right)}{\mathrm{\Gamma }\left(3\right)},$$

and the source term, which approximately reproduces the behavior of the $\delta$ function in (33),

$$\begin{array}{cc}f(x,y,z,t)=\hfill & -e^{-t}(x^{2.2}{y}^2{z}^2-0.1x^{0.4}{y}^2{z}^2+\hfill \\ \hfill & -0.1x^2{y}^{0.2}{z}^2-0.1x^2{y}^2{z}^{0.4}).\hfill \end{array}$$

We impose the boundary conditions

$$\begin{array}{c}p(0,y,z,t)=p(x,0,y,t)=p(x,y,0,t)=0,\\ \\ p(1,y,z,t)=e^{-t}{y}^2{z}^2,p(x,1,y,t)=e^{-t}{x}^{2.2}{z}^2,p(x,y,1,t)=e^{-t}{x}^{2.2}{y}^2,\end{array}$$

and the initial value

$$p_0(x,y,z)=0.$$

The analytic solution to this problem is known to be

$$p(x,y,z,t)=e^{-t}{x}^{2.2}{y}^2{z}^2,$$

(34)

see [2]. Note that, when $(\alpha ,\beta ,\gamma )=(2,2,2)$, we obtain the classical linear forced diffusion equation $p_t=\Delta p+f$.

We now compare the previous numerical solution with $\alpha ,\beta ,\gamma$ in the range $[1.2,1.8]$, computed using our balanced fADI method, with that of a classical (i.e., non-fractional) case, which we can consider rather “close” to it, taking $\alpha =\beta =\gamma =2$ and the same source term that is defined in (34).

In Figure 4, the absolute numerical errors between the exact solution and numerical solution obtained by a fADI method are shown. In Figure 5, the same is done for the absolute numerical errors between the numerical classical ADI method and the numerical solution obtained by the fADI method. Both of the errors are plotted in the $L^2$ norm.

Table 11. $L^2$ norm errors, discrepancies and convergence rates for Example 3, when the balanced scheme is used, with $\alpha =\beta =\gamma =1.8$, at time $T=1$, for $h=1/N$ and several values of N and $\tau$. The two numbers in the rates columns refer to the first and second algorithms, respectively.

N	$\mathit{\tau }$	$\parallel {\mathit{q}}_{\mathit{fADI}}^{\mathit{n}}-{\mathit{p}}^{\mathit{n}}{\parallel }_2$	$\parallel {\mathit{q}}_{\mathit{fADI}}^{\mathit{n}}-{\mathit{q}}_{\mathbf{ADI}}^{\mathit{n}}{\parallel }_2$	Space Conv. Rates	Time Conv. Rates
16	h	$2.0122\times {10}^{-1}$	$2.5684$	–	–
32	h	$3.8524\times {10}^{-2}$	$1.8524\times {10}^{-1}$	–	–
64	h	$2.1852\times {10}^{-3}$	$3.2658\times {10}^{-2}$	–	–
16	$h/2$	$5.7616\times {10}^{-1}$	$1.0226$	1.96–1.82	2.98–2.92
32	$h/2$	$3.1658\times {10}^{-2}$	$2.5802\times {10}^{-1}$	1.99–1.93	2.99–2.95
64	$h/2$	$3.5800\times {10}^{-3}$	$6.3552\times {10}^{-2}$	1.98–1.89	2.99–2.96
16	$h/4$	$1.7525\times {10}^{-2}$	$3.2753$	2.00–1.96	3.00–2.98
32	$h/4$	$2.1358\times {10}^{-3}$	$2.1258\times {10}^{-1}$	2.00–1.98	3.00–2.99
64	$h/4$	$3.3654\times {10}^{-4}$	$9.4528\times {10}^{-2}$	2.00–2.00	3.00–3.01

illustrates the convergence rates of the algorithm, as measured in the $L^2$ norm, in Example 3 for several values of $\tau$ and N, and fixed $\alpha ,\beta$, and $\gamma$. Here, $p^n$ is the exact solution, while $q_{ADI}^n$ is the solution that was obtained by the classical ADI method, and $q_{fADI}^n$ is that provided by the fADI method.

As one would expect in the fADI methods, coupled with the optimized extrapolation, a faster convergence is observed as the grid is refined. In the following, we show these results in a table of computational times, see

Table 12. Computational times (in seconds) for the unbalanced and balanced version of the fADI scheme, respectively, $T_{unbal}$ and $T_{bal}$, required to attain an accuracy of order ${10}^{-2}$, with  $(\alpha ,\beta ,\gamma )=(1.8,1.6,1.4)$, at time $T=1$, for $h=1/N$, and several values of N and $\tau$.

N	$\mathit{\tau }$	${\mathit{T}}_{\mathit{unbal}}$	${\mathit{T}}_{\mathit{bal}}$
16	h	$55.8$	$33.9$
32	h	$111.1$	$67.8$
64	h	$223.4$	$135.7$
16	$h/2$	$117.2$	$71.2$
32	$h/2$	$233.3$	$142.4$
64	$h/2$	$472.3$	$285.0$
16	$h/4$	$234.4$	$142.4$
32	$h/4$	$466.7$	$284.8$
64	$h/4$	$938.3$	$570.0$

.

Table 13. CPU times in clocks ticks units $\left(CT\right)$, and memory ($RAM$ in $MB$) for the unbalanced and the balanced versions of the fADI scheme, $C{T}_{bal},RA{M}_{bal}$ and $C{T}_{unbal},RA{M}_{unbal}$, respectively, with  $(\alpha ,\beta ,\gamma )=(1.8,1.6,1.4)$, at time $T=1$, for $h=1/N$, and several values of N and $\tau$.

N	$\mathit{\tau }$	${\mathit{CT}}_{\mathit{bal}}$	${\mathit{RAM}}_{\mathit{bal}}$	${\mathit{CT}}_{\mathit{unbal}}$	${\mathit{RAM}}_{\mathit{unbal}}$
16	h	$1.944\times {10}^{-3}$	$0.15$	$2.778\times {10}^{-3}$	$0.23$
32	h	$4.416\times {10}^{-3}$	$0.23$	$5.278\times {10}^{-3}$	$0.34$
64	h	$8.889\times {10}^{-2}$	$0.81$	$1.027\times {10}^{-2}$	$0.92$
16	$h/2$	$3.050\times {10}^{-2}$	$0.24$	$3.611\times {10}^{-3}$	$0.33$
32	$h/2$	$5.555\times {10}^{-3}$	$0.42$	$6.944\times {10}^{-3}$	$0.51$
64	$h/2$	$1.028\times {10}^{-2}$	$1.23$	$1.361\times {10}^{-2}$	$1.38$
16	$h/4$	$5.278\times {10}^{-3}$	$0.59$	$6.389\times {10}^{-3}$	$0.67$
32	$h/4$	$1.139\times {10}^{-2}$	$0.83$	$1.310\times {10}^{-3}$	$0.95$
64	$h/4$	$2.778\times {10}^{-2}$	$1.70$	$2.667\times {10}^{-2}$	$1.92$

shows the CPU times and memory used by our algorithm for various grid sizes. The CPU time is evaluated at $T=1$. Table 13 indicates that the balanced ADI method performs slightly worse than that one proposed in [2]. However, this little price is paid in order to obtain a third-order (instead of a second-order) in time method. It was also observed that balanced and unbalanced algorithms require approximately the same computational resources.

Example 4. We consider the Fisher equation, which is the semilinear (reaction–diffusion) equation [48]

$$\frac{\partial p}{\partial t}=C\frac{{\partial }^{\alpha }p}{\partial x^{\alpha }}+D\frac{{\partial }^{\beta }p}{\partial y^{\beta }}+E\frac{{\partial }^{\gamma }p}{\partial z^{\gamma }}+f_{r,k}\left(p\right),$$

(35)

on the set

$$\begin{array}{ccc}\hfill \mathrm{\Omega }& =& {\mathrm{\Omega }}_1\times {\mathrm{\Omega }}_2\times {\mathrm{\Omega }}_3=([-20,10]\times {\overline{I}}_{20}^2)\times ([10,20]\times [2,4]\times {\overline{I}}_{20})\times ([20,100]\times {\overline{I}}_{20}^2),\hfill \end{array}$$

where $I_{20}:=(-20,20)$, $t\ge 0$, and $(D,E,F)$ is the percolation tensor, and $f_{r,k}\left(p\right):=rp\left(1-\frac{p}{k}\right)$ is the well-known Kolmogorov–Fisher function [49,50], which is often adopted in population biology to model the spread of invasive species. Here, r and k are parameters, with r representing the intrinsic increase rate of the fluid, and k the environmental carrying capacity, which is the maximum sustainable fluid density. We computed the numerical solution to the initial-boundary value problem above, assuming the radially symmetric initial condition

$$p(x,y,z,0)=\underset{(x,y,z)\in {\mathrm{\Omega }}_1}{min}\{0.8,10e^{-(x^2+y^2+z^2)}\},$$

(36)

and the boundary conditions

$$\begin{array}{c}\hfill {p(x,y,z,t)|}_{\partial \mathrm{\Omega }}=p_y(x,\pm 20,z,t)=p_x(\pm 20,y,z,t)=p_x(10,y,z,t)=0.\end{array}$$

(37)

Next, we consider the solution to a fPDE, like that in (35), but with a reaction term having space variable coefficients. Let $C=0.15,D=0,4,E=1,r=0.2$, and assume that k varies in space, as follows: for $(x,y,z)\in {\mathrm{\Omega }}^{\prime }:={\mathrm{\Omega }}_1^{\prime }\cup {\mathrm{\Omega }}_2^{\prime }\cup {\mathrm{\Omega }}_3^{\prime }$,

$$k=k(x,y,z):=\left\{\begin{array}{cc}{10}^{-6}\hfill & for(x,y,z)\in {\mathrm{\Omega }}_1^{\prime }:=(-30,10)\times I_{20}^2\hfill \\ 1\hfill & for(x,y,z)\in {\mathrm{\Omega }}_2^{\prime }:=(20,10)\times I_{20}^2,\hfill \end{array}\right.$$

and k is smoothly interpolated in ${\mathrm{\Omega }}_3^{\prime }:=(10,20)\times (2,4)\times I_{20}$, see Figure 6, Figure 7 and Figure 8.

In many applications to meteorology, this case may model a region that can contain, at most, a certain given amount of fluid, due to certain environmental conditions. The geometry is a silt barrier through which the fluid will eventually penetrate. We first consider the case $\alpha =\beta =\gamma =2$. In Figure 5 the solution pertaining to this case is shown, in a plan view, at time $T=90$. Here, the pressure can be seen to penetrate the barrier very slowly due to classical diffusion along x.

We then changed parameters, choosing $\alpha =1.7,\beta =\gamma =2$, in order to represent a certain anomalous diffusion. In Figure 8, it is shown that, at time $T=50$, even before the “snapshot time” $T=90$ (which refers to Figure 7), the pressure has significantly penetrated the barrier, and it spreads at the same time in the y direction.

This is a striking peculiarity of fractional reaction-diffusion model, which allows for predicting the effects of controlling the fluid flow, for instance, describing pollution due to a pollutant expanding from a given environment to another.

5. Conclusions and Future Directions

In this paper, we introduced a new, well "balanced", fractional version of the ADI method, for numerically solving a number of 3D diffusion as well as reaction-diffusion problems for fPDEs, which are important in a variety of problems in porous media modelling. We proved that such a method is unconditionally stable for every fractional order of space derivatives, second-order accurate in space, and third-order accurate in time. The speed of convergence has been improved while adopting an extrapolation technique, coupled with the optimization method that is used by the PageRank algorithm.

Future directions of research should consider: (a) using Riesz fractional space operators, in order to symmetrize the RL operators; (b) better investigating the anisotropic behavior of solutions in modeling physical phenomena, possibly designing numerical schemes that might properly take anisotropy into account (adopting differente space step-sizes in different directions, so to make the numerical solution more efficient); (c) take the issue of imposing boundary conditions (BCs) into account, while facing nonlocal operators, when the problem is posed on bounded domains. (Here, we implicitly assumed Dirichlet BCs identically zero solutions outside the domain).