Fractional SIS Epidemic Models
Abstract
1. Introduction
1.1. Statement of the Problem
1.2. Motivations
1.3. State of the Art
1.4. Main Results
1.5. Outline
2. The Settings
2.1. The Fractional Derivatives
- (P1)
- Let u be a constant function. Then .
- (P2)
- Let such that and , exist almost everywhere. Then, .
- (P3)
- Let be such that and exist almost everywhere in . Let . Then, exists almost everywhere in . In particular,
- (P4)
- Let . Then,pointwise in .
2.2. The Fractional SIS Model
3. Proof of the Main Results
4. Numerical Comparison
4.1. Numerical Approximation
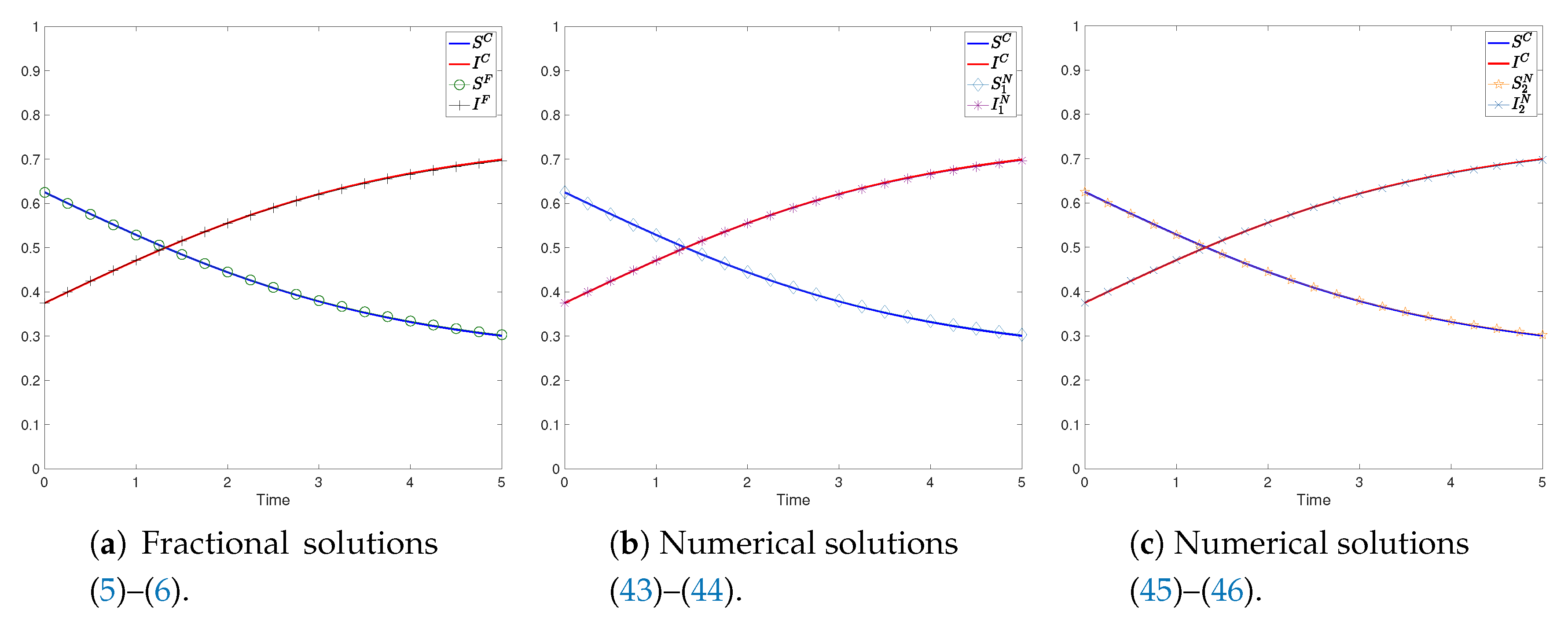
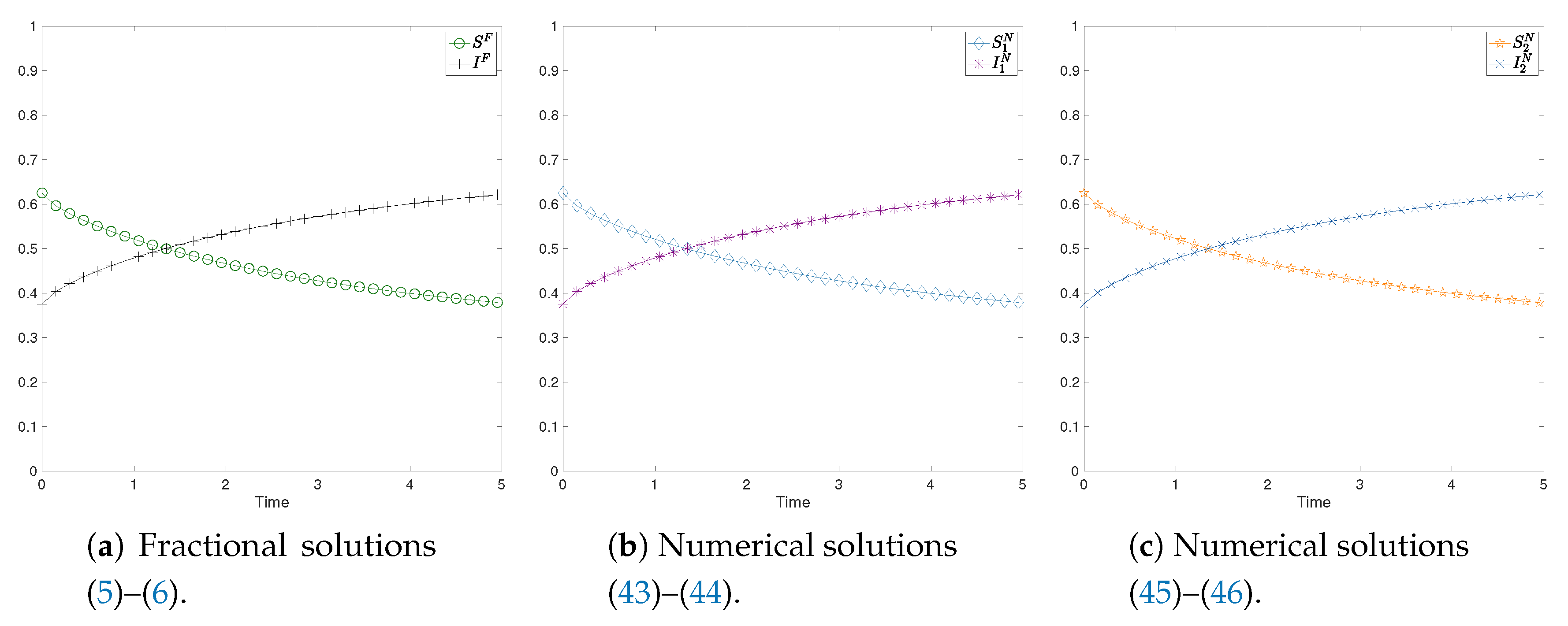
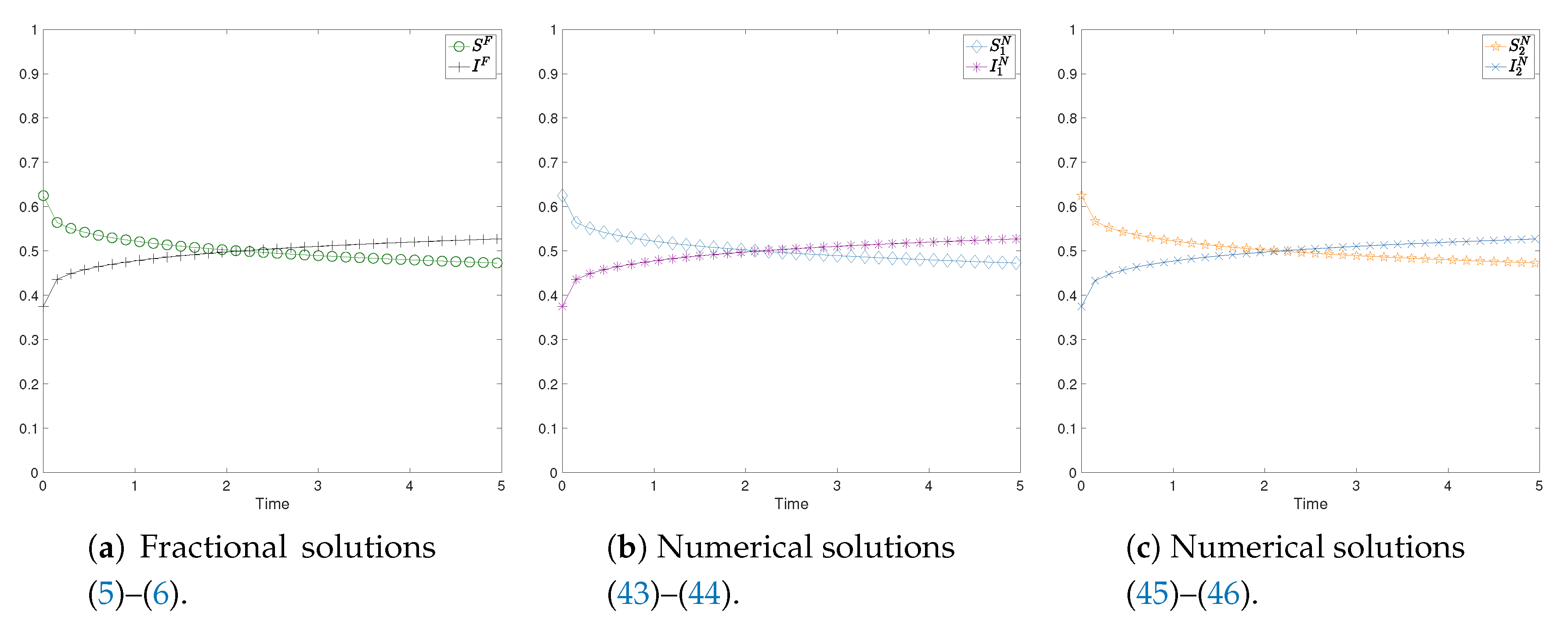
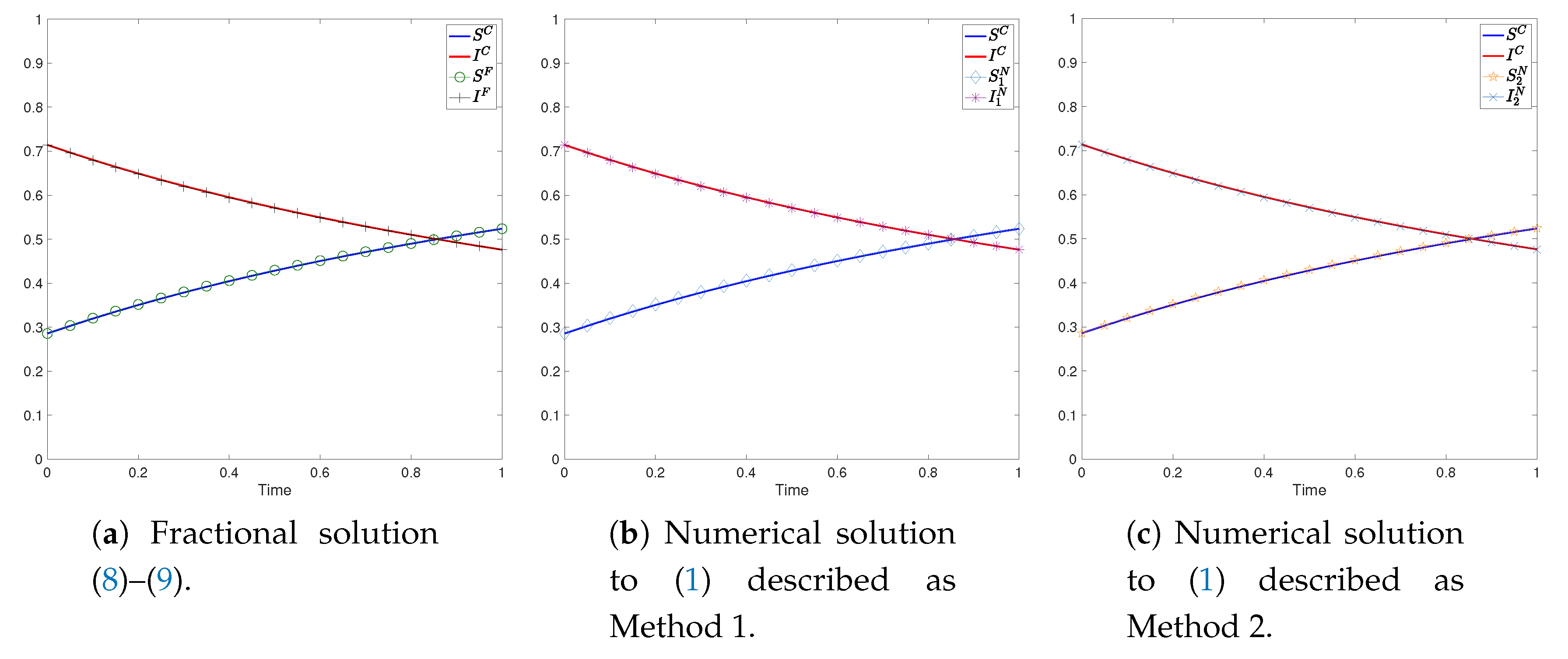
4.2. Numerical Tests
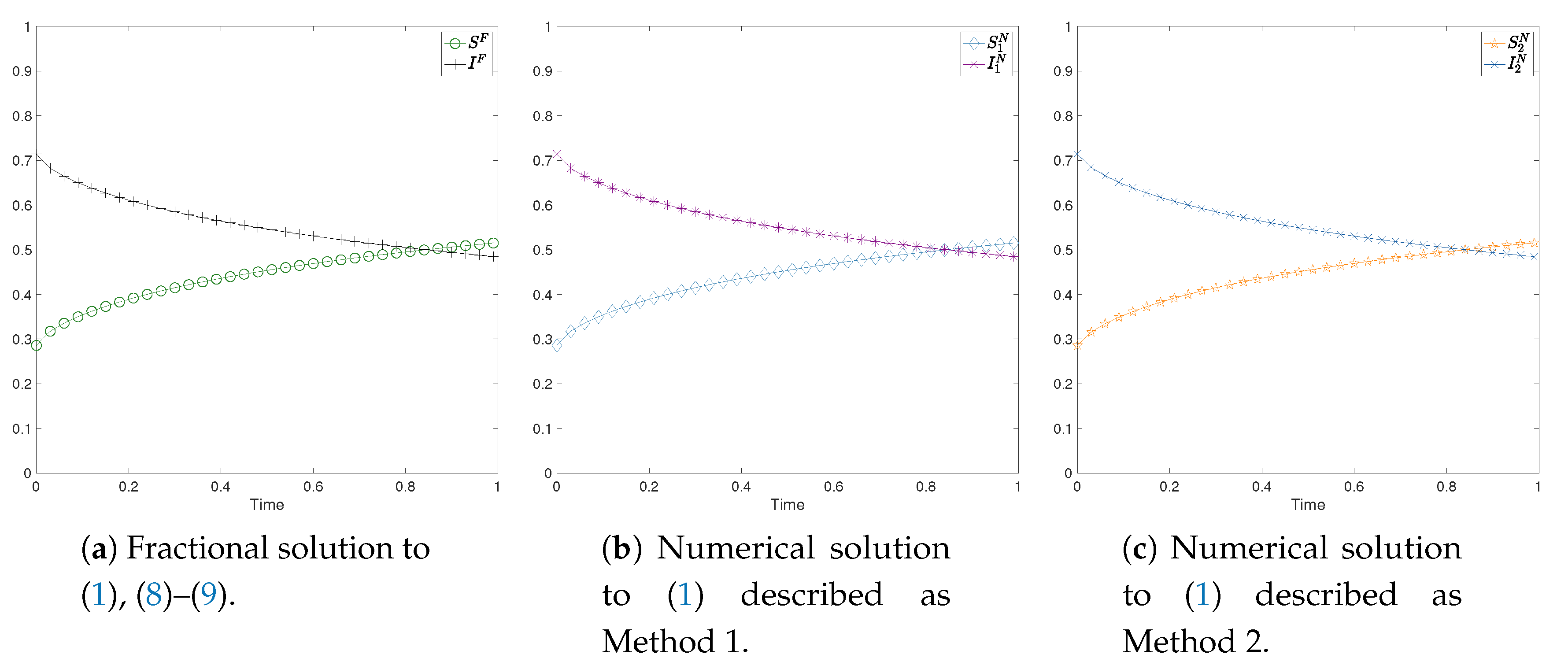
- the solutions to the SIS model, our aim is to show the correspondence with the case ,
4.2.1. Test with
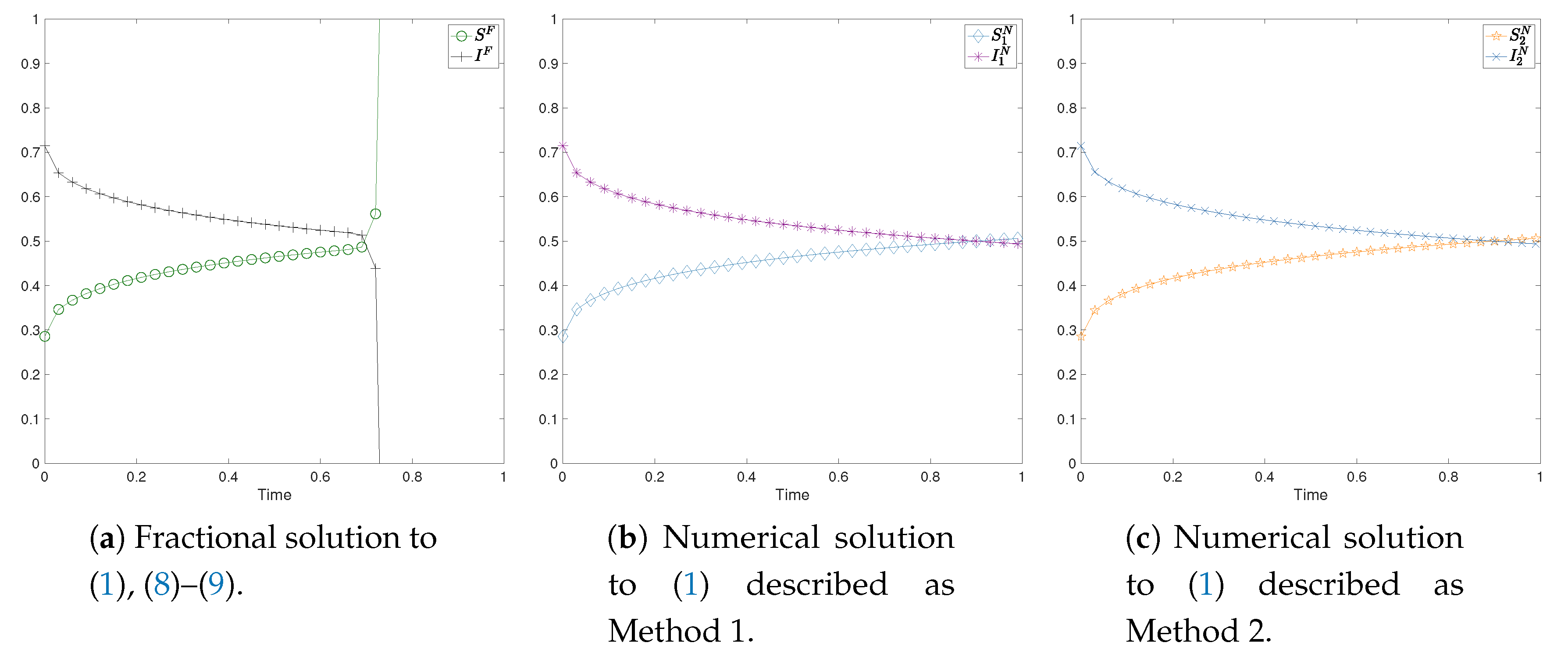
4.2.2. Test with
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. A Math. Phys. 1927, 115, 700–721. [Google Scholar]
- Hethcote, H.W. Three basic epidemiological models. In Applied Mathematical Ecology (Trieste, 1986); Springer: Berlin, Germany, 1989; Volume 18, pp. 119–144. [Google Scholar]
- Verhulst, P.F. Notice sur la loi que la population suit dans son accroissement. Corresp. Math. Phys. 1838, 10, 113–126. [Google Scholar]
- El-Sayed, A.; El-Mesiry, A.; El-Saka, H. On the fractional-order logistic equation. Appl. Math. Lett. 2007, 20, 817–823. [Google Scholar] [CrossRef]
- Area, I.; Losada, J.; Nieto, J.J. A note on the fractional logistic equation. Physica A 2016, 444, 182–187. [Google Scholar] [CrossRef]
- West, B. Exact solution to fractional logistic equation. Physica A 2015, 429, 103–108. [Google Scholar] [CrossRef]
- Yang, X.J.; Tenreiro Machado, J. A new insight into complexity from the local fractional calculus view point: Modelling growths of populations. Math. Mod. Meth. Appl. Sci. 2017, 40, 6070–6075. [Google Scholar] [CrossRef]
- Hassouna, M.; Ouhadan, A.; El Kinania, E. On the solution of fractional order SIS epidemic model. Chaos Solitons Fractals 2018, 117, 168–174. [Google Scholar] [CrossRef] [PubMed]
- El-Saka, H. The fractional-order SIS epidemic model with variable population size. J. Egypt. Math. Soc. 2014, 22, 50–54. [Google Scholar] [CrossRef]
- D’Ovidio, M.; Loreti, P. Solutions of fractional logistic equations by Euler’s numbers. Physica A 2018, 506, 1081–1092. [Google Scholar] [CrossRef]
- Angstmann, C.N.; Henry, B.I.; McGann, A.V. A Fractional-Order Infectivity and Recovery SIR Model. Fractal Fract. 2017, 1, 1–11. [Google Scholar]
- Pooseh, S.; Rodrigues, H.S.; Torres, D.F. Fractional derivatives in dengue epidemics. AIP Conf. Proc. 2011, 1389, 739–742. [Google Scholar] [CrossRef]
- Rositch, A.F.; Koshiol, J.; Hudgens, M.G.; Razzaghi, H.; Backes, D.M.; Pimenta, J.M.; Franco, E.L.; Poole, C.; Smith, J.S. Patterns of persistent genital human papillomavirus infection among women worldwide: A literature review and meta-analysis. Int. J. Cancer 2013, 133, 1271–1285. [Google Scholar] [CrossRef] [PubMed]
- Anderson, R.M.; May, R.M. The population dynamics of microparasites and their invertebrate hosts. Philos. Trans. R. Soc. B 1981, 291, 451–524. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Ferrari, F. Weyl and Marchaud Derivatives: A Forgotten History. Mathematics 2018, 6, 6. [Google Scholar] [CrossRef]
- Zhou, J.; Hethcote, H.W. Population size dependent incidence in models for diseases without immunity. J. Math. Biol. 1994, 32, 809–834. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.W.; Nie, L.F. Dynamics of SIS epidemic model with varying total population and multivaccination control strategies. Stud. Appl. Math. 2017, 139, 533–550. [Google Scholar] [CrossRef]
- Ahmed, E.; El-Sayed, A.M.A.; El-Mesiry, A.E.M.; El-Saka, H.A.A. Numerical solution for the fractional replicator equation. Int. J. Mod. Phys. C 2005, 16, 1017–1026. [Google Scholar] [CrossRef]
- Diethelm, K.; Freed, A.D. The FracPECE Subroutine for the Numerical Solution of Differential Equations of Fractional Order. Forsch. Wiss. Rechn. 1998, 1999, 57–71. [Google Scholar]
- Quarteroni, A.; Sacco, R.; Saleri, F. Numerical Mathematics, 2nd ed.; Springer: Berlin, Germany, 2007; Volume 37, p. xviii+655. [Google Scholar]
- Giga, Y.; Liu, Q.; Mitake, H. On a discrete scheme for time fractional fully nonlinear evolution equations. Asymptot. Anal. 2019, 1–12. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Mathematics in Science and Engineering; Academic Press: Cambridge, MA, USA, 1999; Volume 198. [Google Scholar]
- Diethelm, K.; Ford, N.; Freed, A. A Predictor-Corrector Approach for the Numerical Solution of Fractional Differential Equations. Nonlinear Dyn. 1999, 29, 3–22. [Google Scholar] [CrossRef]
- Ford, N.J.; Simpson, A. The numerical solution of fractional differential equations: Speed versus accuracy. Numer. Algorithms 2001, 26, 333–346. [Google Scholar] [CrossRef]
| () | |||
|---|---|---|---|
| 0.99 | 1 × 10 | 9 × 10 | 9 × 10 |
| 0.7 | 1 × 10 | 2 × 10 | 2 × 10 |
| 0.3 | 3 × 10 | 8 × 10 | 8 × 10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balzotti, C.; D’Ovidio, M.; Loreti, P. Fractional SIS Epidemic Models. Fractal Fract. 2020, 4, 44. https://doi.org/10.3390/fractalfract4030044
Balzotti C, D’Ovidio M, Loreti P. Fractional SIS Epidemic Models. Fractal and Fractional. 2020; 4(3):44. https://doi.org/10.3390/fractalfract4030044
Chicago/Turabian StyleBalzotti, Caterina, Mirko D’Ovidio, and Paola Loreti. 2020. "Fractional SIS Epidemic Models" Fractal and Fractional 4, no. 3: 44. https://doi.org/10.3390/fractalfract4030044
APA StyleBalzotti, C., D’Ovidio, M., & Loreti, P. (2020). Fractional SIS Epidemic Models. Fractal and Fractional, 4(3), 44. https://doi.org/10.3390/fractalfract4030044






