Analysis of Fractional Order Chaotic Financial Model with Minimum Interest Rate Impact
Abstract
1. Introduction
2. Preliminaries
3. Liouville–Caputo Sense
4. Atangana–Baleanu–Caputo Sense
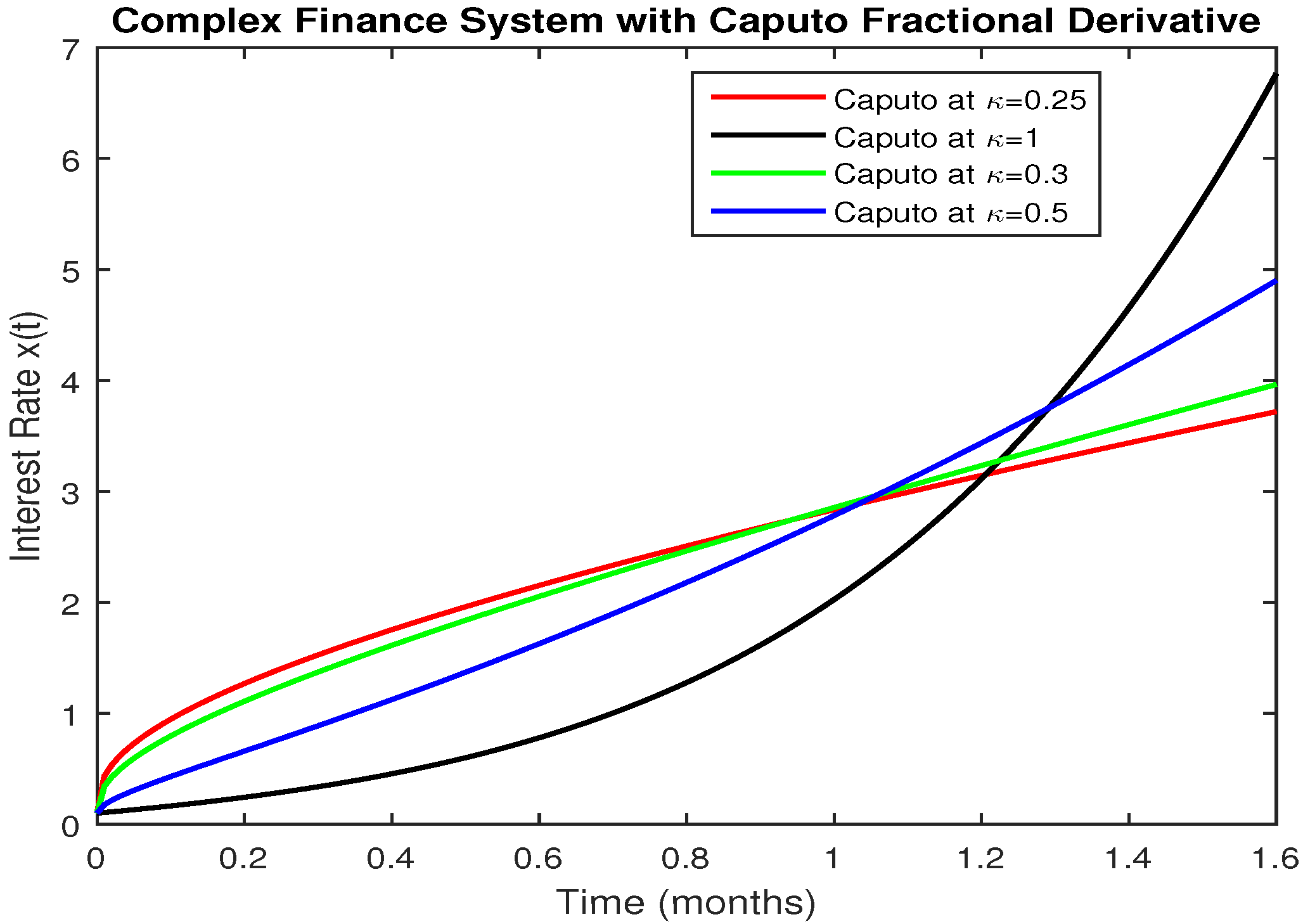
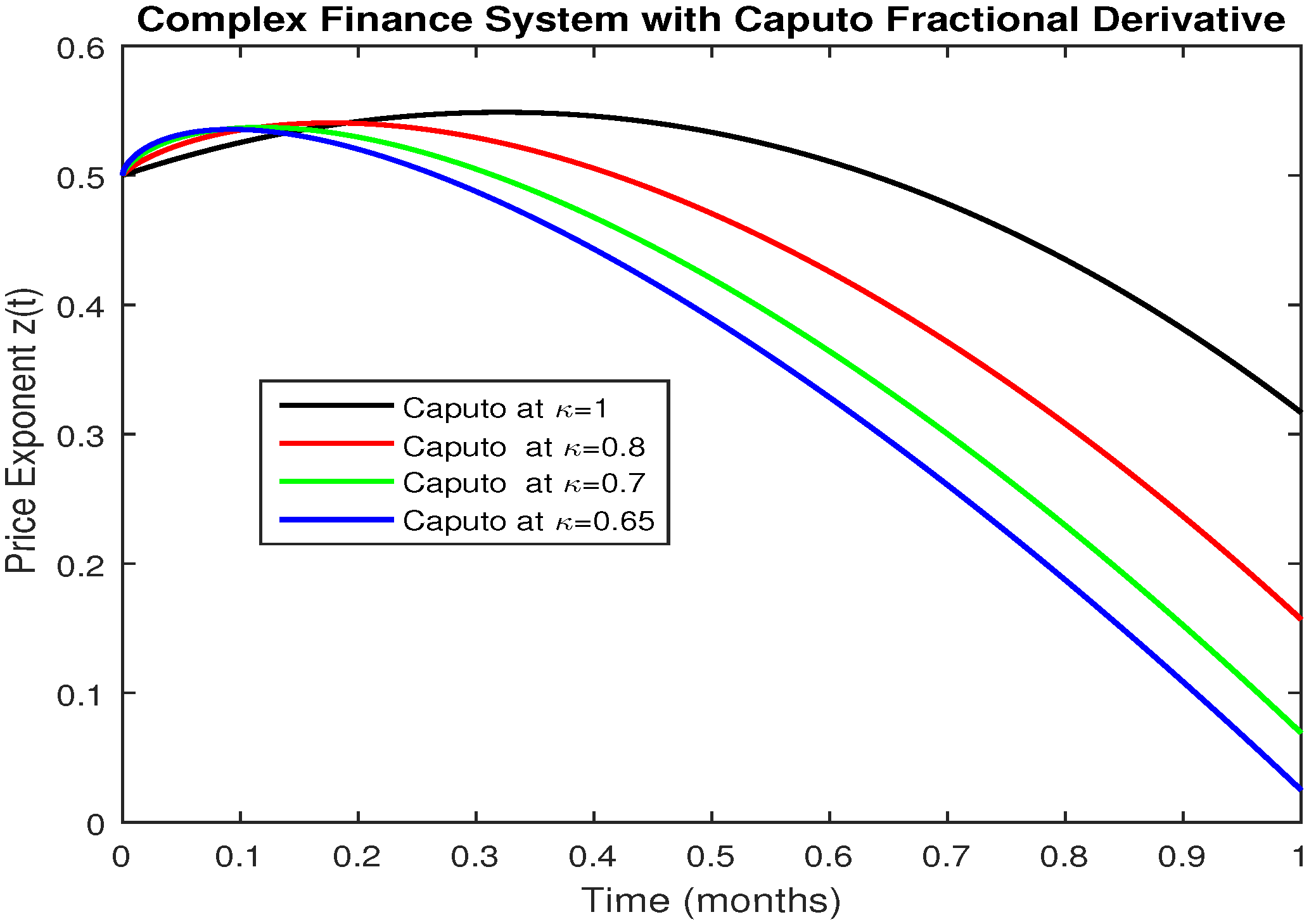
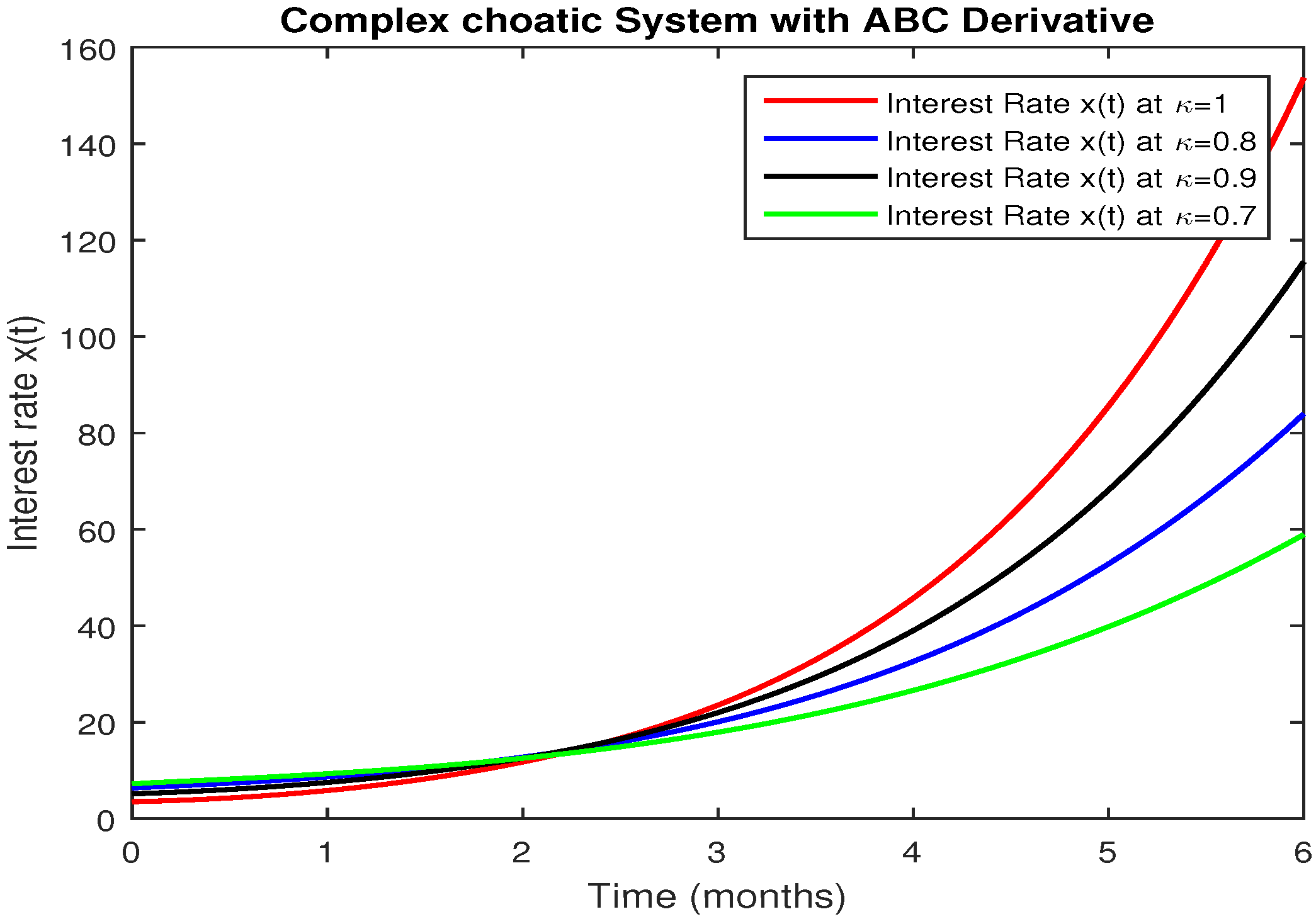
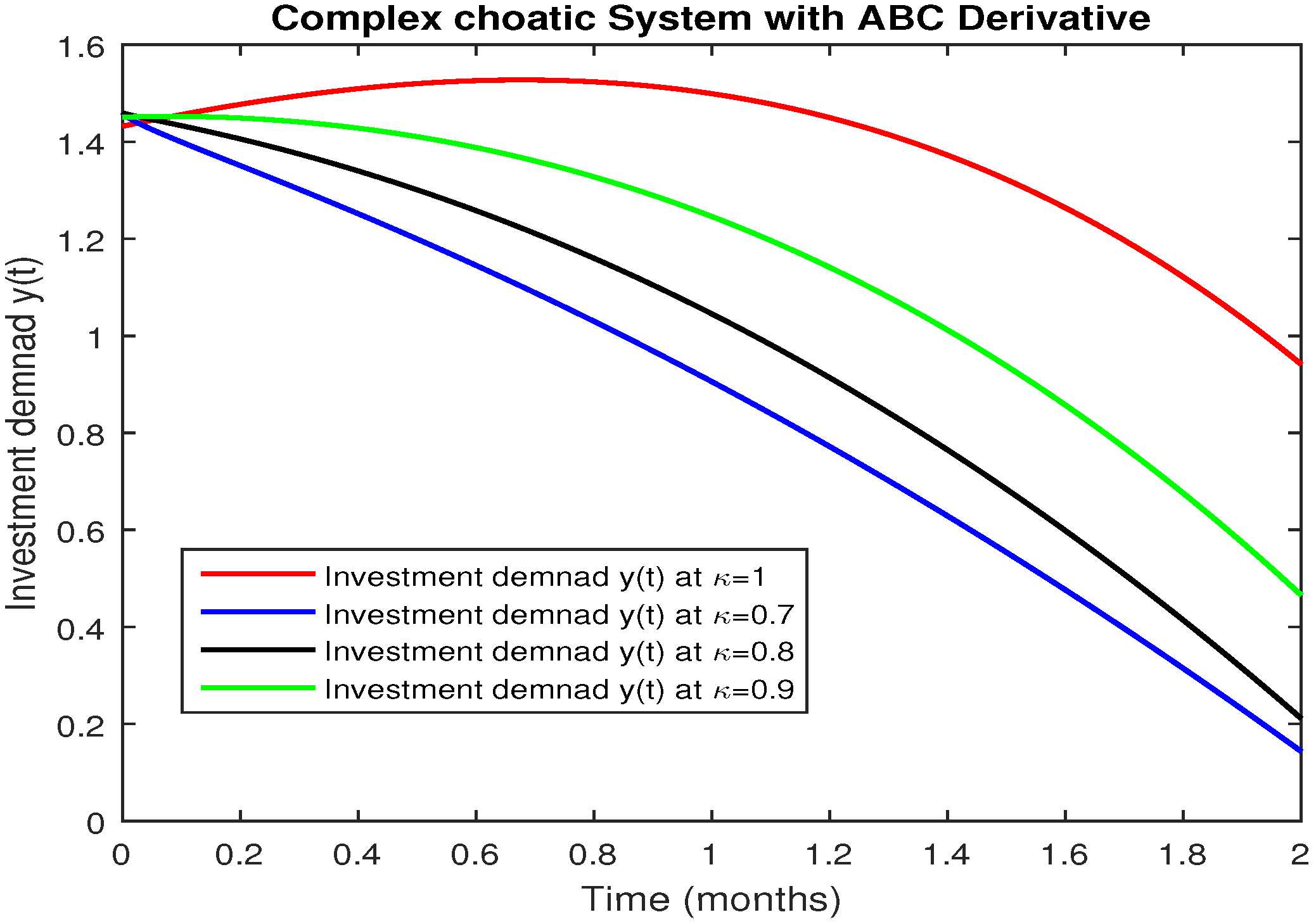
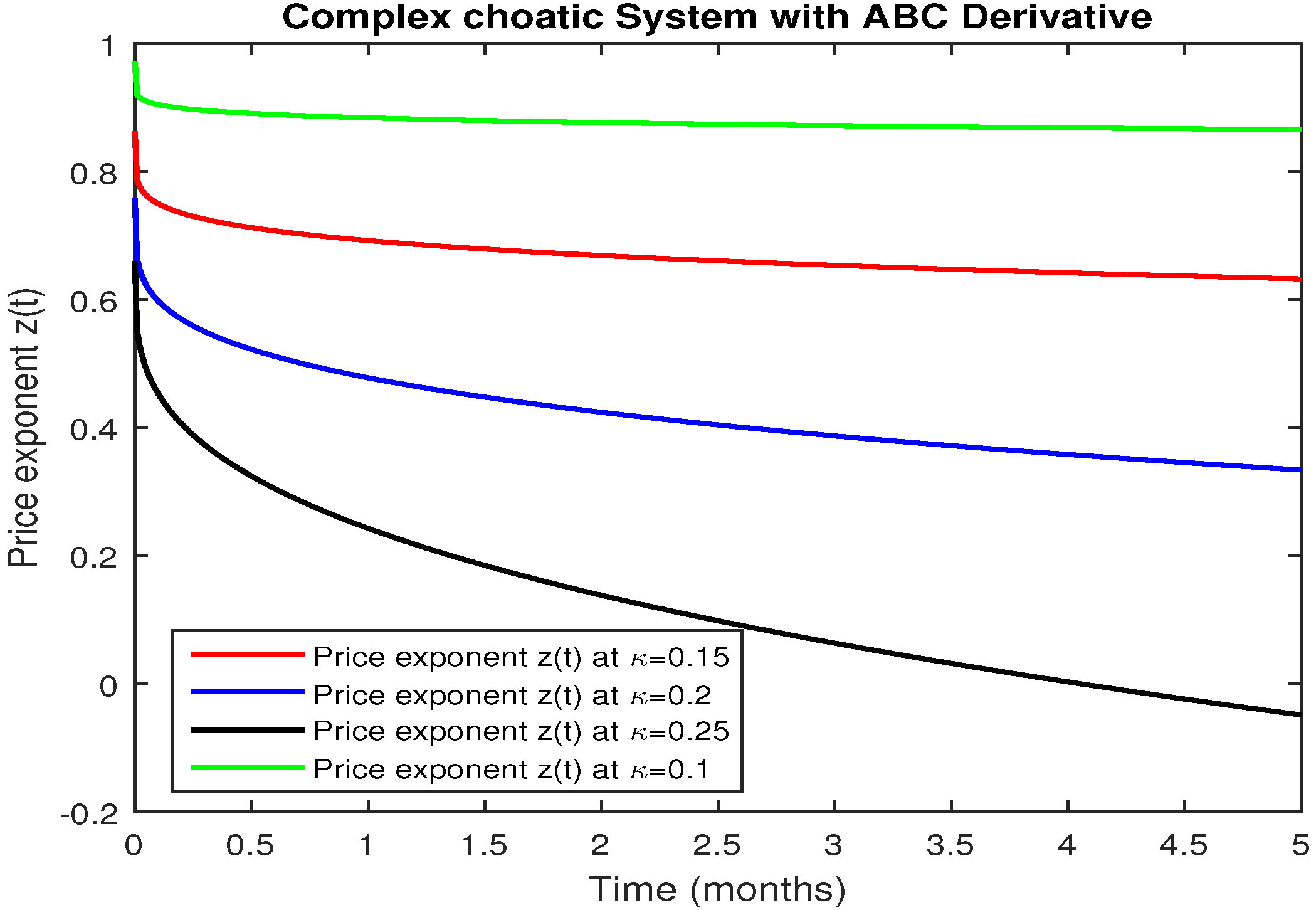
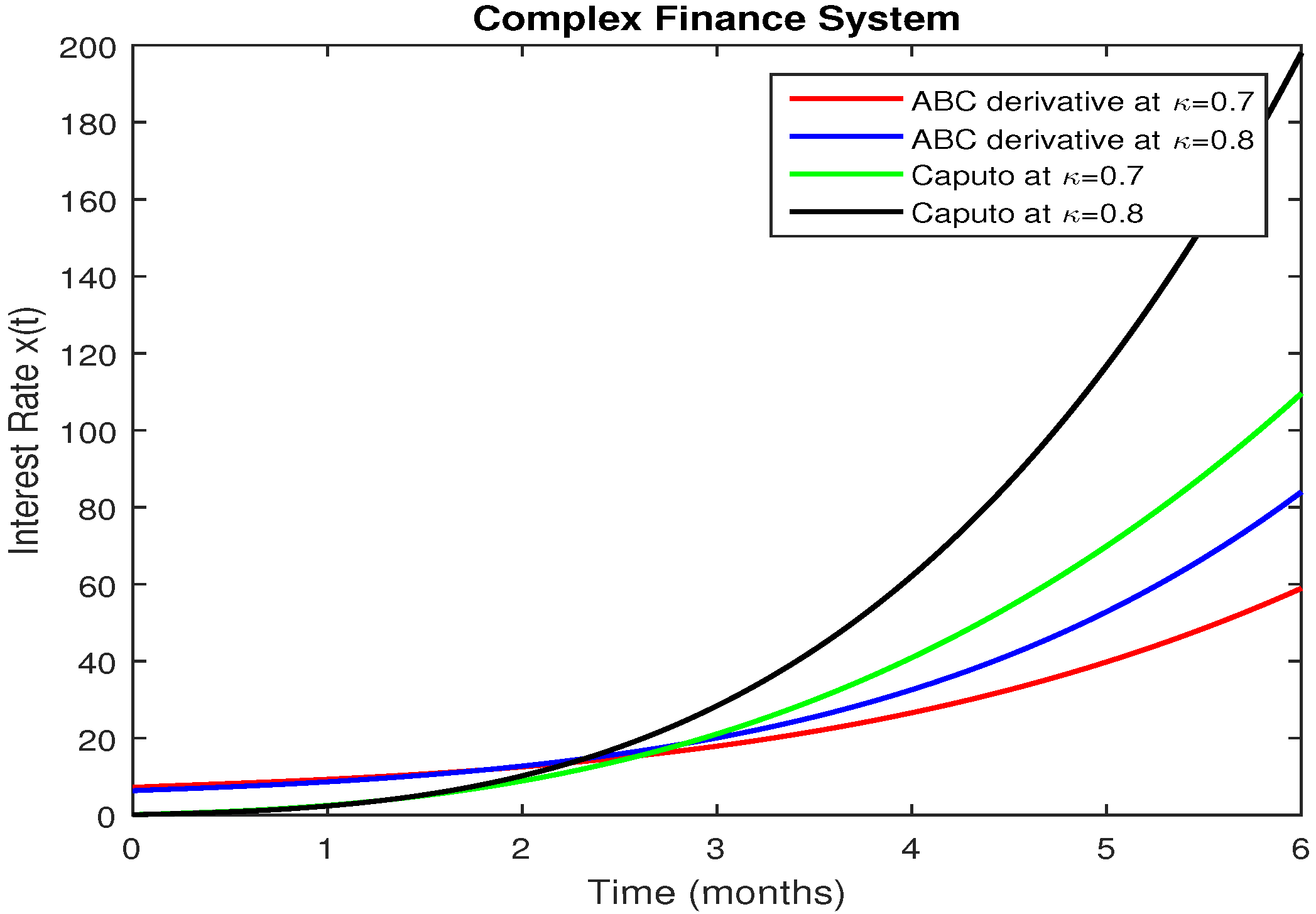
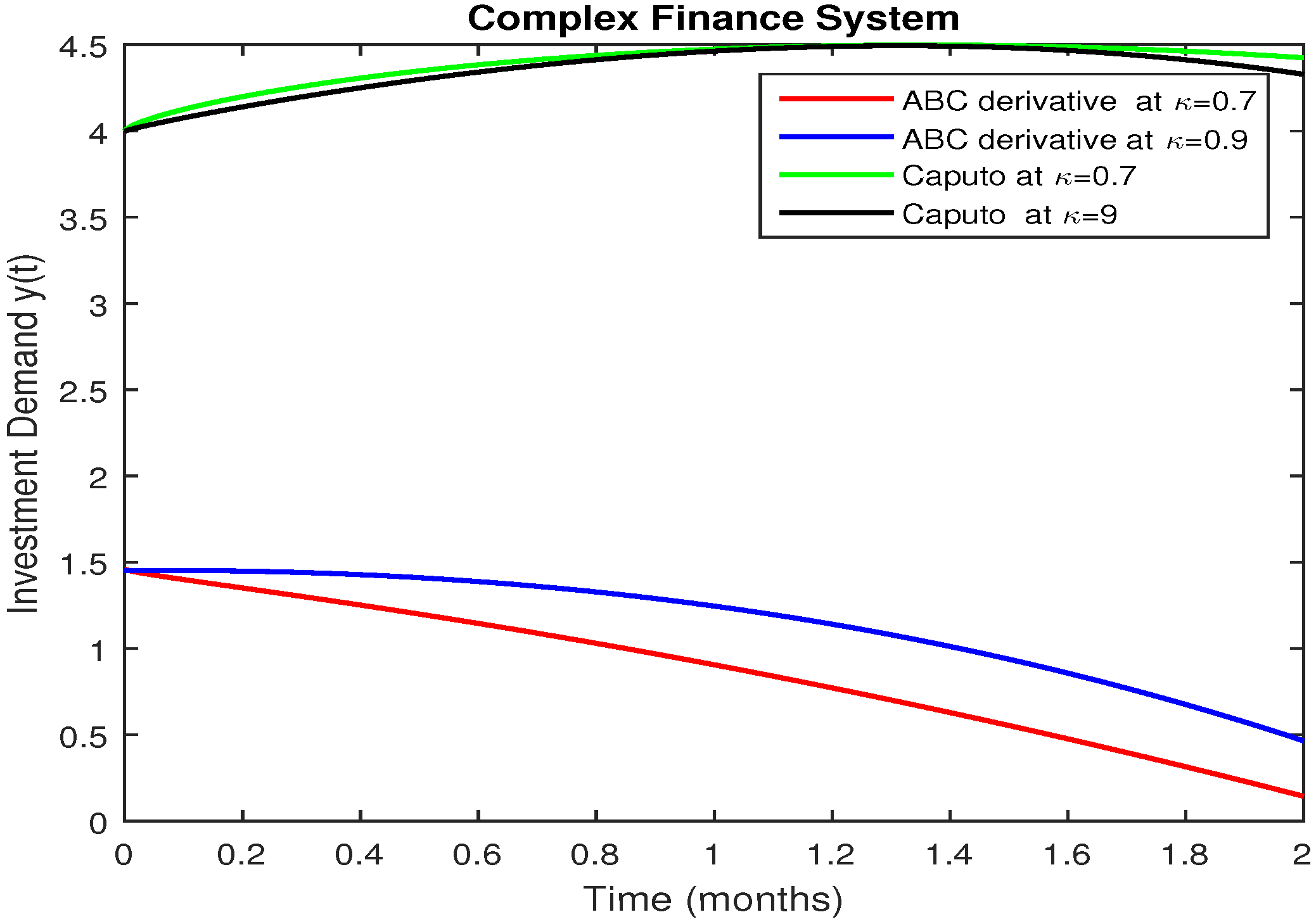
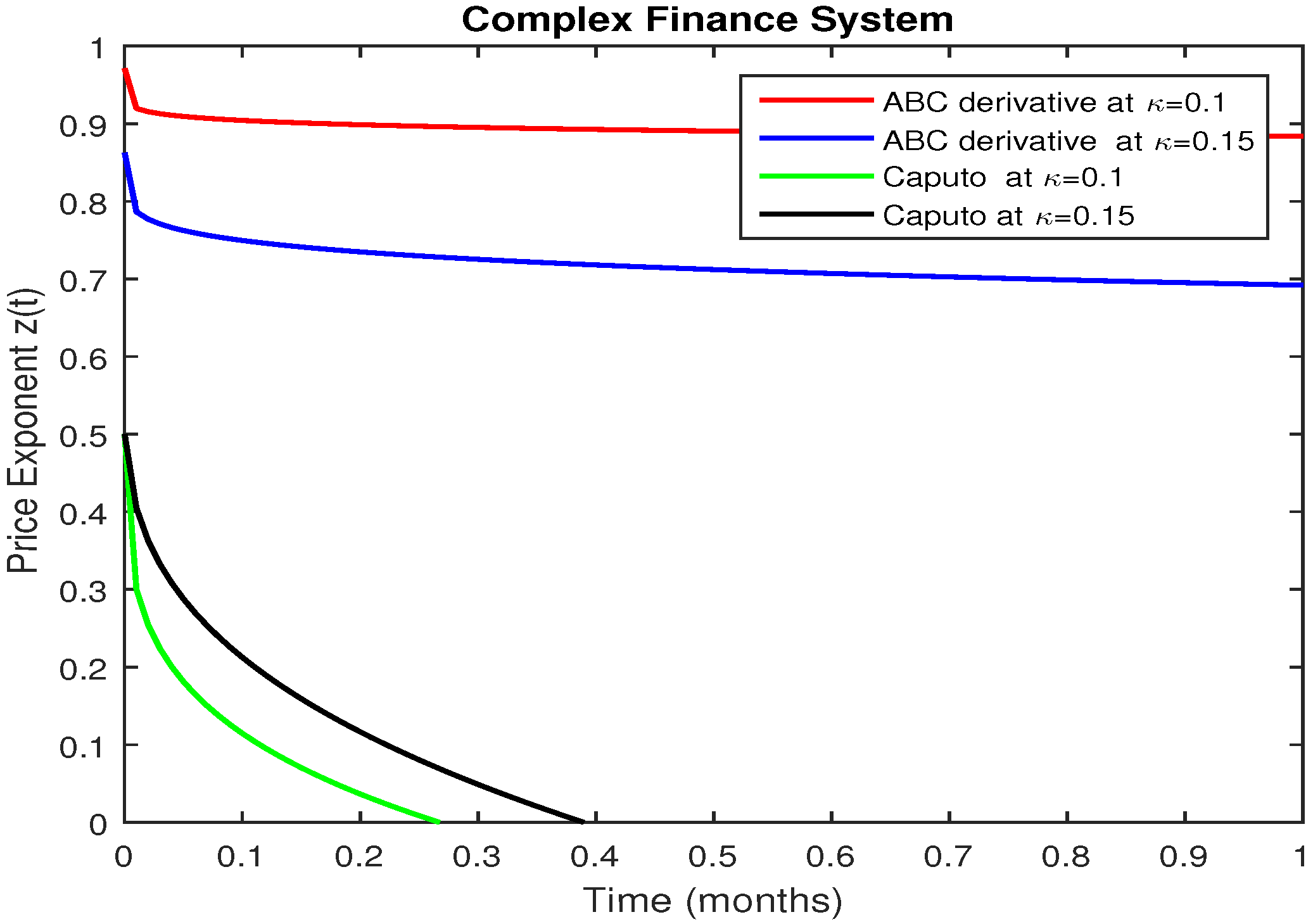
5. Numerical Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Neumaier, A. Mathematical Modelling. Available online: http://www.mat.univie.ac.at/~neum/ms/model.pdf (accessed on 18 January 2011).
- Merton, R.C.; Simons, R.V.; Wilkie, A.D. Influence of mathematical models in finance on practice: Past, present and future. Philos. Trans. Phys. Sci. Eng. 1994, 347, 451–463. [Google Scholar]
- Karatzas, I. Lectures on the Mathematics of Finance 8; American Mathematical Society: Providence, RI, USA, 1997. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000; pp. 87–130. [Google Scholar]
- Kumar, D.; Singh, J.; Baleanu, D. Modified Kawahara equation within a fractional derivative with non-singular kernel. Therm. Sci. 2017, 22, 789–796. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D.; Sushila. Analysis of regularized long-wave equation associated with a new fractional operator with Mittag–Leffler type kernel. Physica A 2018, 492, 155–167. [Google Scholar] [CrossRef]
- Baleanu, D.; Jajarmi, A.; Hajipour, M. A new formulation of the fractional optimal control problems involving Mittag–Leffler nonsingular kernel. J. Optim. Theory Appl. 2017, 175, 718–737. [Google Scholar] [CrossRef]
- Baleanu, D.; Jajarmi, A.; Asad, J.H.; Blaszczyk, T. The motion of a bead sliding on a wire in fractional sense. Acta Phys. Pol. A 2017, 131, 1561–1564. [Google Scholar] [CrossRef]
- Jajarmi, A.; Hajipour, M.; Baleanu, D. New aspects of the adaptive synchronization and hyperchaos suppression of a financial model. Chaos Solitons Fractals 2017, 99, 285–296. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Baleanu, D.; Guvenc, Z.B.; Machado, J.A.T. New Trends in Nanotechnology and Fractional Calculus Applications; Springer: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Yang, X.J.; Srivastava, H.M.; Machado, J.A.T. A new fractional derivative without singular kernel: Application to the modelling of the steady heat flow. Therm. Sci. 2016, 20, 753–756. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Atangana, A. On the new fractional derivative and application to nonlinear Fisher’s reaction diffusion equation. Appl. Math. Comput. 2016, 273, 948–956. [Google Scholar] [CrossRef]
- Panda, S.K.; Karapınar, E.; Atangana, A. A numerical schemes and comparisons for fixed point results with applications to the solutions of Volterra integral equations in dislocated extended b a metric space. Alex. Eng. J. 2020, 59, 815–827. [Google Scholar] [CrossRef]
- Yavuz, M.; Özdemir, N. European vanilla option pricing model of fractional order without singular kernel. Fractal Fract. 2018, 2, 3. [Google Scholar] [CrossRef]
- Keten, A.; Yavuz, M.; Baleanu, D. Nonlocal Cauchy problem via a fractional operator involving power kernel in Banach Spaces. Fractal Fract. 2019, 3, 27. [Google Scholar] [CrossRef]
- Yavuz, M.; Abdeljawad, T. Nonlinear regularized long-wave models with a new integral transformation applied to the fractional derivative with power and Mittag–Leffler kernel. Adv. Differ. Equ. 2020, 2020, 367. [Google Scholar] [CrossRef]
- Yavuz, M.; Ozdemir, N.; Baskonus, H.M. Solutions of partial differential equations using the fractional operator involving Mittag–Leffler kernel. Eur. Phys. J. Plus 2018, 133, 215. [Google Scholar] [CrossRef]
- Gao, W.; Baskonus, H.M.; Shi, L. New investigation of Bats-Hosts Reservoir-People coronavirus model and apply to 2019-nCoV system. Adv. Differ. Equ. 2020, 2020, 1–11. [Google Scholar]
- Gao, W.; Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. Novel dynamical structures of 2019-nCoV with nonlocal operator via powerful computational technique. Biology 2020, 9, 107. [Google Scholar] [CrossRef]
- Gao, W.; Veeresha, P.; Baskonus, H.M.; Prakasha, D.G.; Kumar, P. A new study of unreported cases of 2019-nCOV epidemic outbreaks. Chaos Solitons Fractals 2020, 138, 109929. [Google Scholar] [CrossRef]
- MoralesDelgadoa, V.F.; Aguilarb, J.F.; Taneco, M.A.; Escobar, R.F. Mathematical modeling of the smoking dynamics using fractional differential equations with local and nonlocal kernel. J. Nonlinear Sci. Appl. 2018, 11, 994–1014. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non Singular Kernel: Theory and Application to Heat Transfer Model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, A.; Argyros, I.K. A new analysis for the Keller-Segel model of fractional order. Numer. Algorithms 2017, 75, 213–228. [Google Scholar] [CrossRef]
- Kumar, S.; Rashidi, M.M. New analytical method for gas dynamic equation arising in shock fronts. Comput. Phys. Commun. 2014, 185, 1947–1954. [Google Scholar] [CrossRef]
- Odibat, Z.; Bataineh, A.S. An adaptation of homotopy analysis method for reliable treatment of strongly nonlinear problems: Construction of homotopy polynomials. Math. Methods Appl. Sci. 2015, 38, 991–1000. [Google Scholar] [CrossRef]
- Ma, J.H.; Chen, Y.S. Study for the bifurcation topological structure and the global complicated character of a kind of nonlinear finance system, I. Appl. Math. Mech. 2011, 22, 1240–1251. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Al Qurashi, M.; Baleanu, D. A new fractional model for giving up smoking dynamics. Adv. Differ. Equ. 2017, 2017, 88. [Google Scholar] [CrossRef]
- Li, C.P.; Tao, C.X. On the fractional Adams method. Comput. Math. Appl. 2009, 58, 1573–1588. [Google Scholar] [CrossRef]
- Alkahtani, B.S.T. Chua’s circuit model with Atangana Baleanu derivative with fractional order. Chaos Solitons Fractals 2016, 89, 547–551. [Google Scholar] [CrossRef]
- Zhen, W.; Huang, X.; Shi, G. Analysis of nonlinear dynamics and chaos in a fractional-order financial system with time delay. Comput. Math. Appl. 2011, 62, 1531–1539. [Google Scholar]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farman, M.; Akgül, A.; Baleanu, D.; Imtiaz, S.; Ahmad, A. Analysis of Fractional Order Chaotic Financial Model with Minimum Interest Rate Impact. Fractal Fract. 2020, 4, 43. https://doi.org/10.3390/fractalfract4030043
Farman M, Akgül A, Baleanu D, Imtiaz S, Ahmad A. Analysis of Fractional Order Chaotic Financial Model with Minimum Interest Rate Impact. Fractal and Fractional. 2020; 4(3):43. https://doi.org/10.3390/fractalfract4030043
Chicago/Turabian StyleFarman, Muhammad, Ali Akgül, Dumitru Baleanu, Sumaiyah Imtiaz, and Aqeel Ahmad. 2020. "Analysis of Fractional Order Chaotic Financial Model with Minimum Interest Rate Impact" Fractal and Fractional 4, no. 3: 43. https://doi.org/10.3390/fractalfract4030043
APA StyleFarman, M., Akgül, A., Baleanu, D., Imtiaz, S., & Ahmad, A. (2020). Analysis of Fractional Order Chaotic Financial Model with Minimum Interest Rate Impact. Fractal and Fractional, 4(3), 43. https://doi.org/10.3390/fractalfract4030043






