1. Introduction
In this article, produced from a part of PhD thesis number 519846 from the Council of Higher Education, an iterative approach of reproducing kernel method (RKM) is considered for obtaining an approximate solution of the Burgers’ equation with fractional order as follows:
Here,
is fractional differential operator in Caputo sense with respect to time variable
and also
,
,
,
,
are continuous functions. For this model problem, initial-Neumann boundary conditions:
and initial-Dirichlet boundary conditions:
will be taken as above.
The Burgers’ equation is a simplified version of the Navier–Stokes equation. It was obtained by use of removing the pressure term from the Navier–Stokes equation by Burgers [
1] in 1939. In other words, the Burgers’ equation can be expressed as a result of combining nonlinear wave motion with linear diffusion. Lately, many scientists have focused on Burgers’ equation by using several methods and different approaches. For instance, existence and uniqueness of local and global solution for Burgers’ equation was presented in [
2] by Guesmia and Daili. Lombard and Matignon used a diffusive approximation for fractional-order Burgers’ equation in [
3]. The averaging principle was proposed by Dong et al. for stochastic Burgers’ equation in [
4]. Nojavan et al. obtained a numerical solution of Burgers’ equation by using discretization in reproducing kernel Hilbert space [
5]. The Chebyshev wavelet method was developed by Oruc et al. for the numerical solution of time-fractional Burgers’ equation [
6]. Pei et al. presented the local discontinuous Galerkin method for modified Burgers’ equation in [
7]. The Petrov–Galerkin method was used by Roshan and Bhamra for modified Burgers’ equation in [
8]. The collocation method was presented by Ramadan and Danaf for modified Burgers’ equation in [
9]. Bahadir and Saglam constructed a mixed method for one dimensional Burgers’ equation [
10]. Dag et al. used the cubic B-splines method [
11]. Caldwell et al. proposed a finite element approximation for Burgers’ equation [
12]. A finite difference method was used by Kutluay et al. for one-dimensional Burgers’ equation [
13]. An approximate solution obtained by using the reproducing kernel method for Burgers’ equation [
14]. A hybrid technique for the unsteady flow of a Burgers’ fluid is given by Raza et al. [
15]. Laplace and finite Hankel transformations were proposed by Safdar et al. for generalized Burgers’ fluid with fractional derivative [
16]. Time-fractional coupled Burgers’ equations were solved with generalized differential transform method by Liu and Hou [
17]. Zhang et al proposed an analytical and numerical approach for multi-term time-fractional Burgers’ fluid model [
18]. The Adomian decomposition method was applied to space-and time-fractional Burgers’ equation by Momani [
19]. A generalized Taylor series technique was proposed by Ajou et al. for fractional nonlinear KdV-Burgers’ equation [
20]. Mittal and Arora presented a numerical approach by using cubic B-spline functions for coupled viscous Burgers’ equation [
21]. Jiwari used a hybrid numerical scheme for Burgers’ equation [
22]. Kutluay et al. proposed a B-spline finite element method for Burgers’ equation [
23].
Reproducing kernel concept is introduced by Zaremba [
24]. In his study, Zaremba focused on the boundary value problem, which includes the Dirichlet boundary condition. Furthermore, the theoretical concept of reproducing kernel is developed in [
25,
26]. Reproducing kernel spaces of polynomial and trigonometric functions are constructed in [
27]. Many studies have been conducted by using reproducing kernel method. For instance, eighth order boundary value problems [
28], fractional advection-dispersion equation [
29], fractional order systems of Dirichlet function types [
30], fractional order Bagley–Torvik equation [
31], time fractional telegraph equation [
32], a local reproducing kernel method for Burgers’ equation [
33], time-fractional partial integro differential equations [
34], Riccati differential equations [
35], nonlinear hyperbolic telegraph equation [
36], time-fractional Tricomi and Keldysh equations [
37], one-dimensional sine–Gordon equation [
38], reaction-diffusion equations [
39], integro differential equations of Fredholm operator type [
40], fredholm integro-differential equations [
41], nonlinear system of PDEs [
42], class of fractional partial differential equation [
43], Bagley–Torvik and Painlevé equations [
44], nonlinear coupled Burgers equations [
45] and so on [
46,
47,
48,
49,
50,
51,
52,
53,
54,
55,
56,
57,
58,
59].
This research is organized as: Specific definitions and Hilbert spaces are demonstrated in
Section 2. Reproducing kernel solution is identified by RKM in
Section 3. Convergence analysis of the approximate solution is proved in
Section 4. Error estimation of the method is presented in
Section 5. Two examples of fractional order Burgers’ equation are examined by the RKM and the algorithm of the process is given in
Section 6. Finally, a short conclusion is given in
Section 7.
The notation table
Table 1 is given as follow:
3. Obtaining of Reproducing Kernel Solution for Equations (1) and (2a,b) in
In the reproducing kernel method, an approximate solution will be obtained with the help of kernel function and linear operator
L. The choosing of
L is arbitrary. One can choose the whole linear part of the model problem or any linear part of it. Here, the whole linear part of the model problem is chosen as follow:
The new statement of Equations (1)-(2a-2b) can be expressed as:
and
.
Let
be a countable dense subset in
. Now,
basis function will be defined by applying the kernel function to the operator
L.
Now, it will be shown that basis function belong to space and satisfies the initial-boundary condition of space. For this purpose, the following theorem will be given.
Theorem 2. The basis function is belong to reproducing space for .
Proof. To prove the theorem, we must show that the following conditions are provided.
It should be shown that .
is completely continuous function.
basis function satisfies the initial and boundary conditions.
One can see that any elements of
satisfy the above conditions. Now, the following equation can be written using the property of the kernel function
Here, both
and
are continuous in
. These functions are bounded because they are continuous in
. So, it can be written
In the same way, one can write that
Here,
and
are positive constants. From (
17),
Therefore, . Furthermore, is completely continuous in since is closed region. Finally, basis function satisfies initial-boundary conditions such that and . Therefore, . □
Theorem 3. is a complete system in .
Proof. Clearly, for each fixed
, if
then
,
. Therefore,
is dense in
. Hence,
. By using of inverse operator
, it can be seen that
. So, theorem is proven. □
The orthonormal basis system
of
can be obtained by the way of Gram–Schmidt orthogonalization process of
as follow:
In Equation (
20),
and
are orthogonalization coefficients.
Theorem 4. If is dense in Θ, then the solution (16) is Proof. It is known that
system is complete in
from the previous theorem. So, it can be written
So, theorem is proven. □
In Equation (
21),
is described as infinite term sum. In the next equation, finitely
n-terms solution will be given as
:
4. Convergence of Reproducing Kernel Solution
In this section, it will be shown that
If we take
then (21) can be described as
Now,
is found by taking
from the initial conditions of problem. Furthermore, by choosing
, the
n-term approximation to
is expressed as follows:
here
Now, some theoretical results will be given for convergence of and , respectively.
Lemma 1. If is continuous and for , then Proof. Using reproducing kernel feature, it can be written that
It can be said that there exists
from the convergence of
such that
In a similar way, it can be proven
by using Equation (
14). So,
In a similar way it can be shown that
So, lemma is proven. □
Theorem 5. Assume that (16) has a unique solution, is a bounded and is dense in Θ. Then, converges to and Proof. Firstly, we aim to show that
is convergence. Following equality can be written
from the Equation (
27). Using the orthonormality of
, we have
Therefore,
satisfies from (40). Here, it seems that
is bounded. So, one can know that
is convergent. Therefore, there exists a constant
b so that
So, above equation shows that
. If
, then
The following equation is obtained
and consequently
The completeness of
shows that
for
. Next, it will be shown that
is the representation solution of (16). If the limit is taken both sides of Equation (
27), the following equation can be written:
From (28), the following equation can be expressed
For each
,
is dense in
. Therefore, there exists a subsequence
such that
,
. It is known that
By using Lemma 1 and continuity of
F, it can be seen that
Equation (
52) implies that
satisfies Equation (
16). So, proof is completed. □
Theorem 6. uniformly converges to for and .
Proof. The convergence of
is given in the previous theorem. Now,
6. Numerical Applications and Algorithm of Method
In this section, two fractional Burgers’ problems with variable and constant coefficient are considered. Exact solutions of problems include the fractional parameter . Reproducing kernel method will be applied for these problems and outcomes will be presented with tables and graphics.
6.1. Algorithm Process of RKM
The algorithm process of RKM is given as follow:
Case 1. Choosing of iteration number as .
Case 2. Start .
Case 3. Obtaining of coefficients.
Case 4. Set for .
Case 5. Start initial approximation .
Case 6. Calculate for .
Case 7. Calculate for .
6.2. Numerical Applications
Example 1. It will be examined that the following fractional-order Burgers’ problem with Dirichlet boundary condition: The exact solution of problem:
and
is the function that provides the Equation (
62). Taking
,
and
n-th term of approximate solution is selected as
. Absolute error values for Example 1 is computed for
,
,
and
. Error values are given in
Table 2,
Table 3 and
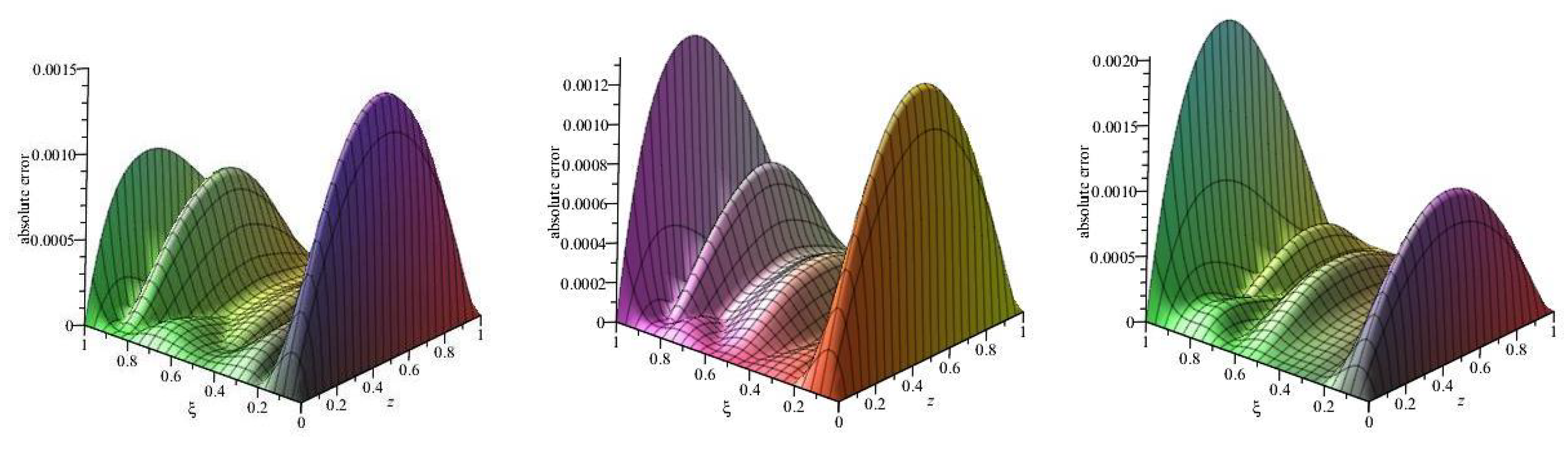
Table 4 in order to observe of applicability and influence of method. The graphics of absolute errors are given for
,
, and
in
Figure 1.
Example 2. It will be examined that the fractional-order Burgers’ equation with Neumann boundary condition as follow: The exact solution of problem is:
and
is the function that provides the Equations (65). Taking
,
and
. Absolute error of Example 2 is computed for
,
,
and
. Error values are given in
Table 5,
Table 6 and
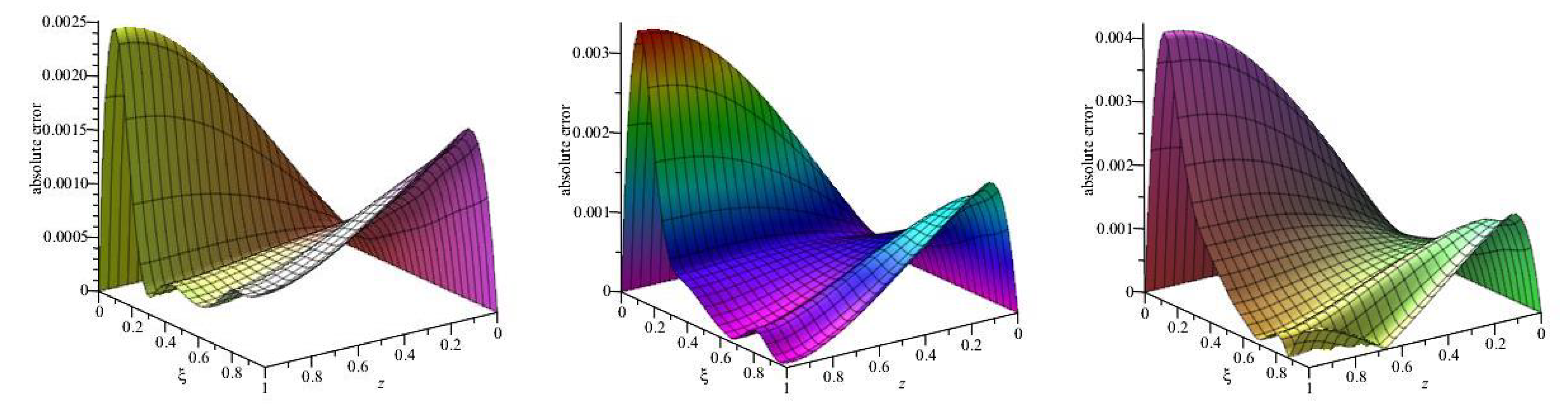
Table 7 in order to observe of applicability and influence of method. The graphics of absolute errors are given for
,
, and
in
Figure 2.