Fractional State Space Description: A Particular Case of the Volterra Equations

Abstract

To tackle several limitations recently highlighted in the field of fractional differentiation and fractional models, some authors have proposed new kernels for the definition of fractional integration/differentiation operators. Some limitations still remain, however, with these kernels, whereas solutions prior to the introduction of fractional models exist in the literature. This paper shows that the fractional pseudo state space description, a fractional model widely used in the literature, is a special case of the Volterra equations, equations introduced nearly a century ago. Volterra equations can thus be viewed as a serious alternative to fractional pseudo state space descriptions for modelling power law type long memory behaviours. This paper thus presents a new class of model involving a Volterra equation and several kernels associated with this equation capable of generating power law behaviours of various kinds. One is particularly interesting as it permits a power law behaviour in a given frequency band and, thus, a limited memory effect on a given time range (as the memory length is finite, the description does not exhibit infinitely slow and infinitely fast time constants as for pseudo state space descriptions).

1. Introduction

For 30 years, research on fractional differentiation and integration operators has steadily increased. While from a mathematical point of view these operators are now well defined, this is not the case for their physical interpretations or for their use in the definition of fractional models.

In the field of automatic control, the literature abounds with papers based on a generalisation of the classical state space description denoted “fractional pseudo state space description”. It is mathematically defined by the following equations:

$$\{\begin{array}{c}\frac{d^{\nu }}{d{t}^{\nu }}\left[x\left(t\right)\right]=Ax\left(t\right)+u\left(t\right)\\ y\left(t\right)=Cx\left(t\right).\end{array}$$

(1)

In relation (1), $\frac{d^{\nu }}{d{t}^{\nu }}\left[x\left(t\right)\right]$ replaces the usual derivative and denotes the fractional derivative of order $\nu$ of the variable (or vector of the variable) $x\left(t\right)$. A first difficulty related to such a representation is the considerable number of possible definitions for the fractional differentiation operator $\frac{d^{\nu }}{d{t}^{\nu }}\left[ .\right]$. More than 30 are listed in [1], and new definitions of fractional operator have appeared recently [2,3,4,5,6]. These definitions are not equivalent if initial conditions are taken into account, and in many cases each author chooses what suits them according to the results they want to obtain. The most widely used definitions are the Riemann–Liouville and Caputo definitions [7]. The latter takes initial conditions into account very easily (as for classical state space descriptions), but it was demonstrated that this is not done in a physically consistent way [8,9,10,11] (the memory of the model is not taken into account at the initial time). While a similar problem exists with the Riemann–Liouville definition, it nonetheless has the merit of taking into account the entire past of the system at the initial time $t=t_0$, which better reflects the behaviour of the model for $t>t_0$ [9].

A fractional pseudo state space description (1)—which it is better to denote a pseudo state space description, since the variable $x\left(t\right)$ does not meet the definition of a state as shown in [9,12]—is in fact a simple “fractionalisation” of the classical state space description, without physical justification and resulting from the need for models that fit power law type long memory behaviours.

Numerous examples of this kind of behaviour were revealed in various domains, for instance:

• Electrochemistry due to charge diffusion in batteries [13,14];
• Thermal conduction in a semi-infinite medium [15];
• Biology for modelling complex dynamics in biological tissues [16];
• Mechanics with the dynamical property of viscoelastic materials and, in particular, wave propagation problems in these materials [17];
• Acoustics to model visco-thermal losses in wind instruments [18];
• Electrical distribution networks [19].

Given the ubiquity of such systems, efficient modelling tools are needed.

Of course, fractional integration and differentiation operators have the ability to fit these kinds of behaviours. A fractional integration operator that links an input $u\left(t\right)$ to an output $y\left(t\right)$ is defined in the Riemann–Liouville sense by the relation [7]:

$$y\left(t\right)={\int }_0^t\frac{1}{{\left(t-\tau \right)}^{\nu -1}}u\left(\tau \right)d\tau .$$

(2)

Such an operator exhibits a power law behaviour as the modulus of its Fourier transform, denoted $\left|Y\left(j\omega \right)/U\left(j\omega \right)\right|$, is defined by $1/{\omega }^{\nu }$. As it is defined using a fractional integrator operator, the fractional-order differentiation operator has a similar property.

Even if a nice fitting of many systems’ input–output behaviours is obtained with models such as (1), several drawbacks are associated with the description (1) and with fractional differential equations in general:

• The variable $x\left(t\right)$ that plays the role of the state does not have the properties of a state, which is why the name “pseudo state” was introduced [11,12];
• The initial conditions are not well taken into account if the Caputo or Riemann–Liouville definitions are used for the derivative of the pseudo state, and it is better to define the description with a fractional integration to take the model past into account [10,11,12,20];
• This description memory is infinite and it exhibits infinitely slow and infinitely fast time constants (even if they are attenuated, they exist), which excludes the possibility of linking the pseudo-state variable to a physical variable [11];
• Observability results (but also controllability, flatness, etc.) depend on the definition used for fractional differentiation [20,21,22], and exact observability cannot be reached if all the system past must be known to predict its future [20],
• Fractional integration given by relation (2) involves a singular kernel, as mentioned in [2]; this leads to complications in the solution/simulation of the fractional-order differential equations (and that is why some new kernels were proposed; see, for instance, [2,3,4,5,6]);
• The parameter units associated with description (2) (parameters inside matrices A and B) have no physical meaning (e.g., $se{c}^{-\nu }$);
• The physical interpretations proposed in the literature [23,24,25,26,27,28,29] are weakly convincing, and in the case of incommensurate orders, some can invalidate the obtained model [30].

It is therefore necessary to find models that overcome these limitations and that are physically consistent and interpretable.

In this paper, Section 2 highlights that the pseudo state space description frequently encountered in the literature for power law type long memory behaviours is a special case of the Volterra equations in the sense that the kernel used in its definition has a constrained form. In the field of power law type long memory behaviour modelling, it thus appears more general to directly work with Volterra equations, which allow great freedom in the choice of the kernel which composes these equations. Several kernels are proposed in Section 3, with some that never been proposed in the literature, that permit power law type long memory behaviours while solving several drawbacks associated with pseudo state space descriptions. Note that the introduction of special kernels in other integro-differential equations to produce power law type long memory behaviour was done in [31,32]. With Section 4, the paper ends with a discussion of the results presented.

Notation: In the following, the same letter is used to designate a time or a frequency variable, or the Laplace transform of these variables. The argument associated to this variable then makes it possible to lift the indeterminacy:

-

$z\left(t\right)$ denotes a time variable;

-

$z\left(j\omega \right)$ denotes a frequency variable;

-

$z\left(s\right)$ denotes the Laplace transform of $z\left(t\right)$, $z\left(s\right)=ℒ\left\{z\left(t\right)\right\}.$

2. Pseudo State Space Description: A Particular Case of the Volterra Equations

Volterra equations of the first kind were introduced by Volterra himself [33,34] to model population growth. In the linear and scalar case ($x\in ℝ$, $v\in ℝ$) they are defined by

$${\int }_0^t\eta \left(t-\tau \right)x\left(\tau \right)d\tau =v\left(t\right).$$

(3)

Such a representation appears more general than the fractional pseudo state space description (1). To demonstrate this, the operator $\frac{d^{\nu }}{d{t}^{\nu }}\left[\right]$ in relation (1) is assumed to be defined in the Riemann–Liouville sense [7] (for the reasons explained in Section 1). It is also assumed in (1) that $A\in {ℝ}^{n\times n}$, $B\in {ℝ}^{n\times n}$, and $C\in {ℝ}^{1\times n}$.

According to [7] (p. 46) (if the fractional integral of order ν of each component of vector $x\left(t\right)$ exists) and after first-order integration of both sides of the first equation in relation (1), the following equation can be obtained:

$${\int }_0^t{\eta }_f\left(t-\tau \right)x\left(\tau \right)d\tau ={\int }_0^t\left[Ax\left(\tau \right)+Bu\left(\tau \right)\right]d\tau$$

(4)

where the kernel in (4) is ${\eta }_f\left(t\right)=t^{-\nu }/\mathsf{\Gamma }\left(1-\nu \right)$ and multiplies each component of vector $x\left(t\right)$. Representation (1) can thus be rewritten under the form of a Volterra equation of the first kind:

$${\int }_0^t\left(\frac{t^{-\nu }}{\mathsf{\Gamma }\left(1-\nu \right)}{I}_n-A\right)x\left(\tau \right)d\tau =v\left(t\right)\mathrm{with}v\left(t\right)={\int }_0^{t}Bu\left(\tau \right)d\tau ,y\left(t\right)=Cx\left(t\right),$$

(5)

where $I_n$ denotes an identity matrix of dimension $n$. Relation (5) demonstrates that a pseudo state space description is a particular case of a Volterra equation of the first kind, as the kernel in (5) has a fixed structure. Using a Volterra equation, it is thus possible to generalise a pseudo state space description in two ways:

• By adapting the kernel $\eta \left(t\right)$ in relation (3), it is possible to produce, with the same kind of equation, power law behaviours of various types (denoted explicit, implicit), but also many other long memory behaviours;
• In relation (3), if $x\left(t\right)\in {ℝ}^n$, then $\eta \left(t\right)$ is a matrix of kernels such that $\eta \left(t\right)=\left[{\eta }_{i,j}\left(t\right)\right]$, thus permitting great flexibility in the tuning of relation (3). The case $\eta \left(t\right)=diag\left[{\eta }_i\left(t\right)\right]$ comes closer to the non-commensurate fractional pseudo state space representation case, but it should be remembered that physical interpretations invalidate this kind of model [30].

Description (3) has another important advantage. Model memory can be limited by introducing a parameter $T_f$ in the integral bounds such that

$${\int }_{t-T_f}^t\eta \left(t-\tau \right)x\left(\tau \right)d\tau =v\left(t\right).$$

(6)

Using the change of variable $\xi =t-\tau$, relation (6) becomes

$${\int }_0^{T_f}\eta \left(\xi \right)x\left(t-\xi \right)d\xi =v\left(t\right).$$

(7)

Relation (7) explicitly shows that knowledge of the model state $x\left(t\right)$ is required on $\left[0, T_f\right]$ to compute its future. Modification of the lower bound of relation (3) to produce relation (6) is thus of interest in the initialisation problem. Initialisation of relation (6) only requires knowledge of the past of variable $\mathrm{x}\left(t\right)$ on the interval $\left[t_0-T_f,t_0\right]$ if $t_0$ denotes the initial time, while knowledge of the past on $\left]-\infty ,t_0\right]$ is required for fractional model (1).

For all these reasons, in a modelling approach it is better to work with model (6) than with model (1), which is more general as previously demonstrated. This can be done by searching the kernel $\eta \left(t\right)$ directly without any assumption on its structure.

3. A Volterra-Equation-Based Model for Power Law Type Long Memory Behaviour

This section shows that by choosing an appropriate kernel $\eta \left(t\right)$ in relation (3), it is possible to produce power law behaviours of various kinds (explicit, implicit). To highlight this, the following model involving a Volterra equation of the first kind is considered:

$${\int }_0^t\eta \left(t-\tau \right)x\left(\tau \right)d\tau =v\left(t\right)\mathrm{with}v\left(t\right)={\int }_0^{t}u\left(\tau \right)d\tau ,y\left(t\right)=x\left(t\right).$$

(8)

It is assumed that $u\left(t\right)\in ℝ$ denotes the input of the model and that $y\left(t\right)\in ℝ$ is its output. The Laplace transform of relation (8) is, without considering initial conditions,

$$\eta \left(s\right)x\left(s\right)=v\left(s\right)\mathrm{with}v\left(s\right)=\frac{1}{s}u\left(s\right),y\left(s\right)=x\left(s\right),$$

(9)

and from an input–output point of view, the following transfer function is thus obtained:

$$\frac{y\left(s\right)}{u\left(s\right)}=\frac{1}{s\eta \left(s\right)}.$$

(10)

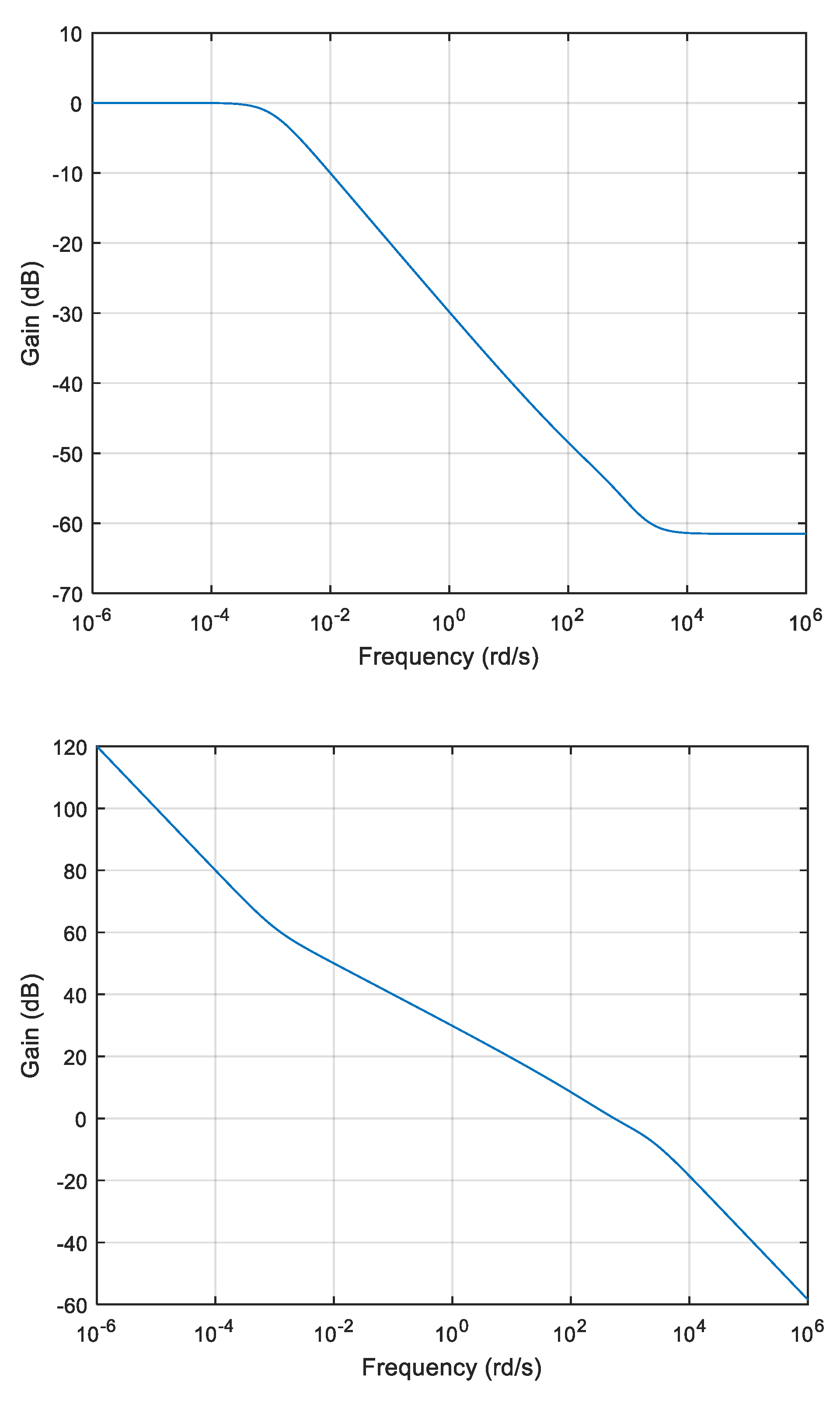
3.1. A First Kernel

The paper by Cole and Cole [35] is considered by some as the first application of fractional differentiation. As Volterra equations of the first kind were introduced by Volterra himself [33] at least 20 years before the Cole and Cole paper, instead of using their empirical formula (see relation (1) in [35])

$${\epsilon }^{*}-{\epsilon }_{\infty }=\frac{{\epsilon }_0-{\epsilon }_{\infty }}{1+{\left(j\omega {\tau }_0\right)}^{1-\nu }}$$

(11)

for dispersion and absorption modelling in dielectrics, model (8) (or, more generally, a Volterra equation of the first kind) could have been used with

$${\eta }_1\left(t\right)=\frac{1}{\left({\epsilon }_0-{\epsilon }_{\infty }\right)}H\left(t\right)+\frac{{\tau }_0{}^{1-\nu }}{\left({\epsilon }_0-{\epsilon }_{\infty }\right)}\frac{t^{\nu -1}}{\mathsf{\Gamma }\left(\nu \right)}$$

(12)

in which $H\left(t\right)$ denotes the Heaviside function. The Laplace transform of relation (12) is

$${\eta }_1\left(s\right)=\frac{1}{\left({\epsilon }_0-{\epsilon }_{\infty }\right)s}+\frac{{\tau }_0{}^{1-\nu }}{\left({\epsilon }_0-{\epsilon }_{\infty }\right)}\frac{1}{{\mathrm{s}}^{\nu }}=\frac{1}{\left({\epsilon }_0-{\epsilon }_{\infty }\right)s}\left(1+{\left({\tau }_{0}s\right)}^{1-\nu }\right)$$

(13)

and thus leads to the frequency response (11) for the transfer function (10), a frequency response that exhibits a power law behaviour of order $\nu -1$ on the frequency domain $\left[\frac{1}{{\tau }_0},\infty \right]$. However, this kernel is singular at $t=0$. Moreover, computation of the impulse response of the transfer function (13) using Cauchy’s theorem as detailed in Section 3.5 gives

$${\eta }_1\left(t\right)=\frac{1}{\left({\epsilon }_0-{\epsilon }_{\infty }\right)}H\left(t\right)+\frac{sin\left(\nu \pi \right){\tau }_0{}^{1-\nu }}{\pi \left({\epsilon }_0-{\epsilon }_{\infty }\right)\mathsf{\Gamma }\left(\nu \right)}{\int }_0^{\infty }{x}^{-\nu }{e}^{-tx}dx.$$

(14)

Laplace transform applied to relation (14) leads to

$${\eta }_1\left(s\right)=\frac{1}{\left({\epsilon }_0-{\epsilon }_{\infty }\right)s}+\frac{sin\left(\nu \pi \right){\tau }_0{}^{1-\nu }}{\pi \left({\epsilon }_0-{\epsilon }_{\infty }\right)\mathsf{\Gamma }\left(\nu \right)}{\int }_0^{\infty }\frac{x^{-\nu }}{s+x}dx.$$

(15)

Relation (15) shows that the transfer function ${\eta }_1\left(s\right)$ exhibits a distribution of poles within the interval $\left]-\infty ,0\right]$. Kernel ${\eta }_1\left(t\right)$ thus exhibits infinitely slow and infinitely fast time constants, and is not a candidate to solve the drawbacks mentioned in the introduction.

3.2. A Second Kernel

The following kernel is now considered:

$${\eta }_2\left(t\right)=-{\omega }_{min}{\left({\omega }_{min}t\right)}^{-\nu }{e}^{-{\omega }_{min}t}{E}_{1,1-\nu }\left({\omega }_{min}t\right)$$

(16)

where $E_{\alpha ,\beta }\left(z\right)$ is the Mittag-Leffler function defined by [7]

$$E_{\alpha ,\beta }\left(z\right)=\sum _{k=0}^{\infty }\frac{z^k}{\mathsf{\Gamma }\left(\alpha k+\beta \right)}.$$

(17)

This kernel is the so-called tempered (or truncated) Mittag-Leffler memory kernel, which has been investigated in different contexts and especially in generalised diffusion equations [36,37], in generalised diffusion-wave equations [38], and in generalised Langevin equations [39,40].

As $ℒ\left\{t^{\alpha }{E}_{1,1+\mathsf{\alpha }}\left(at\right)\right\}=s^{-\alpha }/\left(s-a\right)$ [41], and using the shift rule of the Laplace transform, the Laplace transform of kernel ${\eta }_2\left(t\right)$ is given by

$${\eta }_2\left(s\right)=\frac{{\left(\frac{s}{{\omega }_{min}}+1\right)}^{\nu }}{s}$$

(18)

and the transfer function of model (8) is thus

$$\frac{y\left(s\right)}{u\left(s\right)}=\frac{1}{{\left(\frac{s}{{\omega }_{min}}+1\right)}^{\nu }}.$$

(19)

This is also known as the Davidson–Cole transfer function, which also exhibits a power law behaviour of order $-\nu$ on the frequency domain $\left[{\omega }_{min},\infty \right]$. Such a kernel remains singular at $t=0$. Computation of the impulse response of the transfer function (18) using Cauchy’s theorem as detailed in Section 3.5 gives

$${\eta }_2\left(t\right)=H\left(t\right)+\frac{sin\left(\nu \pi \right)}{\pi }{\int }_{{\omega }_{min}}^{\infty }\frac{{\left(\frac{x}{{\omega }_{min}}-1\right)}^{\nu }}{x}{e}^{-tx}dx.$$

(20)

Laplace transform applied to relation (20) leads to

$${\eta }_2\left(s\right)=\frac{1}{s}+\frac{sin\left(\nu \pi \right)}{\pi }{\int }_{{\omega }_{min}}^{\infty }\frac{{\left(\frac{x}{{\omega }_{min}}-1\right)}^{\nu }}{x\left(s+x\right)}dx.$$

(21)

Relation (15) shows that the transfer function ${\eta }_2\left(s\right)$ exhibits a distribution of poles within the interval $\left]-\infty ,-{\omega }_{min}\right]$ (without taking into account the $1/s$ term). Kernel ${\eta }_2\left(t\right)$ thus does not exhibit infinitely slow time constants, which should simplify the initialisation of the equation in which this kernel will be used. However, this kernel still has infinitely fast time constants, which can be problematic for a physical interpretation.

3.3. A Third Kernel

The third kernel studied is defined by

$${\eta }_3\left(t\right)=E_{\nu ,1}\left(-{\left({\omega }_{min}t\right)}^{\nu }\right).$$

(22)

The Laplace transform of this kernel is defined by

$${\eta }_3\left(s\right)=\frac{{\left(\frac{s}{{\omega }_{min}}\right)}^{\nu }}{s\left({\left(\frac{s}{{\omega }_{min}}\right)}^{\nu }+1\right)}$$

(23)

and the transfer function (10) is thus defined by

$$\frac{y\left(s\right)}{u\left(s\right)}=\frac{\left({\left(\frac{s}{{\omega }_{min}}\right)}^{\nu }+1\right)}{{\left(\frac{s}{{\omega }_{min}}\right)}^{\nu }}.$$

(24)

This transfer function exhibits a power law behaviour of order $-\nu$ on the frequency domain $\left[0,{\omega }_{min}\right]$. Moreover, as $\underset{s\to \infty }{\lim }s{\eta }_3\left(s\right)\ne 0$, using the initial value theorem, it can be concluded that kernel ${\eta }_3\left(t\right)$ is not singular at time $t=0$. Computation of the impulse response of the transfer function (23) using Cauchy’s theorem as detailed in Section 3.5 gives

$${\eta }_3\left(t\right)=\frac{sin\left(\nu \pi \right)}{\pi }{\int }_0^{\infty }\frac{{\left(\frac{x}{{\omega }_{min}}\right)}^{\nu }}{x\left({\left(\frac{x}{{\omega }_{min}}\right)}^{2\nu }+2cos\left(\nu \pi \right){\left(\frac{x}{{\omega }_{min}}\right)}^{\nu }+1\right)}{e}^{-tx}dx.$$

(25)

Laplace transform applied to relation (25) leads to

$${\eta }_3\left(t\right)=\frac{sin\left(\nu \pi \right)}{\pi }{\int }_0^{\infty }\frac{{\left(\frac{x}{{\omega }_{min}}\right)}^{\nu }}{x\left({\left(\frac{x}{{\omega }_{min}}\right)}^2+2cos\left(\nu \pi \right)\left(\frac{x}{{\omega }_{min}}\right)+1\right)\left(s+x\right)}dx.$$

(26)

Relation (21) shows that the transfer function ${\eta }_2\left(s\right)$ exhibits a distribution of poles within the interval $\left]-\infty ,0\right]$ as kernel ${\eta }_1\left(t\right)$.

3.4. A Fourth Kernel

The fourth kernel studied is defined by

$${\eta }_4\left(t\right)=H\left(t\right)-E_{\nu ,1}\left(-{\left({\omega }_{min}t\right)}^{\nu }\right).$$

(27)

The Laplace transform of this kernel is defined by

$${\eta }_4\left(s\right)=\frac{1}{s\left({\left(\frac{s}{{\omega }_{min}}\right)}^{\nu }+1\right)}$$

(28)

and the transfer function (10) is thus defined by

$$\frac{y\left(s\right)}{u\left(s\right)}=\left({\left(\frac{s}{{\omega }_{min}}\right)}^{\nu }+1\right).$$

(29)

This transfer function exhibits a power law behaviour of order $+\nu$ on the frequency domain $\left[{\omega }_{min},\infty \right]$. As $\underset{s\to \infty }{\lim }s{\eta }_4\left(s\right)=0$, using the initial value theorem, it can be concluded that kernel ${\eta }_4\left(t\right)$ is not singular at time $t=0$. Computation of the impulse response of the transfer function (28) using Cauchy’s theorem as detailed in Section 3.5 gives

$${\eta }_4\left(t\right)=H\left(t\right)-\frac{sin\left(\nu \pi \right)}{\pi }{\int }_0^{\infty }\frac{e^{-tx}}{x\left({\left(\frac{x}{{\omega }_{min}}\right)}^{2\nu }+2cos\left(\nu \pi \right){\left(\frac{x}{{\omega }_{min}}\right)}^{\nu }+1\right)}dx.$$

(30)

Laplace transform applied to relation (30) leads to

$${\eta }_4\left(s\right)=\frac{1}{s}-\frac{sin\left(\nu \pi \right)}{\pi }{\int }_{{\omega }_{min}}^{\infty }\frac{1}{x\left({\left(\frac{x}{{\omega }_{min}}\right)}^{2\nu }+2cos\left(\nu \pi \right){\left(\frac{x}{{\omega }_{min}}\right)}^{\nu }+1\right)\left(s+x\right)}dx.$$

(31)

Relation (15) shows that transfer function ${\eta }_4\left(s\right)$ exhibits a distribution of poles within the interval $\left]-\infty ,-{\omega }_{min}\right]$ (without taking into account the $1/s$ term). Kernel ${\eta }_4\left(t\right)$ thus does not exhibit infinitely slow time constants, which should simplify the initialisation of the equation in which this kernel is used. However, this kernel still has infinitely fast time constants, which can be problematic for a physical interpretation.

3.5. A Fifth Kernel

The following kernel is now considered:

$$\begin{array}{l}{\eta }_5\left(t\right)={\left({\omega }_{min}\right)}^{\nu }{\left({\omega }_{max}\right)}^{1-\nu }{e}^{-{\omega }_{min}t}{F}_1\left(1-\nu ,1,\left({\omega }_{min}-{\omega }_{max}\right)t\right)+K\delta \left(t\right)\\ \mathrm{with}K=1/{\left(2\right)}^{\frac{1-\nu }{2}}{\left(1+{\left(\frac{{\omega }_{max}}{{\omega }_{min}}\right)}^2\right)}^{\frac{\nu }{2}}.\end{array}$$

(32)

In relation (32), function $F_1\left(–,–,–\right)$ is a confluent hypergeometric function [42]. The Laplace transform of this kernel is defined by [43] (p. 238):

$${\eta }_5\left(s\right)=\frac{1}{{\left(\frac{s}{{\omega }_{min}}+1\right)}^{\nu }{\left(\frac{s}{{\omega }_{max}}+1\right)}^{1-\nu }}+K.$$

(33)

Note that this kernel can be represented in terms of the three-parameter Mittag-Leffler function due to the following link with confluent hypergeometric function $F_1\left(\delta ,1,a\right)=E_{1,1}^{\delta }\left(az\right)$.

The model (10) input–output Laplace transform is thus

$$\frac{y\left(s\right)}{u\left(s\right)}=\frac{1}{s{\eta }_5\left(s\right)}=H_5\left(s\right)=\frac{{\left(\frac{s}{{\omega }_{min}}+1\right)}^{\nu }{\left(\frac{s}{{\omega }_{max}}+1\right)}^{1-\nu }}{s\left(1+K{\left(\frac{s}{{\omega }_{min}}+1\right)}^{\nu }{\left(\frac{s}{{\omega }_{max}}+1\right)}^{1-\nu }\right)}.$$

(34)

The gain diagrams of transfer functions ${\eta }_5\left(s\right)$ and $H_5\left(s\right)$ are shown in Figure 1 with ${\omega }_{min}=0.001$ rd/s, ${\omega }_{max}=1000$ rd/s, and $\nu =0.5$. These transfer functions exhibit power law behaviour in the frequency band $\left[{\omega }_{min},{\omega }_{max}\right]$.

A property (and advantage) of this kernel is a distribution of its poles on a limited frequency band. To demonstrate such a property, the impulse of the transfer function

$$G\left(s\right)=\frac{1}{{\left(\frac{s}{{\omega }_{min}}+1\right)}^{\nu }{\left(\frac{s}{{\omega }_{max}}+1\right)}^{1-\nu }}$$

(35)

(which is in the definition of ${\eta }_5\left(s\right)$) is computed using Cauchy’s theorem over the path $\mathsf{\Gamma }={\gamma }_0\cup \dots \cup {\gamma }_7$ represented by Figure 2.

For $0<\mathsf{\nu }<1$, the transfer function $G\left(s\right)$ has no pole inside $\mathsf{\Gamma }$ and, thus,

$$\sum _{\begin{array}{c}poles\\ in\mathsf{\Gamma }\end{array}}\mathrm{Res}\left[G\left(s\right)e^{ts}\right]=0.$$

(36)

With the operator $G\left(s\right)$ being strictly proper, by Jordan’s lemma, integrals on the large circular arcs of radius R, R → ∞ can be neglected:

$${\int }_{{\gamma }_1+{\gamma }_7}G\left(s\right)e^{ts}ds=0.$$

(37)

Let $s=x{e}^{j\pi }$ and $x\in \left]\infty ,{\omega }_{max}\right]$ on ${\gamma }_2$; thus, $ds=e^{j\pi }dx$. Let also $s=x{e}^{-j\pi }$ and $x\in \left[{\omega }_{max},\infty \right[$ on ${\gamma }_6$; thus, $ds=e^{-j\pi }dx$. Then

$$\begin{array}{c}\underset{{\gamma }_{2+}\gamma 6}{\int }G\left(s\right)e^{ts}ds=J_{{\gamma }_2+{\gamma }_6}\left(t\right)=\frac{{\omega }_{min}{}^{\nu }}{{\omega }_{max}{}^{\nu -1}}\underset{\infty }{\overset{{\omega }_{max}}{\int }}\frac{{\left(x{e}^{j\pi }+{\omega }_{max}\right)}^{\nu -1}}{{\left(x{e}^{j\pi }+{\omega }_{min}\right)}^{\nu }}{e}^{-xt}{e}^{j\pi }dx+\\ \frac{{\omega }_{min}{}^{\nu }}{{\omega }_{max}{}^{\nu -1}}{\int }_{{\omega }_{max}}^{\infty }\frac{{\left(x{e}^{-j\pi }+{\omega }_{max}\right)}^{\nu -1}}{{\left(x{e}^{-j\pi }+{\omega }_{min}\right)}^{\nu }}{e}^{-xt}{e}^{-j\pi }dx,\end{array}$$

(38)

or

$$\begin{array}{l}{J}_{{\gamma }_2+{\gamma }_6}\left(t\right)=\frac{{\omega }_{min}{}^{\nu }}{{\omega }_{max}{}^{\nu -1}}\underset{\infty }{\overset{{\omega }_{max}}{\int }}\frac{e^{j\left(\nu -1\right)\pi }{\left(x-{\omega }_{max}\right)}^{\nu -1}}{e^{j\nu \pi }{\left(x-{\omega }_{min}\right)}^{\nu }}{e}^{j\pi }{e}^{-xt}dx\\ +\frac{{\omega }_{min}{}^{\nu }}{{\omega }_{max}{}^{\nu -1}}\underset{{\omega }_{max}}{\overset{\infty }{\int }}\frac{e^{-j\left(\nu -1\right)\pi }{\left(x-{\omega }_{max}\right)}^{\nu -1}}{e^{-j\nu \pi }{\left(x-{\omega }_{min}\right)}^{\nu }}{e}^{-j\pi }{e}^{-xt}dx,\end{array}$$

(39)

and, thus,

$$J_{{\gamma }_2+{\gamma }_6}\left(t\right)=0.$$

(40)

Let $s=-{\omega }_{min}+\rho e^{j\theta }$, $\theta \in \left]-\pi ,\pi \right]$ on ${\gamma }_4$, and, thus, $ds=j\rho e^{j\theta }d\theta$ with $\rho \to 0$. Then

$${\int }_{{\gamma }_4}G\left(s\right)e^{ts}ds=\frac{{\omega }_b{}^{\nu }}{{\omega }_h{}^{\nu -1}}{\int }_{\pi }^{-\pi }\frac{{\left(-{\omega }_b+{\omega }_h+\rho e^{j\theta }\right)}^{\nu -1}}{{\left(\rho e^{j\theta }\right)}^{\nu }}j\rho e^{j\theta }{e}^{t\left(-{\omega }_b+\rho e^{j\theta }\right)}d\theta .$$

(41)

As $\rho \to 0$,

$${\int }_{{\gamma }_4}G\left(s\right)e^{ts}ds=0.$$

(42)

Let $s=x{e}^{j\pi }$ and $x\in \left[{\omega }_{min},{\omega }_{max}\right]$ on ${\gamma }_3$; thus, $ds=e^{j\pi }dx$. Also let $s=x{e}^{-j\pi }$ and $x\in \left[{\omega }_{min},{\omega }_{max}\right]$ on ${\gamma }_5$; thus, $ds=e^{-j\pi }dx$. Then

$$\begin{array}{l}\underset{{\gamma }_3+{\gamma }_5}{\int }G\left(s\right)e^{ts}ds\\ =\frac{{\omega }_{min}{}^{\nu }}{{\omega }_{max}{}^{\nu -1}}\underset{{\omega }_{max}}{\overset{{\omega }_{min}}{\int }}\frac{{\left(x{e}^{j\pi }+{\omega }_{max}\right)}^{\nu -1}}{{\left(x{e}^{j\pi }+{\omega }_{min}\right)}^{\nu }}{e}^{-xt}{e}^{j\pi }dx\frac{{\omega }_{min}{}^{\nu }}{{\omega }_{max}{}^{\nu -1}}\underset{{\omega }_{min}}{\overset{{\omega }_{max}}{\int }}\frac{{\left(x{e}^{-j\pi }+{\omega }_{max}\right)}^{\nu -1}}{{\left(x{e}^{-j\pi }+{\omega }_{min}\right)}^{\nu }}{e}^{-xt}{e}^{-j\pi }dx\end{array}$$

(43)

and

$$\begin{array}{l}\underset{{\gamma }_3+{\gamma }_5}{\int }G\left(s\right)e^{ts}ds=\frac{{\omega }_{min}{}^{\nu }}{{\omega }_{max}{}^{\nu -1}}\underset{{\omega }_{min}}{\overset{{\omega }_{max}}{\int }}\frac{{\left({\omega }_{max}-x\right)}^{\nu -1}}{{\left(x-{\omega }_{min}\right)}^{\nu }}\left(e^{j\nu \pi }-e^{-j\nu \pi }\right)e^{-xt}dx\\ =2j\text{sin}\left(\nu \pi \right)\frac{{\omega }_{max}{}^{\nu }}{{\omega }_{min}{}^{\nu -1}}\underset{{\omega }_{min}}{\overset{{\omega }_{max}}{\int }}\frac{{\left({\omega }_{max}-x\right)}^{\nu -1}}{{\left(x-{\omega }_{min}\right)}^{\nu }}{e}^{-xt}dx.\end{array}$$

(44)

As (taking into account relation (36))

$$G\left(t\right)=-\frac{1}{2\pi j}\underset{\Gamma -{\gamma }_0}{\int }G\left(s\right)e^{ts}ds,$$

(45)

using relations (37), (38), (42), and (44), the impulse response of $G\left(s\right)$ is given by, for t > 0,

$$G\left(t\right)=\frac{\sin \left(\nu \pi \right)}{\pi }\frac{{\omega }_{min}{}^{\nu }}{{\omega }_{max}{}^{\nu -1}}{\int }_{{\omega }_{min}}^{{\omega }_{max}}\frac{{\left({\omega }_{max}-x\right)}^{\nu -1}}{{\left(x-{\omega }_{min}\right)}^{\nu }}{e}^{-xt}dx.$$

(46)

Relation (38) demonstrates that the poles (variable $x$ in relation (46)) of the impulse response $G\left(t\right)$ (and thus of the kernel ${\eta }_5\left(t\right)$) are distributed in a limited frequency band defined by $\left[{\omega }_{min},{\omega }_{max}\right]$.

Now, still with kernel ${\eta }_5\left(t\right)$, the definition of model (8) is modified (as in relation (6)) in order to limit its memory:

$${\int }_{t-T_f}^t{\eta }_5\left(t-\tau \right)x\left(\tau \right)d\tau =v\left(t\right)\mathrm{with}v\left(t\right)={\int }_0^{t}u\left(\tau \right)d\tau ,y\left(t\right)=x\left(t\right).$$

(47)

Using the change of variable $\xi =t-\tau$ and, thus, $d\xi =-d\tau$, relation (47) becomes

$${\int }_0^{T_f}{\eta }_5\left(\xi \right)x\left(t-\xi \right)d\xi =v\left(t\right)\mathrm{with}\left(t\right)={\int }_0^{t}u\left(\tau \right)d\tau y\left(t\right)=x\left(t\right).$$

(48)

The Laplace transform of relation (48) without considering initial conditions is

$$x\left(s\right){\int }_0^{T_f}{\eta }_5\left(\xi \right)e^{-\xi s}d\xi =v\left(s\right)\mathrm{with}v\left(s\right)=\frac{1}{s}u\left(s\right),y\left(s\right)=x\left(s\right)$$

(49)

and thus, the transfer function $H_5^{T_f}\left(s\right)$ linking the input $u\left(s\right)$ to the input $y\left(s\right)$ is defined by

$$H_5^{T_f}\left(s\right)=\frac{y\left(s\right)}{u\left(s\right)}=\frac{1}{s{\int }_0^{T_f}{\eta }_5\left(\xi \right)e^{-\xi s}d\xi }.$$

(50)

Figure 3 compares the gain diagram of $H_5^{T_f}\left(s\right)$ (computed numerically) with the gain diagram of $H_5\left(s\right)$ given by relation (34) in the domain of interest (the whole gain diagram is shown in Figure 1). It shows that the frequency response of $H_5^{T_f}\left(s\right)$ remains similar to that of $H_5\left(s\right)$ under the condition $T_f>5/{\omega }_{min}$. In such a situation, parameter $T_f$ can be viewed as the memory length of this kernel. Note that the memory length is connected to the corner frequency below which the kernel frequency response has a constant gain.

4. Conclusions

Dynamic systems with power law type long memory behaviours are generally modelled in the literature using fractional models. However, several studies have highlighted severe limitations of these models. This situation is, in fact, surprising as all the material required for power law type long memory behaviours existed before the introduction of fractional models, in the form of Volterra equations.

The paper first showed that the fractional pseudo state space description currently used in the literature is, in fact, a particular case of the Volterra equations. This class of equations was introduced by Volterra himself in the 1910s. This is 20 years before the paper by Cole and Cole, which is perceived by some as the first application of fractional differentiation and models, and who could have used this equation to model dispersion and adsorption phenomena in dielectrics. As shown in the present paper, by defining a new class of model involving a Volterra equation, and by choosing appropriate kernels in the Volterra equation, various kinds of power law type long memory behaviours can be generated. One kernel was more deeply studied as it permits power law behaviour in a given frequency band and thus avoids infinitely small and infinitely large time constants. With this kernel, it was also shown that the model memory can be limited without affecting its input–output behaviour provided that a condition linking the memory length and the lowest time constant of the kernel is met.

Some of the kernels proposed in Section 3 are continuous. These kernels can solve many of the questions currently raised by the classical and historical definitions of fractional operators. In relation to the list of drawbacks given in the introduction with the analysed kernels associated with model (3) or (8),

• There is no question of state in Equations (3) and (8);
• The mathematical operators used in Equations (3) and (8) are clearly defined, and this equation also well defines how the model past (initial conditions) should be taken into account;
• The choice of kernel is free in Relations (3) and (8), and as shown in this paper with kernel ${\eta }_5\left(t\right)$ (Relation (24)), the model time constant can be limited within an interval, and as shown with relation (35), the model history can be limited;
• Relations (3) and (8) are uniquely defined, which cannot lead to different conclusions on the properties of this equation;
• non-singular kernel can be used in relations (3) and (8), such as kernels ${\eta }_3\left(t\right)$ and ${\eta }_4\left(t\right)$, to produce power law type long memory behaviours;
• In Relations (3) and (8), if variables $v\left(t\right)$ and $x\left(\tau \right)$ are physically consistent, kernel $\eta \left(t\right)$ is also physically consistent;
• Several physical interpretations can be found in the literature for Relation (3) (see, for instance, [34]).

In contradiction with the results published in [44], these kernels are not restrictive. The author of [44] reached this conclusion because its analysis was based on the idea that initial conditions can be defined only using information at time $t=0$ of the variable on which the differential equation relates ($u\left(x,0\right)=\varphi \left(0\right)$ in [44]). As previously claimed, it was indeed shown in [9] and [11] that for the classical Caputo’s or Riemann–Liouiville kernels, the entire past of this variable is required from -∞ to ensure proper initialisation of the equation. The problem is not continuous kernels, but how initialisation is defined. This also joins the work of Lorenzo and Hartley [45], in which an initialisation function was added to the equation solution to take into account the entire equation past. A similar situation holds in a distributed delay equation, in which the past must be known within the time interval on which the integral is defined [46].

To finish, the author argues that the current trend to redefine fractional differentiation operators in the hope of solving the limitations of fractional models, such as the one given by Relation (1) or more generally those based on fractional differential equations, is not a profitable strategy. It seems more interesting and general to work directly on integro-differential equations and select appropriate kernels. The author thus intends now to study in greater depth the properties of Volterra equations for power law type long memory behaviours.