A Survey of Fractional Order Calculus Applications of Multiple-Input, Multiple-Output (MIMO) Process Control
Abstract
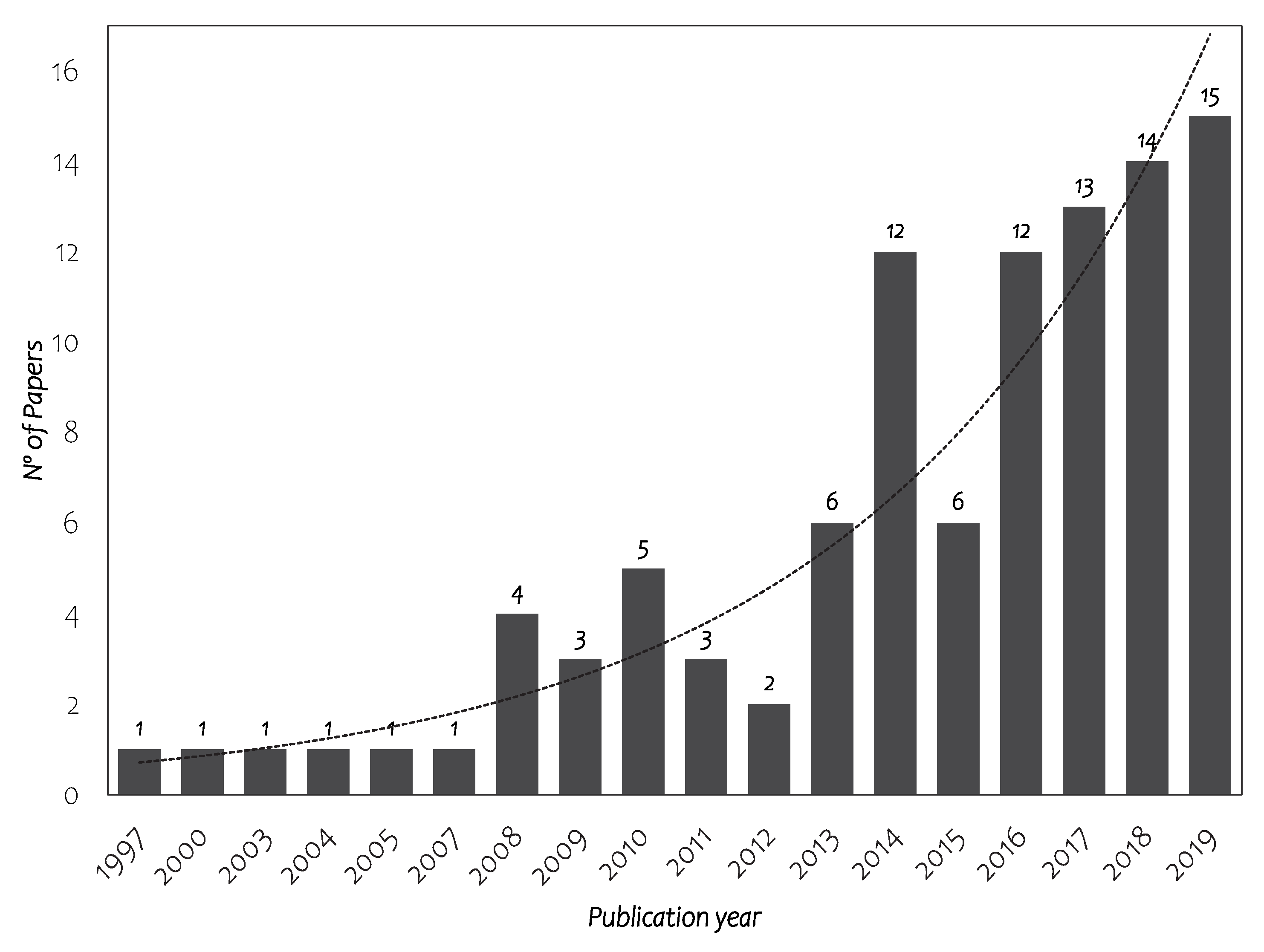
1. Introduction
2. FOC Applications in MIMO Control
2.1. Distillation Column
2.2. Coupled Tanks
2.3. Robotics and Automotive
2.4. Miscellaneous and Generic Applications
3. Simulation and/or Experimental Validation
3.1. Theoretical/Simulation Works
3.2. Theoretical/Simulation Works with Experimental Validation
4. FO-MIMO Controller Scheme and Topology
- Multi-loop control: multiple simple loops in a single control strategy.
- Multivariable control: a complex loop control where each manipulated variable is adjusted based on the error of all controlled variables.
5. Tuning Methods and Techniques
- Stability of responses in closed-loop;
- Rejection to disturbances;
- Set-point tracking;
- Elimination of offset errors;
- Robustness, avoiding saturation in control actions.
- Integral of the absolute value of the error (IAE):
- Integral of the squared error (ISE):
- Integral of the time-weighted absolute error (ITAE):
- Frequency domain tuning method: determination the parameters of the controller by solving a system of nonlinear equations expressing specifications related to phase margin, gain crossover frequency, sensitivity functions and robustness to gain changes in a limited interval;
- Tuning methods based on time-domain cost functions and optimization routines: based on the minimization of the IAE, ISE and ITAE indexes.
- Other tuning methods;
- Autotuning controllers.
6. Decoupling Techniques
7. Software
MATLAB
8. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, X.J. General Fractional Derivatives: Theory, Methods and Applications; CRC Press Taylor and Francis Group: Boca Raton, FL, USA, 2019. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction To The Fractional Calculus and Fractional Differential Equations; Springer Science Business Media: Berlin, Germany, 1993. [Google Scholar]
- Atangana, A.; Gómez-Aguilar, J. Numerical approximation of Riemann-Liouville definition of fractional derivative: From Riemann-Liouville to Atangana-Baleanu. Numer. Methods Part. Differ. Equ. 2018, 34, 1502–1523. [Google Scholar] [CrossRef]
- Atangana, A.; Gómez-Aguilar, J. Fractional derivatives with no-index law property: Application to chaos and statistics. Chaos Solitons Fract. 2018, 114, 516–535. [Google Scholar] [CrossRef]
- Smith, C.A.; Corripio, A.B. Principles and Practice of Automatic Process Control, 3rd ed.; John Wiley and Sons: New York, NY, USA, 2005. [Google Scholar]
- Seborg, D.E.; Edgar, T.F.; Mellichamp, D.A.; Doyle, F.J., III. Process Dynamics and Control, 3rd ed.; John Wiley and Sons: New York, NY, USA, 2011. [Google Scholar]
- Giona, M.; Roman, H.E. A theory of transport phenomena in disordered systems. Chem. Eng. J. 1992, 49, 1–10. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-Order Systems and PIλDμ—Controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Axtell, M.; Bise, M.E. Fractional calculus application in control systems. In Proceedings of the IEEE Conference on Aerospace and Electronics, Dayton, OH, USA, 21–25 May 1990. [Google Scholar]
- Oustaloup, A. La Commande CRONE; Hermès: Paris, France, 1991. [Google Scholar]
- Oustaloup, A.; Melchior, P. The great principles of the CRONE control. In Proceedings of the IEEE Systems Man and Cybernetics Conference, SMC, Le Touquet, France, 17–20 October 1993; pp. 118–129. [Google Scholar]
- Oustaloup, A.; Mathieu, B.; Lanusse, P. The CRONE Control of Resonant Plants: Application to a Flexible Transmission. Eur. J. Control 1995, 1, 113–121. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-Order Systems and Fractional-Order Controllers; Technical Report UEF-03-94; Slovak Academy of Science, Institute of Experimental Physics: Kosise, Slovakia, 1994. [Google Scholar]
- Huang, S.; Wang, J. Fixed-time fractional-order sliding mode control for nonlinear power systems. J. Vib. Control 2020. [Google Scholar] [CrossRef]
- Girgis, M.E.; Fahmy, R.A.; Badr, R.I. Optimal fractional-order PID control for plasma shape, position, and current in Tokamaks. Fusion Eng. Des. 2020, 150, 111361. [Google Scholar] [CrossRef]
- Zhang, F.; Yang, C.; Zhou, X.; Gui, W. Optimal Setting and Control Strategy for Industrial Process Based on Discrete-Time Fractional-Order PIλDμ. IEEE Access 2019, 7, 47747–47761. [Google Scholar] [CrossRef]
- Wang, D.; Zou, H.; Tao, J. A new design of fractional-order dynamic matrix control with proportional–integral–derivative-type structure. Meas. Control 2019, 52, 567–576. [Google Scholar] [CrossRef]
- Ayres Junior, F.A.D.C.; da Costa Junior, C.T.; de Medeiros, R.L.P.; Junior, W.B.; das Neves, C.C.; Lenzi, M.K.; Veroneze, G.D.M. A Fractional Order Power System Stabilizer Applied on a Small-Scale Generation System. Energies 2018, 11, 2052. [Google Scholar] [CrossRef]
- Manage, S. The Non-integer Integral and its Application to Control Systems. J. Inst. Electr. Eng. Jpn. 1960, 80, 589–597. [Google Scholar] [CrossRef]
- Lanusse, P.; Oustaloup, A.; Sutter, D. CRONE control of multivariable plants with a multi-scalar approach. In Proceedings of the International Symposium of Quantitative Feedback Theory, Glasgow, Scotland, 20–22 August 1997; pp. 73–79. [Google Scholar]
- Lanusse, P.; Oustaloup, A.; Mathieu, B. Robust Control of LTI Square Mimo Plants Using Two Crone Control Design Approaches. IFAC Proc. Vol. 2000, 33, 379–384. [Google Scholar] [CrossRef]
- Liang, S.; Ishitobi, M.; Zhu, Q. Improvement of stability of zeros in discrete-time multivariable systems using fractional-order hold. Int. J. Control 2003, 76, 1699–1711. [Google Scholar] [CrossRef]
- Silva, M.F.; Machado, J.A.T.; Lopes, A.M. Fractional Order Control of a Hexapod Robot. Nonlinear Dyn. 2004, 38, 417–433. [Google Scholar] [CrossRef]
- Gruel, D.N.; Lanusse, P.; Oustaloup, A. Robust Control System Design for Multivariable Plants with Lightly Damped Modes. In Proceedings of the ASME/IEEE International Conference on Mechatronic and Embedded Systems and Applications, Las Vegas, NV, USA, 4–7 September 2007; p. 1. [Google Scholar]
- Pommier-Budinger, V.; Janat, Y.; Nelson-Gruel, D.; Lanusse, P.; Oustaloup, A. CRONE control of a multivariable lightly damped plant. In Proceedings of the MELECON 2008—The 14th IEEE Mediterranean Electrotechnical Conference, Ajaccio, France, 5–7 May 2008. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order; Dover Publications: New York, NY, USA, 2006. [Google Scholar]
- Das, S. Functional Fractional Calculus, 2nd ed.; Springe: Mumbai, India, 2011. [Google Scholar]
- Oustaloup, A.; Bluteau, B.; Nouillant, M. First generation scalar CRONE control: Application to a two DOF manipulator and comparison with non linear decoupling control. In Proceedings of the IEEE Systems Man and Cybernetics Conference—SMC, Le Touquet, France, 17–20 October 1993; pp. 453–458. [Google Scholar]
- Oustaloup, A. La Commande CRONE: Du Scalaire au Multivariable, 2nd ed.; Hermès: Paris, France, 1991. [Google Scholar]
- Oustaloup, A.; Melchior, P.; Lanusse, P.; Cois, O.; Danda, F. The CRONE toolbox for Matlab. In Proceedings of the IEEE International Symposium on Computer-Aided Control System Design, Anchorage, AK, USA, 25–27 September 2000; pp. 190–195. [Google Scholar]
- Gruel, D.N.; Lanusse, P.; Oustaloup, A. Robust control design for multivariable plants with time-delays. Chem. Eng. J. 2009, 146, 414–427. [Google Scholar] [CrossRef]
- Wood, R.K.; Berry, M.W. Terminal composition control of a binary distillation column. Chem. Eng. Sci. 1973, 28, 1707–1717. [Google Scholar] [CrossRef]
- Nguyen, V.Q.; Arunsawatwong, S. Fractional Controller Design for a Binary Distillation Column Using the Method of Inequalities. In Proceedings of the SICE Annual Conference 2008, Tokyo, Japan, 20–22 August 2008. [Google Scholar]
- Silpsrikul, W.; Arunsawatwong, S. Design of Fractional PI Controllers for a Binary Distillation Column with Disturbances Restricted in Magnitude and Slope. In Proceedings of the 18th International Federation of Automatic Control (IFAC) World Congress, Milano, Italy, 28 August–2 September 2011; pp. 7702–7707. [Google Scholar]
- Sivananaithaperumal, S.; Baskar, S. Design of multivariable fractional order PID controller using covariance matrix adaptation evolution strategy. Arch. Control Sci. 2014, 24, 235–251. [Google Scholar] [CrossRef]
- Woiciechovski, C.; Lenzi, E.K.; Santos, A.F.; Lenzi, M.K. Simulation of multivariable fractional control applied to binary distillation. Int. Rev. Chem. Eng. 2017, 9, 60–69. [Google Scholar] [CrossRef]
- Baruah, G.; Majhi, S.; Mahanta, C. Auto-tuning of FOPI Controllers for TITO Processes with Experimental Validation. Int. J. Autom. Comput. 2019, 16, 589–603. [Google Scholar] [CrossRef]
- Haji, V.H.; Monje, C.A. Fractional-order PID control of a MIMO distillation column process using improved bat algorithm. Soft Comput. 2019, 23, 8887–8906. [Google Scholar] [CrossRef]
- Wang, Q.G.; Zhang, Y.; Chiu, M.S. Decoupling internal model control for multivariable systems with multiple time delays. Chem. Eng. Sci. 2002, 57, 115–124. [Google Scholar] [CrossRef]
- Edet, E.; Katebi, R. On Fractional-order PID Controllers. Int. J. Syst. Sci. 2018, 51, 739–744. [Google Scholar] [CrossRef]
- Ogunnaike, B.A.; Lemaire, J.P.; Morari, M.; Ray, W.H. Advanced multivariable control of a pilot-plant distillation column. AICHE J. 1983, 29, 632–640. [Google Scholar] [CrossRef]
- Muresan, C.I.; Dulf, E.H.; Both, R.; Palfi, A.; Caprioru, M. Microcontroller Implementation of a Multivariable Fractional Order PI Controller. In Proceedings of the 19th International Conference on Control Systems and Computer Science, Bucharest, Romania, 29–31 May 2013; pp. 44–51. [Google Scholar]
- Muresan, C.I.; Dulf, E.H.; Ionescu, C. Robustness evaluation of a multivariable fractional order PI controller for time delay processes. Control Intell. Syst. 2014, 42, 112–118. [Google Scholar] [CrossRef]
- Muresan, C.I.; Dulf, E.H.; Ionescu, C.M.; Both, R.; Nascu, I. Improving performance for a 13C isotope separation plant using multivariable fractional order controllers. In Proceedings of the ICFDA’14 International Conference on Fractional Differentiation and Its Applications, Catania, Italy, 23–25 June 2014. [Google Scholar]
- Dulf, E.H.; Kovacs, L. Fractional order control of the cyber-physical cryogenic isotope separation columns cascade system. In Proceedings of the 2018 IEEE International Conference on Automation, Quality and Testing, Robotics (AQTR), Cluj-Napoca, Romania, 24–26 May 2018. [Google Scholar]
- Delavari, H.; Ranjbar, A.N.; Ghaderi, R.; Momani, S. Fractional order control of a coupled tank. Nonlinear Dyn. 2010, 61, 383–397. [Google Scholar] [CrossRef]
- Delavari, H.; Ranjbar, A.N.; Ghaderi, R.; Momani, S. Fuzzy fractional order sliding mode controller for nonlinear systems. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 963–978. [Google Scholar] [CrossRef]
- Tepljakov, A.; Petlenkov, E.; Belikov, J. Gain and order scheduled fractional-order PID control of fluid level in a multi-tank system. In Proceedings of the 2014 International Conference on Fractional Differentiation and its Applications, Catania, Italy, 23–25 June 2014; pp. 1–6. [Google Scholar]
- Tepljakov, A. Fractional-Order Modeling and Control of Dynamic Systems. Ph.D. Thesis, Tallinn University of Technology, Tallinn, Estonia, 2015. [Google Scholar]
- Pradeepkannan, D.; Sathiyamoorthy, S. Design and modeling of fractional order PI controller for a coupled spherical tank MIMO system. Aust. J. Basic Appl. Sci. 2015, 9, 477–485. [Google Scholar]
- Banu, U.S.; Lakshmanaprabu, S.K. Adaptive Multi-Loop Fractional Order PID Controller Tuning Using Bat Colony Optimization for Quadruple Tank Process. In Proceedings of the International Conference on Robotics, Automation, Control and Embedded Systems, Chennai, India, 18–20 February 2015; pp. 18–20. [Google Scholar]
- Banu, U.S.; Lakshmanaprabu, S.K. Multivariable Centralized Fractional Order PID Controller tuned using Harmony search Algorithm for Two Interacting Conical Tank Process. In Proceedings of the SAI Intelligent Systems Conference, London, UK, 10–11 November 2015; pp. 320–327. [Google Scholar]
- Muresan, C.I.; Dutta, A.; Dulf, E.H.; Pinar, Z.; Maxim, A.; Ionescu, C.M. Tuning algorithms for fractional order internal model controllers for time delay processes. Int. J. Control 2016, 89, 579–593. [Google Scholar] [CrossRef]
- Muresan, C.I.; Dulf, E.H.; Copot, C.; de Keyser, R.; Ionescu, C. Design and analysis of a multivariable fractional order controller for a non-minimum phase system. J. Vib. Control 2016, 22, 2187–2195. [Google Scholar] [CrossRef]
- Roy, P.; Roy, B.K. Fractional order PI control applied to level control in coupled two tank MIMO system with experimental validation. Control Eng. Pract. 2016, 48, 119–135. [Google Scholar] [CrossRef]
- Roy, P.; Roy, B.K. Dual mode adaptive fractional order PI controller with feedforward controller based on variable parameter model for quadruple tank process. ISA Trans. 2016, 63, 365–376. [Google Scholar] [CrossRef] [PubMed]
- Lakshmanaprabu, S.K.; Banu, S. Optimal Tuning of Multivariable Centralized Fractional Order PID Controller Using Bat Optimization and Harmony Search Algorithms for Two Interacting Conical Tank Process. Intell. Syst. Appl. 2016, 650, 215–235. [Google Scholar] [CrossRef]
- Castro, F.A. Aplicação de Controladores PID Inteiro e Fracionário com Auto Sintonia Através de lóGica FUZZY. Master’s Thesis, Programa de Pós-Graduação em Engenharia de Controle e Automação, Instituto Federal do Espírito Santo, Vitória, Brazil, 2017. [Google Scholar]
- Lakshmanaprabu, S.K.; Banu, U.S.; Hemavathy, P.R. Fractional order IMC based PID controller design using Novel Bat optimization algorithm for TITO Process. In Proceedings of the 1st International Conference on Power Engineering, Computing and Control, Vellore, India, 2–4 March 2017; pp. 1125–1133. [Google Scholar]
- Lakshmanaprabu, S.K.; Nasir, A.W.; Banu, U.S. Design of Centralized Fractional order PI Controller for Two Interacting Conical Frustum Tank Level Process. J. Appl. Fluid Mech. 2017, 10, 23–32. [Google Scholar]
- Chuong, V.L.; Vu, T.N.L.; Linh, L. Fractional PI Control for Coupled-Tank MIMO System. In Proceedings of the 4th International Conference on Green Technology and Sustainable Development, Ho Chi Minh City, Vietnam, 23–24 November 2018; pp. 347–352. [Google Scholar]
- Gurumurthy, G.; Das, D.K. An FO-[PI]λ controller for inverted decoupled two-input two-output coupled tank system. Int. J. Syst. Sci. 2019, 50, 392–402. [Google Scholar] [CrossRef]
- Lakshmanaprabu, S.K.; Najumnissa, J.D.; Sabura, B.U. Multiloop FOPID Controller Design for TITO Process Using Evolutionary Algorithm. Int. J. Energy Optim. Eng. 2019, 8. [Google Scholar] [CrossRef]
- Lakshmanaprabu, S.K.; Elhoseny, M.; Shankar, K. Optimal tuning of decentralized fractional order PID controllers for TITO process using equivalent transfer function. Cogn. Syst. Res. 2019, 58, 292–303. [Google Scholar] [CrossRef]
- Yousfi, N.; Melchior, P.; Rekik, C.; Derbel, N.; Oustaloup, A. Path tracking design based on Davidson–Cole prefilter using a centralized CRONE controller applied to multivariable systems. Nonlinear Dyn. 2013, 71, 701–712. [Google Scholar] [CrossRef]
- Rojas-Moreno, A. An Approach to Design MIMO FO Controllers for Unstable Nonlinear Plants. IEEE/CAA J. Autom. Sin. 2016, 3, 338–344. [Google Scholar] [CrossRef]
- Yousfi-Allagui, N.; Derbel, N.; Melchior, P. Non-diagonal multivariable fractional prefilter in motion control. Int. J. Model. Identif. Control 2017, 28. [Google Scholar] [CrossRef]
- Yousfi, N.; Allagui, M.; Melchior, P.; Derbel, N. Optimization of a fractional PID controller and prefilter in motion control: MIMO systems. In Proceedings of the 15th International Multi-Conference on Systems, Signals and Devices (SSD), Hammamet, Tunisia, 19–22 March 2018; pp. 99–104. [Google Scholar]
- Yousfi-Allagui, N.; Melchior, P.; Lanusse, P.; Derbel, N. Fractional Approaches Based on Fractional Prefilters in MIMO Path Tracking Design. Control Eng. Appl. Inform. 2018, 20, 33–41. [Google Scholar]
- Allagui, M.; Yousfi, N.; Derbel, N.; Melchior, P. Robust Fractional Order Controller and prefilter tuning in MIMO motion control. In Proceedings of the 15th International Multi-Conference on Systems, Signals and Devices (SSD), Hammamet, Tunisia, 19–22 March 2018; pp. 122–126. [Google Scholar]
- Damodaran, S.; Kumar, T.K.S.; Sudheer, A.P. Model-Matching Fractional-Order Controller Design Using AGTM/AGMP Matching Technique for SISO/MIMO Linear Systems. IEEE Access 2019, 7, 41715–41728. [Google Scholar] [CrossRef]
- Lamara, A.; Lanusse, P.; Colin, G.; Charlet, A.; Chamaillard, Y. A Non-square MIMO Fractional Robust Control for the Airpath of a Diesel Engine. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 3482–3487. [Google Scholar]
- Nelson-Gruel, D.; Chamaillard, Y.; Charlet, A.; Colin, G. Robust control applied to minimize NOx emissions. In Proceedings of the 2014 IEEE Conference on Control Applications (CCA), Juan Les Antibes, France, 8–10 October 2014. [Google Scholar]
- Lamara, A.; Colin, G.; Lanusse, P.; Charlet, A.; Nelson-Gruel, D.; Chamaillard, Y. Pollutant Reduction of a Turbocharged Diesel Engine Using a Decentralized Mimo Crone Controller. Fract. Calc. Appl. Anal. 2015, 18, 307–332. [Google Scholar] [CrossRef]
- Lanusse, P.; Gruel, D.N.; Lamara, A.; Lesobre, A.; Wang, X.; Chamaillard, Y.; Oustaloup, A. Development of a fractional order based MIMO controller for high dynamic engine testbeds. Control Eng. Pract. 2016, 56, 174–189. [Google Scholar] [CrossRef]
- Isfer, L.; Teixeira, G.; Lenzi, E.; Lenzi, M. Fractional control of an industrial furnace. Acta Sci. Technol. 2010, 32, 279–285. [Google Scholar]
- Lin, T.; Balas, V.E.; Lee, T. Synchronization of uncertain fractional order chaotic systems via adaptive interval type-2 fuzzy sliding mode control. In Proceedings of the 2011 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 2011), Taipei, Taiwan, 27–30 June 2011; pp. 2882–2889. [Google Scholar]
- Chenikher, S.; Abdelmalek, S.; Sedraoui, M. Control of uncertainly multi-variable system with fractional PID. In Proceedings of the 16th IEEE Mediterranean Electrotechnical Conference, Yasmine Hammamet, Tunisia, 25–28 March 2012; pp. 1079–1082. [Google Scholar]
- Lei, S.; Zhao, Z.; Zhang, J. Design of fractional order smith predictor controller for non-square system. In Proceedings of the 2016 12th World Congress on Intelligent Control and Automation (WCICA), Guilin, China, 12–15 June 2016; pp. 1703–1707. [Google Scholar]
- Xue, D.; Li, T.; Liu, L. A MATLAB toolbox for multivariable linear fractional-order control systems. In Proceedings of the 2017 29th Chinese Control And Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 1894–1899. [Google Scholar]
- Wang, D.; Zhang, R. Design of distributed PID-type dynamic matrix controller for fractional-order systems. Int. J. Syst. Sci. 2018, 49, 435–448. [Google Scholar] [CrossRef]
- Xue, D.; Li, T. An approach to design controllers for MIMO fractional-order plants based on parameter optimization algorithm. ISA Trans. 2018, 82, 145–152. [Google Scholar] [CrossRef] [PubMed]
- Chekari, T.; Mansouri, R.; Bettayeb, M. Improved Internal Model Control-Proportional-Integral-Derivative Fractional-Order Multiloop Controller Design for Non Integer Order Multivariable Systems. J. Dyn. Syst. Meas. Control 2019, 141, 011014. [Google Scholar] [CrossRef]
- Li, D.; He, X.; Song, T.; Jin, Q. Fractional Order IMC Controller Design for Two-input-two-output Fractional Order System. Int. J. Control Autom. Syst. 2019, 17, 936–947. [Google Scholar] [CrossRef]
- Chu, M.; Xu, C.; Chu, J. Graphical PID tuning method for uncertain fractional-order multivariable systems. J. Vibroeng. 2019, 21, 2273–2285. [Google Scholar] [CrossRef]
- Tar, J.K.; Bencsik, A.L. Fractional order adaptive control for hydraulic differential cylinders. In Proceedings of the IEEE 3rd International Conference on Computational Cybernetics, Mauritius, Mauritius, 13–16 April 2005. [Google Scholar]
- Victor, S.; Melchior, P.; Oustaloup, A. Flatness principle extension to linear fractional MIMO systems: Thermal application. In Proceedings of the 14th IEEE Mediterranean Electrotechnical Conference, Ajaccio, France, 5–7 May 2008; pp. 82–88. [Google Scholar]
- Victor, S.; Melchior, P.; Oustaloup, A. Robust path tracking using flatness for fractional linear MIMO systems: A thermal application. Comput. Math. Appl. 2010, 59, 1667–1678. [Google Scholar] [CrossRef]
- Pisano, A.; Rapaic, M.R.; Jelicic, Z.D.; Usai, E. Sliding mode control approaches to the robust regulation of linear multivariable fractional-order dynamics. Int. J. Robust Nonlinear Control 2010, 20, 2045–2056. [Google Scholar] [CrossRef]
- Jiacai, H.; Hongsheng, L.; Fulin, T.; Di, L. Fractional order sliding mode controller for the speed control of a permanent magnet synchronous motor. In Proceedings of the 2012 24th Chinese Control and Decision Conference (CCDC), Taiyuan, China, 23–25 May 2012; pp. 1203–1208. [Google Scholar]
- Bučanović, L.J.; Lazarević, M.P.; Batalov, S.N. The fractional PID controllers tuned by genetic algorithms for expansion turbine in the cryogenic air separation process. Hem. Ind. 2014, 68, 519–528. [Google Scholar] [CrossRef]
- Luo, J.; Liu, H. Adaptive Fractional Fuzzy Sliding Mode Control for Multivariable Nonlinear Systems. Discret. Dyn. Nat. Soc. 2014, 2014, 10. [Google Scholar] [CrossRef]
- Moradi, M. A genetic-multivariable fractional order PID control to multi-input multi-output processes. J. Process Control 2014, 24, 336–343. [Google Scholar] [CrossRef]
- Das, S. Gramian for Control of Fractional Order Multivariate Dynamic System. Int. J. Appl. Math. Stat. 2013, 37, 71–96. [Google Scholar]
- Vinagre, B.M.; Tejado, I.; Romero, M.; Sierociuk, D. Loop transfer recovery for fractional order control systems. First results. In Proceedings of the 17th International Carpathian Control Conference (ICCC), Tatranska Lomnica, Slovakia, 29 May–1 June 2016; pp. 782–787. [Google Scholar]
- Aguila-Camacho, N.; Leroux, J.D.; Duarte-Mermoud, M.A.; Orchard, M.E. Control of a grinding mill circuit using fractional order controllers. J. Process Control 2017, 53, 80–94. [Google Scholar] [CrossRef]
- Nasirpour, N.; Balochian, S. Optimal design of fractional-order PID controllers for multi-input multi-output (variable air volume) air-conditioning system using particle swarm optimization. Intell. Build. Int. 2017, 9, 107–119. [Google Scholar] [CrossRef]
- Feliu-Batlle, V.; Rivas-Perez, R.; Linares-Saez, A. Fractional Order Robust Control of a Reverse Osmosis Seawater Desalination Plant. IFAC PapersOnLine 2017, 50, 14545–14550. [Google Scholar] [CrossRef]
- Aguiar, R.A.; Franco, I.C.; Leonardi, F.; Lima, F. Fractional PID Controller Applied to a Chemical Plant with Level and pH Control. Chem. Prod. Process. Model. 2018, 13. [Google Scholar] [CrossRef]
- Yin, C.; Dadras, S.; Huang, X.; Cheng, Y.; Malek, H. The design and performance analysis of multivariate fractional-order gradient-based extremum seeking approach. Appl. Math. Model. 2018, 62, 680–700. [Google Scholar] [CrossRef]
- Kumar, L.; Kumar, P.; Narang, D. Tuning of Fractional Order PIλDμ Controllers using Evolutionary Optimization for PID Tuned Synchronous Generator Excitation System. IFAC PapersOnLine 2018, 51, 859–864. [Google Scholar] [CrossRef]
- Roy, P.; Das, A.; Roy, B.K. Cascaded fractional order sliding mode control for trajectory control of a bal and plate system. Trans. Inst. Meas. Control 2018, 40, 701–711. [Google Scholar] [CrossRef]
- Juchem, J.; Muresan, C.; Dekeyser, R.; Ionescu, C.M. Robust fractional-order auto-tuning for highly-coupled MIMO systems. Heliyon 2019, 5, e02154. [Google Scholar] [CrossRef] [PubMed]
- Mondal, R.; Dey, J. Fractional Order (FO) Two Degree of Freedom (2-DOF) control of Linear Time Invariant (LTI) plants. ISA Trans. 2019. [Google Scholar] [CrossRef]
- Quadros, T.D. Identificação e Controle de Sistema Térmico Multivariável Experimental. Master’s Thesis, Pós-Graduação em Engenharia Química, Universidade Federal do Paraná, Curitiba, Brazil, 2019. [Google Scholar]
- Yousfi, N.; Melchior, P.; Jallouli-Khlif, R.; Lanusse, P.; Derbel, N.; Oustaloup, A. Input/Output Fractional Transfer Function in Path Tracking Design using multivariable CRONE controller. In Proceedings of the 10th International Multi-Conference on Systems, Signals and Devices (SSD), Hammamet, Tunisia, 18–21 March 2013; pp. 1–8. [Google Scholar]
- Yousfi-Allagui, N.; Lanusse, P.; Khlif, R.J.; Derbel, N.; Melchior, P.; Oustaloup, A. Path tracking design by frequency band limited fractional differentiator prefilter: Square MIMO systems. In Proceedings of the ICFDA’14 International Conference on Fractional Differentiation and Its Applications, Catania, Italy, 23–25 June 2014; pp. 1–7. [Google Scholar]
- Yousfi, N.; Melchior, P.; Lanusse, P.; Derbel, N.; Oustaloup, A. Decentralized CRONE control of nonsquare multivariable systems in path-tracking design. Nonlinear Dyn. 2014, 76, 447–457. [Google Scholar] [CrossRef]
- Song, X.; Chen, Y.; Tejado, I.; Vinagre, B.M. Multivariable fractional order PID controller design via LMI approach. In Proceedings of the 18th IFAC World Congress (IFAC’11), Milano, Italy, 2 September 2011; pp. 13960–13965. [Google Scholar]
- Song, J.; Wang, L.; Cai, G.; Qi, X. Nonlinear fractional order proportion-integral-derivative active disturbance rejection control method design for hypersonic vehicle attitude control. Acta Astronaut. 2015, 111, 160–169. [Google Scholar] [CrossRef]
- Jakovljevic, B.; Pisano, A.; Rapaic, M.R.; Usai, E. On the sliding-mode control of fractional-order nonlinear uncertain dynamics. Int. J. Robust Nonlinear Control 2016, 26, 782–798. [Google Scholar] [CrossRef]
- Lanusse, P.; Tari, M. Simplified fractional-order design of a MIMO robust controller. Fract. Calc. Appl. Anal. J. 2019, 22, 1177–1202. [Google Scholar] [CrossRef]
- Chuong, V.L.; Vu, T.N.L.; Truong, N.T.N.; Jung, J.H. A Novel Design of Fractional PI/PID Controllers for Two-Input-Two-Output Processes. Appl. Sci. 2019, 9, 5262. [Google Scholar] [CrossRef]
- Chekari, T.; Mansouri, R.; Bettayeb, M. IMC-PID Fractional Order Filter Multi-loop Controller Design for Multivariable Systems Based on Two Degrees of Freedom Control Scheme. Int. J. Control Autom. Syst. 2018, 16, 689–701. [Google Scholar] [CrossRef]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control: Analysis and Design, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2005. [Google Scholar]
- Luyben, W.L. Simple method for tuning SISO controllers in multivariable systems. Ind. Eng. Chem. Process. Des. Dev. 1986, 25, 654–660. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Y.Q. Ideal, Simplified and Inverted Decoupling of Fractional Order TITO Processes. In Proceedings of the 19th World Congress The International Federation of Automatic Control (IFAC), Cape Town, South Africa, 24–29 August 2014. [Google Scholar]
- Wang, Q.G.; Huanga, B.; Guo, X. Auto-tuning of TITO decoupling controllers from step tests. ISA Trans. 2000, 39, 407–418. [Google Scholar] [CrossRef]
- Morsi, A.; Abbas, H.S.; Mohamed, A.M. Wind turbine control based on a modified model predictive control scheme for linear parameter-varying systems. IET Control Theory Appl. 2017, 11, 3056–3068. [Google Scholar] [CrossRef]
- Zennir, Y.; Guechi, E.; Bendib, R. Robust fractional multi-controller design of inverted pendulum system. In Proceedings of the 2016 20th International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 13–15 October 2016; pp. 277–282. [Google Scholar]
- Mishra, S.K.; Purwar, S. To design optimally tuned FOPID controller for twin rotor MIMO system. In Proceedings of the 2014 Students Conference on Engineering and Systems, Allahabad, India, 28–30 May 2014. [Google Scholar]
- Cajo, R.; Muresan, C.I.; Ionescu, C.M.; de Keyser, R.; Plaza, D. Multivariable Fractional Order PI Autotuning Method for Heterogeneous Dynamic Systems. IFAC PapersOnLine 2018, 51, 865–870. [Google Scholar] [CrossRef]
- Dworak, P. On Dynamic Decoupling of MIMO Fractional Order Systems. Theor. Dev. Appl. Non-Integer. Order Syst. 2016, 357, 217–232. [Google Scholar] [CrossRef]
- Hunek, W.P.; Wach, L. A New Stability Theory for Grünwald–Letnikov Inverse Model Control in the Multivariable LTI Fractional-Order Framework. Symmetry 2019, 11, 1322. [Google Scholar] [CrossRef]
- Hunek, W.P.; Wach, L. New Approaches to Minimum-Energy Design of Integer and Fractional-Order Perfect Control Algorithms. In Proceedings of the International Conference Energy, Environment and Material Systems, Osaka, Japan, 23 October 2017. [Google Scholar]
- Cheng, S.; Wei, Y.; Chen, Y.; Wang, Y.; Liang, Q. Fractional-order multivariable composite model reference adaptive control. Int. J. Adapt. Control Signal Process. 2017, 31, 1467–1480. [Google Scholar] [CrossRef]
- Khanra, M.; Pal, J.; Biswas, K. Reduced Order Approximation of MIMO Fractional Order Systems. IEEE J. Emerg. Sel. Top. Circuits Syst. 2013, 3, 451–458. [Google Scholar] [CrossRef]
- Wang, Q.G.; Hang, C.; Zhang, Y.; Bi, Q. Multivariable Controller Auto Tinning With Its Application In HVAC Systems. In Proceedings of the American Control Conference, San Diego, CA, USA, 2–4 June 1999; pp. 4353–4357. [Google Scholar]
- Podlubny, I.; Petráš, I.; Vinagre, B.M.; O’Leary, P.; Dorčák, L. Analogue Realizations of Fractional-Order Controllers. Nonlinear Dyn. 2002, 29, 281–296. [Google Scholar] [CrossRef]
- Shah, P.; Agashe, S. Review of fractional PID controller. Mechatronics 2016, 38, 29–41. [Google Scholar] [CrossRef]
- Tepljakov, A.; Alagoz, B.B.; Yeroglu, C.; Gonzalez, E.; HosseinNia, S.H.; Petlenkov, E. FOPID Controllers and Their Industrial Applications: A Survey of Recent Results. IFAC PapersOnLine 2018, 51, 25–30. [Google Scholar] [CrossRef]
- Birs, I.; Muresan, C.; Nascu, I.; Ionescu, C. A Survey of Recent Advances in Fractional Order Control for Time Delay Systems. IEEE Access 2019, 7, 30951–30965. [Google Scholar] [CrossRef]
- Chevalier, A.; Francis, C.; Copot, C.; Ionescu, C.M.; Keyser, R.D. Fractional-order PID design: Towards transition from state-of-art to state-of-use. ISA Trans. 2019, 84, 178–186. [Google Scholar] [CrossRef] [PubMed]
- Nelson-Gruel, D.; Lanusse, P.; Oustaloup, A. Decentralized CRONE Control of mxn Multivariable System with Time-Delay. New Trends Nanotechnol. Fract. Calc. Appl. 2010, 377–391. [Google Scholar] [CrossRef]
- Liu, F.; Li, X.; Liu, X.; Tang, Y. Parameter identification of fractional-order chaotic system with time delay via multi-selection differential evolution. Syst. Sci. Control Eng. Open Access J. 2017, 5, 42–48. [Google Scholar] [CrossRef]
- Isfer, L.A.D. Aplicação de Técnicas de Identificação e Controle Fracionários à Indústria Petroquímica. Master’s Thesis, Pós-Graduação em Engenharia Química, Universidade Federal do Paraná, Curitiba, Brazil, 2009. [Google Scholar]
- Normey-Rico, J.E.; Camacho, E.F. Control of Dead-Time Processes; Springer: London, UK, 2007. [Google Scholar]
- Ziegler, J.G.; Nichols, N.B. Optimum Settings for Automatic Controllers. Trans. Am. Soc. Mech. Eng. 1942, 64, 759–768. [Google Scholar] [CrossRef]
- O’Dwyer, A. Handbook of PI and PID Controller Tuning Rules, 3rd ed.; Imperial College Press: London, UK, 2009. [Google Scholar]
- Hovd, M.; Skogestad, S. Sequential design of decentralized controllers. Automatica 1994, 30, 1601–1607. [Google Scholar] [CrossRef]
- Grosdidier, P.; Morari, M. A computer aided methodology for the design of decentralized controllers. Comput. Chem. Eng. 1987, 11, 423–433. [Google Scholar] [CrossRef]
- Skogestad, S.; Morari, M. Robust performance of decentralized control systems by independent designs. Comput. Chem. Eng. 1989, 25, 119–125. [Google Scholar] [CrossRef]
- Murill, P.W. Automatic Control of Processes; International Textbook: Scranton, PA, USA, 1967. [Google Scholar]
- Awouda, A.E.A.; Mamat, R.B. Refine PID tuning rule using ITAE criteria. In Proceedings of the 2nd International Conference on Computer and Automation Engineering (ICCAE), Singapore, 26–28 February 2010; pp. 171–176. [Google Scholar]
- Åström, K.J.; Hägglund, T. Revisiting the Ziegler–Nichols step response method for PID control. J. Process Control 2004, 14, 635–650. [Google Scholar] [CrossRef]
- Hägglund, T.; Åström, K.J. Revisiting The Ziegler-Nichols Tuning Rules For PI Control. Asian J. Control 2002, 4, 364–380. [Google Scholar] [CrossRef]
- Martelli, G. Technical communique: Stability of PID-controlled second-order time-delay feedback systems. Automatica 2009, 45, 2718–2722. [Google Scholar] [CrossRef]
- Hafsi, S.; Laabidi, K.; Farkh, R. Synthesis of a fractional PI controller for a first-order time delay system. Trans. Inst. Meas. Control 2013, 35, 997–1007. [Google Scholar] [CrossRef]
- Zhao, X.W.; Ren, J.Y. PID stabilization of retarded-type time-delay system. Asian J. Control 2014, 16, 1229–1237. [Google Scholar] [CrossRef]
- Valério, D.; da Costa, J.S. A review of tuning methods for fractional PIDs. In Proceedings of the 4th IFAC Workshop on Fractional Differentiation and Its Applications, Badajoz, Spain, 18–20 October 2010; p. 10. [Google Scholar]
- Valério, D.; Costa, J. Ninteger: A non-integer control toolbox for Matlab. In Proceedings of the IFAC Workshop on Fractional Differentiation and Its Applications, Bordeaux, France, 19–21 July 2004; pp. 208–213. [Google Scholar]
- Bristol, E. On a new measure of interaction for multivariable process control. IEEE Trans. Autom. Control 1966, 11, 133–134. [Google Scholar] [CrossRef]
- Liu, C.H. General Decoupling Theory of Multivariable Process Control Systems (Lecture Notes in Control and Information Sciences), 1st ed.; Springer: Berlin, Germany, 1983. [Google Scholar]
- Lanusse, P.; Malti, R.; Melchior, P. CRONE control system design toolbox for the control engineering community: Tutorial and case study. Philos. Trans. R. Soc. 2013, 371, 120–149. [Google Scholar] [CrossRef]
- Wach, L.; Hunek, W.P. Perfect Control for Fractional-Order Multivariable Discrete-Time Systems. Theor. Dev. Appl. Non-Integer. Order Syst. Lect. Notes Electr. Eng. 2016, 357, 233–237. [Google Scholar] [CrossRef]
- Tepljakov, A.; Petlenkov, E.; Belikov, J. FOMCON: Fractional-order modeling and control toolbox for MATLAB. In Proceedings of the 18th International Conference Mixed Design of Integrated Circuits and Systems—MIXDES, Gliwice, Poland, 16–18 June 2011; pp. 684–689. [Google Scholar]
- Monje, C.A.; Vinagre, Y.C.B.M.; Xue, D.; Feliu, V. Fractional-order Systems and Controls: Fundamentals and Applications; Springer Science Business Media: Glasgow, UK, 2010. [Google Scholar]
| References | Applications | Controller | CV * | MV * | PS * |
|---|---|---|---|---|---|
| [21] | LTI square MIMO uncertain plants | Multi-SISO and MIMO CRONE | Not specified | Not specified | |
| [22] | Electronic circuit 2 × 2 | Adaptive control with AFROH * | Voltage (V) output 1 and 2 | Voltage (V) input 1 and 2 | Zeros of the discrete-time |
| [86] | Differential hydrauIic cylinders 2 × 2 | FO Adaptive control | Pressure ( and ) | Oil volume ( and ) | Not specified |
| [24] | Active-suspension system 2 × 2 | CRONE generation | |||
| [25] | Aircraft wing model 2 × 2 | CRONE generation | Wing vibrations | Vibration attenuators | Frequency domain and the Bode diagrams |
| [89] | Long aluminum rod FO model 3 × 3 | SMC * | Temperature | Thermal flux | - |
| [87,88] | Long aluminum rod 2 × 2 | CRONE generation and PID | and two extreme points | Heat flow density | Nichols diagram and output error |
| [77] | FO Duffing–Holmes chaotic systems 2 × 2 | AITFSMC * | trajectories states x and y | Trajectory of the control effort | Mean square errors |
| [106,107,108] | FO-MIMO systems 2 × 2 and 3 × 2 | CRONE and QFT * | Amplitude responses and | and | |
| [109,110] | FO-LTI MIMO systems and Hypersonic vehicle and 6-DOF model | nonlinear | State responses and attack angles | Input and input parameters | ITAE |
| [79,95,111] | NSS */ARSV */ FOPDT * 3 × 3 and 3 × 2 and 3 × 3 | FSMC */ LTR-FOKF */ FO-IMCSP * | State space and output | Input | ITAE and LQR * cost function |
| [96] | Single stage ore milling plant 5×3 | FOPI FOMRAC * | Particle size, ore load and mud volume | CFF *, OF *, CFW *, MFW *, MBF * | NRMSE *, NRMSI * |
| [81,82] | FO-MIMO with dead time and without dead time 3 × 3 and 2 × 2 | FFO-DDMC | Output | Input | Developed by authors and Nyquist and Bode diagram |
| [83,84,85] | FO-MIMO with dead time and without dead time 2 × 2 and 3 × 2 and 3 × 3 | PID, FO-IMC, FO-PID | Output | Input | Bode diagram, ITAE, settling time, overshoot, maximum sensitivity |
| References | Applications | Controller | CV * | MV * | PS * |
|---|---|---|---|---|---|
| [112] | Refrigeration system TITO | CRONE decentralized, PID | * and * | * and * | Nichols analysis and objective function |
| [33,34,38] | Binary distillation column by [32] | Multi-loop FO-PID, FO-PI, IO-PI | and | R and S | ISE, IAE, ITSE, ITAE, overshoot, cost function defined by authors |
| [113] | Heavy oil fractionator by [115], distillation column by [32], flash distillation column by [116] | IMC FO-PI/PID and Smith predictor | and | and | IAE, ITAE and TV * |
| [36,117] | FO-TITO systems: binary distillation column by [32] and thermal system by [117] | FO-PI and IO-PI multiloop | and , and | R and S, and | ISE, ITAE, settling time, overshoot |
| [65,68,69,70] | SCARA * robot model TITO | FO-PD and *, CRONE and , - | Amplitude | and | Rise time, settling time, cost function defined by authors |
| [31,35,40,114] | Distillation column by [32,39,41,118] | IMC-PID, FO-PI, optimal PI, FO-PID, PID, PI, CRONE 3th generation | Distillate and bottom composition | Reflux flow and reboiler steam flow | Overshoot, settling time, IAE, analysis of responses in frequency domain |
| [45] | Isotopic separation column cascade 9 × 9 | FO observer and FO-PI | Top and bottom pressure, liquid CO level | Waste flow, feed flow, electrical power supplied to the boiler | Gain crossover frequency, phase margin, isodamping property |
| [43,44] | 13C isotope separation plant 3 × 3 | FO-PI with Smith’s predictor, PI | , , | , , | Overshoot, settling time |
| [90,101] | Synchronous generator excitation system, permanent magnet synchronous motor (PMSM) | Cascaded IO-PID and FO-PID, FOSMC * | Excitation voltage, rotor speed | Synchronous voltage obtained by synchronous transformer, Current, torque | Routh’s criterion, ISE, minimization of robustness stability scale function, control effort |
| [119] | Wind turbine with space state model 2 × 5 | MPC-LPV * and LFT * | RS *, AS *, TF *, GT *, BP * | GT reference, BP reference | Wind speed variation, power efficiency coefficien |
| [97] | Air-conditioning VAV * system 2 × 2 | PSO *-, PSO-PID, GA *-PID | Temperature supply air, temperature thermal space | Flow of cold water, flow air supply | Rise time, overshoot, settling time, ITSE |
| [110,120] | Inverted pendulum system, hypersonic vehicle 6-DOF model | FO-PID, IO-PID | Pendulum angle (rad), pendulum velocity (rad/s), state responses and attack angles | Input , input parameters | Control error, ITAE |
| [121] | Twin rotor TITO system | FO-PID, IO-PID | Pitch (elevation) angle, yaw (azimuth) angle | Input voltage main rotor, input voltage tail rotor | Control effort, ISE |
| [91] | Expansion turbine in cryogenic air separation TITO process | FO-PID, IO-PID | Inlet temperature and air flow in the expansion turbine | Air outlet and inlet flow in the separator | Overshoot, settling time, IAE |
| [87,88,89] | Long aluminum rod 2 × 2, 3 × 3 | CRONE generation, PID, SMC * | Temperature | Heat flow density, thermal flux | Nichols diagram and output error |
| [46,47] | Coupled tanks 2 × 2, 2-DOF polar robot manipulator | PD-SMC, FO-PD, FO-PID, SMC, FO-PD, Fuzzy-SMC | Level , , tracking response of joint 1 and 2 | The inflow rate into Tank 1, control signal and | ISE, cost function defined by authors |
| [24] | Widely studied TITO active-suspension system | CRONE generation | Output and | Intput and | Minimizes the robustness cost function |
| [86] | Differential hydrauIic cylinders | FO adaptive control | Piston trajectory | Variation of the pressure | Not specified |
| References | Applications | Controller | PS * |
|---|---|---|---|
| [80,82,85] | FOPDT TITO model | PID FO-EOTF *, optimal FO-PID | Nyquist and Bode diagram |
| [83,84] | FO-TITO system by [117,123] | FO-IMC and FO-PID | Maximum sensitivity, overshoot, settling time |
| [109,124,125] | LTI MIMO plant 3 × 2 and 2 × 2 | FO-MIMO, FO-PID and SOF * | |
| [79,81] | FO-MIMO FOPDT model 3 × 3 and 3 × 2 | FO-DDMC, DDMC *, IMC and FO-Smith predictor | *, *, ITAE, undamped oscillation frequency, overshoot, the peak time |
| [122,126,127] | TITO models of heterogeneous systems, Generic FO-TITO system | FO-PI, FO-IMC, MRAC *, CMRAC * | ISE, IAE, tracking error, control cost |
| [111] | State space model single input 1 × 3 and multiple inputs 3 × 3 | Sliding-mode-based fractional control and PI based | Not specified |
| [106,107,108] | MIMO uncertain system 3 × 2, 2 × 2 | CRONE generation and QFT, Davidson–Cole prefilter MIMO QFT and CRONE | SSE *, overshoot, integral gap optimization |
| [92] | Non-linear MIMO systems: generic system 2 × 2 and a chaotic 3D saturated multiscroll system 3 × 3 | Adaptive FO-FUZZY and IO-FUZZY | Tracking errors, time response of Fuzzy system parameters |
| [93] | HVAC pilot system TITO model by [78] | -FOPID, GA-FOPID | IAE, ISE, ITAE |
| [78] | TITO plant with time delay proposed by [128] | FO-PID, IO-PID | Stability robustness, tracking with disturbance and noise minimization |
| References | Applications | Controller | CV * | MV * | PS * |
|---|---|---|---|---|---|
| [105] | EMBFL * | FO-PI, IO-PI | Temperature and luminescence | Air flow through the fan voltage, energy flow through the heating lamp voltage | IAE, ISE, ITAE, OS * |
| [104] | IPN *, LML *, CIP *, TRM * | 2-DOF FO-PID, IO-PID | Amplitude, pitch angle, yaw angle | Not specified | OS *, ST *, FLTF *, pole positions |
| [57,60,63,64] | TITO system of two coupled conical tanks, flash distillation column proposed by [116] | Multiloop FO-PID, IMC-PID, IO-PI, FO-PI, FO-PID, CFO-PID * and FO-PI, C/D-PI * | Level , and , | Pump rotation speed (flow into the tanks) | IAE, ISE, ITAE |
| [103] | Experimental test bench for an office lighting system 8 × 8 | FO-PI, IO-PI | Light intensity of the lamps | Lamps voltage | IAE, power consumption |
| [71] | FO/IO MIMO plants with time delays, wheeled mobile robot | FO-PID, IO-PID | Amplitude, velocity profiles right wheel and left wheel | Defined only as input | |
| [37] | TITO systems: binary distillation column by [32] and an experimental module with four coupled tanks | Auto-tuning FOPI, IO-PI | Distilled top and bottom composition, level tanks | Output flow tanks | IAE, ITAE, ISE, TV * |
| [61,62] | TITO system of coupled tanks | FO-, FO-, IO-PI, IO-PID, FO-PI | Level , | Flow rates of inlet streams | ST *, OS *, IAE, NCI *, MAV *, Bode diagram |
| [58] | Laboratory scale pressure and level control modules | FO-PID Fuzzy, IO-PID | Level and pressure | Not specified | ISE, IAE, ITAE, ITSE, OS *, rise time, ST * |
| [51,52,55,56] | TITO system of coupled tanks | FF * FO-PI, FF * PI/PID/2DOF-PI/ 3DOF-PI, FF-DMAFOPI *, centralized FO-PID,FO-PID | Level , | Flow rates of inlet streams | ISE, OS *, ST *, tracking error, rise time, IAE, ITAE |
| [53,54] | Experimental module with four coupled tanks for TITO problem | FO-IMC with Smith’s predictor, IO-IMC, decoupled FO-PI, decentralized FO-PI, IMC | Level , | Flow rates of inlet (voltage pumps) | Bode diagram, control effort, ISE |
| [50] | TSCT * | FO-PI, IO-PI | Level , | Feed flow tanks | OS *, *, RT *, ISE, IAE |
| [48,49] | Several examples of FO-FOPDT * systems: TCT *, MTL *, MLS * | FO-PID, FO-PI, IO-PID, IO-PI | Output y, level tanks, ball position in the levitation module | Input u, feed flow tanks | ISE, IAE, ITSE, ITAE, stability analysis of time and frequency domain |
| [102] | Experimental TITO non-linear ball and plate system | Cascaded FO-SMC, SMC | Motion along the x and y axes | Applied current to the actuator | IAE, *, *, *, *, * |
| [100] | MISO nonlinear system, light leds and sensor experimental model with Arduino 2560 board | FO-GESC *, IO-GESC, PID | Time responses of , indoor illumination | Energy consumption | Minimization of energy consumption |
| [99] | Laboratory scale pH neutralization TITO | FO-PID, IO-PID | pH and tank level | Speed Rotating pumps of and | Control effort, ITAE |
| [98] | Reverse Osmosis Seawater Desalination Plant TITO | FO-PI, IO-PI | Permeate flow rate, permeate conductivity | Feed pressure, brine flow rate | OS *, *, frequency specifications |
| [75] | High dynamic engine testbeds TITO | CRONE MIMO | Engine speed (rpm) and torque (Nm) | Variation of current and throttle | Bode analysis and regression analysis for identification |
| [66] | RAM *, CTM * 2DOF | FO-PID MIMO and SISO | APM *, CAPTM * | Input u not specified | Control force |
| [72,74] | Diesel engine 2 × 3 and 3 × 2 | Decentralized CRONE MIMO | Air-flow and boost pressure | EGR *, WG *, * | Bode plots and Nichols chart, robustness cost function |
| [73] | Engine–dynamometer test-bed: diesel engine 3 × 3 | CRONE MIMO based on generation | Mass air flow, boost pressure, NOx emissions | EGR *, geometry turbine, start of injection | Bode diagram of the real system |
| [25] | MIMO lightly damped plant: aircraft wing model 2 × 2 | CRONE MIMO based on generation | Wing vibrations | Vibration attenuators | Frequency domain and the Bode diagrams |
| [23] | Hexapod robot 2 × 2 | FO-PD, IO-PD | Motion trajectories of the multi-legged robot | Joint torques | Nyquist plots, indexes based on robot dynamics, indexes based on hip trajectory tracking errors |
| [22] | Electronic circuit 2 × 2 | Adaptive control with AFROH * | Voltage (V) output 1 and 2 | Voltage (V) input 1 and 2 | Zeros of the discrete-time |
| References | Applications | Controller | Experimental, Simulation or Both? |
|---|---|---|---|
| [112] | Refrigeration system TITO | CRONE decentralized, PID | Simulation |
| [65,67,69] | SCARA robot model TITO | CRONE and QFT MIMO using fractional prefilter of type Davidson Cole | Simulation |
| [75] | High dynamic engine testbeds TITO | FO-MIMO CRONE Control-System Design (CSD) | Experimental and Simulation |
| [72,74] | Diesel engine, 2 × 3 and 3 × 2 | Decentralized CRONE | Experimental and Simulation |
| [106,107,108] | MIMO systems, 3 × 2 and 2 × 2 | MIMO-QFT multi-SISO CRONE and Davidson–Cole prefilter | Simulation |
| [24,31,73,134] | Engine–dynamometer test-bed 3 × 3, distillation column by [39,118] 2 × 2, MIMO plants with time-delay, active-suspension system 2 × 2 | Third generation CRONE | Experimental and Simulation |
| [88] | Aluminum metal rod TITO system | Third generation CRONE, IO-PID | Simulation |
| [25] | MIMO lightly damped plant: aircraft wing model 2 × 2 | Third generation CRONE | Experimental and Simulation |
| [20,21] | MIMO uncertain LTI system | Multi-scalar, multi-SISO and MIMO CRONE | Simulation |
| References | Applications | Controller | Experimental, Simulation or Both? |
|---|---|---|---|
| [105] | Experimental module composed of box, fan, lamp and sensors for TITO problem | FO-PI, IO-PI | Experimental and Simulation |
| [104] | Immersed plate in a Newtonian fluid, LTI unstable Magnetic Levitation system, cart-inverted pendulum SIMO system, twin rotor MIMO system | 2-DOF FO-PID, IO-PID | Experimental and Simulation |
| [80,82,85] | FO-FOPDT model TITO | PID with FO-EOTF *, optimal FO-PID | Simulation |
| [51,52,57,60,63,64] | Coupled conical tanks TITO, flash distillation column by [116], module with four coupled tanks for TITO problem | MCFOPID *, FO-PID, IMC, FO-PI, CFO-PI *, C-PI *, D-PI *, CFO-PID * | Experimental and Simulation |
| [103] | Experimental test bench for an office lighting system 8 × 8 | FO-PI, IO-PI | Experimental and Simulation |
| [38] | Binary distillation column by [32] | Multi-loop FO-PID | Simulation |
| [71] | FO/IO MIMO plants with time delays, wheeled mobile robot | FO-PID, IO-PID | Experimental and Simulation |
| [37] | TITO systems: binary distillation column by [32] and an experimental module with four coupled tanks | Auto-tuning FOPI | Experimental and Simulation |
| [61,62] | TITO system of coupled tanks | FO-, FO-, IO-PI, IO-PID, FO-PI | Experimental and Simulation |
| [36] | FO-TITO systems: binary distillation column by [32] and thermal system by [117] | FO-PI and IO-PI multiloop | Simulation |
| [68,70] | SCARA * robot model TITO | FO-PD and QFT, and QFT | Simulation |
| [101] | Synchronous generator excitation system | Cascaded IO-PID, FO-PID | Simulation |
| [40] | Distillation column by [41] 3 × 3 | FO-PI, optimal PI | Simulation |
| [122] | Two models of heterogeneous TITO systems | FO-PI (cross-gain method), FO-PI (KC method), FO-IMC | Simulation |
| [99] | Laboratory scale pH neutralization TITO | FO-PID, IO-PID | Experimental and Simulation |
| [50,98] | Reverse Osmosis Seawater Desalination Plant TITO, process with two spherical coupled tanks TITO | FO-PI, IO-PI | Experimental and Simulation |
| [120] | Inverted Pendulum system | FO-PID multi-controller approach, IO-PID | Simulation |
| [58] | Laboratory scale pressure and level control modules | FO-PID Fuzzy, IO-PID | Experimental and Simulation |
| [96] | Single stage ore milling plant | FO-PI, FOMRAC * | Experimental and Simulation |
| [54] | Experimental module with four coupled tanks for TITO problem | Decoupled FO-PI, DFO-PI *, IMC | Experimental and Simulation |
| [42,43,44] | 13C isotope separation plant 3 × 3 | FO-PI with Smith’s predictor, FO-PI, IO-PI | Simulation |
| [66] | Robot armt manipulator 2DOF, car with translational manipulator 2DOF | FO-PID MIMO and SISO | Experimental and Simulation |
| [109,110] | FO-LTI MIMO systems and Hypersonic vehicle | nonlinear, FO-PID and SOF * | Simulation |
| [48,49] | FO-FOPDT * systems: TITO coupled tanks, multi-tank laboratory system, magnetic levitation system | FO-PID, FO-PI, IO-PID, IO-PI | Experimental and Simulation |
| [35] | Binary distillation columns by [32] (2 × 2) and by [41] (3 × 3) | FO-PI, FO-PID, IO-PI, IO-PID | Simulation |
| [93] | VAC pilot system TITO model by [78] | -FOPID, GA-FOPID | Simulation |
| [121] | Twin rotor TITO system | FO-PID, IO-PID | Simulation |
| [91] | Expansion turbine in the cryogenic air separation TITO process | FO-PID, IO-PID | Simulation |
| [78] | TITO plant with time delay proposed by [128] | FO-PID, IO-PID from literature | Simulation |
| [34] | Binary distillation column by [32] | FO-PI, IO-PI | Simulation |
| [46,47] | Coupled tanks 2 × 2, 2-DOF polar robot manipulator | PD-SMC, FO-PD, FO-PID, SMC, FO-PD, Fuzzy-SMC | Simulation |
| [136] | Two common systems in the petrochemical industry with multivariable parameter estimation | P, PI, PD and PID of fractional order and FO-IMC | Simulation |
| [33] | Binary distillation column by [32] | Decentralized and centralized FO-PI, IO-PI | Simulation |
| [23] | Hexapod robot 2 × 2 | FO-PD, IO-PD | Experimental and Simulation |
| References | Applications | Controller | Experimental, Simulation or Both? |
|---|---|---|---|
| [84] | FO-TITO system proposed by [117] | FFO-IMC, FO-PID | Simulation |
| [124] | LTI FO-MIMO plant 3 × 2 | GL-IMC | Simulation |
| [113] | Heavy oil fractionator by [115], distillation column by [32], flash distillation column by [116] | IMC FO-PI/PID and Smith predictor | Simulation |
| [83] | FO-TITO system by [117,123] | FO-IMC and FO-PID | Simulation |
| [45] | Isotopic separation column cascade 9 × 9 | FO observer and FO-PI | Simulation |
| [79,81] | FO-MIMO FOPDT model 3 × 3 and 3 × 2 | FO-DDMC, DDMC *, IMC and FO-Smith predictor | Simulation |
| [102] | Experimental TITO non-linear ball and plate system | Cascaded FO-SMC, SMC * | Experimental and Simulation |
| [114] | TITO system with transfer function matrix by [137], distillation column according by [41] | IMC-PID FO-Filter | Simulation |
| [135] | Chaotic system of n-dimensional fractional order with time delay model | MS-DE * | Simulation |
| [59] | Transfer function matrix of coupled conical tanks | IMC-PID, FO-IMC-, FO-IMC- | Simulation |
| [126] | Generic FO-TITO system | MRAC *, CMRAC * | Simulation |
| [119] | Wind turbine with space state model 2 × 5 | MPC-LPV * and LFT * | Simulation |
| [125] | TITO LTI system in state space defined by authors | EMPC * | Simulation |
| [97] | Air-conditioning VAV * system 2 × 2 | PSO *-, PSO-PID, GA *-PID | Simulation |
| [55,56] | TITO system of coupled tanks | FF * FO-PI, FF * PI/PID/2DOF-PI/3DOF-PI, FF-DMAFOPI * | Simulation |
| [95] | Aircraft roll-dynamics, servomotor velocity-dynamics 3 × 3 | LTR-FOKF * | Simulation |
| [111] | State space model single input 1 × 3 and multiple inputs 3 × 3 | Sliding-mode-based fractional control and PI based | Simulation |
| [53] | Experimental module with four coupled tanks for TITO problem | FO-IMC with Smith’s predictor, IO-IMC | Experimental and Simulation |
| [92] | Non-linear MIMO systems: generic system 2 × 2 and a chaotic 3D saturated multiscroll system 3 × 3 | Adaptive FO-FUZZY and IO-FUZZY | Simulation |
| [90] | TITO permanent magnet synchronous motor (PMSM) | FOSMC * | Simulation |
| [89] | Test bench involving long aluminum rod heated from one of its sides 3 × 3 | FSMC *, MSTSSMC * | Simulation |
| [86] | Differential hydrauIic cylinders | FO adaptive control | Simulation |
| [22] | Electronic circuit 2 × 2 | Adaptive control and AFROH * | Experimental and Simulation |
| References | Applications | Tuning Methods | What Type FO-Controller? |
|---|---|---|---|
| [63,64] | Coupled conical tanks TITO | GA *, CS *, BA * | FO-PID multi-loop, FO-PI |
| [38] | Binary distillation column by [32] | DBA *, BA *, DiBA *, EBA *, PSO * | FO-PID multi-loop decentralized |
| [36] | FO-TITO systems: binary distillation column by [32] and thermal system by [117] | GA * | FO-PI |
| [71] | FO/IO MIMO plants with time delays, wheeled mobile robot | Minimum ITAE for equivalent transfer function and BA * | FO-PID |
| [45] | Isotopic separation column cascade 9 × 9 | PSO * | FO observer and FO-PI |
| [101] | Synchronous generator excitation system | MEO * | Cascaded FO-PID |
| [57,59,60] | Coupled conical tanks | NBAO *, BA *, FGS *, HS * | FO-IMC-, FO-IMC-, centralized FO-PID, FO-PI, MCFOPID * |
| [58] | Laboratory scale pressure and level control modules | GA * | FO-PID Fuzzy |
| [96] | Single stage ore milling plant | PSO * | FO-PI, FOMRAC * |
| [79] | FO-MIMO FOPDT model 3 × 2 | DPP *, PSO * | IMC and FO-Smith predictor |
| [110] | Hypersonic vehicle 6-DOF model | NSPSO * | FO-PID |
| [51,52] | Module with four coupled tanks, two conical tank process | BA *, HS * | Adaptive multi-loop FO-PID, centralized FO-PID |
| [121] | Twin rotor TITO system | PSO * | FO-PID |
| [91] | Expansion turbine in the cryogenic air separation TITO process | GA * | FO-PID |
| [35] | Binary distillation columns by [32] and by [41] | Optimization with CMAES * and BLT * | FO-PI, FO-PID |
| [46] | 2-DOF polar robot manipulator, twin-tank model | GA * | FO-PD and SMC, FSMC * |
| [136] | Two common systems in the petrochemical industry with multivariable parameter estimation | MNDH * | FO-P/PI/PD/PID, FO-IMC |
| References | Applications | Tuning Methods | What Type FO-Controller? |
|---|---|---|---|
| [105] | EMBFL * | IMC method and pole allocation method | FO-PI |
| [44,85] | FO-FOPDT model TITO, ISP * | Graphical tuning method | PID and FO-EOTF *, FO-PI |
| [21,24,25,31,73,75,83,88,112,120] | RS *, FOSLD *, IPS *, HDE *, EDT *, AMR *, DCW *, AWM *, ASS *, MULTI * | Based on CRONE methodology through Oustaloup’s approximation method | CRONE decentralized, FO-IMC/FO-PID, FO-PID, CRONE, CRONE generation |
| [37,72,104] | IPN *, LUML *, CIP *, BDW *, EMCT *, Diesel engine | Method based on frequency domain, Response analysis of controlled variables in closed loop | 2-DOF FO-PID, Auto-tuning FO-PI, decentralized CRONE |
| [84,89,92,111,126] | FO-TITO system by [117], FO-TITO system generic, State space model SISO and MIMO, Non-linear MIMO systems, long aluminum rod | Maximum sensitivity method, stability analysis by Lyapunov’s method | FFO-IMC *, FO-PID, MRAC *, CMRAC *, FOSMC *, adaptive FO-Fuzzy, FSMC *, MSTSSMC * |
| [103] | Test bench for an office lighting | Based on Kissing Circle (KC) method | FO-PI |
| [124] | LTI FO-MIMO plant | Energy-based approach to perfect control robustness | GL-IMC * |
| [113] | HOF *, DCW *, FDL * | Tuning rules proposed by authors | IMC FO-PI/PID and Smith predictor |
| [62] | Coupled tanks | Specifications in the frequency domain: phase margin, crossover gain frequency and constant speed error | FO-, FO- |
| [69,70] | SCARA * robot | New tuning method and frequency responses, based on local optimization of the fractional pre-filter parameters | FO-PD and QFT, CRONE and QFT |
| [81] | FO-MIMO FOPDT model | Nash optimization and Monte Carlo method | FO-DDMC, DDMC * |
| [102] | Non-linear ball and plate system | Lyapunov’s finite time stability criterion and Oustaloup’s recursive approximation method | Cascaded FO-SMC * |
| [40] | Distillation column by [41] | Biggest Log-modulus Tuning (BLT) algorithm with IMC | FO-PI |
| [61] | TITO system of coupled tanks | Two methods proposed on literature | FO-PI |
| [68,107] | SCARA * robot model, MIMO uncertain system | Multiobjective optimization FO with anoptimized fractional prefilter of type FBLFD * | and QFT, CRONE generation |
| [100,125] | Light leds and sensor experimental model, LTI MIMO plant | Arbitrated without specified rules | FO-GESC *, FO-perfect control |
| [114] | TITO system by [137], distillation column by [41] | Three steps described in paper using the Bode method for optimal closed-loop transfer function | IMC-PID and FO-Filter |
| [122] | Heterogeneous TITO systems | Self-tuning cross-gain method and KC method | FO-PI (cross-gain method), FO-PI (KC method), FO-IMC |
| [48,65,78,80,99,108,109,117,119] | LpHN *, FO-FOPDT model, WT *, CMT *, FO-MIMO systems, TTM * and DCW *, SCARA robot, PTD *, FO-LTI MIMO systems | FOMCON, FOTF, tuning, optimization, CRONE, Ninteger by [151], LMI * - toolboxes of MATLAB | FO-PID, optimal FO-PID, MPC-LPV * and LFT *, FO-PI, CRONE and QFT, nonlinear |
| [135] | CNFO * | MS-DE * and DE * | MS-DE * |
| [67] | SCARA robot model | Davidson–Cole fractional prefilter optimisation | CRONE and QFT |
| [55,56] | Coupled tanks | Tuning performed using a numerical solution and methods found on literature and parameter estimation algorithm | FF * FO-PI, FF *-PI/PID/2DOF-PI/ 3DOF-PI, FF-DMAFOPI * |
| [42,44,54] | Experimental module with four coupled tanks, ISP * | Tuning algorithm developed by the authors for 1st and 2nd order models with time delay and Oustaloup’s recursive approximation method, set of equations according to [42,152] | FO-IMC and FO-PI with Smith’s predictor, decoupled FO-PI, decentralized FO-PI |
| [95] | Aircraft roll-dynamics, servomotor velocity-dynamics | By minimizing a cost function defined by the authors | LTR-FOKF * |
| [66] | Robot arm manipulator, car with translational manipulator | Trial and error method | FO-PID |
| [50] | Two spherical coupled tanks | Optimization by minimum search algorithm for ISE and Ziegler–Nichols method | FO-PI |
| [49] | Coupled tanks, multi-tank laboratory system, magnetic levitation system | Optimization by Levenberg–Marquardt and Nelder–Mead simplex algorithm, Ziegler–Nichols, Cohen–Coon and AMIGO algorithm | FO-PI, FO-PID |
| [74] | Diesel engine | Based on ad-hoc trial and error methods | Decentralized CRONE MIMO |
| [106] | FO-MIMO systems | Based on direct optimization of the closed loop output | CRONE and QFT * |
| [34] | Binary distillation column by [32] | Method proposed by the authors | FO-PI |
| [77] | FO Duffing–Holmes chaotic systems | Tuned on line by output feedback control law and adaptive law by using Lyapunov synthesis approach | AITFSMC * |
| [31] | Non-square multivariable plants with time-delay | Based on the use of the BRG * for the pairing of the manipulated inputs and controlled outputs | CRONE 3th generation |
| [33] | Binary distillation column by [32] | Inequality method | Decentralized and centralized FO-PI |
| [87] | Long aluminum rod | Flatness principle using polynomial matrices for linear fractional MIMO systems | CRONE 3th generation |
| [23] | Hexapod robot | Systematic method when establishing a compromise between the minimization indexes | FO-PD |
| [22] | Electronic circuit | Improvement of the stability properties of the zeros | AFROH * |
| References | Applications | Has Decoupling? |
|---|---|---|
| [105] | EMBFL * | Yes, unspecified type |
| [85] | FO-FOPDT model TITO | FO-EOTF * method |
| [104] | IPN *, LTIML *, CIP *, TRMS * | , |
| [84] | FO-TITO system proposed by [117] | , |
| [59,60,64] | TCCT *, FDL * | EOTF * method and decoupler by [118] where the extra time delay is incorporated |
| [103] | Experimental test bench for an office lighting system | Static decoupler: |
| [61,113] | HOF *, DCW *, FDL *, two coupled tanks | F-SDSP *: |
| [51,52,83] | FO-TITO system by [117,123], two interacting conical tank | Inverted decoupler and |
| [37] | DCW * and an experimental module with four coupled tanks | Ideal decoupler: |
| [62] | TITO system of coupled tanks | |
| [36] | FO-TITO systems: binary distillation column by [32] and thermal system by [117] | |
| [45] | Isotopic separation column cascade | Decoupled models |
| [98] | Reverse osmosis seawater desalination plant | |
| [80] | FO-FOPDT model TITO | Pseudodiagonalisation method |
| [97] | Air-conditioning VAV * system | Diagonal matrix method: |
| [79] | FO-MIMO FOPDT model | Cascade decoupler: |
| [53,54] | Experimental module with four coupled tanks | From the approximate decoupled process transfer function matrix |
| [50] | Process with two spherical coupled tanks | , |
| [42,43,44] | 13C isotope separation plant | Through the decoupled process transfer function matrix and the inverse of the steady state gain matrix |
| [35] | Binary distillation columns by [32] and by [41] | Through the CMAES * algorithm |
| [117] | TITO system of a thermoelectric temperature control test module, distillation column by [32] | Simplified, ideal and inverted decoupler |
| [91] | Expansion turbine in the cryogenic air separation | Simplified decoupler |
| [72,74,75,112] | Diesel engine, refrigeration system, high dynamic engine testbeds | Through CRONE methodology, matrix: |
| [65,106] | SCARA robot model, TITO systems | Through CRONE methodology, matrix: |
| [89] | Long aluminum rod | Yes, unspecified type |
| [25,31] | Distillation column by [39,118], aircraft wing model | Through CRONE methodology, matrix: |
| [21,24] | Active-suspension system, MIMO uncertain LTI system | Perfect decoupling through CRONE methodology, matrix: |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almeida, A.M.d.; Lenzi, M.K.; Lenzi, E.K. A Survey of Fractional Order Calculus Applications of Multiple-Input, Multiple-Output (MIMO) Process Control. Fractal Fract. 2020, 4, 22. https://doi.org/10.3390/fractalfract4020022
Almeida AMd, Lenzi MK, Lenzi EK. A Survey of Fractional Order Calculus Applications of Multiple-Input, Multiple-Output (MIMO) Process Control. Fractal and Fractional. 2020; 4(2):22. https://doi.org/10.3390/fractalfract4020022
Chicago/Turabian StyleAlmeida, Alexandre Marques de, Marcelo Kaminski Lenzi, and Ervin Kaminski Lenzi. 2020. "A Survey of Fractional Order Calculus Applications of Multiple-Input, Multiple-Output (MIMO) Process Control" Fractal and Fractional 4, no. 2: 22. https://doi.org/10.3390/fractalfract4020022
APA StyleAlmeida, A. M. d., Lenzi, M. K., & Lenzi, E. K. (2020). A Survey of Fractional Order Calculus Applications of Multiple-Input, Multiple-Output (MIMO) Process Control. Fractal and Fractional, 4(2), 22. https://doi.org/10.3390/fractalfract4020022







