Fractional Kinetic Equations Associated with Incomplete I-Functions
Abstract
1. Introduction
2. Arbitrary-Order Kinetic Equation
3. Special Cases and Remarks
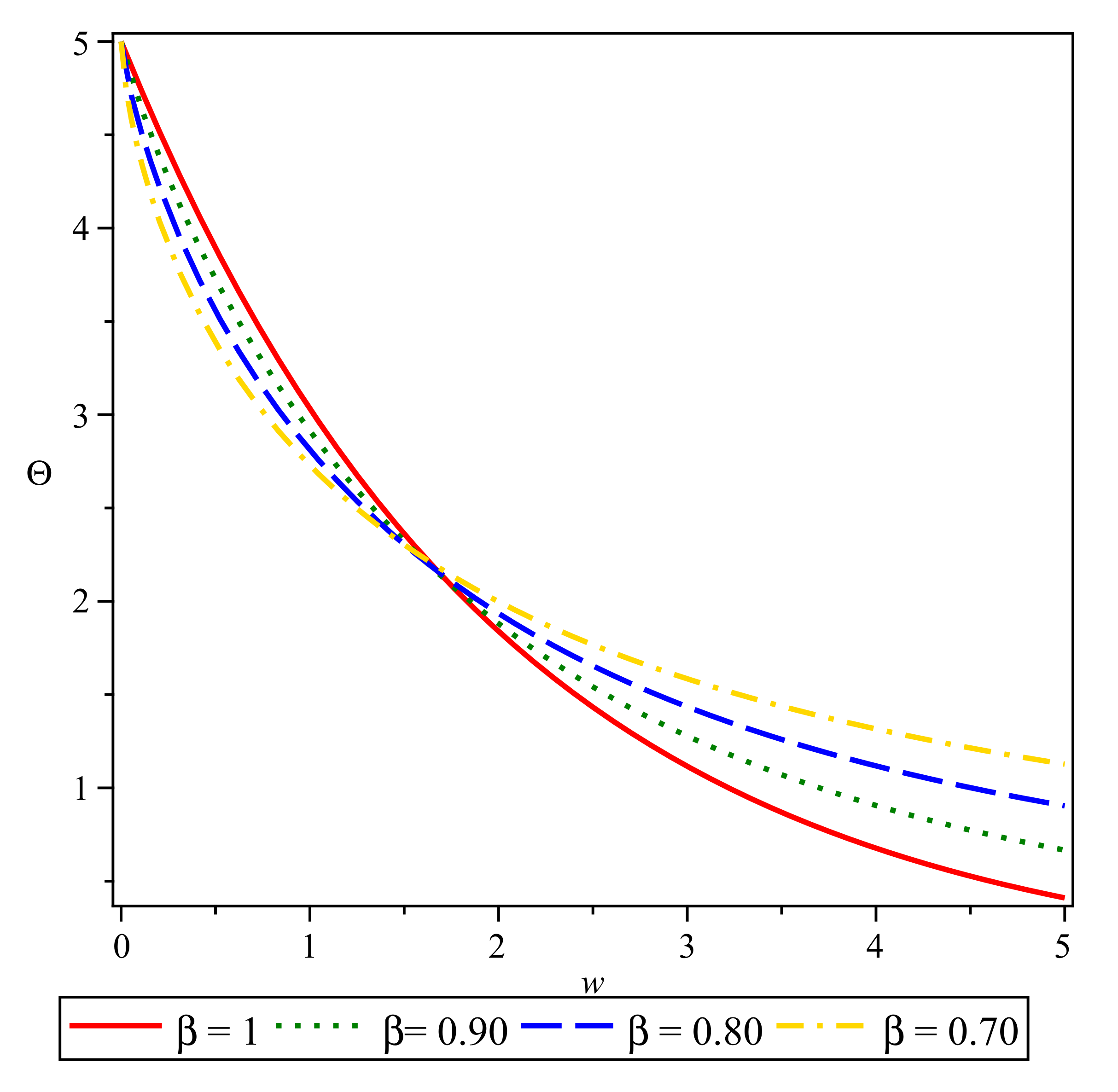
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley & Sons, INC.: New York, NY, USA, 1993. [Google Scholar]
- Oldham, K.; Spanier, J. Fractional Calculus: Theory and Applications of Differentiation and Integration of Arbitrary Order; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematical Studies; Elsevier (North-Holland) Science Publishers: Amsterdam, The Netherlands; London, UK; New York, NY, USA, 2006; Volume 204. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Srivastava, H.M.; Saxena, R.K. Operators of Fractional Integration and Their Applications. Appl. Math. Comput. 2001, 118, 1–52. [Google Scholar] [CrossRef]
- Haubold, H.J.; Mathai, A.M. The fractional kinetic equation and thermonuclear functions. Astrophys. Space Sci. 2000, 273, 53–63. [Google Scholar] [CrossRef]
- Saichev, A.I.; Zaslavsky, G.M. Fractional kinetic equations: Solutions and applications. Chaos 1997, 7, 753–764. [Google Scholar] [CrossRef] [PubMed]
- Saxena, R.K.; Mathai, A.M.; Haubold, H.J. On generalized fractional kinetic equations. Physics A 2004, 344, 657–664. [Google Scholar] [CrossRef]
- Saxena, R.K.; Kalla, S.L. On the solutions of certain fractional kinetic equations. Appl. Math. Comput. 2008, 199, 504–511. [Google Scholar] [CrossRef]
- Chaurasia, V.B.L.; Pandey, S.C. On the new computable solution of the generalized fractional kinetic equations involving the generalized function for the fractional calculus and related functions. Astrophys. Space Sci. 2008, 317, 213–219. [Google Scholar] [CrossRef]
- Goswami, A.; Singh, J.; Kumar, D.; Sushila. An efficient analytical approach for fractional equal width equations describing hydro-magnetic waves in cold plasma. Physics A 2019, 524, 563–575. [Google Scholar] [CrossRef]
- Habenom, H.; Suthar, D.L.; Gebeyehu, M. Application of Laplace Transform on Fractional Kinetic Equation Pertaining to the Generalized Galué Type Struve Function. Adv. Math. Phys. 2019, 2019, 1–8. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Tanwar, K.; Baleanu, D. A new fractional exothermic reactions model having constant heat source in porous media with power, exponential and Mittag-Leffler Laws. Int. J. Heat Mass Transf. 2019, 138, 1222–1227. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Qurashi, M.A.; Baleanu, D. A new fractional SIRS-SI malaria disease model with application of vaccines, anti-malarial drugs, and spraying. Adv. Differ. Equ. 2019, 2019, 278. [Google Scholar] [CrossRef]
- Saxena, R.K.; Mathai, A.M.; Haubold, H.J. On Fractional Kinetic Equations. Astrophys. Space Sci. 2002, 282, 281–287. [Google Scholar] [CrossRef]
- Yavuz, M.; Özdemir, N. Numerical inverse Laplace homotopy technique for fractional heat equations. Therm. Sci. 2018, 22, 185–194. [Google Scholar] [CrossRef]
- Yavuz, M.; Özdemir, N. European vanilla option pricing model of fractional order without singular kernel. Fractal Fract. 2018, 2, 3. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas; Graphs; and Mathematical Tables; Applied Mathematics Series; National Bureau of Standards: Washington, DC, USA, 1964; Dover Publications: New York, NY, USA, 1965; Volume 55. [Google Scholar]
- Andrews, L.C. Special Functions for Engineers and Applied Mathematicians; Macmillan Company: New York, NY, USA, 1985. [Google Scholar]
- Bansal, M.K.; Kumar, D.; Jain, R. Interrelationships Between Marichev–Saigo–Maeda Fractional Integral Operators, the Laplace Transform and the H-Function. Int. J. Appl. Comput. Math 2019, 5, 103. [Google Scholar] [CrossRef]
- Bansal, M.K.; Jolly, N.; Jain, R.; Kumar, D. An integral operator involving generalized Mittag-Leffler function and associated fractional calculus results. J. Anal. 2019, 27, 727–740. [Google Scholar] [CrossRef]
- Bansal, M.K.; Kumar, D.; Jain, R. A Study of Marichev-Saigo-Maeda Fractional Integral Operators Associated with S-Generalized Gauss Hypergeometric Function. Kyungpook Math. J. 2019, 59, 433–443. [Google Scholar]
- Goswami, A.; Singh, J.; Kumar, D.; Gupta, S.; Sushila. An efficient analytical technique for fractional partial differential equations occurring in ion acoustic waves in plasma. J. Ocean Eng. Sci. 2019, 4, 85–99. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D. On the analysis of vibration equation involving a fractional derivative with Mittag-Leffler law. Math. Methods Appl. Sci. 2020, 43, 443–457. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Purohit, S.D.; Swroop, R. A hybrid analytical algorithm for nonlinear fractional wave-like equations. Math. Model. Nat. Phenom. 2019, 14, 304. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Baleanu, D. New aspects of fractional Biswas-Milovic model with Mittag-Leffler law. Math. Model. Nat. Phenom. 2019, 14, 303. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Chaudhry, M.A.; Agarwal, R.P. The incomplete Pochhammer symbols and their applications to hypergeometric and related functions. Integral Transform. Spec. Funct. 2012, 23, 659–683. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Bansal, M.K.; Harjule, P. A study of fractional integral operators involving a certain generalized multi-index Mittag-Leffler function. Math. Methods Appl. Sci. 2018, 41, 6108–6121. [Google Scholar] [CrossRef]
- Bansal, M.K.; Kumar, D. On the integral operators pertaining to a family of incomplete I-functions. AIMS Math. 2020, 5, 1247–1259. [Google Scholar] [CrossRef]
- Saxena, V.P. Formal solution of certain new pair of dual integral equations involving H-functions. Proc. Natl. Acad. Sci. India Sect. A 1982, 52, 366–375. [Google Scholar]
- Srivastava, H.M.; Saxena, R.K.; Parmar, R.K. Some Families of the Incomplete H-Functions and the Incomplete H-Functions and Associated Integral Transforms and Operators of Fractional Calculus with Applications. Russ. J. Math. Phys. 2018, 25, 116–138. [Google Scholar] [CrossRef]
- Bansal, M.K.; Choi, J. A Note on Pathway Fractional Integral Formulas Associated with the Incomplete H-Functions. Int. J. Appl. Comput. Math. 2019, 5, 133. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Gupta, K.C.; Goyal, S.P. The H-Functions of One and Two Variables with Applications; South Asian Publishers: New Delhi, India, 1982. [Google Scholar]
- Sneddon, I.N. The Use of Integral Transforms; Tata McGrawHill: New Delhi, India, 1979. [Google Scholar]
- Chaurasia, V.B.L.; Kumar, D. On the solutions of generalized fractional kinetic equations. Adv. Stud. Theor. Phys. 2010, 4, 773–780. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar Bansal, M.; Kumar, D.; Harjule, P.; Singh, J. Fractional Kinetic Equations Associated with Incomplete I-Functions. Fractal Fract. 2020, 4, 19. https://doi.org/10.3390/fractalfract4020019
Kumar Bansal M, Kumar D, Harjule P, Singh J. Fractional Kinetic Equations Associated with Incomplete I-Functions. Fractal and Fractional. 2020; 4(2):19. https://doi.org/10.3390/fractalfract4020019
Chicago/Turabian StyleKumar Bansal, Manish, Devendra Kumar, Priyanka Harjule, and Jagdev Singh. 2020. "Fractional Kinetic Equations Associated with Incomplete I-Functions" Fractal and Fractional 4, no. 2: 19. https://doi.org/10.3390/fractalfract4020019
APA StyleKumar Bansal, M., Kumar, D., Harjule, P., & Singh, J. (2020). Fractional Kinetic Equations Associated with Incomplete I-Functions. Fractal and Fractional, 4(2), 19. https://doi.org/10.3390/fractalfract4020019






