Fractional Model for a Class of Diffusion-Reaction Equation Represented by the Fractional-Order Derivative

Abstract

This paper proposes the analytical solution for a class of the fractional diffusion equation represented by the fractional-order derivative. We mainly use the Grunwald–Letnikov derivative in this paper. We are particularly interested in the application of the Laplace transform proposed for this fractional operator. We offer the analytical solution of the fractional model as the diffusion equation with a reaction term expressed by the Grunwald–Letnikov derivative by using a double integration method. To illustrate our findings in this paper, we represent the analytical solutions for different values of the used fractional-order derivative.

1. Introduction

Fractional diffusion equations have many applications and used in many domains in mechanics, in physics, in electrical circuits, in cable models, in sciences and engineering, see in the following papers [1,2,3,4,5]. The diffusion–reaction equation is a class of diffusion equations. In the diffusion–reaction equations, this present investigation is new. It contributes to the application of the Laplace transform of the Grunwald–Letnikov fractional derivative for solving the fractional differential equations. We will prove by this paper; our results are in good agreement with the classical results in the literature. The fractional diffusion equations receive many investigations in the literature; Henry in [6] proposed the analytical solutions of the fractional diffusion–reaction equations, Metzler in [7] studied the fractional diffusion equation by proposing the analytical solutions using the Laplace transforms and the Fourier transform, Mainardi et al. in [8] proposed the analytical solutions of the fractional diffusion equations using the Riemann–Liouville integral. They have used the Mittag–Leffler function and H-fox function to represent the obtained solutions. Li et al. [9] proposed investigations in fractional diffusion equations too. The diffusion equation is also used in finance, for example, getting the value of call options. In other words, it is known that the fractional Black and Scholes equation is a fractional diffusion Equation [10]. There exist many other examples where the diffusion equation can be used [10].

The differentiation and integration with non-integer order has attracted many researchers since 1965. Nowadays, we note many works related to the fractional derivatives and their applications in many fields. For recent applications of the fractional derivatives see [2,10,11,12,13,14,15,16]. This paper contributes to a new application of the fractional calculus in real-world problems. It is known that the Grunwald–Letnikov derivative is a fractional derivative with which the numerical scheme is utilized to study the physical phenomena [17]. The Grunwald–Letnikov derivative was one of the proposed derivatives to answer Leibniz’s question related to the definition of the fractional derivative; many investigations were done related to the effective use of this derivative. Ortigueira et al. in [18] and Podlubny in [19] have proposed in their studies the Laplace transform of this derivative. It is well known that the Laplace transformation is essential for getting the solutions of the fractional differential equations, notably to propose the approximate solution or the exact solution of the differential equations. One of our motivations in this paper is the use of the Laplace transform of this derivative. We also want to use this derivative to study and to determine the exact solutions of the fractional diffusion equations with a reaction term. In the literature, the fractional diffusion equations with Grunwald–Letnikov derivative are studied by utilizing the numerical schemes. The Laplace transform of the Grunwald–Letnikov derivative proposed in [18,19] opens new doors, in the physical applications and the resolution of the fractional equations.

The fractional context is recent in the diffusion equations, note that the fractional derivatives describe more accurately all physical phenomena due to the fact the fractional derivatives are derivatives with memory effect. The memory effect is crucial in modeling dynamical systems. To be more precise, in this paper, we will study the fractional diffusion equation described by the Grunwald–Letnikov derivative. For history, there exist many discussions related to the good definition of the fractional derivatives, and many papers were addressed in these directions, see [20,21]. Nowadays the most used fractional derivatives in fractional calculus are: Caputo–Liouville derivative [19], Liouville–Riemann derivative [19], conformable derivative, Grunwald–Letnikov derivative, Atangana–Baleanu derivative [22], Caputo–Fabrizio derivative [23]. There exist also the discrete form of all the fractional derivatives previously cited, please see [24,25,26]. For the advancement in the solutions of the fractional diffusion equations, we have the following investigations [1,27].

The analytical solution of the fractional diffusion equation with a reaction term with the Grunwald–Letnikov derivative using an integral method is proposed, too. We will determine as well the physical number like the square of the penetration depth of our proposed model using the Laplace transform of the Grunwald–Letnikov derivative. The similarity variable and the analytical solution of the Cauchy problem will be discussed as well. In comparison with the investigation in the literature [6,7,8,9], which all investigate the analytical solutions using Fourier transform or with the numerical schemes. In this paper, we propose a new procedure of getting the analytical solution of the fractional diffusion–reaction equation with a novel method. This method is called a double integration method.

The paper is partitioned as follows: In Section 2, we will discuss the basic definitions related to the fractional derivatives, notably the Grunwald–Letnikov derivative and all properties associated with this fractional derivative. In Section 3, we propose the fractional diffusion with reaction term studied in this present paper. We also consider three categories of problems: the Cauchy problem, the fractional diffusion equation without a reaction term, and the fractional diffusion equation with a reaction term. In Section 4, we represent the analytical solutions and discuss the physics applications of our results. In Section 5, we give the concluding remarks.

2. Basics Definitions and Lemmas

This section proposes the definitions and the lemmas fundamental for our investigations. We have many fractional derivatives that can be classified into many classes. We cite two most important classes: the first class of derivatives is defined with the singular kernels as the Riemann–Liouville derivative [19] and the Caputo–Liouville derivatives, the second class of derivatives is defined without singular kernels as the Atangana–Balenau fractional derivative [22] and Caputo–Liouville fractional derivative [19]. In this section, we recall another type of fractional derivative represented by series and developed in many works in the literature [20,28]. We particularly focus on the Grunwald–Letinov derivative [20,21] proposed to study some fractional phenomena. There exist many discussions related to the fractional derivatives operators, but all of them develop have advantages and inconveniences. There exist many criteria for the classification of the existing derivatives, those which respect Leibniz rule as presented in [20,21] and those which do not satisfies this property. The commutativity property is considered and discussed in the work of Atangana et al. [29]. All the derivatives used in this section are considered definite on the left side. We have the following definition for the Grunwald–Letnikov derivative.

Definition 1.

[18,19,20,21] We consider the function $g:\mathbb{R}⟶\mathbb{R}$, the Grunwald–Letnikov fractional derivative of order α of the function h is given by the equation

$${}^{GL}{D}^{\alpha }g\left(t\right)=\underset{h\to 0}{lim}\frac{1}{h^{\alpha }}\sum _{j=0}^{\infty }\frac{{\left(-\alpha \right)}_j}{j!}g\left(t-jh\right),$$

(1)

with the condition $t\in \mathbb{R}$ and where we have the following condition

$${\left(\alpha \right)}_j=\alpha \left(\alpha +1\right)\dots \left(\alpha +j-1\right).$$

(2)

The above derivative is also called Forward Grunwald–Letnikov fractional derivative, see more detail in Ortigeira et al. in [20]. There exists another form of the Grunwald–Letnikov fractional derivative, which is useful; we have the following definition.

Definition 2.

[19,28] We consider the function $g:\mathbb{R}⟶\mathbb{R}$, the truncated Grunwald–Letnikov fractional derivative of order α of the function h is given by the equation

$${}^{GL}{D}^{\alpha }g\left(t\right)=\underset{h\to 0}{lim}{h}^{-\alpha }\sum _{j=0}^N\frac{{\left(-\alpha \right)}_j}{j!}g\left(t-jh\right),$$

(3)

with the condition $t>t_0$ and where we have the following condition

$$N=⌈\frac{t-t_0}{h}⌉.$$

(4)

Note that it is essential to mention that before going further, there exists a relation between the Riemann–Liouville derivative and the Forward Grunwald–Letnikov fractional derivative; it is described as follows [28].

$${}^{GL}{D}^{\alpha }g\left(t\right){=}^{RL}{D}^{\alpha }g\left(t\right),$$

(5)

where the Riemann–Liouville derivative for all $\alpha <1$ is defined as the following form

$${}^{RL}{D}^{\alpha }g\left(t\right)=\frac{1}{\mathsf{\Gamma }(1-\alpha )}\frac{d}{dt}{\int }_0^t{\left(t-s\right)}^{-\alpha }g\left(s\right)ds,$$

(6)

where the function $\mathsf{\Gamma }(\dots )$ represents the gamma Euler function. One of the main remarks the forward Grunwald–Letnikov fractional derivative is, this derivative is very useful for numerical methods, see, for example, in [17]. The numerical scheme of the Grunwald–Letnikov fractional derivative for the fractional diffusion equations is proposed in [1]. In this paper, we are interested by another aspect of this derivative, which can be used to get analytical solutions. We mean the Laplace transformation of the forward Grunwald–Letnikov fractional derivative introduced in [21]. Note that this form of the Laplace transform open new doors on the applications of many methods as the homotopy methods, the Fourier transforms, and other [30,31], to solve the fractional differential equations. The Laplace transform is also beneficial for getting the transfer functions. We recall the Laplace transform of the forward Grunwald–Letnikov fractional derivative proposed by Ortigeira et al. in [18] and is given by the following form

$$\mathcal{L}\left\{{}^{GL}{D}^{\alpha }g\left(t\right)\right\}=q^{\alpha }\mathcal{L}\left\{g\left(t\right)\right\}=q^{\alpha }G\left(q\right).$$

(7)

where the operator $\mathcal{L}$ designs the classical Laplace transform and where G designs the Laplace transform of the function $g.$ In physic, the initial condition is important; thus, we define the Laplace transform, taking into account the initial condition. Considering the initial condition characterized by $\left(I^{1-\alpha }g\right)\left(0\right)$ due to the relation existing between the Riemann–Liouville and the truncated Grunwald–Letnikov fractional derivative Equation (5), we get the following Laplace Transform for the derivative represented in Equation (3)

$$\mathcal{L}\left\{{}^{GL}{D}^{\alpha }g\left(t\right)\right\}=q^{\alpha }G\left(q\right)-\left(I^{1-\alpha }g\right)\left(0\right).$$

(8)

Related to the use of the Laplace transform, there exist many points of view. The first, Equation (7) is the Laplace Transform of the fractional derivative defined in Definition 1, and take into account that the boundary condition is fixed by the physics of the problem [18]. There exists also another point of view, Equation (8) is the Laplace transform of the truncated Grunwald–Letnikov fractional derivative, which takes into account the integral initial condition explicitly; in other words, it satisfies the initial condition of the proposed physical model. Motivated by Equation (5), for the rest of the paper, we decide to work with the Laplace Transform in Equation (8). Note that this question related to the initial condition is still an unsolved problem, we hope that in the future some more deep studies on this subject would shed some light on this controversial question.

We also recall a fundamental function used in many fractional differential equations to represent the form of the analytical solutions, namely the Mittag–Leffler function [32]. Note that the Mittag–Leffler function is used to express the Atangana–Baleanu fractional derivative, a derivative with the nonsingular kernel. The Mittag–Leffler function with two parameters is represented as the form

$$E_{\alpha ,\beta }\left(z\right)=\sum _{k=0}^{\infty }\frac{z^k}{\mathsf{\Gamma }(\alpha k+\beta )},$$

(9)

with $\alpha >0,$ $\beta \in \mathbb{R}$ and $z\in \mathbb{C}$. It is also important to mention the condition of the convergence of the series (9). Furthermore, when the parameter $\alpha >0$ and $\beta >0$ the series represented in Equation (9) is convergent. The Mittag–Leffler function is fundamental in fractional calculus. For example, the Mittag–Leffler function is used to represent the final results of [31]. Atangana and Baleanu use the Mittag-Lefler function to express the fractional derivative with a nonsingular kernel. This fractional derivative has many applications in real-world problems for more information; see [22,33]. To see another importance of the Mittag–Leffler function, we recall the Atangana–Baleanu derivative in terms of the above definition of the Mittag–Leffler function in the following lines.

Definition 3.

[22,33] The Atangana–Baleanu derivative in Caputo sense for a given function $g:\mathbb{R}\times [0,+\infty [⟶\mathbb{R}$, of order $\alpha \in (0,1]$ is represented with the Mittag–Leffler function as the following form

$$D_{\alpha }^{ABC}g\left(t\right)=\frac{B\left(\alpha \right)}{1-\alpha }{\int }_0^t{g}^{\prime }\left(s\right)E_{\alpha }\left(-\frac{\alpha }{1-\alpha }{(t-s)}^{\alpha }\right)ds,$$

(10)

for all $t>0,$ where the function $\mathsf{\Gamma }(\dots )$ represents the Euler Gamma function, $E_{\alpha }(.)$ represents the Mittag–Leffler function with $\beta =1$ in Equation (9), and with the normalization term $B\left(\alpha \right)$ obeying the relationships $B\left(0\right)=B\left(1\right)=1$.

Many other properties such as the causality, associativity, neutral element, additivity, and commutativity, and the integration by part have already been discussed in the literature.

3. Fractional Model with the Grunwald–Letnikov Fractional Derivative

This section concerns the diffusion equation with a reaction term but considered as defined the help of the Grunwald–Letnikov fractional derivative. The objective of this section is not to focus on the numerical schemes of the fractional diffusion equations and to study the convergence of the numerical schemes already proposed in [1], but to suggest the analytical solution of the fractional diffusion equation with a reaction term by using the Laplace transform of the Grunwald–Letnikov fractional derivative proposed by Ortigeira et al. in [18]. The following equation defines the fractional differential model described by the Grunwald–Letnikov fractional derivative under consideration in this paper

$${}^{GL}{D}^{\alpha }u=\nu \frac{{\partial }^{2}u}{\partial x^2}-bu,$$

(11)

where $\nu$, is the diffusion coefficient, b the reaction parameter, and we consider as the Goodman’s boundary conditions [34] the equation as follows

$$u(0,t)=1 \mathrm{and} u\left(\lambda \right)=\frac{\partial u(\lambda ,t)}{\partial t},\hspace{1em}t\ge 0.$$

(12)

The diffusion coefficient plays an important role in the diffusion processes. The variable u represents the temperature distribution of the material, the concentration of the material, the density distribution of the particle, or the numbers of a particular species per unit volume [6]. The parameter $\lambda$ denotes the penetration depth of the model and satisfies for $x\ge \lambda$ the temperature change from the initial temperature or concentration is negligible [35,36]. Note that the parameter $\lambda$ also depend on time t. For the rest of the paper for simplification, $\lambda \left(t\right)$ is denoted by $\lambda$. It is important to comment on Equation (12). In comparison to the diffusion equation with reaction studied in [6], our problem is defined respecting Goodman’s boundary condition [34,37]. This condition explains the use of the double integration method [38]. For getting the analytical solution, this method imposes the use of condition (12). Note that for the diffusion–reaction model presented in [6], the delta function (Dirac function) as initial condition gives the possibility to the authors to focus in particular on the mean square displacement and to get the analytical solutions using Laplace transforms and Fourier transform. The procedure for getting solutions in [6] is not possible in our model, due to Goodman’s boundary conditions [3]. In Equation (11), we can when $\nu =0$, we have no diffusion, and the problem becomes a Cauchy problem in terms of the truncated Grunwald–Letnikov fractional derivative, that is

$${}^{GL}{D}^{\alpha }u=-bu,$$

(13)

we add the initial condition $\left(I^{1-\alpha }u\right)\left(t_0\right)=u_{t_0}=1$. The analytical solution can be obtained by applying the Laplace transform to both sides of Equation (13). As a solution, we describe the following procedure for getting the solution to the Cauchy problem (13). We apply the Laplace transform proposed in Equation (8) into both sides of Equation (13) we get that

$$\begin{array}{ccc}\hfill q^{\alpha }\overline{u}\left(q\right)-\left(I^{1-\alpha }u\right)\left(t_0\right)& =& -b\overline{u}\left(q\right),\hfill \\ \hfill q^{\alpha }\overline{u}\left(q\right)+b\overline{u}\left(q\right)& =& 1,\hfill \\ \hfill \overline{u}\left(q\right)& =& \frac{u_0}{q^{\alpha }+b}\hfill \end{array}$$

(14)

After inverse of the Laplace transform the Cauchy problem with the Grunwald–Letnikov fractional derivative is described by the following analytical solution, using the Mittag–Leffler function, we have, for example

$$u\left(t\right)={\left(t-t_0\right)}^{\alpha -1}{E}_{\alpha ,\alpha }\left(-b{\left(t-t_0\right)}^{\alpha }\right).$$

(15)

We now continue when the diffusion coefficient is not null, but the reaction term $b=0$. In this case, we have a fractional diffusion equation described by the following equation

$${}^{GL}{D}^{\alpha }u=\nu \frac{{\partial }^{2}u}{\partial x^2},$$

(16)

where $\nu$, is the diffusion coefficient, and we consider as the initial condition the equation as follows

$$u(0,t)=1 \mathrm{and} u\left(\lambda \right)=\frac{\partial u(\lambda ,t)}{\partial t},\hspace{1em}t\ge 0.$$

(17)

The analytical solution for the fractional diffusion equation described by truncated Grunwald–Letnikov fractional derivative (16) can be got using the physical procedure. We particularly use the double integration method presented by Hristov in [38]; see also the recent application of this method in [3]. The idea of this procedure of solution stated by Goodman in [37] and recently developed by Myers and Mitchell in [35,36]. Applying the double integral to both sides to Equation (16), we get the following relationship

$${\int }_0^{\lambda }{\int }_x^{\lambda }\left[{}^{GL}{D}^{\alpha }u\right]dxdx=\nu {\int }_0^{\lambda }{\int }_x^{\lambda }\frac{{\partial }^{2}u}{\partial x^2}dxdx,$$

(18)

We add the assumption the form of the analytical solution for the fractional diffusion Equation (16) is defined by the following Equation [35,36]

$$u(x,t)={\left(1-\frac{x}{\lambda }\right)}^n.$$

(19)

It is important to mention again the penetration depth $\lambda$ depend on time $t.$ Furthermore, Equation (19) is subject to discussions in the literature, notably the exponent n. There exist methods to get the exponent n consisting of minimizing the Langhord function as explained in [35,36]. In many investigations it was proved for the diffusion equation $n=2$ is the better for the approximate solution [3,35,36,37,38]. For the rest of the paper, we work with $n=2.$ Using Equation (19) into Equation (18), we get the following fractional differential equation with truncated Grunwald–Letnikov fractional derivative

$${}^{GL}{D}^{\alpha }{\lambda }^2=12u(0,t)=12.$$

(20)

We have to apply the Laplace transform to both sides of Equation (20) by using the Laplace transform of the truncated Grunwald–Letnikov fractional derivative, we have

$$\begin{array}{ccc}\hfill q^{\alpha }{\overline{\lambda }}^2\left(q\right)-\left(I^{1-\alpha }\lambda \right)\left(0\right)& =& \frac{12\nu }{q},\hfill \\ \hfill q^{\alpha }{\overline{\lambda }}^2\left(q\right)& =& \frac{12\nu }{q},\hfill \\ \hfill {\overline{\lambda }}^2\left(q\right)& =& \frac{12\nu }{q^{1+\alpha }}\hfill \end{array}$$

(21)

After application of the inverse of the Laplace transform, we get the following form for the penetration depth

$${\lambda }^2\left(t\right)=\frac{12}{\mathsf{\Gamma }\left(1+\alpha \right)}\nu t^{\alpha }.$$

(22)

Finally, the analytical solution of the fractional diffusion Equation (16) with the truncated Grunwald–Letnikov fractional derivative is given by

$$u(x,t)={\left(1-\frac{x}{2\sqrt{\frac{3\nu }{\mathsf{\Gamma }\left(1+\alpha \right)}{t}^{\alpha }}}\right)}^2.$$

(23)

We clearly observe when $\alpha =1$, the form of the similarity variable is $\eta =\frac{x}{2\sqrt{3\nu t}}$ which correspond to the similarity variable in the classical diffusion. We will represent graphically and discuss this point in the next section. There exist a similar algorithm called the Heat integral balance method, which can be applied in our equation to get the analytical solution satisfying Goodman’s conditions. In contrary to the double integral balance method, the Heat integral balance method [35,36] uses single integration and the penetration depth. This method is not applied here, but the result is approximatively the same.

We now propose the analytical solution of the fractional diffusion equation when the diffusion coefficient and the reaction parameter are not zero. In this case, we have to solve the following fractional diffusion equation

$${}^{GL}{D}^{\alpha }u=\nu \frac{{\partial }^{2}u}{\partial x^2}-bu,$$

(24)

we consider as the boundary condition the equation defined as follows

$$u(0,t)=1.$$

(25)

We adopt the same procedure as previously described. We apply the double integral to both sides of the Equation (24), we get the following form

$${\int }_0^{\lambda }{\int }_x^{\lambda }\left[{}^{GL}{D}^{\alpha }u\right]dxdx=\nu {\int }_0^{\lambda }{\int }_x^{\lambda }\frac{{\partial }^{2}u}{\partial x^2}dxdx-b{\int }_0^{\lambda }{\int }_x^{\lambda }udxdx,$$

(26)

Using the proposed analytical solution in Equation (19), we have to solve the following fractional differential equation with the truncated Grunwald–Letnikov fractional derivative

$${}^{GL}{D}^{\alpha }{\lambda }^2=-b{\lambda }^2+12.$$

(27)

We have the choice to use Equation (15) or to apply the Laplace transform of the truncated Grunwald–Letnikov fractional derivative to both sides of Equation (27) and we get the following form

$$\begin{array}{ccc}\hfill q^{\alpha }{\overline{\lambda }}^2\left(q\right)-\left(I^{1-\alpha }\lambda \right)\left(0\right)& =& -b{\overline{\lambda }}^2\left(q\right)+\frac{12\nu }{q},\hfill \\ \hfill (q^{\alpha }+b){\overline{\lambda }}^2\left(q\right)& =& \frac{12\nu }{q},\hfill \\ \hfill {\overline{\lambda }}^2\left(q\right)& =& \frac{12\nu }{b}\left\{\frac{1}{q}-\frac{q^{\alpha -1}}{q^{\alpha }+b}\right\}.\hfill \end{array}$$

(28)

From the inverse of the Laplace transform yields that, the penetration depth is in the following form

$${\lambda }^2\left(t\right)=\frac{12\nu }{b}\left\{1-E_{\alpha }\left(-b{t}^{\alpha }\right)\right\},$$

(29)

from which the analytical solution of the fractional diffusion Equation (24) with a reaction term is given by the following relationship

$$u(x,t)={\left(1-\frac{x}{2\sqrt{\frac{3\nu }{b}\left\{1-E_{\alpha }\left(-b{t}^{\alpha }\right)\right\}}}\right)}^2.$$

(30)

The solution of the fractional diffusion equation with a reaction term is also in consideration in [6]. The difference between the investigations is due to the fact in [6], they investigate with the initial condition, and here we investigate with Goodman’s conditions and with double integration method. In our context combining the Laplace transform and the Fourier transform is not possible with Goodman’s boundary conditions. Therefore the comparison study between the results is not trivial. Another remark is our method can be applied in the fractional diffusion equation in [6], but further assumptions will be posed. For the assumptions, see [36].

We discuss all the solutions in the next section; in this section, we have applied the Laplace transform of the truncated Grunwald–Letnikov fractional derivative successfully.

4. Graphical Representations and Interpretations

In this section, we analyze the analytical solutions found in the previous section. We represent and analyze the analytical solutions in all the cases previously addressed.

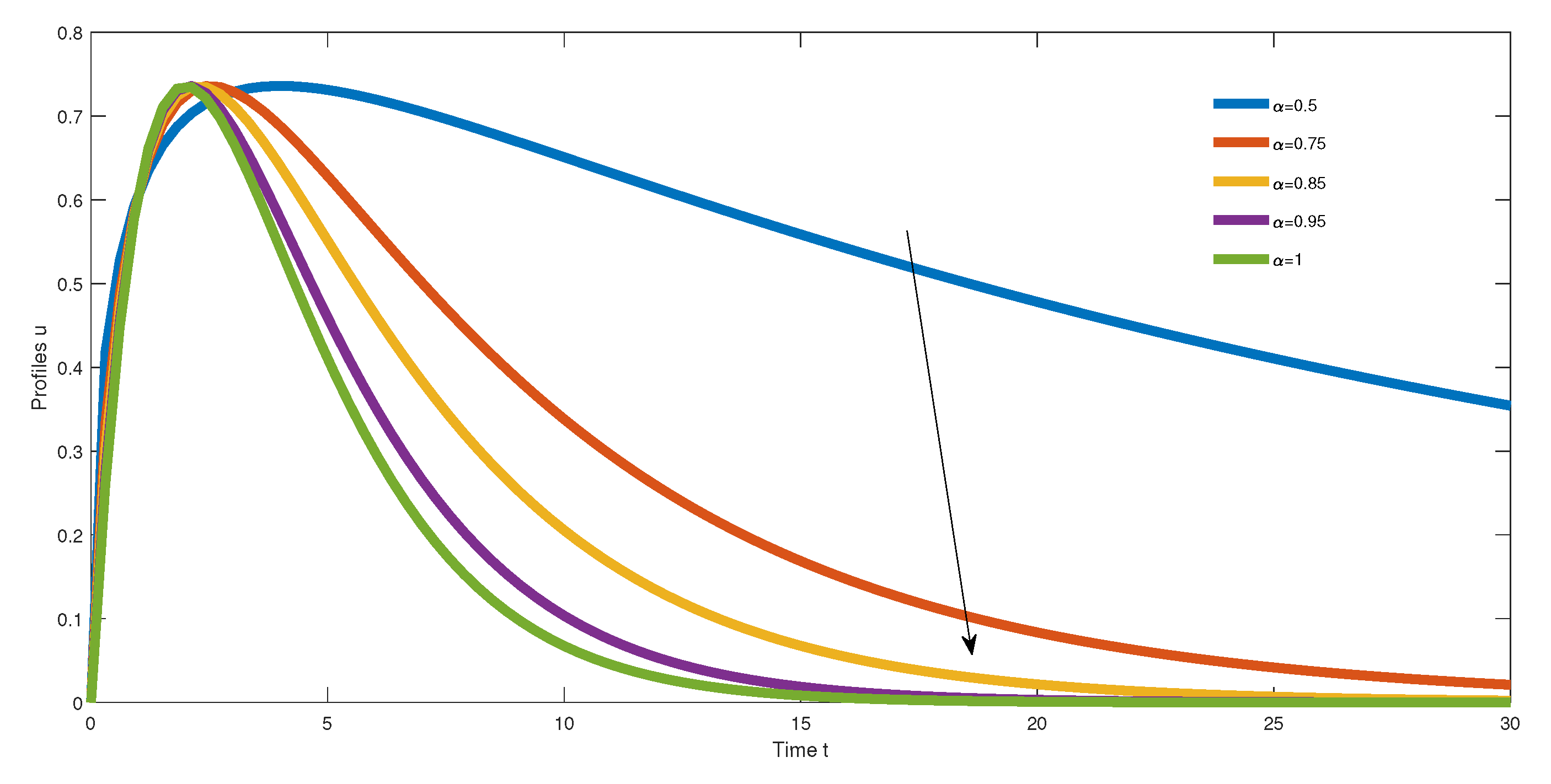
We begin by the Cauchy problem, the representation of the analytical solution of Equation (13) is done with the following assumptions $t_0=0$ and $b=0.5$. For our Cauchy problem, we can observe by the definition of the Mittag–Leffler stability, the trivial solution of the fractional differential Equation (13) with the truncated Grunwald–Letnikov fractional derivative is Mittag–Leffler stable [39]. We can observe in Figure 1 all the solutions converge to zero for a long time of the process. The Figure 1 is depicted with $x=0.5$.

We note, in this case, when the fractional order of the truncated Grunwald–Letnikov fractional derivative increase, we notice the profiles converge rapidly to zero, see the direction of the arrow for more details.

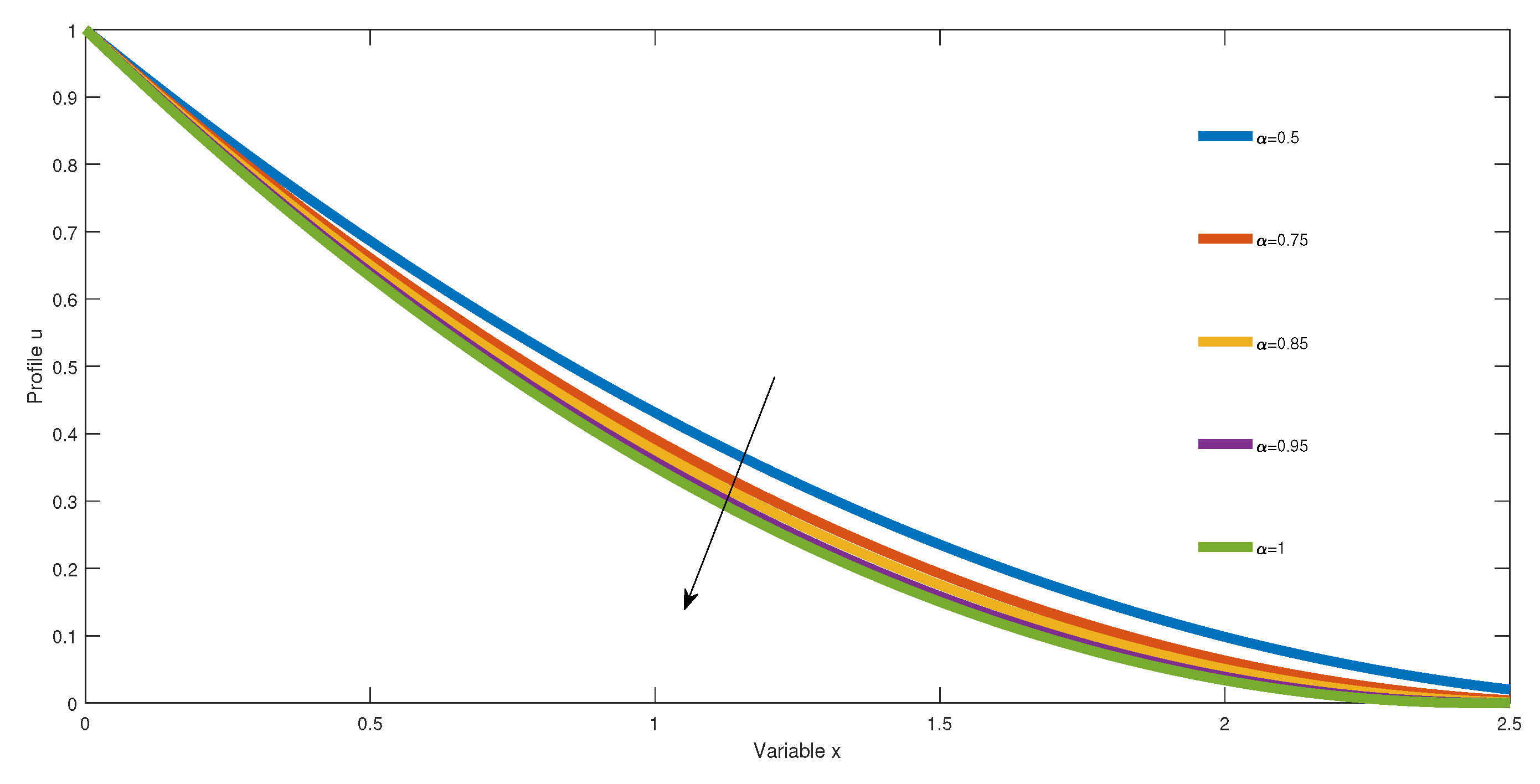
We continue our analysis with the second case, that is when we work without a reaction term Equation (16). We make the following assumption, for simplification due to the fact we do not analyze the impact of the parameter of the diffusion equation, we suppose the diffusion coefficient is unit, and we maintain $b=0$. We depict the solutions with time $t=0.5$. The behaviors of the analytical solutions for different values of the order of the truncated Grunwald–Letnikov fractional derivative are represented in Figure 2. In Figure 2, we depict the figure with the assumption $t=0.2$.

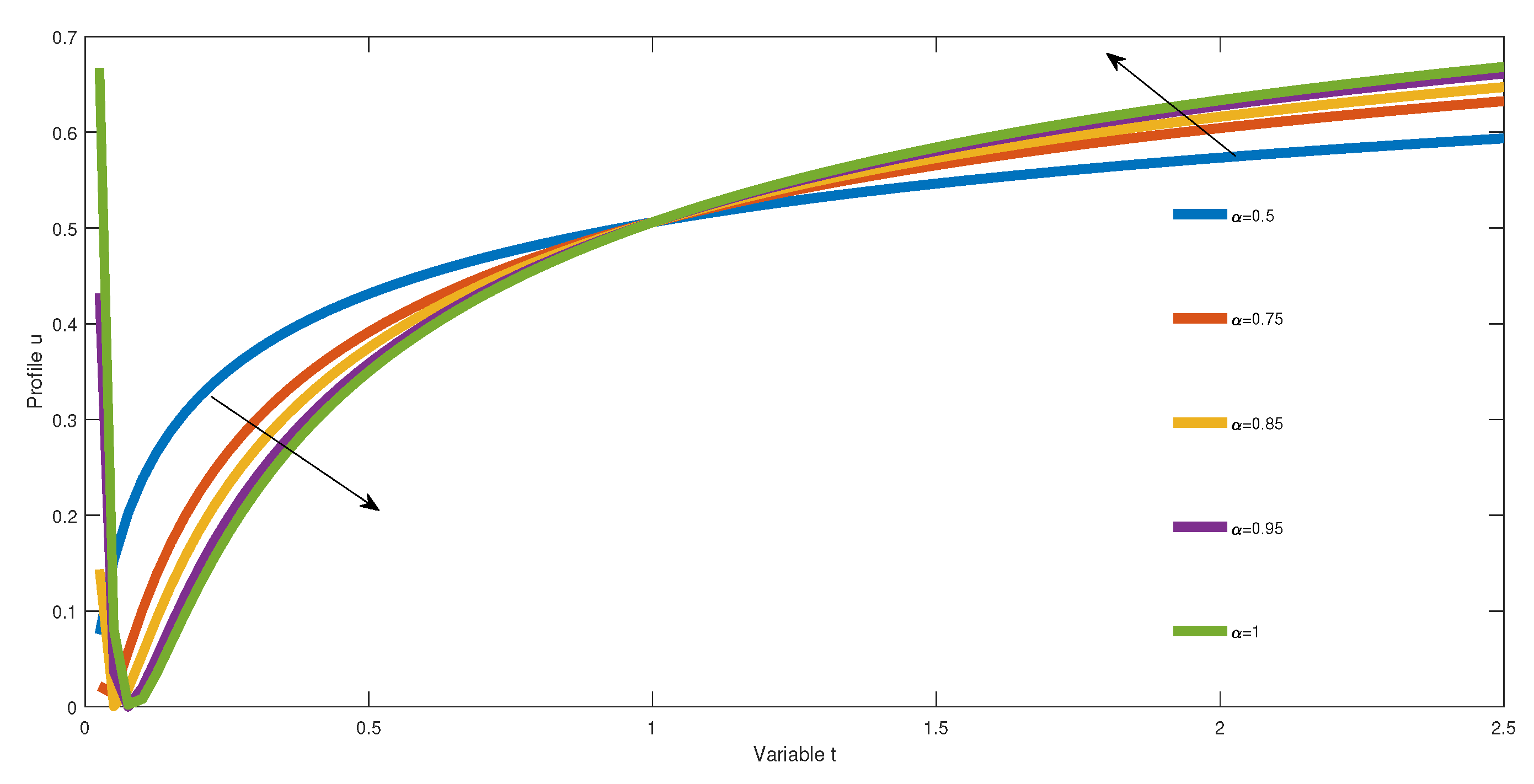
We observe that all the profiles represented with different values of the order of the truncated Grunwald–Letnikov fractional derivative when the time is fixed decrease and convergence rapidly to zero, when the order increase. These processes are explained by the fractional-order creates acceleration effect and the fact the diffusion process is subdiffusive that is $\alpha \le 1.$ In Figure 3, we depict the figure with the assumption $x=1$, we note in the neighbor of the origin the concentrations decrease after a certain time, but after that, all the profiles increase following the increase of the orders (see the arrow). After a certain time, the behaviors change entirely, but the profiles continue to grow as well (see the arrow in Figure 3). These behaviors are not new for us because it is well known that when we fix the state x, the similarity of the diffusion equation increases linearly in time. In other words, the increase of the similarity variable generates this behavior into the diffusion process. The convergence to zero after certain can be explained by the fact the penetration depth converges to 1, which is the value of $x=1$; we can observe this behavior in Equation (30). In other words, the similarity variable converges to 1, which implies the convergence of the solution to zero after a certain time.

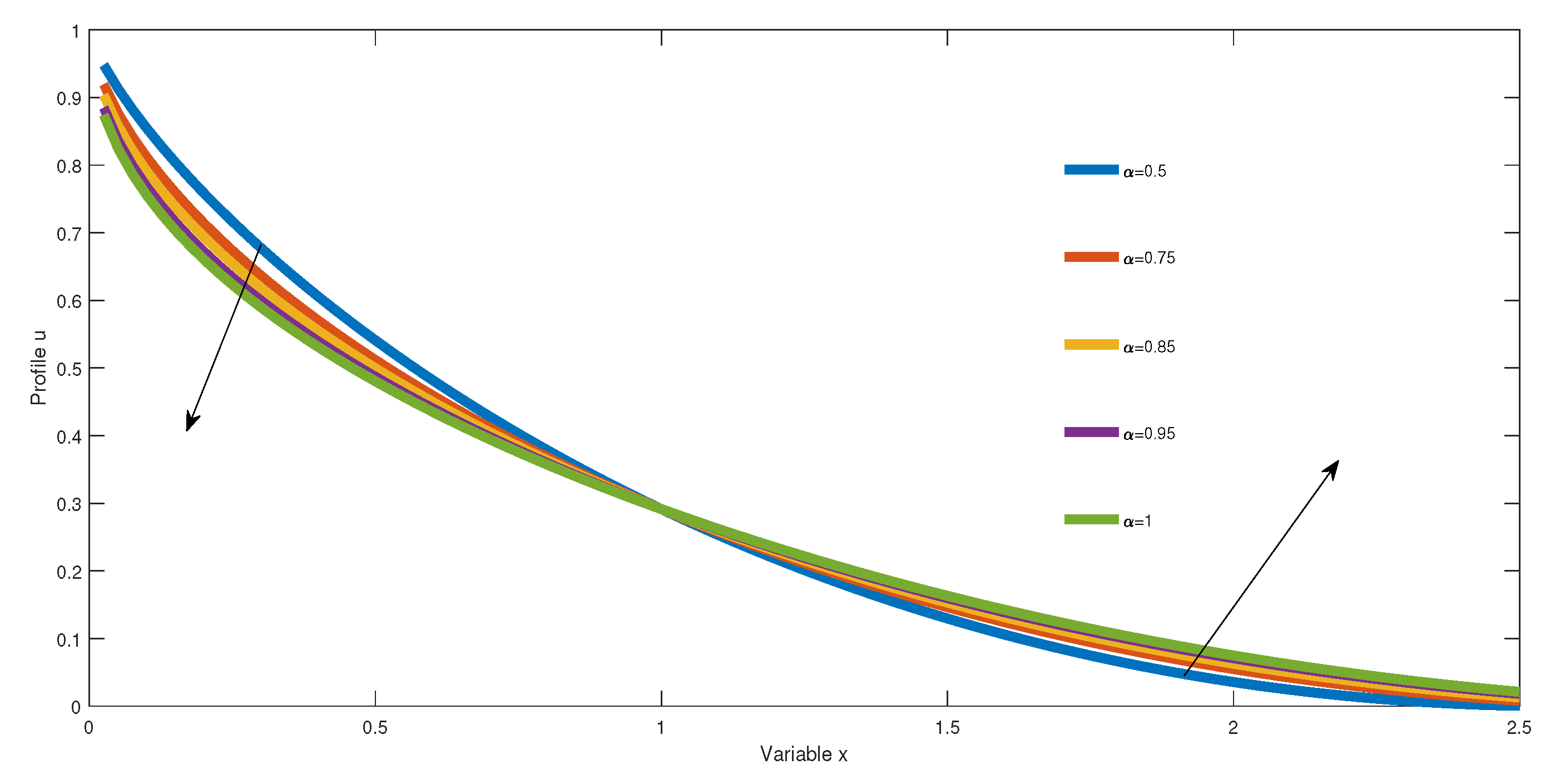
We finish by analyzing now all the profiles into the diffusion–reaction Equation (24). We make the following assumption, we suppose for simplicity, the diffusion coefficient equals the unit, and we let the reaction parameter $b=0.5$. In Figure 4, we depict the profiles with different orders; we observe all the profiles decrease in time and converge rapidly to zero. The form of the reaction does not have many impacts on the nature of the diffusion process; that is, we note the same behavior as in the subdiffusion process studied in the previous case. The subdiffusion process explains the decrease of all the analytical solutions. In other words, the increase in the order accelerates the diffusion process.

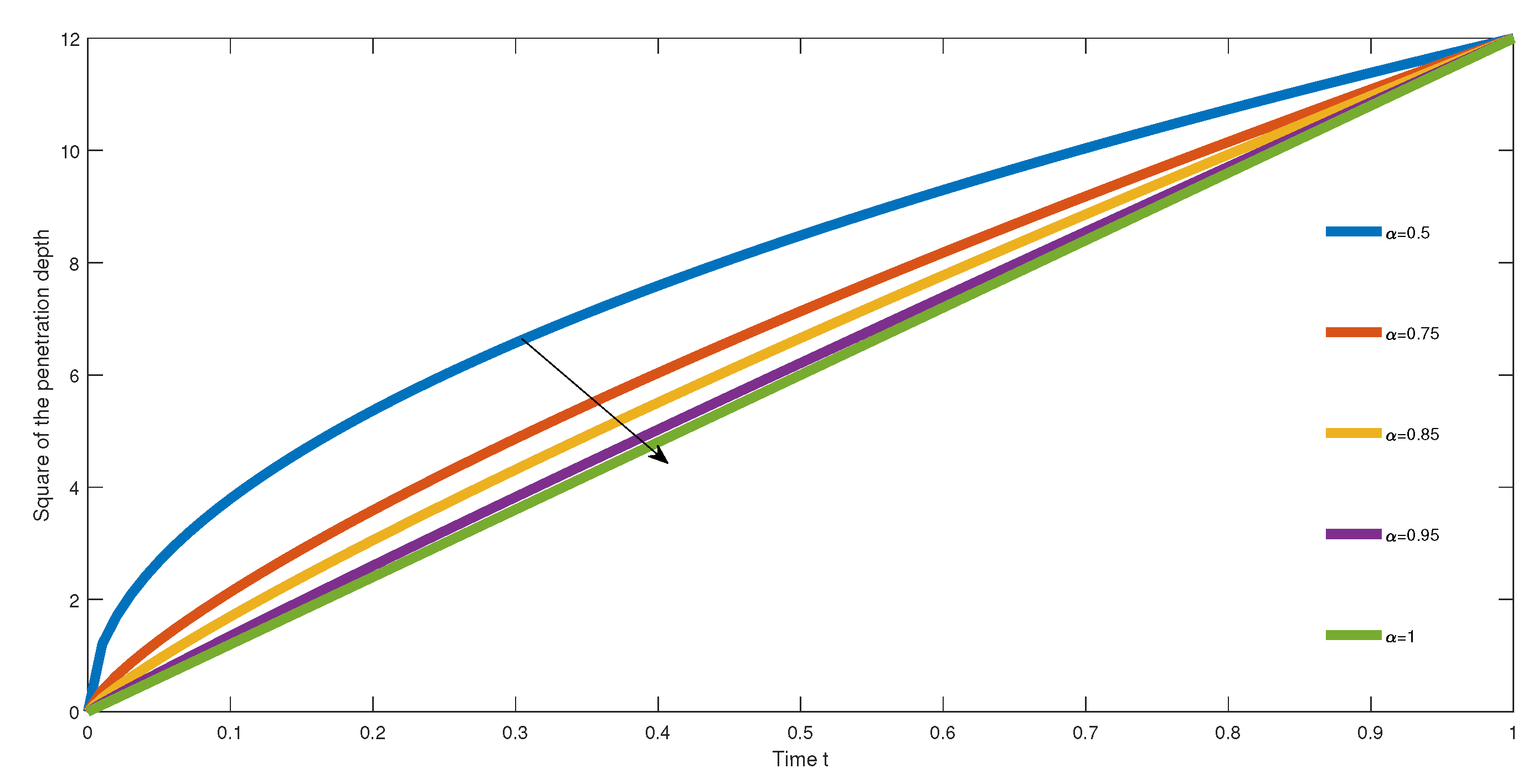
Equation (22) is the square of the penetration depth which represents the mean square displacement for the fractional diffusion equation. In other words, the nature of the diffusion process can be obtained by analyzing the value of the square of the penetration depth. We have many types of diffusion; we recall some of them as follows: subdiffusion, hyperdiffusion, superdiffusion, ballistic diffusion, and Richardson diffusion and normal diffusion process. In this paper, we work in the context of subdiffusion because the fractional-order derivative is into (0,1). In Figure 5, we represent the square of the penetration depth for different values of the fractional order. We notice when the order increases, the square of the penetration depth becomes linear. In other words, the penetration depth of the fractional model converges to the penetration depth of the classical diffusion equation obtained with a classical derivative.

5. Conclusions

This paper gives the response to the possible use of the Laplace transform of the Grunwald–Letnikov fractional derivative in fractional diffusion equations with reaction terms. We also represent and analyze the analytical solutions obtained with the double integration method and the Laplace transform, the square of the penetration depth. A physical analysis is well addressed.