Admissibility of Fractional Order Descriptor Systems Based on Complex Variables: An LMI Approach

Abstract

This paper is devoted to the admissibility issue of singular fractional order systems with order $\alpha \in (0,1)$ based on complex variables. Firstly, with regard to admissibility, necessary and sufficient conditions are obtained by strict LMI in complex plane. Then, an observer-based controller is designed to ensure system admissible. Finally, numerical examples are given to reveal the validity of the theoretical conclusions.

1. Introduction

Singular systems have attracted much increasing attention which have not only theoretical value but also play an important role in practice in recent years. As everyone knows, singular systems have always been the focus of attention and have extensive application in economic systems, power systems, electronic systems and other areas in the development of control theory [1,2,3,4]. Due to the diversity of applications, descriptor systems have better performance than normal systems. Duan et al. [5] generalize the normal systems into the case of descriptor linear systems and examine some of the basic equivalent structures and the solution of a general descriptor linear system. In [6], the paper considers the issue of stabilization for a class of singular FOS by using appropriate matrix variable decoupling technique. In fact, a lot of notations and significative results have been spread from standard systems to singular systems.

At present, with the further study of fractional order systems, many scholars find that FOS have better performance than the integer order counterpart. In recent years, scientists have found that the dynamical behavior of many real world physical systems can be described by fractional order differential equations more completely and precisely than the ordinary integer order differential equations [7]. The relationship between FOS and normal system is verified in [8]. Sabatier et al. [9] deal with LMI stability conditions for FOS. Tavazoei et al. [10] present a new approach to investigate stability of fractional order linear time invariant systems with order between 1 and 2. In [11,12,13,14], papers focus on the issue of initialization of fractional order systems including theory and application. Some stability properties of fractional order systems are presented in [13]. The application of control methods for initialized fractional order systems are shown in [14]. Later on, the observability of fractional order systems are shown in [15]. Trigeassou et al. [16] consider state variables of fractional order differential systems to verify that $x\left(t\right)$ is pseudo state instead of real state. Sabatier et al. [17] reveal advantages of fractional integration operator. A lot of results are given about the stability analysis of FOS in [18,19,20,21,22]. Lu et al. [19] research robust stability of FOS with order $\alpha$: the $0<\alpha <1$ case. Zhang et al. [20] propose the new stability criteria of FOS. The most important conclusion is obtained by linear matrix inequality (LMI) in [23,24,25,26]. Wang et al. [23] focus on robust control issues of uncertain FOS based on model approximation in terms of LMI. In [27,28,29], many important results about FOS have been studied and widely used. Podlubny [27] studies fractional order systems and $P{I}^{\lambda }{D}^{\mu }$-controllers are designed. In [28,29], Sabatier et al. analyze the stability and stabilization of FOS.

With the rapid development of SFOS, many difficult and challenging problems have been solved on this aspect in [29,30,31,32,33]. In [30], Zhang et al. propose the new admissibility conditions of linear SFOS with the order $0<\alpha <1$ in terms of strict linear matrix inequalities. Ji et al. [33] discuss the state and static output feedback stabilization of singular FOS with uncertainty. Yu et al. [34] propose a original admissibility condition for SFOS. To remove the equality constraint in admissibility criterion, Saliha et al. [35] provide a concise criterion. A novel necessary and sufficient condition for the admissibility of singular fractional order systems is derived in terms of linear matrix inequalities in [36]. Wei et al. [37,38] propose new results for stabilizing singular FOS and expect the sufficient and necessary condition for output feedback control which are better than the existing works. Through the above discussion, we know that singular fractional order systems where many challenging and unsolved theoretical problems have been addressed in [34,35,36,37,38]. However, in our knowledge, the problem of admissibility of singular FOS based on complex domain is still incomplete.

Based on these previous works, new sufficient and necessary admissibility conditions in terms of strict LMI are proposed.

The contributions of this work can be summarized as follows:

• The purpose of this paper is to consummate the issue for singular FOS with the fractional order $\alpha$ between $(0,1)$ to complex domain by presenting new theorems.
• Based on thinking about previous studies, we propose the new admissibility conditions by strict LMI in complex domain.
• Finally, we design a novel observer-based controller for SFOS to guarantee the systems to be admissible.

The rest of this paper is briefly outlined as follows. Some preliminaries are presented in Section 2. Section 3 is devoted to the main results. In Section 4 numerical examples are presented to illustrate the applicability of the results and finally conclusion is given in Section 5.

Throughout the text, $X^T$, $\overline{X}$ and $X^{*}$ denote the transpose, the conjugate and the conjugate transpose of a matrix $X$, respectively. $\mathrm{sym}\left\{X\right\}$ denotes the expression $X+X^T$. $\Re \left(r\right)$ denotes the real part of the complex number. r Matrices are the appropriate dimension without special description.

2. Preliminaries

Consider the following SFOS described by,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}E{D}^{\alpha }x\left(t\right)=Ax\left(t\right)+Bu\left(t\right)\\ y=Cx\left(t\right)\\ \hspace{1em}x\left(0\right)=x_0\end{array}\right.\end{array}$$

(1)

where $x\left(t\right)\in {\mathrm{C}}^n$ is the pseudo state vector, $u\left(t\right)\in {\mathrm{R}}^m$ is the control input, $x_0$ is the compatible initial condition without introducing impulse behavior. $E\in {\mathrm{R}}^{n\times n}$ may be singular satisfying $0\le rank\left(E\right)=r\le n$. $A\in {\mathrm{R}}^{n\times n}$, $B\in {\mathrm{R}}^{n\times m}$, C is matrix with appropriate dimensions. The symbol $D^{\alpha }x\left(t\right)$ denotes the Caputo fractional derivatives of $\alpha$ of function $x\left(t\right)$ which is defined as [20]

$${}_c{D}_t^{\alpha }x\left(t\right)=\frac{d^{\alpha }f\left(t\right)}{d{t}^{\alpha }}=\frac{1}{\mathsf{\Gamma }(m-\alpha )}{\int }_0^t\frac{f^{\left(m\right)}\left(\tau \right)}{{(t-\tau )}^{\alpha +1-m}}d\tau ,$$

(2)

where $m-1<\alpha \le m,m\in Z^{+}$, and the gamma function $\mathsf{\Gamma }\left(x\right)={\int }_0^{\infty }{e}^{-t}{t}^{x-1}dt$. For convenience, we simplify ${}_c{D}_t^{\alpha }x\left(t\right)$ to $D^{\alpha }x\left(t\right)$.

System (1) can be rewritten in the following form:

$$\begin{array}{c}\hfill E{D}^{\alpha }x\left(t\right)=Ax\left(t\right).\end{array}$$

(3)

System (3) reduces normal fractional order system as matrix $E(=I)$ is nonsingular,

$$D^{\alpha }x\left(t\right)=Ax\left(t\right).$$

(4)

Then, we introduce the admissibility definition of SFOS which is similar to the integer order system.

Definition 1

([37]). System (3) is said to be regular if $\det (s^{\alpha }E-A)$ is not identially zero. System (3) is said to be impulse free if $\mathrm{deg}\left(\det \right(sE-A\left)\right)=\mathrm{rank}\left(E\right).$ System (3) is said to be stable if all the finite generalized eigenvalues of $\det (\lambda E-A)=0$ lie in $D_{\alpha }=\{\lambda :|arg\left(\lambda \right)|>\frac{\alpha \pi }{2}\}.$ System (3) is said to be admissibility if it is regular, impulse free and stable.

Next, we introduce some lemmas that will be needed in the sequel.

Lemma 1

([20]). $X\in {\mathrm{C}}^{n\times n}>0$ iff

$$\begin{array}{c}\hfill \left[\begin{array}{cc}\Re \left(X\right)& \Im \left(X\right)\\ -\Im \left(X\right)& \Re \left(X\right)\end{array}\right]>0.\end{array}$$

Lemma 2

([20]). System (4) is asymptotically stable iff there exist two matrices $X,Y\in {\mathrm{R}}^{n\times n},$ such that

$$\left[\begin{array}{cc}X& Y\\ -Y& X\end{array}\right]>0,$$

(5)

$$\mathrm{s}\left(\alpha \right)AX-\mathrm{c}\left(\alpha \right)AY+\mathrm{s}\left(\alpha \right)X{A}^T+\mathrm{c}\left(\alpha \right)Y{A}^T<0,$$

(6)

where $\mathrm{s}\left(\alpha \right)=sin\left(\alpha \frac{\pi }{2}\right)$, $\mathrm{c}\left(\alpha \right)=cos\left(\alpha \frac{\pi }{2}\right)$.

Lemma 3

([30]). Suppose that system (3) is regular, and two nonsingular matrices M and N such that

$$MEN=\left[\begin{array}{cc}{I}_m& 0\\ 0& N_{n-m}\end{array}\right],MAN=\left[\begin{array}{cc}\overline{A_1}& 0\\ 0& I_{n-m}\end{array}\right],$$

(7)

where $N_{n-m}$ is nilpotent matrix, then we have:

(a) 

System (3) is impulse free if and only if $N_{n-m}=0$.

(b) 

System (3) is stable if and only if $|\arg \left(spec(\overline{A_1},\alpha )\right)|>\alpha \frac{\pi }{2}$.

(c) 

System (3) is admissible if and only if $N_{n-m}=0$ and $|\arg \left(spec(\overline{A_1},\alpha )\right)|>\alpha \frac{\pi }{2}$.

When the regularity of system (3) is not known, there always exist two nonsingular matrices M and N such that

$$MEN=\left[\begin{array}{cc}{I}_m& 0\\ 0& 0\end{array}\right],MAN=\left[\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right]$$

(8)

Lemma 4.

$X\in {\mathrm{C}}^{n\times n}>0$if and only if$\overline{X}\in {\mathrm{C}}^{n\times n}>0$.

3. Results

According to the above lemmas, the new admissibility criteria for system (3) is presented as follow.

Theorem 1.

The unforced SFOS in (3) with order $0<\alpha <1$ is admissible iff the following equivalent statements hold:

(i) There exist$X_1\in {\mathrm{C}}^{n\times n}$, $X_2\in {\mathrm{C}}^{n\times n}$such that

$$\begin{array}{c}\hfill E{X}_1\ge 0,E{X}_2\ge 0,\end{array}$$

(9)

$$\begin{array}{c}\hfill \mathrm{sym}\{rA{X}_1+\overline{r}A{X}_2\}<0.\end{array}$$

(10)

(ii) There exists$X\in {\mathrm{C}}^{n\times n}$such that

$$\begin{array}{c}\hfill EX\ge 0,\end{array}$$

(11)

$$\begin{array}{c}\hfill \mathrm{sym}\{rAX+\overline{r}A\overline{X}\}<0,\end{array}$$

(12)

where$r=e^{j(1-\alpha )\frac{\pi }{2}}$.

Proof. 

First of all, the equivalence of admissibility and $\left(ii\right)$ are proved.

[Sufficiency:] Suppose the inequalities (11) and (12) hold, since E is singular, there exist invertible matrices M and N satisfying (8).

Due to the invertibility of the matrix $M$, let

$$N^{-1}X{M}^T=\left[\begin{array}{cc}{X}_{11}& X_{12}\\ X_{21}& X_{22}\end{array}\right].$$

(13)

Replacing (13) into (11), we obtain the following formula:

$$\begin{array}{cc}EX\hfill & =M^{-1}\left[\begin{array}{cc}I& 0\\ 0& 0\end{array}\right]N^{-1}N\left[\begin{array}{cc}{X}_{11}& X_{12}\\ X_{21}& X_{22}\end{array}\right]M^{-T}\hfill \\ \hfill & =M^{-1}\left[\begin{array}{cc}{X}_{11}& X_{12}\\ 0& 0\end{array}\right]M^{-T}\ge 0,\hfill \end{array}$$

(14)

so it is shown that $X_{11}\ge 0$, $X_{12}=0$.

Considering (13), and using the expressions in (8), we have

$$\begin{array}{ccc}\mathrm{sym}\{rAX+\overline{r}A\overline{X}\}\hfill & =\hfill & \mathrm{sym}\{r{M}^{-1}\left[\begin{array}{cc}{A}_{11}{X}_{11}+A_{12}{X}_{21}& A_{12}{X}_{22}\\ A_{21}{X}_{11}+A_{22}{X}_{21}& A_{22}{X}_{22}\end{array}\right]M^{-T}\hfill \\ \hfill & \hfill & +\overline{r}{M}^{-1}\left[\begin{array}{cc}{A}_{11}\overline{X_{11}}+A_{12}\overline{X_{21}}& A_{12}\overline{X_{22}}\\ A_{21}\overline{X_{11}}+A_{22}\overline{X_{21}}& A_{22}\overline{X_{22}}\end{array}\right]M^{-T}\}<0\hfill \end{array}$$

(15)

.

Then, it induces $A_{22}$ reversible that represents system (3) is regular and impulse free. Then, invertible matrices L and R can be defined such that

$$LER=\left[\begin{array}{cc}{I}_{r1}& 0\\ 0& 0\end{array}\right],LAR=\left[\begin{array}{cc}{A}_1& 0\\ 0& I\end{array}\right],$$

(16)

where $A_1\in {\mathrm{R}}^{r_1\times r_1}$, then let

$$X=R\left[\begin{array}{cc}{X}_{11}& 0\\ X_{21}& X_{22}\end{array}\right]L^{-T}.$$

(17)

From (16) and (17), it induces the equivalence of the following inequalities and conditions (12),

$$\left[\begin{array}{cc}{\mathsf{\Psi }}_{11}& {\mathsf{\Psi }}_{21}^T\\ {\mathsf{\Psi }}_{21}& {\mathsf{\Psi }}_{22}\end{array}\right]<0,$$

where

$$\begin{array}{c}{\mathsf{\Psi }}_{11}=\mathrm{sym}\{r{A}_1{X}_{11}+\overline{r}{A}_1{\overline{X}}_{11}\},\hfill \\ {\mathsf{\Psi }}_{21}=\mathrm{sym}\{r{X}_{21}+\overline{r}{\overline{X}}_{21}\},\hfill \\ {\mathsf{\Psi }}_{22}=\mathrm{sym}\{r{X}_{22}+\overline{r}{\overline{X}}_{22}\}.\hfill \end{array}$$

(18)

It follows that ${\mathsf{\Psi }}_{11}<0$. We deduce that the system $D^{\alpha }{x}_1\left(t\right)=A_{1}x\left(t\right)$ is stable, so system (3) is also stable. Therefore, We conclude that system (3) is admissibile since it is regular, impulse free and stable.

[Necessity:] Suppose that system (3) is admissible. Then, there exist invertible matrices such that (8) holds and $D^{\alpha }{x}_1\left(t\right)=A_{1}x\left(t\right)$ is stable. There exists a matrix ${\widehat{X}}_1={\widehat{X}}_1^{*}\in C^{n\times n}>0$ such that

$$\mathrm{sym}\left\{A_1(r\widehat{X_1}+\overline{r}{\overline{\widehat{X}}}_1)\right\}<0,$$

(19)

with $r=e^{j(1-\alpha )\frac{\pi }{2}}$, then let

$$X=R\left[\begin{array}{cc}{\widehat{X}}_1& 0\\ 0& -I\end{array}\right]L^{-T}.$$

(20)

It is easy to show that $EX\ge 0$, then, we get

$$\begin{array}{c}\hfill \mathrm{sym}(rAX+\overline{r}A\overline{X})=\mathrm{sym}(L^{-1}\left[\begin{array}{cc}r{A}_1{\widehat{X}}_1& 0\\ 0& -I\end{array}\right]L^{-T}+L^{-1}\left[\begin{array}{cc}\overline{r}{A}_1{\overline{\widehat{X}}}_1& 0\\ 0& -I\end{array}\right]L^{-T})<0.\end{array}$$

(21)

Therefore, it proves that the equivalence of $\left(ii\right)$ and admissibility of SFOS (3). Afterwards, the equivalence of $\left(i\right)$ and $\left(ii\right)$ is given.

$\left(ii\right)$⇒$\left(i\right)$: Taking $X_1=X$ and $X_2=\overline{X}$, it is obtained easily.

$\left(i\right)$⇒$\left(ii\right)$: It is proved in the following form, $\exists E{X}_1\ge 0,$$E{X}_2\ge 0$ s.t.

$$\overline{r}{X}_1^{*}{A}^T+rA{X}_1+r{X}_2^{*}{A}^T+\overline{r}A{X}_2<0.$$

⇔$\exists E{X}_1\ge 0,$ $E{X}_2\ge 0$ s.t.

$$\overline{\overline{r}{X}_1^{*}{A}^T+rA{X}_1+r{X}_2^{*}{A}^T+\overline{r}A{X}_2}<0.$$

This implies that $\exists E{X}_1\ge 0,$ $E{X}_2\ge 0$ s.t.

$$\overline{r}{X}_1^{*}{A}^T+rA{X}_1+r{X}_2^{*}{A}^T+\overline{r}A{X}_2+\overline{\overline{r}{X}_1^{*}{A}^T+rA{X}_1+r{X}_2^{*}{A}^T+\overline{r}A{X}_2}<0.$$

When $X=X_1+{\overline{X}}_2$, the inequality (12) is obtained. □

Remark 1.

Because the inequalities in (10) and (12) contain equality constraint, it has difficulty in solving. Therefore, the following theorem introduces a matrix $S\in {\mathrm{C}}^{n\times (n-m)}$ which is of full column rank and $ES=0$. With the help of the matrix S, a strict LMI without equality constraint condition is given.

Theorem 2.

System (3) is admissible iff there exist matrices $X,Y\in {\mathrm{C}}^{n\times n},Q\in {\mathrm{C}}^{(n-m)\times n}$ such that (5) holds and

$$sym\{rA(X{E}^T+SQ)+\overline{r}AY{E}^T\}<0.$$

(22)

Proof. 

Suppose that there exist matrices $X,Y,$ Q such that (5) and (22) hold. Let

$${\tilde{X}}_1=X{E}^T+r^{-1}SQ,{\tilde{X}}_2=Y{E}^T.$$

(23)

Then, it is similar to the proof of Theorem 1, so not to be described in detail herein. □

Corollary 1.

System (3) is admissible iff there exist matrices $X,Y\in {\mathrm{C}}^{n\times n},Q\in {\mathrm{C}}^{(n-m)\times n}$ such that (5) holds and

$$\mathrm{sym}\{r(E^{T}X+SQ)A+\overline{r}{E}^{T}YA\}<0.$$

(24)

3.1. Stabilization of SFOS

For a SFOS, it is necessary to ensure the SFO system is admissibile by designing the state feedback controller which is given in the following:

$$u\left(t\right)=Kx\left(t\right),K\in {\mathrm{C}}^{m\times n}.$$

(25)

When system (1) have a controller (25), it obtains the following closed-loop system:

$$\left\{\begin{array}{c}E{D}^{\alpha }x\left(t\right)=(A+BK)x\left(t\right)\\ y=Cx\left(t\right)\end{array}\right.$$

(26)

Then, it has

$$\mathrm{sym}\{r(A+BK)(X{E}^T+SQ)+\overline{r}(A+BK)Y{E}^T\}<0.$$

(27)

For SFOS (1), the closed-loop system in (26) with controller (25) is admissible if and only if there exist matrices $X,Y\in {\mathrm{C}}^{n\times n},$ $Q\in {\mathrm{C}}^{(n-m)\times n}$, and $Z\in {\mathrm{C}}^{m\times n}$ such that (5) holds and

$$\mathrm{sym}(rA(X{E}^T+SQ)+\overline{r}AY{E}^T+BZ)<0.$$

(28)

Afterwards, we obtain the following gain matrix,

$$K=Z{(r(X{E}^T+SQ)+\overline{r}Y{E}^T)}^{-1}.$$

(29)

3.2. Observer-Based Control for SFOS

For SFOS (1), we consider the following form to design the controller:

$$\left\{\begin{array}{c}E{D}^{\alpha }\widehat{x}\left(t\right)=A\widehat{x}\left(t\right)+Bu\left(t\right)+L(C\widehat{x}\left(t\right)-y\left(t\right))\\ \hspace{1em}\hspace{1em}\hspace{1em}u\left(t\right)=K\widehat{x}\left(t\right)\end{array}\right.$$

(30)

where K and L are defined as the parameter gains. The following closed-loop system is given,

$$\check{E}{D}^{\alpha }\nu \left(t\right)=A_{cl}\nu \left(t\right)$$

(31)

with $\check{E}=\left[\begin{array}{cc}E& 0\\ 0& E\end{array}\right]$, $\nu \left(t\right)=\left[\begin{array}{c}x\left(t\right)\\ x\left(t\right)-\widehat{x}\left(t\right)\end{array}\right]$, $A_{cl}=\left[\begin{array}{cc}A+BK& -BK\\ 0& A+LC\end{array}\right]$. Conditions of the admissibility for system (31), or the pair $(\check{E},A_{cl})$ are given by the following results.

Theorem 3.

System in (31) is admissible if and only if there exist matrices$X_1=X_1^{*},X_2=X_2^{*}\in {\mathrm{C}}^{n\times n}>0,$$Y_1=Y_1^{*},Y_2=Y_2^{*}\in {\mathrm{C}}^{n\times n}>0$such that Lemma 2 holds,$Q_1\in {\mathrm{C}}^{(n-q)\times n},$$Q_2\in {\mathrm{C}}^{n\times (n-q)},$$W_1\in {\mathrm{C}}^{m\times n},$$W_2\in {\mathrm{C}}^{n\times m},$satisfying

$$\mathrm{sym}\{rA(X_1{E}^T+S_1{Q}_1)+\overline{r}A{Y}_1{E}^T+B{W}_1\}<0,$$

(32)

$$\mathrm{sym}\{r(E^T{X}_2+Q_2{S}_2)A+\overline{r}{E}^T{Y}_{2}A+W_{2}C\}<0,$$

(33)

where$S_1\in {\mathrm{C}}^{n\times (n-q)}$and$S_2\in {\mathrm{C}}^{(n-q)\times n}$are full column rank and$E{S}_1=0,$$S_{2}E=0$. The following gain matrices are given,

$$\begin{array}{c}K=W_1{(r(X_1{E}^T+S_1{Q}_1)+\overline{r}{Y}_1{E}^T)}^{-1},\\ L={(r(E^T{X}_2+Q_2{S}_2)+\overline{r}{E}^T{Y}_2)}^{-1}{W}_2.\end{array}$$

(34)

Proof. 

[Sufficiency:] From Theorem 2 and (32), it obtains that $(E,A+BK)$ is admissible.

Therefore, the system $(E,A+BK)$ is admissible if and only if there exist matrix $X_1=X_1^{*}\in {\mathrm{C}}^{n\times n}>0$ satisfying

$$\mathsf{\Lambda }=\mathrm{sym}\{r(A+BK)({\tilde{X}}_2{E}^T+S_1{\tilde{Q}}_2)+\overline{r}(A+BK)Y_1{E}^T\}<0.$$

(35)

By (32), it is equivalently expressed as

$$\mathsf{\Omega }=\mathrm{sym}\{r(A+LC)(X_1{E}^T+S_1{Q}_1)+\overline{r}(A+LC)Y_1{E}^T\}<0.$$

(36)

Then, a scalar $ϵ$ satisfying $ϵ>0,$ the LMI holds as follow,

$$\mathrm{sym}\{r{A}_{cl}(\check{X}{\check{E}}^T+{\check{S}}_1\check{Q})+\overline{r}{A}_{cl}{\check{Y}}_1{\check{E}}^T\}=\left[\begin{array}{cc}\mathsf{\Lambda }& -ϵBK({\tilde{X}}_2{E}^T+S_1{\tilde{Q}}_2+Y_1{E}^T)\\ 0& ϵ\mathsf{\Omega }\end{array}\right]<0,$$

(37)

for $\check{X}=\left[\begin{array}{cc}{X}_1& 0\\ 0& ϵ{\tilde{X}}_2\end{array}\right]$, ${\check{Y}}_1=\left[\begin{array}{cc}{Y}_1& 0\\ 0& ϵY_1\end{array}\right],$ $\check{Q}=\left[\begin{array}{cc}{Q}_1& 0\\ 0& ϵ{\tilde{Q}}_2\end{array}\right],$ ${\check{S}}_1=\left[\begin{array}{cc}{S}_1& 0\\ 0& S_1\end{array}\right].$ Hence, we obtain that the closed-loop system (31) is admissible under the conditions of Theorem 2.

[Necessity:] If system (31) is admissible, and $\acute{X},$ ${\acute{Y}}_1,$ $\acute{Q}$ and ${\overline{S}}_1$ with appropriate dimensions satisfying

$$\mathrm{sym}(r{A}_{cl}(\acute{X}{\check{E}}^T+{\overline{S}}_1\acute{Q})+\overline{r}{A}_{cl}{\acute{Y}}_1{\check{E}}^T)<0.$$

(38)

Suppose there exist matrices satisfying $\acute{X}=\left[\begin{array}{cc}{X}_1& 0\\ 0& X_2\end{array}\right],$ ${\acute{Y}}_1=\left[\begin{array}{cc}{Y}_1& 0\\ 0& Y_1\end{array}\right],$ $\acute{Q}=\left[\begin{array}{cc}{Q}_1& 0\\ 0& Q_2\end{array}\right],$ ${\overline{S}}_1=\left[\begin{array}{cc}{S}_1& 0\\ 0& S_1\end{array}\right],$ $W_1=K(r(X_1{E}^T+S_1{Q}_1)+\overline{r}{Y}_1{E}^T).$ Then, we obtain that if $\acute{X}$ such that Lemma 2 holds, so $\left[\begin{array}{cc}{I}_n& 0\end{array}\right]\acute{X}\left[\begin{array}{c}{I}_n\\ 0\end{array}\right]$ such that Lemma 2 holds. Furthermore, one has

$$\begin{array}{c}\left[\begin{array}{cc}{I}_n& 0\end{array}\right]\mathrm{sym}(r{A}_{cl}(\acute{X}{\check{E}}^T+{\overline{S}}_1\acute{Q})+\overline{r}{A}_{cl}{\acute{Y}}_1{\check{E}}^T)\left[\begin{array}{c}{I}_n\\ 0\end{array}\right]\hfill \\ =\mathrm{sym}\{r(A+BK)(X_1{E}^T+S_1{Q}_1)+\overline{r}(A+BK)Y_1{E}^T\}\hfill \\ =\mathrm{sym}(rA(X_1{E}^T+S_1{Q}_1)+\overline{r}A{Y}_1{E}^T+B{W}_1)\hfill \\ <0,\hfill \end{array}$$

(39)

which implies inequality (32). Apparently, (33) is obtained in the similar way. It completes the proof of Theorem 3. □

4. Numerical Example

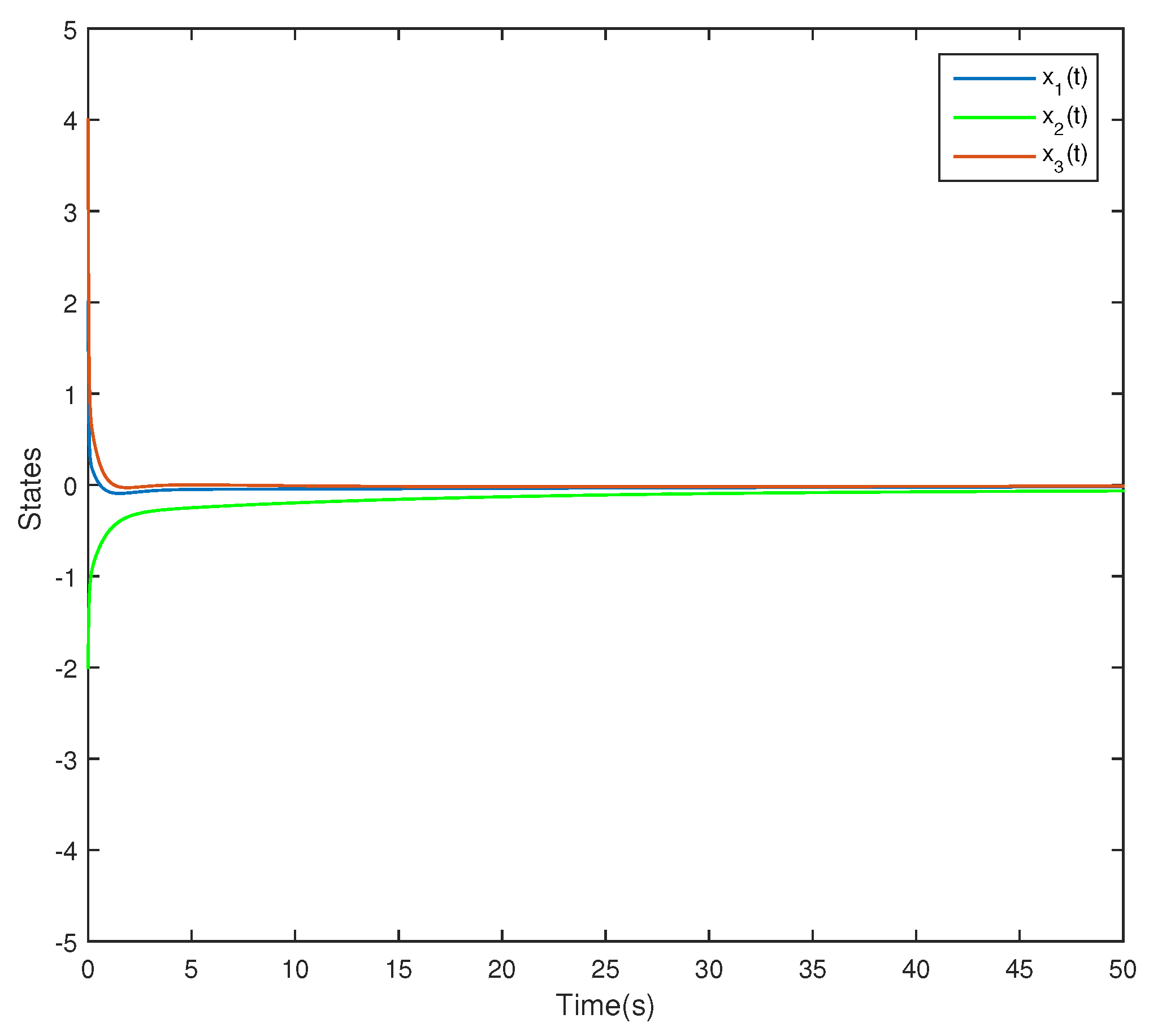
4.1. Admissibility

Example 1.

Consider SFOS (3) with $\alpha =0.5,$ and

$$E=\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 0& 0& 1\end{array}\right],A=\left[\begin{array}{ccc}-1& 1& 0\\ -3& -4& 1\\ 0& 0& -2\end{array}\right].$$

(40)

A feasible solution is given in the following by LMI (22) of Theorem 2:

$$X={10}^8*\left[\begin{array}{ccc}2.8857& 1.0441& 0.4275\\ 1.0441& -1.8416& -0.3945\\ 0.4275& -0.3945& 0.7279\end{array}\right],Y=\left[\begin{array}{ccc}0& -4.2749& 3.9448\\ 4.2749& 0& -7.2789\\ -3.9448& 7.2789& 0\end{array}\right],$$

(41)

$$Q={10}^8*\left[\begin{array}{ccc}-5.1317& 0.4044& -0.5777\end{array}\right].$$

Setting the initial conditions$x\left(0\right)={[2-24]}^T,$the state responses of the resulting closed-loop control systems are illustrated in Figure 1.

4.2. Controller Design

Example 2.

Consider the following SFOS described in (30) with$\alpha =0.3$and

$$E=\left[\begin{array}{ccc}1& 3& 0\\ 2& -1& 0\\ 1& 5& 0\end{array}\right],A=\left[\begin{array}{ccc}1& 1& -1\\ 2& -2& -1\\ 4& 1& -4\end{array}\right],$$

(42)

$$B=\left[\begin{array}{cc}-1& 1\\ 1& -1\\ 1& 1\end{array}\right],C=\left[\begin{array}{ccc}1& 0& 0\\ 0& 0& 1\end{array}\right].$$

(43)

Afterwards, an observer-based controller is designed to ensure the closed-loop system in (30) is admissible. We get the following results by the conditions (32) and (33) of Theorem 3:

$$K=\left[\begin{array}{ccc}-0.1168& 0.2476& -0.5767\\ 0.0028& 0.0060& -0.0140\end{array}\right],$$

(44)

$$L=\left[\begin{array}{cc}3.4074& 0.0210\\ 8.3516& -0.0283\\ 2.8518& -0.0024\end{array}\right].$$

(45)

SFO system in (30) is unstable initially and its states response is shown in Figure 2. Then, the closed-loop SFO system in (31) is stable under the condition of Theorem 3 and its states responses is shown in Figure 3.

5. Conclusions

The issue of admissibility of SFOS is considered based on complex variables in complex domain. We derive the Theorem 1 by an LMI approach as $\alpha$ belonging $0<\alpha <1.$ Then, an observer-based controller is designed to guarantee the stability of the SFOS. Finally, we demonstrate the validity of the proposed results by giving the numerical examples. Further works will still be focused on the series of the issue of SFOS.