Fractional Mass-Spring-Damper System Described by Generalized Fractional Order Derivatives
Abstract
:1. Introduction
2. Generalized Fractional Derivative Operators
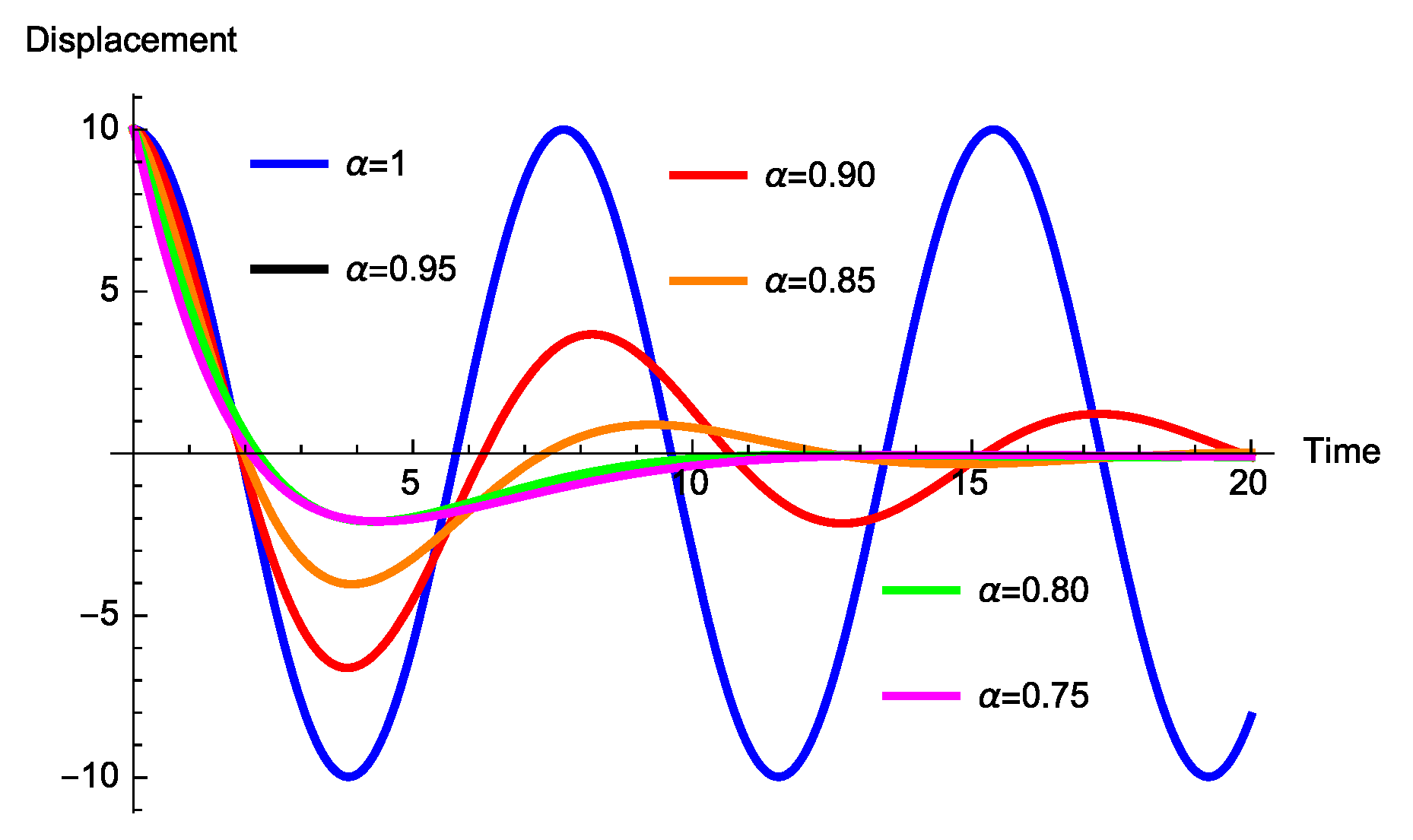
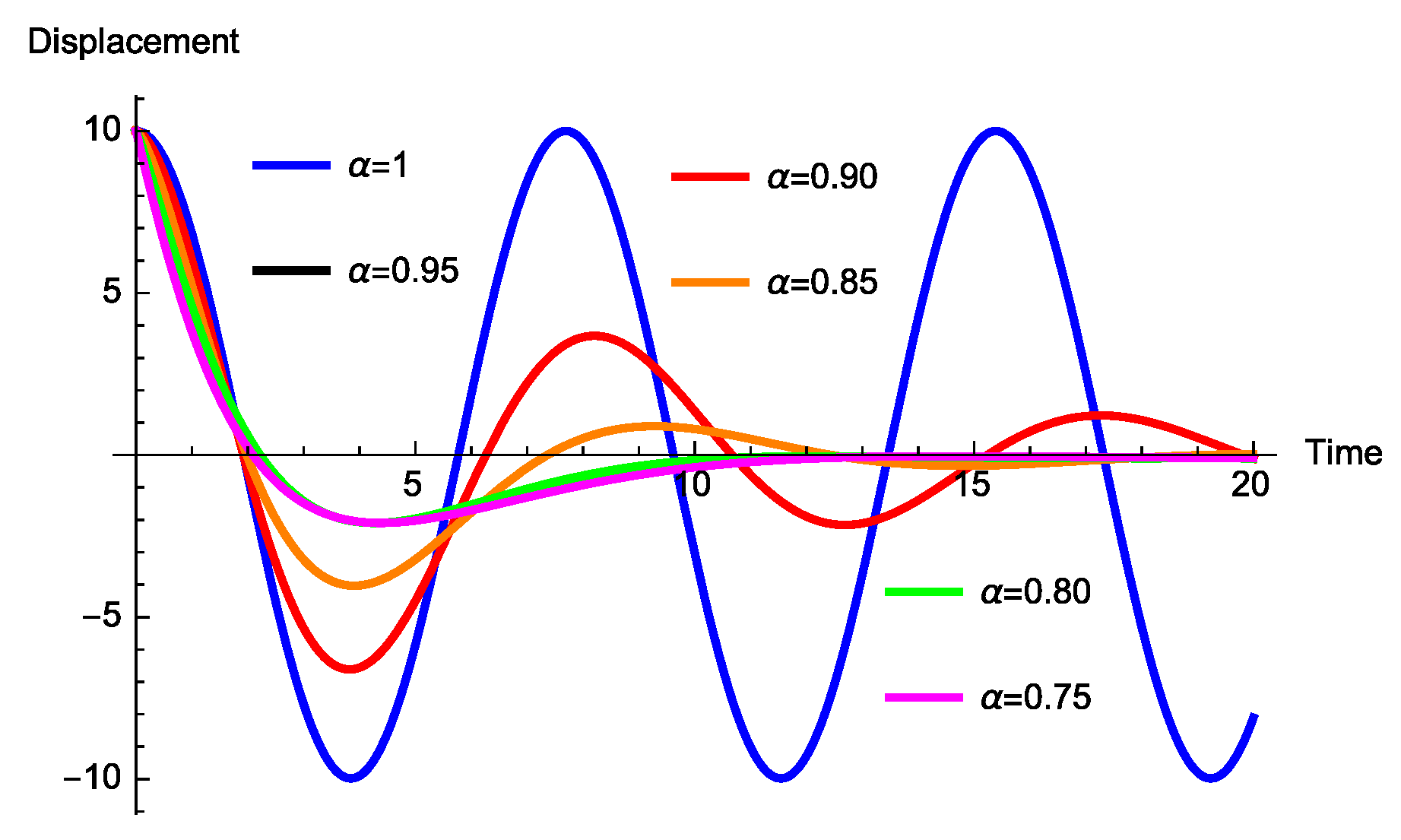
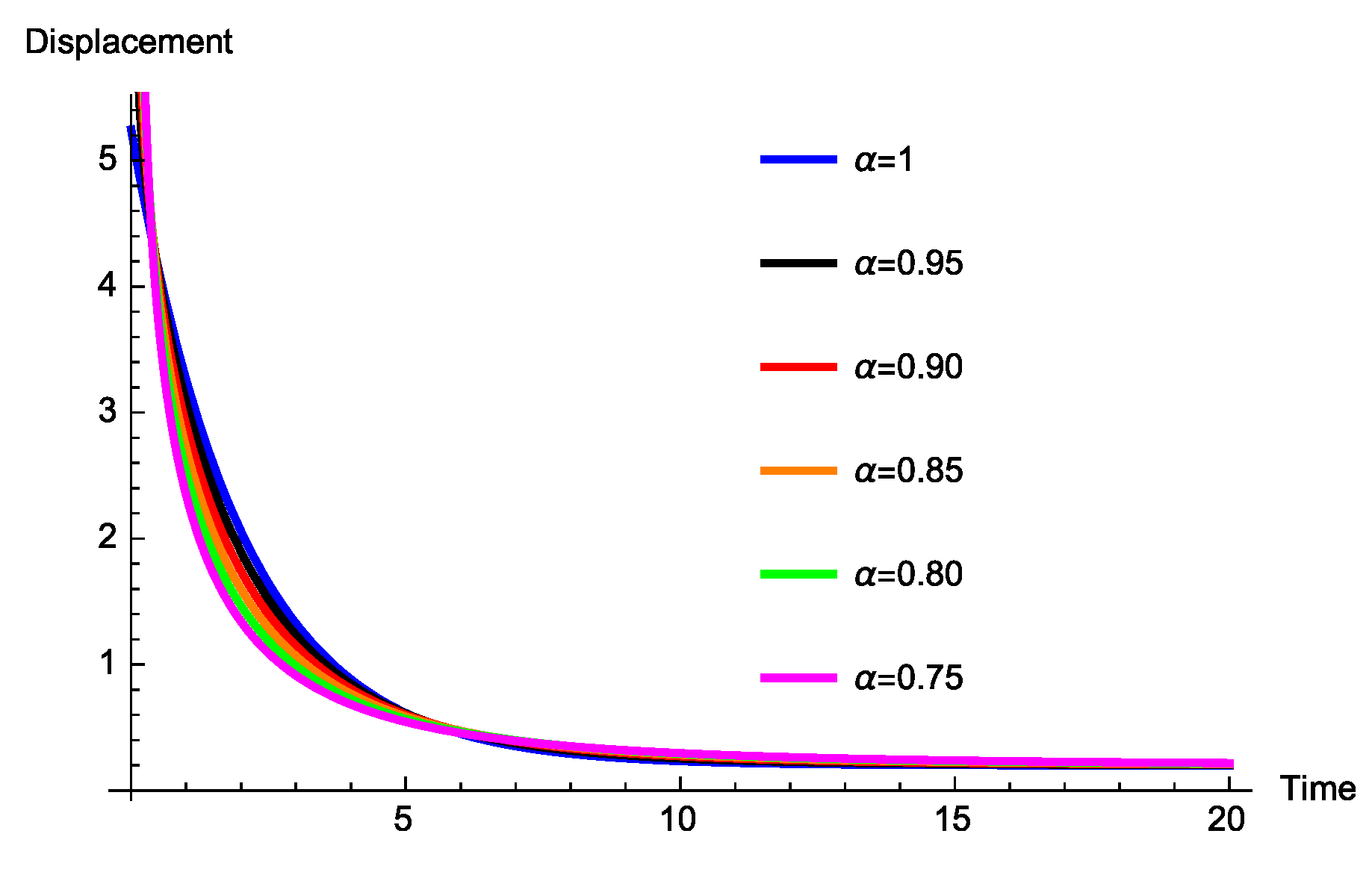
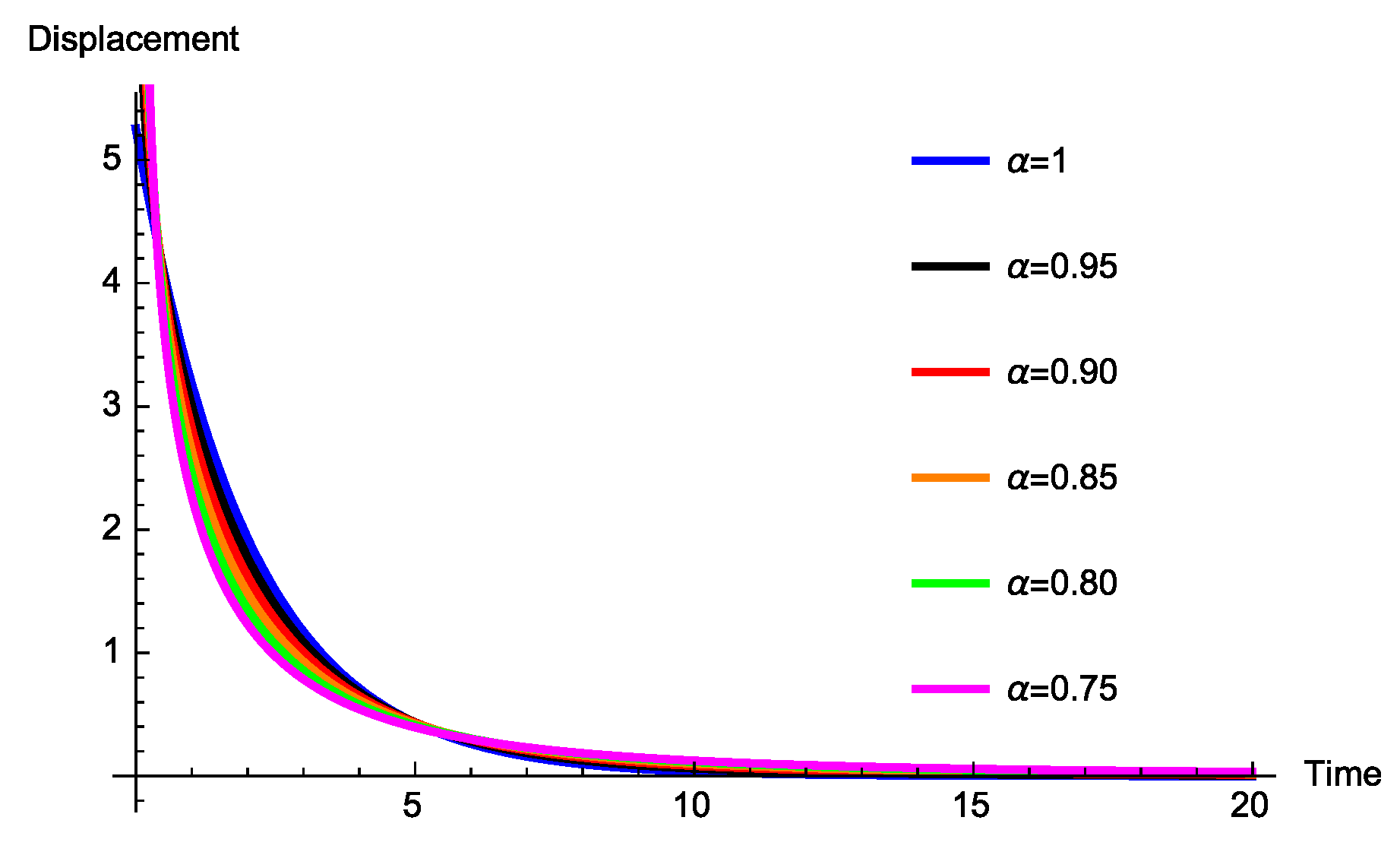
3. Fractional Mass-Spring-Damper Systems
3.1. Caputo Generalized Fractional Derivative
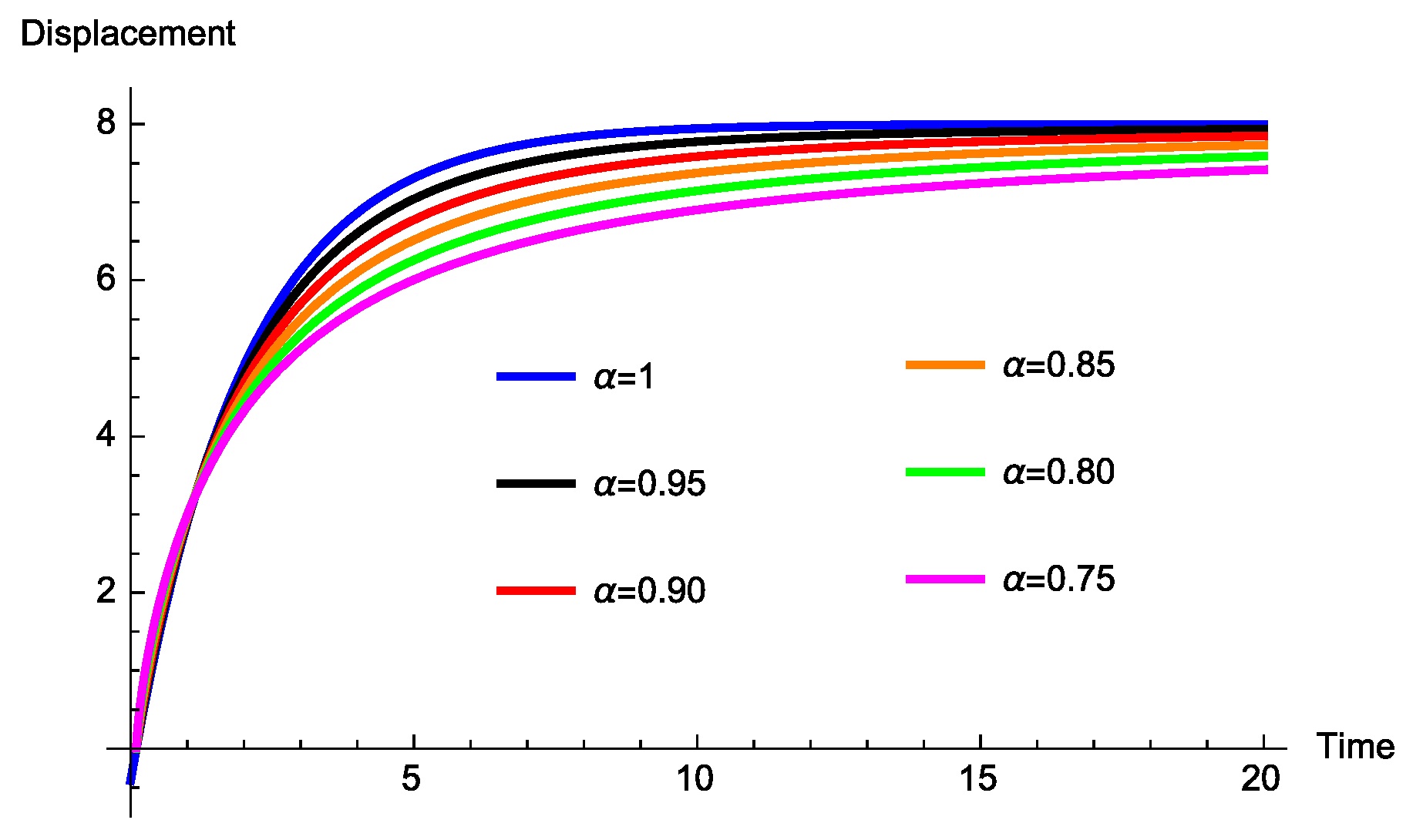
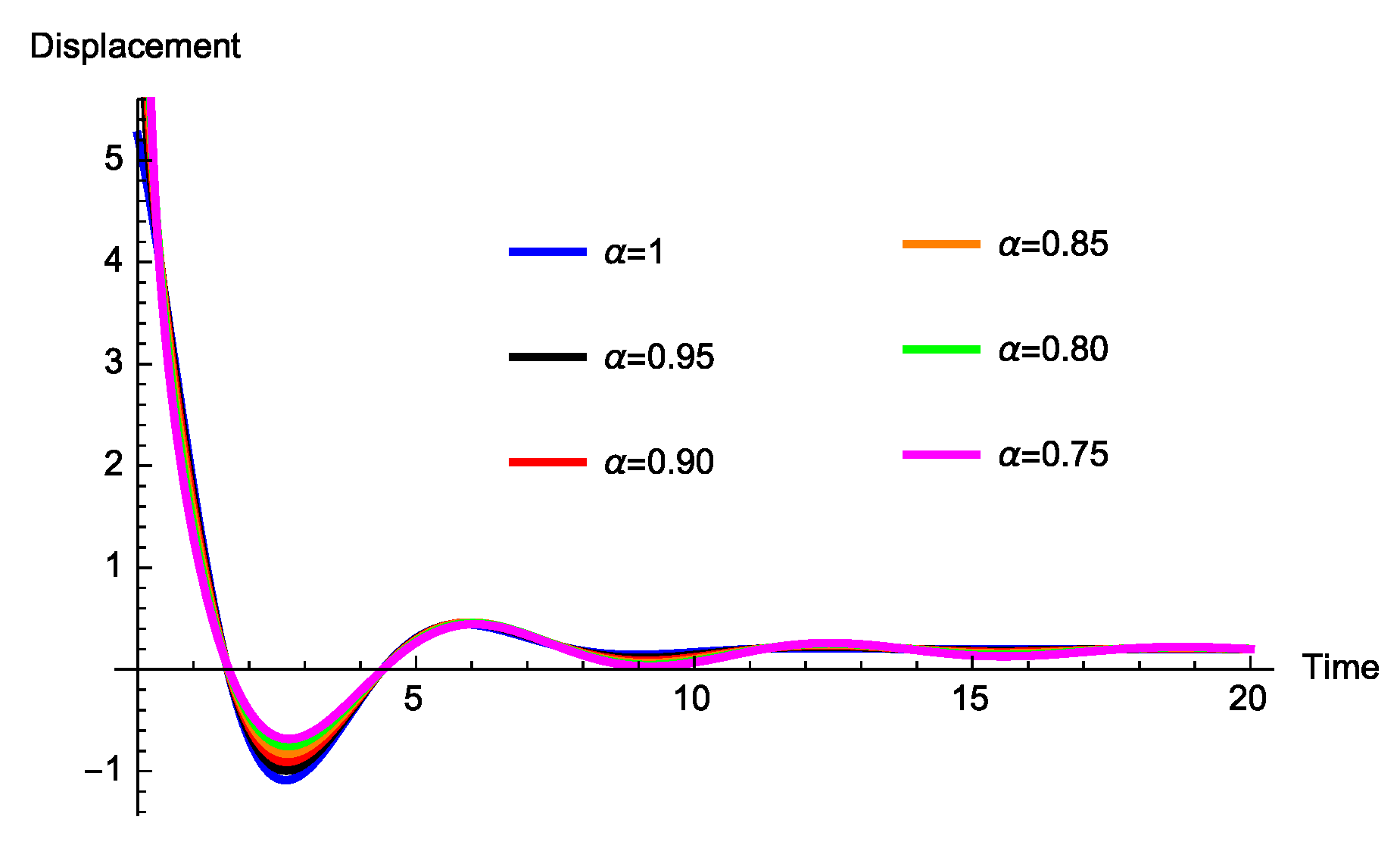
3.1.1. Absence of Mass
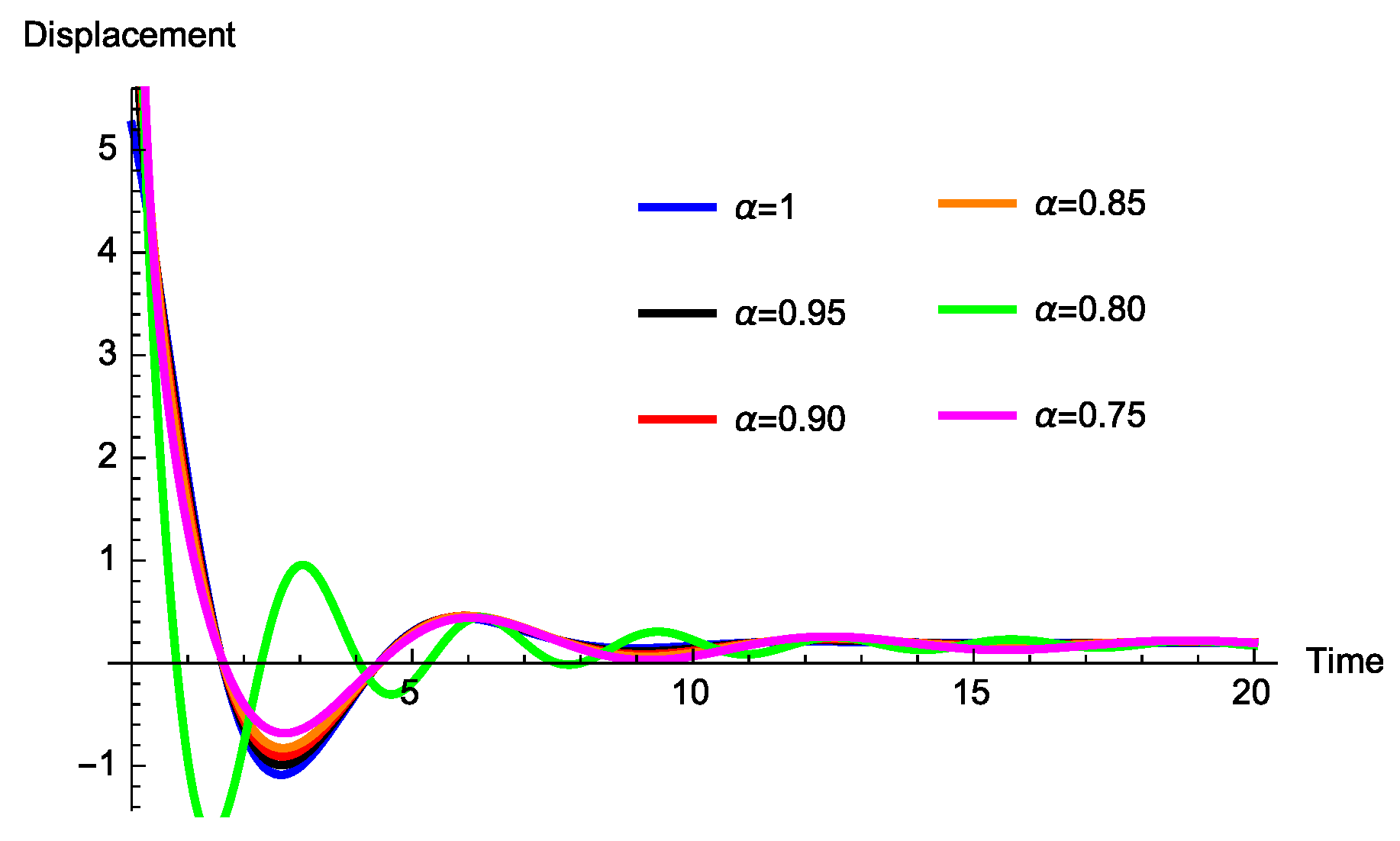
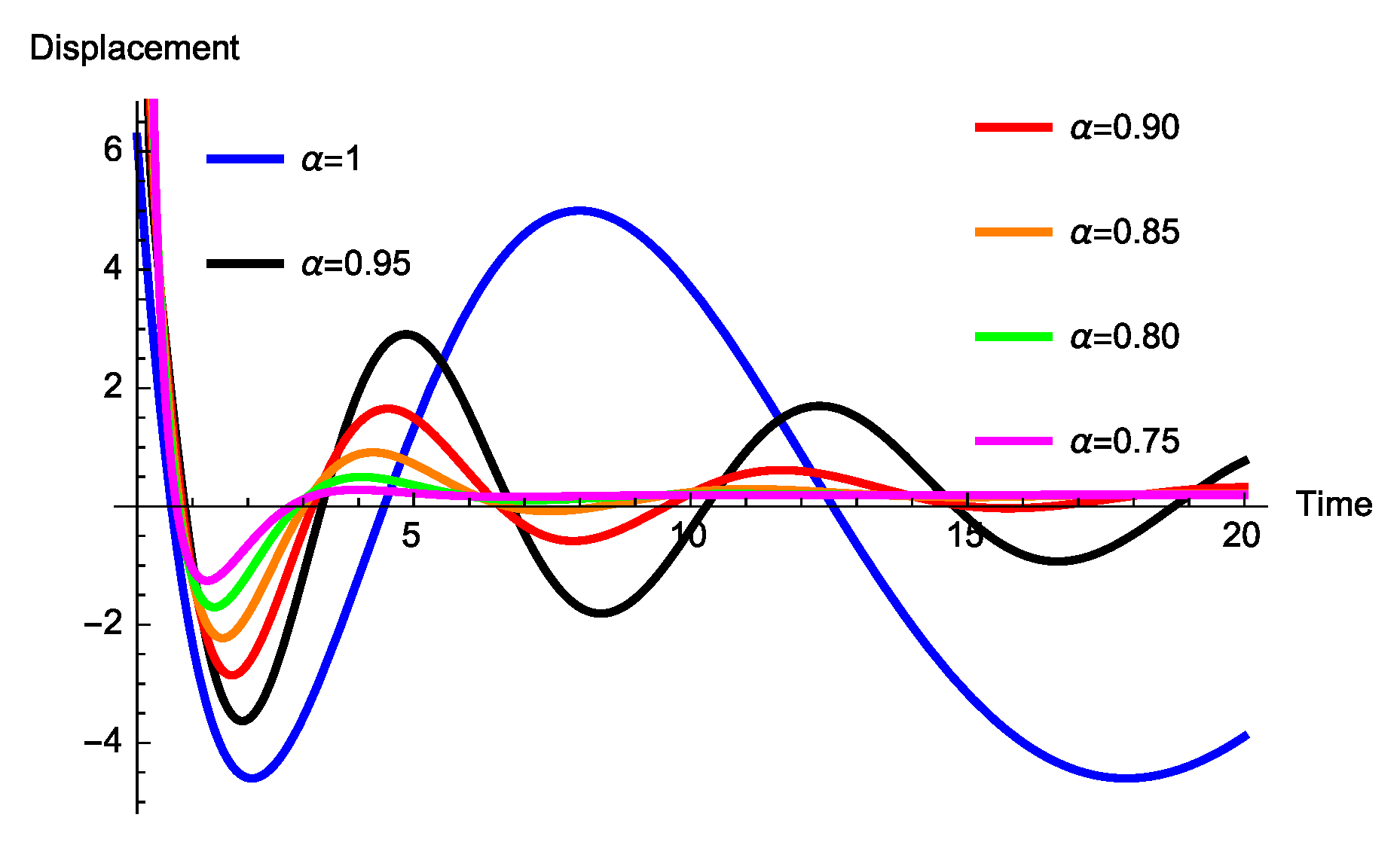
3.1.2. Absence of the Spring Coefficient
3.1.3. In the Presence of Mass and Spring Coefficients
3.2. Left Generalized Fractional Derivative
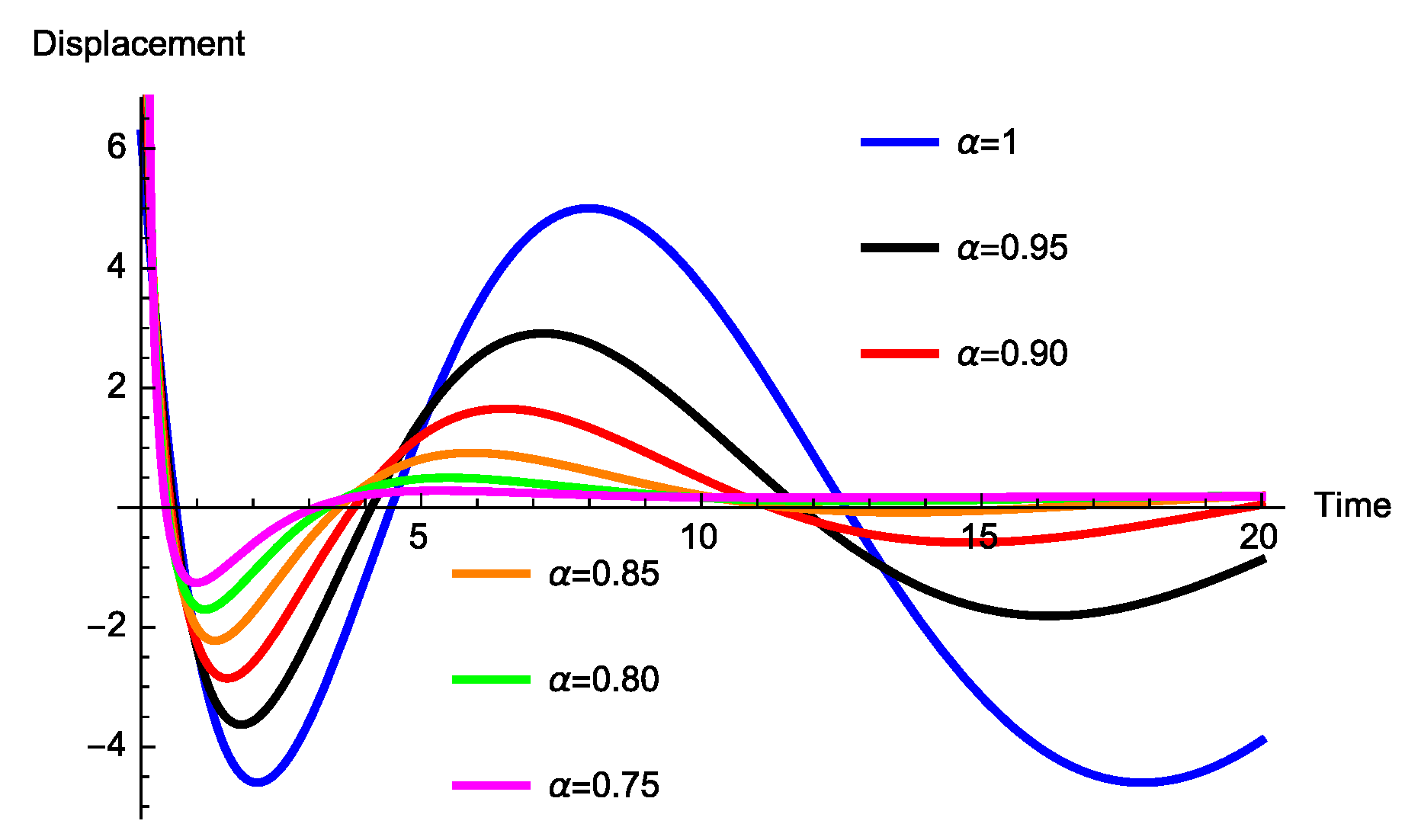
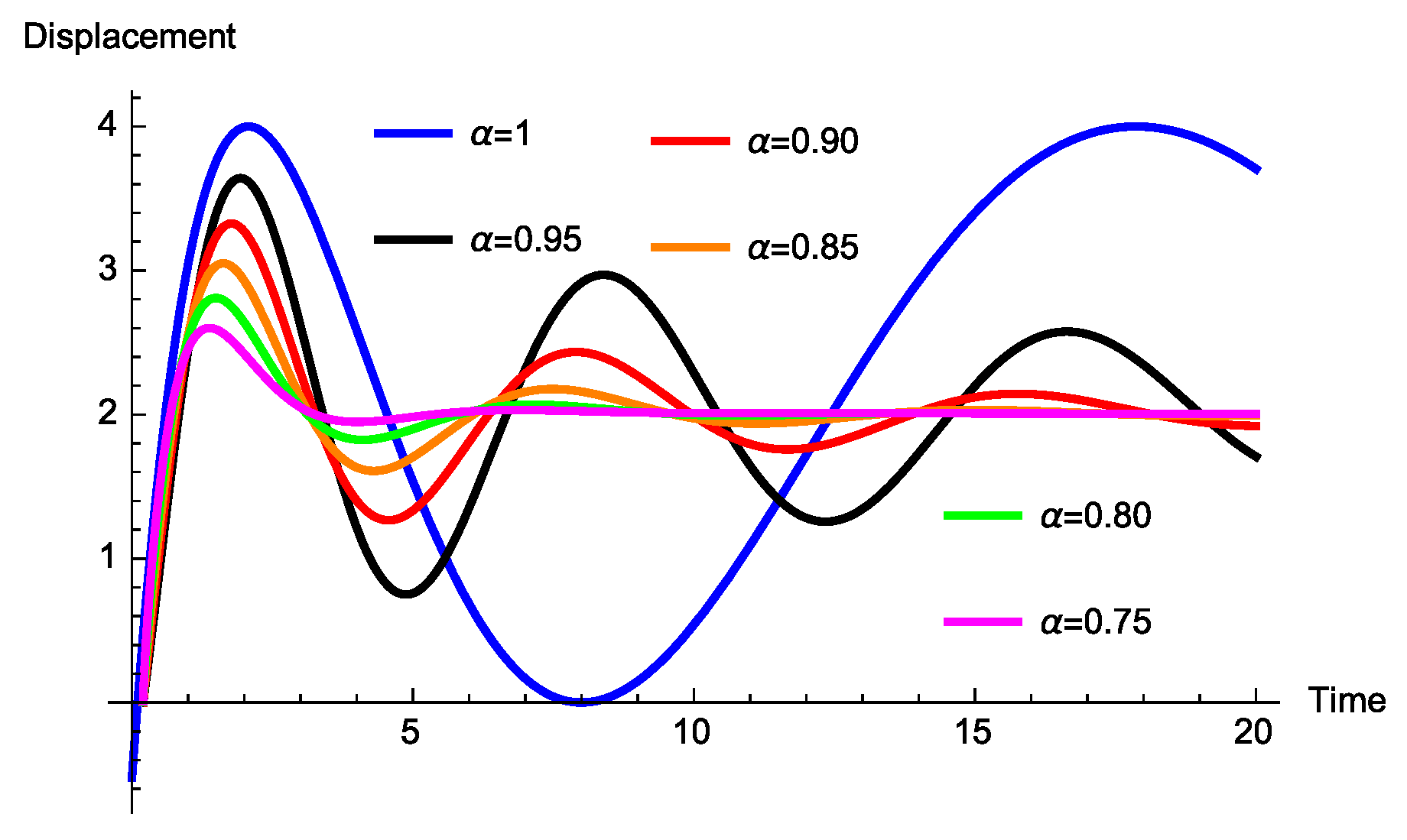
3.2.1. Absence of Mass
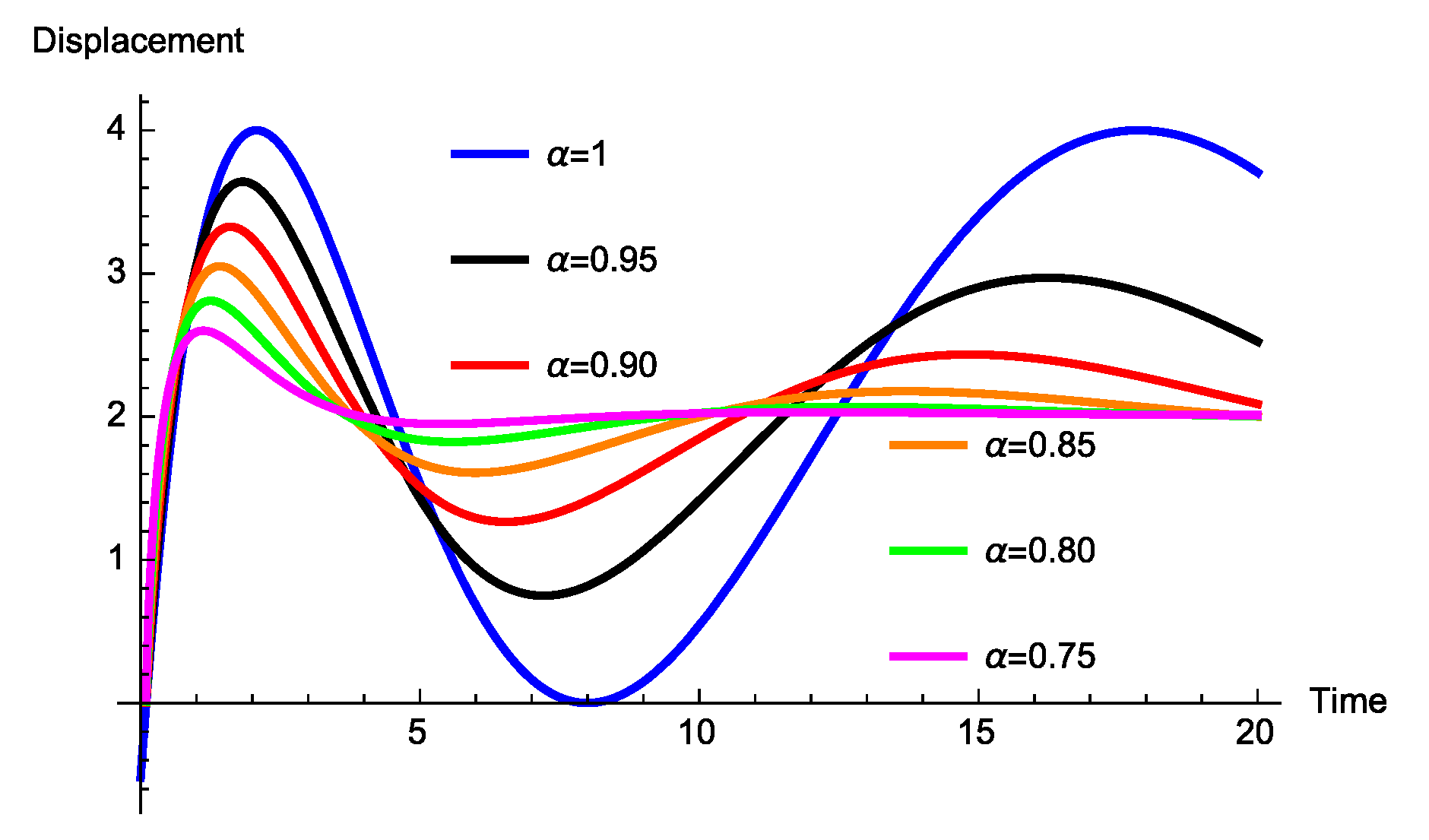
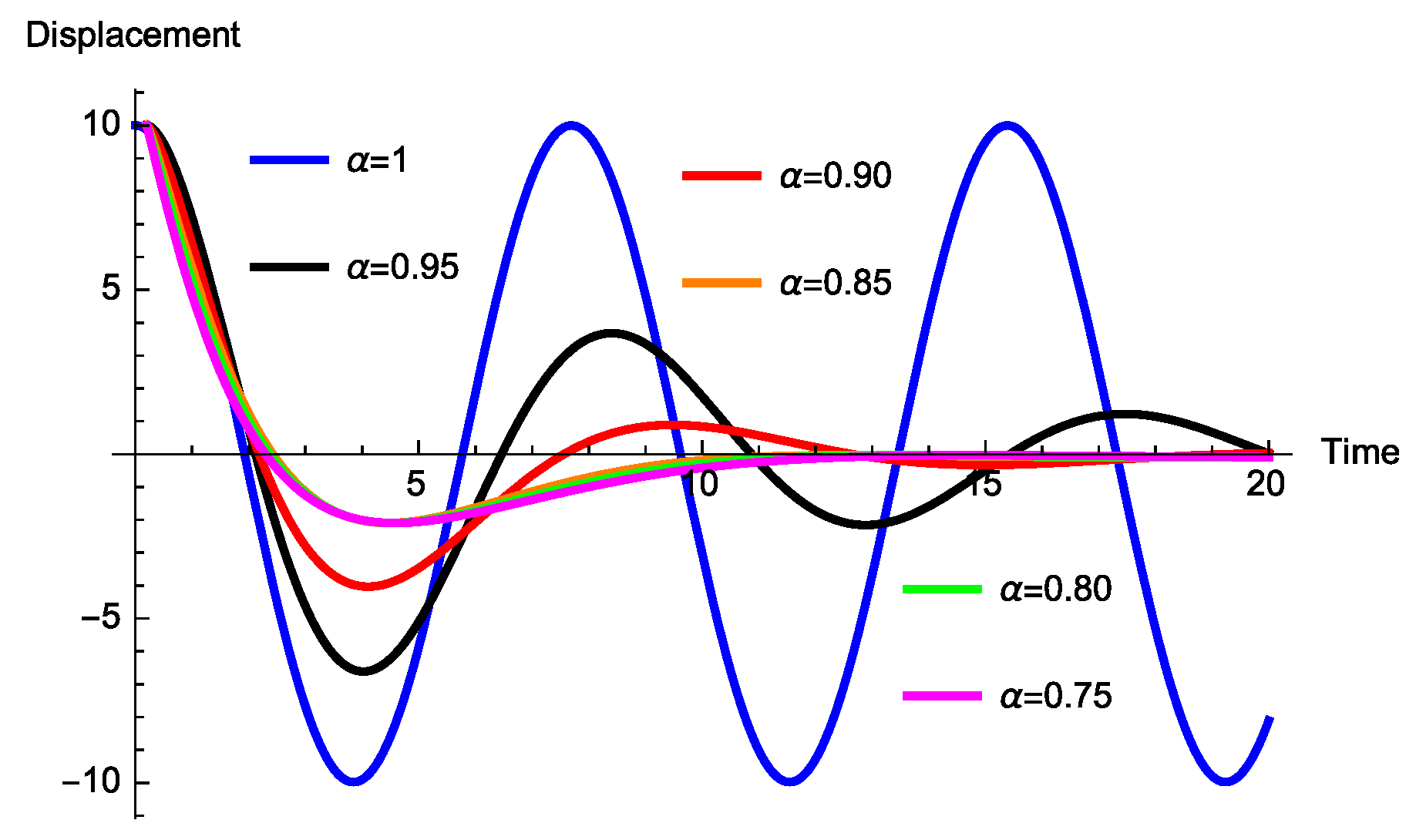
3.2.2. Absence of the Spring Coefficient
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Morales-Delgado, V.F.; Gómez-Aguilar, J.F.; Taneco-Hernández, M.A.; Escobar-Jiménez, R.F. A novel fractional derivative with variable- and constant-order applied to a mass-spring-damper system. Eur. Phys. J. Plus 2018, 133, 78. [Google Scholar] [CrossRef]
- Hristov, J. A transient flow of a non-Newtonian fluid modelled by a mixed time-space derivative: An improved integral-balance approach. In Mathematical Methods in Engineering; Springer: Berlin, Germany, 2019; pp. 153–174. [Google Scholar]
- Sheikh, N.A.; Ali, F.; Saqib, M.; Khan, I.; Jan, S.A.; Alshomrani, A.S.; Alghamdi, M.S. Comparison and analysis of the Atangana–Baleanu and Caputo–Fabrizio fractional derivatives for generalized Casson fluid model with heat generation and chemical reaction. Results Phys. 2017, 7, 789–800. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; Rosales-García, J.J.; Bernal-Alvarado, J.J.; Córdova-Fraga, T.; Gúzman-Cabrera, R. Fractional mechanical oscillators. Rev. Mex. Fís. 2012, 58, 348–352. [Google Scholar]
- Iyiola, O.S.; Zaman, F.D. A fractional diffusion equation model for cancer tumor. AIP Adv. 2014, 4, 107121. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, D.; Singh, J. Numerical computation of fractional Black–Scholes equation arising in financial market. Egyp. J. Basic Appl. Sci. 2014, 1, 177–183. [Google Scholar] [CrossRef]
- Yavuz, M.; Özdemir, N. A different approach to the European option pricing model with new fractional operator. Math. Model. Nat. Phenom. 2018, 13, 1–12. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; Rosales-García, J.J.; Guía-Calderón, M.; Razo-Hernández, J.R. Fractional RC and LC electrical circuits. Ing. Investig. Tecnol. 2014, 15, 311–319. [Google Scholar]
- Sene, N. Analytical solutions of Hristov diffusion equations with non-singular fractional derivatives. Chaos 2019, 29, 023112. [Google Scholar] [CrossRef]
- Hristov, J. Approximate solutions to fractional subdiffusion equations. Eur. Phys. J. Spec. Top. 2011, 193, 229–243. [Google Scholar] [CrossRef] [Green Version]
- Hristov, J. On the Atangana–Baleanu derivative and its relation to the fading memory concept: The diffusion equation formulation. In Trends in Theory and Applications of Fractional Derivatives with Mittag–Leffler Kernel; Springer: Berlin, Germany, 2019; pp. 1–22. [Google Scholar]
- Sene, N. Stokes’ first problem for heated flat plate with Atangana–Baleanu fractional derivative. Chaos Solitons Fractals 2018, 117, 68–75. [Google Scholar] [CrossRef]
- Sene, N.; Fall, A.N. Homotopy Perturbation ρ-Laplace Transform Method and Its Application to the Fractional Diffusion Equation and the Fractional Diffusion–Reaction Equation. Fract. Frac. 2019, 3, 14. [Google Scholar] [CrossRef]
- Sene, N. Solutions of fractional diffusion equations and Cattaneo–Hristov diffusion model. Int. J. Anal. Appl. 2019, 17, 191–207. [Google Scholar]
- Hristov, J. Fourth-order fractional diffusion model of thermal grooving: Integral approach to approximate closed form solution of the Mullins model. Math. Model. Nat. Phenom. 2018, 13, 1–6. [Google Scholar] [CrossRef]
- Hristov, J. The heat radiation diffusion equation: Explicit analytical solutions by improved integral-balance method. Therm. Sci. 2018, 22, 777–788. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Aguilar, J.F.; Yépez-Martínez, H.; Calderón-Ramón, C.; Cruz-Orduña, I.; Eecobar-Jiménez, R.F.; Olivares-Peregrino, V.H. Modeling of a Mass-Spring-Damper System by Fractional Derivatives with and without a Singular Kernel. Entropy 2015, 17, 6289–6303. [Google Scholar] [CrossRef]
- Ray, S.S.; Sahoo, S.; Das, S. Formulation and solutions of fractional continuously variable-order mass-spring damper systems controlled by viscoelastic and viscous-viscoelastic dampers. Adv. Mech. Eng. 2016, 8, 1–13. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F. Analytic solutions and numerical simulations of mass-spring and damper-spring systems described by fractional differential equations. Rom. J. Phys. 2015, 60, 311–323. [Google Scholar]
- Escalante-Martínez, J.E.; Gómez-Aguilar, J.F.; Calderón-Ramón, C.; Morales-Mendoza, L.J.; Cruz-Orduna, I.; Laguna-Camacho, J.R. Experimental evaluation of viscous damping coefficient in the fractional underdamped oscillator. Adv. Mech. Eng. 2016, 8, 1–12. [Google Scholar] [CrossRef]
- Fahd, J.; Abdeljawad, T. A modified Laplace transform for certain generalized fractional operators. Results Nonlinear Anal. 2018, 2, 88–98. [Google Scholar]
- Katugampola, U.N. Theory and applications of fractional differential equations. Appl. Math. Comput. 2011, 218, 860–865. [Google Scholar]
- Fahd, J.; Abdeljawad, T.; Baleanu, D. On the generalized fractional derivatives and their Caputo modification. J. Nonlinear Sci. Appl. 2017, 10, 2607–2619. [Google Scholar] [Green Version]
- Sene, N. Fractional input stability for electrical circuits described by the Riemann–Liouville and the Caputo fractional derivatives. AIMS Math. 2019, 4, 147–165. [Google Scholar] [CrossRef]
- Sene, N. Stability analysis of the generalized fractional differential equations with and without exogenous inputs. J. Nonlinear Sci. Appl. 2019, 12, 562–572. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sene, N.; Gómez Aguilar, J.F. Fractional Mass-Spring-Damper System Described by Generalized Fractional Order Derivatives. Fractal Fract. 2019, 3, 39. https://doi.org/10.3390/fractalfract3030039
Sene N, Gómez Aguilar JF. Fractional Mass-Spring-Damper System Described by Generalized Fractional Order Derivatives. Fractal and Fractional. 2019; 3(3):39. https://doi.org/10.3390/fractalfract3030039
Chicago/Turabian StyleSene, Ndolane, and José Francisco Gómez Aguilar. 2019. "Fractional Mass-Spring-Damper System Described by Generalized Fractional Order Derivatives" Fractal and Fractional 3, no. 3: 39. https://doi.org/10.3390/fractalfract3030039




