Analogues to Lie Method and Noether’s Theorem in Fractal Calculus

Abstract

In this manuscript, we study symmetries of fractal differential equations. We show that using symmetry properties, one of the solutions can map to another solution. We obtain canonical coordinate systems for differential equations on fractal sets, which makes them simpler to solve. An analogue for Noether’s Theorem on fractal sets is given, and a corresponding conservative quantity is suggested. Several examples are solved to illustrate the results.

1. Introduction

In past centuries, discussions in physics included regular objects such as straight lines, squares, spheres, cones, etc. Functions were smooth or involved a few singularities. Fractal sets or curves are shapes that are irregular or whose Hausdorff dimension exceeds their topological dimension. Fractals are certain shapes that share a common feature such as irregularities on a large range of scales and whose properties, like density, length, area, and volume, are not meaningful. The surface of human lungs and snowflakes, the boundaries of clouds, and the folds of mammalian brains are in the category of fractals. The theory of heat and wave transfer in disordered systems was modeled by fractals and random walks on them, such as polymers, fractured and porous rocks, amorphous semiconductors, etc. [1,2,3,4,5,6,7,8,9,10]. Clusters in nature are the points at which the density of points does not have meaning as a quantifier. In processes with fractal structures, we note that there are no perfect Cantor sets, von Koch curves, or Sierpinski gaskets in nature. But, they can be reasonable approximations to natural shapes and are simpler to analyze since they are systematic mathematical constructions [2,3,11,12].

Cantor-like sets are in the class of dusts and totally disconnected sets. Fractal von Koch curves can be used to model natural irregular curves that do not have tangents and for which using smaller yardsticks leads to an increase in the measured length of the curve. The fractal Sierpinski gasket is a good model for objects such as the backbones of percolating clusters [1,13,14].

Motivated by these ideas, mathematicians developed the theory of “analysis on fractals”, with branches including the fractional calculus approach, the probabilistic approach, the measure theory approach, and $F^{\alpha }$-calculus [6,15,16,17,18,19,20,21,22,23,24].

Fractional calculus: Fractional calculus is the subject of derivatives and integrals with arbitrary orders, which is used to model anomalous phenomena [15]. There is a lot of research in this direction, such as fractional Fokker–Planck equations, fractional diffusion equations, fractional master equations, stochastic fractional equations, and so on [25,26,27,28,29,30,31,32]. Fractal features and macroscopic anomalous exploits of systems are connected to the order of fractional derivatives [33,34,35,36,37,38,39,40]. In addition, memory effects in physical models are presented by using fractional derivatives because of their non-local character [41]. To solve this problem, fractional local derivatives were defined and turn out to be applicable to the differentiability of graphs that are fractals [42,43].

Probabilistic approach: In this approach, the Laplacian is defined as an infinitesimal generator of Brownian motion on fractal sets. Using self-similarity properties, Laplacians on connected Sierpinski sets were suggested, and the solutions of equations were obtained by utilizing the self-similarities of fractals [16,44]. Generalized constructions using Brownian motion are given for more general nested fractals [45].

Measure theory approach: Measure theory is used to define suitable derivatives for fractal subsets of ℜ. If $\mathbf{m}$ is a measure and its support is a fractal subset of the real line $F\in [a,b]\in \Re$, then a function $g^{\prime }:F\to \Re$ is called a $\mathbf{m}$-derivative of a given function $g:F\to \Re$ if the following condition is satisfied:

$$g\left(x\right)=g\left(a\right)+{\int }_a^x{g}^{\prime }\left(y\right)d\mathbf{m}\left(y\right),y\in F.$$

(1)

Note that the function $g^{\prime }\left(y\right)$ does not always exist and is not unique for a given $g\left(y\right)$. If $g\in L^2(F,m)$, then it solves both of these problems [6,19,46,47,48,49].

$F^{\alpha }$-Calculus approach: $F^{\alpha }$-Calculus ($F^{\alpha }$-C) is a simple, constructive, and algorithmic approach to the analysis of fractals [20,21]. In [22], $F^{\alpha }$-C was formulated as a calculus framework on fractal sets and fractal curves in higher dimensions. As an application of $F^{\alpha }$-C in celestial mechanics, the motion of simple harmonic oscillators and Kepler’s Third Law on fractal-time spaces were explained and obtained [50]. The existence and uniqueness of the solutions have important roles in applications that were studied on fractal sets [51,52].

Recently, transport through pre-fractal and porous media has been modeled using Lévy flights, Lévy walks, scaled random walks, and corresponding diffusion equations [53,54]. Fractal scaled Brownian motion and ultra-slow fractal scaled Brownian motion were studied and the corresponding fractal mean square displacements are suggested [55,56]. Sub-, normal-, and super-diffusion on middle-$\xi$ Cantor sets was characterized in view of $F^{\alpha }$-C [23].

Lie groups have an important role since they give symmetries of physical laws and help in finding conserved quantities in physics by using Noether’s theorem. For example, Lie symmetries of the Lagrangian of a system give conserved quantities [57,58,59,60,61,62,63,64,65,66]. In this work, we generalize Lie methods for differential equations on fractal Cantor-like sets and Noether’s theorem.

The outline of the paper is as follows: Relevant background and various definitions are given in Section 2. In Section 3, we discuss symmetry and the Lie method for solving differential equations on fractal sets. In Section 4, we give a generalized Noether’s theorem for fractal Cantor-like sets. Section 5 offers a conclusion.

2. Basic Tools

In this section, we review some of the basic definitions of fractal calculus, which was adapted for the middle-$\xi$ Cantor sets. For details see [20,21,23].

Local $C^{\alpha }$-Calculus:

If $C^{\xi }\in K=[r,t],$ and $r,t\in \Re$ is a middle-$\xi$ Cantor set. Then the flag function of $C^{\xi }$ is defined by

$$\vartheta (C^{\xi },K)=\left\{\begin{array}{c}1\mathrm{if}{C}^{\xi }\cap K\ne \varnothing \hfill \\ 0\mathrm{otherwise}.\hfill \end{array}\right.$$

Taking into account the $E_{[r,t]}=\{r=x_0,x_1,x_2,\dots ,x_n=t\}$ subdivision of K, one can define

$${\rho }^{\alpha }[C^{\xi },E]=\sum _{i=1}^n\Gamma (\alpha +1){(x_i-x_{i-1})}^{\alpha }\vartheta (C^{\xi },[x_{i-1},x_i]),$$

where $0<\alpha \le 1$. Let $\delta >0$, then the coarse-grained mass function ${\gamma }_{\delta }^{\alpha }(C^{\xi },r,t)$ is given by

$${\gamma }_{\delta }^{\alpha }(C^{\xi },r,t)=\underset{E_{[r,t]}:|E|\le \delta }{inf}{\rho }^{\alpha }[C^{\xi },E].$$

Here we take infimum over all subdivisions E satisfying $|E|:={max}_{1\le i\le n}(x_i-x_{i-1})\le \delta$.

The mass function ${\gamma }^{\alpha }(C^{\xi },r,t)$ is defined by [20,21,23]:

$${\gamma }^{\alpha }(C^{\xi },r,t)=\underset{\delta \to 0}{lim}{\gamma }_{\delta }^{\alpha }(C^{\xi },r,t).$$

The integral staircase function $S_{C^{\xi }}^{\alpha }\left(x\right)$ of order $\alpha$ for a fractal set $C^{\xi }$ is defined in [20,21] by

$$S_{C^{\xi }}^{\alpha }\left(x\right)=\left\{\begin{array}{c}{\gamma }^{\alpha }(C^{\xi },r_0,x)\mathrm{if}x\ge r_0\hfill \\ -{\gamma }^{\alpha }(C^{\xi },r_0,x)\mathrm{otherwise},\hfill \end{array}\right.$$

where $r_0$ is an arbitrary real number and fixed.

In Figure 1, we present middle-$\xi$ Cantor sets and their staircase functions.

The $\beta$-dimension of $C^{\xi }\cap [r,t]$ is

$$\begin{array}{cc}\hfill {dim}_{\beta }(C^{\xi }\cap [r,t])& =inf\{\alpha :{\gamma }^{\alpha }(C^{\xi },r,t)=0\}\hfill \\ & =sup\{\alpha :{\gamma }^{\alpha }(C^{\xi },r,t)=\infty \}.\hfill \end{array}$$

Remark 1.

For a given ξ, then we have ${dim}_{\beta }(C^{\xi }\cap [r,t])=\alpha$. For example, for $\xi =1/5$ we get $\alpha \approx 0.77$. The plot in Figure 2 indicates the approximation of ${\gamma }_{{\delta }_2}^{\alpha }/{\gamma }_{{\delta }_1}^{\alpha }$ where ${\delta }_2<{\delta }_1$.

This value leads to the $\beta$-dimension since it shows convergence to the finite valve while $\delta \to 0$, which can be seen by choosing different various pairs of $({\delta }_1,{\delta }_2)$.

• The $C^{\alpha }$-Limits: Suppose $h:C^{\xi }\to R$ and $x\in C^{\xi }$. Then l is called to be the limit of h through the points of $C^{\xi }$ as $z\to x$.

  $$z\in C^{\xi }\mathrm{and}|z-x|<\delta \Rightarrow |h\left(z\right)-l|<ϵ.$$

  If l exists, then we can write

  $$l=C^{\alpha }-\underset{z\to x}{lim}h\left(z\right).$$
• The $C^{\alpha }$-Continuity: A function $h:C^{\xi }\to R$ is called to be $C^{\xi }$-continues at $x\in C^{\xi }$ if

  $$h\left(x\right)=C^{\alpha }-\underset{z\to x}{lim}h\left(z\right).$$
• The $C^{\alpha }$-Differentiation: The $C^{\alpha }$-derivative of a function u defined on $C^{\xi }$ at a point x is [20,21,23]:

  $$D_{C^{\xi }}^{\alpha }h\left(x\right)=\left\{\begin{array}{c}{C}^{\alpha }{\text{-lim}}_{z\to x}\frac{h\left(z\right)-h\left(x\right)}{S_{C^{\xi }}^{\alpha }\left(z\right)-S_{C^{\xi }}^{\alpha }\left(x\right)},\mathrm{if}z\in C^{\xi }.\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\right.$$

  In view of infinitesimal calculus and non-standard analysis, Equation (2) is written [67]

  $$h(x+\delta x)=h\left(x\right)+(D_{C^{\xi }}^{\alpha }h)\delta S_{C^{\xi }}^{\alpha }\left(x\right)+ϵ\delta S_{C^{\xi }}^{\alpha }\left(x\right),$$

  (2)

  where $ϵ\approx \delta S_{C^{\xi }}^{\alpha }\left(x\right)=S_{C^{\xi }}^{\alpha }(x+\delta x)-S_{C^{\xi }}^{\alpha }\left(x\right)\approx 0$. A more general form of the Taylor expansion formula is

  $$h(x+\delta x)=h\left(x\right)+D_{C^{\xi }}^{\alpha }h.S_{C^{\xi }}^{\alpha }\left(x\right)+\dots +\frac{1}{n!}{\left(D_{C^{\xi }}^{\alpha }\right)}^{n}h{\left(S_{C^{\xi }}^{\alpha }\left(x\right)\right)}^n+ϵ{\left(S_{C^{\xi }}^{\alpha }\left(x\right)\right)}^n.$$

  (3)
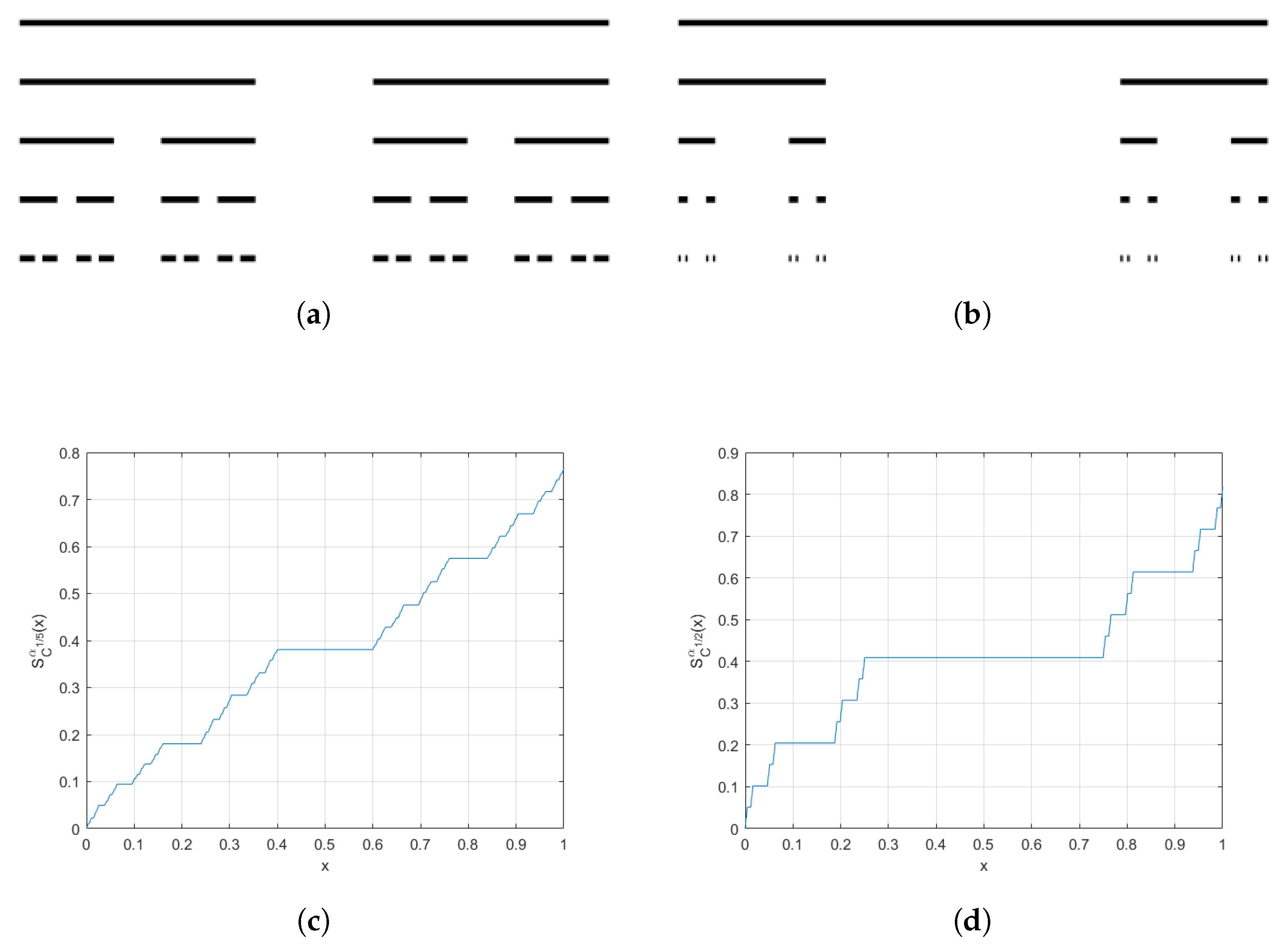
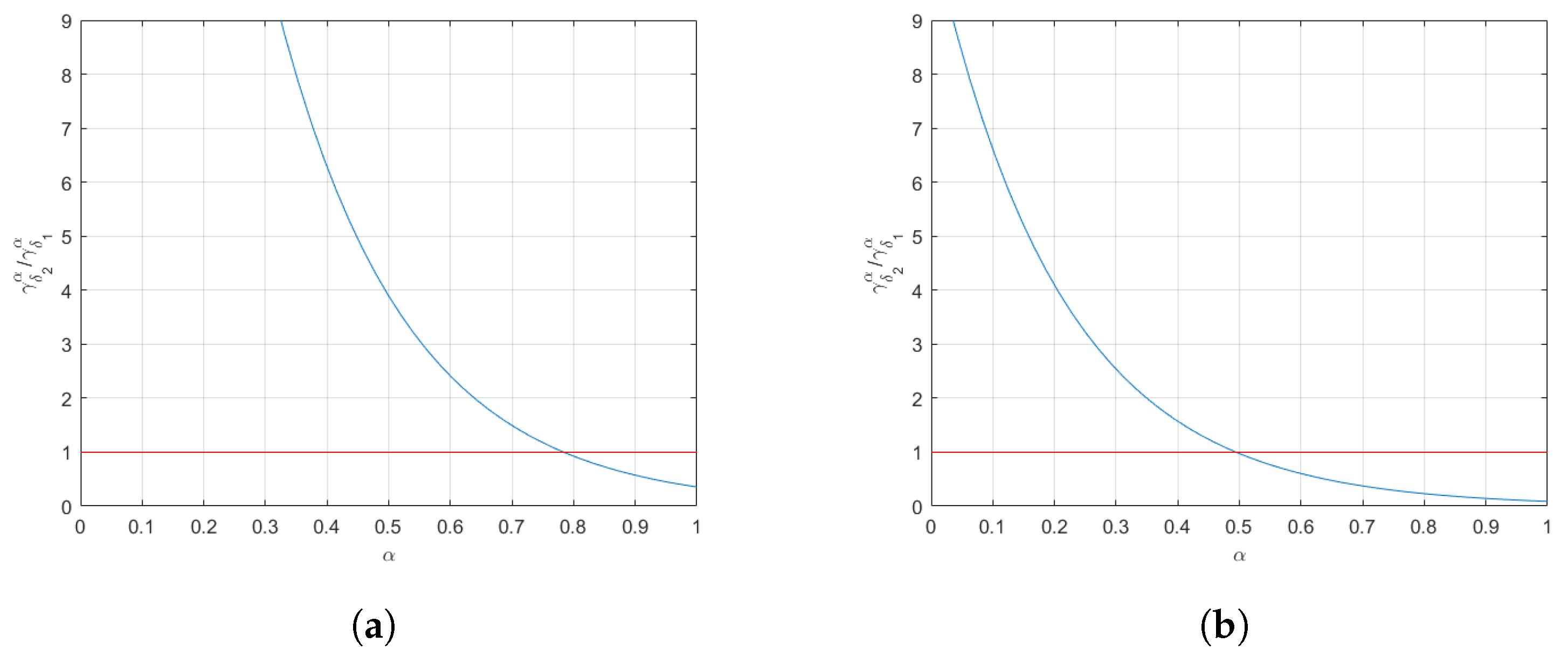
• The $C^{\alpha }$-Integration: For a bounded function h on $C^{\xi }$, one can define [20,21,23]:

  $$\begin{array}{ccc}\hfill \mathcal{M}[h,C^{\xi },K]& =& \underset{x\in C^{\xi }\cap K}{sup}h\left(x\right)\mathrm{if}{C}^{\xi }\cap K\ne 0\hfill \\ & =& 0\mathrm{otherwise},\hfill \end{array}$$

  and similarly,

  $$\begin{array}{ccc}\hfill \mathit{m}[h,C^{\xi },K]& =& \underset{x\in C^{\xi }\cap K}{inf}u\left(x\right)\mathrm{if}{C}^{\xi }\cap K\ne 0\hfill \\ & =& 0\mathrm{otherwise}.\hfill \end{array}$$

  The upper $C^{\alpha }$-sum and lower $C^{\alpha }$-sum for a function h over the subdivision E are given respectively by [20,21,23]

  $${\mathfrak{U}}^{\alpha }[h,C^{\xi },E]=\sum _{j=1}^m\mathcal{M}[h,C^{\xi },[x_j,x_{j-1}]](S_{C^{\xi }}^{\alpha }\left(x_j\right)-S_{C^{\xi }}^{\alpha }\left(x_{j-1}\right)),$$

  and

  $${\mathfrak{L}}^{\alpha }[h,C^{\xi },E]=\sum _{j=1}^m\mathit{m}[h,C^{\xi },[x_j,x_{j-1}]](S_{C^{\xi }}^{\alpha }\left(x_j\right)-S_{C^{\xi }}^{\alpha }\left(x_{j-1}\right)).$$

  We say that h is $C^{\alpha }$-integrable on $C^{\xi }$ if [20,21,23] the following equations are equal.

  $$\begin{array}{cc}\hfill \underline{{\int }_r^t}h\left(x\right)d_{C^{\xi }}^{\alpha }x& =\underset{E_{[r,t]}}{sup}{\mathfrak{L}}^{\alpha }[h,C^{\xi },E],\hfill \end{array}$$

  (4)

  $$\begin{array}{cc}\hfill \overline{{\int }_r^t}h\left(x\right)d_{C^{\xi }}^{\alpha }x& =\underset{E_{[r,t]}}{inf}{\mathfrak{L}}^{\alpha }[h,C^{\xi },E].\hfill \end{array}$$

  (5)

  In that case, the $C^{\alpha }$-integral of h on $C^{\xi }$ is denoted by ${\int }_r^{t}h\left(x\right)d_{C^{\xi }}^{\alpha }x$ and is given by the common value of (4) and (5).

Fundamental Theorems of $C^{\alpha }$-Calculus. Suppose that $h\left(x\right):C^{\xi }\to \Re$ is $C^{\alpha }$-continuous and bounded on $C^{\xi }$. If we define $\mathrm{H}\left(z\right)$ by

$$\mathrm{H}\left(z\right)={\int }_a^{z}h\left(x\right)d_{C^{\xi }}^{\zeta }x,$$

for all $x\in [r,t]$, consequently it follows that [20,21,23]

$${\int }_r^{t}h\left(x\right)d_{C^{\xi }}^{\alpha }x=\mathrm{H}\left(t\right)-\mathrm{H}\left(r\right).$$

3. The Lie Method on ${\mathit{C}}^{\mathit{\alpha }}$-Calculus

In this section, we study Sophus Lie’s method for solving linear and non-linear fractal differential equations [57,58,59]. An infinitesimal generator is defined on the middle-$\xi$ Cantor sets.

A fractal Lie group is a set of maps with parameter $\eta$ such that

$$L_{\eta }:(S_{C^{\xi }}^{\alpha }\left(t\right),x)\rightarrowtail (v(S_{C^{\xi }}^{\alpha }\left(t\right),x,\eta ),w(S_{C^{\xi }}^{\alpha }\left(t\right),x,\eta )),(S_{C^{\xi }}^{\alpha }\left(t\right),x)\in \Re ,\eta \in \Re ,$$

(6)

with the following properties [57,58,59]:

(1)

$L_{\eta }$ onto and one-to-one;

(2)

$L_{{\eta }_2}\circ L_{{\eta }_1}=L_{{\eta }_2+{\eta }_1}$; (Composition Property).

(3)

$L_0=I$;

(4)

$\forall {\eta }_1\in \Re ,\exists {\eta }_2=-{\eta }_1,\Rightarrow L_{{\eta }_2}\circ L_{{\eta }_1}=L_0$.

Symmetry condition of fractal differential equations: Consider a fractal differential equation of the form

$$D_{C^{\xi },t}^{\alpha }x\left(t\right)=h(S_{C^{\xi }}^{\alpha }\left(t\right),x),t\in C^{\xi }.$$

(7)

In order to find the fractal symmetry conditions, we write

$$D_{C^{\xi },t^{\prime }}^{\alpha }{x}^{\prime }\left(t\right)=h(S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right),x^{\prime }),$$

(8)

where $v(S_{C^{\xi }}^{\alpha }\left(t\right),x,\eta )=S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right),w(S_{C^{\xi }}^{\alpha }\left(t\right),x,\eta )=x^{\prime }$. By Equation (8), we have

$$\begin{array}{cc}\hfill D_{C^{\xi },t^{\prime }}^{\alpha }{x}^{\prime }& =\frac{{\mathbf{D}}^{\alpha }{x}^{\prime }}{{\mathbf{D}}^{\alpha }{S}_{C^{\xi }}^{\alpha }\left(t^{\prime }\right)}=h(S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right),x^{\prime }),\hfill \end{array}$$

(9)

where

$${\mathbf{D}}^{\alpha }=D_{C^{\xi },t}^{\alpha }+(D_{C^{\xi },t}^{\alpha }x)D_{C^{\xi },x}^{\alpha }$$

(10)

might be called the fractal total derivative operator. From Equation (10), we obtain

$$\begin{array}{cc}\hfill D_{C^{\xi },t^{\prime }}^{\alpha }{x}^{\prime }& =\frac{D_{C^{\xi },t}^{\alpha }{x}^{\prime }+(D_{C^{\xi },t}^{\alpha }x)D_{C^{\xi },x}^{\alpha }{x}^{\prime }}{D_{C^{\xi },t}^{\alpha }{S}_{C^{\xi }}^{\alpha }\left(t^{\prime }\right)+(D_{C^{\xi },t}^{\alpha }x)D_{C^{\xi },x}^{\alpha }{S}_{C^{\xi }}^{\alpha }\left(t^{\prime }\right)}=h(S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right),x^{\prime }).\hfill \end{array}$$

(11)

Substituting Equation (9) into Equation (11), we obtain

$$\begin{array}{cc}\hfill D_{C^{\xi },t^{\prime }}^{\alpha }{x}^{\prime }& =\frac{D_{C^{\xi },t}^{\alpha }{x}^{\prime }+h(S_{C^{\xi }}^{\alpha }\left(t\right),x)D_{C^{\xi },t}^{\alpha }{x}^{\prime }}{D_{C^{\xi },t}^{\alpha }{S}_{C^{\xi }}^{\alpha }\left(t^{\prime }\right)+h(S_{C^{\xi }}^{\alpha }\left(t\right),x)D_{C^{\xi },x}^{\alpha }{S}_{C^{\xi }}^{\alpha }\left(t^{\prime }\right)}=h(S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right),x^{\prime }),\hfill \end{array}$$

(12)

which might be called the fractal symmetry condition.

Example 1.

The following fractal differential equation

$$D_{C^{\xi },t}^{\alpha }x\left(t\right)=\frac{1-x^2}{S_{C^{\xi }}^{\alpha }\left(t\right)}$$

(13)

has a fractal symmetry

$$(S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right),x^{\prime })=(e^{\eta }{S}_{C^{\xi }}^{\alpha }\left(t\right),x).$$

(14)

To show this, we substitute Equation (14) into Equation (12). Hence we get

$$\frac{D_{C^{\xi },t}^{\alpha }{x}^{\prime }+\frac{1-x^2}{S_{C^{\xi }}^{\alpha }\left(t\right)}{D}_{C^{\xi },x}^{\alpha }{x}^{\prime }}{D_{C^{\xi },t}^{\alpha }{S}_{C^{\xi }}^{\alpha }\left(t^{\prime }\right)+\frac{1-x^2}{S_{C^{\xi }}^{\alpha }\left(t\right)}{D}_{C^{\xi },x}^{\alpha }{S}_{C^{\xi }}^{\alpha }\left(t^{\prime }\right)}=\frac{1-x^{\prime }2}{S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right)}$$

(15)

since $D_{C^{\xi },t}^{\alpha }{x}^{\prime }=0,D_{C^{\xi },x}^{\alpha }{S}_{C^{\xi }}^{\alpha }\left(t^{\prime }\right)=0$, and $D_{C^{\xi },t}^{\alpha }{S}_{C^{\xi }}^{\alpha }\left(t^{\prime }\right)=e^{\eta }$. Then Equation (15) looks like

$$\frac{1-x^2}{e^{\eta }{S}_{C^{\xi }}^{\alpha }\left(t\right)}=\frac{1-x^{\prime }2}{S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right)}.$$

(16)

Consequently, Equation (12) holds.

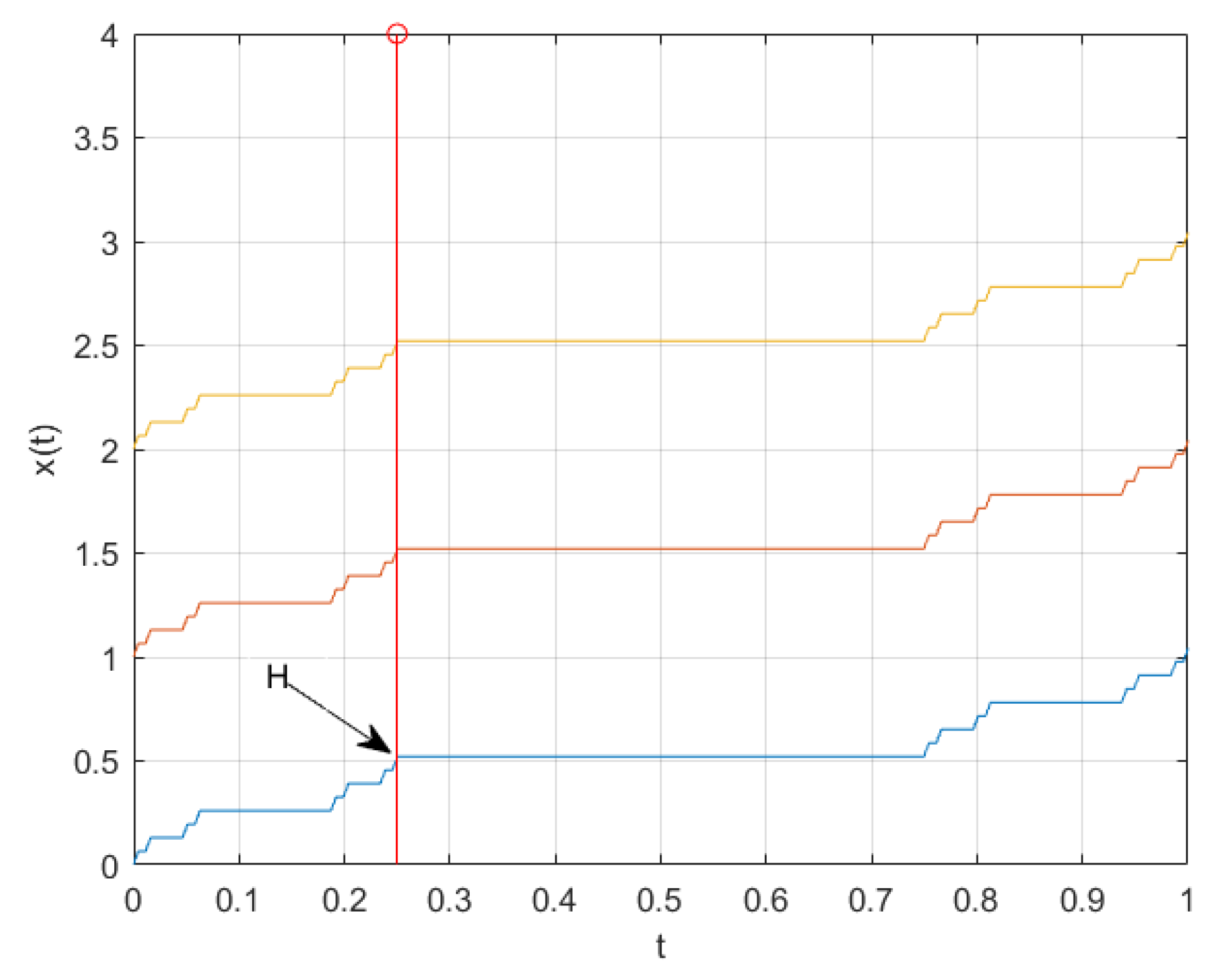
• Orbit of a point in the fractal differential equations: If H is a point on the solution of the fractal differential equation, then given a fractal symmetry map by choosing different values of $\eta$, we get an orbit of the point H. We demonstrate this by giving the following example.

Example 2.

Suppose a fractal differential equation

$$D_{C^{\xi },t}^{\alpha }x={\chi }_{C^{\xi }}\left(t\right),0<t<1,\in C^{\xi }$$

under the following symmetry

$$(S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right),x^{\prime })=({\chi }_{C^{\xi }}\left(t\right),S_{C^{\xi }}^{\alpha }\left(t\right)+\eta ).$$

(17)

For instance, the orbit of point $H=(1/4,0)$ is denoted by ${\mathcal{O}}_H$ and given by

$${\mathcal{O}}_H=\{(1/4,0),(1/4,S_{C^{\xi }}^{\alpha }(1/4)+\eta ),\eta =0.5,1.5,2.5,\dots \}.$$

Figure 3 shows the orbit of point H under the symmetry of Equation (17).

• Analogues to tangent vectors on fractal orbit: Analogues to the tangent vectors/fractal tangent vectors for any given orbit at the point $(S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right),x^{\prime })$ are defined as follows:

  $$\begin{array}{ccc}\hfill \frac{d{S}_{C^{\xi }}^{\alpha }\left(t^{\prime }\right)}{d\eta }& =& \varphi (S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right),x^{\prime }),\hfill \\ \hfill \frac{d{x}^{\prime }}{d\eta }& =& \psi (S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right),x^{\prime }).\hfill \end{array}$$

  (18)

  For the initial point $(S_{C^{\xi }}^{\alpha }\left(t\right),x),$ we set $\eta =0$, namely

  $$\begin{array}{cc}\hfill \left(\frac{d{S}_{C^{\xi }}^{\alpha }\left(t^{\prime }\right)}{d\eta }{{|}_{\eta =0},\frac{d{x}^{\prime }}{d\eta }|}_{\eta =0}\right)& =\hfill \\ & (\varphi (S_{C^{\xi }}^{\alpha }\left(t\right),x),\psi (S_{C^{\xi }}^{\alpha }\left(t\right),x)).\hfill \end{array}$$

  (19)

  In what follows, we want to obtain an invariant solution of Equation (7) by using fractal tangent vectors. Therefore, we can write

  $$D_{C^{\xi },t}^{\alpha }x\left(t\right)=h(S_{C^{\xi }}^{\alpha }\left(t\right),x)=\frac{\psi (S_{C^{\xi }}^{\alpha }\left(t\right),x)}{\varphi (S_{C^{\xi }}^{\alpha }\left(t\right),x)},$$

  (20)

  which is called a fractal symmetric equation. In view of Equation (20), we define $\mathcal{Q}$ as follows:

  $$\mathcal{Q}\left(S_{C^{\xi }}^{\alpha }\left(t\right),x,D_{C^{\xi },t}^{\alpha }x\right)=\psi (S_{C^{\xi }}^{\alpha }\left(t\right),x)-\left(D_{C^{\xi },t}^{\alpha }x\right)\varphi (S_{C^{\xi }}^{\alpha }\left(t\right),x),$$

  (21)

  which might be called a fractal characteristic function. Utilizing Equation (20), we get

  $$\overline{\mathcal{Q}}\left(S_{C^{\xi }}^{\alpha }\left(t\right),x,D_{C^{\xi },t}^{\alpha }x\right)=\psi (S_{C^{\xi }}^{\alpha }\left(t\right),x)-h(S_{C^{\xi }}^{\alpha }\left(t\right),x)\varphi (S_{C^{\xi }}^{\alpha }\left(t\right),x),$$

  which might be called a fractal reduced characteristic function. Under the given symmetry, we conclude $\overline{\mathcal{Q}}=0$.

Example 3.

Consider the fractal Riccati differential equation as follows:

$$D_{C^{\xi },t}^{\alpha }x\left(t\right)=S_{C^{\xi }}^{\alpha }\left(t\right)x^2-\frac{2x}{S_{C^{\xi }}^{\alpha }\left(t\right)}-\frac{1}{S_{C^{\xi }}^{\alpha }{\left(t\right)}^3},S_{C^{\xi }}^{\alpha }\left(t\right)\ne 0.$$

(22)

Hence, Equation (22) has the following symmetry

$$(S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right),x^{\prime })=(e^{\eta }{S}_{C^{\xi }}^{\alpha }\left(t\right),e^{-2\eta }x).$$

(23)

By Equation (19), the fractal tangent vectors are

$$\varphi (S_{C^{\xi }}^{\alpha }\left(t\right),x)=S_{C^{\xi }}^{\alpha }\left(t\right),$$

and

$$\psi (S_{C^{\xi }}^{\alpha }\left(t\right),x)=-2x.$$

Subsequently, the fractal reduced characteristic function is

$$\begin{array}{cc}\hfill \overline{\mathcal{Q}}(S_{C^{\xi }}^{\alpha }\left(t\right),x,D_{C^{\xi },t}^{\alpha }x)& =-2x-\left(S_{C^{\xi }}^{\alpha }\left(t\right)x^2-\frac{2x}{S_{C^{\xi }}^{\alpha }\left(t\right)}-\frac{1}{S_{C^{\xi }}^{\alpha }{\left(t\right)}^3}\right)S_{C^{\xi }}^{\alpha }\left(t\right)\hfill \\ & =-S_{C^{\xi }}^{\alpha }{\left(t\right)}^2{x}^2+\frac{1}{S_{C^{\xi }}^{\alpha }{\left(t\right)}^2}.\hfill \end{array}$$

Therefore, if

$$\overline{\mathcal{Q}}=0⟹x\left(t\right)=\pm S_{C^{\xi }}^{\alpha }{\left(t\right)}^{-2},$$

which is the fractal invariant solution of Equation (22) under symmetry Equation (23).

Example 4.

Suppose one parameter fractal Lie group as follows:

$$L_{\eta }:(S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right),x^{\prime })\rightarrowtail (e^{\eta }{S}_{C^{\xi }}^{\alpha }\left(t\right),e^{k\eta }x),k>0.$$

Then, the associated fractal tangent vectors is given by Equation (18), that is,

$$\varphi (S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right),x^{\prime })=e^{\eta }{S}_{C^{\xi }}^{\alpha }\left(t\right),$$

(24)

and

$$\psi (S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right),x^{\prime })=k{e}^{k\eta }x.$$

(25)

Evaluating Equations (24) and (25) at $\eta =0$, we get

$$\varphi (S_{C^{\xi }}^{\alpha }\left(t\right),x)=S_{C^{\xi }}^{\alpha }\left(t\right),$$

and

$$\psi (S_{C^{\xi }}^{\alpha }\left(t\right),x)=kx.$$

By using Equation (20), we have

$$D_{C^{\xi },t}^{\alpha }x\left(t\right)=\frac{\psi (S_{C^{\xi }}^{\alpha }\left(t\right),x)}{\varphi (S_{C^{\xi }}^{\alpha }\left(t\right),x)}=\frac{kx}{S_{C^{\xi }}^{\alpha }\left(t\right)}.$$

(26)

To solve Equation (26), we use the conjugacy of $C^{\alpha }$-calculus with standard calculus; that is,

$$\int \frac{dx}{x}=k\int \frac{dt}{t}.$$

(27)

Then, it is straightforward to get

$$x\left(t\right)=c{t}^k.$$

By inverse conjugacy, we have

$$x\left(t\right)=c{S}_{C^{\xi }}^{\alpha }{\left(t\right)}^k.$$

An easy computation shows that

$$(v,w)=(\frac{x}{S_{C^{\xi }}^{\alpha }{\left(t\right)}^k},ln{S}_{C^{\xi }}^{\alpha }\left(t\right)),$$

which might be called fractal canonical coordinates.

Example 5.

Consider the fractal equation Riccati equation as follows:

$$D_{C^{\xi },t}^{\alpha }x\left(t\right)=S_{C^{\xi }}^{\alpha }\left(t\right)x^2-\frac{2x}{S_{C^{\xi }}^{\alpha }\left(t\right)}-\frac{1}{S_{C^{\xi }}^{\alpha }{\left(t\right)}^3},S_{C^{\xi }}^{\alpha }\left(t\right)\ne 0,$$

(28)

with the symmetry

$$(S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right),x^{\prime })=(e^{\eta }{S}_{C^{\xi }}^{\alpha }\left(t\right),e^{-2\eta }x).$$

In the same manner, using Equations (24) and (25), we can see that

$$(v,w)=(S_{C^{\xi }}^{\alpha }{\left(t\right)}^{2}x,ln{S}_{C^{\xi }}^{\alpha }\left(t\right)).$$

Using the conjugacy of $C^{\alpha }$-calculus with ordinary calculus, we can write

$$w=\frac{1}{2}ln(\frac{r-1}{r+1})+k.$$

Then, inverting the conjugacy leads to

$$x\left(t\right)=\frac{-k-S_{C^{\xi }}^{\alpha }{\left(t\right)}^2}{S_{C^{\xi }}^{\alpha }{\left(t\right)}^4-k{S}_{C^{\xi }}^{\alpha }{\left(t\right)}^2},$$

(29)

which is the solution of Equation (28).

Remark 2.

Note that by setting $k=0$ in Equation (29), we can obtain the invariant solution.

• Linearized symmetry condition for the fractal differential equations: Solving the fractal symmetry condition in Equation (12) is often very difficult or impossible. Therefore, we linearize Equation (12) by using Taylor series expansion, namely,

  $$\begin{array}{cc}\hfill S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right)& =S_{C^{\xi }}^{\alpha }\left(t\right)+\eta \varphi (S_{C^{\xi }}^{\alpha }\left(t\right),x)+\mathcal{O}({\eta }^2,)\hfill \\ \hfill x^{\prime }& =x+\eta \psi (S_{C^{\xi }}^{\alpha }\left(t\right),x)+\mathcal{O}\left({\eta }^2\right),\hfill \\ \hfill h(S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right),x^{\prime })& =h(S_{C^{\xi }}^{\alpha }\left(t\right),x)\hfill \\ & +\eta \left(D_{C^{\xi },t}^{\alpha }h\varphi (S_{C^{\xi }}^{\alpha }\left(t\right),x)+D_{C^{\xi },x}^{\alpha }h\psi (S_{C^{\xi }}^{\alpha }\left(t\right),x)\right)+\mathcal{O}\left({\eta }^2\right).\hfill \end{array}$$

  (30)

  Here, $\mathcal{O}({\eta }^2)=e\left(\eta \right)$ describes the error function of Taylor series expansions, such that

  $$\underset{\eta \to 0}{lim}\frac{e\left(\eta \right)}{{\eta }^2}=c.$$

  Substituting Equation (30) into Equation (12) and disregarding terms of ${\eta }^2$ or higher orders, we have

  $$D_{C^{\xi },t}^{\alpha }\psi +(D_{C^{\xi },x}^{\alpha }\psi -D_{C^{\xi },t}^{\alpha }\varphi )h-D_{C^{\xi },x}^{\alpha }\varphi h^2=\varphi D_{C^{\xi },t}^{\alpha }h+\psi D_{C^{\xi },x}^{\alpha }h.$$

  (31)

Example 6.

Consider a fractal differential equation

$$D_{C^{\xi },t}^{\alpha }x=\frac{x}{S_{C^{\xi }}^{\alpha }\left(t\right)}+S_{C^{\xi }}^{\alpha }\left(t\right).$$

(32)

Substituting Equation (32) into Equation (31), we get

$$\begin{array}{c}{D}_{C^{\xi },t}^{\alpha }\psi -D_{C^{\xi },x}^{\alpha }\varphi {\left(\frac{x}{S_{C^{\xi }}^{\alpha }\left(t\right)}+S_{C^{\xi }}^{\alpha }\left(t\right)\right)}^2+(D_{C^{\xi },x}^{\alpha }\psi -D_{C^{\xi },t}^{\alpha }\varphi )\left(\frac{x}{S_{C^{\xi }}^{\alpha }\left(t\right)}+S_{C^{\xi }}^{\alpha }\left(t\right)\right)\hfill \\ -\left(\varphi (1-\frac{x}{S_{C^{\xi }}^{\alpha }{\left(t\right)}^2})+\psi (\frac{1}{S_{C^{\xi }}^{\alpha }\left(t\right)})\right)=0.\hfill \end{array}$$

(33)

Then, to solve Equation (33), let $\varphi =0$ so that we have

$$D_{C^{\xi },t}^{\alpha }\psi \left(t\right)-\frac{\psi \left(t\right)}{S_{C^{\xi }}^{\alpha }\left(t\right)}=0.$$

(34)

Conjugacy of the fractal calculus with standard calculus gives

$$\psi \left(t\right)=c{S}_{C^{\xi }}^{\alpha }\left(t\right).$$

(35)

Since $\varphi (S_{C^{\xi }}^{\alpha }\left(t\right),x)=0$, then $v=S_{C^{\xi }}^{\alpha }\left(t\right)$. Consequently, we have

$$w=\int \frac{d_{C^{\xi }}^{\alpha }x}{c{S}_{C^{\xi }}^{\alpha }\left(t\right)}=\frac{x}{c{S}_{C^{\xi }}^{\alpha }\left(t\right)}.$$

(36)

If we set $c=1$, then we get the fractal canonical coordinates

$$(v,w)=(S_{C^{\xi }}^{\alpha }\left(t\right),\frac{x}{S_{C^{\xi }}^{\alpha }\left(t\right)}).$$

(37)

Moreover, since we have

$$\frac{dw}{dv}=\frac{D_{C^{\xi },t}^{\alpha }w+h(S_{C^{\xi }}^{\alpha }\left(t\right),x)D_{C^{\xi },x}^{\alpha }w}{D_{C^{\xi },t}^{\alpha }v+h(S_{C^{\xi }}^{\alpha }\left(t\right),x)D_{C^{\xi },x}^{\alpha }r},$$

(38)

we can write

$$D_{C^{\xi },t}^{\alpha }w=-\frac{x}{S_{C^{\xi }}^{\alpha }{\left(t\right)}^2},D_{C^{\xi },x}^{\alpha }w=\frac{1}{S_{C^{\xi }}^{\alpha }\left(t\right)}.$$

(39)

Substituting Equation (39) into Equation (38), one can obtain following:

$$\frac{dw}{dv}=1,w=v+k,$$

(40)

where k is constant. Replacing $S_{C^{\xi }}^{\alpha }\left(t\right)$ and x back into Equation (40), we obtain

$$x\left(t\right)=S_{C^{\xi }}^{\alpha }{\left(t\right)}^2+k{S}_{C^{\xi }}^{\alpha }\left(t\right).$$

• Infinitesimal fractal generator: In view of the fractal symmetry group of Equation (6), the infinitesimal fractal generator is defined by

  $$X_{C^{\xi }}=\varphi D_{C^{\xi },t}^{\alpha }+\psi D_{C^{\xi },x}^{\alpha },$$

  where $X_{C^{\xi }}$ is called an infinitesimal fractal generator.

Example 7.

Consider the fractal Lie group of the fractal differential equation as follows:

$$(S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right),x^{\prime })=(\frac{S_{C^{\xi }}^{\alpha }\left(t\right)}{1-\eta x},\frac{x}{1-\eta x}).$$

(41)

The associated the fractal tangent vectors are

$$\varphi (S_{C^{\xi }}^{\alpha }\left(t\right),x)=S_{C^{\xi }}^{\alpha }\left(t\right)x,$$

and

$$\psi (S_{C^{\xi }}^{\alpha }\left(t\right),x)=x^2.$$

Then, the fractal infinitesimal generator is

$$X_{C^{\xi }}=S_{C^{\xi }}^{\alpha }\left(t\right)x{D}_{C^{\xi },t}^{\alpha }+x^2{D}_{C^{\xi },x}^{\alpha }.$$

Example 8.

Consider the fractal infinitesimal generator

$$X_{C^{\xi }}=D_{C^{\xi },t}+x{D}_{C^{\xi },x}.$$

(42)

We can calculate the fractal tangent vectors using Equation (18) as follows:

$$\varphi (S_{C^{\xi }}^{\alpha }\left(t\right),x)=1,$$

and

$$\psi (S_{C^{\xi }}^{\alpha }\left(t\right),x)=x.$$

Then, it follows

$$\varphi (S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right),x^{\prime })=1,\psi (S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right),x^{\prime })=e^{\eta }x.$$

In addition, we have

$$\begin{array}{cc}\hfill S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right)& =S_{C^{\xi }}^{\alpha }\left(t\right)+\eta ,\hfill \\ \hfill x^{\prime }& =e^{\eta }x.\hfill \end{array}$$

(43)

Hence, the fractal Lie symmetry of Equation (42) will be

$$(S_{C^{\xi }}^{\alpha }\left(t^{\prime }\right),x^{\prime })=(S_{C^{\xi }}^{\alpha }\left(t\right)+\eta ,e^{\eta }x).$$

4. Noether’s Theorem for Lagrangians with Fractal Set Support

Noether’s theorem presents the connection between conservation laws and Lie symmetries. For every Lie symmetry, there is a conserved quantity in the system. The Lagrangian on middle-$\xi$ Cantor sets is not a differentiable manifold in the sense of standard calculus. Here, we consider fractal calculus to generalize Noether’s Theorem to include the wider class of the Lagrangian.

Consider a fractal Lagrangian as follows:

$$L_{C^{\xi }}(q\left(t\right),D_{C^{\xi }}^{\alpha }q\left(t\right),S_{C^{\xi }}^{\alpha }\left(t\right)),t\in C^{\xi },$$

where $L_{C^{\xi }}$ is $C^{\alpha }$-differentiable. If $T_{\eta }$ is the set of operations such that

$$T_{ϵ}\left(L_{C^{\xi }}\right)=L_{C^{\xi }},$$

(44)

which might be called a fractal Lie group of Lagrangian. The existence of Equation (44) leads to conserved quantities of the system. Equation (44) is a functional equality, so that one can write

$$\begin{array}{l}{T}_{ϵ}(L_{C^{\xi }}(q,D_{C^{\xi }}^{\alpha }q,S_{C^{\xi }}^{\alpha }\left(t\right)))=\\ L_{C^{\xi }}(Q(q,D_{C^{\xi }}^{\alpha }q,S_{C^{\xi }}^{\alpha }\left(t\right),\eta ),D_{C^{\xi }}^{\alpha }Q(q,D_{C^{\xi }}^{\alpha }q,S_{C^{\xi }}^{\alpha }\left(t\right),\eta ),R(q,D_{C^{\xi }}^{\alpha }q,S_{C^{\xi }}^{\alpha }\left(t\right),\eta )).\end{array}$$

(45)

If we expand $L_{C^{\xi }}$ using Taylor series, we have

$$\begin{array}{c}\hfill T_{ϵ}(L_{C^{\xi }}(q,D_{C^{\xi }}^{\alpha }q,S_{C^{\xi }}^{\alpha }\left(t\right)))=L_{C^{\xi }}(q+\varphi \eta ,D_{C^{\xi }}^{\alpha }q+D_{C^{\xi }}^{\alpha }\varphi \eta ,S_{C^{\xi }}^{\alpha }\left(t\right)+\rho \eta ),\end{array}$$

(46)

where $\varphi ,D_{C^{\xi }}^{\alpha }\varphi$, and $\rho$ are defined by

$$\varphi =\frac{\partial Q}{\partial \eta }{|}_{\eta =0},D_{C^{\xi }}^{\alpha }\varphi =\frac{\partial D_{C^{\xi }}^{\alpha }Q}{\partial \eta }{{|}_{\eta =0},\rho =\frac{\partial R}{\partial \eta }|}_{\eta =0}.$$

(47)

Local fractal symmetries are given by Equation (47).

Fractal Noether’s Theorem is given by

$$D_{C^{\xi },t}^{\alpha }\left(\frac{\partial L_{C^{\xi }}}{\partial D_{C^{\xi }}^{\alpha }q}\varphi -H_{C^{\xi }}\rho \right)=0,$$

(48)

where

$$H_{C^{\xi }}=D_{C^{\xi }}^{\alpha }q\frac{\partial L_{C^{\xi }}}{\partial D_{C^{\xi }}^{\alpha }q}-L_{C^{\xi }},$$

(49)

which is called Hamiltonian on fractal sets.

Example 9.

Consider transformation with the following symmetry

$$T_{ϵ}(L_{C^{\xi }}(q,D_{C^{\xi }}^{\alpha }q,S_{C^{\xi }}^{\alpha }\left(t\right)))=L_{C^{\xi }}(q+\eta ,D_{C^{\xi }}^{\alpha }q,S_{C^{\xi }}^{\alpha }\left(t\right)).$$

(50)

Then in view of Equation (47), we obtain

$$\varphi =1,,D_{C^{\xi },t}^{\alpha }\varphi =0,\rho =0.$$

The fractal momentum is conserved and defined by

$$p_{C^{\xi }}=\frac{\partial L_{C^{\xi }}}{\partial D_{C^{\xi }}^{\alpha }q}.$$

Example 10.

Let us consider a fractal Lagrangian with fractal symmetry transformation as follows:

$$T_{ϵ}(L_{C^{\xi }}(q,D_{C^{\xi }}^{\alpha }q,S_{C^{\xi }}^{\alpha }\left(t\right)))=L_{C^{\xi }}(q,D_{C^{\xi }}^{\alpha }q,S_{C^{\xi }}^{\alpha }\left(t\right)-\eta ).$$

(51)

By Equation (47), we get

$$\varphi =0,,D_{C^{\xi },t}^{\alpha }\varphi =0,\rho =-1.$$

Therefore, the fractal conserved quantity is

$$H_{C^{\xi }}=constant.$$

The fractal Lagrangian will be

$$L_{C^{\xi }}(q,D_{C^{\xi }}^{\alpha }q,S_{C^{\xi }}^{\alpha }\left(t\right)))=\frac{1}{2}m{(D_{C^{\xi }}^{\alpha }q)}^2-U\left(q\right),q\in C^{\xi }.$$

The fractal Hamiltonian is obtained by Equation (49):

$$H_{C^{\xi }}=\frac{1}{2}m{(D_{C^{\xi }}^{\alpha }q)}^2+U\left(q\right),$$

(52)

which is conserved.

5. Conclusions

In this paper, the Lie method for solving differential equations was extended to $C^{\alpha }$-calculus. Analogues for the orbit of a point in view of fractal differential equations were defined. Using linearized symmetry conditions, canonical coordinates on fractal differential equations were derived. Analogues to tangent vectors utilizing $C^{\alpha }$-C were suggested. Infinitesimal generators applying symmetry properties were presented. Noether’s Theorem was expanded to non-differentiable manifolds such as Lagrangians with middle-$\xi$ Cantor sets. Some examples were worked out to show the details.