Residual Power Series Method for Fractional Swift–Hohenberg Equation
Abstract
:1. Introduction
2. Preliminaries
3. Basic Idea of Proposed Algorithm
4. Solution for Fractional Swift–Hohenberg (S–H) Equation
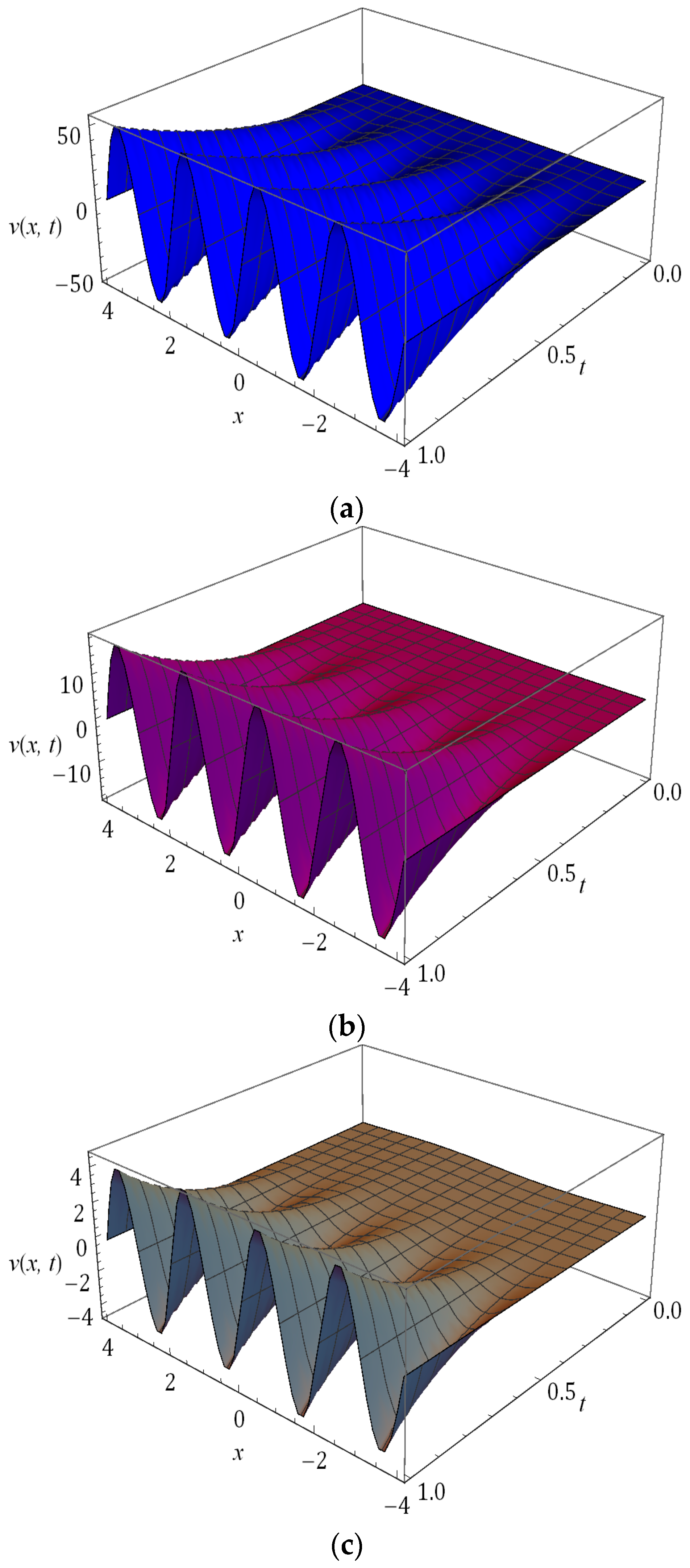
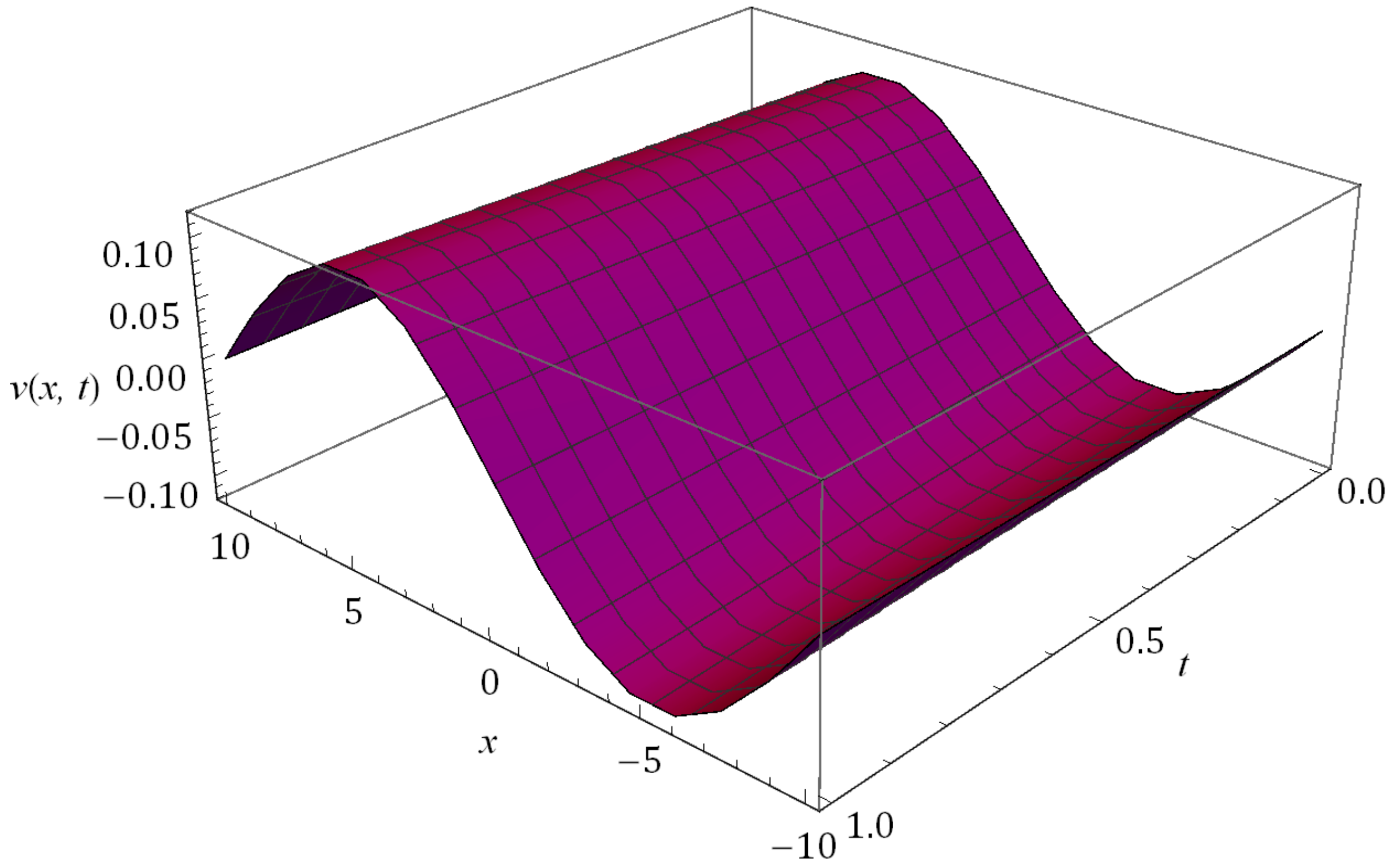
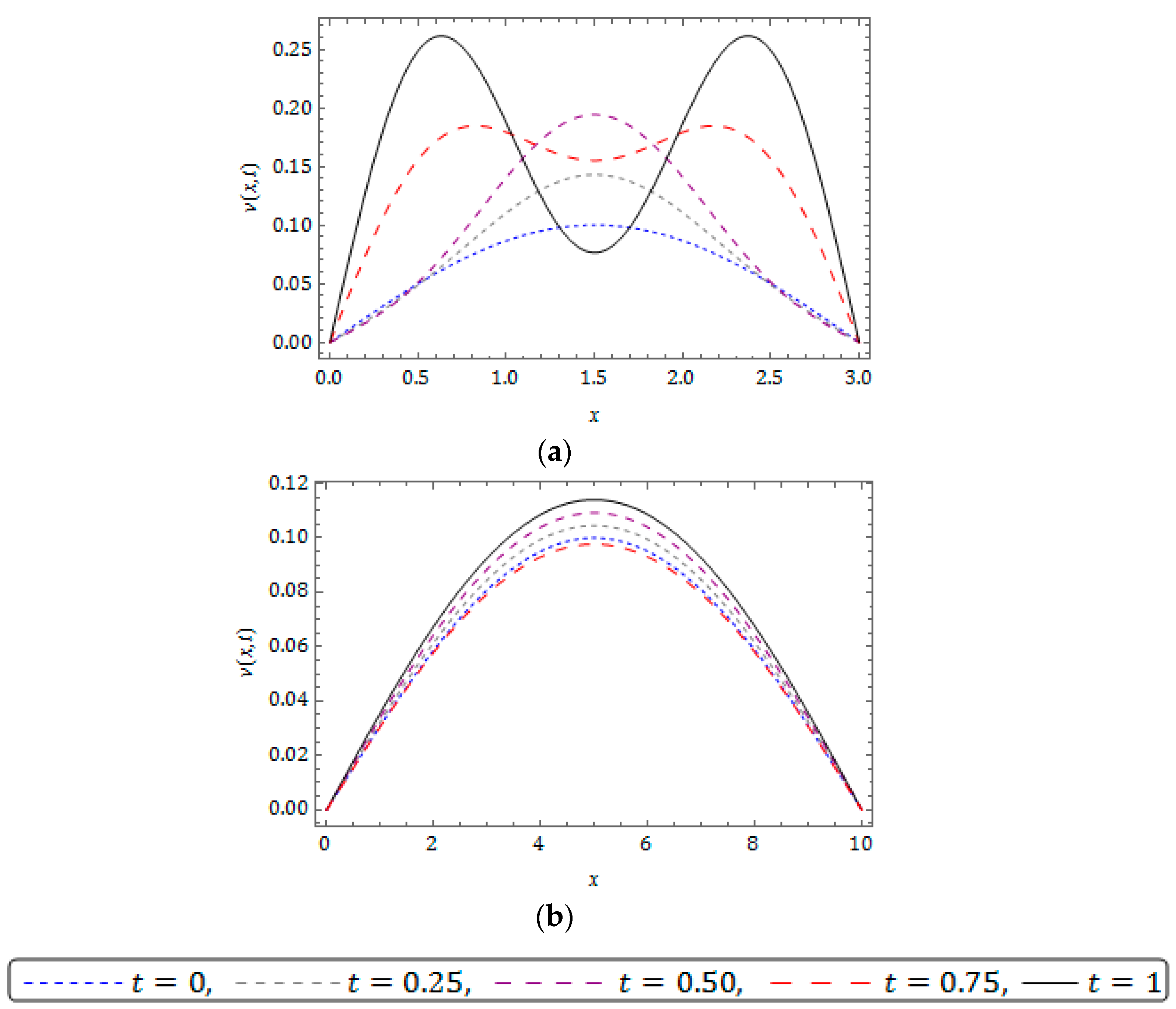
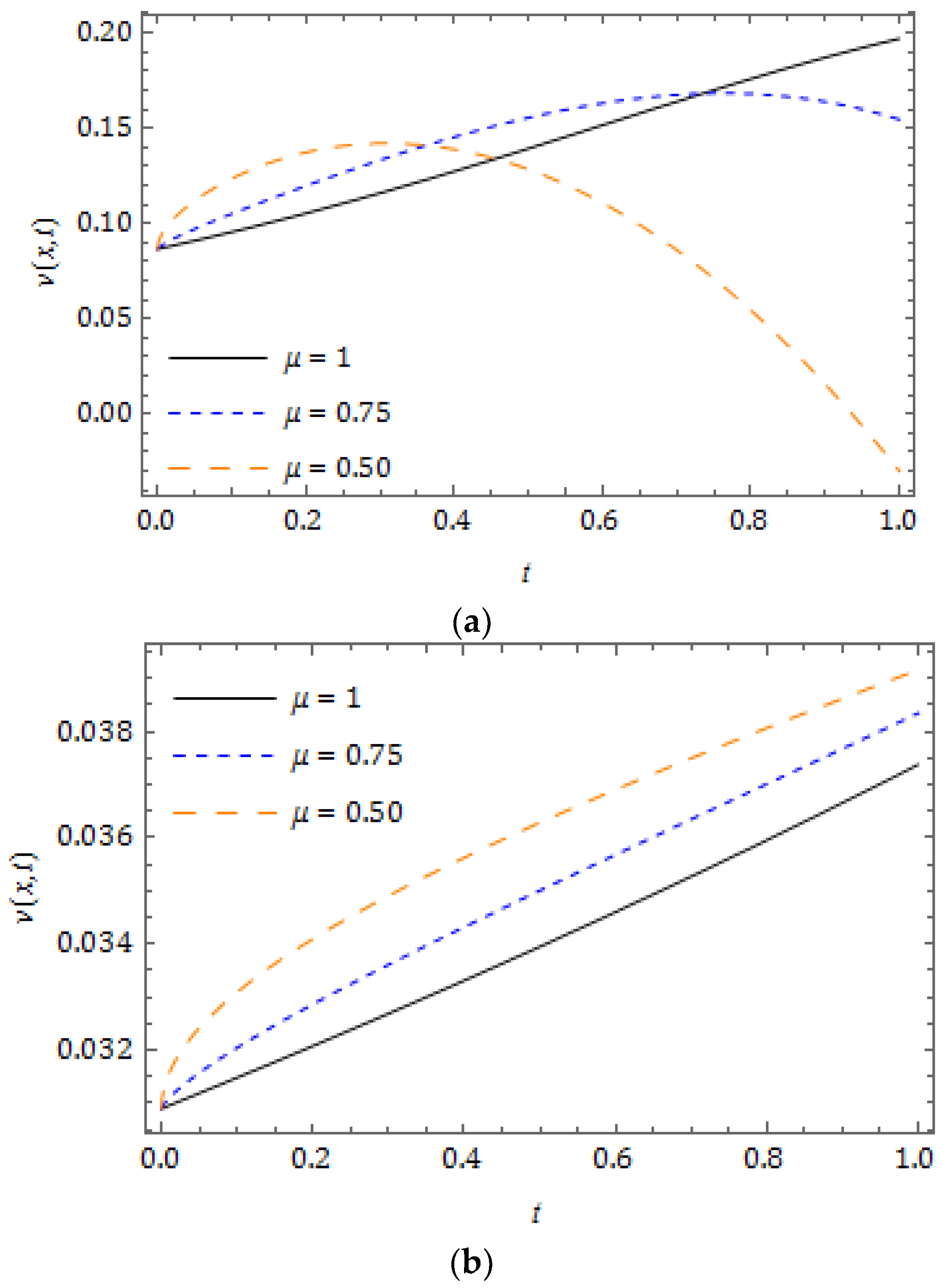
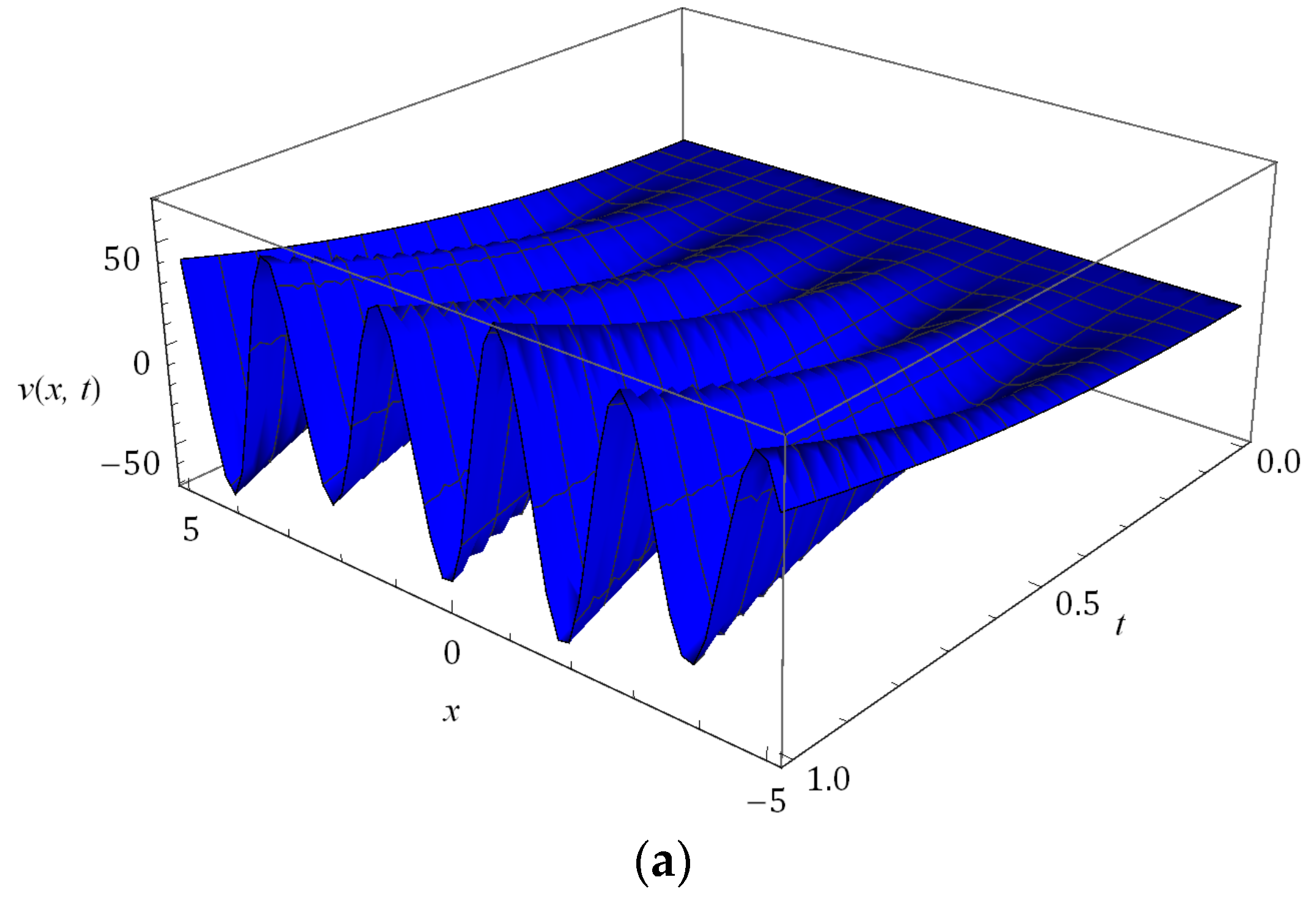
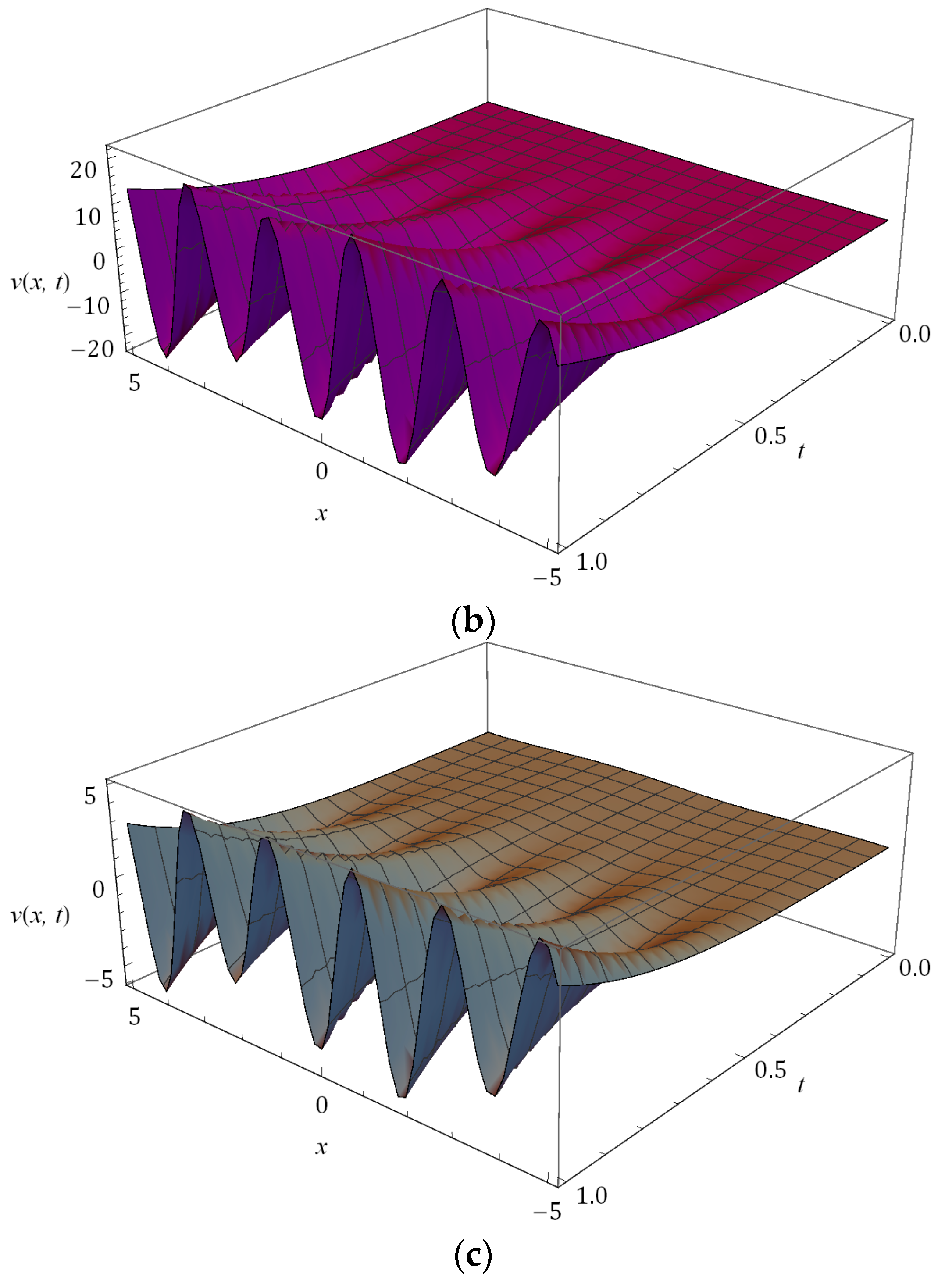
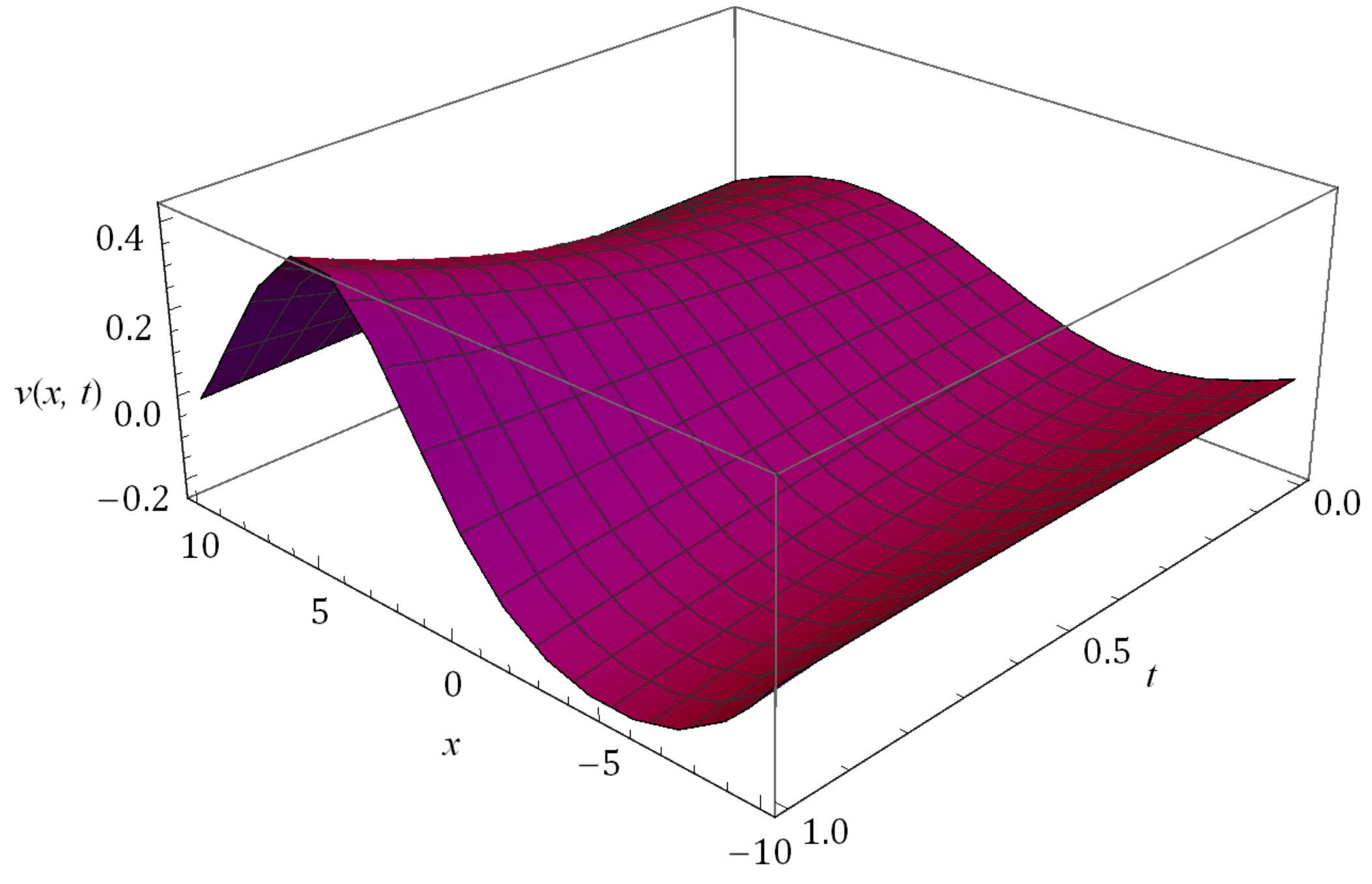
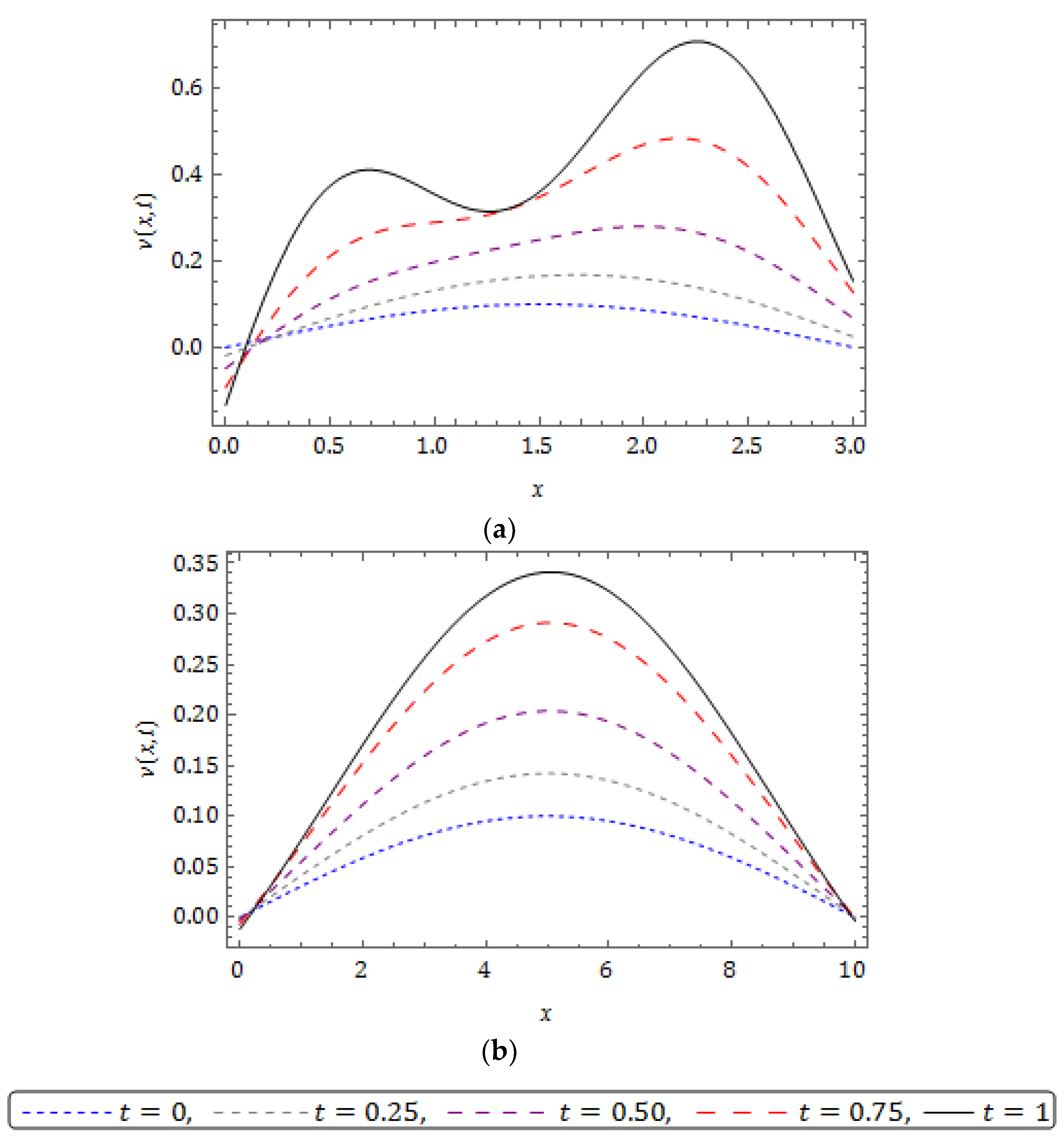
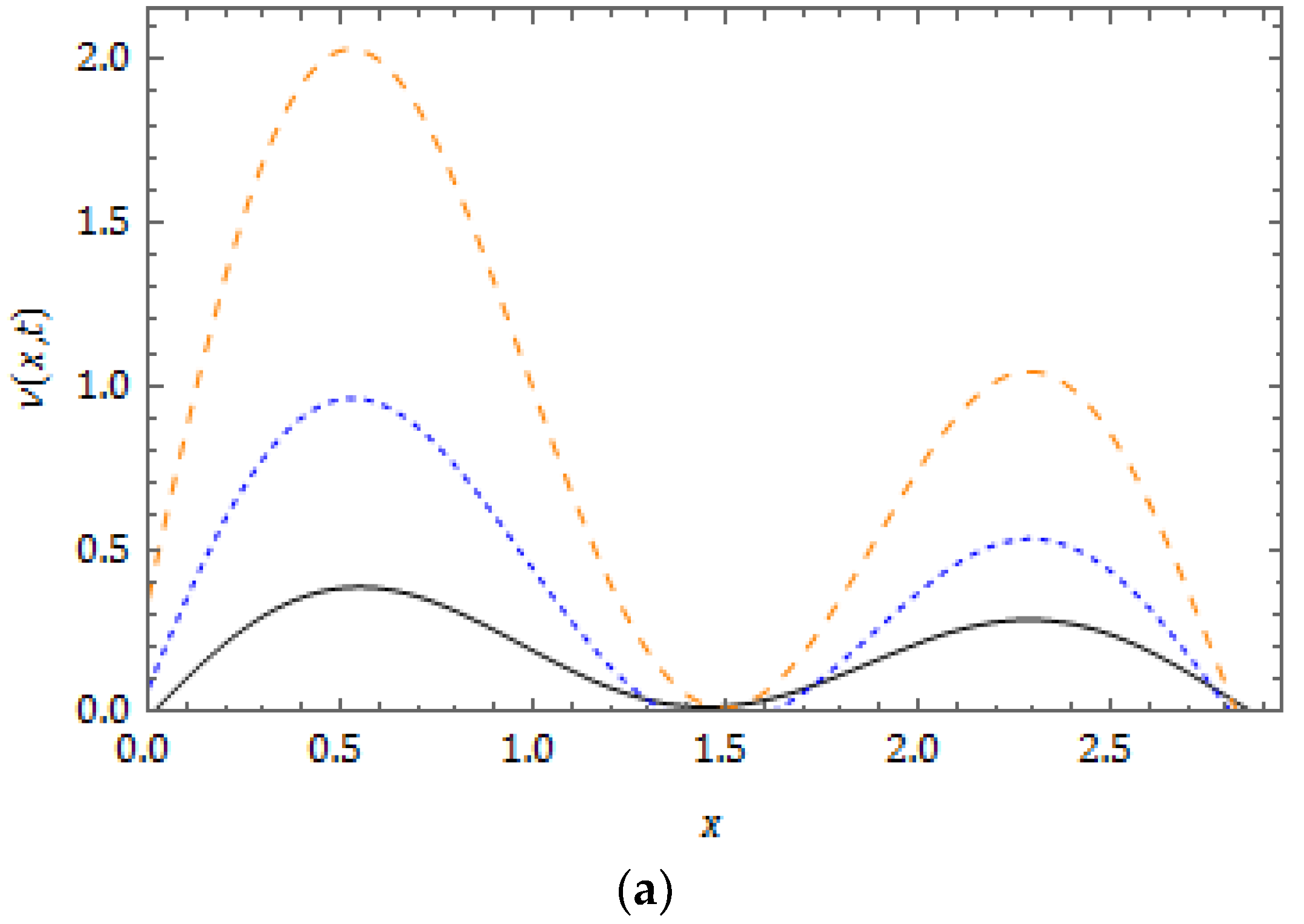
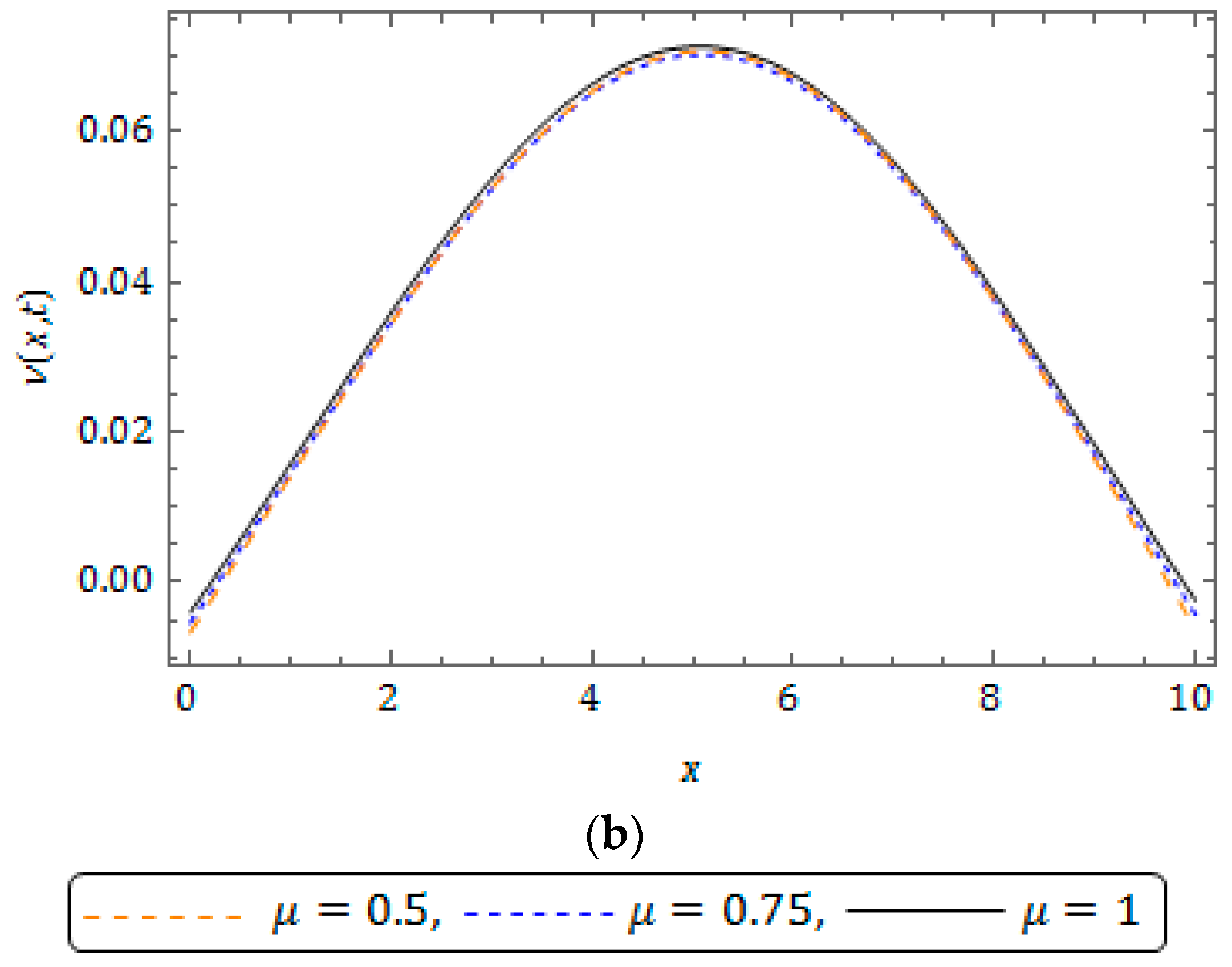
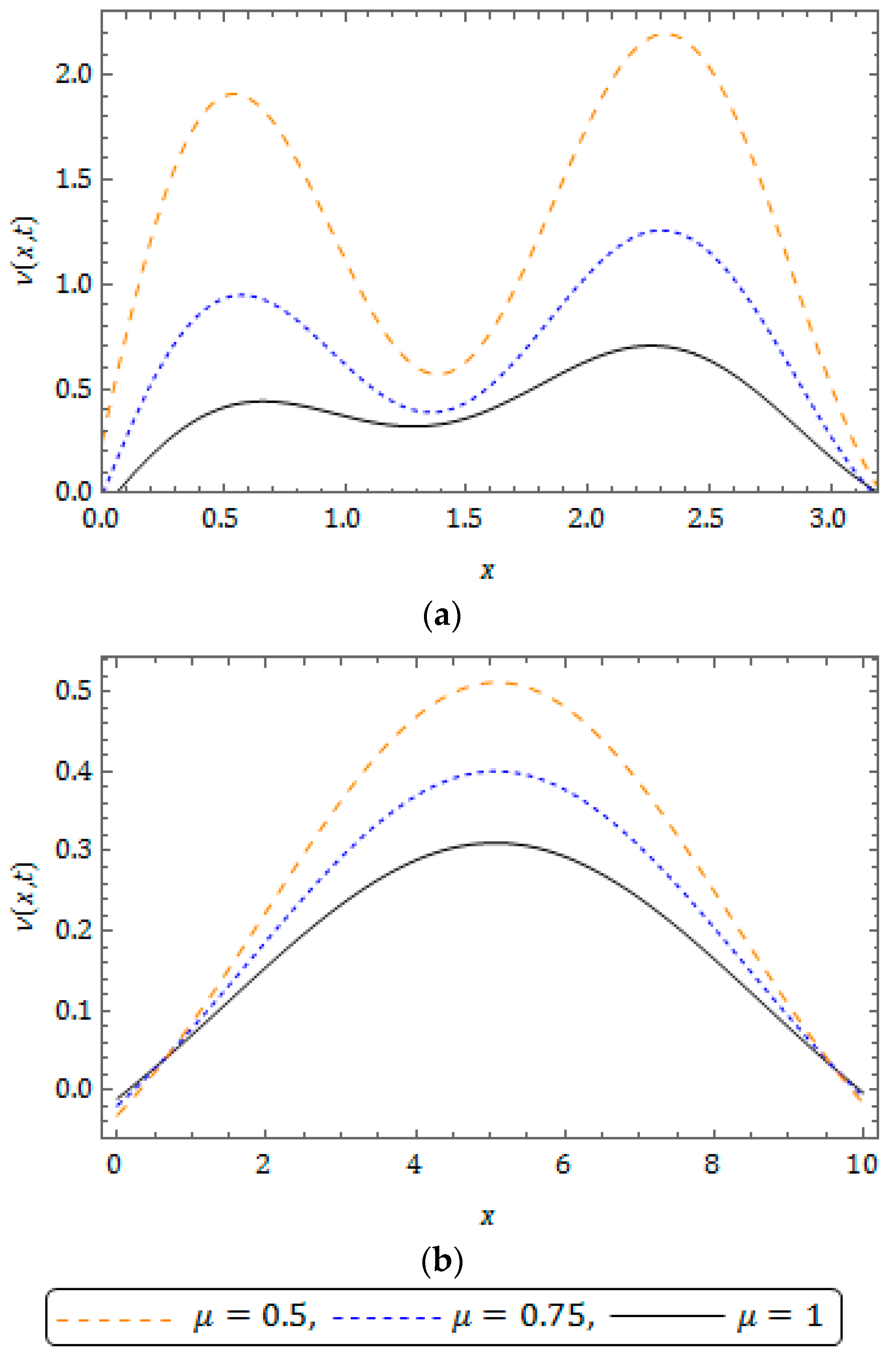
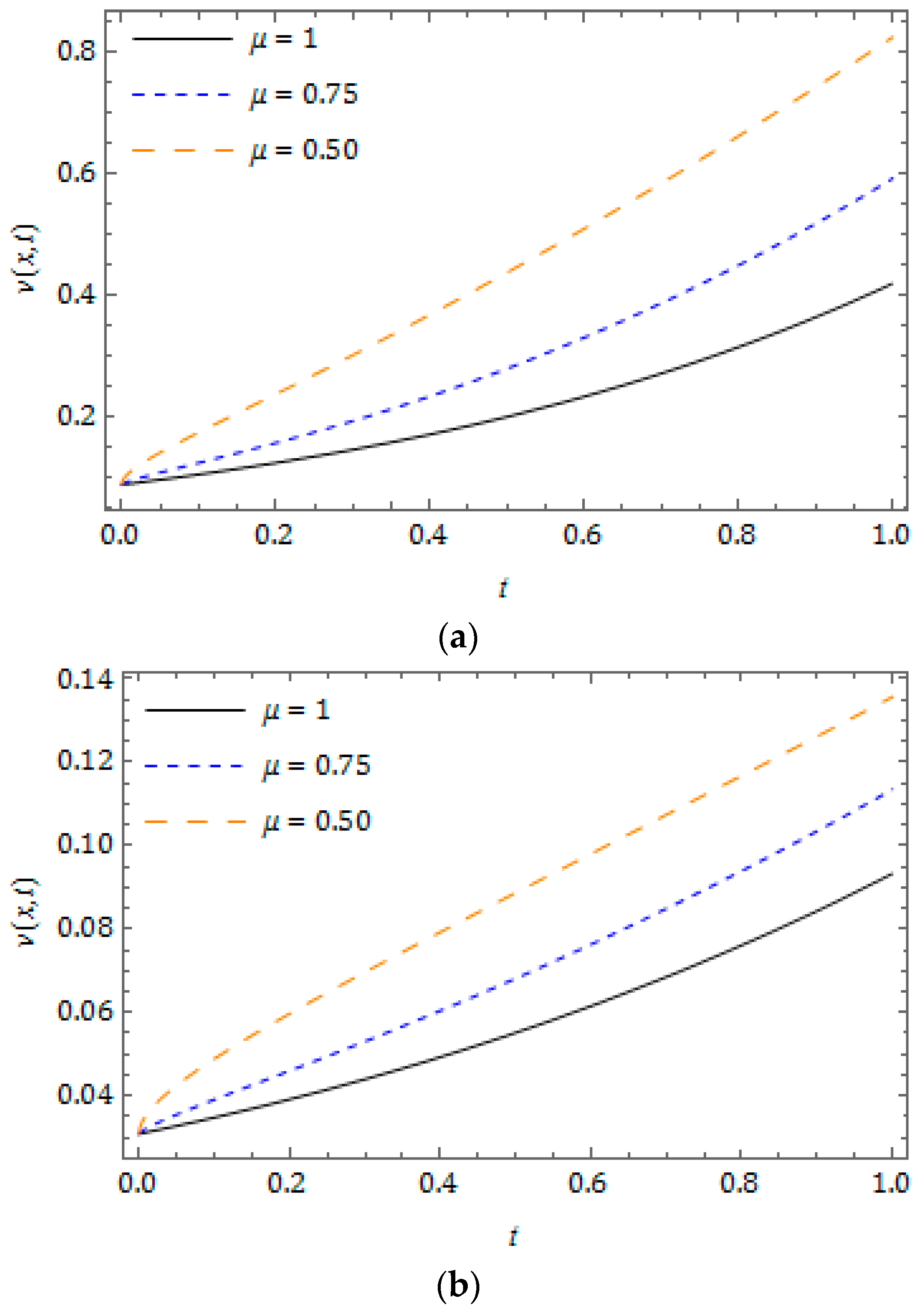
5. Numerical Results and Discussion
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Liouville, J. Mémoire sur quelques questions de géométrie et de mécanique, et sur un nouveau genre de calcul pour résoudre ces questions. J. Ecole. Polytéch. 1832, 13, 1–69. [Google Scholar]
- Riemann, G.F.B. Versuch einer allgemeinen Auffassung der Integration und Differentiation. In Gesammelte Mathematische Werke; Teubner: Leipzig, Germany, 1896. [Google Scholar]
- Caputo, M. Elasticità e Dissipazione; Zanichelli: Bologna, Italy, 1969. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; World Scientific: Boston, MA, USA, 2012. [Google Scholar]
- Povstenko, Y. Linear Fractional Diffusion-Wave Equation for Scientists and Engineers; Birkhäuser: New York, NY, USA, 2015. [Google Scholar]
- Baleanu, D.; Wu, G.-C.; Zeng, S.-D. Chaos analysis and asymptotic stability of generalized Caputo fractional differential equations. Chaos Solitons Fractals 2017, 102, 99–105. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Hasan, M.M.A.; Baleanu, D. New studies for general fractional financial models of awareness and trial advertising decisions. Chaos Solitons Fractals 2017, 104, 772–784. [Google Scholar] [CrossRef]
- Liu, D.Y.; Gibaru, O.; Perruquetti, W.; Laleg-Kirati, T.M. Fractional order differentiation by integration and error analysis in noisy environment. IEEE Trans. Autom. Control 2015, 60, 2945–2960. [Google Scholar] [CrossRef]
- Esen, A.; Sulaiman, T.A.; Bulut, H.; Baskonus, H.M. Optical solitons to the space-time fractional (1+1)-dimensional coupled nonlinear Schrödinger equation. Optik 2018, 167, 150–156. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. New numerical surfaces to the mathematical model of cancer chemotherapy effect in Caputo fractional derivatives. Chaos 2019, 29, 013119. [Google Scholar] [CrossRef] [PubMed]
- Caponetto, R.; Dongola, G.; Fortuna, L.; Gallo, A. New results on the synthesis of FO-PID controllers. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 997–1007. [Google Scholar] [CrossRef]
- Prakash, A.; Veeresha, P.; Prakasha, D.G.; Goyal, M. A homotopy technique for fractional order multi-dimensional telegraph equation via Laplace transform. Eur. Phys. J. Plus 2019, 134, 1–18. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. Novel simulations to the time-fractional Fisher’s equation. Math. Sci. 2019, 1–10. [Google Scholar] [CrossRef]
- Swift, J.B.; Hohenberg, P.C. Hydrodynamics fluctuations at the convective instability. Phys. Rev. A 1977, 15, 319–328. [Google Scholar] [CrossRef]
- Ryabov, P.N.; Kudryashov, N.A. Nonlinear waves described by the generalized Swift-Hohenberg equation. J. Phys. Conf. Ser. 2017, 788, 012032. [Google Scholar] [CrossRef]
- Cross, M.; Hohenberg, P. Pattern formation outside of equilibrium. Rev. Mod. Phys. 1993, 65, 851–1112. [Google Scholar] [CrossRef]
- Fife, P.C. Pattern formation outside of equilibrium. In Handbook of Dynamical Systems; Elsevier: Amsterdam, The Netherlands, 2002; pp. 679–719. [Google Scholar]
- Hoyle, R.B. Pattern Formation; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Lega, L.; Moloney, J.V.; Newell, A.C. Swift–Hohenberg equation for lasers. Phys. Rev. Lett. 1994, 73, 2978–2981. [Google Scholar] [CrossRef] [PubMed]
- Pomeau, Y.; Zaleski, S. Dislocation motion in cellular structures. Phys. Rev. A 1983, 27, 2710–2726. [Google Scholar] [CrossRef]
- Peletier, L.A.; Rottschäfer, V. Large time behaviour of solutions of the Swift–Hohenberg equation. C. R. Acad. Sci. Paris Ser. I 2003, 336, 225–230. [Google Scholar] [CrossRef]
- Vishal, K.; Kumar, S.; Das, S. Application of homotopy analysis method for fractional Swift-Hohenberg equation revisited. Appl. Math. Model. 2012, 36, 3630–3637. [Google Scholar] [CrossRef]
- Khan, N.A.; Khan, N.U.; Ayaz, M.; Mahmood, A. Analytical methods for solving the time-fractional Swift–Hohenberg (S–H) equation. Comput. Math. Appl. 2011, 61, 2181–2185. [Google Scholar] [CrossRef]
- Vishal, K.; Das, S.; Ong, S.H.; Ghosh, P. On the solutions of fractional Swift-Hohenberg equation with dispersion. Appl. Math. Comput. 2013, 219, 5792–5801. [Google Scholar] [CrossRef]
- Arqub, O.A.; Abo-Hammour, Z.; Al-Badarneh, R.; Momani, S. A reliable analytical method for solving higher-order initial value problems. Discret. Dyn. Nat. Soc. 2013, 1–12. [Google Scholar] [CrossRef]
- Arqub, O.A.; El-Ajou, A.; Momani, S. Constructing and predicting solitary pattern solutions for nonlinear time-fractional dispersive partial differential equations. J. Comput. Phys. 2015, 293, 385–399. [Google Scholar] [CrossRef]
- Korpinar, Z.; Inc, M. Numerical simulations for fractional variation of (1+1)-dimensional Biswas-Milovic equation. Optik 2018, 164, 77–85. [Google Scholar] [CrossRef]
- Zhang, Y.; Kumar, A.; Kumar, S.; Baleanu, D.; Yang, X.-J. Residual power series method for time-fractional Schrödinger equations. J. Nonlinear Sci. Appl. 2016, 9, 5821–5829. [Google Scholar] [CrossRef]
- Qurashi, M.M.A.; Korpinar, Z.; Baleanu, D.; Inc, M. A new iterative algorithm on the time-fractional Fisher equation: Residual power series method. Adv. Mech. Eng. 2017, 9, 1–8. [Google Scholar] [CrossRef]
- Bayrak, M.A.; Demir, A. A new approach for space-time fractional partial differential equations by residual power series method. Appl. Math. Comput. 2018, 336, 215–230. [Google Scholar]
- Arafa, A.; Elmahdy, G. Application of residual power series method to fractional coupled physical equations arising in fluids flow. Int. J. Differ. Equ. 2018, 1–10. [Google Scholar] [CrossRef]
- Merdan, M. A numeric–analytic method for time-fractional Swift–Hohenberg (S-H) equation with modified Riemann–Liouville derivative. Appl. Math. Model. 2013, 37, 4224–4231. [Google Scholar] [CrossRef]
- McCalla, S.; Sandstede, B. Snaking of radial solutions of the multi-dimensional Swift-Hohenberg equation: A numerical study. Phys. D 2010, 239, 1581–1592. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Sinelshchikov, D.I. Exact solutions of the Swift–Hohenberg equation with dispersion. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 26–34. [Google Scholar] [CrossRef]
- Li, W.; Pang, Y. An iterative method for time-fractional Swift-Hohenberg equation. Adv. Math. Phys. 2018, 1, 1–13. [Google Scholar] [CrossRef]
- Bakhtiari, P.; Abbasbandy, S.; Gorder, R.A.V. Reproducing kernel method for the numerical solution of the 1D Swift–Hohenberg equation. App. Math. Comput. 2018, 339, 132–143. [Google Scholar] [CrossRef]
- Tchier, F.; Inc, M.; Korpinar, Z.S.; Baleanu, D. Solution of the time fractional reaction-diffusion equations with residual power series method. Adv. Mech. Eng. 2016, 8, 1–10. [Google Scholar] [CrossRef]
- Arqub, O.A. Series solution of fuzzy differential equations under strongly generalized differentiability. J. Adv. Res. Appl. Math. 2013, 5, 31–52. [Google Scholar] [CrossRef]
- Arqub, O.A.; El-Ajou, A.; Bataineh, A.; Hashim, I. A representation of the exact solution of generalized Lane-Emden equations using a new analytical method. Abstr. Appl. Anal. 2013, 2013, 1–10. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prakasha, D.G.; Veeresha, P.; Baskonus, H.M. Residual Power Series Method for Fractional Swift–Hohenberg Equation. Fractal Fract. 2019, 3, 9. https://doi.org/10.3390/fractalfract3010009
Prakasha DG, Veeresha P, Baskonus HM. Residual Power Series Method for Fractional Swift–Hohenberg Equation. Fractal and Fractional. 2019; 3(1):9. https://doi.org/10.3390/fractalfract3010009
Chicago/Turabian StylePrakasha, D. G., P. Veeresha, and Haci Mehmet Baskonus. 2019. "Residual Power Series Method for Fractional Swift–Hohenberg Equation" Fractal and Fractional 3, no. 1: 9. https://doi.org/10.3390/fractalfract3010009
APA StylePrakasha, D. G., Veeresha, P., & Baskonus, H. M. (2019). Residual Power Series Method for Fractional Swift–Hohenberg Equation. Fractal and Fractional, 3(1), 9. https://doi.org/10.3390/fractalfract3010009






