Abstract
In this paper, the approximated analytical solution for the fractional Swift–Hohenberg (S–H) equation has been investigated with the help of the residual power series method (RPSM). To ensure the applicability and efficiency of the proposed technique, we consider a non-linear fractional order Swift–Hohenberg equation in the presence and absence of dispersive terms. The effect of bifurcation and dispersive parameters with physical importance on the probability density function for distinct fractional Brownian and standard motions are studied and presented through plots. The results obtained show that the proposed technique is simple to implement and very effective for analyzing the complex problems that arise in connected areas of science and technology.
1. Introduction
Fractional calculus (FC) is a general expansion of integer order calculus to arbitrary order and was discussed in an early letter between the mathematicians Leibniz and L’Hospital in 1695. In recent years, many authors have started to study the fractional calculus due to its ability to provide an exact description for various types of non-linear phenomena. Fractional order differential equations are the generalization of traditional differential equations having non-local and genetic consequence in material properties. The concept of fractional calculus was studied and described by many senior scholars and they defined revolutionary definitions of fractional calculus, which laid the foundations for fractional calculus [1,2,3,4,5,6,7]. Nowadays, fractional partial differential equations have gained popularity in developing procedure for non-linear models and investigation of dynamical systems. The theory of fractional-order calculus has been related to practical projects and it has been applied to analyze and study different phenomena including chaos theory [8], financial models [9], a noisy environment [10], optics [11], and others [12,13,14,15]. The solutions of fractional differential equations play a vital role in describing the characteristics of non-linear problems that arise in nature. It is difficult to obtain exact solutions for the fractional differential equations describing non-linear phenomena, so we come across various analytical and numerical techniques.
The Swift–Hohenberg (S–H) equation was introduced and nurtured by Jack Swift and Pierre Hohenberg, as a universal model of the Rayleigh–Benard convective instability of the fluid with thermal fluctuations for fluid velocity dynamics and temperature of convection [16].
The Swift–Hohenberg equation plays a vital role in pattern formation theory (specifically, the mechanism of the amplitude of optical electrical field in the interior of cavity, the pattern within thin vibrated granular layers and so on) in fluid layers confined between horizontal well-conducting boundaries [17]. The proposed problem serves as a paradigm for a motivating plethora of localized as well as non-localized patterns that originate in various biological structures [18,19,20]. In many physical phenomena including the study of lasers, hydrodynamics, liquid crystals, flame dynamics and statistical mechanics [21,22,23], the portrayal of the S–H equation is very essential. In the present investigation, we consider the time-fractional non-linear S–H equation [24,25] as follows:
and in the presence of the dispersive term [26] as:
where is probability density function, and are respectively dispersive and bifurcation parameters.
In this paper, the solution for a fractional S–H equation has been investigated by employing the residual power series method (RPSM). The future technique was proposed by Arqub to analyze and find the solution for strongly non-linear problems arising in science and technology [27,28]. This technique does not necessitate any change while moving from the first order to the higher order. Due to this, the future technique can be directly employed to the considered problems by picking suitable initial conditions. By this method, we obtain an analytic Taylor series solution. The proposed scheme does not require linearization, discretization or perturbation and, additionally, it will decrease huge mathematical computations, requires less computer memory, and is free from obtaining difficult polynomials, integrations and physical parameters. It provides us with extremely large freedom to choose the equation type of linear sub-problems, initial guess, and base function of the solution; due to this, complicated non-linear differential equations can often be solved in a simple way. It is worth mentioning that, the proposed method can reduce the computation of the time and work as compared with other traditional techniques while maintaining the efficiency of the results obtained.
Recently, due to its consistency and efficacy, it has aided by many researchers to interpret results for various kinds of nonlinear problem, like the authors in [29]; analyze and find the solution for the Biswas–Milovic equation having fractional order; the arbitrary order Schrodinger equation has been profitably analyzed in [30]; the authors in [31] employed it to find the solution for the Fisher equation with fractional order; the applicability and efficiency of RPSM is presented in [32] to solve PDEs; scholars in [33], have analyzed coupled equations arising in fluid flow; and many other are aided by the considered scheme to analyze and find the solution for complex non-linear problems describing complex phenomena.
The solution for the S–H equation is studied by many scholars using distinct techniques like Vishal et al. who employed Homotopy Analysis Method (HAM) [24] and Homotopy Perturbation Transform Method (HPTM) [26], Merdan who studied with the help of the variational iteration technique using the Riemann–Liouville derivative [34], Khan et al. who used the differential transform technique [25], and others [35,36,37,38]. Motivated by the above work, we find the approximated analytical solution for proposed problem by using RPSM.
2. Preliminaries
We recall the definitions and basic notions of the fractional calculus and Laplace transform, which will be used in the present frame work:
Definition 1.
The Riemann-Liouville fractional integral for a functionis presented [1,2] as:
Definition 2.
The Caputo fractional derivative for a functionis defined as [3]:
Definition 3.
An expanding power series (PS) and the shape of the PS are, respectively, presented as:
and,
is called fractional PS at[39].
Remark 1.
The FPS expanded ofat pointshould be of the shape
which is a generalized Taylor’s series expression.
3. Basic Idea of Proposed Algorithm
In this segment, we present a fundamental solution procedure of the proposed technique. We consider the following generalized non-linear fractional differential equation to present the basic idea of RPSM as follows:
with initial condition,
where symbolised the Caputo fractional derivative for the function , is the non-linear term and is linear term. The solution for Equation (10) in a fractional power series about the initial point is proposed by RPSM as follows:
The truncated series of is defined as follows:
The RPS approximate solution of is given by:
Now, from Equation (13) we have:
We define the residual function for Equation (10) as follows:
Then, the residual function becomes:
As in [40,41], it is clear that and . Therefore, , since the fractional derivative of a constant in the Caputo sense is zero and the fractional derivatives of and are matching at for each ; that is .
Now, we consider , in Equation (13) to evaluate f1(x), f2(x), f3(x), …, and put the obtained values in Equation (15), then on applying the fractional derivative in both results we have:
4. Solution for Fractional Swift–Hohenberg (S–H) Equation
In this part, we consider fractional S–H equation to validate the applicability and efficiency of the considered algorithms.
Example 1.
Consider non-linear fractional S–H equation of the form [24,25]:
Subjected to initial condition:
Now, we define the residual function for Equation (19) as follows:
Now, theresidual functionis given by:
To determine, we considerin Equation (22) and we have:
For, Equation (15) reduces to:
Then, we have:
But, depending on the result of Equation (18) in the case ofwe have. Therefore, we get:
At, Equation (22) reduces to:
Now, from Equation (15) for we have:
Then, we obtained:
Depending on the result of Equation (18) in the case of , we have . Therefore, the above equation simplifies to:
For in Equation (22), one can get:
But from Equation (15) at , we obtain:
On simplification, we get:
For in Equation (18), we obtain and then Equation (31) reduces to:
Similarly, we can find In the present investigation, we find a fourth-order RPSM solution and corresponding analysis has been presented in terms of 2D and 3D plots.
Example 2.
Consider the fractional S–H equation with dispersion of the form [26]:
with initial condition:
For Equation (33), the residual function is defined as:
Now, theresidual functionis given by:
To find, we setin Equation (36), then:
But from Equation (15) at,
Then, Equation (37) becomes:
Now, depending on the result of Equation (18) in the case of, we have, therefore:
At, Equation (36) reduces to:
Since, from Equation (15) at
From the above result, Equation (41) becomes:
Depending on the result of Equation (16) in the case of, we have,
To evaluate, we putin Equation (36) which gives:
But from Equation (15) at,
Then, we have:
For, Equation (18) gives, therefore:
In a similar manner, we can evaluate the values ofIn this paper, we evaluate up to a fourth RPSM series solution, and the corresponding results are presented through plots.
5. Numerical Results and Discussion
The solution for a fractional order non-linear S–H equation is obtained in present framework with the aid of RPSM for both cases in the domain . Furthermore, the consequences of dispersion and bifurcation on the solution obtained are presented in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. The overshoot of Figure 1 reveals that the surfaces of the solution obtained for distinct fractional order considered in Example 1 at , and in the same manner the nature of the RPSM solution for is presented in Figure 2. These plots help us to understand the behaviour of probability density function with changing space and time-scale variables. The nature of obtained solution for Example 1 at distinct values of time () for and is presented in Figure 3, and for the corresponding equation the behaviour of the solution obtained for distinct is plotted in Figure 4.
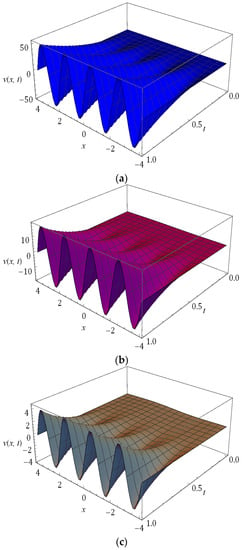
Figure 1.
Surfaces of obtained solution for Example 1 at with and .
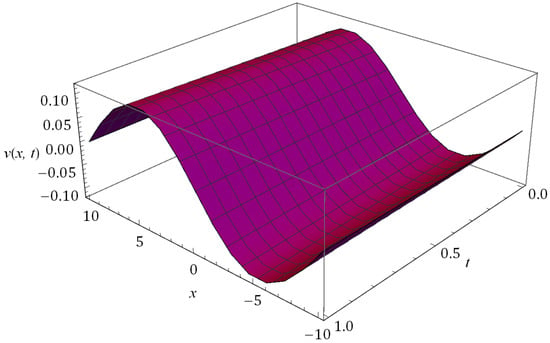
Figure 2.
Behaviour of solution obtained for Example 1 at with and .
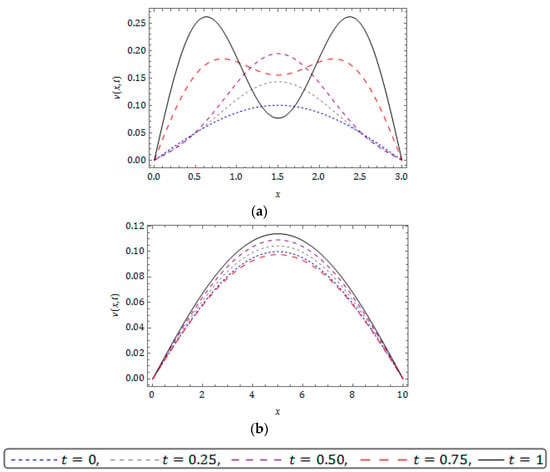
Figure 3.
Nature of solution obtained for Example 1 for distinct at when and .
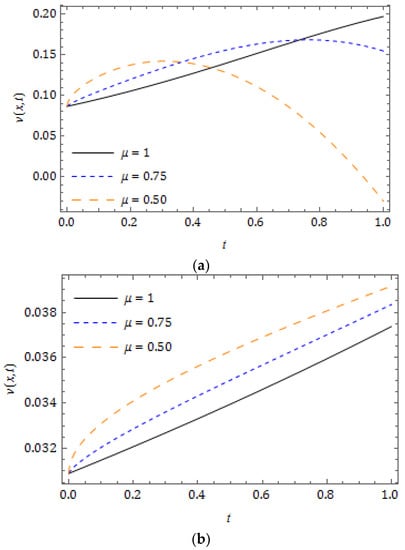
Figure 4.
Plots of -HATM solution for Example 1 for distinct at when and .
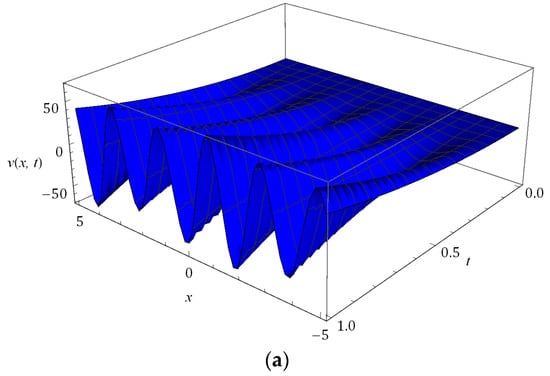
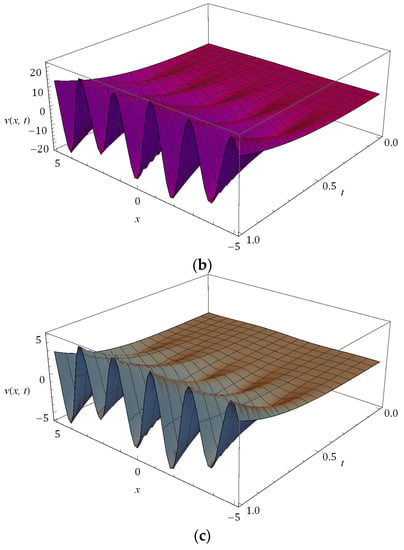
Figure 5.
Surfaces of solution obtained for Example 2 at when and .
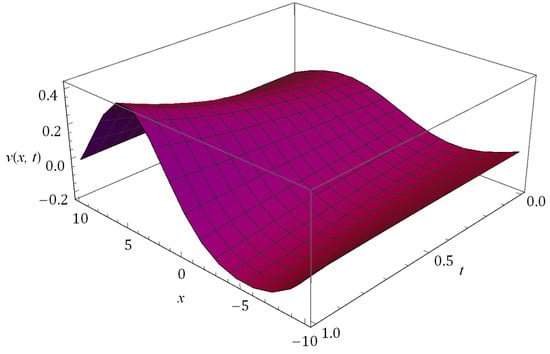
Figure 6.
Behaviour of solution obtained for Example 2 at and .
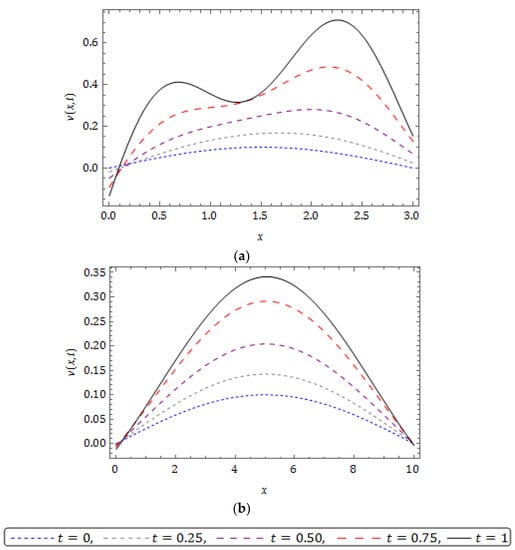
Figure 7.
Plots of solution obtained for Example 2 for distinct at when and .
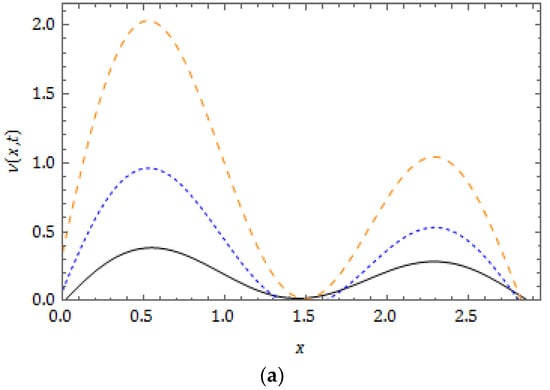
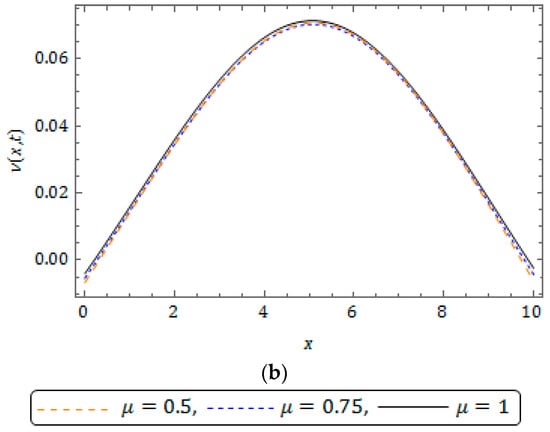
Figure 8.
Nature of residual power series method (RPSM) solution for Example 2 for distinct at when and .
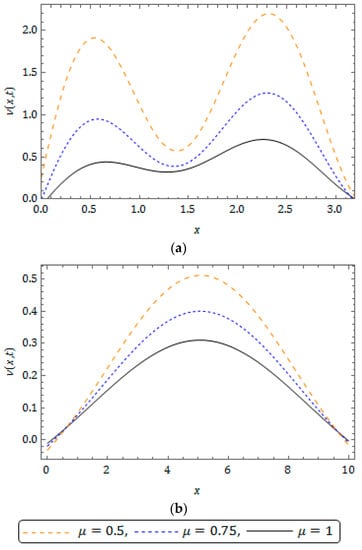
Figure 9.
Behaviour of RPSM solution for Example 2 for distinct at when and .
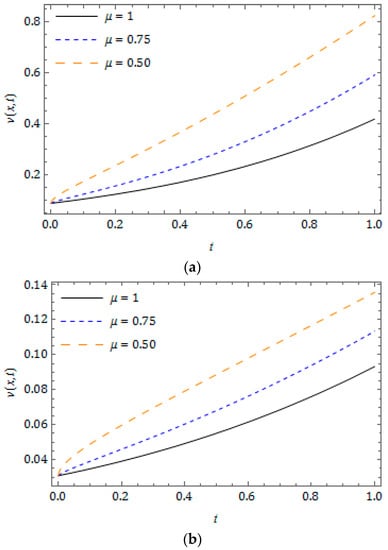
Figure 10.
Plots of RPSM solution for Example 2 for distinct at when and .
The nature of the RPSM solution for the FSH equation considered in Example 2 is captured in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. The surfaces of the solution obtained for the FSH equation with dispersion considered in Equation (33) with diverse is presented in Figure 5 and Figure 6, respectively, for and 10. Figure 7 presents the temperament of the obtained solution with gradual changes of time at and . Figure 8 and Figure 9 show that, for the nature of damping is maximum when and there is no damping at , and increases with decreasing . As compared to , the damping is minimum for the corresponding equation at and is cited in Figure 8 and Figure 9, and we can see that the nature of curves changes and solution lose their periodicity. In Figure 10, we plot the solution obtained for diverse at and . The present investigation will benefit the scholars working in the pattern formation theory, laser patterns and statistical mechanics to understand the behaviour of the probability density function.
6. Conclusions
In this paper, we applied RPSM to find the approximate analytical solution for a non-linear S–H equation of fractional order with the absence and presence of the dispersion term. The consequences of dispersion and bifurcation parameters on the probability density function for the proposed fruition equation is analyzed in terms of plots, and the time and space domain are also illustrated during the investigation. From these results, we learned that both dispersion and fractional order parameters control the nature of the probability density function. The oscillatory value and ) of the bifurcation parameter specifies the behaviour of hydrodynamic stability. Finally, from the results obtained we can conclude that the proposed algorithm is highly efficient and can be employed to examine a wide class of non-linear fractional order mathematical models for understanding the nature of complex phenomena.
Author Contributions
All authors contributed to each part of this work equally, and they read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liouville, J. Mémoire sur quelques questions de géométrie et de mécanique, et sur un nouveau genre de calcul pour résoudre ces questions. J. Ecole. Polytéch. 1832, 13, 1–69. [Google Scholar]
- Riemann, G.F.B. Versuch einer allgemeinen Auffassung der Integration und Differentiation. In Gesammelte Mathematische Werke; Teubner: Leipzig, Germany, 1896. [Google Scholar]
- Caputo, M. Elasticità e Dissipazione; Zanichelli: Bologna, Italy, 1969. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; World Scientific: Boston, MA, USA, 2012. [Google Scholar]
- Povstenko, Y. Linear Fractional Diffusion-Wave Equation for Scientists and Engineers; Birkhäuser: New York, NY, USA, 2015. [Google Scholar]
- Baleanu, D.; Wu, G.-C.; Zeng, S.-D. Chaos analysis and asymptotic stability of generalized Caputo fractional differential equations. Chaos Solitons Fractals 2017, 102, 99–105. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Hasan, M.M.A.; Baleanu, D. New studies for general fractional financial models of awareness and trial advertising decisions. Chaos Solitons Fractals 2017, 104, 772–784. [Google Scholar] [CrossRef]
- Liu, D.Y.; Gibaru, O.; Perruquetti, W.; Laleg-Kirati, T.M. Fractional order differentiation by integration and error analysis in noisy environment. IEEE Trans. Autom. Control 2015, 60, 2945–2960. [Google Scholar] [CrossRef]
- Esen, A.; Sulaiman, T.A.; Bulut, H.; Baskonus, H.M. Optical solitons to the space-time fractional (1+1)-dimensional coupled nonlinear Schrödinger equation. Optik 2018, 167, 150–156. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. New numerical surfaces to the mathematical model of cancer chemotherapy effect in Caputo fractional derivatives. Chaos 2019, 29, 013119. [Google Scholar] [CrossRef] [PubMed]
- Caponetto, R.; Dongola, G.; Fortuna, L.; Gallo, A. New results on the synthesis of FO-PID controllers. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 997–1007. [Google Scholar] [CrossRef]
- Prakash, A.; Veeresha, P.; Prakasha, D.G.; Goyal, M. A homotopy technique for fractional order multi-dimensional telegraph equation via Laplace transform. Eur. Phys. J. Plus 2019, 134, 1–18. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. Novel simulations to the time-fractional Fisher’s equation. Math. Sci. 2019, 1–10. [Google Scholar] [CrossRef]
- Swift, J.B.; Hohenberg, P.C. Hydrodynamics fluctuations at the convective instability. Phys. Rev. A 1977, 15, 319–328. [Google Scholar] [CrossRef]
- Ryabov, P.N.; Kudryashov, N.A. Nonlinear waves described by the generalized Swift-Hohenberg equation. J. Phys. Conf. Ser. 2017, 788, 012032. [Google Scholar] [CrossRef]
- Cross, M.; Hohenberg, P. Pattern formation outside of equilibrium. Rev. Mod. Phys. 1993, 65, 851–1112. [Google Scholar] [CrossRef]
- Fife, P.C. Pattern formation outside of equilibrium. In Handbook of Dynamical Systems; Elsevier: Amsterdam, The Netherlands, 2002; pp. 679–719. [Google Scholar]
- Hoyle, R.B. Pattern Formation; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Lega, L.; Moloney, J.V.; Newell, A.C. Swift–Hohenberg equation for lasers. Phys. Rev. Lett. 1994, 73, 2978–2981. [Google Scholar] [CrossRef] [PubMed]
- Pomeau, Y.; Zaleski, S. Dislocation motion in cellular structures. Phys. Rev. A 1983, 27, 2710–2726. [Google Scholar] [CrossRef]
- Peletier, L.A.; Rottschäfer, V. Large time behaviour of solutions of the Swift–Hohenberg equation. C. R. Acad. Sci. Paris Ser. I 2003, 336, 225–230. [Google Scholar] [CrossRef]
- Vishal, K.; Kumar, S.; Das, S. Application of homotopy analysis method for fractional Swift-Hohenberg equation revisited. Appl. Math. Model. 2012, 36, 3630–3637. [Google Scholar] [CrossRef]
- Khan, N.A.; Khan, N.U.; Ayaz, M.; Mahmood, A. Analytical methods for solving the time-fractional Swift–Hohenberg (S–H) equation. Comput. Math. Appl. 2011, 61, 2181–2185. [Google Scholar] [CrossRef]
- Vishal, K.; Das, S.; Ong, S.H.; Ghosh, P. On the solutions of fractional Swift-Hohenberg equation with dispersion. Appl. Math. Comput. 2013, 219, 5792–5801. [Google Scholar] [CrossRef]
- Arqub, O.A.; Abo-Hammour, Z.; Al-Badarneh, R.; Momani, S. A reliable analytical method for solving higher-order initial value problems. Discret. Dyn. Nat. Soc. 2013, 1–12. [Google Scholar] [CrossRef]
- Arqub, O.A.; El-Ajou, A.; Momani, S. Constructing and predicting solitary pattern solutions for nonlinear time-fractional dispersive partial differential equations. J. Comput. Phys. 2015, 293, 385–399. [Google Scholar] [CrossRef]
- Korpinar, Z.; Inc, M. Numerical simulations for fractional variation of (1+1)-dimensional Biswas-Milovic equation. Optik 2018, 164, 77–85. [Google Scholar] [CrossRef]
- Zhang, Y.; Kumar, A.; Kumar, S.; Baleanu, D.; Yang, X.-J. Residual power series method for time-fractional Schrödinger equations. J. Nonlinear Sci. Appl. 2016, 9, 5821–5829. [Google Scholar] [CrossRef]
- Qurashi, M.M.A.; Korpinar, Z.; Baleanu, D.; Inc, M. A new iterative algorithm on the time-fractional Fisher equation: Residual power series method. Adv. Mech. Eng. 2017, 9, 1–8. [Google Scholar] [CrossRef]
- Bayrak, M.A.; Demir, A. A new approach for space-time fractional partial differential equations by residual power series method. Appl. Math. Comput. 2018, 336, 215–230. [Google Scholar]
- Arafa, A.; Elmahdy, G. Application of residual power series method to fractional coupled physical equations arising in fluids flow. Int. J. Differ. Equ. 2018, 1–10. [Google Scholar] [CrossRef]
- Merdan, M. A numeric–analytic method for time-fractional Swift–Hohenberg (S-H) equation with modified Riemann–Liouville derivative. Appl. Math. Model. 2013, 37, 4224–4231. [Google Scholar] [CrossRef]
- McCalla, S.; Sandstede, B. Snaking of radial solutions of the multi-dimensional Swift-Hohenberg equation: A numerical study. Phys. D 2010, 239, 1581–1592. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Sinelshchikov, D.I. Exact solutions of the Swift–Hohenberg equation with dispersion. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 26–34. [Google Scholar] [CrossRef]
- Li, W.; Pang, Y. An iterative method for time-fractional Swift-Hohenberg equation. Adv. Math. Phys. 2018, 1, 1–13. [Google Scholar] [CrossRef]
- Bakhtiari, P.; Abbasbandy, S.; Gorder, R.A.V. Reproducing kernel method for the numerical solution of the 1D Swift–Hohenberg equation. App. Math. Comput. 2018, 339, 132–143. [Google Scholar] [CrossRef]
- Tchier, F.; Inc, M.; Korpinar, Z.S.; Baleanu, D. Solution of the time fractional reaction-diffusion equations with residual power series method. Adv. Mech. Eng. 2016, 8, 1–10. [Google Scholar] [CrossRef]
- Arqub, O.A. Series solution of fuzzy differential equations under strongly generalized differentiability. J. Adv. Res. Appl. Math. 2013, 5, 31–52. [Google Scholar] [CrossRef]
- Arqub, O.A.; El-Ajou, A.; Bataineh, A.; Hashim, I. A representation of the exact solution of generalized Lane-Emden equations using a new analytical method. Abstr. Appl. Anal. 2013, 2013, 1–10. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).