The Fractal Calculus for Fractal Materials
Abstract
:1. Introduction
2. Preliminaries
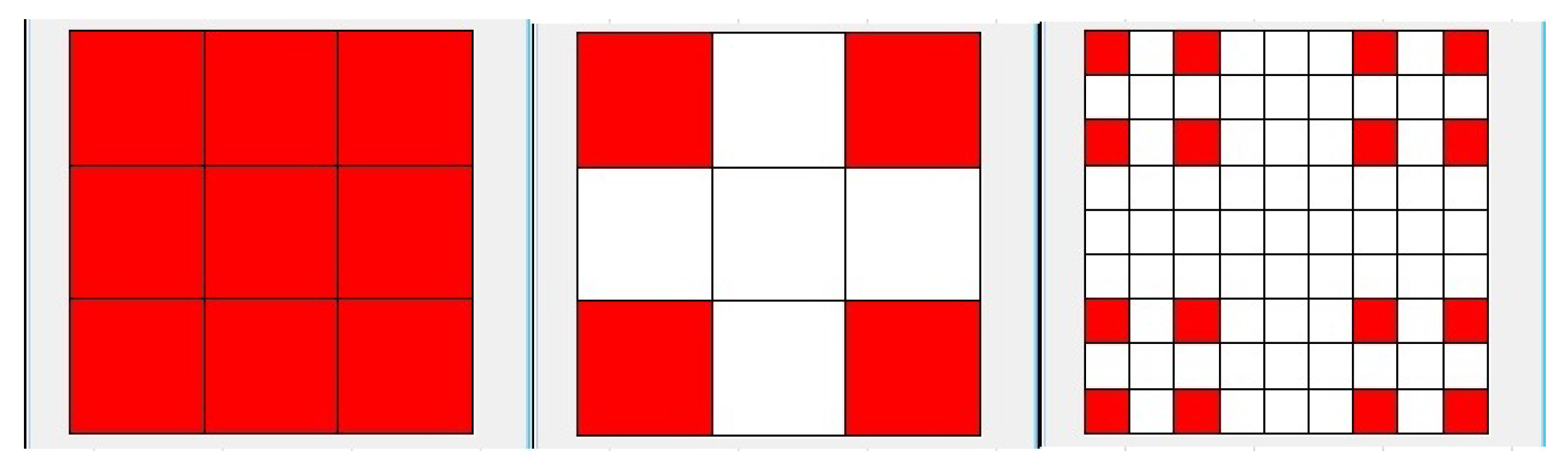
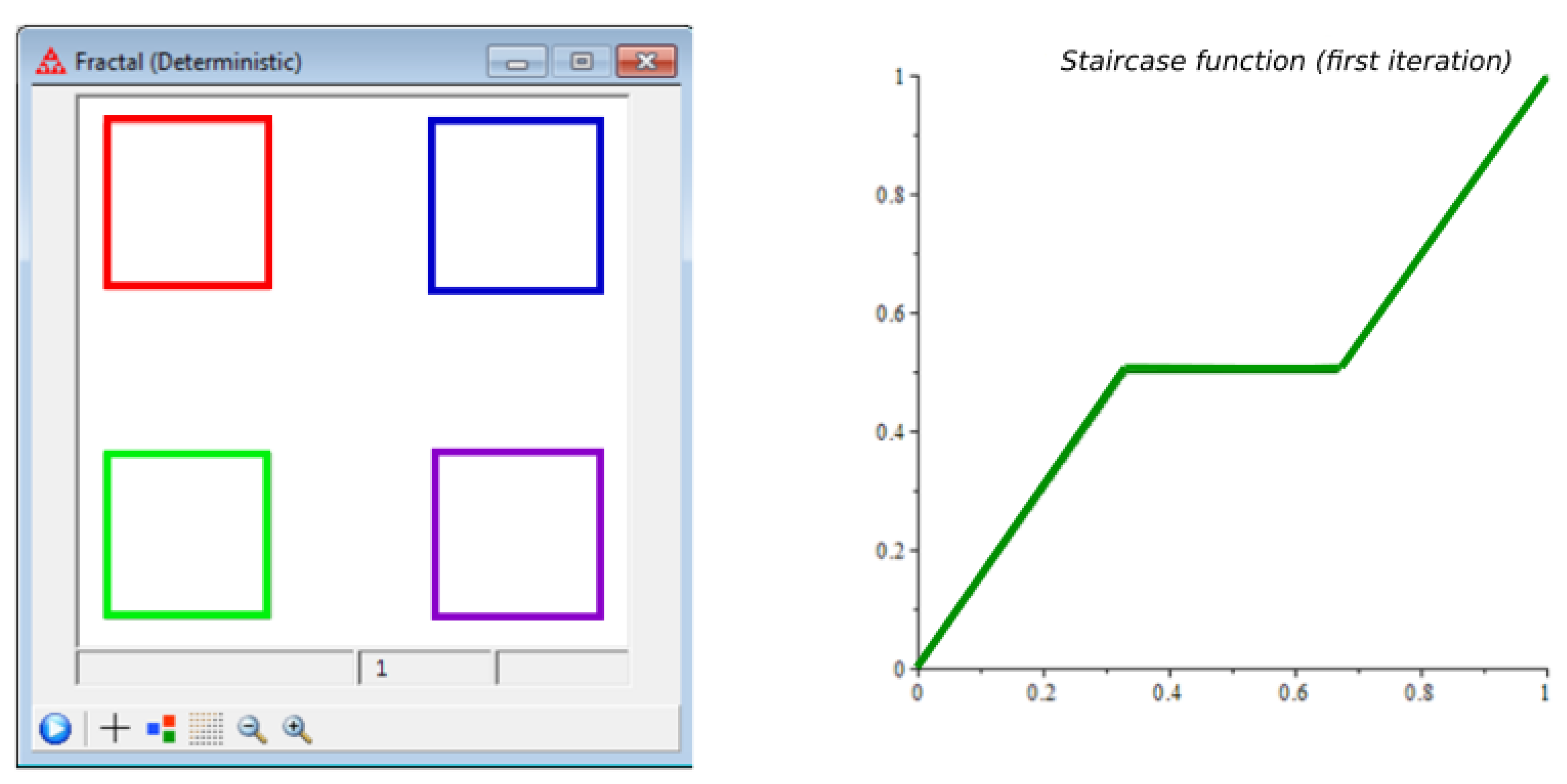
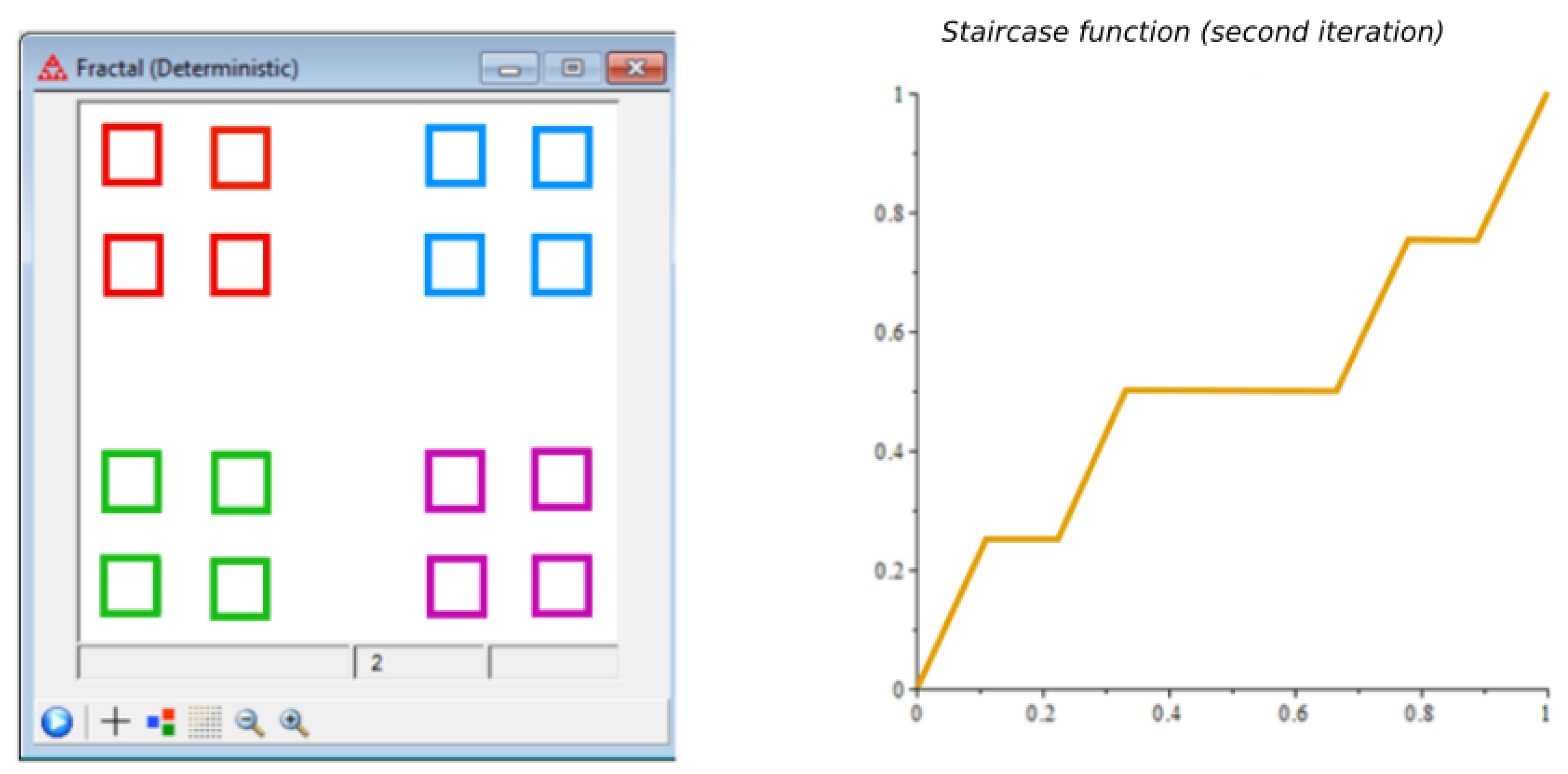
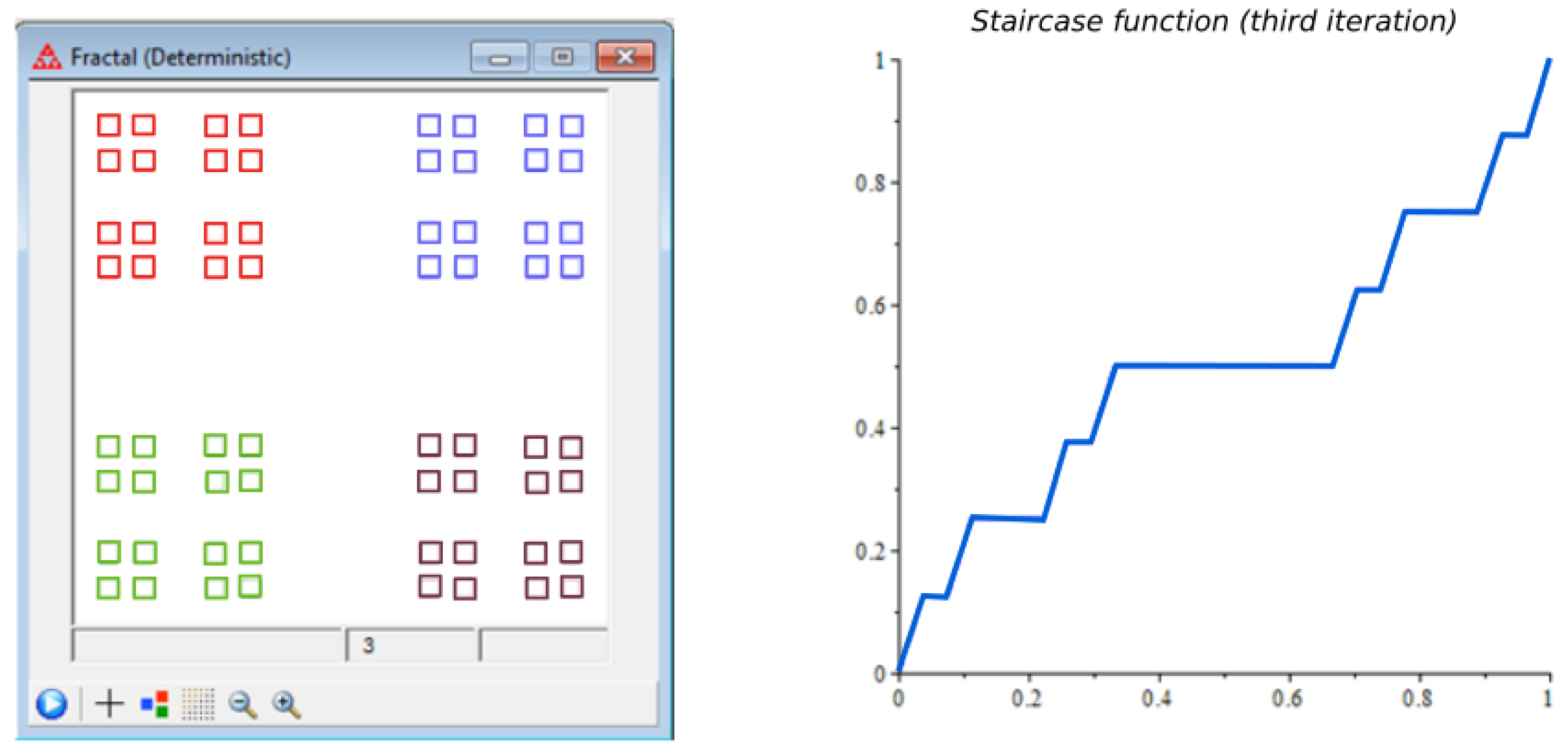
2.1. The Integral Staircase Function on Cantor Cubes
2.2. -Differentiation
3. Results
3.1. Equations of State
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman and Company: New York, NY, USA, 1977. [Google Scholar]
- Falconer, K. Fractal Geometry: Mathematical Foundations and Applications, 2nd ed.; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Peitgen, H.O.; Saupe, D. The Science of Fractal Images; Springer-Verlag: New York, NY, USA, 1988. [Google Scholar]
- Krzysztofik, W.J. Fractal geometry in electromagnetics applications—From antenna to metamaterials. Microw. Rev. 2013, 19, 3–14. [Google Scholar]
- Van Oevelen, T.; Baelmans, M. Numerical topology optimization of heat sinks. In Proceedings of the 15th International Heat Transfer Conference (IHTC-15), Kyoto, Japan, 10–15 August 2014; pp. 1–15. [Google Scholar]
- Yang, X.-J. A Short Note on Local Fractional Calculus of Function of One Variable. J. Appl. Libr. Inf. Sci. 2012, 1, 1–12. [Google Scholar]
- Atangana, A. Fractal-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fractals 2017, 102, 396–406. [Google Scholar] [CrossRef]
- Kolwanka, K.M.; Gangal, A.D. Local Fractional Fokker–Planck Equation. Phys. Rev. Lett. 1998, 80, 214–217. [Google Scholar] [CrossRef]
- Babakhani, A.; Daftardar-Gejji, V. On calculus of local fractional derivatives. J. Math. Anal. Appl. 2002, 270, 66–79. [Google Scholar] [CrossRef]
- Yang, X.J.; Baleanu, D.; Machado, J.A.T. Systems of Navier–Stokes equations on Cantor sets. Math. Probl. Eng. 2013, 2013, 769724. [Google Scholar] [CrossRef]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Springer-Verlag: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Hristov, J. Approximate solutions to fractional subdiffusion equations. Eur. Phys. J. Spec. Top. 2011, 193, 229–243. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations, 1st ed.; Wiley-Interscience: Hoboken, NJ, USA, 1993. [Google Scholar]
- Dos Santos, M.A.F. Non-Gaussian Distributions to Random Walk in the Context of Memory Kernels. Fractal Fract. 2018, 2, 20. [Google Scholar] [CrossRef]
- Tarasov, V.E. Vector calculus in non-integer dimensional space and its applications to fractal media. Commun. Nonlinear. Sci. Numer. Simul. 2015, 20, 360–374. [Google Scholar] [CrossRef]
- Parvate, A.; Gangal, A.D. Calculus on Fractal Subsets of Real Line II: Conjugacy With Ordinary Calculus. Fractals 2011, 19, 271–290. [Google Scholar] [CrossRef]
- Parvate, A.; Gangal, A.D. Fractal differential equations and fractal-time dynamical systems. Pramana 2005, 64, 389–409. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Baleanu, D. Diffraction from fractal grating Cantor sets. J. Mod. Opt. 2016. [Google Scholar] [CrossRef]
- Falconer, K. Techniques in Fractal Geometry; John Wiley & Sons: New York, NY, USA, 1997. [Google Scholar]
- Kigami, J. Analysis on Fractals; Cambridge University Press: Cambridge, UK, 2001; Volume 143. [Google Scholar]
- Parvate, A.; Gangal, A.D. Calculus on fractal subsets of real line—I: Formulation. arXiv, 2003; arXiv:math-ph/0310047. [Google Scholar]
- Stillinger, F.H. Axiomatic basis for spaces with noninteger dimension. J. Math. Phys. 1977, 18, 1224. [Google Scholar] [CrossRef]
- Callen, H.B. Thermodynamics and an Introduction to Themostatics, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1985. [Google Scholar]
- Golmankhaneh, A.K.; Baleanu, D. Heat and Maxwell’s equations on Cantor cubes. Rom. Rep. Phys. 2017, 69, 109. [Google Scholar]
- Golmankhaneh, A.K.; Baleanu, D. Calculus on fractals. In Fractional Dynamics; De Gruyter Open: Basel, Switzerland, 2015; Chapter 18; pp. 307–332. [Google Scholar]
- Dovgosheya, O.; Martiob, O.; Ryazanova, V.; Vuorinenc, M. The Cantor function. Expo. Math. 2006, 24, 1–37. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Baleanu, D. About Maxwell’s equations on fractal subsets of ℝ3. Cent. Eur. J. Phys. 2013, 11, 863–867. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jafari, F.K.; Asgari, M.S.; Pishkoo, A. The Fractal Calculus for Fractal Materials. Fractal Fract. 2019, 3, 8. https://doi.org/10.3390/fractalfract3010008
Jafari FK, Asgari MS, Pishkoo A. The Fractal Calculus for Fractal Materials. Fractal and Fractional. 2019; 3(1):8. https://doi.org/10.3390/fractalfract3010008
Chicago/Turabian StyleJafari, Fakhri Khajvand, Mohammad Sadegh Asgari, and Amir Pishkoo. 2019. "The Fractal Calculus for Fractal Materials" Fractal and Fractional 3, no. 1: 8. https://doi.org/10.3390/fractalfract3010008
APA StyleJafari, F. K., Asgari, M. S., & Pishkoo, A. (2019). The Fractal Calculus for Fractal Materials. Fractal and Fractional, 3(1), 8. https://doi.org/10.3390/fractalfract3010008




