Fractal Image Interpolation: A Tutorial and New Result
Abstract
1. Introduction
2. Iterated Function System
2.1. Fixed Point Theorem
2.2. Partitioned Iterative Function System
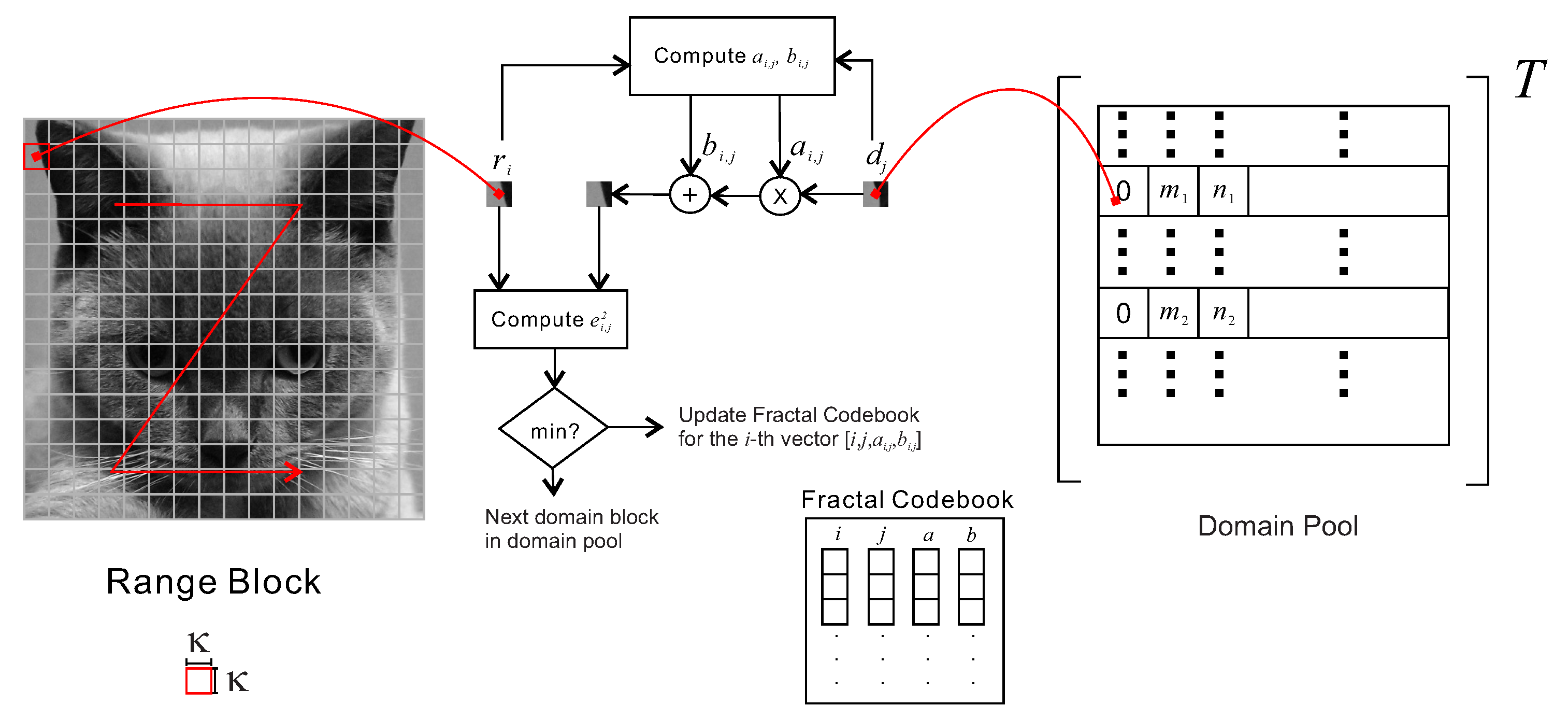
3. Encoding
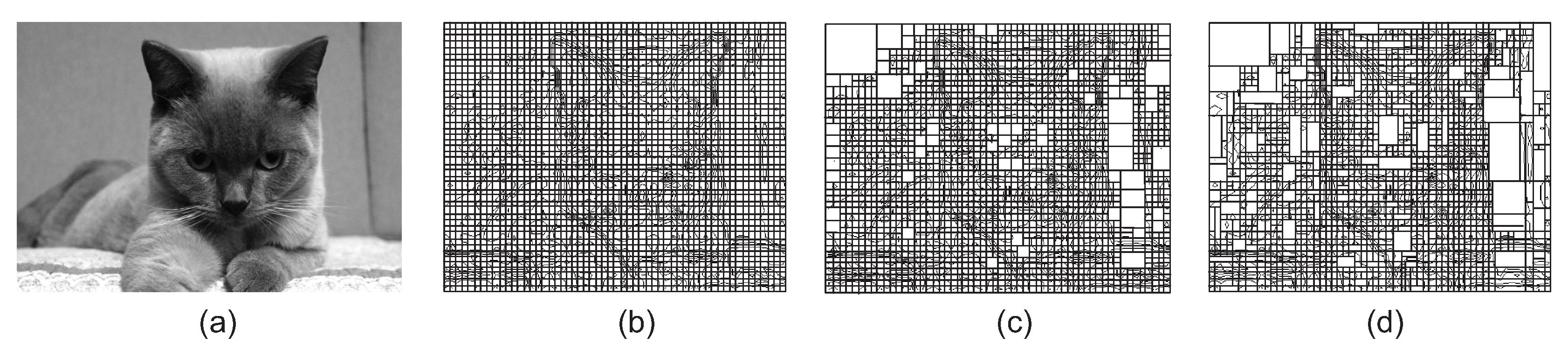
3.1. Range Block Partition
3.2. Domain Block Partition
3.3. Domain Pool Generation
3.4. Grayscale Scaling
4. Decoding
- Constructs the simple domain pool using the down-sampled domain blocks from the previously decoded image. The domain pool generation routine should be the same as that used in the PIFS encoder. Furthermore, if there is no previously decoded image, the “previously decoded image” can be initialized by any image, including the dark image (i.e., all pixels have intensity equal zero). For image interpolation, the initial image can be the original image f, such as to reduce the decoding time (i.e., ).
- Form the i-th range block from the j-th domain block extracted from the initial image with graylevel scaling by a and addition of brightness shift b on each pixel, where the parameters j, a and b are retrieved from the fractal code one-by-one from the codebook and generate the attractor image f, where each range blocks in are generated by applying grayscale scaling a and shifting b to the j-th domain block.
- Glue all the range blocks together to form the fractal decoded image at the k-th iteration.
- If the number of iteration is smaller than a predefined number, and, if the differences between the images in consecutive loops is larger than a specified tolerance, then go back to step 1 for the ()-th fractal decoding iteration using the k-th fractal decoded image as the start image.
Does Size Matter?
5. Decoding with Interpolation
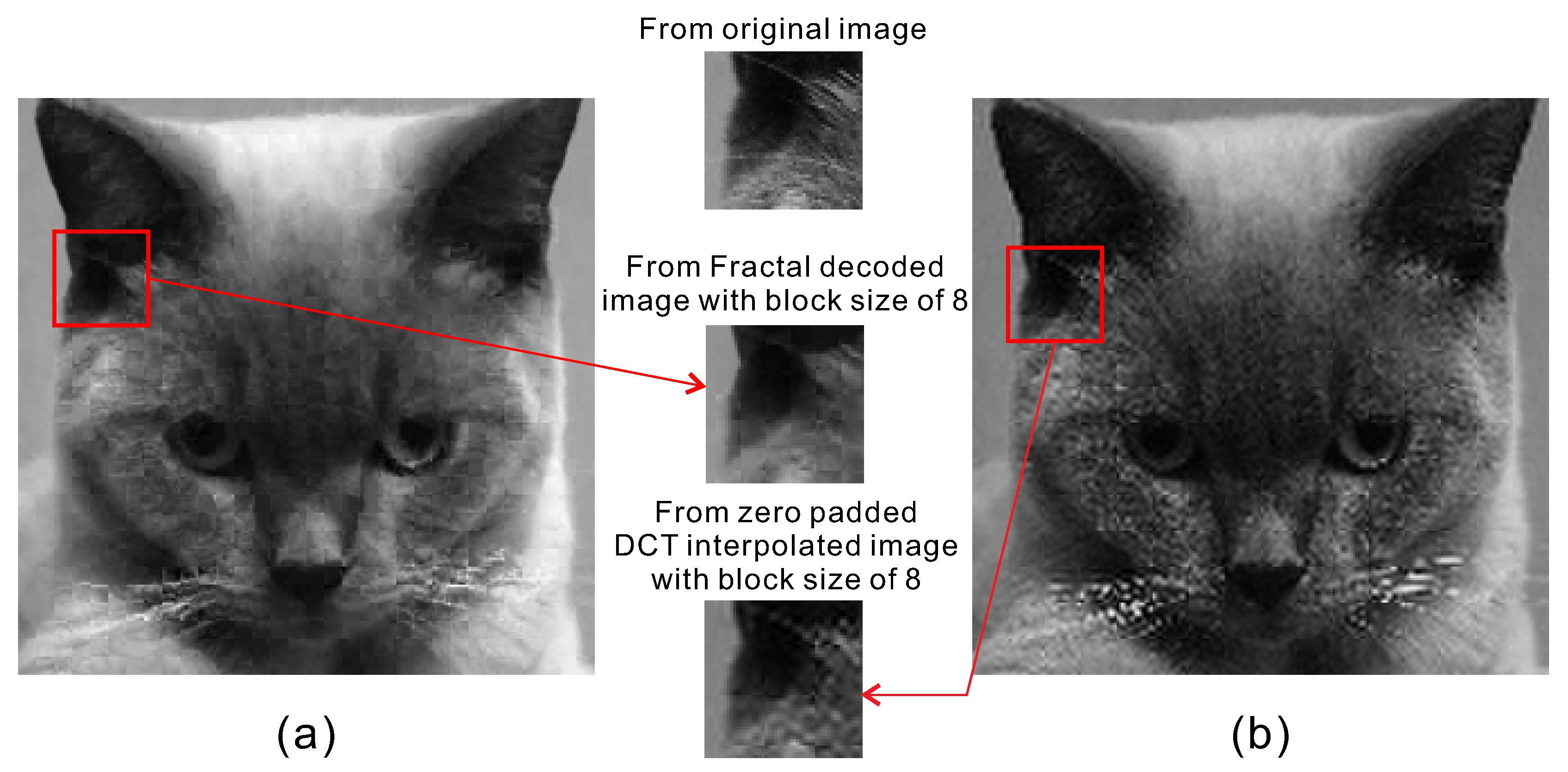
- When edges are well approximated at the original resolution, they are sharp and fairly well preserved in the interpolated image.
- Edges do not always match well at block boundaries.
- The non-fractal blocks are less visually satisfactory, where “notches” are created by non-fractal blocks, which are propagated by iterations onto neighboring blocks.
From Fitting to Interpolation
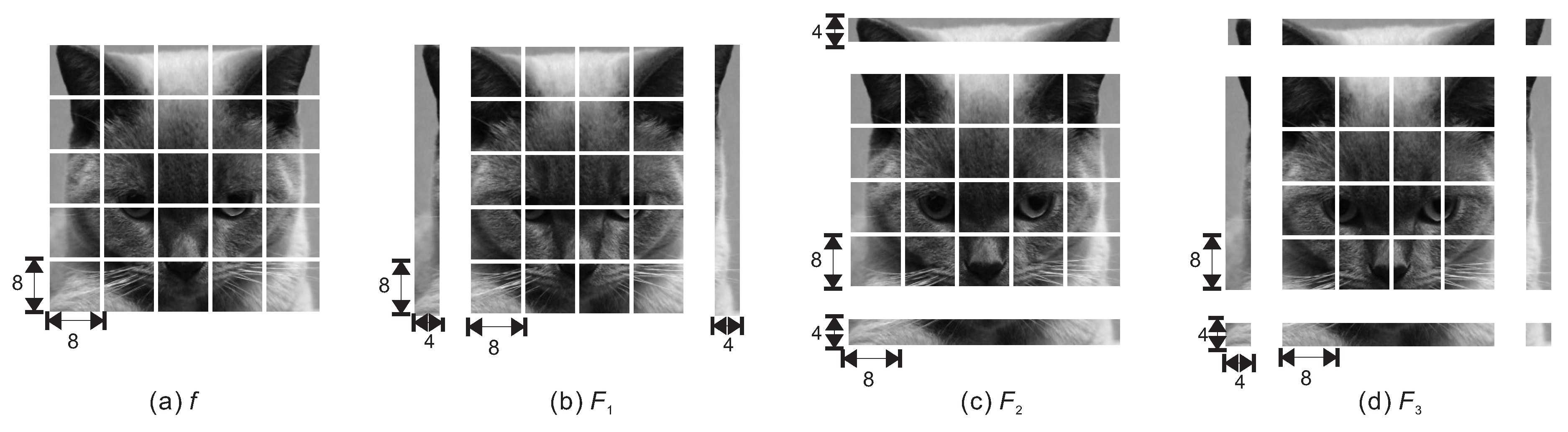
6. Overlapping
7. Conclusions
Author Contributions
Conflicts of Interest
Abbreviations
| IFS | Iterative Function System |
| PIFS | Partitioned Iterative Function System |
| PSNR | Peak Signal to Noise Ratio |
| SSIM | Structural Similarity |
| DCT | Discrete Cosine Transform |
References
- Xu, Y.; Ji, H.; Fermuller, C. Viewpoint invariant texture description using fractal analysis. Int. J. Comput. Vis. 2009, 83, 85–100. [Google Scholar] [CrossRef]
- Wee, Y.C.; Shin, H.J. A Novel Fast Fractal Super Resolution Technique. IEEE Trans. Consum. Electron. 2010, 56, 1537–1541. [Google Scholar] [CrossRef]
- He, S.H.; Wu, Z. Method of Single Image Super-Resolution Enhancement Based on Fractal Coding. In Proceedings of the 3rd International Confernece on Computer Science and Network Technology, Dalian, China, 12–13 October 2013; pp. 1034–1036. [Google Scholar]
- Zhang, Y.; Fan, Q.; Bao, F.; Liu, Y.; Zhang, C. Single-Image Super-Resolution Based on Rational Fractal Interpolation. IEEE Trans. Image Process. 2018, 27, 3782–3797. [Google Scholar] [PubMed]
- Xu, H.; Zhai, G.; Yang, X. Single image super-resolution with detail enhancement based on local fractal analysis of gradient. IEEE Trans. Circuits Syst. Video Technol. 2013, 23, 1740–1754. [Google Scholar] [CrossRef]
- Chaurasia, V.; Gumasta, R.K.; Kurmi, Y. Fractal Image Compression with Optimized Domain Pool Size. In Proceedings of the International Conference on Innovations in Electronics, Signal Processing and Communication, Shillong, India, 6–7 April 2017; pp. 209–212. [Google Scholar]
- Padmashree, S.; Nagapadma, R. Different approaches for implementation of fractal image compression on medical images. In Proceedings of the International Conference on Electrical, Electronics, Communications, Computer and Optimization Techniques, Mysuru, India, 9–10 December 2016; pp. 66–72. [Google Scholar]
- Biswas, A.K.; Karmakar, S.; Sharma, S.; Kowar, M.K. Performance of fractal image compression for medical images: A comprehensive literature review. Int. J. Appl. Inf. Syst. 2015, 8, 14–24. [Google Scholar]
- Ye, R.; Lan, H.; Wu, Q. A fractal interpolation based image encryption scheme. In Proceedings of the IEEE International Conference on Computer and Communication Engineering Technology, Beijing, China, 18–20 August 2018; pp. 291–295. [Google Scholar]
- Liu, M.; Zhao, Y.; Lin, C.; Bai, H.; Yao, C. Resolution-independent up-sampling for depth map using fractal transforms. KSII Trans. Internet Inf. Syst. 2016, 10, 2730–2747. [Google Scholar]
- Banach, S. Sur les operations dans les ensembles abstraits et leur application aux equations integrales. Fundam. Math. 1922, 3, 133–181. [Google Scholar] [CrossRef]
- Hutchinson, J. Fractals and self-similarity. Indiana Univ. J. Math. 1981, 30, 713–747. [Google Scholar] [CrossRef]
- Jacquin, A.E. Image coding based on a fractal theory of iterated contractive image transformations. IEEE Trans. Image Process. 1992, 1, 18–30. [Google Scholar] [CrossRef] [PubMed]
- Barnsley, M.F.; Elton, J.H.; Hardin, D.P. Recurrent iterated function systems. Constr. Approx. 1989, 5, 3–31. [Google Scholar] [CrossRef]
- Fisher, Y. Fractal Image Compression—Theory and Applications; Springer: New York, NY, USA, 1995. [Google Scholar]
- Reusens, E. Overlapped Adaptive Partitioning for Image Coding Based on Theory of Iterated Function systems. In Proceedings of the IEEE Internation Conference on Acoustics, Speech and Signal Processing, Adelaide, SA, Australia, 19–22 April 1994; pp. 569–572. [Google Scholar]
- Davoine, F.; Antonini, M.; Chassery, J.M.; Barlaud, M. Fractal image compression based on Delaunay triangulation and vector quantization. IEEE Trans. Image Process. 1996, 5, 338–346. [Google Scholar] [CrossRef] [PubMed]
- Reusens, E. Partitioning complexity issue for iterated function system based image coding. In Proceedings of the VII-th European Signal Processing Conference, Edinburg, UK, 13–16 September 1994; pp. 171–174. [Google Scholar]
- Kok, C.; Tam, W. Digital Image Interpolation in MATLAB; Wiley-IEEE Press: Hoboken, NJ, USA, 2019. [Google Scholar]
- Lu, N. Fractal Imaging; Academic Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Gharavi-Al., M.; DeNardo, R.; Tenda, Y.; Huang, T.S. Resolution enhancement of images using fractal coding. In Proceedings of the SPICE Visual Communications and Image Processing, San Jose, CA, USA, 10 January 1997; pp. 1089–1100. [Google Scholar]
- Polidori, E.; Dugelay, J.L. Zooming using iterated function systems. Fractals 1997, 5, 111–123. [Google Scholar] [CrossRef]
- Chung, K.H.; Fung, Y.H.; Chan, Y.H. Image enlargement using fractal. In Proceedings of the IEEE International Conference on Acoustic, Speech, and Signal Processing, Hong Kong, China, 6–10 April 2003; pp. 273–276. [Google Scholar]
- Polidori, E.; Dugelay, J.L. Zooming using iterated function systems. In Proceedings of the NATO ASI on Image Encoding and Analysis, Trondheim, Norway, 8–17 July 1995. [Google Scholar]






| n | |||
|---|---|---|---|
| 0 | 1 | 2 | 5 |
| 1 | 3.000000 | 2.250000 | 2.625000 |
| 2 | 2.333333 | 2.236111 | 2.264881 |
| 3 | 2.238095 | 2.236068 | 2.236251 |
| 4 | 2.236069 | 2.236068 | 2.236068 |
| 5 | 2.236068 | 2.236068 | 2.236068 |
| 6 | 2.236068 | 2.236068 | 2.236068 |
| Block Size | ||
|---|---|---|
| Time to Encode | 15 min | 3 min |
| Size of pool | 16 × 62,001 double | 64×58,081 double |
| Fractal Code Size | 0.375 byte/pixel | 0.07 byte/pixel |
| Block Size | Double | Double |
|---|---|---|
| Size of pool | 16 × 62,001 double | 64 × 58,081 double |
| No of Iterations | 30 | 20 |
| Time to decode | 50 mins | 5 mins |
| PSNR | 30.9964 dB | 26.5392 dB |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kok, C.W.; Tam, W.S. Fractal Image Interpolation: A Tutorial and New Result. Fractal Fract. 2019, 3, 7. https://doi.org/10.3390/fractalfract3010007
Kok CW, Tam WS. Fractal Image Interpolation: A Tutorial and New Result. Fractal and Fractional. 2019; 3(1):7. https://doi.org/10.3390/fractalfract3010007
Chicago/Turabian StyleKok, Chi Wah, and Wing Shan Tam. 2019. "Fractal Image Interpolation: A Tutorial and New Result" Fractal and Fractional 3, no. 1: 7. https://doi.org/10.3390/fractalfract3010007
APA StyleKok, C. W., & Tam, W. S. (2019). Fractal Image Interpolation: A Tutorial and New Result. Fractal and Fractional, 3(1), 7. https://doi.org/10.3390/fractalfract3010007





