1. Introduction
The Mandelbrot set, arising from the study of dynamical systems on the complex plane, has been an object of interest ever since its introduction by Robert W. Brooks and Peter Matelski [
1]. With its combination of simplicity of definition and complexity of structure, the set exhibits one of the most classical fractal patterns in mathematics.
The Mandelbrot set gives the set of complex
parameter values c for which the orbit of the initial point
is bounded under iterations of the map
defined by
Definition 1. The Mandelbrot set is the set of complex numbers for which there exists some such that for all , the inequality is satisfied.
The left panel of
Figure 1 shows the Mandelbrot set.
Julia sets, studied by the pioneers of complex dynamics Gaston Julia and Pierre Fatou, are subsets of complex phase space and also exhibit fractal structure.
Definition 2. Fix a polynomial . The filled Julia set associated with f, denoted by , is the set of values for which there exists some such that for all , the inequality is satisfied. The Julia set associated with f, denoted by , is the boundary of .
Julia sets associated with the complex quadratic polynomial
that defines the Mandelbrot set are shown in the center and right panels of
Figure 1. These examples illustrate a surprising connection of a topological nature between Mandelbrot and Julia sets given by the dichotomy theorem.
Dichotomy Theorem. The Mandelbrot set parameterizes the connectedness of filled Julia sets: The filled Julia set is connected if c is in the Mandelbrot set and totally disconnected otherwise.
For the examples of
Figure 1, the choice
for the center panel lies in the Mandelbrot set, and the Julia set is connected; whereas the choice
for the right panel lies outside the Mandelbrot set, and the Julia set is totally disconnected. A discussion and proof of this significant result in complex dynamics may be found in [
2]. The dichotomy theorem showcases the idea of viewing
as both the
parameter space and the
dynamical plane for a dynamical system.
Given the rich results for iterations of quadratic maps on the complex plane, it is natural to wonder about the behavior of dynamics on a less well-known, but also very useful sibling of the complex numbers, the hyperbolic numbers,
[
3]. This number system has connections to diverse topics such as general relativity, differential equations, and the study of abstract algebras [
4,
5].
The first to explore a hyperbolic number analog to the hyperbolic numbers (under the name of
perplex numbers) was Senn [
6], who in 1990 performed numerical experiments revealing that the hyperbolic analog to the Mandelbrot set has a completely different character from the (complex) Mandelbrot set. For the quadratic map
, for
, Senn’s simulations indicated that the set of values of
c for which the orbit
is bounded consists of a square with one of its diagonals on the real axis between
and
. Artzy [
7] and Metzler [
8] independently proved this conjecture. Artzy further showed that Julia sets for quadratic maps with the constant
c in the hyperbolic Mandelbrot set are connected, rectangular sets. This suggests that the dichotomy theorem may also hold for hyperbolic quadratic maps. Artzy states that the hyperbolic Julia set is disconnected for values of
c outside of the Mandelbrot set. Fishback [
9] describes, with reference to Artzy [
7], these disconnected hyperbolic Julia sets as being stretched Cantor sets or products of Cantor sets. Proofs or explicit descriptions of these disconnected hyperbolic Julia sets are, however, not found in [
7] or [
9].
In this paper, we provide explicit descriptions, with proofs, for Julia sets over
. Hyperbolic Julia sets turn out to have one of four characteristics: they may be empty, the product of intervals, the product of a Cantor set and an interval, or the product of two Cantor sets. Our main result is a wall-and-chamber decomposition of the hyperbolic plane, which gives the regions of the parameter space that give rise to each of these types of Julia sets. This clarifies the results and statements of [
7,
9] by providing an explicit statement and proof of the hyperbolic-number analog to the dichotomy theorem:
Quadchotomy Theorem. The hyperbolic Mandelbrot set parameterizes the connectedness of filled hyperbolic Julia sets.
The quadchotomy theorem is stated explicitly as Theorem 2.
Structure of the Paper
In
Section 2, we provide an introduction to the hyperbolic numbers, emphasizing characteristic coordinates.
Section 3 explicitly defines the hyperbolic Mandelbrot and Julia sets (slightly differently from Artzy [
7] in the choice of a hyperbolic analog of boundedness). We give an explicit description of the former, mirroring the results of Artzy [
7] and Metzler [
8]. The main result, the quadchotomy theorem, is proven in
Section 4.
2. Hyperbolic Numbers
The
hyperbolic numbers , sometimes called
perplex numbers, motor variables, split-complex numbers, Lorentz numbers, Minkowski numbers, or a variety of other names, can be understood in several contexts [
3,
4,
5,
10]. Algebraically,
can be identified with the ring
, where we call
the image of
t in the quotient. Hence, they are abstractly isomorphic to
as a module over
, with generators 1 and
. In analogy to the complex numbers, we write
for
, where
, but
.
Seen as a module over , hyperbolic numbers admit an automorphism, which acts trivially on the component generated by 1, called hyperbolic conjugation. If , the hyperbolic conjugate is . Hyperbolic conjugation shares properties with complex conjugation; , , and .
We will refer to
as the
hyperbolic plane in analogy to the complex plane; our usage is entirely distinct from the geometric notion of the plane equipped with a hyperbolic metric, which would typically be modeled with the Poincaré disk or upper half plane. Indeed, the hyperbolic numbers are equipped with a quadratic form, but it does not give rise to a metric or norm. Instead, if
,
Representing the hyperbolic number
as the matrix:
and addition
and multiplication
correspond respectively to matrix addition and multiplication. The matrix approach reveals the natural
characteristic coordinates and
with which to work with hyperbolic numbers, as noted by Fishback [
9]. Representing a hyperbolic number in characteristic coordinates as
the hyperbolic multiplication
is simply
In addition, the quadratic form has a simple form in characteristic coordinates:
The sets and in the hyperbolic plane where either characteristic coordinate vanishes form the axes of the characteristic coordinate system. Note that and are closed under addition and multiplication.
3. The Hyperbolic Mandelbrot Set
The simple representation of multiplication for hyperbolic numbers in characteristic coordinates gives rise to hyperbolic Mandelbrot and Julia sets that contrast significantly with the classical Mandelbrot and Julia sets of complex numbers. Our definitions for hyperbolic Mandelbrot and Julia sets closely follow the corresponding definitions over . If is a function, we again write , , etc.
Definition 3. For each , consider the map The hyperbolic Mandelbrot set is the set of values for which there exists some such that for all , the inequality is satisfied.
Definition 4. Fix a polynomial . The hyperbolic filled Julia set associated with f, denoted by , is the set of values for which there exists some such that for all , the inequality is satisfied. The hyperbolic Julia set associated with f, denoted by , is the boundary of .
The quantity
is equal to zero on the characteristic axes
, and therefore, the bound
automatically holds on these sets even though the real and hyperbolic components of
may be limited to infinity. Artzy [
7] makes a different choice in the definition of the hyperbolic Julia set in that he bounds the real and hyperbolic parts.
The similarities in definition to the complex case lead to several of the same immediate results. We will use the fact that, as for the complex Mandelbrot set [
2],
is invariant under conjugation. We note as well that since both complex and hyperbolic conjugations fix
, we must have
.
Remark 1. The two definitions are in many ways similar, but the Mandelbrot set is a subset of parameter space, whereas a Julia set is said to lie in the dynamical plane. Theorem 2 makes the connection between and explicit for f quadratic.
Key to determining the hyperbolic Mandelbrot and Julia sets is the observation that in characteristic coordinates, the map
decouples into the real quadratic map
on each coordinate. Indeed,
can be written as
or, writing
as a function characteristic coordinates,
where
and
are representations of the constants in characteristic coordinates. In characteristic coordinates, the map decouples into a map on each coordinate, so that under iteration, we have
The map
(for
), whose behavior is well known [
2], is therefore key to finding hyperbolic Julia sets.
For
, the behavior of the dynamical system
may be understood by a change of coordinates to the well-known logistic map. Writing
the dynamical system
becomes the logistic dynamical system
for
.
The case corresponds to , for which all orbits of the logistic map diverge to infinity except for points in a Cantor set. For , the Cantor set is contained in , where . For , this translates to a Cantor set contained in , where . Note that for , , so the Cantor set for is bounded away from zero.
The case corresponds to , for which orbits of the logistic map are bounded for and diverge to infinity otherwise. That is, for , the orbit is bounded if and only if . In this case, the fixed points are ; there is a fixed point equal to zero only for .
That is empty for may be seen as follows: For any , the minimum value of is . Thus, for any and positive integer n, ; . It follows that for , as .
In summary, we have the following:
Lemma 1. Let for . Then, the intersection is
- (i)
a Cantor set not containing zero if ,
- (ii)
the interval if ,
- (iii)
empty if .
The decoupling of the characteristic coordinates endows
with a much simpler structure than
, as detailed in the next theorem, due to Artzy and Metzler [
7,
8].
Theorem 1. Let S be the square given byand let be the union of the diagonals in . Then, . Proof. We need to determine the values of
c for which
is bounded as
n approaches infinity. The expression (
3) for iterates of the map
in characteristic coordinates allows us to write
According to Lemma 1,
are bounded for (and only for)
. Thus,
is bounded for
.
It could also be the case that, without loss of generality, , but in a manner so that their product is bounded. Since only for , such cases occur only for on the union D. D is, in fact, in : Since and are closed under addition and multiplication, the restrictions are well defined. However, since for all , we have that . □
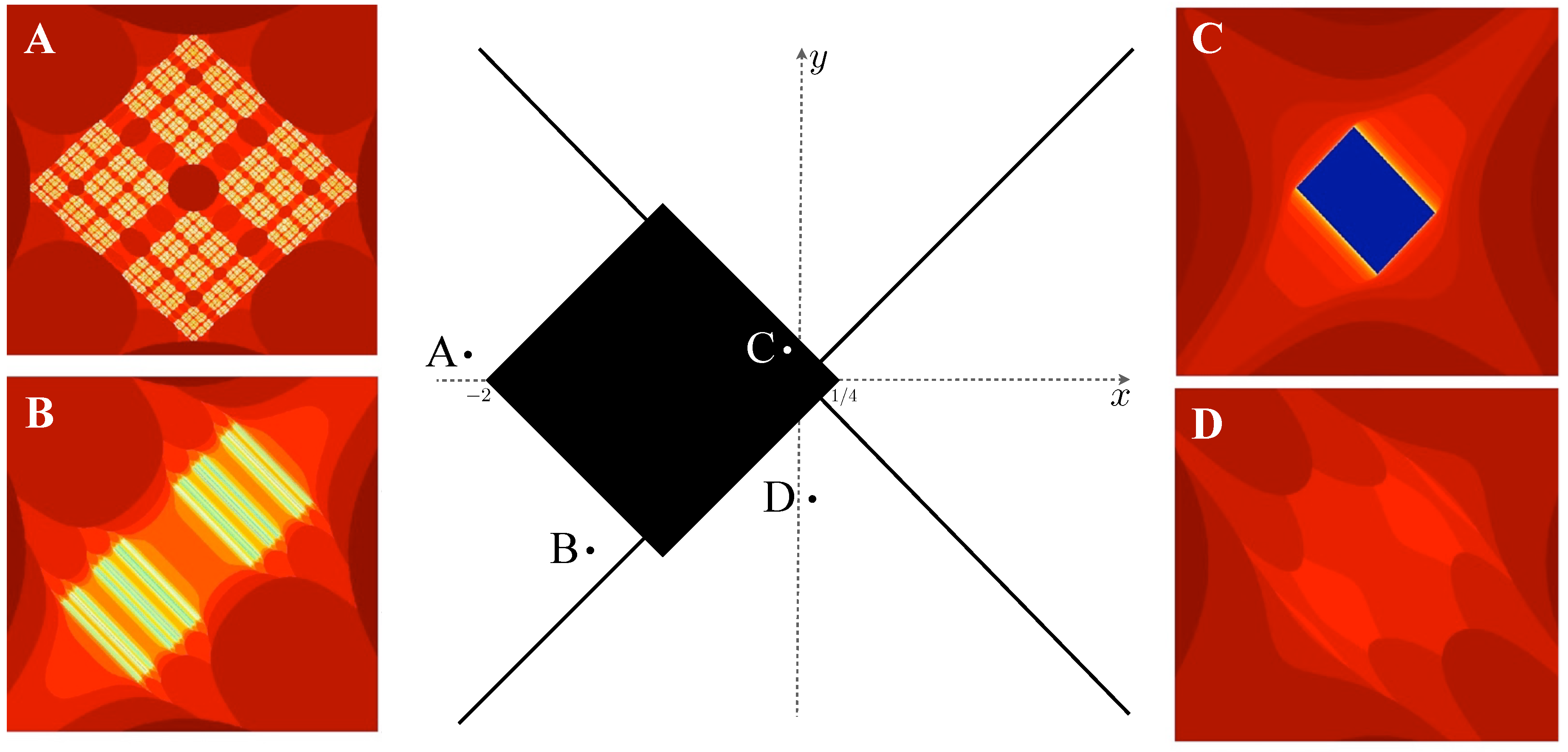
The center panel of
Figure 2 depicts the hyperbolic Mandelbrot set.
Remark 2. As implied by Theorem 2 below, the fact that the part of D outside of S is in the Mandelbrot set is largely an artifact of the fact that and are ideals of .
4. Hyperbolic Julia Sets
Over the complex numbers, determines the points in parameter space that correspond to connected Julia sets. One may ask if performs the analogous role for the hyperbolic numbers. The positive answer may be given more nuance, as as a parameter space admits a wall-and-chamber decomposition based on the form of , in which is the chamber corresponding to connectedness of nonempty filled Julia sets. We now develop this decomposition explicitly.
Proposition 1. For , let be its description in characteristic coordinates, and let . Write and . For , the filled hyperbolic Julia set is equal to the Cartesian product of and .
Proof. Let
in characteristic coordinates. By equation
,
=
. According to the discussion leading to Lemma 1,
only for
. For
, there is a
such that
for all
n if and only if there is some
such that for all
n ,
. However, since
, we have
if and only if
,
. We conclude that, for
,
□
Examples of filled hyperbolic Julia sets are shown in the side panels of
Figure 2. The filled hyperbolic Julia sets may be totally disconnected (Panel A), connected but not totally disconnected (Panel B), connected and nonempty (Panel C), or empty (Panel D). These examples represent the decomposition of
stated in the following analog to the dichotomy theorem of complex Mandelbrot and filled Julia sets and depicted in
Figure 3:
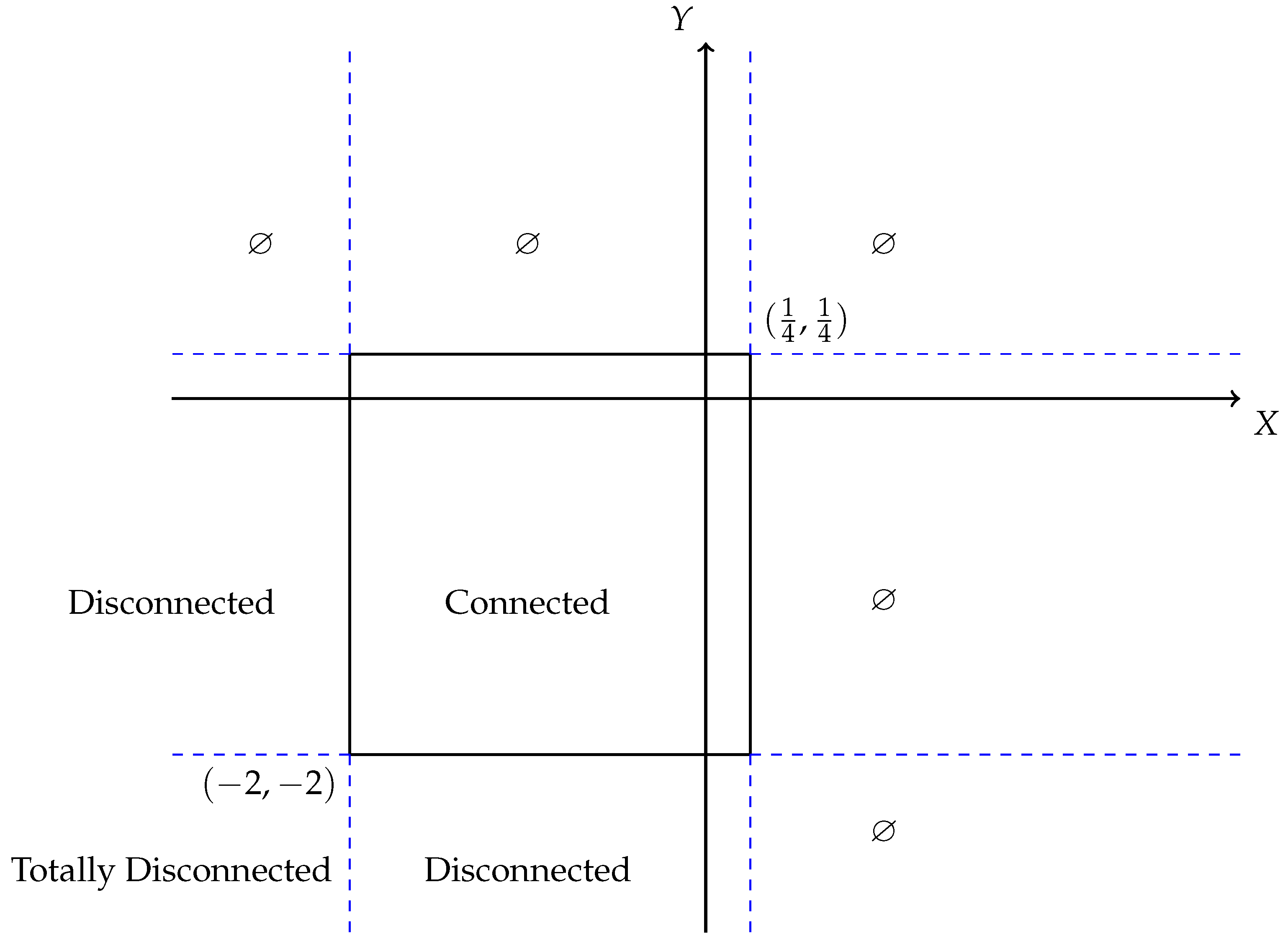
Theorem 2 (Quadchotomy). For , let , and let in characteristic coordinates, with . Then, admits a wall-and-chamber decomposition as follows:
- (i)
if , then is nonempty and connected;
- (ii)
if one of is in and the other is less than or equal to , then is disconnected;
- (iii)
if , then is totally disconnected;
- (iv)
otherwise, is empty.
Proof. By Proposition 1, we need to understand and , which are given in Lemma 1.
Part (i): When , , and and are both simply connected and conjugate-invariant. Thus, and are both connected, so is as well.
Part (ii): In this case, exactly one of or is connected; the other is a Cantor set. The product of a Cantor set and a connected set is a disconnected set.
Part (iii): Both and are Cantor sets, which are totally disconnected, and the product of two totally disconnected sets is again totally disconnected.
Part (iv): By Lemma 1, at least one of or is empty, so their product is as well. □
We ignored the characteristic axes in Theorem 2. We compute their Julia sets as follows: If, say, , then . The ratio of to is , for If is unbounded, then so is this ratio since approaches infinity with x. That is, for , the filled Julia set is empty. For , the Julia set is the product for a Cantor set contained in .