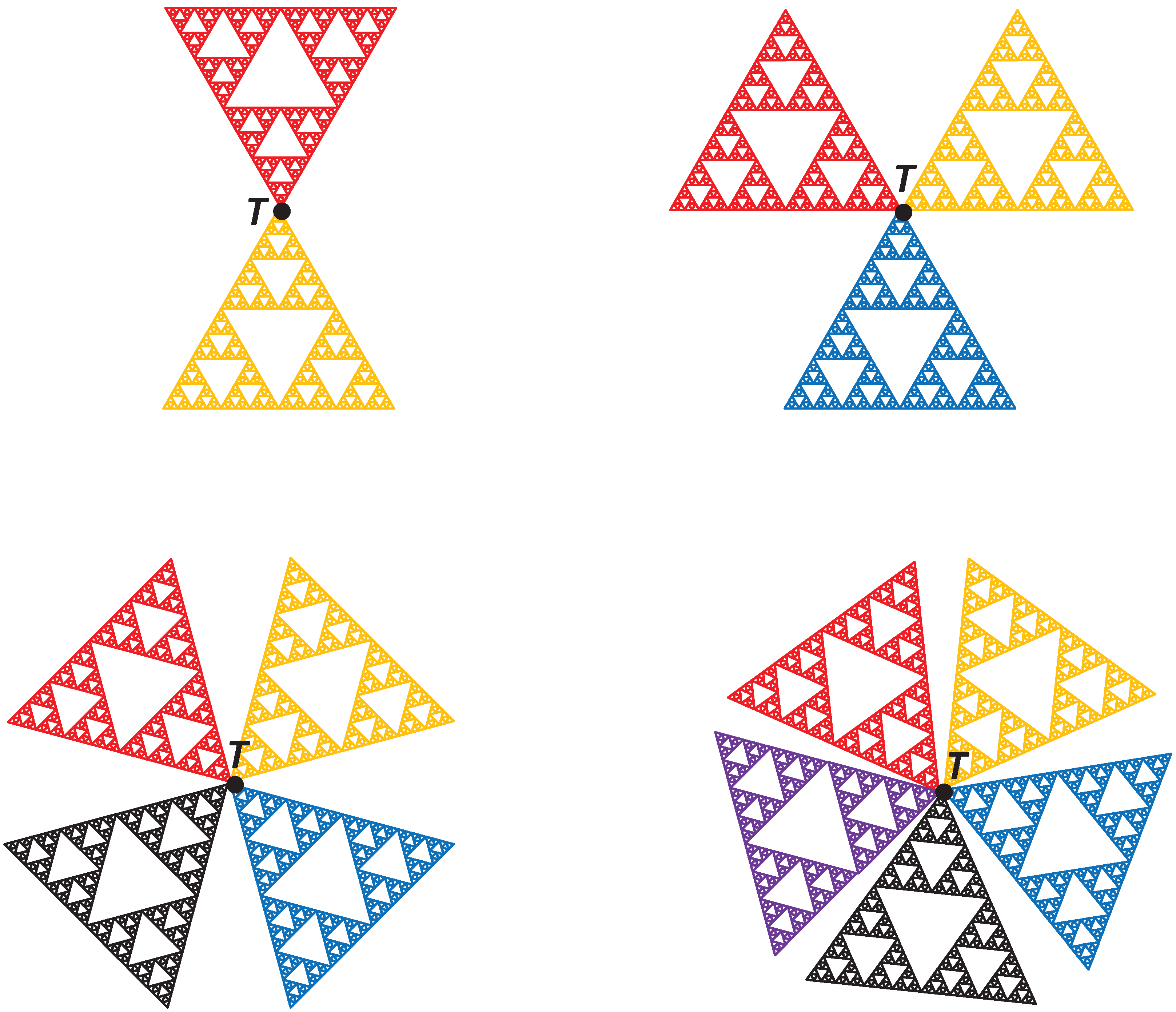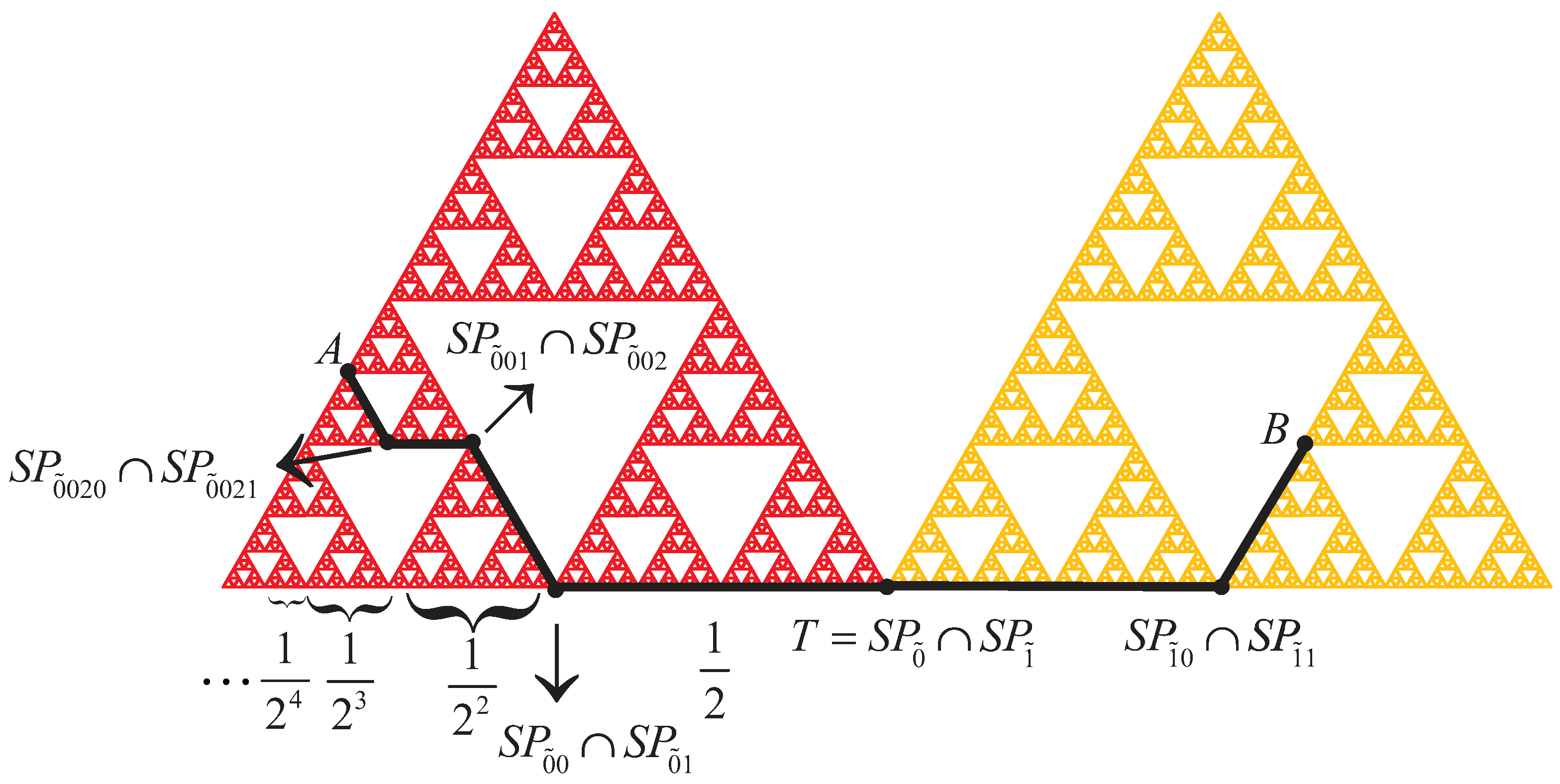1. Introduction
Fractal geometry is one of the most remarkable developments in mathematics in recent years. Since fractals are central to apprehending a wide array of chaotic and nonlinear systems, they have many applications in physics, chemistry, biology, computer science, engineering, economics and so on (for details, see [
1,
2,
3,
4]). One of the common properties of fractals is self-similarity. A geometric shape is self-similar if there is a point such that every neighborhood of the point contains a copy of the entire shape and, if it is self-similar at every point, then it is called strictly self-similar. For example, the Sierpinski gasket, the Cantor set, the Koch curve and the Sierpinski carpet are strictly self-similar sets (for details, see [
5]). There have been different studies on these fractals since the 1970s. Defining the intrinsic metric on these sets is one of them [
6,
7,
8,
9,
10,
11]. In [
12], the intrinsic metric on the code set of the Sierpinski gasket, which is one of the instructive examples of strictly self-similar sets, is formulated by the code representations of its points. Due to this metric formula, important geometrical and topological properties of the Sierpinski gasket are expressed by the code sets, the number of geodesics are determined and the code representations of points are classified according to the number of geodesics (for details, see [
13,
14,
15]). As seen in these studies, defining the intrinsic metrics by using the code representations of the points on fractals provides some facilities for different works. Hence, our aim is to increase such examples in the literature.
In this paper, we define two new fractals which are self-similar but are not strictly self-similar and then we determine the code representations of points on these fractals. To this end, we first constitute a model by using three classical Sierpinski gaskets with edge length one. We also express code representations of the points on this structure. In Theorem 2, we define the intrinsic metric on this structure and present some geometrical properties on its code set in Propositions 3 and 4. Finally, we formulate the intrinsic metric on a second fractal obtained by two right Sierpinski gaskets in Proposition 5. As seen in Examples 1 and 3, one of the advantages of these intrinsic metric formulas is to calculate the distance between the points on these sets easily.
2. The Intrinsic Metric on the Code Set of the Sierpinski Gasket
It is well known that the intrinsic metric on a set
X is defined as
for
(see [
16]). By using the code representations of the points, to express the intrinsic metrics on fractals is a valuable problem, but it is not easy to obtain these formulas for every self-similar set. Therefore, the Sierpinski gasket (
S) is regarded as one of the fundamental models which define the intrinsic metric formulas on fractals (for details, see [
12]). It is well known that the attractor of the iterated function system
such that
is the Sierpinski gasket with the vertices
and
. That is,
Note that, if these coefficients are taken as
and
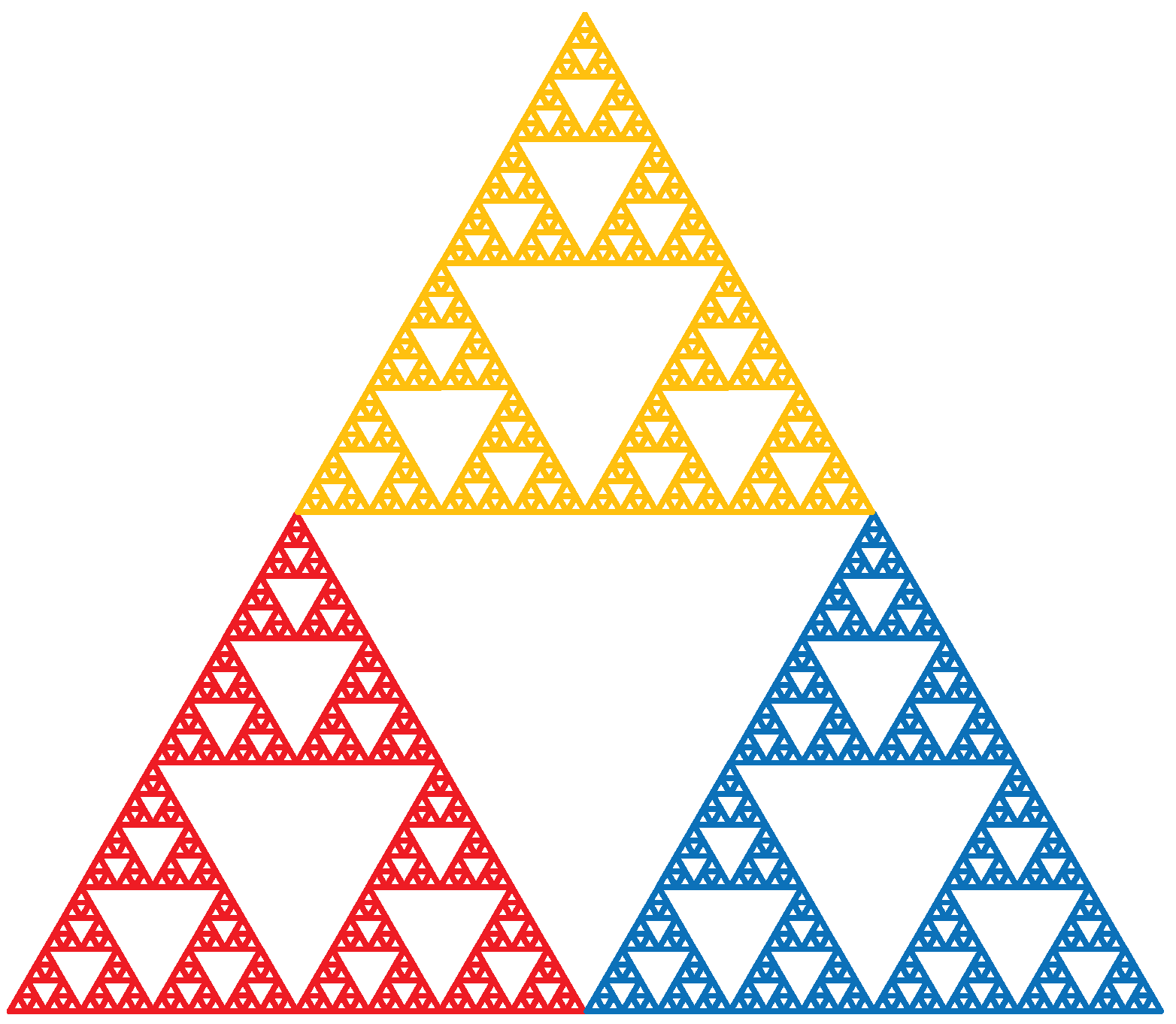
, then the attractor of the iterated function system is the classical Sierpinski gasket (see
Figure 1). In the case of
and
, the so-called right Sierpinski gasket is then obtained as the attractor of the iterated function system.
The intrinsic metric on the code set of the scalene Sierpinski gasket with the vertices
and
is formulated in [
15] as follows:
Let for and where for . If the code representations points A and B on this set are and respectively, then the intrinsic metric formula is defined as follows:
Theorem 1 (15], Theorem 1) Let and andThen, the formulasuch thatgives the length of the shortest path between the points A and B on the scalene Sierpinski gasket. Remark 1. The intrinsic metric formula on the right Sierpinski gasket is defined as follows:such thatandThe intrinsic metric formula on the classical Sierpinski gasket is obtained bywhere(for details, see [12,15]). 3. The Code Representations of Points on the Sierpinski Propellers
Let us first consider identical classical Sierpinski gaskets whose colors are red, yellow, blue, black and purple. As seen in
Figure 2, we combine
m copies of the identical classical Sierpinski gaskets (for
, respectively) at one touching point
T. Note that these shapes are similar to a propeller. Thus, we call these new structures as the Sierpinski propeller (briefly
). Since the fractal dimension of the Sierpinski gasket is
, the fractal dimensions of the Sierpinski propellers are also
. Moreover, the areas of these sets are 0.
The Sierpinski gasket is a strictly self-similar. Although the Sierpinski propellers are self-similar, they are not strictly self-similar. It can easily be seen that T is a special point since every neighborhood of this point contains the scaled copies of the Sierpinski propellers (see
Figure 3 and Proposition 4).
In this section, we only express the code representations of points on the classical Sierpinski propeller for
and we define the intrinsic metric on the code set of this fractal in
Section 4. The intrinsic metric formulas and the code sets of the classical Sierpinski propellers for
can be similarly obtained. Note that the intrinsic metric formula can be expressed more simply for
when a different code representation is used (see Remark 4). However, the following method can be more convenient for the proofs in cases of
and
(the numbers of the code representations of the point
T are 4 and 5, respectively).
Let us denote the red Sierpinski gasket, the yellow Sierpinski gasket and the blue Sierpinski gasket of the Sierpinski propeller by
and
, respectively. It is obvious that
and
Let us state the left-bottom part, the right-bottom part and the upper part of
by
and
, respectively, where
. The smaller triangular pieces of
are denoted by
where
and
We thus obtain
and for a sequence of nested sets
, the Cantor intersection theorem states that the infinite intersection of these sets contains exactly one point:
We denote the point
by
where
and
for
.
The following proposition shows that the points on the Sierpinski propeller have the code representations different from the code representations of points on the Sierpinski gasket:
Proposition 1. The Sierpinski propeller has points whose numbers of the code representations are 1, 2 or 3. Moreover, the point T is the unique point whose number of the code representations is 3.
Proof. T is the unique point which has three code representations such that
,
and
since all of the set sequences
and
contain the point
Note that, for
, if
A is the intersection point of any two sub-triangles in the same level of
, then
A has two different representations such that
and
where
. Otherwise, the code representation of A is unique. □
In
Figure 4, it can be seen that the set of code representations of points on the red Sierpinski gasket is
the set of code representations of points on the yellow Sierpinski gasket is
and the set of code representations of points on the blue Sierpinski gasket is
Generally, the sub-triangles of
for
are expressed as
In addition, the code sets of the Sierpinski propellers are
where
for
4. The Construction of the Intrinsic Metric on the Code Set of SP
In the following theorem, we formulate the intrinsic metric on by using the code representations of its points.
Theorem 2. Suppose that the code representations of the points A and B on the Sierpinski propeller are and respectively such that for and where and for
(i)If , then the shortest distance between A and B is determined bysuch that(ii)If , then Equation (4) gives the desired distance. Proof. (i) Suppose that A and B are two different points of the Sierpinski propeller with the code representations and , respectively, where . It is clear that the shortest path between A and B must pass through the point T since .
Firstly, let us consider the case of
and
(the other cases are done similarly). If
or
, then the shortest path between
A and
T must pass through the points
or
respectively. These points have the code representations
(equivalently
) or
(equivalently
), respectively. Furthermore,
T and
(similarly
T and
) are the points which are the vertices in the sub-triangle
of the Sierpinski gasket. Hence, the length of the shortest path between these points is
. We compute the length of the shortest path between
A and
T as
if the code representations of
A are
(equivalently
) or
(equivalently
). If
and the code representations of
A are not
and
, then the length of the shortest path between
A and
T is less than
. Consequently, in (
5), we get
if
or
and we get
if
.
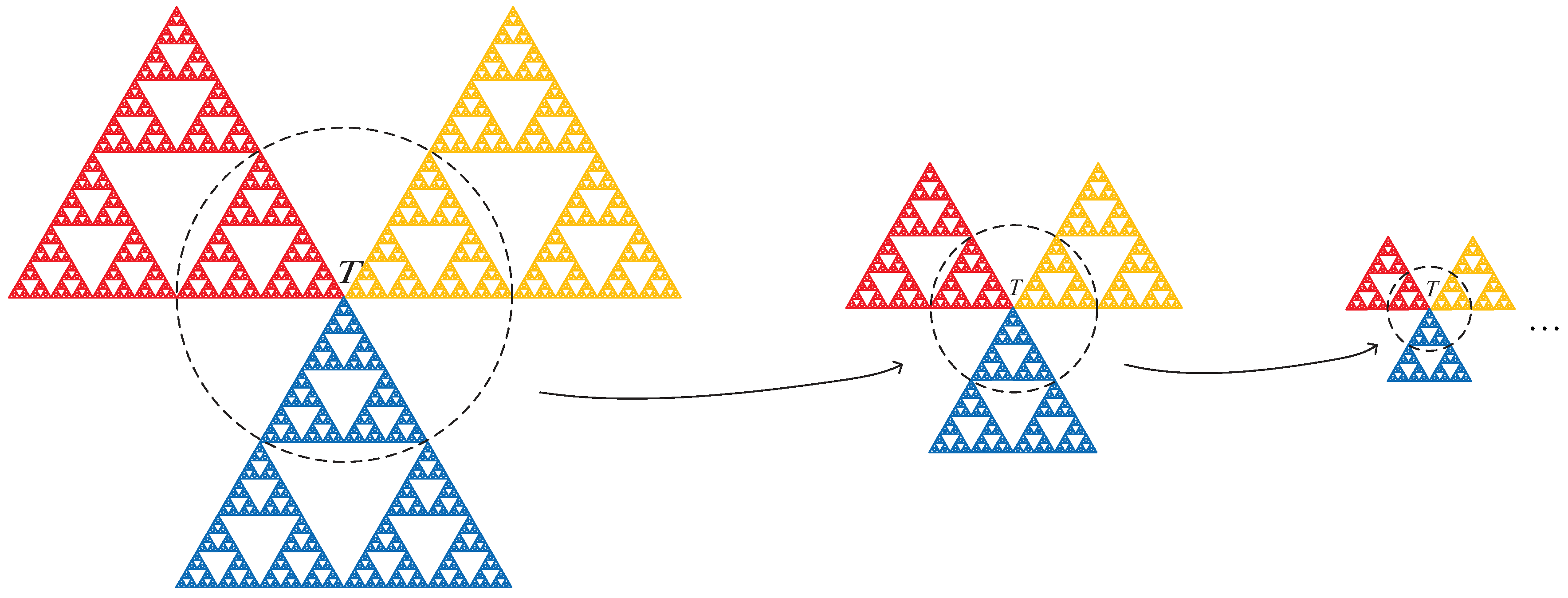
Now, consider
and let us take
or
(see
Figure 5). Then, the shortest path between
A and
must pass through
or
, respectively. Note that these intersections have the code representations
(equivalently
) or
(equivalently
), respectively. In addition,
and
(similarly
and
) are the points that are the vertices in the sub-triangle
of the Sierpinski gasket. Thus, the length of the shortest path between these points is
. We compute the length of the shortest path between
A and
T as
if the code representations of
A are
or
. If
and the code representations of
A are not
and
, then the length of the shortest path between
A and
T is less than
. Consequently, in (
5), we get
if
or
and we get
if
. Generally, for
, we obtain
if
or
and we get
if
. A similar procedure is also valid for the computation of the length of the shortest path between the points
T and
B. □
Remark 2. The point T has three code representations such as , and . Due to Formula (5), it is easily seen that the distance (which is computed by using different codes of this point) is 0. Thus, using a similar method given in [12], the following proposition can be proven. Proposition 2. The metric d defined in Theorem 2 does not depend on the choice of the code representations of the points.
Example 1. Assume that A and B are the points of whose code representations are and , respectively. For the computation of , we must use Formula (8) owing to the fact that the first terms of the code representations of A and B are and respectively. Thus, we getand Proposition 3. If d is the intrinsic metric defined in (5) on , thenMoreover, if and only if the code representations of A are an element of the set and the code representations of B are an element of the sets or , or if the code representations of A are an element of the set and the code representations of B are an element of the sets or . Proof. For the computation of the maximum value of the distances between any two points
A and
B of
,
and
must be 1 for
(see Formula (
5)). Thus, if
and
, then
and
or if
and
, then
and
for
(see Formulas (
6) and (
7)). In addition, if
and
, then
and
(see Formula (
8)). In these cases, we obtain
□
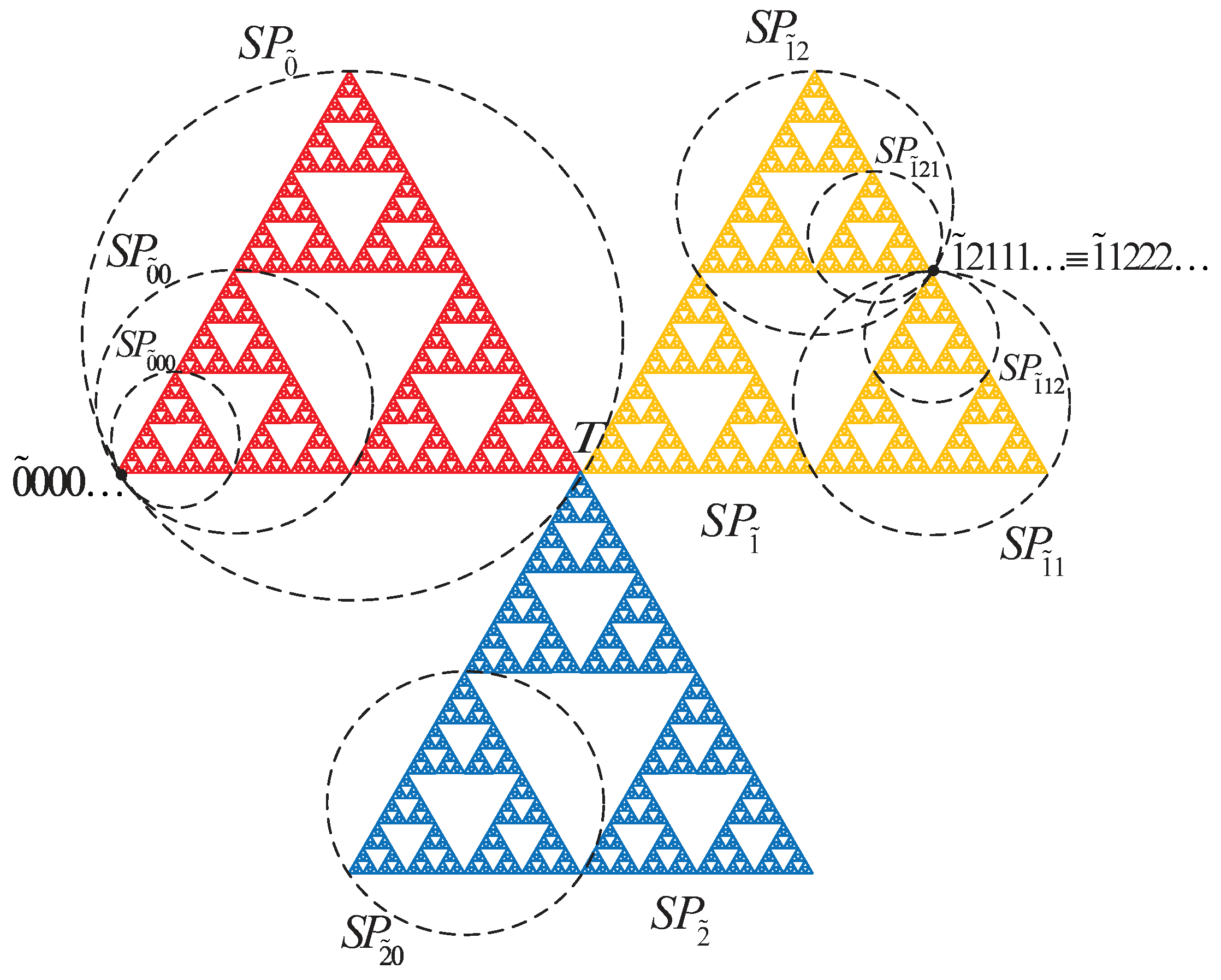
Proposition 4. For , the closed discs of radii with center T are the scaled copy of Sierpinski propeller. Especially, if , then . In addition, the code sets of circles of radii with center T are Proof. We first compute the code representations of the points A satisfying . Without loss of generality, we take as the code representation of T. Let the code representation of A be where and for
Case 1:
Suppose that
Since the terms of code representation of
T (for i=1,2,3,…) are 2, we get
for
. In addition,
must be 1 for
(see Formula (
7)). Otherwise, we compute
. Now, consider that
are 1 for all
. This means that
for
. If
for
, then we obtain
. Therefore, we compute
and this shows that
is one of the parts of the set of the code representations of
A satisfying
for
.
From the construction above, it can be easily seen that, if for , then is one of the parts of the set of the code representations of A.
Case 2:
Let
By using Formula (
8) and following a method similar to Case 1, we obtain that
is one of the parts of the set of the code representations of
A satisfying
. Moreover, we compute if
for
, then
is one of the parts of the set of the code representations of
A.
Case 3:
Assume that
Then, the points
A and
T are in the same Sierpinski gasket. Applying Formula (
4), we obtain that
and
are one of the parts of the set of the code representations of
A satisfying
and
respectively.
Thus, the unions of sets obtained in Cases 1, 2 and 3 give us the code representations of
A satisfying
and
. That is,
and
□
Example 2. Consider the point A of which has the code representation . Obviously, the code set of the closed disc of radius with center A is Remark 3. Proposition 4 and Example 2 show that is a self-similar set but not strictly self-similar.
Remark 4. In the Sierpinski propeller for , if the red Sierpinski gasket is coded by and the yellow Sierpinski gasket is coded by , then the code representations of the point T are determined by , where Thus, the intrinsic metric formula can be expressed bysuch thatfor Moreover, the code sets of circles of radii with center T can be determined by 5. The Intrinsic Metric Formula on Two Adjacent Right Sierpinski Gaskets
By using two right Sierpinski gaskets with vertices
P,
Q and
R where
and
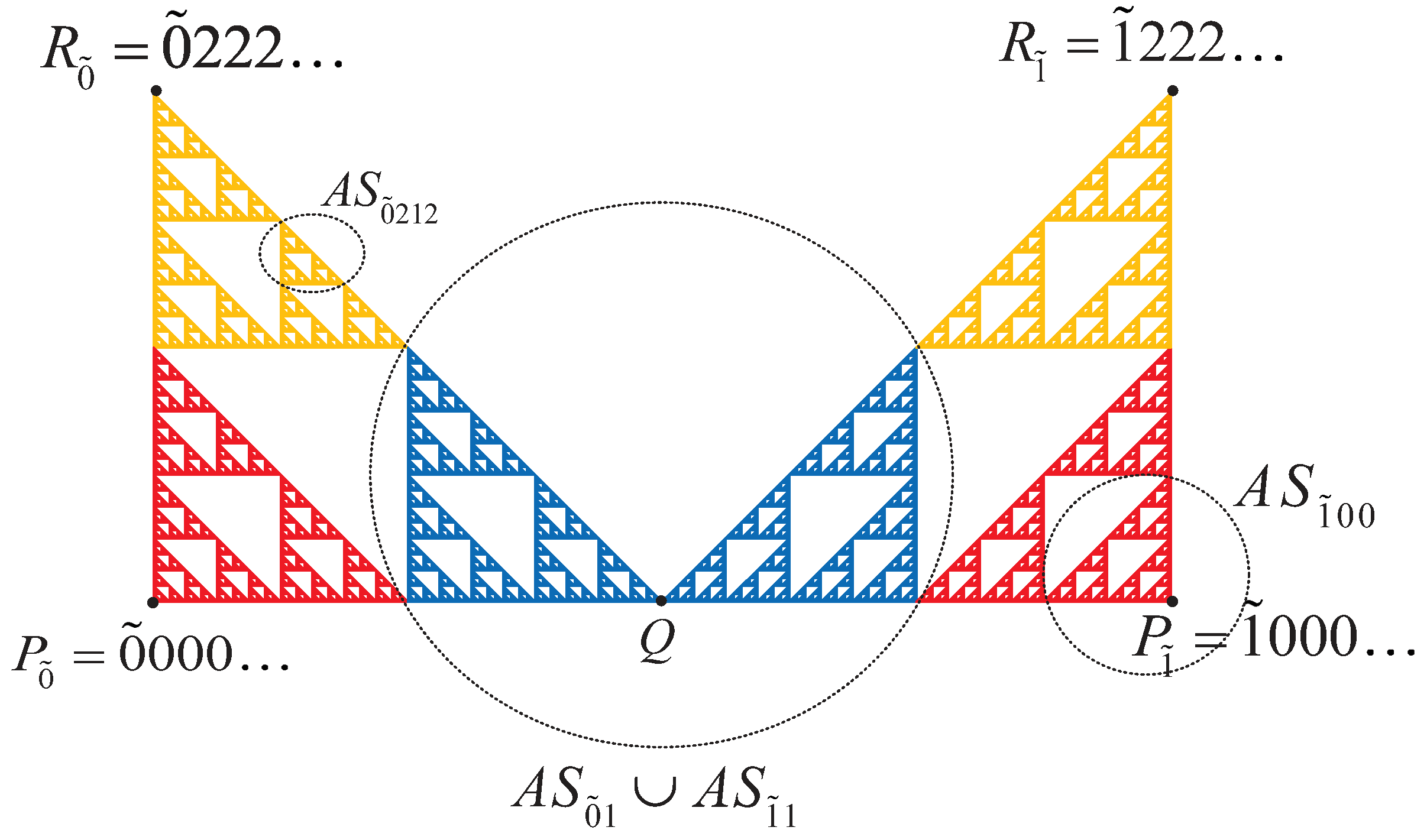
, we now define a second fractal which is self-similar but not strictly self-similar. Consider two identical right Sierpinski gakets whose colors of sub-triangles are red, blue and yellow, and then combine these two triangles at the point Q as in
Figure 6. We call this structure adjacent right Sierpinski gaskets, briefly
.
Let us denote the triangle that is left of the point
Q by
and the triangle that is the right of the point
Q by
. In addition, let us denote the red Sierpinski gaskets by
and
respectively, the blue Sierpinski gaskets by
and
, respectively, and the yellow Sierpinski gaskets by
and
, respectively. It is clear that
and
Thus, two different code representations of
Q are
and
. It is also easily seen that a point of
has either one code representation or two code representations.
In the following proposition, we express the intrinsic metric on the code set of :
Proposition 5. Suppose that the code representations of the points A and B on are and respectively such that for and , where and for
(i)If , then the shortest distance between A and B is determined bysuch that(ii)If , then Equation (3) gives the desired distance. Proof. The proof is omitted since it is similar to the proof of Theorem 2. □
Example 3. Let the code representation of A be and let the code representation of B be . We must use Formula (12) to compute since the first terms of the code representations of A and B are different. Then, we obtainandThus, we get Proposition 6. If d is the intrinsic metric defined in (12) on , thenMoreover, the code representations of A and B satisfying are and , respectively. Proof. As seen in Formula (
12), to obtain the maximum value of the distances between any two points
A and
B of
,
and
must be
for
Then, we get
,
,
and
for
We also have
□
6. Conclusions
In this paper, we express the intrinsic metrics on two new self-similar (but not strictly self-similar) sets created with different combinations of the Sierpinski gaskets. With a similar way, various self-similar sets can be defined by using the different fractals and the intrinsic metrics on these sets can be formulated.