Power Laws in Fractionally Electronic Elements
Abstract
:1. Introduction
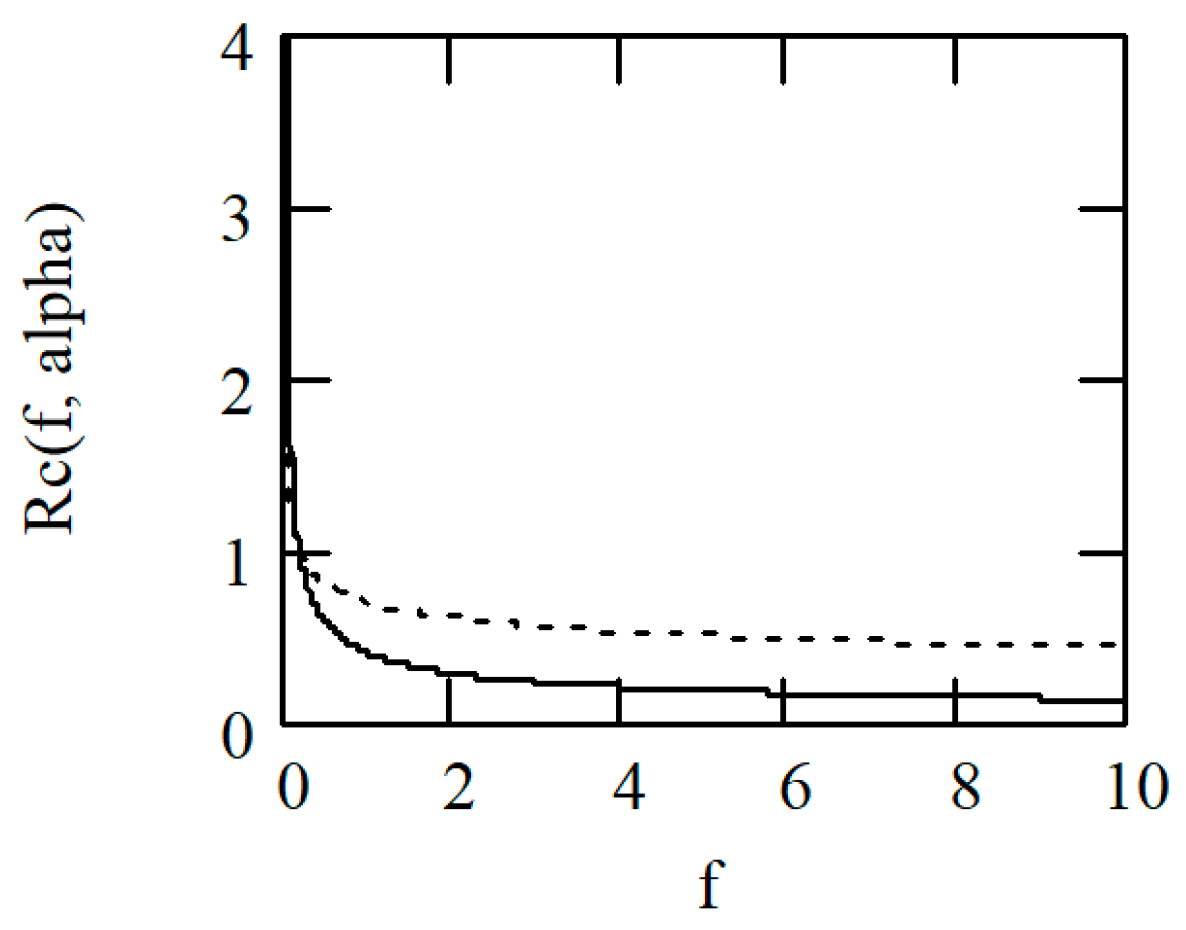
2. Results
3. Concluding Remarks
Funding
Conflicts of Interest
References
- Sarafraz, M.S.; Tavazoei, M.S. Passive realization of fractional-order impedances by a fractional element and RLC components: Conditions and procedure. IEEE Trans. Circuits Syst. I 2017, 64, 585–595. [Google Scholar] [CrossRef]
- Sarafraz, M.S.; Tavazoei, M.S. Passively realisable impedance functions by using two fractional elements and some resistors. IET Circuits Devices Syst. 2018, 12, 280–285. [Google Scholar]
- Malek, H.; Dadras, S.; Chen, Y.-Q. Fractional order equivalent series resistance modelling of electrolytic capacitor and fractional order failure prediction with application to predictive maintenance. IET Power Electron. 2016, 9, 1608–1613. [Google Scholar] [CrossRef]
- Tsirimokou, G.; Psychalinos, C.; Freeborn, T.J.; Elwakil, A.S. Emulation of current excited fractional-order capacitors and inductors using OTA topologies. Microelectron. J. 2016, 55, 70–81. [Google Scholar] [CrossRef]
- Ionescu, C.M. Emerging tools in engineering: Fractional order ladder impedance models for respiratory and neural systems. IEEE J. Emerg. Sel. Top. Circuits Syst. 2013, 3, 425–431. [Google Scholar] [CrossRef]
- Pu, Y.-F.; Yuan, X.; Yu, B. Analog circuit implementation of fractional-order memristor: Arbitrary-order lattice scaling fracmemristor. IEEE Trans. Circuits Syst. I 2018, 65, 2903–2916. [Google Scholar] [CrossRef]
- Ionescu, C.M.; Machado, J.A.T.; Keyser, R.D. Modeling of the lung impedance using a fractional-order ladder network with constant phase elements. IEEE Trans. Biomed. Circuits Syst. 2011, 5, 83–89. [Google Scholar] [CrossRef] [PubMed]
- Beaulieu, A.; Bosse, D.; Micheau, P.; Avoine, O.; Praud, J.-P.; Walti, H. Measurement of fractional order model parameters of respiratory mechanical impedance in total liquid ventilation. IEEE Trans. Biomed. Eng. 2012, 59, 323–331. [Google Scholar] [CrossRef] [PubMed]
- Radwan, A.G.; Shamim, A.; Salama, K.N. Theory of fractional order elements based impedance matching networks. IEEE Microw. Wirel. Compon. Lett. 2011, 21, 120–122. [Google Scholar] [CrossRef]
- Martynyuk, V.; Ortigueira, M.; Fedula, M.; Savenko, O. Methodology of electrochemical capacitor quality control with fractional order model. AEU Int. J. Electron. Commun. 2018, 91, 118–124. [Google Scholar] [CrossRef]
- Atangana, A.; Gómez-Aguilar, J.F. Decolonisation of fractional calculus rules: Breaking commutativity and associativity to capture more natural phenomena. Eur. Phys. J. Plus 2018, 133, 1–22. [Google Scholar] [CrossRef]
- Atangana, A.; Gómez-Aguilar, J.F. Fractional derivatives with no-index law property: Application to chaos and statistics. Chaos Solitons Fract. 2018, 114, 516–535. [Google Scholar] [CrossRef]
- Morales-Delgado, V.F.; Taneco-Hernández, M.A.; Gómez-Aguilar, J.F. On the solutions of fractional order of evolution equations. Eur. Phys. J. Plus 2017, 132. [Google Scholar] [CrossRef]
- Coronel-Escamilla, A.; Gómez-Aguilar, J.F.; Baleanu, D.; Córdova-Fraga, T.; Escobar-Jiménez, R.F.; Olivares-Peregrino, V.H.; Al Qurashi, M.M. Bateman–Feshbach Tikochinsky and Caldirola–Kanai oscillators with new fractional differentiation. Entropy 2017, 19, 55. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Springer: Berlin, Germany, 2013; Volume I. [Google Scholar]
- Lavoie, J.L.; Osler, T.J.; Tremblay, R. Fractional derivatives and special functions. SIAM Rev. 1976, 18, 240–268. [Google Scholar] [CrossRef]
- Raina, R.K.; Koul, C.L. On Weyl fractional calculus. Proc. Am. Math. Soc. 1979, 73, 188–192. [Google Scholar] [CrossRef]
- Gelfand, I.M.; Vilenkin, K. Generalized Functions; Academic Press: New York, NY, USA, 1964; Volume 1. [Google Scholar]
- Zhang, L.; Hu, X.; Wang, Z.; Sun, F.; Dorrell, D.G. Fractional-order modeling and state-of-charge estimation for ultracapacitors. J. Power Sources 2016, 314, 28–34. [Google Scholar] [CrossRef]
- Kanoun, H.; Gabano, J.-D.; Poinot, T. Fractional modeling of ultracapacitors dynamic behavior. IFAC Proc. Vol. 2011, 44, 13978–13983. [Google Scholar] [CrossRef]
- Zou, C.; Zhang, L.; Hu, X.; Wang, Z.; Pecht, M. A review of fractional-order techniques applied to lithium-ion batteries, lead-acid batteries, and supercapacitors. J. Power Sources 2018, 390, 286–296. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M. Power Laws in Fractionally Electronic Elements. Fractal Fract. 2018, 2, 24. https://doi.org/10.3390/fractalfract2040024
Li M. Power Laws in Fractionally Electronic Elements. Fractal and Fractional. 2018; 2(4):24. https://doi.org/10.3390/fractalfract2040024
Chicago/Turabian StyleLi, Ming. 2018. "Power Laws in Fractionally Electronic Elements" Fractal and Fractional 2, no. 4: 24. https://doi.org/10.3390/fractalfract2040024
APA StyleLi, M. (2018). Power Laws in Fractionally Electronic Elements. Fractal and Fractional, 2(4), 24. https://doi.org/10.3390/fractalfract2040024




