Fractional Derivatives with the Power-Law and the Mittag–Leffler Kernel Applied to the Nonlinear Baggs–Freedman Model
Abstract
:1. Introduction
2. Fractional Operators
3. Freedman Model
3.1. Freedman Model with the Power-Law Kernel
3.2. Stability Analysis of the Iteration Method
3.3. Freedman Model with the Mittag–Leffler Kernel
3.4. Stability Analysis of the Iteration Method
- The fixed point set of H has at least one element.
- converges to a point .
3.5. Uniqueness of the Special Solution
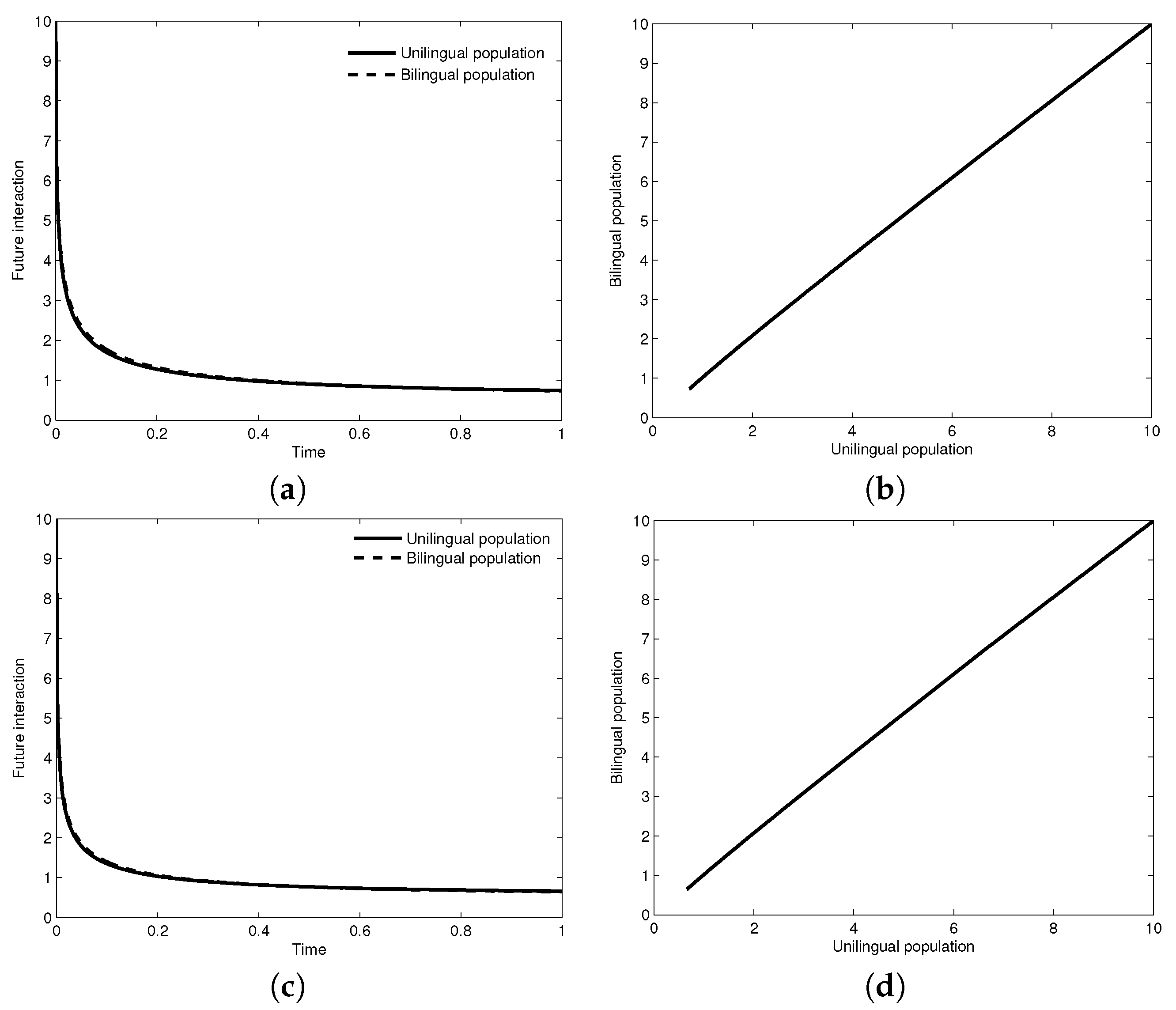
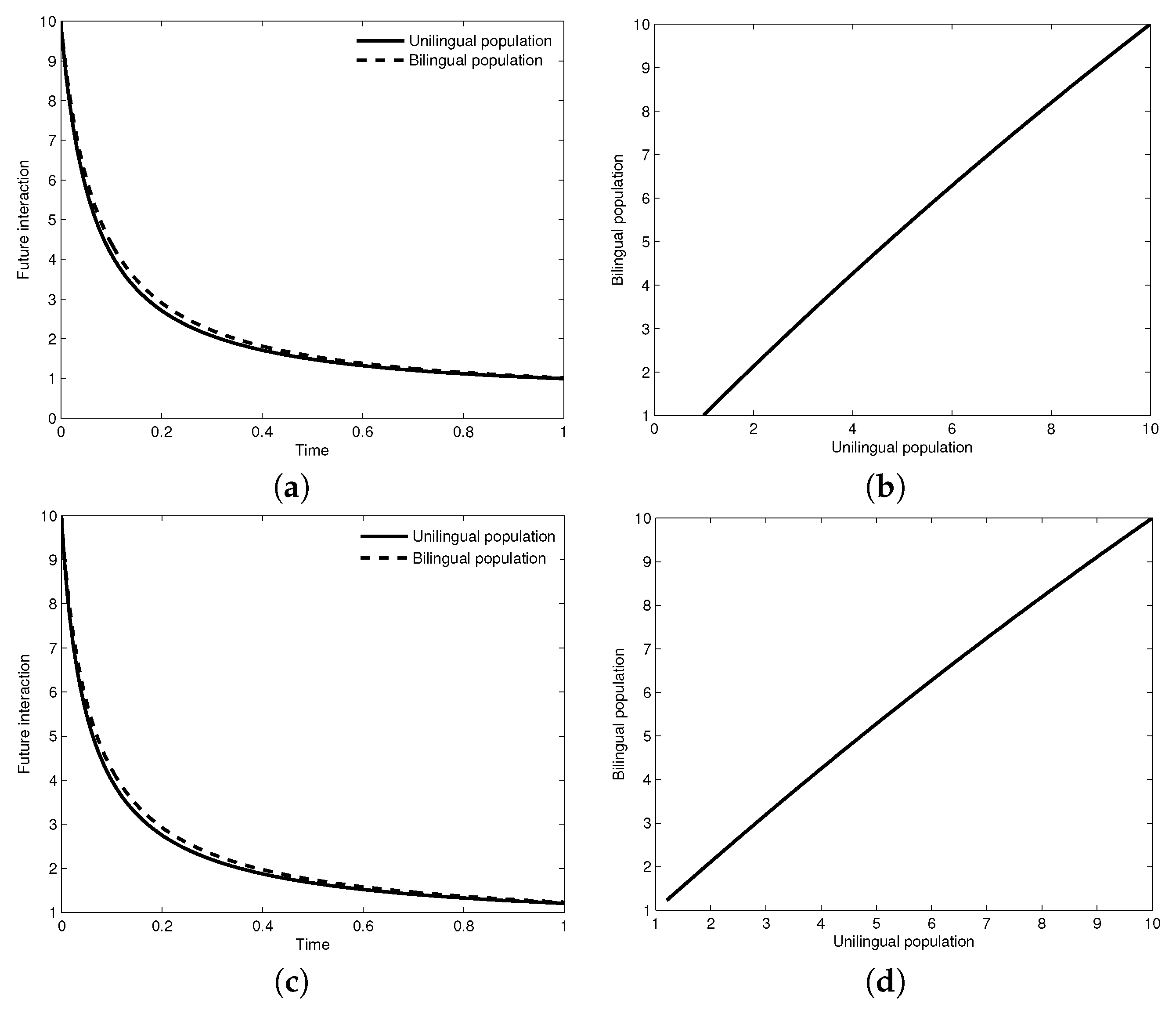
4. Numerical Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Baggs, I.; Freedman, H.I. A mathematical model for the dynamics of interactions between a unilingual and a bilingual population: Persistence versus extinction. J. Math. Sociol. 1990, 16, 51–75. [Google Scholar] [CrossRef]
- Baggs, I.; Freedman, H.I.; Aiello, W.G. Equilibrium characteristics in models of unilingual-bilingual population interactions. In Ocean Wave Mechanics, Computational Fluid Dynamics, and Mathematical Modeling; Rahman, M., Ed.; Computational Mechanics Publ.: Southampton, UK, 1990; pp. 879–886. [Google Scholar]
- Duan, B.; Zheng, Z.; Cao, W. Spectral approximation methods and error estimates for Caputo fractional derivative with applications to initial-value problems. J. Comput. Phys. 2016, 319, 108–128. [Google Scholar] [CrossRef]
- Gómez, J.F. Comparison of the Fractional Response of a RLC Network and RC Circuit. Prespacetime J. 2012, 3, 736–742. [Google Scholar]
- Ito, K.; Jin, B.; Takeuchi, T. On the sectorial property of the Caputo derivative operator. Appl. Math. Lett. 2015, 47, 43–46. [Google Scholar] [CrossRef]
- Kochubei, A.N. General fractional calculus, evolution equations, and renewal processes. Integral Equ. Oper. Theory 2011, 71, 583–600. [Google Scholar] [CrossRef]
- Sandev, T.; Metzler, R.; Tomovski, Z. Velocity and displacement correlation functions for fractional generalized Langevin equations. Fract. Calc. Appl. Anal. 2012, 15, 426–450. [Google Scholar] [CrossRef]
- Sandev, T.; Tomovski, Z.; Dubbeldam, J.L. Generalized Langevin equation with a three parameter Mittag–Leffler noise. Phys. A Stat. Mech. Appl. 2011, 390, 3627–3636. [Google Scholar] [CrossRef]
- Eab, C.H.; Lim, S.C. Fractional generalized Langevin equation approach to single-file diffusion. Phys. A Stat. Mech. Appl. 2010, 389, 2510–2521. [Google Scholar] [CrossRef]
- Ahmad, B.; Nieto, J.J.; Alsaedi, A.; El-Shahed, M. A study of nonlinear Langevin equation involving two fractional orders in different intervals. Nonlinear Anal. Real World Appl. 2012, 13, 599–606. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. Subdiffusive transport close to thermal equilibrium: from the Langevin equation to fractional diffusion. Phys. Rev. E 2000, 61, 6308–6311. [Google Scholar] [CrossRef]
- Lutz, E. Fractional langevin equation. In Fractional Dynamics: Recent Advances; World Scientific: Singapore, 2012; pp. 285–305. [Google Scholar]
- Wiman, A. Über den Fundamentalsatz in der Teorie der Funktionen Ea(x). Acta Math. 1905, 29, 191–201. [Google Scholar] [CrossRef]
- Prabhakar, T.R. A singular integral equation with a generalized Mittag–Leffler function in the kernel. Yokohama Math. J. 1971, 19, 7–15. [Google Scholar]
- Shukla, A.K.; Prajapati, J.C. On a generalization of Mittag–Leffler function and its properties. J. Math. Anal. Appl. 2007, 336, 797–811. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Tomovski, Z. Fractional calculus with an integral operator containing a generalized Mittag–Leffler function in the kernel. Appl. Math. Comput. 2009, 211, 198–210. [Google Scholar] [CrossRef]
- Saxena, R.K.; Ram, J.; Vishnoi, M. Fractional differentiation and fractional integration of the generalized Mittag–Leffler function. J. Indian Acad. Math. 2010, 32, 153–162. [Google Scholar]
- Kiryakova, V.S. Multiple (multiindex) Mittag–Leffler functions and relations to generalized fractional calculus. J. Comput. Appl. Math. 2000, 118, 241–259. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New Fractional Derivatives with Nonlocal and Non-Singular Kernel: Theory and Application to Heat Transfer Model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Alkahtani, B.S.T. Chua’s circuit model with Atangana–Baleanu derivative with fractional order. Chaos Solitons Fractals 2016, 89, 547–551. [Google Scholar] [CrossRef]
- Algahtani, O.J.J. Comparing the Atangana–Baleanu and Caputo-Fabrizio derivative with fractional order: Allen Cahn model. Chaos Solitons Fractals 2016, 89, 552–559. [Google Scholar] [CrossRef]
- Alkahtani, B.S.T. Analysis on non-homogeneous heat model with new trend of derivative with fractional order. Chaos Solitons Fractals 2016, 89, 566–571. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; López-López, M.G.; Alvarado-Martínez, V.M.; Reyes-Reyes, J.; Adam-Medina, M. Modeling diffusive transport with a fractional derivative without singular kernel. Phys. A Stat. Mech. Appl. 2016, 447, 467–481. [Google Scholar] [CrossRef]
- Atangana, A.; Koca, I. Chaos in a simple nonlinear system with Atangana–Baleanu derivatives with fractional order. Chaos Solitons Fractals 2016, 89, 447–454. [Google Scholar] [CrossRef]
- Atangana, A.; Koca, I. On the new fractional derivative and application to nonlinear Baggs and Freedman model. J. Nonlinear Sci. Appl. 2016, 9, 2467–2480. [Google Scholar] [CrossRef]
- Wyburn, J.; Hayward, J. The future of bilingualism: an application of the Baggs and Freedman model. J. Math. Sociol. 2008, 32, 267–284. [Google Scholar] [CrossRef]
- Caputo, M.; Mainardi, F. A new dissipation model based on memory mechanism. Pure Appl. Geophys. 1971, 91, 134–147. [Google Scholar] [CrossRef]
- Watugala, G.K. Sumudu transform: A new integral transform to solve differential equations and control engineering problems. Integr. Educ. 1993, 24, 35–43. [Google Scholar] [CrossRef]
- Li, C.; Tao, C. On the fractional Adams method. Comput. Math. Appl. 2009, 58, 1573–1588. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. Detailed error analysis for a fractional Adams method. Numer. Algorithms 2004, 36, 31–52. [Google Scholar] [CrossRef]
- Katatbeh, Q.K.; Belgacem, F.B.M. Applications of the Sumudu transform to fractional differential equations. Nonlinear Stud. 2011, 18, 99–112. [Google Scholar]
- Bulut, H.; Baskonus, H.M.; Belgacem, F.B.M. The analytical solutions of some fractional ordinary differential equations by Sumudu transform method. Abstr. Appl. Anal. 2013, 2013, 203875. [Google Scholar] [CrossRef]

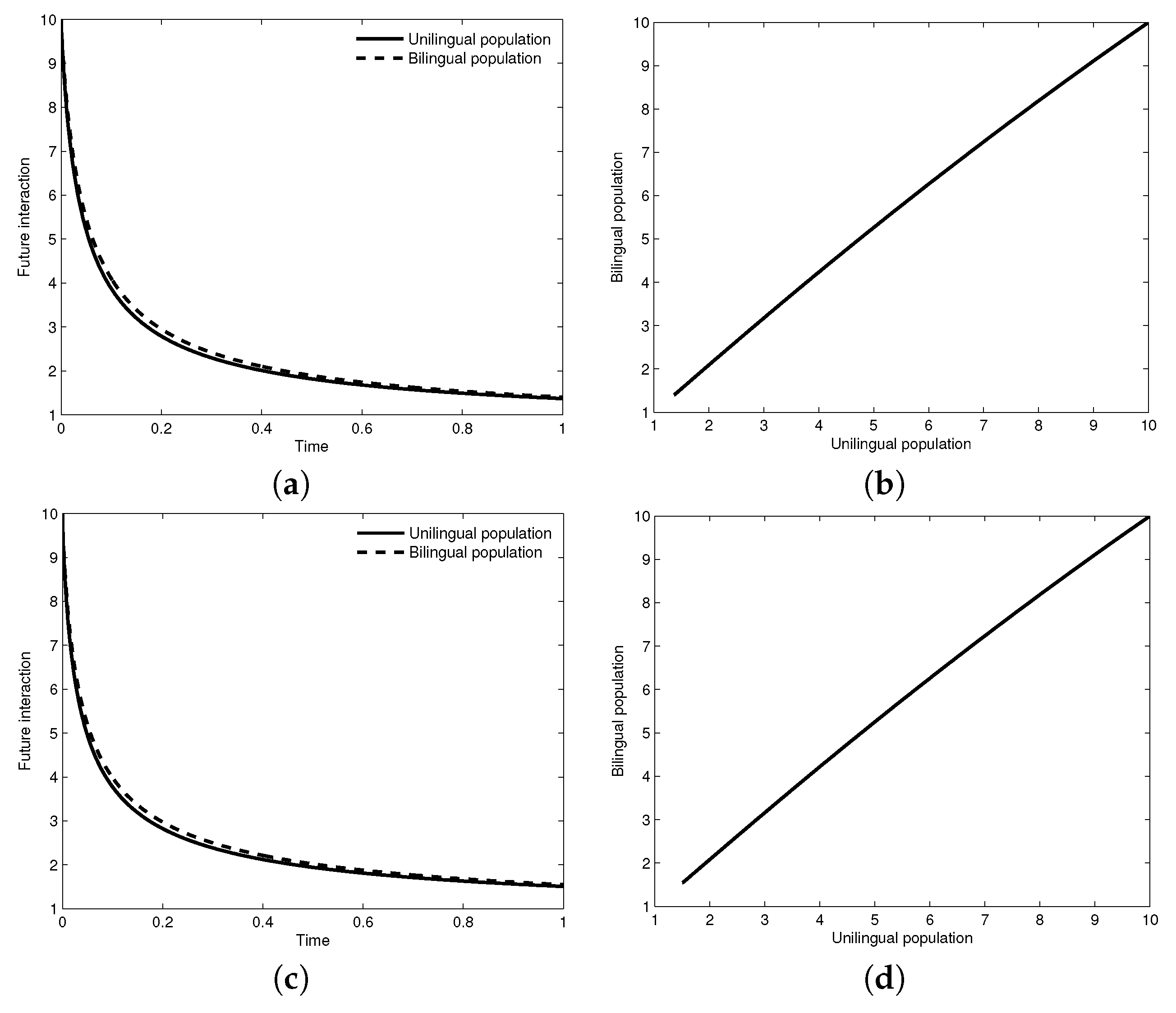
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez-Aguilar, J.F.; Atangana, A. Fractional Derivatives with the Power-Law and the Mittag–Leffler Kernel Applied to the Nonlinear Baggs–Freedman Model. Fractal Fract. 2018, 2, 10. https://doi.org/10.3390/fractalfract2010010
Gómez-Aguilar JF, Atangana A. Fractional Derivatives with the Power-Law and the Mittag–Leffler Kernel Applied to the Nonlinear Baggs–Freedman Model. Fractal and Fractional. 2018; 2(1):10. https://doi.org/10.3390/fractalfract2010010
Chicago/Turabian StyleGómez-Aguilar, José Francisco, and Abdon Atangana. 2018. "Fractional Derivatives with the Power-Law and the Mittag–Leffler Kernel Applied to the Nonlinear Baggs–Freedman Model" Fractal and Fractional 2, no. 1: 10. https://doi.org/10.3390/fractalfract2010010
APA StyleGómez-Aguilar, J. F., & Atangana, A. (2018). Fractional Derivatives with the Power-Law and the Mittag–Leffler Kernel Applied to the Nonlinear Baggs–Freedman Model. Fractal and Fractional, 2(1), 10. https://doi.org/10.3390/fractalfract2010010





