Research on High-Reliability Energy-Aware Scheduling Strategy for Heterogeneous Distributed Systems

Abstract

With the demand for workflow processing driven by edge computing in the Internet of Things (IoT) and cloud computing growing at an exponential rate, task scheduling in heterogeneous distributed systems has become a key challenge to meet real-time constraints in resource-constrained environments. Existing studies now attempt to achieve the best balance in terms of time constraints, energy efficiency, and system reliability in Dynamic Voltage and Frequency Scaling environments. This study proposes a two-stage collaborative optimization strategy. With the help of an innovative algorithm design and theoretical analysis, the multi-objective optimization challenges mentioned above are systematically solved. First, based on a reliability-constrained model, we propose a topology-aware dynamic priority scheduling algorithm (EAWRS). This algorithm constructs a node priority function by incorporating in-degree/out-degree weighting factors and critical path analysis to enable multi-objective optimization. Second, to address the time-varying reliability characteristics introduced by DVFS, we propose a Fibonacci search-based dynamic frequency scaling algorithm (SEFFA). This algorithm effectively reduces energy consumption while ensuring task reliability, achieving sub-optimal processor energy adjustment. The collaborative mechanism of EAWRS and SEFFA has well solved the dynamic scheduling challenge based on DAG in heterogeneous multi-core processor systems in the Internet of Things environment. Experimental evaluations conducted at various scales show that, compared with the three most advanced scheduling algorithms, the proposed strategy reduces energy consumption by an average of 14.56% (up to 58.44% under high-reliability constraints) and shortens the makespan by 2.58–56.44% while strictly meeting reliability requirements.

1. Introduction

In recent advancements, processor technology has experienced a rapid evolution, transitioning from the initial single-core designs to sophisticated multi-core architectures. This progression has witnessed a shift from homogeneous to heterogeneous multi-core systems [1]. With the continuous increase in architectural complexity, the performance capabilities of systems have significantly improved. As a result, heterogeneous distributed systems have been widely adopted in several critical domains, particularly in environments with high demands for computational power and efficiency, such as artificial intelligence, drones, smart homes, and edge computing scenarios in the Internet of Things (IoT) [2,3,4]. These systems typically integrate multiple types of processors, with significant variations in task execution efficiency among different processors, enhancing the flexibility of resource utilization. Particularly in large-scale, real-time IoT applications, the adoption trend of heterogeneous distributed systems has become increasingly prominent [5]. In IoT environments, typical computational tasks include signal processing (e.g., fast Fourier transform), data analysis (e.g., Gaussian Elimination), and others. These tasks are often mapped to Directed Acyclic Graphs (DAGs) to facilitate parallelized scheduling and optimization [6,7]. The DAG structure can clearly represent dependencies between tasks, making it conducive to achieving efficient scheduling and resource allocation on multi-core heterogeneous platforms [8].

In the recent past, energy consumption has become a critical challenge in heterogeneous distributed systems, particularly for battery-powered end devices such as new energy vehicles, edge sensors, and drones [9]. To alleviate the energy bottleneck, researchers have explored various technical solutions, including Dynamic Voltage and Frequency Scaling (DVFS) [10], virtualization-based consolidation [11], and task replication strategies [12,13]. Among these, DVFS has gained prominence as a mainstream technique for enhancing processor energy efficiency by dynamically adjusting the voltage and frequency levels. However, applying DVFS in heterogeneous IoT multi-processor systems introduces considerable complexity into task scheduling. The scheduling algorithms must now address multiple dimensions simultaneously, such as task prioritization, processor assignment, and power management. Since different processors support different voltage-frequency ranges, the same task may exhibit significant variations in both execution time and energy consumption depending on the core it is assigned to. Consequently, achieving energy-efficient execution while optimizing task completion time and maintaining system reliability has become an urgent and challenging research problem [14,15,16]. Energy-aware scheduling is of critical importance in IoT and edge computing. First, battery-powered devices need to operate for long periods under strict energy budgets—for instance, a 10% reduction in energy consumption can triple the lifespan of devices in environmental monitoring systems [17]. Second, edge servers handling real-time workflows must meet deadlines while avoiding thermal throttling, and dynamic frequency scaling can reduce peak power by 18–22% [18]. Third, large-scale distributed energy optimization can collectively save megawatt-level power each year. Our work meets these needs through reliability-guaranteed DVFS control.

This paper introduces two novel scheduling algorithms designed for parallel applications in heterogeneous distributed systems, with the dual objectives of minimizing energy consumption and operational timelines while adhering to reliability standards. The principal contributions of this paper are delineated as follows:

• We propose a novel search-based optimal energy frequency adjustment algorithm (SEFFA). Predicated on the assumption that all nodes are pre-allocated, this algorithm strives to minimize energy consumption while fulfilling reliability prerequisites through strategic frequency adjustments.
• We introduce an energy-aware scheduling algorithm based on the weight method under reliability constraints (EAWRS). This methodology integrates both the out-degree and in-degree of the DAG and employs a combination of task completion times, energy consumption metrics, and reliability factors, expressed through normalized and linear combinations, to optimize node allocation.
• The efficacy of the proposed algorithms is validated through comprehensive experimental simulations. The findings demonstrate that these methods outperform existing techniques in terms of energy consumption and makespan.

2. Related Work

In recent years, with the continuous advancement in computing capabilities and the widespread deployment of large-scale workflows in IoT edge computing scenarios, the demand for high-performance computing has exhibited a significant upward trend [17,18,19]. In parallel, heterogeneous distributed systems are facing increasingly stringent performance requirements in terms of reliability, energy efficiency, and task completion time [20]. These challenges are especially pronounced in resource-constrained environments with high real-time demands characteristics typical of many IoT applications where they have become critical bottlenecks for ensuring system stability and achieving efficient task scheduling. For reliability, the objective is to mitigate the occurrence of failures during task execution, which are predominantly related to hardware issues, temperature fluctuations, and other factors. These failures are categorized into transient and permanent types, with transient failures occurring much more frequently than permanent ones. Consequently, most research has focused on transient failures [21,22,23]. A widely accepted reliability model uses $1-e^{-\lambda t}$ to represent the probability of a transient failure occurring within a time interval $t$, demonstrating that reliability increases as execution time decreases. Therefore, a common approach to enhancing reliability is the reduction in task execution time.

Energy consumption presents another significant challenge within heterogeneous distributed systems [24]. Current research on optimizing energy usage during task scheduling in such systems predominantly utilizes Dynamic Voltage and Frequency Scaling (DVFS) technology [10]. Since high-frequency operation is a major cause of high energy consumption, DVFS can be employed to reduce power consumption by lowering the operational voltage and frequency during the runtime. In terms of reducing completion times, current research aims to minimize the makespan and the total completion time. The heterogeneous earliest finish time (HEFT) algorithm is one of the most popular high-performance scheduling algorithms and is widely regarded as capable of achieving the shortest completion times in many scenarios [25]. Additionally, there are approaches that consider both energy consumption and reliability, such as the low energy consumption (LEC) [26] and minimum reliability (MR) methods [27]. Research has also proposed scheduling algorithms that consider both reliability and energy consumption, such as optimal dynamic scheduling (ODS) and the self-optimizing evolutionary algorithm (SOEA), and has combined these algorithms to optimize reliability, energy use, and scheduling duration, thereby achieving the optimization of energy consumption, reliability, and makespan [28].

The latest advancements in energy-aware computing and IoT security further highlight the need for efficient resource scheduling. Schieber et al. demonstrated a polynomial-time algorithm for interleaving energy harvesting tasks with real-time jobs in battery-free IoT devices, achieving maximum throughput under intermittent power supply—similar to our dynamic scheduling based on DVFS (Dynamic Voltage and Frequency Scaling) in resource-constrained environments [29]. In the field of IoT security, hyperdimensional computing (HDC) has shown remarkable efficiency: Ghajari et al. [30] achieved 99.54% intrusion detection accuracy on NSL-KDD with low computational overhead, while [31] reported 91.55% accuracy for unknown attack patterns, emphasizing the value of lightweight algorithms for edge devices. Similarly, Rastgoo et al. proposed an intelligent control method for electric vehicle charging microgrids, which stabilizes voltage through reactive power compensation while reducing the charging time—paralleling our processor-level energy–time-reliability trade-offs [32]. Collectively, these works validate that cross-layer optimization (from job scheduling to security) is critical for IoT systems. Our EAWRS + SEFFA provides a unified framework for heterogeneous task scheduling.

Although existing studies have made significant progress in understanding the trade-off between energy and time, there are still key issues that remain unaddressed: most algorithms overlook the correlation between reliability and energy consumption, and their performance is suboptimal. Our EAWRS + SEFFA strategy explicitly addresses these gaps through energy-aware priority scheduling and adaptive frequency search.

In summary, as heterogeneous distributed systems find widespread applications across various sectors, enhancing system reliability, reducing energy consumption, and shortening completion times have become focal points of research. The improved scheduling algorithms proposed in this paper aim to optimize scheduling strategies, thereby further reducing energy consumption and shortening completion times while meeting reliability requirements, offering more efficient solutions for the application of heterogeneous distributed systems.

3. Models

In this section, we discuss the mathematical models. The reader can refer to

Table 1. Notation and list of definitions.

Notation	Definition
${\omega }_{i,j}$	Execution time of task $t_i$ in processor $u_j$
$e_{i,j}$	The edge between task $t_i$ and task $t_j$
$c_{i,j}$	Communication time from $t_i$ to $t_j$
$\overline{{\omega }_i}$	Average execution time of task $t_i$
$P_{ind}$	Dynamic power consumption independent of processor frequency
$P_s$	Static energy consumption
$h$	System state
$P_d$	Power consumption related to processor frequency
$C_{\left\{k,ef\right\}}$	The effective capacitance of processor $u_k$
$m_k$	Dynamic power index of processor $u_k$
$E\left(G\right)$	Energy consumption of application $G$
$R\left(t_i,u_k\right)$	Reliability value of task $t_i$ in processor $u_k$
$R\left(G\right)$	Reliability value of application $G$
$ran{k}_{up}\left(t_i\right)$	Upward rank value of task $t_i$
$succ\left(t_i\right)$	The successor to task $t_i$
$Ft\left(t_i,u_k\right)$	The finish time of executing task $t_i$ on processor $u_k$
$F{t}_{min}\left(t_i\right)$	The minimum values of finish time of executing task $t_i$
$F{t}_{max}\left(t_i\right)$	The maximum values of finish time of executing task $t_i$
$R_{req}$	Reliability requirement of application $G$
$R_{min}\left(t_i\right)$	Reliability value of task $t_i$ under the minimum redundancy of the task
$R_{max}\left(t_i\right)$	Reliability value of task $t_i$ under the maximum redundancy of the task
$W_i$	The execution time of sub-task $t_i$ on a processor with its maximum frequency
${\mathsf{\lambda }}_k$	Failure rate of processor $u_k$

for the notation and list of definitions used in this work.

3.1. System Model

We conceptualize heterogeneous distributed systems as a model comprising a set of heterogeneous processors ($U=\left\{u_1, u_2,\dots , u_m\right\}$), where $m$ denotes the number of processors. An application is represented by a Directed Acyclic Graph (DAG), designated as $G=\left\{N, E\right\}$. Here, $N$ signifies a set of tasks, and $E$ represents a collection of directed edges within the DAG. Each edge $e_{i,j}\in E$ illustrates the dependency and correlation between tasks $t_i$ and $t_j$, indicating that $t_i$ is a prerequisite task for $t_j$, with the latter commencing only upon the completion of the former. Additionally, each edge $e_{i,j}$ carries a weight $c_{i,j}$, denoting the communication time between tasks $t_i$ and $t_j$. If the two tasks are assigned to the same processor, their intercommunication time is considered to be zero. The execution time of the tasks is represented by $W$, where ${\omega }_{i,j}$ denotes the execution time of task $t_i$ on processor $p_j$. The average execution cost of task $t_i$ can be defined as

$$\stackrel{-}{{\omega }_i}=\frac{{\sum }_{j=1}^m {\omega }_{\{i,j\}}}{m}$$

(1)

Through this approach, we can effectively evaluate the execution times of tasks, thereby optimizing scheduling strategies to enhance the overall performance of the system.

Figure 1 illustrates an example of a Directed Acyclic Graph (DAG) with ten tasks. In this DAG, tasks $t_2, t_3, t_4, t_5,$ and $t_6$ can only commence after the completion of task $t_1$.

Table 2. The execution time of tasks on processors.

Task	${\mathit{u}}_1$	${\mathit{u}}_2$	${\mathit{u}}_3$
$t_1$	$14$	$16$	$9$
$t_3$	$11$	$13$	$19$
$t_4$	$13$	$8$	$17$
$t_2$	$13$	$19$	$18$
$t_5$	$12$	$13$	$10$
$t_6$	$13$	$16$	$9$
$t_9$	$18$	$12$	$20$
$t_7$	$7$	$15$	$11$

provides the execution times for this example when operated at the maximum frequency across three processors. Specifically, the value “14” in the table denotes that the execution time of task $t_1$ on processor $u_1$ is 14 units.

Table 3. Power parameters of processors.

${\mathit{u}}_{\mathit{k}}$	${\mathit{P}}_{\left\{\mathit{k},\mathit{i}\mathit{n}\mathit{d}\right\}}$	${\mathit{C}}_{\left\{\mathit{k},\mathit{e}\mathit{f}\right\}}$	${\mathit{m}}_{\mathit{k}}$	${\mathit{f}}_{\left\{\mathit{k},\mathit{l}\mathit{o}\mathit{w}\right\}}$	${\mathit{f}}_{\left\{\mathit{k},\mathit{m}\mathit{a}\mathit{x}\right\}}$
$u_1$	$0.03$	$0.8$	$2.9$	$0.26$	$1.0$
$u_2$	$0.04$	$0.8$	$2.5$	$0.26$	$1.0$

shows all the processor parameters such as the frequency-independent dynamic power $P_{\left\{k,ind\right\}}$; this will be explained in more detail in subsequent chapters.

3.2. Energy Model

In this study, we employed an advanced system-level power model, which has been widely applied in various contexts. Within the framework of Dynamic Voltage and Frequency Scaling (DVFS) technology, voltage and frequency are interrelated in a nearly linear relationship. Consequently, adjustments in frequency under DVFS inherently necessitate corresponding alterations in voltage. The system power calculation model utilized in this research is articulated as follows:

$$\begin{array}{c}P\left(f\right)=P_s+h\left(P_{ind}+P_d\right)=P_s+h\left(P_{ind}+C_{\left\{k,ef\right\}}{f}^{m_k}\right)\end{array}$$

(2)

In the model, $P_s$ represents the static power consumption, which is omnipresent except when the system is in an idle state. $P_{ind}$ denotes frequency-independent power consumption, while $P_d$ corresponds to the dynamic power consumption that varies with frequency changes. The parameter $h$ symbolizes the system state, and $C_{\left\{k,ef\right\}}$ represents the effective capacitance.

Given that dynamic power consumption constitutes the primary component within the system ($h=1$) and managing static power consumption poses challenges, this study opts to exclude static energy consumption from consideration. Therefore, the power consumption formula utilized in this research simplifies to the following expression:

$$\begin{array}{c}P\left(f\right)=P_{ind}+C_{\left\{k,ef\right\}}{f}^{m_k}\end{array}$$

(3)

Among them, $m_k$ represents the characteristic constant of processor $u_k$ itself. At the same time, due to the heterogeneity of the processors, each processor has its own set of operational parameters. We have defined the following parameter set to accommodate these variations:

The set of $P_{ind}:\left\{P_{\left\{1,ind\right\}}, P_{\left\{2,ind\right\}},\dots ,P_{\left\{\left|U\right|,ind\right\}}\right\};$

The set of $P_d:\left\{P_{\left\{1,d\right\}}, P_{\left\{2,d\right\}},\dots ,P_{\left\{\left|U\right|,d\right\}}\right\};$

The set of $C_{ef}:\left\{C_{\left\{1,ef\right\}}, C_{\left\{2, ef\right\}},\dots ,C_{\left\{\left|U\right|,ef\right\}}\right\};$

The set of $m:\left\{m_1, m_2,\dots ,m_{\left|U\right|}\right\}.$

The actual effective frequency set for the processors is defined as follows:

$$\left\{\begin{array}{c}\left\{f_{\left\{1,low\right\}},f_{\left\{1,\alpha \right\}},\dots ,f_{\left\{1,max\right\}}\right\},\\ \left\{f_{\left\{2,low\right\}},f_{\left\{2,\alpha \right\}},\dots ,f_{\left\{2,max\right\}}\right\},\\ \dots \\ \left\{f_{\left\{\left|U\right|,low\right\}},f_{\left\{\left|U\right|,\alpha \right\}},\dots ,f_{\left\{\left|U\right|,max\right\}}\right\},\end{array}\right.$$

Based on the definitions of the parameters provided, the execution time of task $t_i$ on processor $u_k$ at frequency $f_{\left\{k, h\right\}}$ can be calculated using the following formula:

$$\begin{array}{c}{\omega }_{\left\{i,k,h\right\}}={\omega }_{\left\{i,k\right\}}\times {\displaystyle \frac{f_{\left\{k,max\right\}}}{f_{\left\{k,h\right\}}}}\end{array}$$

(4)

Among these, $f_{\left\{k,max\right\}}$ represents the maximum frequency on processor $u_k$.

Therefore, we can compute the energy consumption of task $t_i$ on processor $u_k$ operating at frequency $f_{\left\{k, h\right\}}$ as follows:

$$\begin{array}{c}E\left(t_i,u_k,f_i\right)=P_{\left\{k,h\right\}}\times W_i\times {\displaystyle \frac{1}{f_i}}=(P_{ind}+C_{ef}{f}^m)\times {\displaystyle \frac{W_i}{f_i}}\end{array}$$

(5)

The total energy consumption of application $G$ can be represented as follows:

$$\begin{array}{c}E\left(G\right)={{\displaystyle \sum }}_{i=1}^{\left|N\right|}E\left(t_i,u_k,f_{\left\{k,h\right\}}\right)\end{array}$$

(6)

3.3. Reliability Model

There are two primary types of faults within computing systems: transient faults (also known as random hardware faults) and permanent faults. Once a permanent fault occurs, the affected processor cannot recover autonomously and must be replaced. Transient faults, on the other hand, appear and last only briefly, disappearing without causing lasting damage to the processor. Therefore, this research primarily focuses on transient faults. Typically, in applications based on Directed Acyclic Graphs (DAGs), the occurrence of transient faults in tasks follows a Poisson distribution. The reliability of an event within time interval $t$ can be expressed as

$$\begin{array}{c}R\left(t\right)=e^{-\mathsf{\lambda }\mathrm{t}}\end{array}$$

(7)

The symbol $\mathsf{\lambda }$ represents the total fault rate per time unit for a processor. We use ${\mathsf{\lambda }}_k$ to denote the constant fault rate per time unit on processor $u_k$. Thus, the fault rate can be expressed as

$$\begin{array}{c}{\mathsf{\lambda }}_k\left(f_i\right)={\mathsf{\lambda }}_F·{10}^{{\displaystyle \frac{d\left(1-f_i\right)}{1-f_{min}}}}\end{array}$$

(8)

where ${\mathsf{\lambda }}_F$ is the average number of faults per second at the maximum frequency.

For the task $t_i$ executed on processor $u_k$, the reliability during its execution time is expressed as

$$\begin{array}{c}R\left(t_i,u_k,f_i\right)=e^{-{\mathsf{\lambda }}_k{w}_{\left\{i,k\right\}}}=e^{-{\mathsf{\lambda }}_k\left(f_i\right){\displaystyle \frac{W_i}{f_i}}}=e^{-{\mathsf{\lambda }}_F·{10}^{{\displaystyle \frac{d\left(1-f_i\right)}{1-f_{min}}}}}\end{array}$$

(9)

In the formula, $W_i$ represents the execution time of task $t_i$ at the maximum frequency. From this, the failure probability of task $t_i$ can be expressed as

$$\begin{array}{c}1-R\left(t_i,u_k\right)=1-e^{-{\mathsf{\lambda }}_k{\omega }_{\left\{i,k\right\}}}\end{array}$$

(10)

So, the reliability of a parallel application with priority constraints is given by

$$\begin{array}{c}R\left(G\right)={\displaystyle {\displaystyle \prod }_{t_i\in N}}R\left(t_i\right)\end{array}$$

(11)

3.4. Problem Description

This research focuses on optimizing task allocation and frequency levels within heterogeneous distributed systems to minimize both the makespan and energy consumption. Using the model described above, we can formulate our problem as follows: Given a Directed Acyclic Graph as $G=\left\{N, E\right\}$ and a set of processors ($U=\left\{u_1, u_2,\dots , u_m\right\}$) that support Dynamic Voltage and Frequency Scaling (DVFS) technology, our objective is to find a scheduling algorithm that minimizes both the makespan and energy consumption, denoted as $R\left(G\right)$, while also meeting reliability requirements.

$$\begin{array}{l}Minimize\left\{Makespan\left(G\right),E\left(G\right)\right\}\\ subject to: R\left(G\right)\ge R_{req}\left(G\right)\end{array}$$

(12)

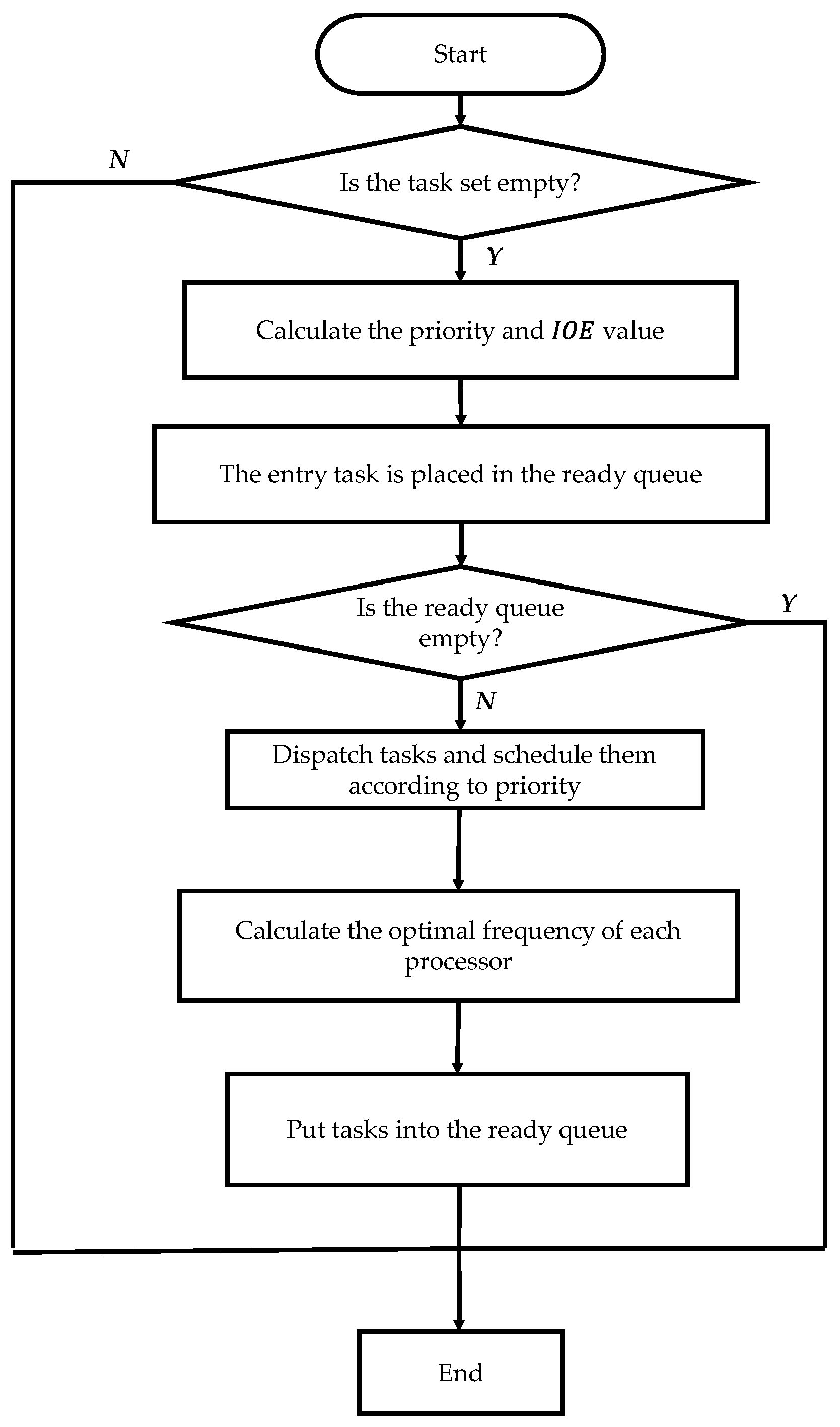
4. Energy-Aware Weighted Scheduling Algorithm with Reliability Constraints

In this section, we introduce the energy-aware weighted scheduling algorithm with reliability constraints. The algorithm is structured into two main phases: the task priority ordering phase and the processor allocation phase.

4.1. The Task Priority Ordering Phase

In task scheduling for heterogeneous distributed systems, the first step involves determining the execution order of the tasks. For this purpose, we employ a widely used method, specifically the HEFT (heterogeneous earliest finish time) algorithm. This algorithm utilizes the calculation of the upward rank value ($ran{k}_{up}$), which is computed as follows:

$$\begin{array}{c}ran{k}_{up}\left(t_i\right)=\left\{\begin{array}{c}\overline{{\omega }_i},if\left(t_i=t_{exit}\right)\\ \overline{{\omega }_i}+\underset{t_j\in succ\left(t_i\right)}{\max }\left\{\overline{c_{i,j}}+ran{k}_{up}\left(t_j\right)\right\},if\left(t_i\ne t_{exit}\right)\end{array}\right. \end{array}$$

(13)

In the formula, $t_{exit}$ represents the exit task, and $succ\left(t_i\right)$ is the set of direct successors to task $t_i$. The term $\overline{c_{i,j}}$ refers to the average communication cost between tasks $t_i$ and $t_j.$ After calculating the upward rank values ($ran{k}_{up}$), these are sorted in descending order. A higher $ran{k}_{up}$ value signifies a higher priority for the task.

4.2. The Processor Allocation Phase

Considering task reliability, energy consumption, and completion times, this paper introduces a new method for allocating processors. The complexity of scheduling in a Directed Acyclic Graph (DAG) primarily arises from the dependencies among its nodes, where the in-degree and out-degree of node tasks and their execution times are crucial to the scheduling outcomes. In the HEFT algorithm, while the upward rank values ($ran{k}_{up}$) guide scheduling decisions, it fails to account for other influential factors, thereby potentially impacting the DAG’s makespan.

Here, we have designed a metric to evaluate the criticality of the current node, referred to as the index of execution ($IOE$). The design of this metric is as follows:

$$\begin{array}{c}IOE\left(t_i\right)={\displaystyle \frac{ID\left(t_i\right)\times \overline{{\omega }_i}+OD\left(t_i\right)\times \overline{{\omega }_i}}{2}}\end{array}$$

(14)

In this formulation, $ID\left(t_i\right)$ represents the in-degree of task $t_i$, and $OD\left(t_i\right)$ represents its out-degree. The index of execution ($IOE$) employs a weighted approach to holistically consider the dependencies before and after a task, as well as the impact of execution times on scheduling outcomes. This optimization explicitly gives priority to the high-degree DAG nodes on the critical path and directly adjusts the task allocation based on the graph topological characteristics. The main steps of the energy-aware weighted scheduling algorithm under reliability constraints (EAWRS) and its presentation in Algorithm 1 are as follows:

Algorithm 1: EAWRS
Input: $G=\left\{N, E\right\}$, $R_{given}$ Output: $E\left(G\right),Makespan\left(G\right),R\left(G\right)$
1:	Calculate $ran{k}_{up}$ of all tasks
2:	Calculate $IOE\left(t_i\right)$ according to Equation (14)
3:	Push $ran{k}_{up}$ valuese into queue $urv$
4:	Push $IOE$ values into queue $VQ$ in decreasing order
5:	for (∀$i$,$t_i\in urv$) do
6:	if $t_i\in \left[VQ\left[0\right], VQ\left[l\right]\right]$ then
7:	Assign $t_i$ to processor satisfying:
8:	$u_k\leftarrow \underset{1\le k\le m}{min}\left\{\alpha ·{\displaystyle \frac{E_{max}\left(t_i\right)-E\left(t_i,u_k\right)}{E_{max}\left(t_i\right)-E_{min}{t}_i}}+\left(1-\alpha \right){\displaystyle \frac{Ft\left(t_i,u_k\right)-F{t}_{min}\left(t_i\right)}{F{t}_{max}\left(t_i\right)-F{t}_{min}\left(t_i\right)}}\right\}$
9:	else
10:	Assign $n_i$ to processor satisfying:
11:	$u_k\leftarrow \underset{1\le k\le m}{min}E\left(\left(t_i,u_k\right)\right)$
12:	end if
13:	end for
14:	return $E\left(G\right),Makespan\left(G\right), R(G$)

• Calculate the $IOE$ value for each task.
• Place the calculated IOE values in queue $VQ$ in decreasing order.
• If task $t_i$ is within the range of $\left(\left[VQ\right[0\right], VQ\left[l\right])$, it indicates a high criticality level, and it is then assigned to processor $u_k$ with

  $$\begin{array}{c}\underset{1\le k\le m}{min}\left\{\alpha ·{\displaystyle \frac{E_{max}\left(t_i\right)-E\left(t_i,u_k\right)}{E_{max}\left(t_i\right)-E_{min}{t}_i}}+\left(1-\alpha \right){\displaystyle \frac{Ft\left(t_i,u_k\right)-F{t}_{min}\left(t_i\right)}{F{t}_{max}\left(t_i\right)-F{t}_{min}\left(t_i\right)}}\right\}\end{array}$$

  (15)

  where $Ft\left(t_i,u_k\right)$ represents the completion time of task $t_i$ on processor $u_k$.
• If task $t_i$ is within the range of $\left(\left[VQ\right[l+1\left], VQ\right[n-1\right])$, it indicates a lower criticality level, and it should then be assigned to processor $u_k$ with $\underset{1\le k\le m}{min}E\left(\left(t_i,u_k\right)\right)$.
• Calculate the upward rank values ($ran{k}_{up}$) for each task and assign tasks to the appropriate processors according to Formulas (14) and (15). The final result is a scheduling solution.

Among them, the parameter $\alpha \left(\alpha \ge 0\right)$ is used to balance completion time and energy consumption. When $l=n$ and $\alpha =0$, we obtain maximum reliability allocation. Here, we change $\alpha$ from 0.0 to 1.0 with a step size of 0.1 so as to gradually find the near-optimal solution. The time complexity of EAWRS is $O\left(n{m}^3{L}_{\alpha }\right)$, where the parameter $L_{\alpha }$ is related to the considered frequency range and represents the accuracy of reliability constraints. $L_{\alpha }$ is the number of iterations on α, and the number of iterations on $l$ is equal to the number of subtasks $n$.

5. Search-Based Optimal Energy Frequency Adjustment Algorithm

After selecting suitable processors for each task using the EAWRS in the previous section, the next step is to find the optimal frequency that satisfies reliability constraints while minimizing energy consumption, thereby achieving further optimization. In this subsection, we introduce a frequency search algorithm, SEFFA (search-based optimal energy frequency adjustment algorithm), which aims to minimize energy consumption under energy constraints. Utilizing the EAWRS (energy-aware weighted scheduling algorithm with reliability constraints), we obtain an initial processor allocation and scheduling result. We then adjust the frequencies to reduce energy consumption even more. Given that different heterogeneous processors may have optimal frequencies for energy consumption that vary, our objective now becomes

$$\begin{array}{l}Minimize E\left(G\right)\\ subject to: R\left(G\right)\ge R_{req}\left(G\right)\end{array}$$

(16)

In this context, we can employ the Karush–Kuhn–Tucker (KKT) conditions to solve the problem. Therefore, we can construct a Lagrangian function as follows:

$$\begin{array}{c}L\left(f,\sigma \right)=E\left(G,f\right)+\sigma \left(R_{req}\left(\mathrm{G}\right)-R\left(G,f\right)\right)\end{array}$$

(17)

In this formulation, $f=\left(f_1,f_2,\dots ,f_n\right)$ represents the vector of frequencies for the processors; $E\left(G,f\right)$ denotes the total energy consumption of the DAG, expressed as $E\left(G,f\right)={{\displaystyle \sum }}_{i=1}^{n}E\left(t_i,f_i\right)$, and $R\left(G,f\right)$ indicates the reliability of the DAG, given by $R\left(G,f\right)={{\displaystyle \prod }}_{i=1}^{n}R\left(t_i,f_i\right)$.

Next, we will proceed with the derivative with respect to $f_i$:

$$\begin{array}{c}{\displaystyle \frac{\partial L\left(f,\sigma \right)}{\partial f_i}}={\displaystyle \frac{\partial E\left(G,f\right)}{\partial f_i}}-\sigma {\displaystyle \frac{\partial R\left(G,f\right)}{\partial f_i}}\end{array}$$

(18)

The energy function $E\left(G,f\right)$ is the sum of the energy consumption of each subtask, while $R\left(G,f\right)$ is the product of the reliability of each task.

Next, the derivative of the energy function $E\left(t_i,u_k,f_i\right)$ with respect to $f_i$ is

$$\begin{array}{ll}& {\displaystyle \frac{\partial E\left(t_i,u_k,f_i\right)}{\partial f_i}}={\displaystyle \frac{W_i}{f_i}}{\displaystyle \frac{\partial (P_{ind}+C_{\left\{k,ef\right\}}{f}_i^{m_k})}{\partial f_i}}-(P_{ind}+C_{\left\{k,ef\right\}}{f}_i^{m_k}){\displaystyle \frac{W_i}{f_i^2}}\\ & ={\displaystyle \frac{W_i}{f_i}}\left(m_k{C}_{\left\{k,ef\right\}}{f}_i^{m_k-1}\right)-(P_{ind}+C_{\left\{k,ef\right\}}{f}_i^{m_k}){\displaystyle \frac{W_i}{f_i^2}}\\ & =W_i\left({\displaystyle \frac{m_k{C}_{\left\{k,ef\right\}}{f}_i^{m_k-1}}{f_i}}-{\displaystyle \frac{P_{ind}+C_{\left\{k,ef\right\}}{f}_i^{m_k}}{f_i^2}}\right)\\ & =W_i\left({\displaystyle \frac{m_k{C}_{\left\{k,ef\right\}}{f}_i^{m_k-1}}{f_i}}-{\displaystyle \frac{P_{ind}}{f_i^2}}-{\displaystyle \frac{C_{\left\{k,ef\right\}}{f}_i^{m_k}}{f_i^2}}\right)\\ & =W_i\left({\displaystyle \frac{m_k{C}_{\left\{k,ef\right\}}{f}_i^{m_k-2}}{f_i^0}}-{\displaystyle \frac{P_{ind}}{f_i^2}}-{\displaystyle \frac{C_{\left\{k,ef\right\}}{f}_i^{m_k}}{f_i^2}}\right)\\ & =W_i\left(m_k{C}_{\left\{k,ef\right\}}{f}_i^{m_k-2}-{\displaystyle \frac{P_{ind}}{f_i^2}}-C_{\left\{k,ef\right\}}{f}_i^{m_k-2}\right)\\ & =W_i\left(\left(m_k-1\right)C_{\left\{k,ef\right\}}{f}_i^{m_k-2}-{\displaystyle \frac{P_{ind}}{f_i^2}}\right)\end{array}$$

(19)

The derivative of the reliability function $R\left(t_i,u_k,f_i\right)$ with respect to $f_i$ is

$$\begin{array}{c}{\displaystyle \frac{\partial R\left(t_i,u_k,f_i\right)}{\partial f_i}}=R\left(t_i,u_k,f_i\right)\cdot \left(-{\displaystyle \frac{\partial ({\lambda }_k\left(f_i\right)\frac{W_i}{f_i})}{\partial f_i}}\right)\end{array}$$

(20)

where ${\mathsf{\lambda }}_k\left(f_i\right)={\mathsf{\lambda }}_F·{10}^{{\displaystyle \frac{d\left(1-f_i\right)}{1-f_{min}}}}$; its derivative is calculated as follows:

$$\begin{array}{c}{\displaystyle \frac{\partial {\lambda }_k\left(f_i\right)}{\partial f_i}}={\lambda }_F\cdot \mathit{ln}\left(10\right)\cdot d\cdot {\displaystyle \frac{-1}{1-f_{min}}}\cdot {10}^{{\displaystyle \frac{d\left(1-f_i\right)}{1-f_{min}}}}\end{array}$$

(21)

So:

$$\begin{array}{ll}& {\displaystyle \frac{\partial R\left(t_i,u_k,f_i\right)}{\partial f_i}}=R\left(t_i,u_k,f_i\right)\left(-{\displaystyle \frac{W_i}{f_i}}{\lambda }_F\cdot \mathit{ln}\left(10\right)\cdot d\cdot {\displaystyle \frac{-1}{1-f_{min}}}\cdot {10}^{{\displaystyle \frac{d\left(1-f_i\right)}{1-f_{min}}}}+{\lambda }_k\left(f_i\right){\displaystyle \frac{W_i}{f_i^2}}\right)\\ & \begin{array}{c}=R\left(t_i,u_k,f_i\right)\left({\displaystyle \frac{W_i{\lambda }_F\cdot \mathit{ln}\left(10\right)\cdot d\cdot \frac{-1}{1-f_{min}}\cdot {10}^{\frac{d\left(1-f_i\right)}{1-f_{min}}}}{\left(1-f_{min}\right)f_i}}+{\displaystyle \frac{{\lambda }_k\left(f_i\right)W_i}{f_i^2}}\right)\end{array}\end{array}$$

(22)

The derivative of total reliability is

$$\begin{array}{c}{\displaystyle \frac{\partial R\left(G,f\right)}{\partial f_i}}=R\left(G,f\right)\cdot {{\displaystyle \sum }}_{j=1}^n\left[{\displaystyle \frac{\partial R\left(t_j,u_k,f_j\right)}{\partial f_j}}\right]\end{array}$$

(23)

For $f_i$:

$$\begin{array}{c}{\displaystyle \frac{\partial R\left(G,f\right)}{\partial f_i}}=R\left(G,f\right)\cdot \left[{\displaystyle \frac{W_i{\lambda }_F\cdot \mathit{ln}\left(10\right)\cdot d\cdot {10}^{\frac{d\left(1-f_i\right)}{1-f_{min}}}}{\left(1-f_{min}\right)f_i}}+{\displaystyle \frac{{\lambda }_k\left(f_i\right)W_i}{f_i^2}} \right]\end{array}$$

(24)

Simultaneously solving the equations by substituting the derivatives of the energy function and the reliability function into the KKT conditions yields the following:

$$W_i\left(\left(m-1\right)C_e{f}_i^{m-2}-{\displaystyle \frac{P_{ind}}{f_i^2}}\right)=\sigma R\left(G,f\right)\left[{\displaystyle \frac{W_i{\lambda }_F\cdot \mathit{ln}\left(10\right)\cdot d\cdot {10}^{\frac{d\left(1-f_i\right)}{1-f_{min}}}}{\left(1-f_{min}\right)f_i}}+{\displaystyle \frac{{\lambda }_k\left(f_i\right)W_i}{f_i^2}}\right]$$

(25)

$$\left(m-1\right)C_e{f}_i^{m-2}-{\displaystyle \frac{P_{ind}}{f_i^2}}=\sigma R\left(G,f\right)\cdot \left[{\displaystyle \frac{{\lambda }_F\cdot \mathit{ln}\left(10\right)\cdot d\cdot {10}^{\frac{d\left(1-f_i\right)}{1-f_{min}}}}{\left(1-f_{min}\right)f_i}}+{\displaystyle \frac{{\lambda }_k\left(f_i\right)}{f_i^2}}\right]$$

(26)

As seen from Equation (26), the left-hand side is an increasing function of $f_i$, while the right-hand side is a decreasing function of $f_i$. Therefore, within the domain of $f_i$, there exists only one intersection point, i.e., a unique solution, which demonstrates the existence of a unique optimal frequency for $f_i$. Due to the monotonicity of the energy and reliability functions with respect to frequency, the KKT condition indicates the existence of a unique global optimum. Although the computational complexity of directly solving the KKT system is large, we utilize the Fibonacci search algorithm as a numerically effective method for locating the minimum value of the energy function under reliability constraints. The concave–convex structure of this problem ensures that the Fibonacci search converges to the same solution as the optimal point based on KKT and has predefined precision.

In this study, we have designed a simple Fibonacci search algorithm to find the set of frequencies for $f_i$ that satisfies R$\left(G,f\right)=R_{given}$, thereby identifying the optimal frequency. As shown in Algorithm 2, the steps are as follows:

Algorithm 2: SEFFA
Input: $G=\left(N, E\right),U, R_{given}$ Output: $f_1,f_2,\dots ,f_n$
1:	Initialize Fibonacci sequence $F_n$ with sufficient length
2:	Compute the upper and lower bounds of the search region $ub$ and $lb$
3:	while $\left(ub-lb>\epsilon \right)$ do
4:	$n$ = length_of_$F_n$
5:	Compute $\sigma 1$ and $\sigma 2$
6:	for each processor $u_k$ do:
7:	$f_{lb}$ = $f_{k,min}$, $f_{ub}$ = $f_{k,max}$
8:	while ($f_{ub}$ − $f_{lb}$ > $\epsilon$) do
9:	$f$ = ($f_{lb}$ + $f_{ub})$/2
10:	if $\sigma$ $\left(f\right)$ < $mid$ then
11:	$f_{lb}$ = $f$
12:	else
13:	$f_{lb}$ = $f$
14:	end if
15:	end while
16:	for each task $t_i$ allocated to the processor $u_k$ do
17:	$f_i$ = $f$
18:	end for
19:	Compute $R\left(G,f\right)$
20:	if $R\left(G, f\right)$ < $R_{given}$ then
21:	$lb$ = $mid$
22:	else
23:	$ub$ = $mid$
24:	end if
25:	Update $F_n$ for next iteration
26:	end while
27:	return $f_1,f_2,\dots ,f_n$

Generating a Fibonacci Sequence: Generate a sufficiently long Fibonacci sequence of length $F_n$ to determine the search interval. The sequence is defined as $F_0$= 0, $F_1$= 1, and $F_{n }$ = $F_{n-1}$ +$F_{n-2}$. Choose an appropriate $n$ to ensure that the length of the sequence meets the needs of the search interval.

Initializing the Search Interval: Set the initial search interval as [a, b], where $a$ and $b$ represent the possible range of values for the frequency f. Typically, a = 0, while b is a larger value.

Fibonacci search steps: Use the Fibonacci sequence to progressively narrow the search interval until the desired precision is achieved. First, two initial points are calculated; then the corresponding frequency $f_i$ is calculated for each $\sigma$ value; then total reliability is calculated and compared with the reliability requirements, and the iteration stops when the reliability requirements are met. The algorithm returns the optimal frequency setting for each task. In Step 3, the two initial points are calculated as follows:

$$\begin{array}{c}{\sigma }_1=a+{\displaystyle \frac{F_{n-2}}{F_n}}\left(b-a\right)\end{array}$$

(27)

$$\begin{array}{c}{\sigma }_2=a+{\displaystyle \frac{F_{n-1}}{F_n}}\left(b-a\right)\end{array}$$

(28)

The complexity of SEFFA is $O\left(mnlogL\right)$, and the overall scheduling process is shown in Figure 2.

6. Experiments

In this section, we integrate the proposed EAWRS (energy-aware weighted scheduling algorithm with reliability constraints) and the SEFFA (search-based energy frequency adjustment algorithm) to address the scheduling of Directed Acyclic Graphs (DAGs) on heterogeneous distributed systems. Simultaneously, we consider constraints on reliability, as well as objectives related to energy consumption and makespan under these constraints. This subsection will evaluate the performance from various perspectives, including the diversity of DAG applications.

6.1. Comparative Algorithms

We compare our EAWRS + SEFFA approach with the state-of-the-art methods ODS + SOEA, MR + SEFFA, and HEFT + SEFFA. Since MR and HEFT focus solely on task allocation, we employ the SEFFA to assist in determining processor frequencies for a fairer comparison.

6.2. Experimental Platform and DAG Applications

The probability of task failures in real system is very small and difficult to control. So, similar to most existing studies, we ran simulations. These experiments were carried out on a laptop with 16 GB of RAM and a 12th Gen Intel(R) Core(TM) i7-12650H processor (Intel Corporation, Santa Clara, CA, USA) using Python version 3.9.12. The processor parameters were randomly set within the following ranges: $(P_{ind}\in \left[0.4, 0.8\right]$, $C_{k,ef}\in \left[0.8, 1.3\right]$, $f\in \left[0.3, 1.0\right]$, and $m_k\in \left[2.7, 3.0\right]$, ${\lambda }_F\in$ [0.1 × 10⁻⁵, 1.0 × 10⁻⁵], and $d\in \left[1, 3\right]$). They reflect the characteristics of the real world, such as for Intel Mobile Pentium III (Intel Corporation, Santa Clara, CA, USA) and ARM Cortex-A9 (ARM Holdings, Cambridge, UK). The purpose of performing this is to ensure that the experimental environment can simulate the diversity of real heterogeneous computing platforms. It is important to note that this work does not consider redundancies that can be deployed to achieve extremely high reliability. For the actual deployment of other systems, these parameters can be adjusted based on the specific hardware configuration and reliability requirements of the target platform while preserving the core scheduling logic of our algorithm. The adjustments include calibrating processor-specific parameters and fine-tuning frequency adjustment thresholds to align with the actual DVFS capabilities of the deployed system.

We evaluated the performance under three different DAG applications: fast Fourier transform (FFT), Gaussian Elimination (GE), and random DAGs. Each has distinct characteristics:

Fast Fourier Transform (FFT): This is an efficient algorithm for computing discrete Fourier transforms in computers, significantly reducing the number of multiplications required. FFT applications exhibit high levels of parallelism. An example of a parallel FFT application DAG for $\rho$ = 4 is shown in Figure 3. The parameter $\rho$ is used to denote the computational scale of FFT and can be used to determine the number of FFT tasks $\left|N\right|$, as shown in formula $\left|N\right|=\left(2+\rho \right)\times 2^{\rho }-1$, where $\rho =2^x$ and $x$ is an integer. The calculation formula is as follows:

$$\begin{array}{c}\left|N\right|=\left(2\times \rho -1\right)+\rho \times {\log }_2\rho =\left(2+\rho \right)\times 2^{\rho }-1\end{array}$$

(29)

Gaussian Elimination (GE) is primarily used for solving systems of linear equations and can also be used to compute the rank of a matrix or its inverse, making it an essential algorithm in linear algebra. The method involves a series of row transformations to convert a matrix into an upper triangular form, followed by back substitution to obtain particular solutions or a set of solutions. GE has a lower degree of parallelism compared to other methods. An illustration of the Gaussian Elimination DAG for ρ = 5 is shown in Figure 4 The parameter $\rho$ is utilized to indicate the computational scale of GE. The calculation of the number of GE tasks $\left|N\right|$ is given in formula $\left|N\right|={\rho }^2+\rho -2/2$, where $\rho$ is an integer.

The random parameter settings for the task sets subject the randomly generated DAG task sets to constraints within specified parameter ranges. These tasks set exhibit random parallelism, and their computational and communication costs are also determined randomly.

6.3. Evaluation Metrics

To ensure the fairness of the comparison, we meticulously designed the following evaluation scenario: By establishing reliability as a strict constraint for the four methods and constructing diverse scenarios through adjusting its value, we executed three other algorithms under this hard reliability constraint to pursue the optimal energy consumption and makespan. Subsequently, we conducted a comparative analysis with the optimal solution in the solution set generated by the EAWRS + SEFFA method across two dimensions: makespan and energy consumption.

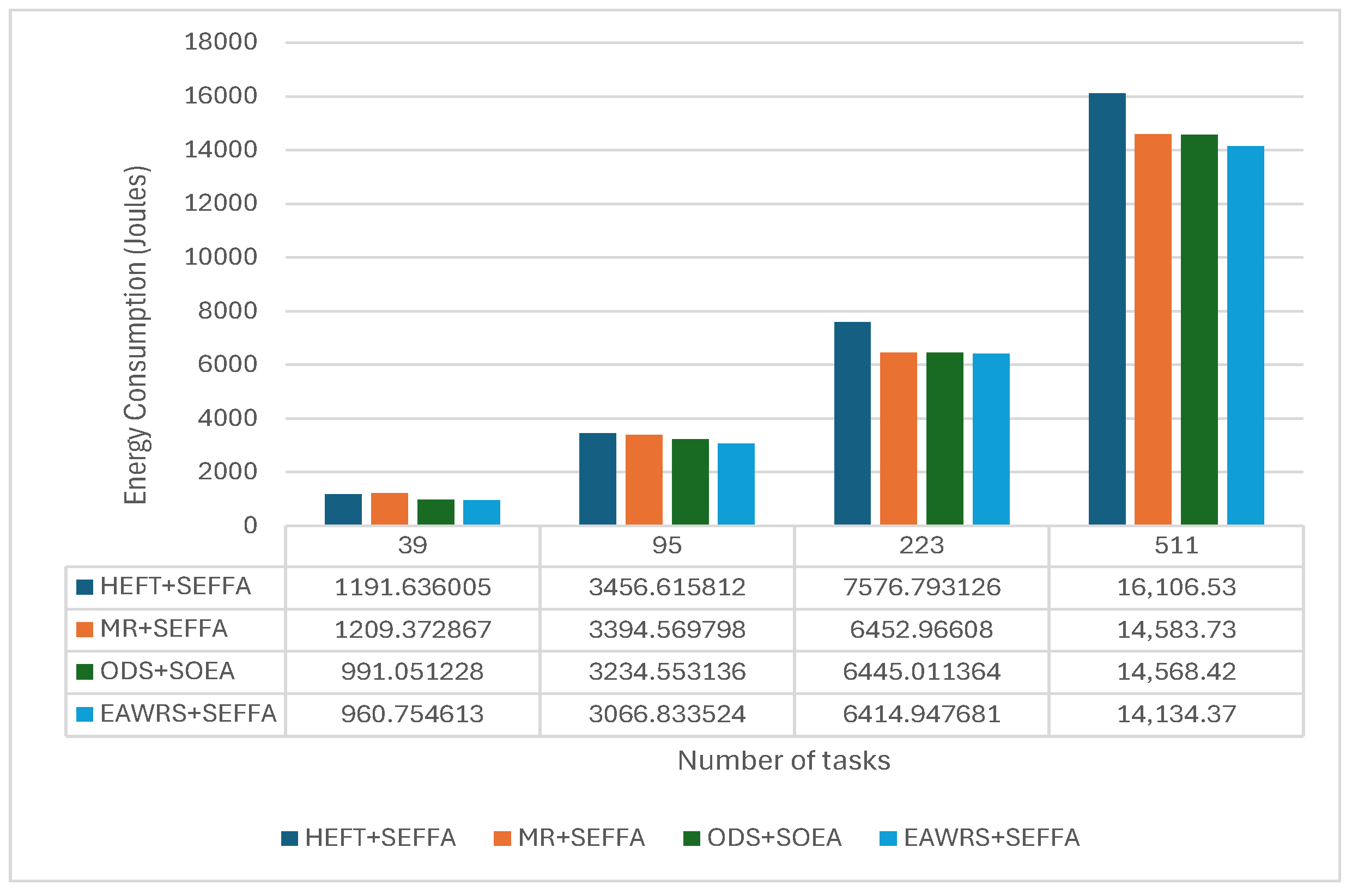
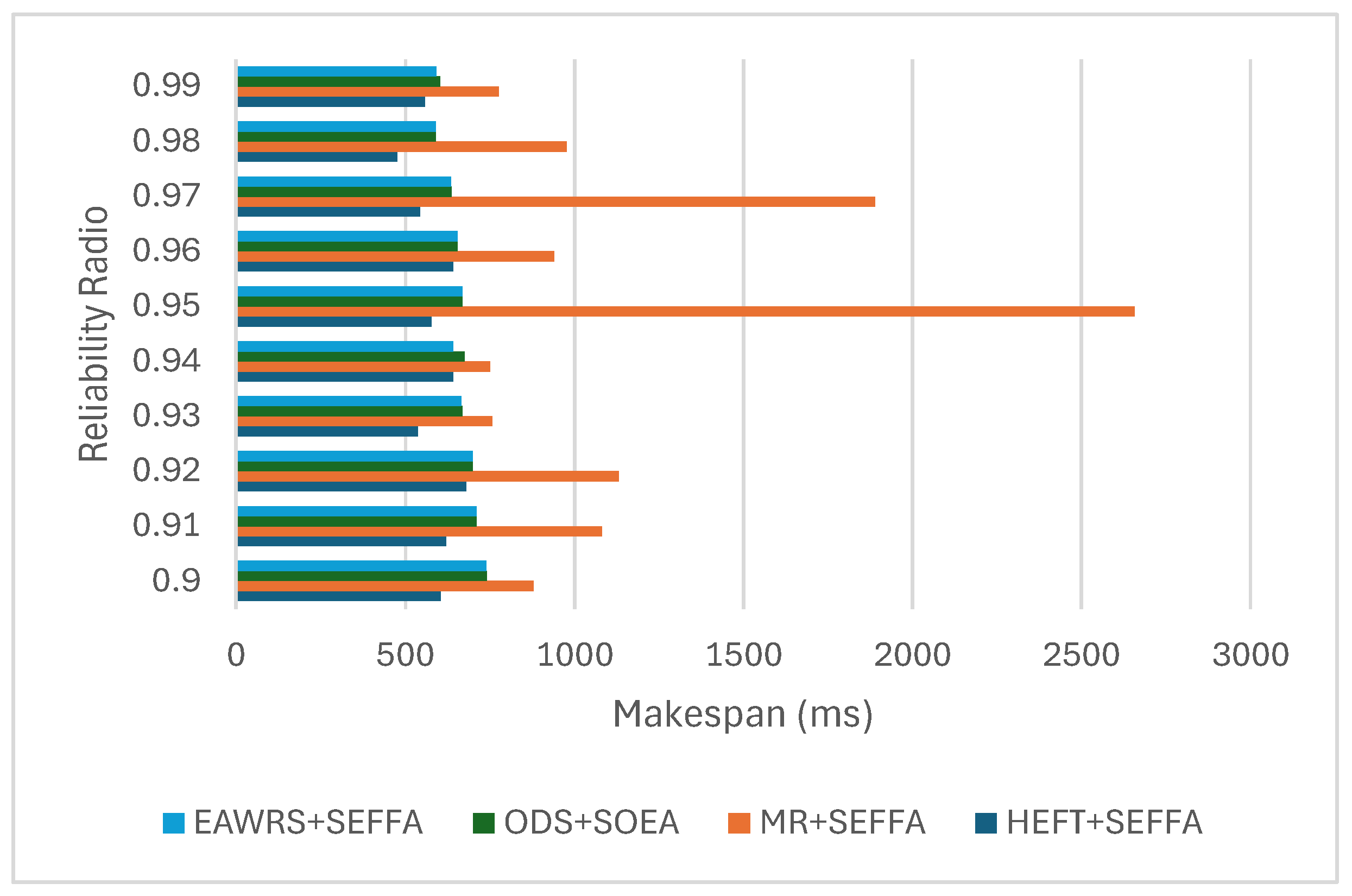
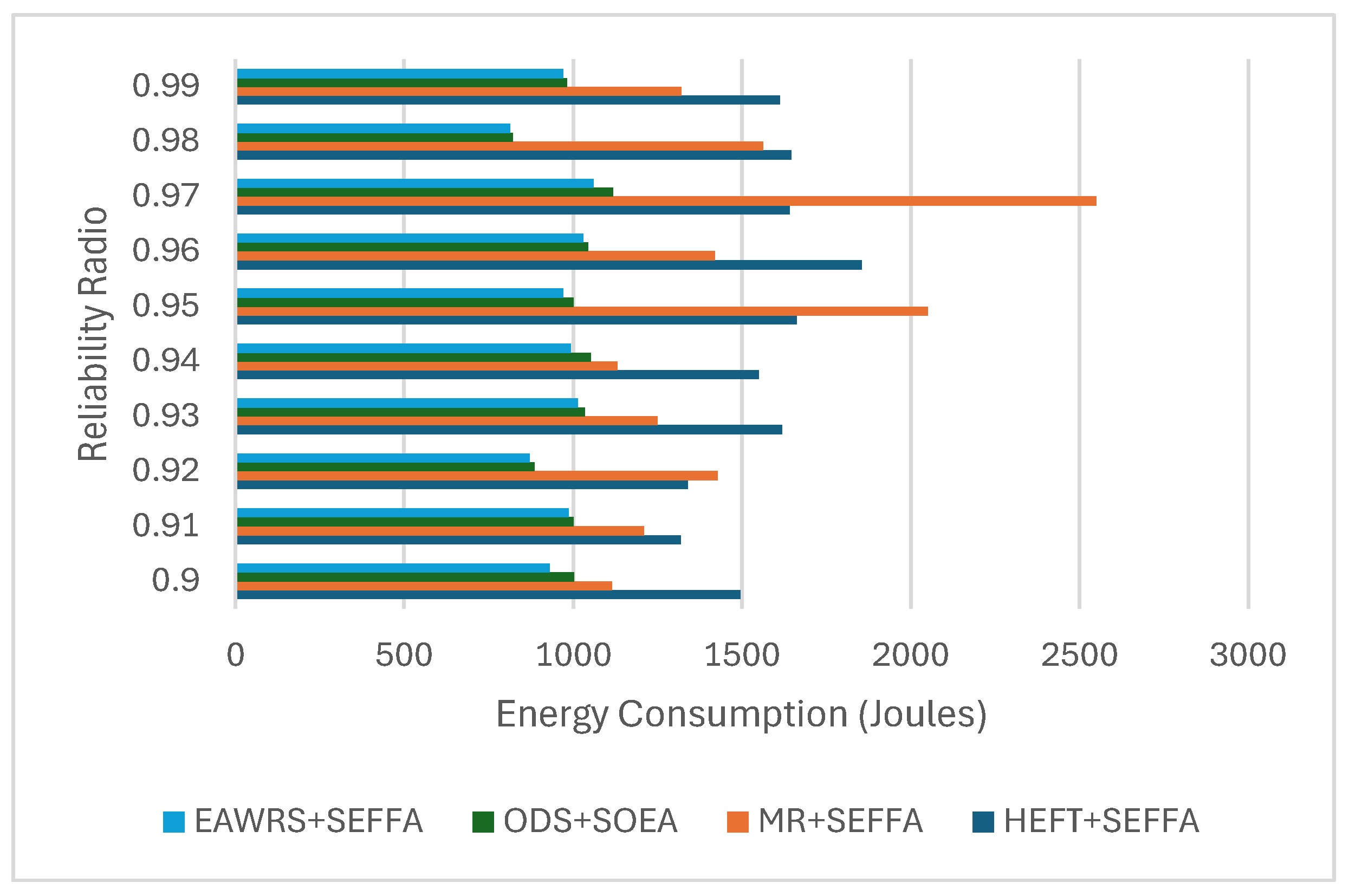
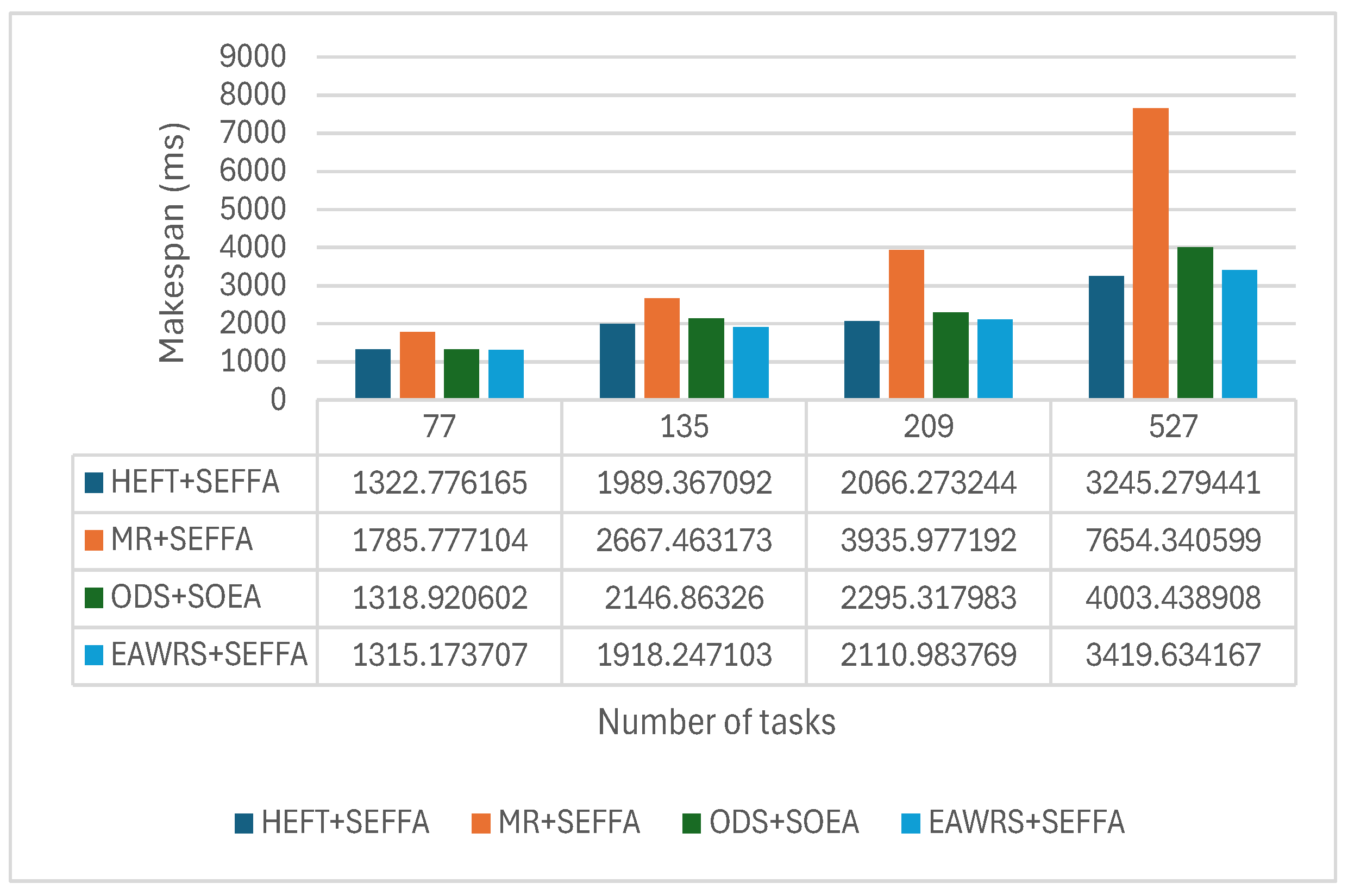
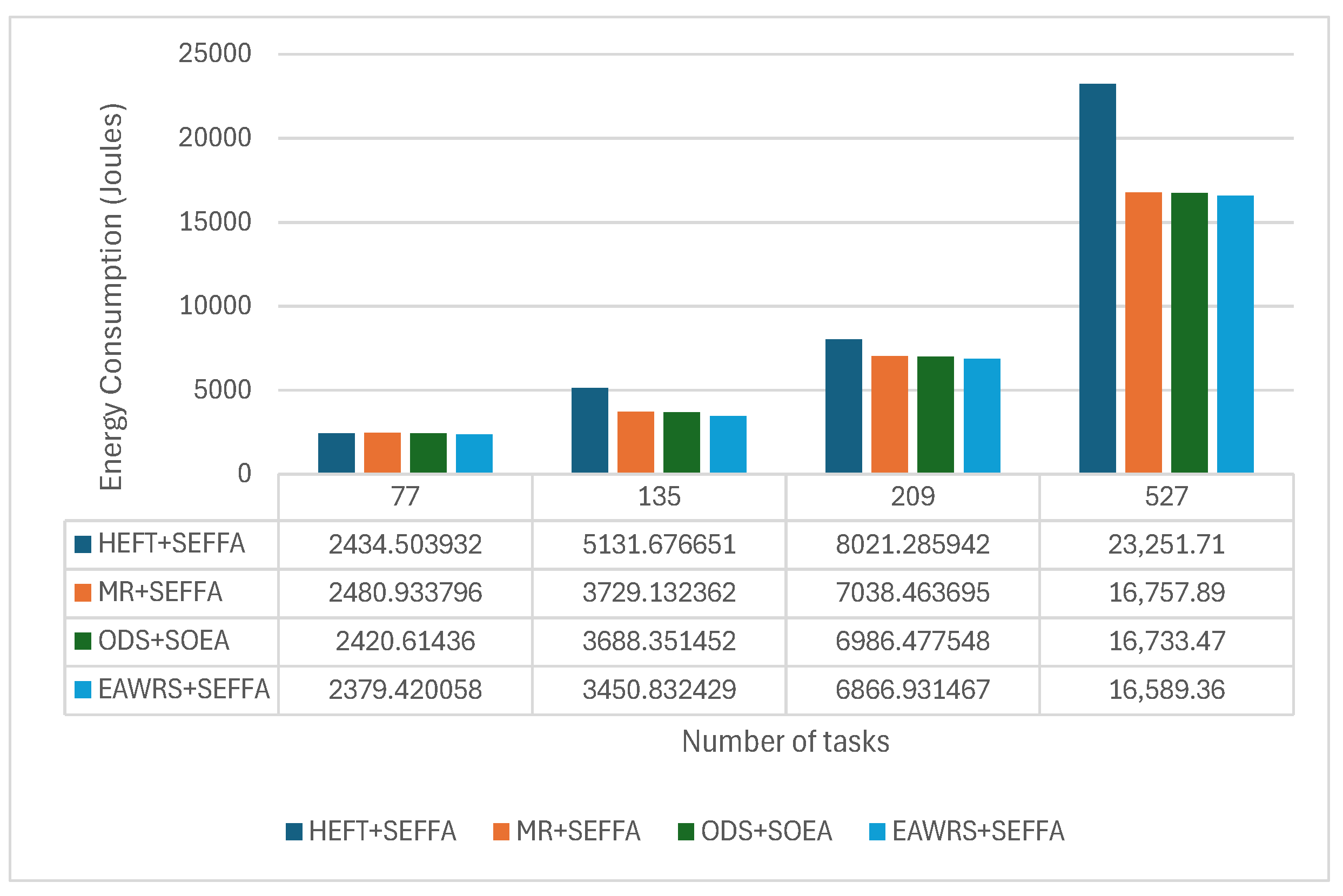
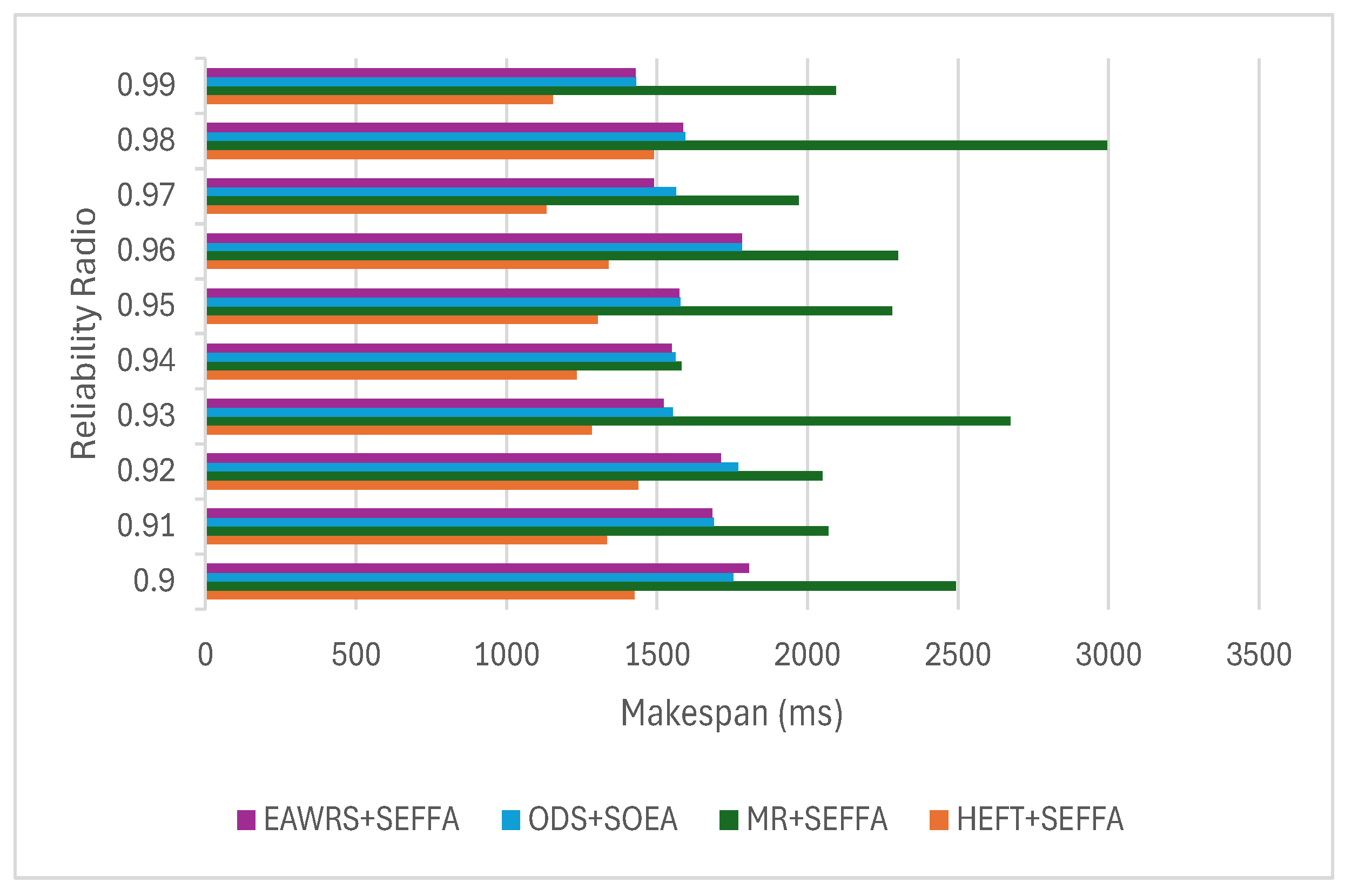
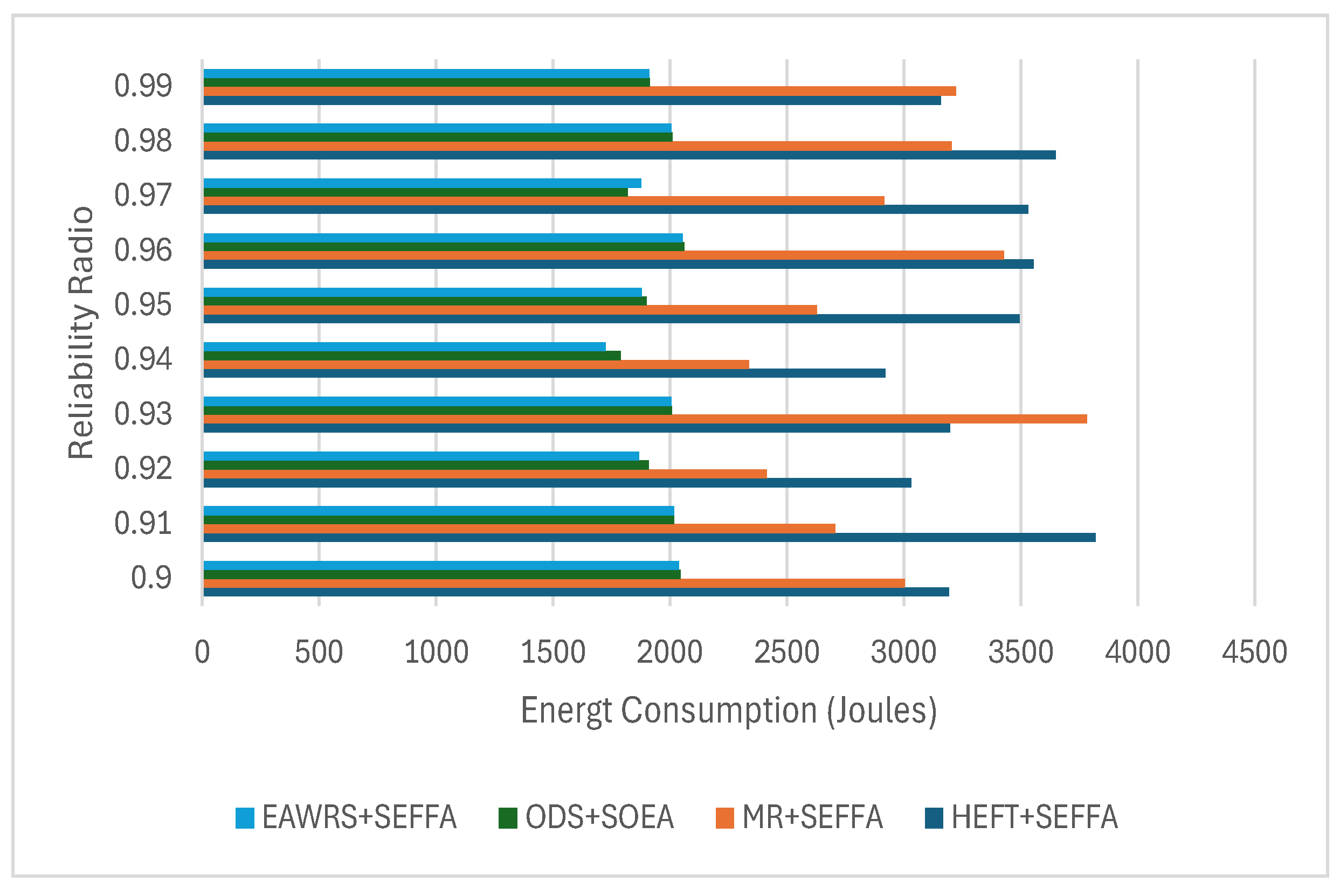
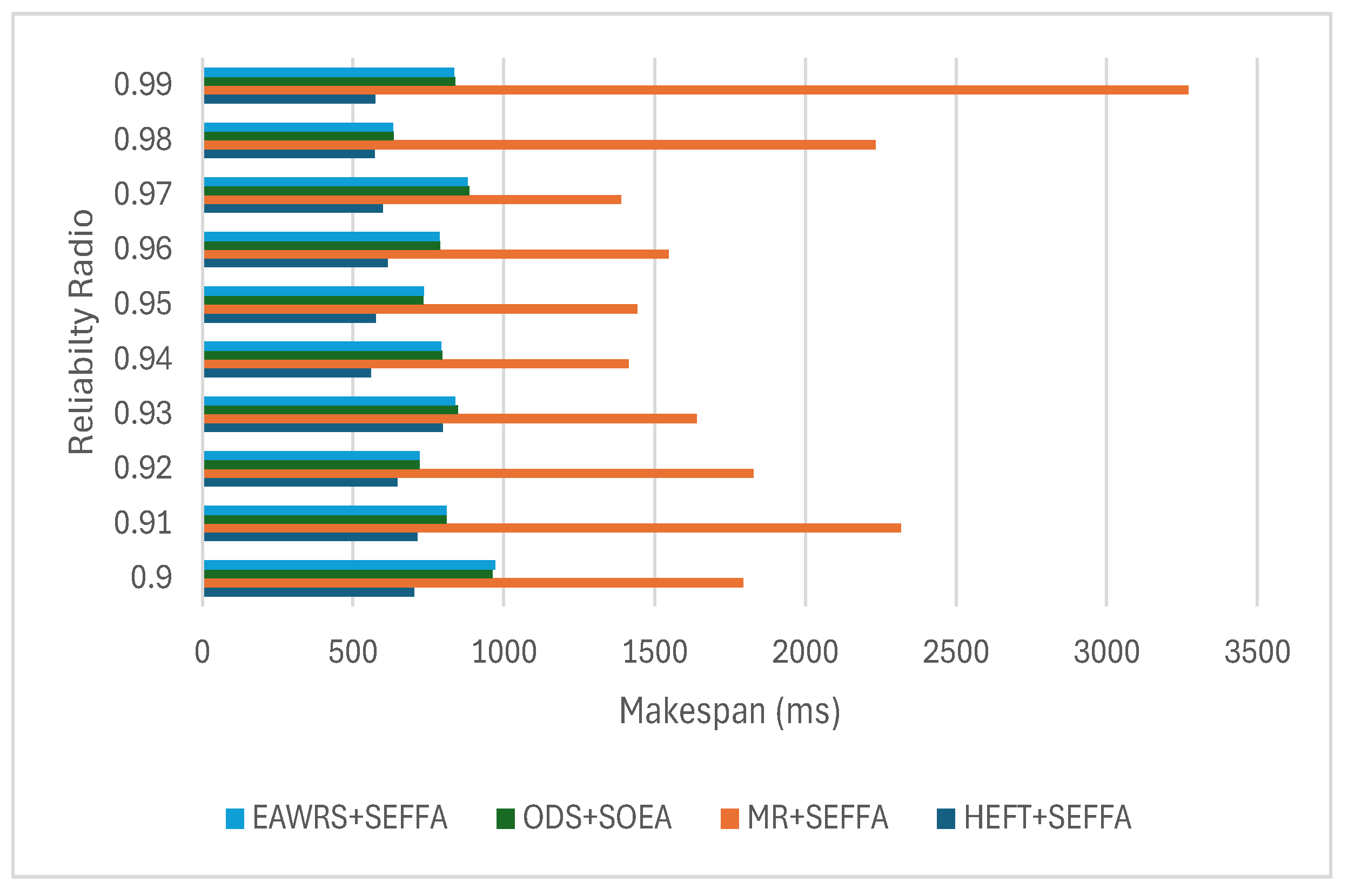
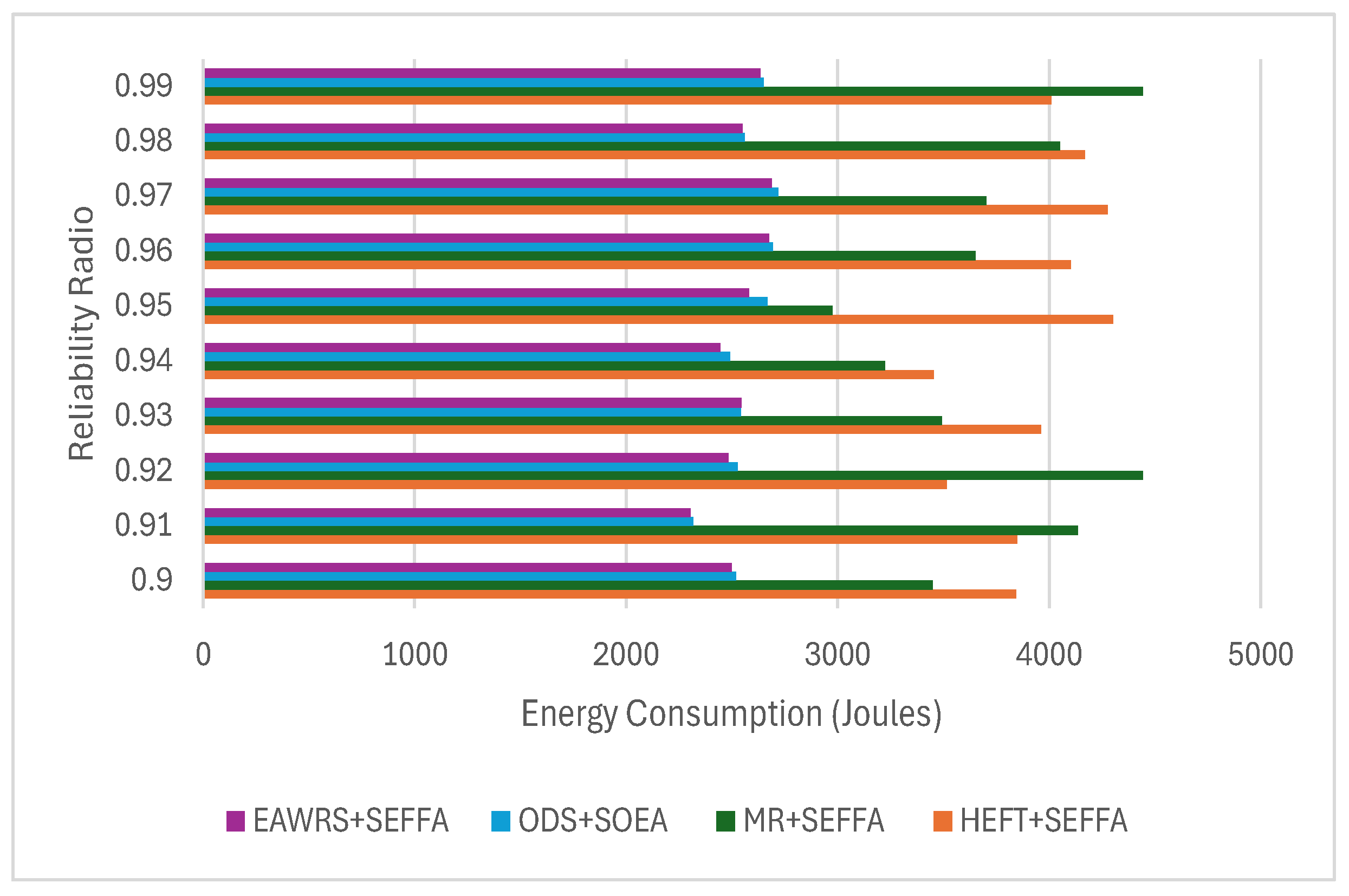
6.4. Results and Analysis

This section presents the experiment and result analysis based on real parallel applications. The MR algorithm, the ODS algorithm, and the HEFT algorithm are selected as benchmark algorithms for evaluating scheduling performance. Since HEFT and MR only perform task allocation, the SEFFA is employed to determine processor operating frequencies. The application data used in the experiments consists of real parallel applications, including the parallel implementations of FFT and GE. The following will be five implementations. Experiments 1 and 3 evaluate scalability by changing the number of tasks in FFT and GE applications, respectively, while Experiments 2 and 4 assess the trade-offs among energy, completion time, and reliability under fixed workloads but dynamic constraints. Experiment 5 uses unpredictable parallel random DAGs to test the generalization ability. These experiments collectively verify the adaptability of EAWRS + SEFFA to workload sizes (Experiments 1 and 3), reliability-critical scenarios (Experiments 2 and 4), and unstructured workflows (Experiment 5).

Experiment 1: Analysis of energy consumption and makespan under different task numbers in the FFT application: In the DAG application generated by FFT, the EAWRS + SEFFA method is compared with three existing methods: HEFT + SEFFA, MR + SEFFA, and ODS + SOEA. The number of subtasks in the FFT application is controlled by the parameter ρ, with values of 3, 4, 5, and 6, corresponding to 39, 95, 223, and 511 subtasks, respectively. As shown in Figure 5, an increase in the number of tasks leads to a rise in makespan for all algorithms. The EAWRS + SEFFA method achieves competitive makespan values across all scenarios. Specifically, when the number of tasks is 39, 95, 223, and 511, the makespan values for EAWRS + SEFFA are 514.81, 708.19, 867.55, and 1158.84, respectively. On average, it reduces the makespan by 2.58% compared to HEFT + SEFFA, by 56.44% compared to MR + SEFFA, and by 4.76% compared to ODS + SOEA.

Figure 6 illustrates the energy consumption of the FFT application under different numbers of tasks. The EAWRS + SEFFA method demonstrates outstanding energy efficiency across all task scales. When the number of tasks increases from 39 to 511, the energy consumption of EAWRS + SEFFA is 960.75, 3066.83, 6414.95, and 14,134.37, respectively. Compared with HEFT + SEFFA, the algorithm achieves an average energy reduction of 14.56%; compared with MR + SEFFA, it reduces energy consumption by an average of 8.47%; and compared with the energy-optimized ODS + SOEA method, it still achieves an average reduction of 2.92%. These results collectively demonstrate the significant energy efficiency advantage of EAWRS + SEFFA under dynamic task loads.

Taken together, in the FFT application, the EAWRS + SEFFA method demonstrates clear advantages in energy consumption control compared to the other three algorithms as the number of tasks varies.

Experiment 2: Energy consumption and makespan under different reliability constraints in FFT applications: According to Figure 7, the makespan performance of each algorithm under different reliability constraints is examined in the FFT application. The EAWRS + SEFFA method exhibits complex yet competitive performance. When the reliability constraint varies between 0.9 and 0.99, at certain values such as 0.93, the makespan of EAWRS + SEFFA is 665.64, which is lower than HEFT’s 536.61. Compared to MR, the advantage of EAWRS + SEFFA is even more pronounced. Across the entire range of reliability constraints, the makespan of EAWRS + SEFFA is significantly lower than that of MR + SEFFA. For example, with a reliability constraint of 0.95, the makespan of MR reaches 2657.56, while that of EAWRS + SEFFA is only 667.67, demonstrating remarkable efficiency. Compared to ODS + SOEA, EAWRS + SEFFA performs similarly in most cases but slightly better in some instances. For example, at a reliability constraint of 0.93, EAWRS + SEFFA achieves a makespan of 665.64, which is lower than ODS + SOEA’s 668.07. The results indicate that EAWRS + SEFFA delivers excellent makespan performance under different reliability constraints, especially under high-reliability constraints, where its advantages become more prominent.

Figure 8 presents the energy consumption results under different reliability constraints. The EAWRS + SEFFA method achieves outstanding energy efficiency. Compared to HEFT + SEFFA, the average energy consumption level is reduced by approximately 38.38%. For instance, at a reliability constraint of 0.9, HEFT + SEFFA consumes 1495.76, whereas EAWRS + SEFFA only consumes 930.71, reducing energy consumption by 37.77%. Compared to MR + SEFFA, EAWRS + SEFFA achieves an average energy reduction of approximately 31.78%. At a reliability constraint of 0.97, EAWRS + SEFFA exhibits remarkable energy efficiency, with an energy reduction of up to 58.44%. Even when compared to the energy-efficient ODS + SOEA method, EAWRS + SEFFA still maintains a slight advantage, achieving an average energy reduction of approximately 2.91%.

Collectively, under different reliability constraints, the EAWRS + SEFFA method demonstrates significant advantages in energy consumption control compared to the other three algorithms, effectively reducing energy consumption and exhibiting superior energy-saving characteristics.

Experiment 3: Energy consumption and makespan under different numbers of tasks in GE applications: In GE-generated DAG applications, the proposed EAWRS + SEFFA method is compared with five existing methods. The number of tasks is controlled by parameter $\rho$, which is set to 12, 16, 20, and 32, corresponding to subtask counts $N$ of 77, 135, 209, and 527, respectively. Each subtask’s computation and communication costs are randomly generated within the range of [10, 100].

As shown in Figure 9, the makespan results of the GE application reveals the differentiated performance of the EAWRS + SEFFA method. Under lower task volumes (77 and 135 tasks), EAWRS + SEFFA achieves slightly shorter makespans than HEFT + SEFFA, with reductions of 0.58% and 3.57%, respectively. However, under higher task volumes (209 and 527 tasks), its makespan increases by 2.16% and 5.37% compared to HEFT + SEFFA, with the gap widening as the task volume grows. In contrast, EAWRS + SEFFA significantly outperforms MR + SEFFA across all task volumes, achieving an average makespan reduction of 39.03%, with a maximum reduction of 46.36% at 209 tasks. Compared to ODS + SOEA, EAWRS + SEFFA maintains a consistent advantage, with an average makespan reduction of 8.39%, though the improvement is less pronounced than that over MR + SEFFA.

Figure 10 presents the energy consumption results for the GE application, demonstrating the sustained energy efficiency advantage of the EAWRS + SEFFA method. Compared to HEFT + SEFFA, the algorithm achieves significant energy savings across all task volumes, notably reducing energy consumption by 32.75% at 135 tasks (from 5131.68 to 3450.83) and by 28.65% at 527 tasks (from 23,251.71 to 16,589.36), with an average energy reduction of 19.51%. Compared to MR + SEFFA, it achieves an average energy saving of 3.75%, with a maximum of 7.46% for 135 tasks. Even when compared with the energy-optimized ODS + SOEA method, EAWRS + SEFFA maintains an average energy advantage of 2.68%, with a typical case being a 0.86% reduction at 527 tasks (from 16,733.47 to 16,589.36).

To sum up, under different task counts in the GE application, EAWRS + SEFFA performs well in terms of both energy consumption and makespan.

Experiment 4: Energy consumption and makespan results under different reliability constraints in the GE application: Figure 11 presents the makespan performance of EAWRS + SEFFA in the GE application under different reliability constraints. The results indicate that compared to the MR algorithm, EAWRS + SEFFA demonstrates a significant advantage, achieving a consistently shorter makespan across various reliability constraint levels. This suggests that EAWRS + SEFFA is more efficient than MR + SEFFA under specific conditions. When compared to ODS + SOEA, the two algorithms exhibit similar performance, with EAWRS + SEFFA achieving slight improvements in certain scenarios. Overall, in the GE application, EAWRS + SEFFA demonstrates competitive makespan optimization under different reliability constraints, showing clear advantages over MR + SEFFA and maintaining comparable performance with ODS + SOEA.

Figure 12 illustrates the energy consumption performance of EAWRS + SEFFA under different reliability constraints, where the algorithm exhibits a clear advantage in energy efficiency. Compared to HEFT + SEFFA, EAWRS + SEFFA achieves an average energy reduction of approximately 42.99%. At various reliability levels, such as 0.91, HEFT + SEFFA consumes 3819.81, whereas EAWRS + SEFFA reduces energy consumption to 2015.81, a reduction of 47.23%, demonstrating its effectiveness in minimizing energy consumption when compared to HEFT. Against the MR algorithm, EAWRS + SEFFA continues to excel, with an average energy reduction of 32.46%. For example, at a reliability level of 0.93, the energy consumption of MR + SEFFA is 3783.66, while EAWRS + SEFFA reduces it to 2006.22, a reduction of 46.98%, further proving its energy-saving efficiency. Even when compared to ODS + SOEA, which is known for its energy efficiency, EAWRS + SEFFA still achieves a slight improvement, with an average energy reduction of 3.73%. For instance, at a reliability level of 0.94, ODS + SOEA consumes 1790.98, while EAWRS + SEFFA reduces it to 1724.24.

Through this experiment, it is evident that EAWRS + SEFFA demonstrates outstanding energy-saving performance across different reliability constraints in the GE application, making it highly competitive in energy efficiency.

Experiment 5: Experimental results and analysis based on random DAG task sets: This experiment was conducted using randomly generated DAG task graphs, with the number of tasks set to 100. The results indicate that as reliability constraints become more stringent, EAWRS + SEFFA effectively balances the makespan and energy consumption.

Figure 13 illustrates the makespan performance of EAWRS + SEFFA under different reliability constraints for random task graphs. Compared to HEFT, the makespan of EAWRS + SEFFA is, on average, 27.91% longer. In most reliability constraint conditions, HEFT + SEFFA achieves faster task completion. For example, at a reliability level of 0.94, the makespan of HEFT is 558.6, whereas EAWRS + SEFFA increases it to 791.31, an increase of 41.66%. However, when compared to MR, EAWRS + SEFFA shows a significant advantage, reducing the makespan by an average of 54.75%. At a reliability level of 0.99, MR + SEFFA results in a makespan of 3270.84, whereas EAWRS + SEFFA reduces it to 835.75, an impressive 74.45% reduction, demonstrating the effectiveness of EAWRS + SEFFA in handling high-reliability requirements. When compared to ODS + SOEA, the two algorithms exhibit highly similar performances, with only minor variations across different reliability constraints. Overall, while EAWRS + SEFFA lags behind HEFT in terms of makespan, it significantly outperforms MR + SEFFA and remains competitive against ODS + SOEA.

Figure 14 presents the energy consumption performance of EAWRS + SEFFA under different reliability constraints in random task graphs, highlighting its remarkable energy-saving capabilities. Compared to HEFT + SEFFA, EAWRS + SEFFA reduces energy consumption by an average of 35.56%. At various reliability levels, such as 0.91, HEFT + SEFFA consumes 3847.39, whereas EAWRS + SEFFA reduces it to 2303.04, achieving a 40.14% reduction. Against MR + SEFFA, EAWRS + SEFFA also demonstrated superior performance, reducing energy consumption by an average of 30.23%. For instance, at a reliability level of 0.92, MR + SEFFA consumes 4443.08, whereas EAWRS + SEFFA lowers it to 2483.09, achieving a 44.11% reduction and showcasing the algorithm’s ability to effectively save energy under varying reliability constraints. Even when compared to ODS + SOEA, while the reduction is relatively small, EAWRS + SEFFA still achieves a noticeable improvement, with an average energy reduction of 1.20%. At a reliability level of 0.95, ODS + SOEA consumes 2668.64, while EAWRS + SEFFA reduces it to 2580.42, a 3.30% reduction.

In brief, EAWRS + SEFFA performs exceptionally well in energy consumption reduction under different reliability constraints for random DAG task graphs, proving its strong energy-saving effectiveness.

Summary: EAWRS + SEFFA demonstrates robust energy optimization capabilities across varying reliability constraints. It effectively reduces the makespan while ensuring reliability, showcasing strong comprehensive scheduling performance. This makes it particularly suitable for heterogeneous distributed systems with stringent requirements for both reliability and energy efficiency. It is worth noting that we repeated each experiment 10 times and took the average value. The standard deviation of the results is always lower than 10% of the average value, indicating that our algorithm has high stability.

6.5. Key Limitations

This study simplifies hardware heterogeneity by simulating processor parameters within a limited range (e.g., the DVFS scope), which may not fully capture the behavior of systems with extreme heterogeneity, such as those containing both ultra-low-power and high-performance cores. Additionally, the reliability model only considers transient faults and does not include permanent faults that may significantly impact the long-term stability of the system.

7. Conclusions

This paper introduces two algorithms: the energy-aware scheduling algorithm based on the weight method under reliability constraints (EAWRS), which considers the in-degree and out-degree of DAG nodes and optimizes execution time and energy consumption within a unified range via normalization, and the optimal energy frequency adjustment algorithm based on Fibonacci search (SEFFA), which further optimizes energy consumption under reliability constraints. Experimental results demonstrate that combining these two algorithms achieves superior performance, outperforming comparative algorithms in terms of energy efficiency and completion time.

The contributions of this work provide valuable insights and guidance for the energy-efficient design of parallel applications in heterogeneous distributed systems. In our study, we only considered scenarios where a single application runs within a heterogeneous distributed system, whereas, in real-world settings, systems typically operate multiple applications simultaneously. Although our methods provide feasible and reasonable solutions within a relatively short period, we are interested in exploring more effective techniques to enhance the overall problem-solving performance. To this end, future research will focus on developing multi-objective optimization models, such as the joint optimization of energy consumption, latency, and reliability, as well as enhancing task allocation strategies for IoT edge nodes and designing cross-platform heterogeneous resource scheduling algorithms. At the same time, we will evaluate the adaptability and practical effectiveness of the proposed algorithms in representative IoT application scenarios, including smart manufacturing, environmental monitoring, and intelligent transportation systems, to facilitate their deployment and practical implementation in real-world systems.