Improving Early Detection of Dementia: Extra Trees-Based Classification Model Using Inter-Relation-Based Features and K-Means Synthetic Minority Oversampling Technique
Abstract
1. Introduction
2. Literature Review
2.1. Features Used for Dementia Classification Models
2.2. Feature Engineering for Disease Prediction
2.3. Data Balancing for ML Model Construction
2.4. Machine Learning Classification for Dementia Prediction
2.5. Proposed Work
3. Research Methodology
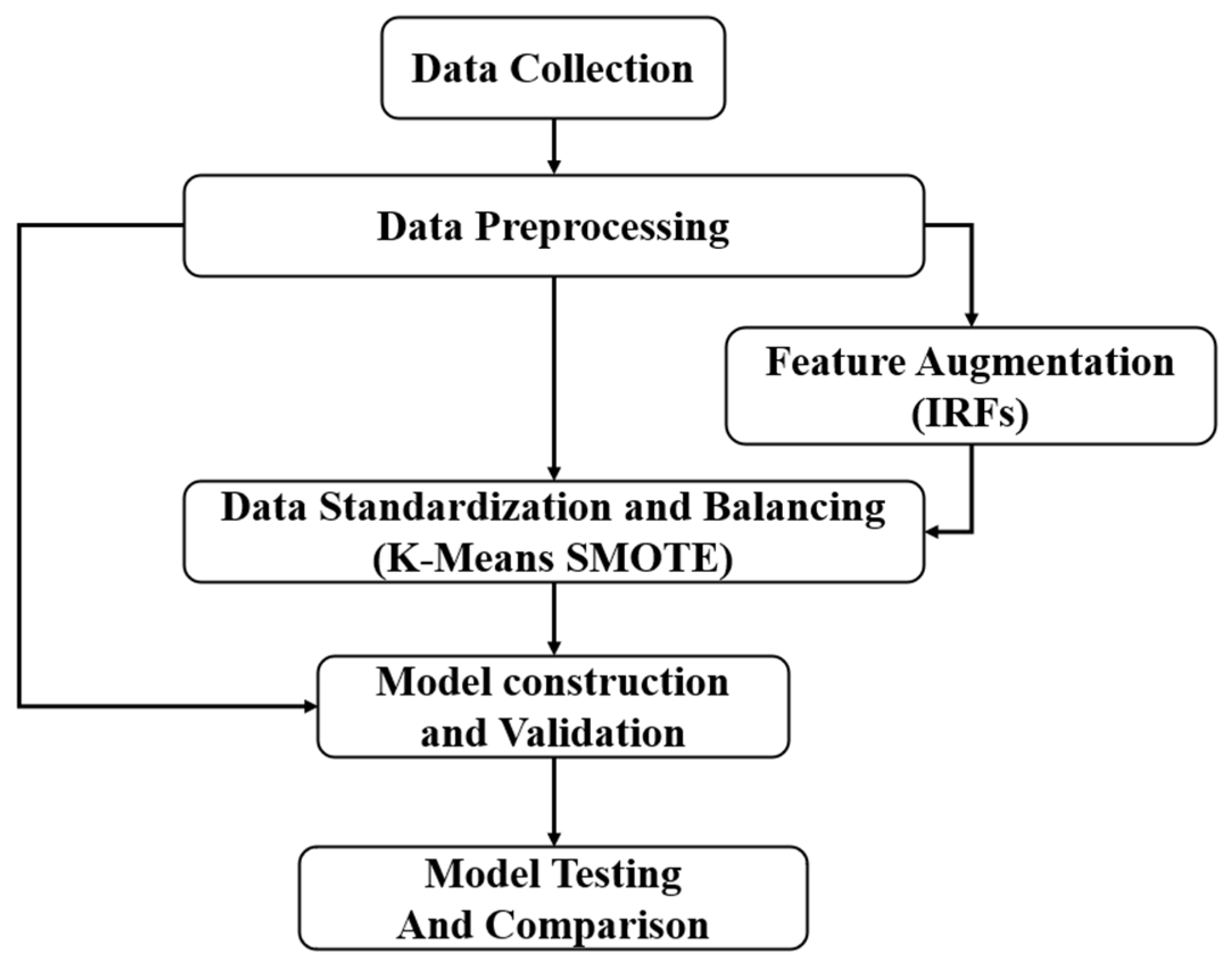
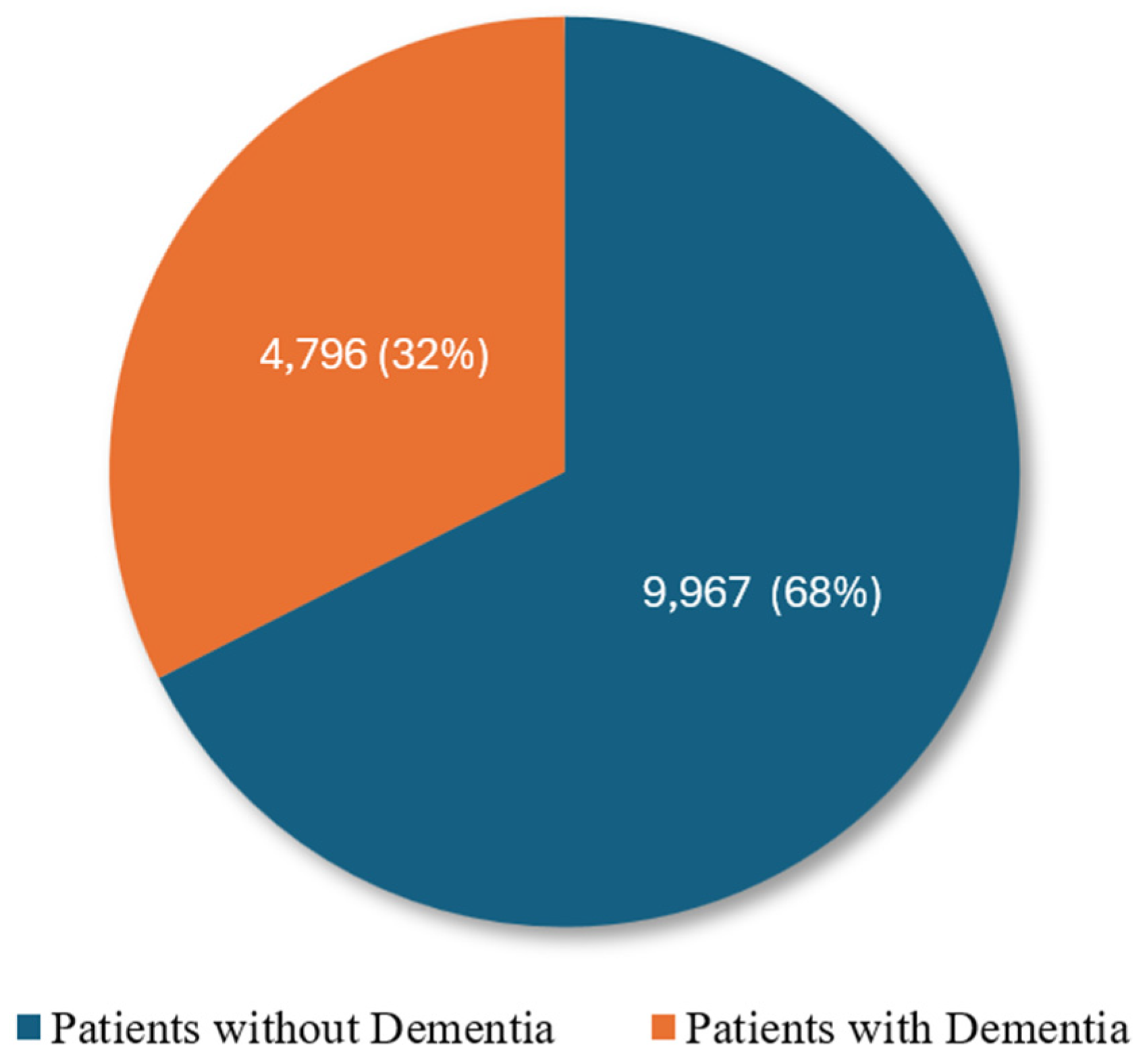
3.1. Data Collection
3.2. Data Preprocessing
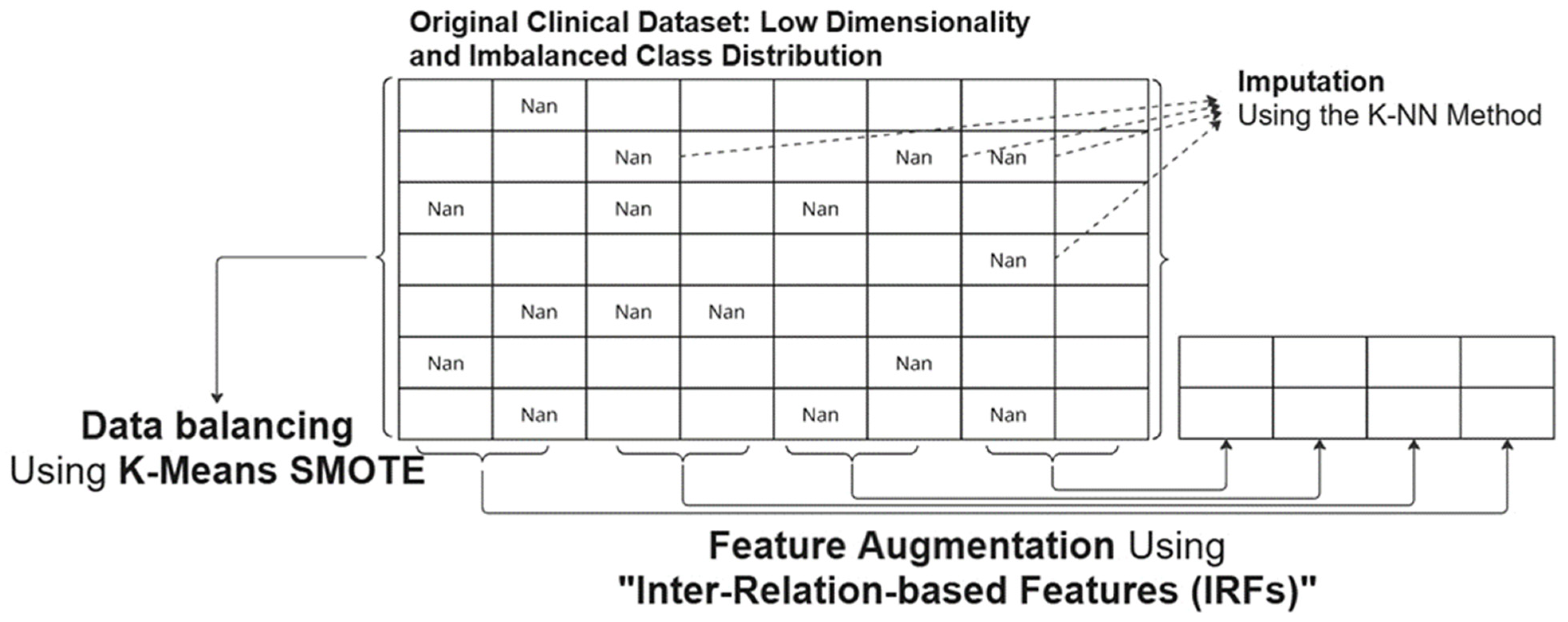
3.3. Feature Augmentation
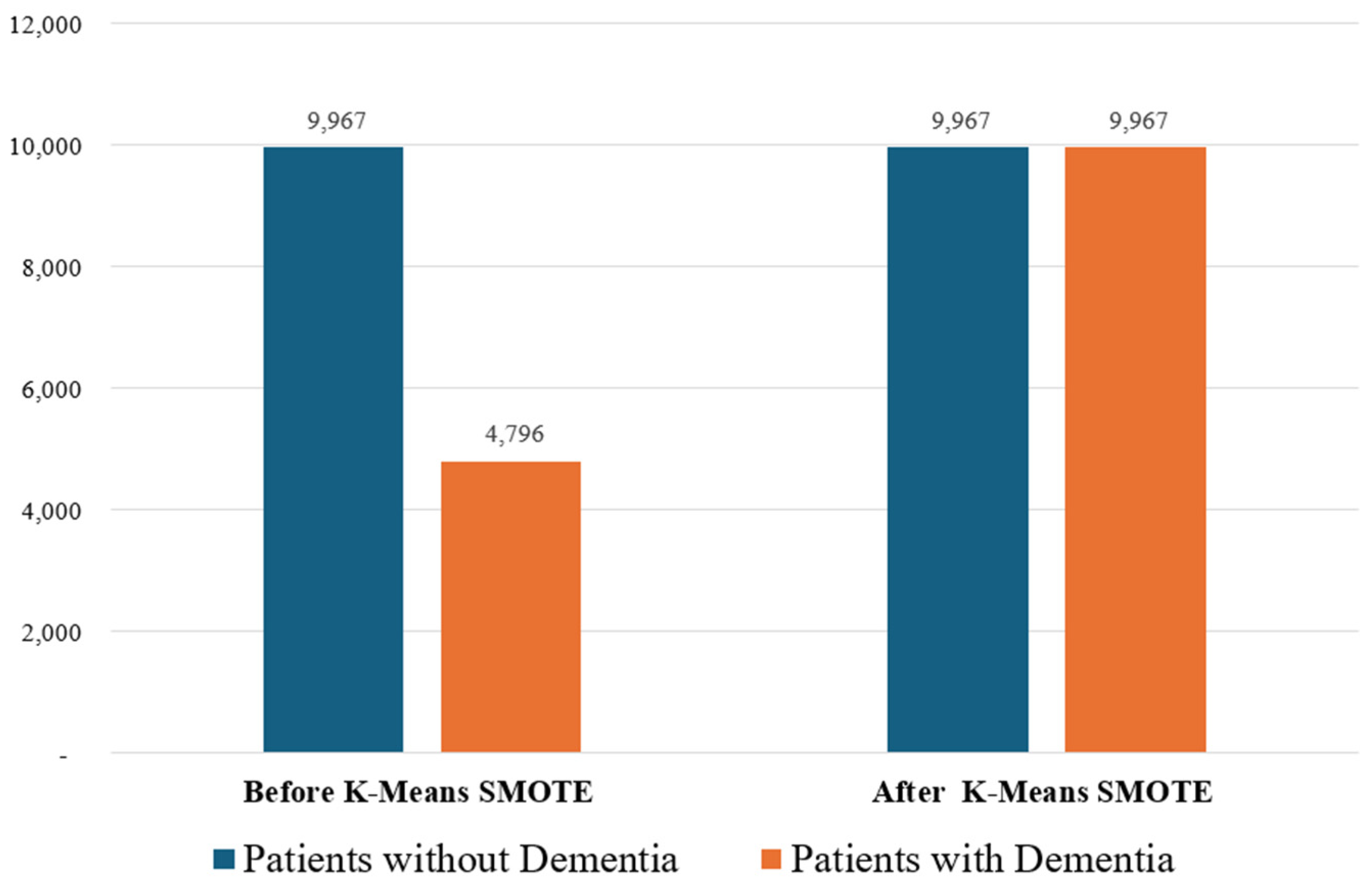
3.4. Data Standardization and Balancing
3.5. Model Construction and Validation
3.6. Model Comparison
4. Results
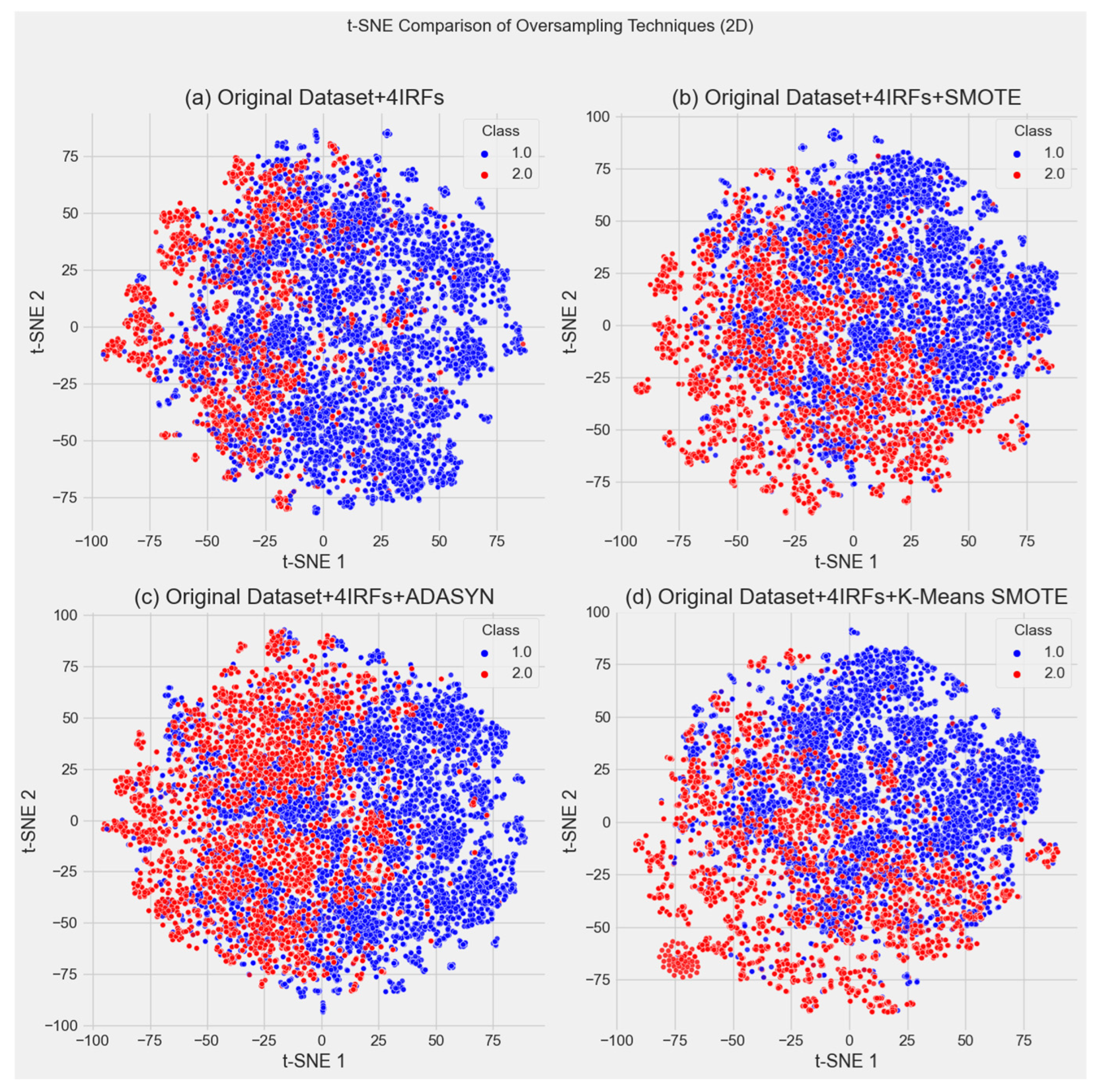
4.1. Evaluation of Synthetic Data
4.1.1. Data Distribution Similarity
4.1.2. Model Performance Consistency
4.1.3. Generalization Capability
4.1.4. Optimal Oversampling Method
4.2. Evaluation of Effective Classification Model
4.2.1. Descriptive Summary of 10-Fold Cross-Validation Results
4.2.2. Model Performance Based on Accuracy
4.2.3. Model Performance Based on Precision
4.2.4. Model Performance Based on Recall
4.2.5. Model Performance Based on F1 Score
4.2.6. Model Performance Based on Average AUC-ROC
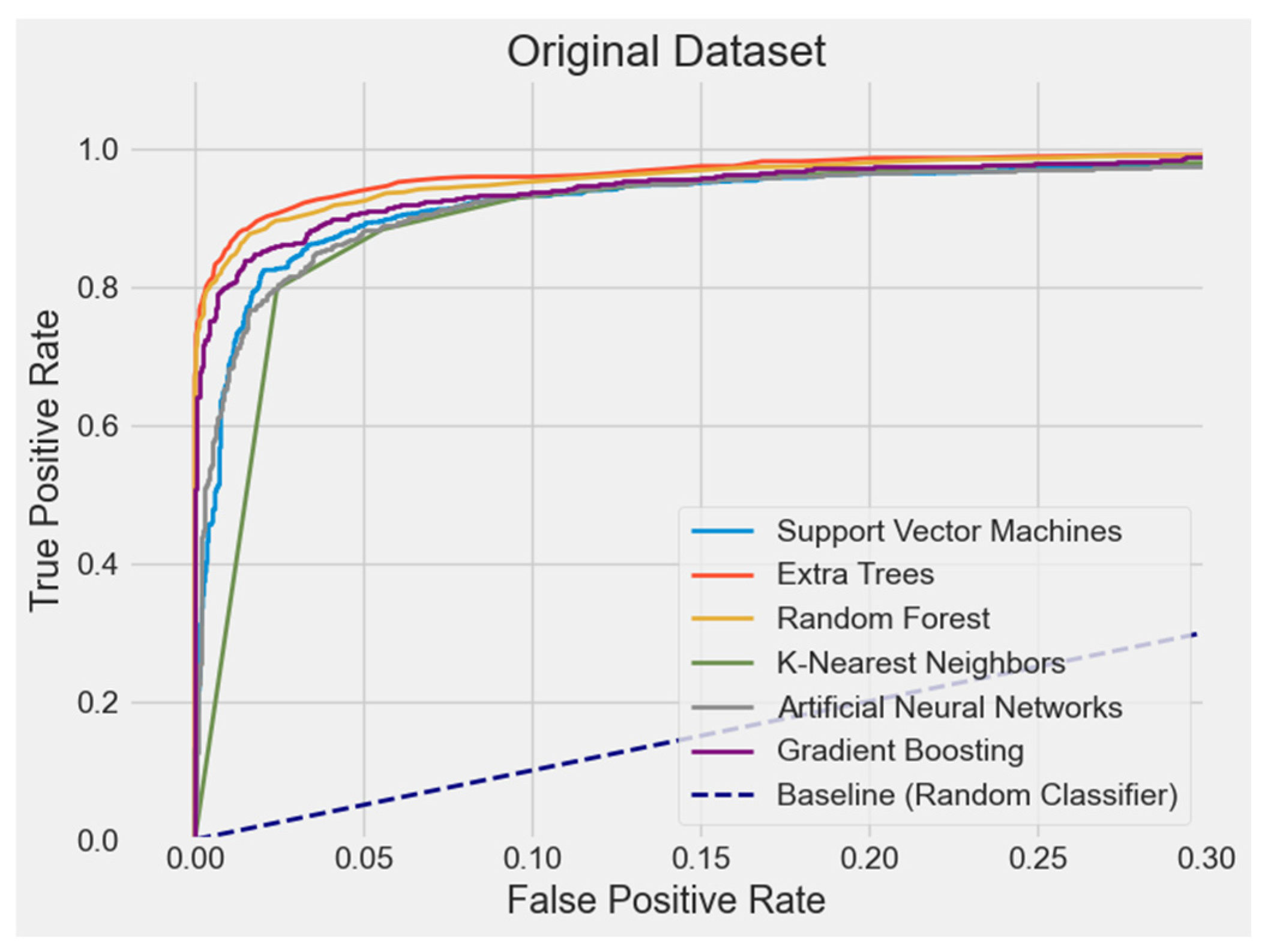
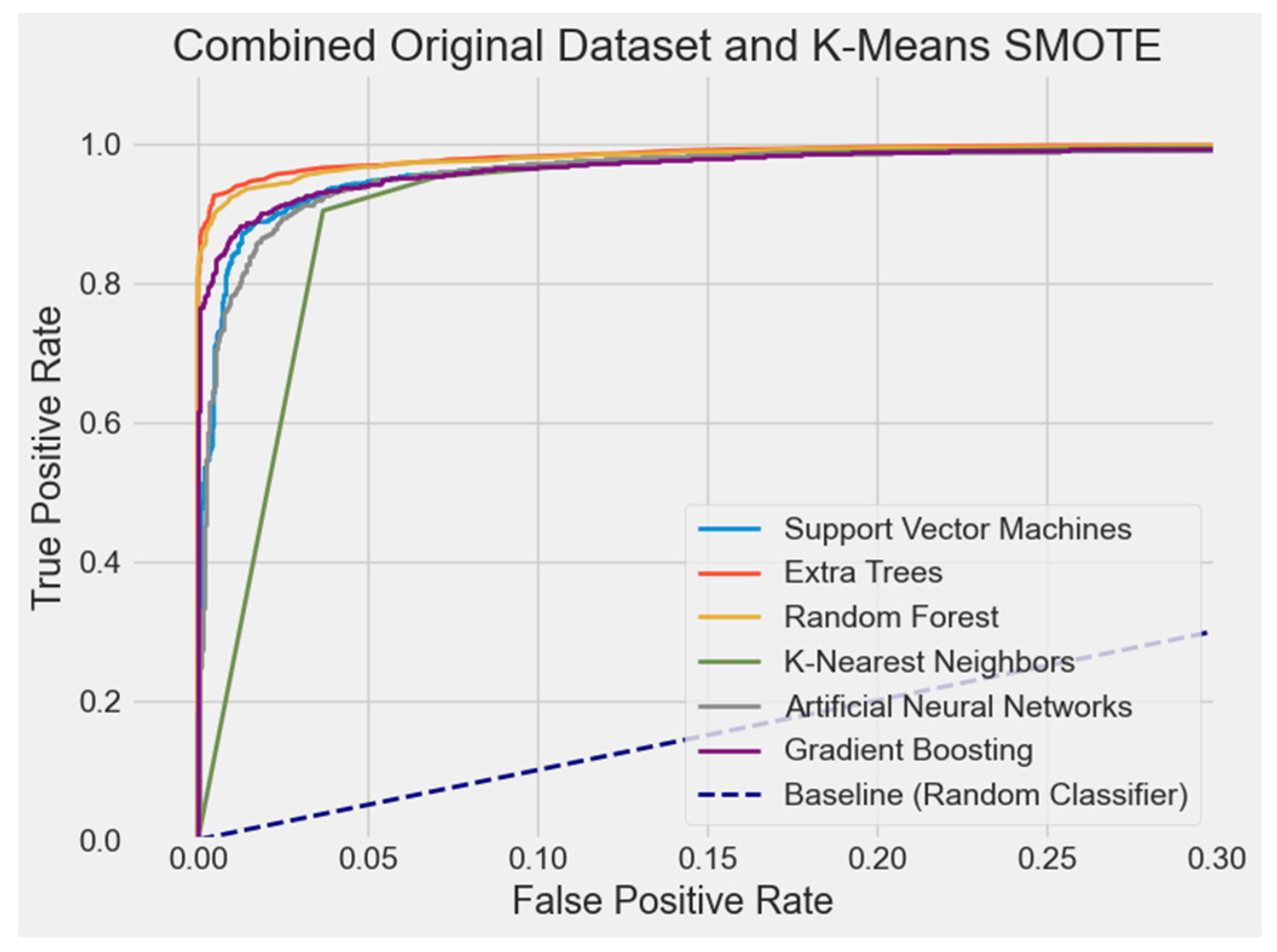
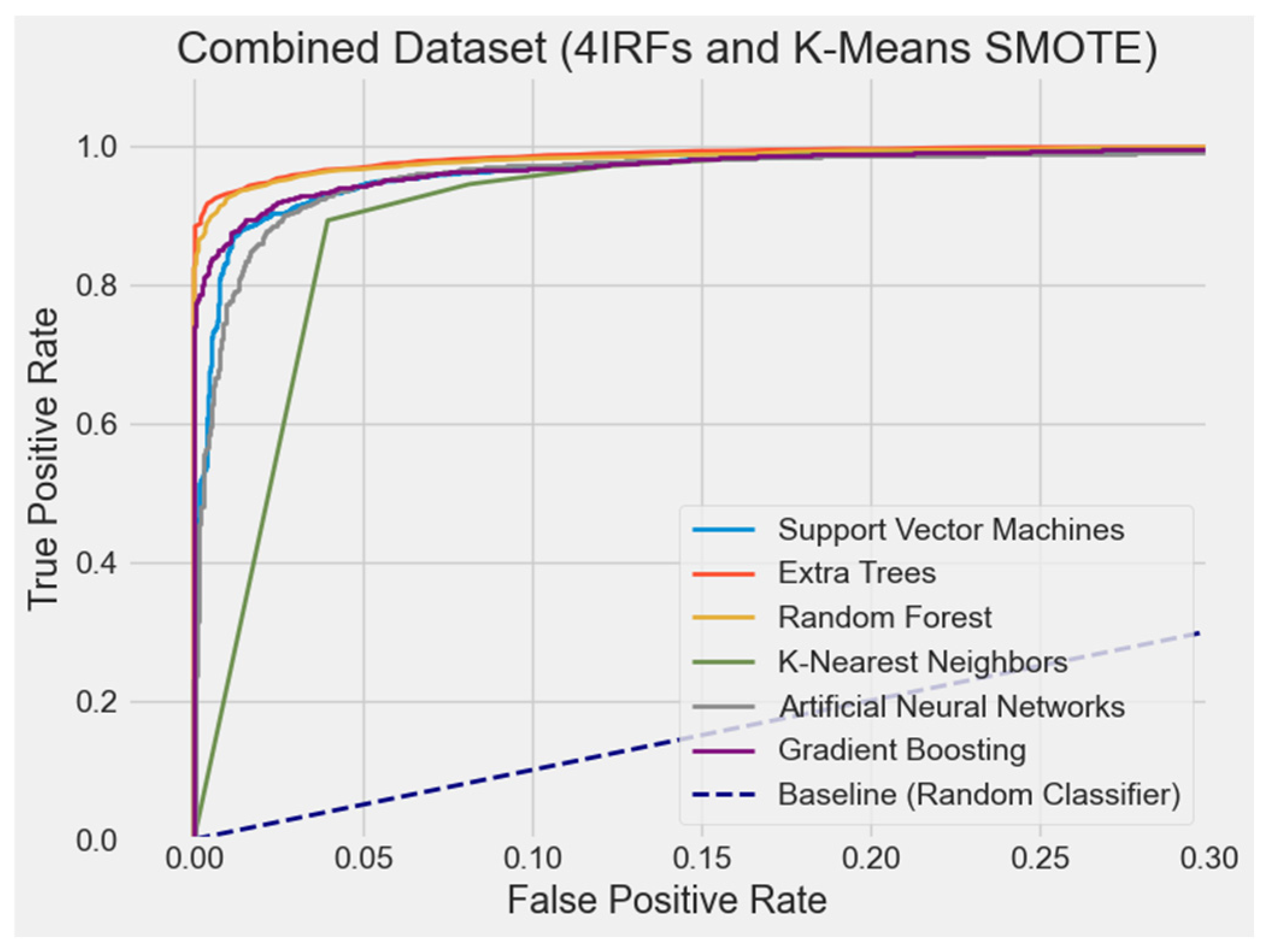
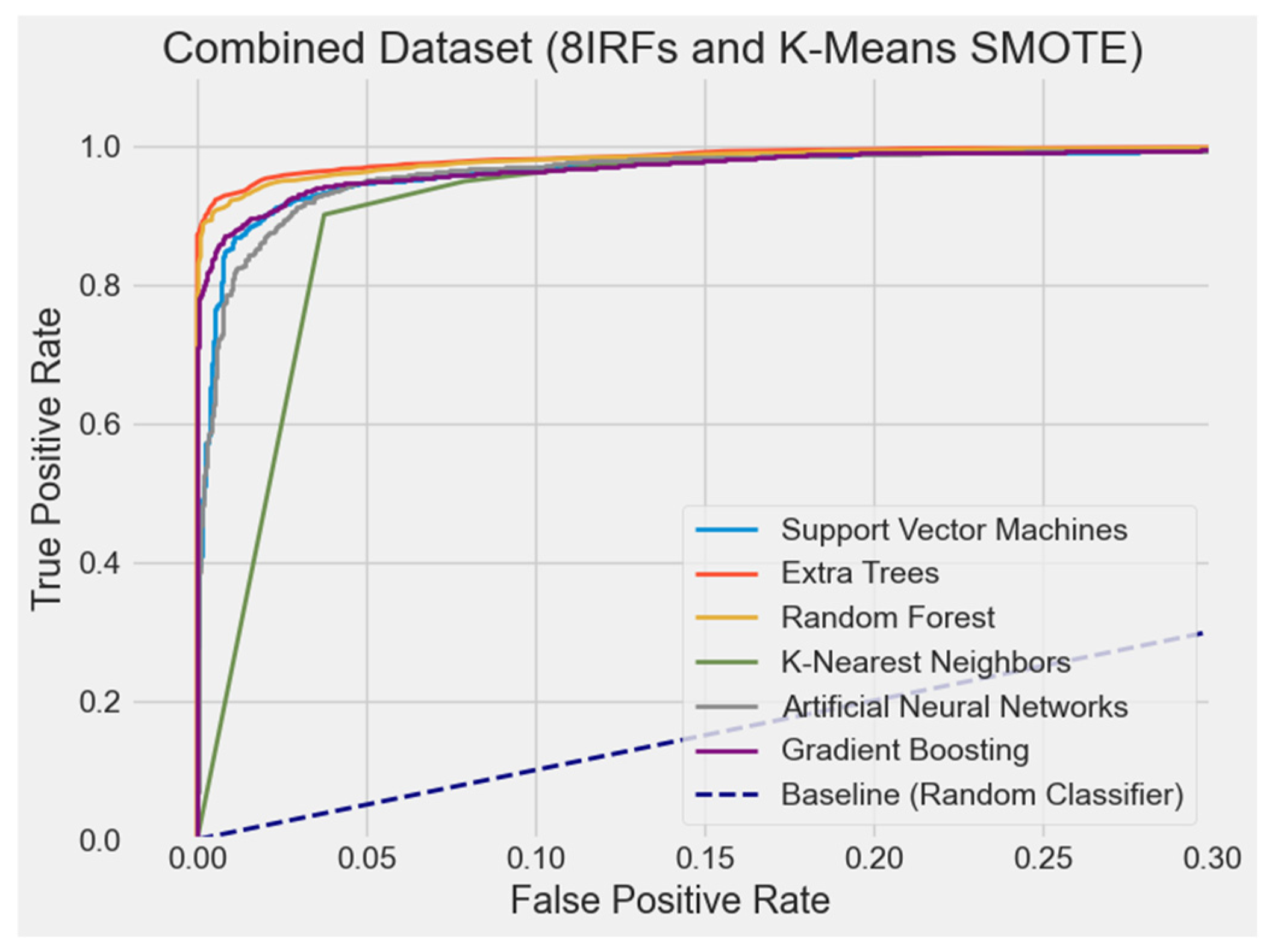
4.2.7. ROC Curve Comparison
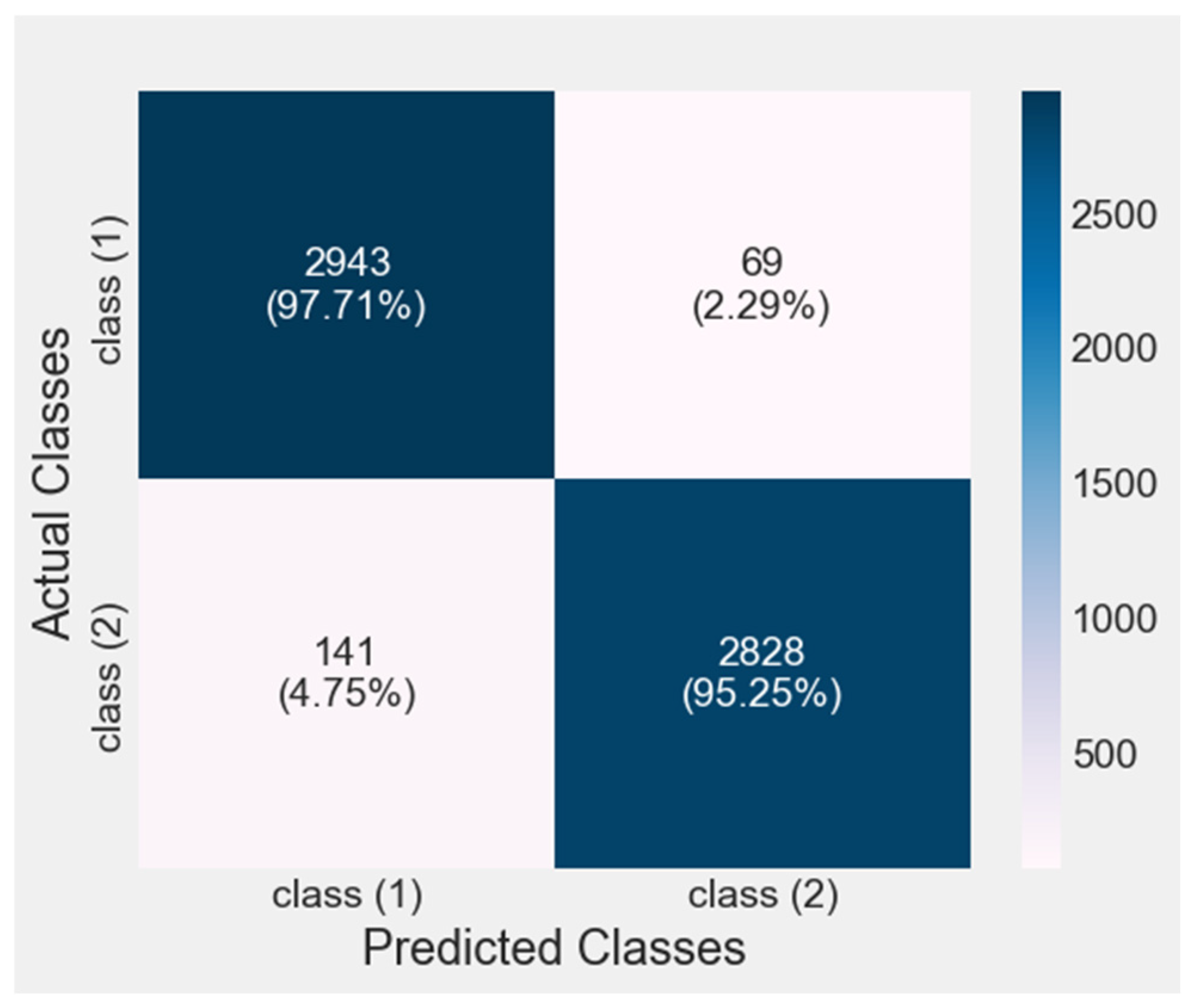
4.3. Confusion Matrix
4.4. Ablation Study
4.5. Sensitivity Analysis
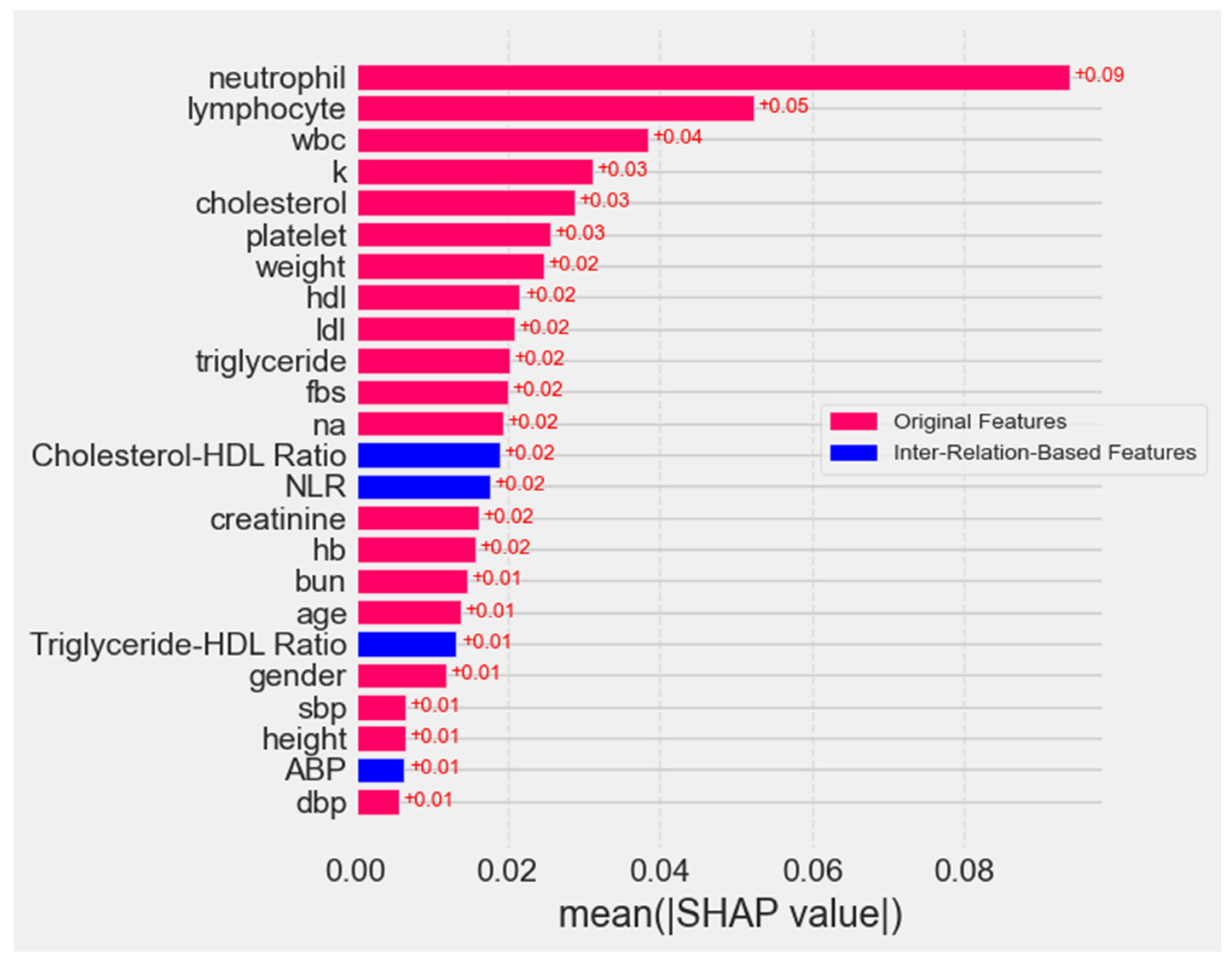
4.5.1. Mean Absolute Feature Importance Scores
4.5.2. Mean SHAP Value
5. Discussion
5.1. K-Means SMOTE Effect
5.2. IRF Effect
5.3. IRF and K-Means SMOTE Effect
5.4. The Findings
5.5. Suggestions and Future Studies
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Castellazzi, G.; Cuzzoni, M.G.; Cotta Ramusino, M.; Martinelli, D.; Denaro, F.; Ricciardi, A.; Vitali, P.; Anzalone, N.; Bernini, S.; Palesi, F.; et al. A machine learning approach for the differential diagnosis of Alzheimer and vascular dementia fed by MRI selected features. Front. Neuroinform. 2020, 14, 25. [Google Scholar] [CrossRef] [PubMed]
- Gustavsson, A.; Norton, N.; Fast, T.; Frölich, L.; Georges, J.; Holzapfel, D.; Kirabali, T.; Krolak-Salmon, P.; Rossini, P.M.; Ferretti, M.T.; et al. Global estimates on the number of persons across the Alzheimer’s disease continuum. Alzheimer’s Dement. 2023, 19, 658–670. [Google Scholar] [CrossRef] [PubMed]
- Nichols, E.; Steinmetz, J.D.; Vollset, S.E.; Fukutaki, K.; Chalek, J.; Abd-Allah, F.; Abdoli, A.; Abualhasan, A.; Abu-Gharbieh, E.; Akram, T.T.; et al. Estimation of the global prevalence of dementia in 2019 and forecasted prevalence in 2050: An analysis for the Global Burden of Disease Study 2019. Lancet Public Health 2022, 7, e105–e125. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Risk Reduction of Cognitive Decline and Dementia: WHO Guidelines; World Health Organization: Rome, Italy, 2019. [Google Scholar]
- Lastuka, A.; Bliss, E.; Breshock, M.R.; Iannucci, V.C.; Sogge, W.; Taylor, K.V.; Pedroza, P.; Dieleman, J.L. Societal costs of dementia: 204 countries, 2000–2019. J. Alzheimer’s Dis. 2024, 101, 277–292. [Google Scholar] [CrossRef]
- Muangpaisan, W. Dementia: Prevention, Assessment and Care; Parbpim: Bangkok, Thailand, 2013. [Google Scholar]
- Thongwachira, C.; Jaignam, N.; Thophon, S. A model of dementia prevention in older adults at Taling Chan District Bangkok Metropolis. KKU Res. J. 2019, 19, 96–108. [Google Scholar]
- Gómez, C.; Vaquerizo-Villar, F.; Poza, J.; Ruiz, S.J.; Tola-Arribas, M.A.; Cano, M.; Hornero, R. Bispectral analysis of spontaneous EEG activity from patients with moderate dementia due to Alzheimer’s disease. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju, Republic of Korea, 11–15 July 2017; IEEE: New York, NY, USA, 2017; pp. 422–425. [Google Scholar]
- Jeong, J.; Chae, J.H.; Kim, S.Y.; Han, S.H. Nonlinear dynamic analysis of the EEG in patients with Alzheimer’s disease and vascular dementia. J. Clin. Neurophysiol. 2001, 18, 58–67. [Google Scholar] [CrossRef]
- Nancy, A.; Balamurugan, M.; Vijaykumar, S. A brain EEG classification system for the mild cognitive impairment analysis. In Proceedings of the 2017 4th International Conference on Advanced Computing and Communication Systems (ICACCS), Coimbatore, India, 6–7 January 2017; IEEE: New York, NY, USA, 2017; pp. 1–6. [Google Scholar]
- Trambaiolli, L.R.; Spolaôr, N.; Lorena, A.C.; Anghinah, R.; Sato, J.R. Feature selection before EEG classification supports the diagnosis of Alzheimer’s disease. Clin. Neurophysiol. 2017, 128, 2058–2067. [Google Scholar] [CrossRef]
- Rodrigues, P.M.; Bispo, B.C.; Freitas, D.R.; Teixeira, J.P.; Carreres, A. Evaluation of EEG spectral features in Alzheimer disease discrimination. In Proceedings of the 21st European Signal Processing Conference (EUSIPCO 2013), Marrakech, Morocco, 9–13 September 2013; IEEE: New York, NY, USA, 2013; pp. 1–5. [Google Scholar]
- Pritchard, W.S.; Duke, D.W.; Coburn, K.L.; Moore, N.C.; Tucker, K.A.; Jann, M.W.; Hostetler, R.M. EEG-based, neural-net predictive classification of Alzheimer’s disease versus control subjects is augmented by non-linear EEG measures. Electroencephalogr. Clin. Neurophysiol. 1994, 91, 118–130. [Google Scholar] [CrossRef]
- Shorten, C.; Khoshgoftaar, T.M. A survey on image data augmentation for deep learning. J. Big Data 2019, 6, 1–48. [Google Scholar] [CrossRef]
- Ullah, H.T.; Onik, Z.; Islam, R.; Nandi, D. Alzheimer’s disease and dementia detection from 3D brain MRI data using deep convolutional neural networks. In Proceedings of the 3rd International Conference for Convergence in Technology (I2CT 2018), Pune, India, 6–8 April 2018; IEEE: New York, NY, USA, 2018; pp. 1–3. [Google Scholar]
- Bansal, D.; Khanna, K.; Chhikara, R.; Dua, R.K.; Malhotra, R. Comparative analysis of artificial neural networks and deep neural networks for detection of dementia. Int. J. Soc. Ecol. Sustain. Dev. 2022, 13, 1–18. [Google Scholar] [CrossRef]
- Narmatha, C.; Hayam, A.; Qasem, A.H. An analysis of deep learning techniques in neuroimaging. J. Comput. Sci. Intell. Technol. 2021, 2, 7–13. [Google Scholar]
- Vardhini, K.V.; Vishnumolakala, L.D.; Palanki, S.U.A.; Yarramsetty, M.; Raja, G. Alzheimer’s Research and Early Diagnosis Through Improved Deep Learning Models. In Proceedings of the 2024 5th International Conference on Electronics and Sustainable Communication Systems (ICESC), Coimbatore, India, 7–9 August 2024; IEEE: New York, NY, USA, 2024; pp. 1577–1583. [Google Scholar]
- Almubark, I.; Alsegehy, S.; Jiang, X.; Chang, L.C. Early detection of mild cognitive impairment using neuropsychological data and machine learning techniques. In Proceedings of the 2020 IEEE Conference on Big Data and Analytics (ICBDA), Kota Kinabalu, Malaysia, 17–19 November 2020; IEEE: New York, NY, USA, 2020; pp. 32–37. [Google Scholar]
- Javeed, A.; Dallora, A.L.; Berglund, J.S.; Idrisoglu, A.; Ali, L.; Rauf, H.T.; Anderberg, P. Early prediction of dementia using feature extraction battery (FEB) and optimized support vector machine (SVM) for classification. Biomedicines 2023, 11, 439. [Google Scholar] [CrossRef] [PubMed]
- Yongcharoenchaiyasit, K.; Arwatchananukul, S.; Temdee, P.; Prasad, R. Gradient boosting-based model for elderly heart failure, aortic stenosis, and dementia classification. IEEE Access 2023, 11, 48677–48696. [Google Scholar] [CrossRef]
- Mirzaei, G.; Adeli, H. Machine learning techniques for diagnosis of Alzheimer’s disease, mild cognitive disorder, and other types of dementia. Biomed. Signal Process. Control. 2022, 72, 103293. [Google Scholar] [CrossRef]
- Mohammed, B.A.; Senan, E.M.; Rassem, T.H.; Makbol, N.M.; Alanazi, A.A.; Al-Mekhlafi, Z.G.; Almurayziq, T.S.; Ghaleb, F.A. Multi-method analysis of medical records and MRI images for early diagnosis of dementia and Alzheimer’s disease based on deep learning and hybrid methods. Electronics 2021, 10, 2860. [Google Scholar] [CrossRef]
- Cura, O.K.; Yilmaz, G.C.; Ture, H.S.; Akan, A. Deep time-frequency feature extraction for Alzheimer’s dementia EEG classification. In Proceedings of the 2022 Medical Technologies Congress (TIPTEKNO), Antalya, Turkey, 31 October–2 November 2022; IEEE: New York, NY, USA, 2022; pp. 1–4. [Google Scholar]
- Hanai, S.; Kato, S.; Sakuma, T.; Ohdake, R.; Masuda, M.; Watanabe, H. A dementia classification based on speech analysis of casual talk during a clinical interview. In Proceedings of the 2022 IEEE 4th Global Conference on Life Sciences and Technologies (LifeTech), Osaka, Japan, 7–9 March 2022; IEEE: New York, NY, USA, 2022; pp. 38–40. [Google Scholar]
- Mumuni, A.; Mumuni, F. Data augmentation: A comprehensive survey of modern approaches. Array 2022, 16, 100258. [Google Scholar] [CrossRef]
- Jha, A.; John, E.; Banerjee, T. Multi-class classification of dementia from MRI images using transfer learning. In Proceedings of the 2022 IEEE 13th Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), New York, NY, USA, 26–29 October 2022; IEEE: New York, NY, USA, 2022; pp. 597–602. [Google Scholar]
- Reddy, T.S.; Saikiran, V.; Samhitha, S.; Moin, S.; Kumar, T.P.; Charan, V.S. Early detection of Alzheimer’s disease using data augmentation and CNN. In Proceedings of the 2023 4th IEEE Global Conference for Advancement in Technology (GCAT), Bangalore, India, 6–8 October 2023; IEEE: New York, NY, USA, 2023; pp. 1–6. [Google Scholar]
- Samanta, S.; Mazumder, I.; Roy, C. Deep learning-based early detection of Alzheimer’s disease using image enhancement filters. In Proceedings of the 2023 Third International Conference on Advances in Electrical, Computing, Communication and Sustainable Technologies (ICAECT), Bhilai, India, 5–6 January 2023; IEEE: New York, NY, USA; pp. 1–5. [Google Scholar]
- Liu, Q.S.; Xue, Y.; Li, G.; Qiu, D.; Zhang, W.; Guo, Z.; Li, Z. Application of KM-SMOTE for rockburst intelligent prediction. Tunn. Undergr. Space Technol. 2023, 138, 105180. [Google Scholar] [CrossRef]
- Hairani, H.; Saputro, K.E.; Fadli, S. K-means-SMOTE untuk menangani ketidakseimbangan kelas dalam klasifikasi penyakit diabetes dengan C4.5, SVM, dan naive Bayes. J. Teknol. Dan Sist. Komput. 2020, 8, 89–93. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, 1–8 June 2008; IEEE: New York, NY, USA, 2008; pp. 1322–1328. [Google Scholar]
- Ranjan, N.; Kumar, D.U.; Dongare, V.; Chavan, K.; Kuwar, Y. Diagnosis of Parkinson disease using handwriting analysis. Int. J. Comput. Appl. 2022, 184, 13–16. [Google Scholar] [CrossRef]
- Öcal, H. A novel approach to detection of Alzheimer’s disease from handwriting: Triple ensemble learning model. Gazi Univ. J. Sci. Part C Des. Technol. 2024, 12, 214–223. [Google Scholar] [CrossRef]
- Shen, Y.; Zhu, J.; Deng, Z.; Lu, W.; Wang, H. EnsDeepDP: An ensemble deep learning approach for disease prediction through metagenomics. IEEE/ACM Trans. Comput. Biol. Bioinform. 2022, 20, 986–998. [Google Scholar] [CrossRef]
- Goel, A.; Lal, M.; Javadekar, A.N. Comparative analysis of the machine and deep learning classifier for dementia prediction. In Proceedings of the 2023 Advanced Computing and Communication Technologies for High Performance Applications (ACCTHPA), Ernakulam, India, 20–21 January 2023; IEEE: New York, NY, USA, 2023; pp. 1–8. [Google Scholar]
- Rahman, M.A.; Shafique, R.; Ullah, S.; Choi, G.S. Cardiovascular Disease Prediction System Using Extra Trees Classifier. Res. Sq. 2019, 11, 51. [Google Scholar]
- Aashima; Bhargav, S.; Kaushik, S.; Dutt, V. A Combination of Decision Trees with Machine Learning Ensembles for Blood Glucose Level Predictions; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Hanczár, G.; Stippinger, M.; Hanák, D.; Kurbucz, M.T.; Törteli, O.M.; Chripkó, Á.; Somogyvári, Z. Feature space reduction method for ultrahigh-dimensional, multiclass data: Random forest-based multiround screening (RFMS). arXiv 2023, arXiv:2305.15793. [Google Scholar] [CrossRef]
- Zhou, Z.-H.; Feng, J. Deep forest: Towards an alternative to deep neural networks. In Proceedings of the IJCAI’17: 26th International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017. [Google Scholar]
- Fernández, A.; García, S.; Galar, M.; Prati, R.C.; Krawczyk, B.; Herrera, F. Learning from Imbalanced Data Streams; Springer: Cham, Switzerland, 2018; Volume 10. [Google Scholar]
- Kim, K. Noise avoidance SMOTE in ensemble learning for imbalanced data. IEEE Access 2021, 9, 143250–143265. [Google Scholar] [CrossRef]
- Wen, J.; Thibeau-Sutre, E.; Diaz-Melo, M.; Samper-González, J.; Routier, A.; Bottani, S.; Dormont, D.; Durrleman, S.; Burgos, N.; Alzheimer’s Disease Neuroimaging Initiative; et al. Convolutional neural networks for classification of Alzheimer’s disease: Overview and reproducible evaluation. Med. Image Anal. 2020, 63, 101694. [Google Scholar]
- Fernández-Delgado, M.; Cernadas, E.; Barro, S.; Amorim, D. Do we need hundreds of classifiers to solve real world classification problems? J. Mach. Learn. Res. 2014, 15, 3133–3181. [Google Scholar]
- Kourou, K.; Exarchos, T.P.; Exarchos, K.P.; Karamouzis, M.V.; Fotiadis, D.I. Machine learning applications in cancer prognosis and prediction. Comput. Struct. Biotechnol. J. 2015, 13, 8–17. [Google Scholar] [CrossRef]
- Wang, X.; Yu, H.; Zhang, Y.; Yu, Y. An ensemble learning framework for early detection of Alzheimer’s disease using multiple biomarkers. Comput. Biol. Med. 2021, 133, 104399. [Google Scholar]
- Beebe-Wang, N.; Okeson, A.; Althoff, T.; Lee, S.I. Efficient and explainable risk assessments for imminent dementia in an aging cohort study. IEEE J. Biomed. Health Inform. 2021, 25, 2409–2420. [Google Scholar] [CrossRef]
- Pujianto, U.; Wibawa, A.P.; Akbar, M.I. K-nearest neighbor (K-NN) based missing data imputation. In Proceedings of the 2019 5th International Conference on Science in Information Technology (ICSITech), Yogyakarta, Indonesia, 10–11 October 2019; IEEE: New York, NY, USA, 2019; pp. 83–88. [Google Scholar]
- Jameson, J.L.; Fauci, A.S.; Kasper, D.L.; Hauser, S.L.; Longo, D.L.; Loscalzo, J. Harrison’s Principles of Internal Medicine, 21st ed.; McGraw Hill: New York, NY, USA, 2022. [Google Scholar]
- Skerrett, P.J. Lipid Disorders: Diagnosis and Treatment; Harvard Health Publications: Boston, MA, USA, 2014. [Google Scholar]
- Bishop, M.L. Clinical Chemistry: Principles, Techniques, and Correlations, Enhanced Edition: Principles, Techniques, and Correlations; Jones & Bartlett Learning: Burlington, MA, USA, 2023. [Google Scholar]
- Guyton, A.C.; Hall, J.E. Guyton and Hall Textbook of Medical Physiology, 13th ed.; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Noble, W.S. What is a support vector machine? Nat. Biotechnol. 2006, 24, 1565–1567. [Google Scholar] [CrossRef]
- Almasoud, M.; Ward, T.E. Detection of chronic kidney disease using machine learning algorithms with least number of predictors. Int. J. Soft Comput. Its Appl. 2019, 10, 14–23. [Google Scholar] [CrossRef]
- Justin, B.N.; Turek, M.; Hakim, A.M. Heart disease as a risk factor for dementia. Clin. Epidemiol. 2013, 5, 135–145. [Google Scholar] [CrossRef] [PubMed]
- Kramer, O. Dimensionality Reduction with Unsupervised Nearest Neghbors; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Zhang, Z. Generalized Linear Models: Modern Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Kunapuli, G. Ensemble Methods for Machine Learning; Simon and Schuster: New York, NY, USA, 2023. [Google Scholar]
- Zhang, Y.; Chen, X. Explainable recommendation: A survey and new perspectives. Found. Trends® Inf. Retr. 2020, 14, 1–101. [Google Scholar] [CrossRef]


| No. | Group | Feature | Data Range |
|---|---|---|---|
| 1. | Personal data | Age Weight (W) Height (H) Gender (S) | 73.17 ± 8.54 56.37 ± 9.70 155.03 ± 7.62 0–1 |
| 2. | Blood pressure | Systolic Blood Pressure (SBP) Diastolic Blood Pressure (DBP) | 130.00 ± 16.34 68.93 ± 9.9 |
| 3. | Lipid levels | Cholesterol (Chol) Triglyceride (TG) Low-Density Lipoprotein (LDL) High-Density Lipoprotein (HDL) | 171.02 ± 28.77 115.81 ± 33.59 112.19 ± 21.17 44.95 ± 8.67 |
| 4. | Blood sugar level | Fasting Blood Sugar (FBS) | 123.47 ± 62.52 |
| 5. | Minerals and chemical substances | Creatinine (Cr) Blood Urea Nitrogen (BUN) Hemoglobin (Hb) Potassium (K) Sodium (Na) | 1.59 ± 1.45 25.96 ± 16.44 11.34 ± 1.72 3.96 ± 0.49 137.67 ± 3.02 |
| 6. | Blood cells | White Blood Cell (WBC) Neutrophil (Neut) Platelet (Plt) Lymphocyte (Lymph) | 9006.04 ± 2639.41 74.65 ± 12.80 238,667.17 ± 60,548.65 18.12 ± 7.45 |
| No. | Features Detail | Description |
|---|---|---|
| 1. | Average blood pressure (ABP) | ABP, a key indicator of circulation, is calculated from systolic and diastolic pressures during heart contraction and relaxation, respectively. |
| 2. | Cholesterol–HDL Ratio (CHR) | CHR, used to assess cardiovascular risk, is calculated by dividing total cholesterol by HDL. |
| 3. | Neutrophil-to-Lymphocyte Ratio (NLR) | NLR, used to assess inflammation and immune response, is calculated by dividing neutrophils by lymphocytes and is commonly applied in chronic disease and cancer evaluation. |
| 4. | Modification of Diet in Renal Disease (MDRD) | MDRD, used to assess kidney function, is calculated from serum creatinine adjusted for age, gender, and ethnicity, and is commonly used in chronic kidney disease management. |
| 5. | Neutrophil Count (NC) | NC, used to assess immune function, measures the number of neutrophils (white blood cells) in the blood. |
| 6. | Triglyceride–HDL Ratio (TG/HDL Ratio) | TG/HDL, used to assess cardiovascular risk and insulin resistance, is calculated by dividing triglyceride levels by HDL cholesterol; higher ratios indicate greater risk. |
| 7. | Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) | CKD-EPI, used for accurate kidney function assessment, improves upon MDRD by incorporating serum creatinine, age, gender, and ethnicity, aiding in chronic kidney disease diagnosis. |
| 8. | HDL-LDL ratio (HDL/LDL Ratio) | HDL/LDL Ratio, used to assess cardiovascular health, is calculated by dividing HDL by LDL; higher ratios indicate better cholesterol balance and reduced risk. |
| Original Features | IRFs | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AGE | W | H | S | SBP | DBP | Chol | TG | LDL | HDL | FBS | Cr | BUN | Hb | K | Na | WBC | Neut | Plt | … | ABP | CHR | NLR | MDRD |
| 74 | 60.73 | 153.02 | 0 | 128.38 | 64.84 | 145.67 | 86.94 | 89.57 | 41.7 | 116.28 | 1.03 | 17.63 | 11.078 | 4.20 | 137.09 | 12,210 | 91.09 | 292,530 | … | 193.22 | 0.4655 | 1.6263 | 2.0848 |
| 74 | 54.56 | 147.21 | 0 | 129.39 | 62.59 | 170.64 | 133.04 | 119.45 | 42.28 | 158.7 | 0.97 | 16.93 | 12.259 | 3.90 | 139.36 | 12,276 | 91.65 | 287,970 | … | 191.98 | 0.3539 | 1.4285 | 3.1466 |
| 74 | 61.34 | 155.71 | 0 | 127.37 | 63.89 | 146.03 | 81.67 | 89.81 | 40.19 | 99.48 | 1.0045 | 20.07 | 10.969 | 4.09 | 137.15 | 10,725 | 91.30 | 246,440 | … | 191.26 | 0.4475 | 1.6259 | 2.0320 |
| 83 | 47.16 | 143.69 | 1 | 134.49 | 58.61 | 170.93 | 120.31 | 119.3 | 43.95 | 142.23 | 1.75 | 28 | 9.400 | 2.40 | 137.80 | 10,862 | 86.40 | 390,000 | … | 193.10 | 0.3683 | 1.4327 | 2.7374 |
| Oversampling Method | Features with D > 0.05 | Max D-Value | Most Affected Features |
|---|---|---|---|
| K-Means SMOTE | 3 | 0.4692 | Height (0.4692), ABP (0.3405), sbp (0.2024) |
| SMOTE | 4 | 0.1595 | Height (0.0801), dbp (0.1595), sbp (0.0527), ABP (0.0792) |
| ADASYN | 3 | 0.2474 | Height (0.2474), platelet (0.0531), na (0.0551) |
| Dataset | Best Model | Accuracy | Precision | Recall | F1 Score | AUC-ROC | Avg Rank (Mean) |
|---|---|---|---|---|---|---|---|
| Original + 4 IRFs | ET | 1.20 | 1.15 | 1.45 | 1.30 | 1.00 | 1.22 |
| Original + 4 IRFs + ADASYN | ET | 1.10 | 1.00 | 1.10 | 1.00 | 1.00 | 1.04 |
| Original + 4 IRFs + SMOTE | ET | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Original + 4 IRFs + K-Means SMOTE | ET | 1.05 | 1.00 | 1.10 | 1.20 | 1.00 | 1.07 |
| Dataset | Best Model | Accuracy | Precision | Recall | F1 Score | AUC |
|---|---|---|---|---|---|---|
| Original | ET | 95.15% | 95.98% | 93.00% | 94.29% | 98.85% |
| Original + ADASYN | ET | 94.74% | 93.85% | 94.21% | 94.03% | 98.76% |
| Original + SMOTE | ET | 94.94% | 94.72% | 93.68% | 94.17% | 98.73% |
| Original + K-Means SMOTE | ET | 95.26% | 95.68% | 93.48% | 94.47% | 98.81% |
| Model | Original Dataset Features (No. of Features = 20) | ||||
|---|---|---|---|---|---|
| Precision (%) | Recall (%) | F1 Score (%) | Accuracy (%) | AUC | |
| GB | 0.93 ± 0.01 | 0.92 ± 0.01 | 0.93 ± 0.01 | 0.94 ± 0.01 | 0.98 ± 0.00 |
| RF | 0.95 ± 0.01 | 0.92 ± 0.01 | 0.94 ± 0.01 | 0.95 ± 0.01 | 0.99 ± 0.00 |
| ET | 0.96 ± 0.01 | 0.93 ± 0.01 | 0.94 ± 0.01 | 0.95 ± 0.01 | 0.99 ± 0.00 |
| SVM | 0.34 ± 0.00 | 0.50 ± 0.00 | 0.40 ± 0.00 | 0.68 ± 0.00 | 0.78 ± 0.01 |
| KNN | 0.86 ± 0.01 | 0.84 ± 0.01 | 0.85 ± 0.01 | 0.87 ± 0.01 | 0.92 ± 0.01 |
| ANN | 0.55 ± 0.14 | 0.58 ± 0.09 | 0.53 ± 0.12 | 0.68 ± 0.02 | 0.76 ± 0.02 |
| Model | Original Dataset with 4 IRFs and K-Means SMOTE (No. of Features = 24) | ||||
|---|---|---|---|---|---|
| Precision (%) | Recall (%) | F1 Score (%) | Accuracy (%) | AUC | |
| GB | 0.95 ± 0.01 | 0.95 ± 0.01 | 0.95 ± 0.01 | 0.95 ± 0.01 | 0.99 ± 0.00 |
| RF | 0.96 ± 0.00 | 0.96 ± 0.00 | 0.96 ± 0.00 | 0.96 ± 0.00 | 0.99 ± 0.00 |
| ET | 0.96 ± 0.01 | 0.96 ± 0.01 | 0.96 ± 0.01 | 0.96 ± 0.01 | 0.99 ± 0.00 |
| SVM | 0.76 ± 0.01 | 0.75 ± 0.01 | 0.74 ± 0.01 | 0.75 ± 0.01 | 0.83 ± 0.01 |
| KNN | 0.90 ± 0.01 | 0.90 ± 0.01 | 0.90 ± 0.01 | 0.90 ± 0.01 | 0.96 ± 0.01 |
| ANN | 0.75 ± 0.05 | 0.68 ± 0.08 | 0.64 ± 0.13 | 0.68 ± 0.08 | 0.77 ± 0.07 |
| Model | Original Dataset with 8 IRFs and K-Means SMOTE (No. of Features = 28) | ||||
|---|---|---|---|---|---|
| Precision (%) | Recall (%) | F1 Score (%) | Accuracy (%) | AUC | |
| GB | 0.95 ± 0.00 | 0.95 ± 0.00 | 0.95 ± 0.00 | 0.95 ± 0.00 | 0.99 ± 0.00 |
| RF | 0.96 ± 0.01 | 0.96 ± 0.01 | 0.96 ± 0.01 | 0.96 ± 0.01 | 0.99 ± 0.00 |
| ET | 0.96 ± 0.01 | 0.96 ± 0.01 | 0.96 ± 0.01 | 0.96 ± 0.01 | 0.99 ± 0.00 |
| SVM | 0.77 ± 0.01 | 0.76 ± 0.01 | 0.75 ± 0.01 | 0.76 ± 0.01 | 0.84 ± 0.01 |
| KNN | 0.91 ± 0.01 | 0.91 ± 0.01 | 0.91 ± 0.01 | 0.91 ± 0.01 | 0.96 ± 0.01 |
| ANN | 0.79 ± 0.04 | 0.76 ± 0.06 | 0.75 ± 0.06 | 0.76 ± 0.06 | 0.82 ± 0.05 |
| Accuracy (%) | ||||
|---|---|---|---|---|
| Model | Original Dataset | Original Dataset + K-Means SMOTE | Original Dataset + K-Means SMOTE + 4 IRFs | Original Dataset + K-Means SMOTE + 8 IRFs |
| SVM | 93.05 | 94.73 | 94.52 | 94.50 |
| GB | 93.84 | 94.58 | 94.67 | 95.10 |
| ET | 95.08 | 96.39 | 96.47 | 96.52 |
| RF | 94.63 | 96.02 | 96.10 | 96.27 |
| KNN | 91.24 | 92.58 | 92.44 | 92.56 |
| ANN | 92.68 | 94.70 | 94.95 | 94.90 |
| Precision (%) | ||||
|---|---|---|---|---|
| Model | Original Dataset | Original Dataset + K-Means SMOTE | Original Dataset + K-Means SMOTE + 4 IRFs | Original Dataset + K-Means SMOTE + 8 IRFs |
| SVM | 94.35 | 94.26 | 94.25 | 94.05 |
| GB | 94.44 | 93.98 | 94.07 | 93.92 |
| ET | 94.01 | 94.72 | 94.79 | 94.47 |
| RF | 93.66 | 94.14 | 93.99 | 93.82 |
| KNN | 97.34 | 97.55 | 97.46 | 97.57 |
| ANN | 94.78 | 95.03 | 95.10 | 95.13 |
| Recall (%) | ||||
|---|---|---|---|---|
| Model | Original Dataset | Original Dataset + K-Means SMOTE | Original Dataset + K-Means SMOTE + 4 IRFs | Original Dataset + K-Means SMOTE + 8 IRFs |
| SVM | 94.96 | 94.22 | 93.85 | 94.16 |
| GB | 96.53 | 95.31 | 95.11 | 95.49 |
| ET | 98.79 | 97.97 | 97.86 | 97.57 |
| RF | 98.55 | 97.76 | 97.66 | 97.34 |
| KNN | 93.40 | 91.03 | 90.94 | 91.13 |
| ANN | 94.85 | 94.35 | 94.34 | 94.36 |
| F1 Score (%) | ||||
|---|---|---|---|---|
| Model | Original Dataset | Original Dataset + K-Means SMOTE | Original Dataset + K-Means SMOTE + 4 IRFs | Original Dataset + K-Means SMOTE + 8 IRFs |
| SVM | 94.66 | 94.24 | 94.05 | 94.11 |
| GB | 95.47 | 94.64 | 94.59 | 94.70 |
| ET | 96.34 | 96.32 | 96.30 | 96.00 |
| RF | 96.04 | 95.92 | 95.79 | 95.55 |
| KNN | 95.33 | 94.18 | 94.09 | 94.24 |
| ANN | 94.81 | 94.69 | 94.72 | 94.75 |
| Average AUC-ROC (%) | ||||
|---|---|---|---|---|
| Model | Original Dataset | Original Dataset + K-Means SMOTE | Original Dataset + K-Means SMOTE + 4 IRFs | Original Dataset + K-Means SMOTE + 8 IRFs |
| SVM | 97.10 | 98.59 | 98.57 | 98.68 |
| GB | 98.03 | 98.87 | 98.89 | 98.91 |
| ET | 98.74 | 99.49 | 99.51 | 99.45 |
| RF | 98.59 | 99.39 | 99.35 | 99.33 |
| KNN | 96.20 | 97.12 | 96.82 | 96.96 |
| ANN | 96.98 | 98.44 | 98.56 | 98.44 |
| Model Configuration | IRFs | K-Means SMOTE | Classifier | Accuracy (%) | Recall (%) | Precision (%) | F1 Score (%) | AUC-ROC (%) |
|---|---|---|---|---|---|---|---|---|
| Full Model | included | included | ET | 96.47 | 97.86 | 94.79 | 96.30 | 99.51 |
| w/o IRFs | not included | included | ET | 96.30 | 98.01 | 94.73 | 96.26 | 99.49 |
| w/o SMOTE | included | not included | ET | 94.85 | 99.05 | 93.64 | 96.22 | 98.88 |
| w/o IRFs and SMOTE | not included | not included | ET | 95.08 | 98.63 | 93.96 | 96.34 | 98.74 |
| RF instead of ET | included | included | RF | 96.10 | 97.66 | 93.99 | 95.79 | 99.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaiyo, Y.; Rueangsirarak, W.; Hristov, G.; Temdee, P. Improving Early Detection of Dementia: Extra Trees-Based Classification Model Using Inter-Relation-Based Features and K-Means Synthetic Minority Oversampling Technique. Big Data Cogn. Comput. 2025, 9, 148. https://doi.org/10.3390/bdcc9060148
Chaiyo Y, Rueangsirarak W, Hristov G, Temdee P. Improving Early Detection of Dementia: Extra Trees-Based Classification Model Using Inter-Relation-Based Features and K-Means Synthetic Minority Oversampling Technique. Big Data and Cognitive Computing. 2025; 9(6):148. https://doi.org/10.3390/bdcc9060148
Chicago/Turabian StyleChaiyo, Yanawut, Worasak Rueangsirarak, Georgi Hristov, and Punnarumol Temdee. 2025. "Improving Early Detection of Dementia: Extra Trees-Based Classification Model Using Inter-Relation-Based Features and K-Means Synthetic Minority Oversampling Technique" Big Data and Cognitive Computing 9, no. 6: 148. https://doi.org/10.3390/bdcc9060148
APA StyleChaiyo, Y., Rueangsirarak, W., Hristov, G., & Temdee, P. (2025). Improving Early Detection of Dementia: Extra Trees-Based Classification Model Using Inter-Relation-Based Features and K-Means Synthetic Minority Oversampling Technique. Big Data and Cognitive Computing, 9(6), 148. https://doi.org/10.3390/bdcc9060148








