Assessing the Transformation of Armed Conflict Types: A Dynamic Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Construction of the SCDi and Its Transformation Types
2.3. Modeling the SCDi Transformation
3. Results
3.1. Spatiotemporal Characteristics of Armed Conflict Type Transformation
3.2. Simulation Results of the Dynamic Transformations of SCDi Types
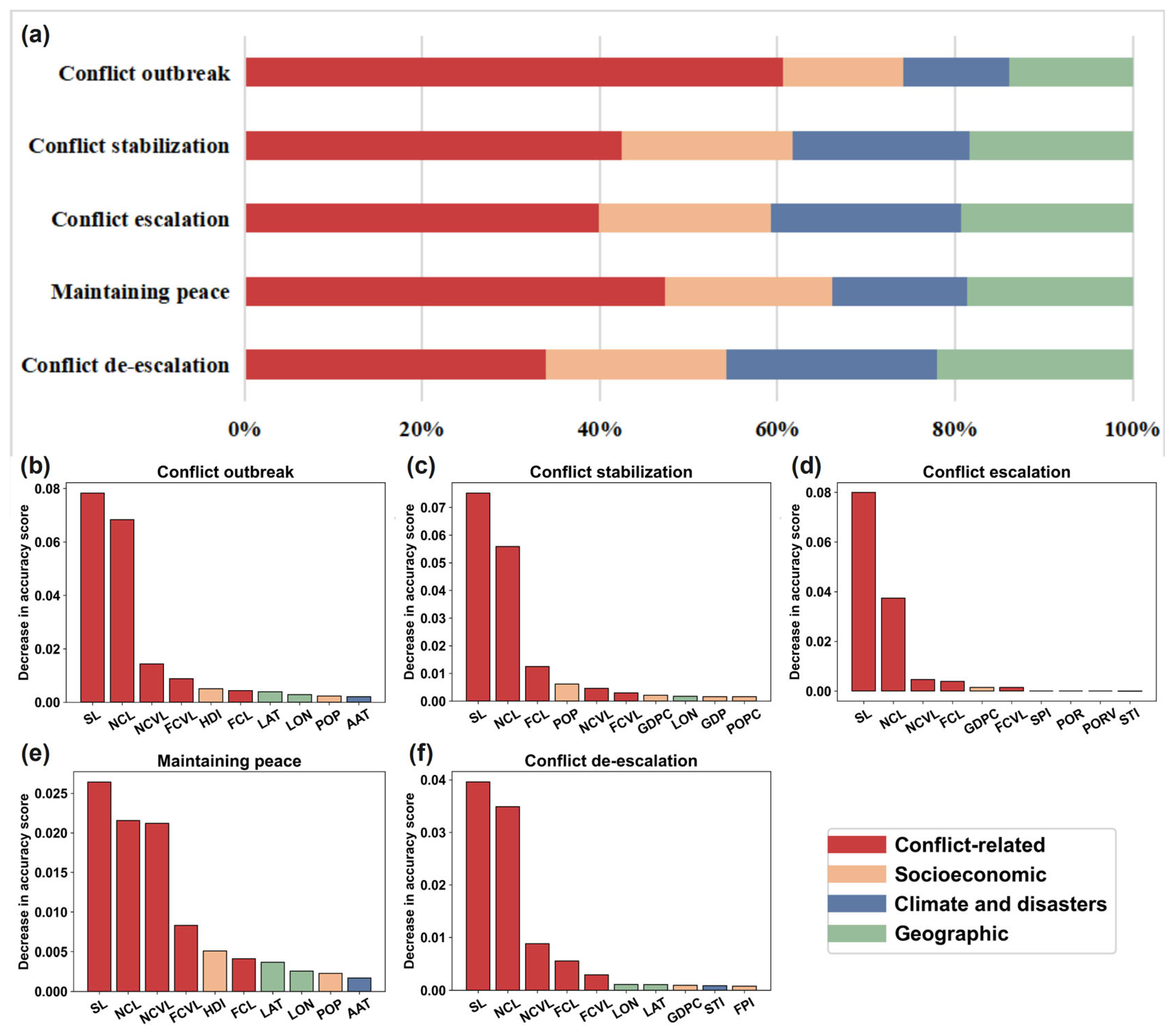
3.3. Potential Driving Factors of Different Transformation of Armed Conflict Types
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Petrić Howe, N.; Gaind, N.; Van Noorden, R. Nature’s Take: How the War in Ukraine Is Impacting Science. Available online: https://www.nature.com/articles/d41586-022-03155-z (accessed on 26 April 2025).
- Alexander, P.; Arneth, A.; Henry, R.; Maire, J.; Rabin, S.; Rounsevell, M.D.A. High Energy and Fertilizer Prices Are More Damaging than Food Export Curtailment from Ukraine and Russia for Food Prices, Health and the Environment. Nat. Food 2022, 4, 84–95. [Google Scholar] [CrossRef] [PubMed]
- International Organization for Migration Sudan Conflict Displaces Nearly Four Million: UN Migration Agency. Available online: https://news.un.org/en/story/2023/08/1139352 (accessed on 31 March 2025).
- Leaning, J.; Guha-Sapir, D. Natural Disasters, Armed Conflict, and Public Health. N. Engl. J. Med. 2013, 369, 1836–1842. [Google Scholar] [CrossRef] [PubMed]
- Lane, L. Mitigating Humanitarian Crises during Non-International Armed Conflicts—The Role of Human Rights and Ceasefire Agreements. J. Int. Humanit. Action 2016, 1, 2. [Google Scholar] [CrossRef]
- Cederman, L.-E.; Weidmann, N.B. Predicting Armed Conflict: Time to Adjust Our Expectations? Science 2017, 355, 474–476. [Google Scholar] [CrossRef]
- De Bruin, S.P.; Hoch, J.M.; Von Uexkull, N.; Buhaug, H.; Demmers, J.; Visser, H.; Wanders, N. Projecting Long-Term Armed Conflict Risk: An Underappreciated Field of Inquiry? Glob. Environ. Chang. 2022, 72, 102423. [Google Scholar] [CrossRef]
- Goldstone, J.A.; Bates, R.H.; Epstein, D.L.; Gurr, T.R.; Lustik, M.B.; Marshall, M.G.; Ulfelder, J.; Woodward, M. A Global Model for Forecasting Political Instability. Am. J. Political Sci. 2010, 54, 190–208. [Google Scholar] [CrossRef]
- Buhaug, H.; Rød, J.K. Local Determinants of African Civil Wars, 1970–2001. Political Geogr. 2006, 25, 315–335. [Google Scholar] [CrossRef]
- Cederman, L.-E.; Buhaug, H.; Rød, J.K. Ethno-Nationalist Dyads and Civil War: A GIS-Based Analysis. J. Confl. Resolut. 2009, 53, 496–525. [Google Scholar] [CrossRef]
- Raleigh, C.; Hegre, H. Population Size, Concentration, and Civil War. A Geographically Disaggregated Analysis. Political Geogr. 2009, 28, 224–238. [Google Scholar] [CrossRef]
- Colaresi, M.; Mahmood, Z. Do the Robot: Lessons from Machine Learning to Improve Conflict Forecasting. J. Peace Res. 2017, 54, 193–214. [Google Scholar] [CrossRef]
- Weidmann, N.B.; Ward, M.D. Predicting Conflict in Space and Time. J. Confl. Resolut. 2010, 54, 883–901. [Google Scholar] [CrossRef]
- Hegre, H.; Buhaug, H.; Calvin, K.V.; Nordkvelle, J.; Waldhoff, S.T.; Gilmore, E. Forecasting Civil Conflict along the Shared Socioeconomic Pathways. Environ. Res. Lett. 2016, 11, 054002. [Google Scholar] [CrossRef]
- Vesco, P.; Håvard, H.; Michael, C.; Remco Bastiaan, J.; Adeline, L.; Gregor, R.; Weidmann, N.B. United They Stand: Findings from an Escalation Prediction Competition. Int. Interact. 2022, 48, 860–896. [Google Scholar] [CrossRef]
- Tollefsen, A.F.; Strand, H.; Buhaug, H. PRIO-GRID: A Unified Spatial Data Structure. J. Peace Res. 2012, 49, 363–374. [Google Scholar] [CrossRef]
- Mueller, H.; Rauh, C. Using Past Violence and Current News to Predict Changes in Violence. Int. Interact. 2022, 48, 579–596. [Google Scholar] [CrossRef]
- Vestby, J.; Brandsch, J.; Larsen, V.B.; Landsverk, P.; Tollefsen, A.F. Predicting (de-)Escalation of Sub-National Violence Using Gradient Boosting: Does It Work? Int. Interact. 2022, 48, 841–859. [Google Scholar] [CrossRef]
- Walther, O.J.; Radil, S.M.; Russell, D.G.; Trémolières, M. Introducing the Spatial Conflict Dynamics Indicator of Political Violence. Terror. Political Violence 2023, 35, 533–552. [Google Scholar] [CrossRef]
- Idler, A. Change in Armed Conflict: An Introduction. Int. Political Sci. Rev. 2024, 45, 3–14. [Google Scholar] [CrossRef]
- Hauge, W.; Ellingsen, T. Beyond Environmental Scarcity: Causal Pathways to Conflict. J. Peace Res. 1998, 35, 299–317. [Google Scholar] [CrossRef]
- Hao, M.; Fu, J.; Jiang, D.; Ding, F.; Chen, S. Simulating the Linkages Between Economy and Armed Conflict in India with a Long Short-Term Memory Algorithm. Risk Anal. 2020, 40, 1139–1150. [Google Scholar] [CrossRef]
- Gizelis, T.-I.; Wooden, A.E. Water Resources, Institutions, & Intrastate Conflict. Political Geogr. 2010, 29, 444–453. [Google Scholar] [CrossRef]
- Buhaug, H.; Benjaminsen, T.A.; Sjaastad, E.; Magnus Theisen, O. Climate Variability, Food Production Shocks, and Violent Conflict in Sub-Saharan Africa. Environ. Res. Lett. 2015, 10, 125015. [Google Scholar] [CrossRef]
- Koubi, V.; Spilker, G.; Böhmelt, T.; Bernauer, T. Do Natural Resources Matter for Interstate and Intrastate Armed Conflict? J. Peace Res. 2013, 51, 227–243. [Google Scholar] [CrossRef]
- Shumilova, O.; Tockner, K.; Sukhodolov, A.; Khilchevskyi, V.; De Meester, L.; Stepanenko, S.; Trokhymenko, G.; Hernández-Agüero, J.A.; Gleick, P. Impact of the Russia–Ukraine Armed Conflict on Water Resources and Water Infrastructure. Nat. Sustain. 2023, 6, 578–586. [Google Scholar] [CrossRef]
- Fisk, K. Refugee Geography and the Diffusion of Armed Conflict in Africa. Civ. Wars 2014, 16, 255–275. [Google Scholar] [CrossRef]
- Augsten, L.; Gagné, K.; Su, Y. The Human Dimensions of the Climate Risk and Armed Conflict Nexus: A Review Article. Reg. Environ. Chang. 2022, 22, 42. [Google Scholar] [CrossRef]
- Basedau, M.; Strüver, G.; Vüllers, J.; Wegenast, T. Do Religious Factors Impact Armed Conflict? Empirical Evidence from Sub-Saharan Africa. Terror. Political Violence 2011, 23, 752–779. [Google Scholar] [CrossRef]
- Svensson, I. One God, Many Wars: Religious Dimensions of Armed Conflict in the Middle East and North Africa. Civ. Wars 2013, 15, 411–430. [Google Scholar] [CrossRef]
- Fjelde, H.; von Uexkull, N. Climate Triggers: Rainfall Anomalies, Vulnerability and Communal Conflict in Sub-Saharan Africa. Political Geogr. 2012, 31, 444–453. [Google Scholar] [CrossRef]
- Mach, K.J.; Kraan, C.M.; Adger, W.N.; Buhaug, H.; Burke, M.; Fearon, J.D.; Field, C.B.; Hendrix, C.S.; Maystadt, J.-F.; O’Loughlin, J.; et al. Climate as a Risk Factor for Armed Conflict. Nature 2019, 571, 193–197. [Google Scholar] [CrossRef]
- Helman, D.; Zaitchik, B.F.; Funk, C. Climate Has Contrasting Direct and Indirect Effects on Armed Conflicts. Environ. Res. Lett. 2020, 15, 104017. [Google Scholar] [CrossRef]
- Ge, Q.; Hao, M.; Ding, F.; Jiang, D.; Scheffran, J.; Helman, D.; Ide, T. Modelling Armed Conflict Risk under Climate Change with Machine Learning and Time-Series Data. Nat. Commun. 2022, 13, 2839. [Google Scholar] [CrossRef] [PubMed]
- Hao, M.; Ding, F.; Xie, X.; Fu, J.; Qian, Y.; Ide, T.; Maystadt, J.-F.; Chen, S.; Ge, Q.; Jiang, D. Varying Climatic-Social-Geographical Patterns Shape the Conflict Risk at Regional and Global Scales. Humanit. Soc. Sci. Commun. 2022, 9, 276. [Google Scholar] [CrossRef]
- Sundberg, R.; Melander, E. Introducing the UCDP Georeferenced Event Dataset. J. Peace Res. 2013, 50, 523–532. [Google Scholar] [CrossRef]
- Walter, B.F. Why Bad Governance Leads to Repeat Civil War. J. Confl. Resolut. 2015, 59, 1242–1272. [Google Scholar] [CrossRef]
- Hegre, H.; Nygård, H.M.; Ræder, R.F. Evaluating the Scope and Intensity of the Conflict Trap: A Dynamic Simulation Approach. J. Peace Res. 2017, 54, 243–261. [Google Scholar] [CrossRef]
- Buhaug, H.; Gleditsch, K.S. Contagion or Confusion? Why Conflicts Cluster in Space. Int. Stud. Q. 2008, 52, 215–233. [Google Scholar] [CrossRef]
- Urdal, H. People vs. Malthus: Population Pressure, Environmental Degradation, and Armed Conflict Revisited. J. Peace Res. 2005, 42, 417–434. [Google Scholar] [CrossRef]
- Vestby, J.; Buhaug, H.; von Uexkull, N. Why Do Some Poor Countries See Armed Conflict While Others Do Not? A Dual Sector Approach. World Dev. 2021, 138, 105273. [Google Scholar] [CrossRef]
- Salehyan, I.; Gleditsch, K.S. Refugees and the Spread of Civil War. Int. Organ. 2006, 60, 335–366. [Google Scholar] [CrossRef]
- Eck, K. From Armed Conflict to War: Ethnic Mobilization and Conflict Intensification. Int. Stud. Q. 2009, 53, 369–388. [Google Scholar] [CrossRef]
- Zhukov, Y.M. Roads and the Diffusion of Insurgent Violence: The Logistics of Conflict in Russia’s North Caucasus. Political Geogr. 2012, 31, 144–156. [Google Scholar] [CrossRef]
- Tatem, A.J. WorldPop, Open Data for Spatial Demography. Sci. Data 2017, 4, 170004. [Google Scholar] [CrossRef]
- Chen, J.; Gao, M.; Cheng, S.; Hou, W.; Song, M.; Liu, X.; Liu, Y. Global 1 Km × 1 Km Gridded Revised Real Gross Domestic Product and Electricity Consumption during 1992–2019 Based on Calibrated Nighttime Light Data. Sci. Data 2022, 9, 202. [Google Scholar] [CrossRef]
- Kummu, M.; Taka, M.; Guillaume, J.H.A. Gridded Global Datasets for Gross Domestic Product and Human Development Index over 1990–2015. Sci. Data 2018, 5, 180004. [Google Scholar] [CrossRef]
- Niva, V.; Horton, A.; Virkki, V.; Heino, M.; Kosonen, M.; Kallio, M.; Kinnunen, P.; Abel, G.J.; Muttarak, R.; Taka, M.; et al. World’s Human Migration Patterns in 2000–2019 Unveiled by High-Resolution Data. Nat. Hum. Behav. 2023, 7, 2023–2037. [Google Scholar] [CrossRef]
- Wucherpfennig, J.; Weidmann, N.B.; Girardin, L.; Cederman, L.-E.; Wimmer, A. Politically Relevant Ethnic Groups across Space and Time: Introducing the GeoEPR Dataset1. Confl. Manag. Peace Sci. 2011, 28, 423–437. [Google Scholar] [CrossRef]
- Vogt, M.; Bormann, N.-C.; Rüegger, S.; Cederman, L.-E.; Hunziker, P.; Girardin, L. Integrating Data on Ethnicity, Geography, and Conflict: The Ethnic Power Relations Data Set Family. J. Confl. Resolut. 2015, 59, 1327–1342. [Google Scholar] [CrossRef]
- Meijer, J.R.; Huijbregts, M.A.J.; Schotten, K.C.G.J.; Schipper, A.M. Global Patterns of Current and Future Road Infrastructure. Environ. Res. Lett. 2018, 13, 64006. [Google Scholar] [CrossRef]
- Mu, H.; Li, X.; Wen, Y.; Huang, J.; Du, P.; Su, W.; Miao, S.; Geng, M. A Global Record of Annual Terrestrial Human Footprint Dataset from 2000 to 2018. Sci. Data 2022, 9, 176. [Google Scholar] [CrossRef]
- Nirandjan, S.; Koks, E.E.; Ward, P.J.; Aerts, J.C.J.H. A Spatially-Explicit Harmonized Global Dataset of Critical Infrastructure. Sci. Data 2022, 9, 150. [Google Scholar] [CrossRef] [PubMed]
- Cil, D.; Fjelde, H.; Hultman, L.; Nilsson, D. Mapping Blue Helmets: Introducing the Geocoded Peacekeeping Operations (Geo-PKO) Dataset. J. Peace Res. 2020, 57, 360–370. [Google Scholar] [CrossRef]
- Winkler, K.; Fuchs, R.; Rounsevell, M.D.A.; Herold, M. HILDA+ Global Land Use Change between 1960 and 2019 2020. Available online: https://doi.pangaea.de/10.1594/PANGAEA.921846 (accessed on 10 March 2025).
- Food and Agriculture Organization of the United Nations FAO Food Price Index. Available online: https://www.fao.org/worldfoodsituation/foodpricesindex/en/ (accessed on 27 April 2025).
- Felbermayr, G.; Kirilakha, A.; Syropoulos, C.; Yalcin, E.; Yotov, Y.V. The Global Sanctions Data Base. Eur. Econ. Rev. 2020, 129, 103561. [Google Scholar] [CrossRef]
- Schleussner, C.-F.; Donges, J.F.; Donner, R.V.; Schellnhuber, H.J. Armed-Conflict Risks Enhanced by Climate-Related Disasters in Ethnically Fractionalized Countries. Proc. Natl. Acad. Sci. USA 2016, 113, 9216–9221. [Google Scholar] [CrossRef]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS Monthly High-Resolution Gridded Multivariate Climate Dataset. Sci. Data 2020, 7, 109. [Google Scholar] [CrossRef]
- Center For Hazards And Risk Research-CHRR-Columbia University; Center For International Earth Science Information Network-CIESIN-Columbia University; International Bank For Reconstruction And Development-The World Bank Global Multihazard Frequency and Distribution. Available online: https://access.earthdata.nasa.gov/collections/C179001775-SEDAC (accessed on 10 March 2025).
- Fearon, J.D.; Laitin, D.D. Ethnicity, Insurgency, and Civil War. Am. Political Sci. Rev. 2003, 97, 75–90. [Google Scholar] [CrossRef]
- Buhaug, H.; Gates, S. The Geography of Civil War. J. Peace Res. 2002, 39, 417–433. [Google Scholar] [CrossRef]
- De Rouen Jr, K.R.; Sobek, D. The Dynamics of Civil War Duration and Outcome. J. Peace Res. 2004, 41, 303–320. [Google Scholar] [CrossRef]
- NASA Ocean Biology Processing Grou Distance to Nearest Coastline: 0.04-Degree Grid. Available online: https://www.pacioos.hawaii.edu/metadata/dist2coast_4deg.html (accessed on 10 March 2025).
- Tucker, C.J.; Pinzon, J.E.; Brown, M.E.; Slayback, D.A.; Pak, E.W.; Mahoney, R.; Vermote, E.F.; El Saleous, N. An Extended AVHRR 8-km NDVI Dataset Compatible with MODIS and SPOT Vegetation NDVI Data. Int. J. Remote Sens. 2005, 26, 4485–4498. [Google Scholar] [CrossRef]
- Pinzon, J.E.; Tucker, C.J. A Non-Stationary 1981–2012 AVHRR NDVI3g Time Series. Remote Sens. 2014, 6, 6929–6960. [Google Scholar] [CrossRef]
- World Bank Group World Bank Group Strategy for Fragility, Conflict, and Violence 2020–2025; World Bank Group: Washington, DC, USA, 2020.
- Hossin, M.; Sulaiman, M.N. A Review on Evaluation Metrics for Data Classification Evaluations. Int. J. Data Min. Knowl. Manag. Process 2015, 5, 1–11. [Google Scholar] [CrossRef]
- Ma, W.; Feng, Z.; Cheng, Z.; Chen, S.; Wang, F. Identifying Forest Fire Driving Factors and Related Impacts in China Using Random Forest Algorithm. Forests 2020, 11, 507. [Google Scholar] [CrossRef]
- Pollins, B.M. Globalization and Armed Conflict among Nations. Confl. Manag. Peace Sci. 2008, 25, 191–205. [Google Scholar] [CrossRef]
- Wenger, A.; Mason, S.J.A. The Civilianization of Armed Conflict: Trends and Implications. Int. Rev. Red Cross 2009, 90, 835–852. [Google Scholar] [CrossRef]
- Elfversson, E.; Höglund, K. Are Armed Conflicts Becoming More Urban? Cities 2021, 119, 103356. [Google Scholar] [CrossRef]
- Schutte, S.; Weidmann, N.B. Diffusion Patterns of Violence in Civil Wars. Political Geogr. 2011, 30, 143–152. [Google Scholar] [CrossRef]
- Pearlman, L. Cities in Crisis: Riots, Rebellion, and Repression on a Global Scale. J. Urban Hist. 2017, 43, 672–677. [Google Scholar] [CrossRef]
- Raleigh, C.; Nsaibia, H.; Dowd, C. The Sahel Crisis since 2012. Afr. Aff. 2021, 120, 123–143. [Google Scholar] [CrossRef]
- Hoch, J.M.; De Bruin, S.P.; Buhaug, H.; Von Uexkull, N.; Van Beek, R.; Wanders, N. Projecting Armed Conflict Risk in Africa towards 2050 along the SSP-RCP Scenarios: A Machine Learning Approach. Environ. Res. Lett. 2021, 16, 124068. [Google Scholar] [CrossRef]
- Ding, F.; Ge, Q.; Jiang, D.; Fu, J.; Hao, M. Understanding the Dynamics of Terrorism Events with Multiple-Discipline Datasets and Machine Learning Approach. PLoS ONE 2017, 12, e0179057. [Google Scholar] [CrossRef]
- Bundschuh, T. Economic, Social, and Cultural Rights in Armed Conflict. Nord. J. Hum. Rights 2017, 35, 74–79. [Google Scholar] [CrossRef]
- Garcia Corrales, L.M.; Avila, H.; Gutierrez, R.R. Land-Use and Socioeconomic Changes Related to Armed Conflicts: A Colombian Regional Case Study. Environ. Sci. Policy 2019, 97, 116–124. [Google Scholar] [CrossRef]
- Le Billon, P. The Political Ecology of War: Natural Resources and Armed Conflicts. Political Geogr. 2001, 20, 561–584. [Google Scholar] [CrossRef]
- Mach, K.J.; Adger, W.N.; Buhaug, H.; Burke, M.; Fearon, J.D.; Field, C.B.; Hendrix, C.S.; Kraan, C.M.; Maystadt, J.-F.; O’Loughlin, J.; et al. Directions for Research on Climate and Conflict. Earth’s Future 2020, 8, e2020EF001532. [Google Scholar] [CrossRef]
- Ide, T. Rise or Recede? How Climate Disasters Affect Armed Conflict Intensity. Int. Secur. 2023, 47, 50–78. [Google Scholar] [CrossRef]
- Hegre, H.; Karlsen, J.; Nygård, H.M.; Strand, H.; Urdal, H. Predicting Armed Conflict, 2010–2050. Int. Stud. Q. 2013, 57, 250–270. [Google Scholar] [CrossRef]
- Lee, E.D.; Daniels, B.C.; Myers, C.R.; Krakauer, D.C.; Flack, J.C. Scaling Theory of Armed-Conflict Avalanches. Phys. Rev. E 2020, 102, 42312. [Google Scholar] [CrossRef]
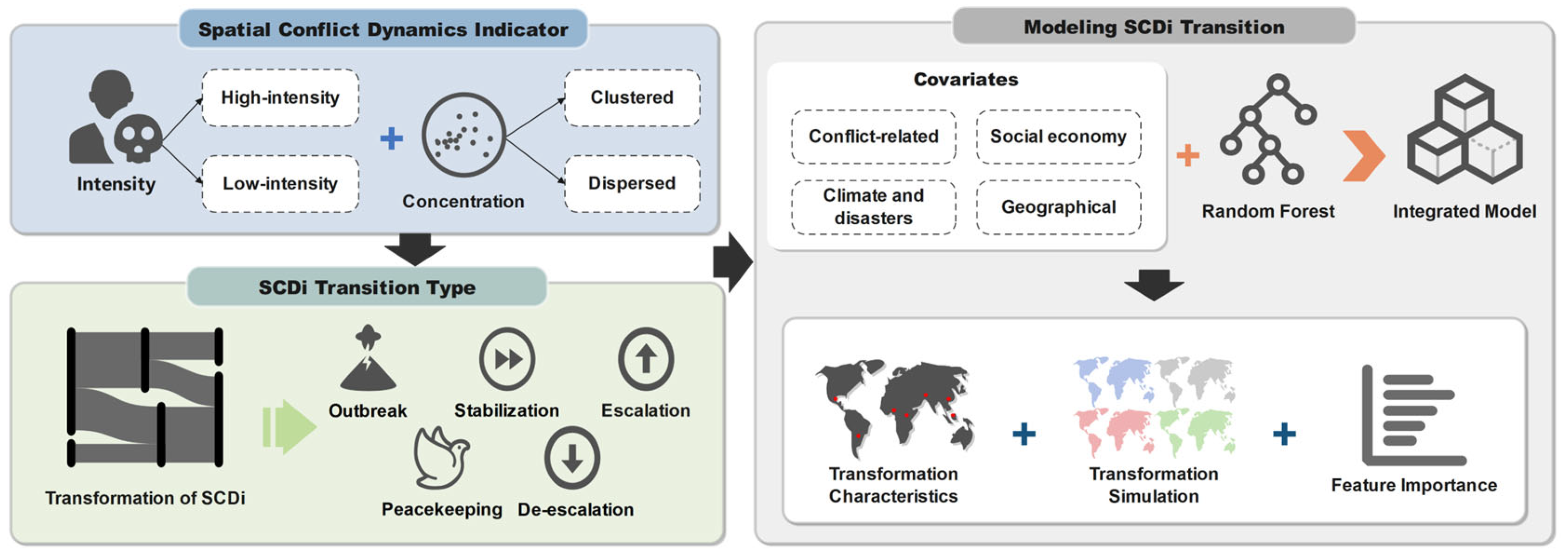


| Type | Covariates | Abbreviation |
|---|---|---|
| Conflict-related | SCDi last year Total number of conflicts last year Fatalities of conflicts last year Total number of conflicts in the vicinity last year Fatalities of conflicts in the vicinity last year Total number of conflicts in 1989–1999 Fatalities of conflicts in 1989–1999 Number of years of conflict in 1989–1999 Total number of conflicts in the vicinity in 1989–1999 Fatalities of conflicts in the vicinity in 1989–1999 Number of years of conflict in the vicinity in 1989–1999 Total number of global conflicts last year Fatalities of global conflicts last year | SL NCL |
| Socioeconomic | Population Population change Gross domestic product (GDP) GDP change Human development index (HDI) Net migration Excluded ethnic groups Road density Urban proportion Farmland proportion Human footprint Peacekeeping operations records Peacekeeping operations records in the vicinity Critical infrastructure index Food price index Oil price index Frequency of major international sanctions | POP POPC GDP GDPC HDI NM EEG RD UP FLP HF POR PORV CISI FPI OPI SAC |
| Climate and disasters | Multi-hazard frequency Standard precipitation index Standard temperature index Mean annual temperature Mean annual precipitation | MF SPI STI AAT AP |
| Geographic | Longitude Latitude Elevation mean Elevation standard deviation Mountain coverage Travel times to cities Distance to nearest country anywhere Distance to own borders Distance to capital Distance to the coastline Forest proportion Normalized Difference Vegetation Index (NDVI) | LON LAT EM ESD MC TTC DNCT DOB DCA DNCS FRP NDVI |
| Transformation | Meaning | Type |
|---|---|---|
| NC → NC | Remain non-conflict | Maintaining peace |
| NC → DL NC → DH NC → CL NC → CH | From non-conflict state to conflict state | Conflict outbreak |
| DL → DL DH → DH CL → CL CH → CH DH → CH CH → DH DL → CL CL → DL | Maintain the original conflict level | Conflict stabilization |
| DL → NC DH → NC CL → NC CH → NC DH → DL CH → DL DH → CL CH → CL | Reduce conflict level | Conflict de-escalation |
| DL → DH; DL → CH; CL → DH; CL → CH; | Raise conflict level | Conflict escalation |
| Types of Armed Conflict Transformation | Precision | Recall | F1-Score |
|---|---|---|---|
| Maintaining peace | 0.918 | 0.878 | 0.897 |
| Conflict outbreak | 0.884 | 0.921 | 0.902 |
| Conflict stabilization | 0.669 | 0.598 | 0.631 |
| Conflict de-escalation | 0.544 | 0.545 | 0.544 |
| Conflict escalation | 0.587 | 0.648 | 0.615 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, D.; Zhuo, J.; Fan, P.; Ding, F.; Hao, M.; Chen, S.; Dong, J.; Wu, J. Assessing the Transformation of Armed Conflict Types: A Dynamic Approach. Big Data Cogn. Comput. 2025, 9, 123. https://doi.org/10.3390/bdcc9050123
Jiang D, Zhuo J, Fan P, Ding F, Hao M, Chen S, Dong J, Wu J. Assessing the Transformation of Armed Conflict Types: A Dynamic Approach. Big Data and Cognitive Computing. 2025; 9(5):123. https://doi.org/10.3390/bdcc9050123
Chicago/Turabian StyleJiang, Dong, Jun Zhuo, Peiwei Fan, Fangyu Ding, Mengmeng Hao, Shuai Chen, Jiping Dong, and Jiajie Wu. 2025. "Assessing the Transformation of Armed Conflict Types: A Dynamic Approach" Big Data and Cognitive Computing 9, no. 5: 123. https://doi.org/10.3390/bdcc9050123
APA StyleJiang, D., Zhuo, J., Fan, P., Ding, F., Hao, M., Chen, S., Dong, J., & Wu, J. (2025). Assessing the Transformation of Armed Conflict Types: A Dynamic Approach. Big Data and Cognitive Computing, 9(5), 123. https://doi.org/10.3390/bdcc9050123







