A Formal Model of Trajectories for the Aggregation of Semantic Attributes
Abstract
1. Introduction
2. Related Works
- Distributive: In this method, it is assumed that the only measure stored in each cell is its presence. To calculate the presence of R, the presences of the cells that compose R are added. Note that, in this method, if the same trajectory passes, e.g., through two cells that compose R, then this trajectory is counted twice; therefore, this method may produce inaccurate results.
- Algebraic: In this method, it is assumed that in addition to the presence, three additional measures (calculated by a previous process) are stored in each cell: (i) the number of distinct trajectories crossing the spatial border (i.e., the common border, perpendicular to the X-axis, of two adjacent cells) between two adjacent cells, (ii) same as (i) but for the border, perpendicular to the Y-axis, and (iii) same as (i) but for the temporal border between two adjacent cells, e.g., if a cell is defined in the intervals (8 am, 10 am] and (10 am, 12 m], then the temporal border occurs at 10 am. Based on these four measures, the presence of R is calculated. For example, to calculate the presence of two adjacent cells that have in common a border perpendicular to the X-axis, their presences are added and the number of distinct trajectories crossing such border is subtracted. This method, although more accurate than the distributive method, can also generate inaccurate results.
- −
- It supports uncertainty, i.e., given two consecutive points (x, y, t) of a trajectory, if between these two points, there are several road sections, it is unknown which of these road sections the moving object followed. That is, the method considers sparse trajectory samples.
- −
- It considers the problem of repetition counting, i.e., when a moving object visits the same region multiple times, to avoid counting it several times. For this reason, the authors use indexes and specialized data structures (histograms, hash tables, B+ trees, among others) to achieve a good level of accuracy and obtain it efficiently. The experimental results showed that the method ensures accuracy by adjusting some parameters.
3. A Formal Model of Trajectories for the Aggregation of Semantic Attributes
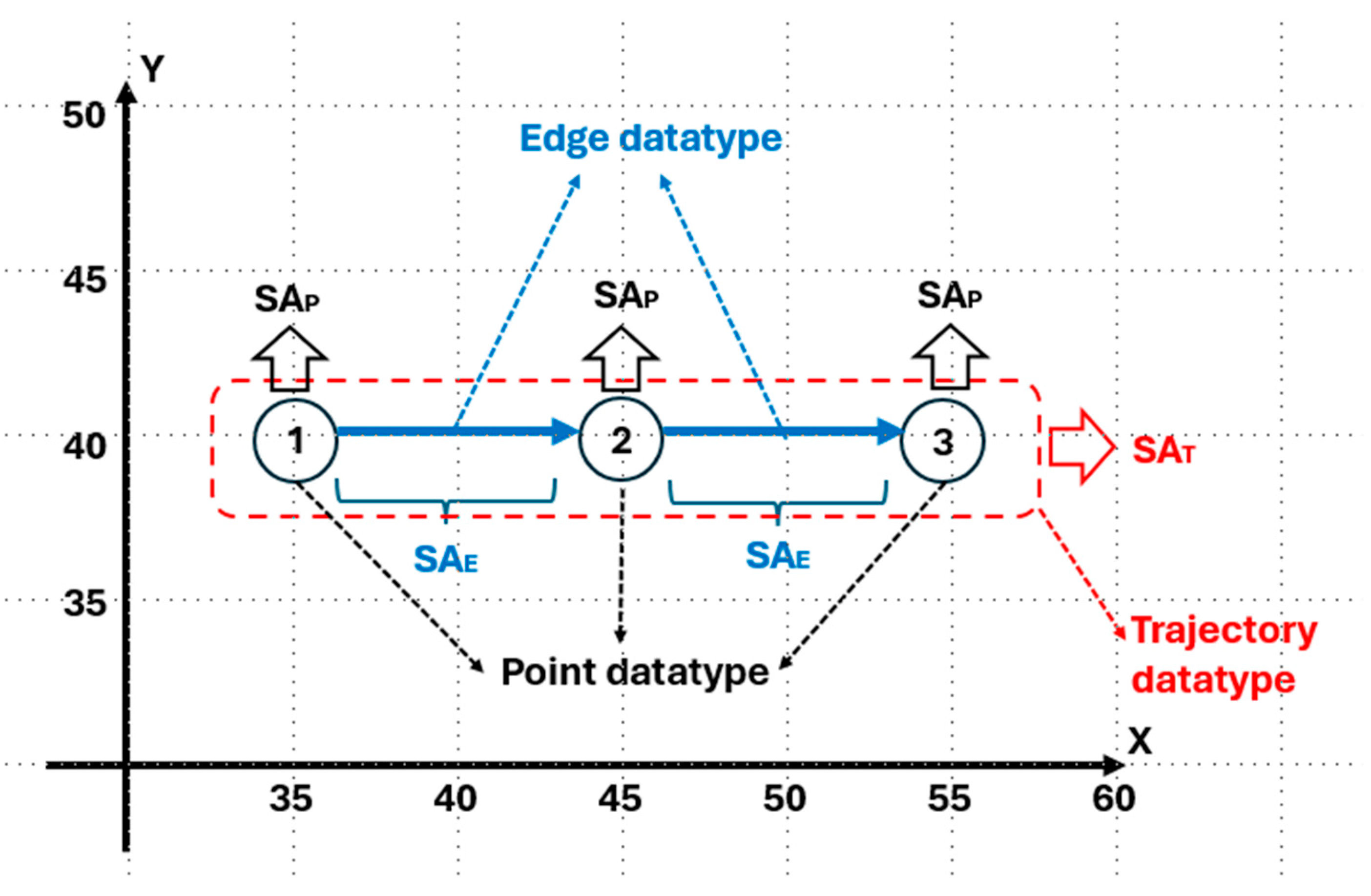
3.1. Basic Datatypes and Attributes
- Example:
3.2. Point Datatype
- (i)
- PointId is the point identifier, DTF(PointId) = Z+.
- (ii)
- x represents the point latitude, DTF(x) = Latitude. For simplicity, in our examples, x is just a positive integer (in a Cartesian coordinate system), i.e., DTF(x) = Z+.
- (iii)
- y represents the point longitude, DTF(y) = Longitude. For simplicity, in our examples, y is just a positive integer (in a Cartesian coordinate system), i.e., DTF(y) = Z+.
- (iv)
- t is the point time, DTF(t) = Timestamp.
- (v)
- SAP is a set of semantic attributes, SAP = {sap1, sap2, …, sapn}. Each semantic attribute has its corresponding datatype DTF(sapi), for i = 1, …, n. For example, if SAP = {busy, gasolineLevel, numberofPassengers}, then DTF(busy) = Boolean, DTF(gasolineLevel) = Z+, and DTF(numberofPassengers) = Z+.
3.3. Aggregation Functions for the Semantic Attributes of a Point Datatype
- Example:
- Example:
3.4. Edge Datatype
- (i)
- PointId1 is the identifier of a point, DTF(PointId1) = Z+.
- (ii)
- PointId2 is the identifier of a point, DTF(PointId2) = Z+.
- (iii)
- SAE is a set of semantic attributes, SAE = {sae1, sae2, …, saen}. Each semantic attribute has its corresponding datatype DTF(saei), for i = 1, …, n. For example, if SAE = {distance, passengersActivity}, then DTF(distance) = R+ and DTF(passengersActivity) = String.
3.5. Aggregation Functions for the Semantic Attributes of an Edge Datatype
- Example:
- Example:
3.6. Trajectory Datatype
- (i)
- TrajId is the identifier of a trajectory, DTF(TrajId) = Z+.
- (ii)
- PDT is a set of point datatypes, PDT = {pdt1, pdt2, …, pdtn}.
- (iii)
- EDT is a set of edge datatypes, EDT = {edt1, edt2, …, edtn − 1}.
- (iv)
- SAT is, in a similar way to SAP and SAE, a set of semantic attributes, SAT = {sat1, sat2, …, satk}. Each semantic attribute has its corresponding datatype DTF(sati), for i = 1, …, k. For example, if SAT = {vehicleType}, then DTF(vehicleType) = String.
3.7. Aggregation Functions for the Semantic Attributes of a Trajectory Datatype
- Example:
3.8. Point Value (Point Instance)
- (i)
- value(PointId) is a value of DTF(PointId) datatype, i.e., Z+.
- (ii)
- value(x) is a value of DTF(x) datatype, i.e., Latitude (for simplicity, a positive integer, Z+).
- (iii)
- value(y) is a value of DTF(y) datatype, i.e., Longitude (for simplicity, a positive integer, Z+).
- (iv)
- value(t) is a value of DTF(t) datatype, i.e., Timestamp.
- (v)
- SApvalue = {value(sap1), value(sap2), …, value(sapn)}, where value(sapi), for i = 1, …, n, is a value of DTF(sapi) datatype, i.e., SApvalue is the set of values of the semantic attributes of the point.
- Example:
3.9. Edge Value (Instance)
- (i)
- value(PointId1) is a value of DTF(PointId) datatype, i.e., Z+.
- (ii)
- value(PointId2) is a value of DTF(PointId) datatype, i.e., Z+.
- (iii)
- SAEvalue = {value(sae1), value(sae2), …, value(saen)}, where value(saei), for i = 1, …, n, is a value of DTF(saei) datatype, i.e., SAEvalue is the set of values of the semantic attributes of the edge.
- Example:
3.10. Trajectory Value (Instance)
- (i)
- value(TrajId) is a value of DTF(TrajId) datatype, i.e., Z+.
- (ii)
- Pvalue = {pv1, pv2, …, pvn}, where pvi, for i = 1, …, n, is a point value.
- (iii)
- Evalue = {ev1, ev2, …, evn − 1}, where evi, for i = 1, …, n − 1; n > 1, is an edge value.
- (iv)
- SATvalue = {value(sat1), value(sat2), …, value(satk)}, where value(sati), for i = 1, …, k, is a value of DTF(sati) datatype, i.e., SATvalue is the set of values of the semantic attributes of the trajectory.
- (i)
- If the set of point values is empty, then the set of edge values is also empty and vice versa.
- (ii)
- If n = 1 (i.e., the trajectory has only one point value), the set of edge values is empty.
- (iii)
- There cannot be, in Pvalue, two point values with the same PointId nor with the same t (time). Indeed, the point values of Pvalue are enumerated as follows. The point value with the smallest time (t) has PointId = 1, the point value with the second smallest time has PointId = 2, and so on. Therefore, given two point values pvi, pvj ∈ Pvalue, pvi ≠ pvj, if the PointId of pvi is less than the PointId of pvj, then the time of pvi is less than the time of pvj.
- (iv)
- Given an edge value evi, its corresponding PointIds, i.e., PointId1 and PointId2, meet the following two conditions: (i) PointId1 and PointId2 correspond to the PointIds of two point values pvi, pvj ∈ Pvalue, pvi ≠ pvj and (ii) PointId1 = PointId2 − 1, i.e., an edge value is created between two point values of Pvalue with consecutive PointIds.
- Example:
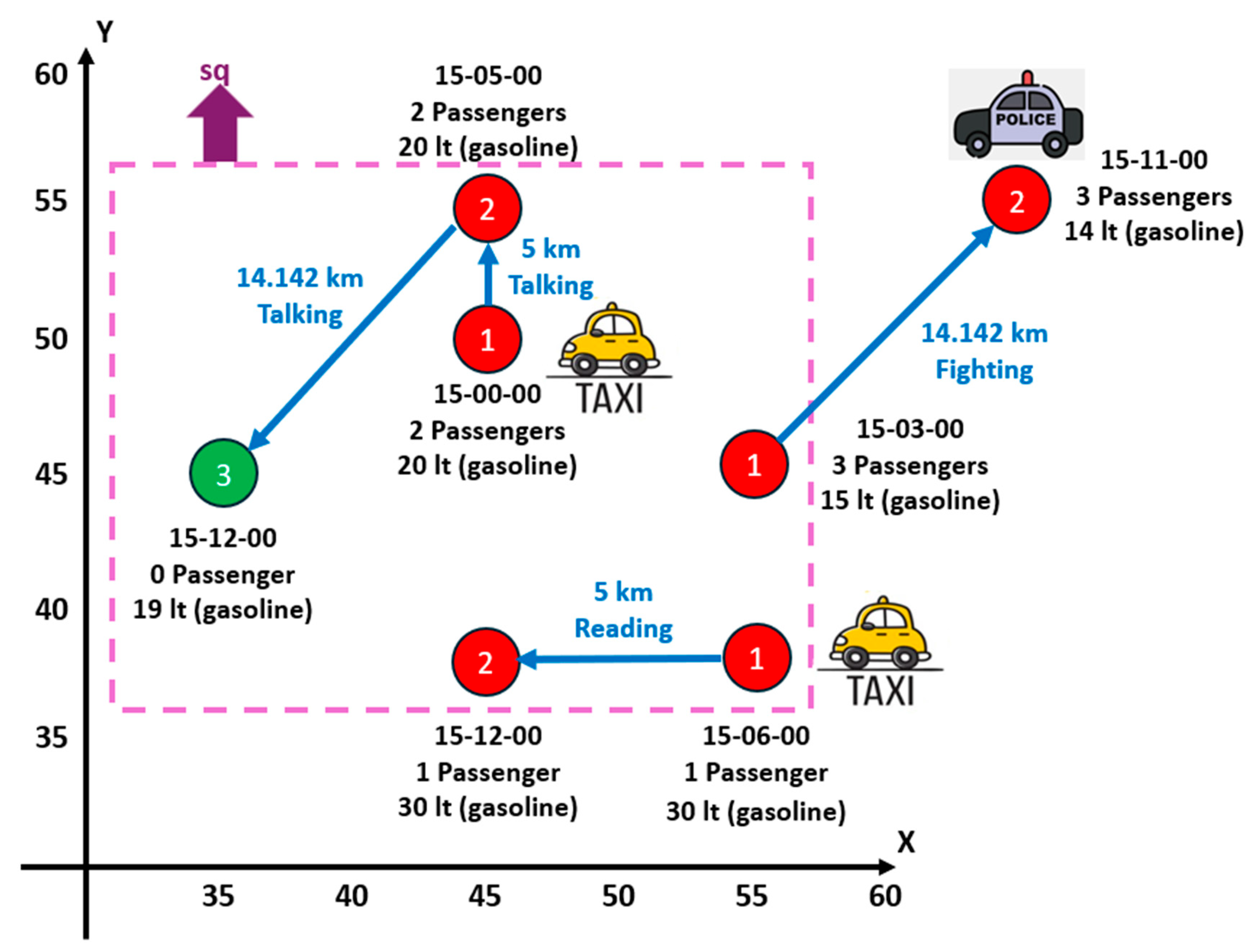
- (i)
- Pvalue = {pv1, pv2, pv3} with pv1 = (1, 45, 50, 25-Apr-2024:15-00-00, {true, 20, 2}), pv2 = (2, 45, 55, 25-Apr-2024:15-05-00, {true, 20, 2}), and pv3 = (3, 35, 45, 25-Apr-2024:15-12-00, {false, 19, 0}). In this example, the three point values have the same set of semantic attributes: SAP = {busy, gasolineLevel, numberofPassengers}. Although our proposal allows the analyst to define point values that have different sets of semantic attributes, for simplicity, it is assumed that all the point values of the same trajectory have the same set of semantic attributes.
- (ii)
- Evalue = {ev1, ev2} with ev1 = (1, 2, {5, “Talking”}) and ev2 = (2, 3, {14.142, “Talking”}). In this example, the two edge values have the same set of semantic attributes: SAE = {distance, passengersActivity}. Although the present proposal allows the analyst to define edge values that have different sets of semantic attributes, for simplicity, it is assumed that all the edge values of the same trajectory have the same set of semantic attributes.
- (i)
- For semantic attributes of points: Given that AggFnumberofPassengers = {AVG, SUM}, then AVG([2, 2, 0]) = 1.333 (note that this is the average of the number of passengers by point) and SUM([2, 2, 0]) = 4. Now, for AggFgasolineLevel = {AVG}, AVG([20, 20, 19]) = 19.666.
- (ii)
- For semantic attributes of edges: Given that AggFdistance = {SUM}, SUM([5, 14.142]) = 19.142. Now, for AggFpassengersActivity = {MODE}, MODE([“Talking”, “Talking”]) = “Talking”.
3.11. Aggregation of a Set of Trajectories
| Algorithm 1. AggregateTrajectoriesSAPoint. |
| Function AggregateTrajectoriesSAPoint(sq, TRAJ, ti, sa, aggf) |
| Input: sq ∈ Square; TRAJ ∈ PowerSet(TRAJECTORY); ti ∈ Time Interval; sa ∈ ATTR; |
| aggf ∈ AGGF; |
| Output: aggvalue ∈ DTF(aggf) /* DTF(aggf) is the resulting datatype of applying aggf to a |
| multiset of values each of DTF(sa) */ |
| Variables: multisetsa ∈ multiset of DTF(sa); // An array of DTF(sa) values |
| BEGIN |
| 1. IF aggf ∉AggFsa THEN /* Check if the aggf function is valid to be applied to the attribute |
| sa */ |
| 2. RETURN error; |
| 3. END IF |
| 4. FOREACH trajectory Tv ∈ TRAJ LOOP |
| 5. FOREACH point Pv ∈ Tv LOOP |
| 6. IF (Pv.x, Pv.y) IS INSIDE sq AND /* Check spatial containment of the point in the square */ |
| 7. Pv.t ∈ ti THEN // Check temporal containment of the point in the time interval |
| 8. multisetsa.Add(Pv.sa); // Add value of sa to the multiset |
| 9. END IF |
| 10. END FOREACH |
| 11. END FOREACH |
| 12. aggvalue = aggf(multisetsa); // Apply the aggregate function aggf to the multiset |
| 13. RETURN aggvalue; |
| END Function |
| Algorithm 2. AggregateTrajectoriesSAEdge. |
| Function AggregateTrajectoriesSAEdge(sq, TRAJ, ti, sa, aggf) |
| Input: sq ∈ Square; TRAJ ∈ PowerSet(TRAJECTORY); ti ∈ Time Interval; sa ∈ ATTR; |
| aggf ∈ AGGF; |
| Output: aggvalue ∈ DTF(aggf) /* DTF(aggf) is the resulting datatype of applying aggf to a multiset of values each of DTF(sa) */ |
| Variables: multisetsa ∈ multiset of DTF(sa); // An array of DTF(sa) values |
| BEGIN |
| 1. IF aggf ∉AggFsa THEN /* Check if the aggf function is valid to be applied to the attribute sa */ |
| 2. RETURN error; |
| 3. END IF |
| 4. FOREACH trajectory Tv ∈ TRAJ LOOP |
| 5. FOREACH edge Ev ∈ Tv LOOP |
| 6. IF (getPoint(Ev.pointId1).x, getPoint(Ev.pointId1).y) IS INSIDE sq AND |
| 7. (getPoint(Ev.pointId2).x, getPoint(Ev.pointId2).y) IS INSIDE sq AND /* Check spatial containment of the two points of the edge in the square. A straight line between PointId1 and PointId2 is assumed */ |
| 8. getPoint(Ev.pointId1).t ∈ // Add value of sa to the multiset |
| 9. multisetsa.Add(Ev.sa); ti AND getPoint(Ev.pointId2).t THEN /* Check temporal containment of the edge in the time interval */ |
| 10. END IF |
| 11. END FOREACH |
| 12. END FOREACH |
| 13. aggvalue = aggf(multisetsa); // Apply the aggregate function aggf to the multiset |
| 14. RETURN aggvalue; |
| END Function |
| Algorithm 3. AggregateTrajectoriesSATrajectory. |
| Function AggregateTrajectoriesSATrajectory(sq, TRAJ, ti, sa, aggf) |
| Input: sq ∈ Square; TRAJ ∈ PowerSet(TRAJECTORY); ti ∈ Time Interval; sa ∈ ATTR; |
| aggf ∈ AGGF; |
| Output: aggvalue ∈ DTF(aggf) /* DTF(aggf) is the resulting datatype of applying aggf to a multiset of values each of DTF(sa) */ |
| Variables: multisetsa ∈ multiset of DTF(sa); // An array of DTF(sa) values flag ∈ Boolean; // Check spatial and temporal containment of a trajectory |
| BEGIN |
| 1. IF aggf ∉AggFsa THEN /* Check if the aggf function is valid to be applied to the attribute sa */ |
| 2. RETURN error; |
| 3. END IF |
| 4. FOREACH trajectory Tv ∈ TRAJ LOOP |
| 5. flag = TRUE; |
| 6. FOREACH edge Ev ∈ Tv LOOP |
| 7. IF (Pv.x, Pv.y) IS NOT INSIDE sq OR/* Check spatial containment of the point in the square */ |
| 8. Pv.t ∉ ti THEN // Check temporal containment of the point in the time interval |
| 9. flag = FALSE; EXIT LOOP; |
| 10. END IF |
| 11. END FOREACH |
| 12. IF flag = TRUE THEN /* Check if all the points of the trajectory were inside the square and inside the time interval */ |
| 13. multisetsa.Add(Tv.sa); // Add value of sa to the multiset |
| 14. END IF |
| 15. END FOREACH |
| 16. aggvalue = aggf(multisetsa); // Apply the aggregate function aggf to the multiset |
| 17. RETURN aggvalue; |
| END Function |
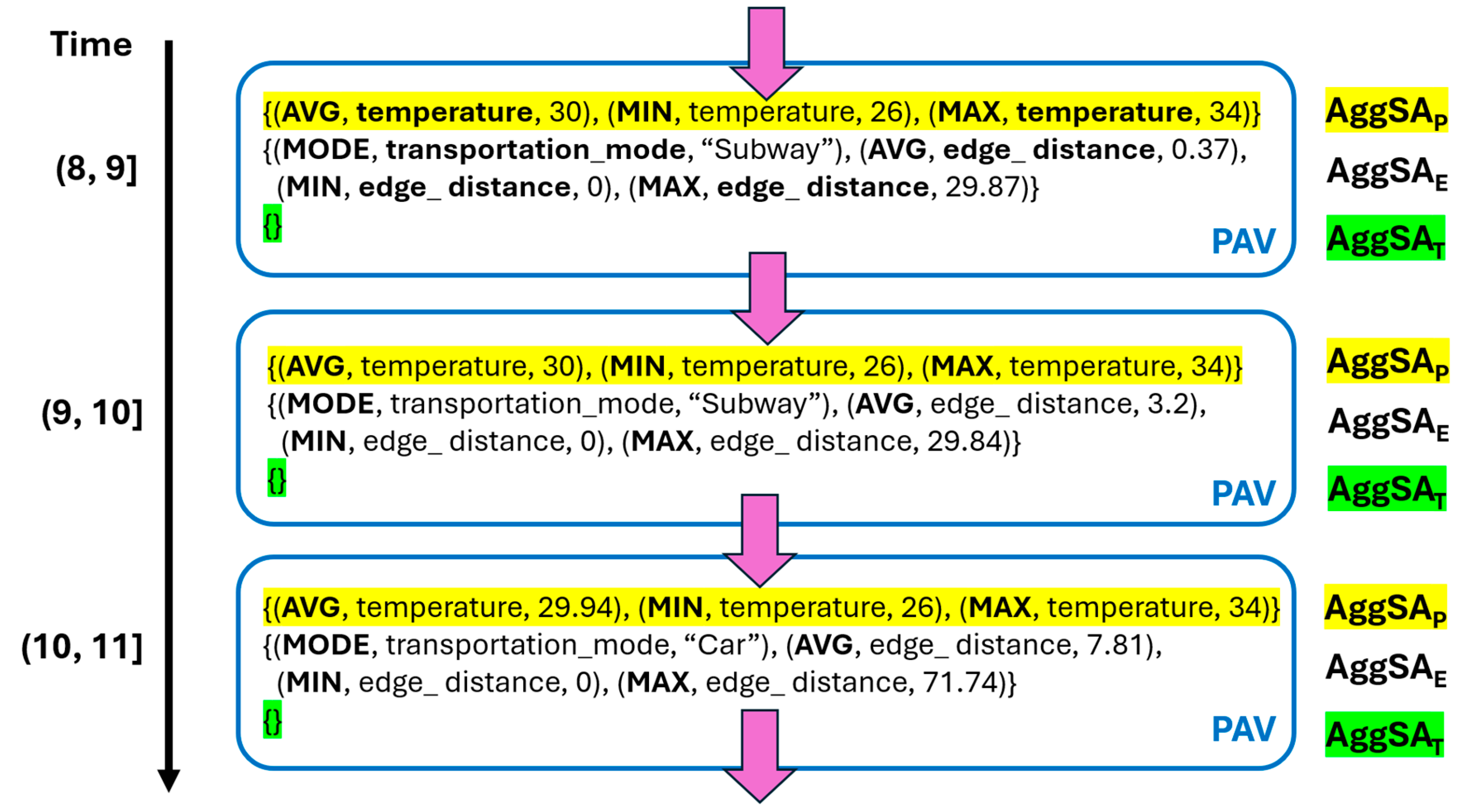
3.12. Package of Aggregate Values of a Set of Trajectories
- Example:
4. Experiments
Data Enrichment
- (i)
- Semantic attribute of a point
- (ii)
- Semantic attribute of an edge
- (iii)
- Semantic attributes of a trajectory
- (i)
- Mode (MODE): transportation_mode.
- (ii)
- Average (AVG): edge_distance, temperature, total_trajectory_time, and total_trajectory_ distance.
- (iii)
- Minimum (MIN): edge_distance, temperature, total_trajectory_time, and total_trajectory_ distance.
- (iv)
- Maximum (MAX): edge_distance, temperature, total_trajectory_time, and total_trajectory_distance.
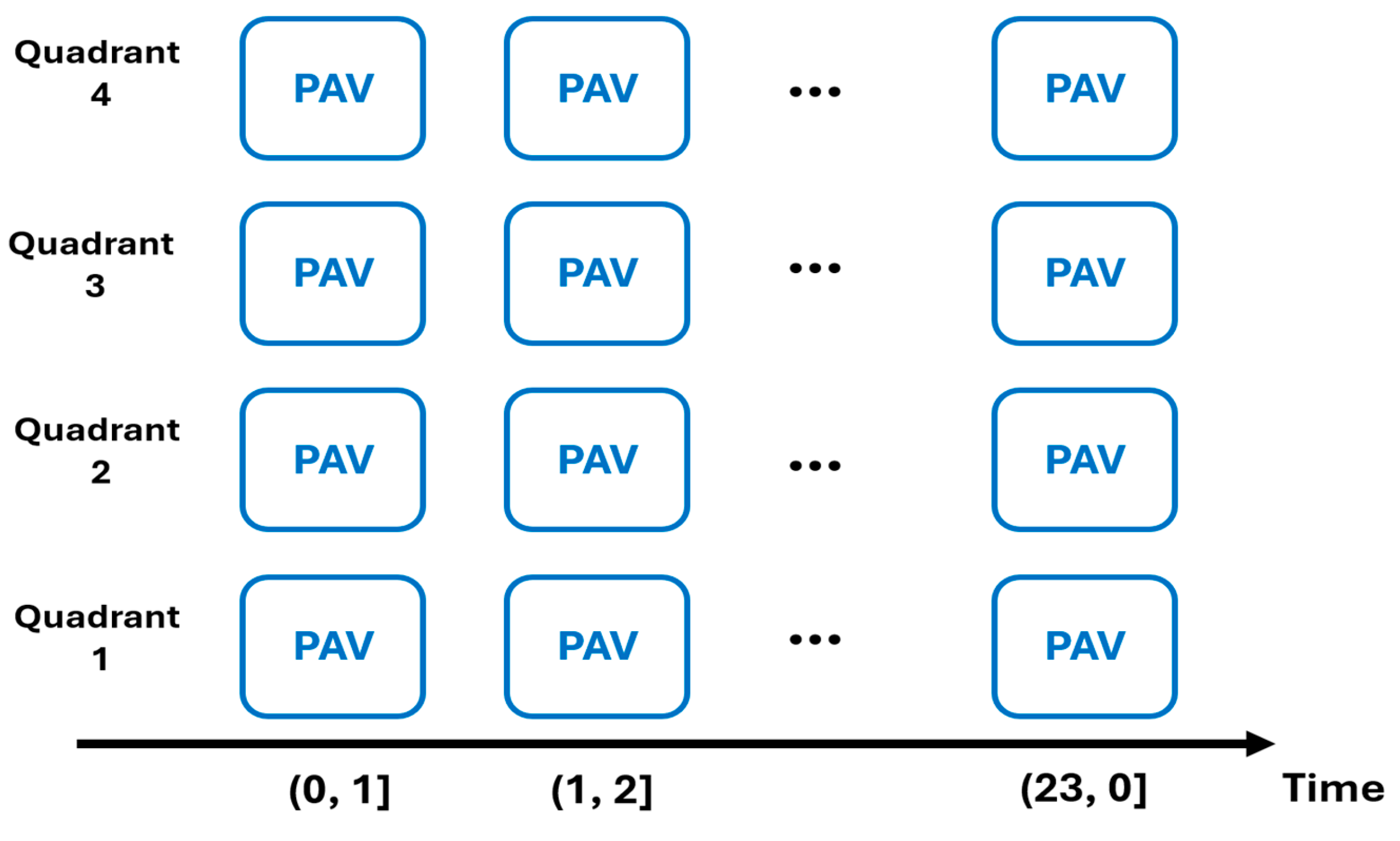
- (i)
- First quadrant: latitudes between 40 and 41 and longitudes between 115 and 116.
- (ii)
- Second quadrant: latitudes between 40 and 41 and longitudes between 116 and 117.
- (iii)
- Third quadrant: latitudes between 39 and 40 and longitudes between 115 and 116.
- (iv)
- Fourth quadrant: latitudes between 39 and 40 and longitudes between 116 and 117.
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. AggregateTrajectoriesSAPoint: Average (AVG) of Temperature
|
CREATE OR REPLACE FUNCTION AggregateTrajectoriesSAPoint( Sq_inf_x FLOAT, -- Longitude of the bottom-left corner of a square region (sq) Sq_inf_y FLOAT, -- Latitude of the bottom-left corner of a square region (sq) Sq_sup_x FLOAT, -- Longitude of the top-right corner of a square region (sq) Sq_sup_y FLOAT, -- Latitude of the top-right corner of a square region (sq) Ti_start TIMESTAMP WITHOUT TIME ZONE, -- Time interval start time Ti_end TIMESTAMP WITHOUT TIME ZONE -- Time interval end time ) RETURNS FLOAT AS $$ DECLARE aggvalue FLOAT; -- Average of temperature BEGIN -- Execute a query to calculate the average of the temperature attribute from the point table -- Spatial and temporal windows are checked SELECT AVG(“temperature”) INTO aggvalue FROM public.point WHERE -- Check latitude to fall within the square region “Latitude” BETWEEN Sq_inf_y AND Sq_sup_y -- Check longitude to fall within the square region AND “Longitude” BETWEEN Sq_inf_x AND Sq_sup_x -- Check datetime to be within the specified time interval AND “Datetime” BETWEEN Ti_start AND Ti_end; -- Return average of temperature RETURN aggvalue; END; $$ LANGUAGE plpgsql; |
Appendix B. AggregateTrajectoriesSAEdge: Mode (MODE) of Transportation_Mode
|
CREATE
OR REPLACE FUNCTION ( Sq_inf_x FLOAT, -- Longitude of the bottom-left corner of a square region (sq) Sq_inf_y FLOAT, -- Latitude of the bottom-left corner of a square region (sq) Sq_sup_x FLOAT, -- Longitude of the top-right corner of a square region (sq) Sq_sup_y FLOAT, -- Latitude of the top-right corner of a square region (sq) Ti_start TIMESTAMP WITHOUT TIME ZONE, -- Time interval start time Ti_end TIMESTAMP WITHOUT TIME ZONE -- Time interval end time ) RETURNS TEXT AS $$ DECLARE aggvalue TEXT; -- Mode of transportation mode BEGIN -- Execute a query to find the mode of the transportation mode attribute from the point table -- Spatial and temporal windows are checked SELECT MODE() WITHIN GROUP (ORDER BY “transportation_mode”) INTO aggvalue FROM public.point WHERE -- Check latitude to fall within the square region “Latitude” BETWEEN Sq_inf_y AND Sq_sup_y -- Check longitude to fall within the square region AND “Longitude” BETWEEN Sq_inf_x AND Sq_sup_x -- Check datetime to be within the specified time interval AND “Datetime” BETWEEN Ti_start AND Ti_end; -- Return mode of the transportation mode RETURN aggvalue; END; $$ LANGUAGE plpgsql; |
Appendix C. AggregateTrajectoriesSATrajectory: Maximum (MAX) of Total_Trajectory_Distance
|
CREATE
OR REPLACE FUNCTION AggregateTrajectoriesSATrajectory( Sq_inf_x FLOAT, -- Longitude of the bottom-left corner of a square region (sq) Sq_inf_y FLOAT, -- Latitude of the bottom-left corner of a square region (sq) Sq_sup_x FLOAT, -- Longitude of the top-right corner of a square region (sq) Sq_sup_y FLOAT, -- Latitude of the top-right corner of a square region (sq) Ti_start TIMESTAMP WITHOUT TIME ZONE, -- Time interval start time Ti_end TIMESTAMP WITHOUT TIME ZONE -- Time interval end time ) RETURNS FLOAT AS $$ DECLARE aggvalue NUMERIC; -- Maximum of total distance BEGIN -- Execute a query to calculate the maximum total distance attribute from the trajectory table -- Spatial and temporal windows are checked SELECT MAX(“total_trajectory_distance”) INTO aggvalue FROM public.trajectory WHERE -- Check start latitude to fall within the square region “start_latitude” BETWEEN Sq_inf_y AND Sq_sup_y -- Check end latitude to fall within the square region AND “end_latitude” BETWEEN Sq_inf_y AND Sq_sup_y -- Check start longitude to fall within the square region AND “start_longitude” BETWEEN Sq_inf_x AND Sq_sup_x -- Check end longitude to fall within the square region AND “end_longitude” BETWEEN Sq_inf_x AND Sq_sup_x -- Check start time to be within the specified time interval AND “start_time” BETWEEN Ti_start AND Ti_end -- Check end time to be within the specified time interval AND “end_time” BETWEEN Ti_start AND Ti_end; -- Return maximum of total distance RETURN aggvalue; END; $$ LANGUAGE plpgsql; |
References
- Spaccapietra, S.; Parent, C.; Damiani, M.L.; Fernandes de Macedo, J.A.; Porto, F.; Vangenot, C. A conceptual view on trajectories. Data. Knowl. Eng. 2008, 65, 126–146. [Google Scholar] [CrossRef]
- Oueslati, W.; Tahri, S.; Limam, H.; Akaichi, J. A systematic review on moving objects’ trajectory data and trajectory data warehouse modeling. Comput. Sci. Rev. 2023, 47, 100516. [Google Scholar] [CrossRef]
- Andrienko, G.; Andrienko, N.; Rinzivillo, S.; Nanni, M.; Pedreschi, D.; Giannotti, F. Interactive visual clustering of large collections of trajectories. In Proceedings of the 2009 IEEE Symposium on Visual Analytics Science and Technology, Atlantic City, NJ, USA, 12–13 October 2009; pp. 3–10. [Google Scholar] [CrossRef]
- Zhang, Y.; Klein, K.; Deussen, O.; Gutschlag, T.; Storandt, S. Robust visualization of trajectory data. It Inf. Technol. 2022, 64, 181–191. [Google Scholar] [CrossRef]
- Orlando, S.; Orsini, R.; Raffaeta, A.; Roncato, A.; Silvestri, C. Trajectory Data Warehouses: Design and Implementation Issues. Comput. Sci. Eng. 2007, 1, 211–232. [Google Scholar] [CrossRef]
- Meratnia, N.; de By, R.A. Aggregation and comparison of trajectories. In Proceedings of the GIS ‘02: 10th ACM International Symposium on Advances in Geographic Information Systems, McLean, VA, USA, 8–9 November 2002; pp. 49–54. [Google Scholar] [CrossRef]
- Braz, F.; Orlando, S.; Orsini, R.; Raffaeta, A.; Roncato, A.; Silvestri, C. Approximate Aggregations in Trajectory Data Warehouses. In Proceedings of the IEEE 23rd International Conference on Data Engineering Workshop (ICDEW), Istanbul, Turkey, 17 April 2007; pp. 536–545. [Google Scholar] [CrossRef]
- Baltzer, O.; Dehne, F.; Hambrusch, S.E.; Rau-Chaplin, A. OLAP for Trajectories. In Proceedings of the 19th International Workshop on Database and Expert Systems Applications, DEXA 2008, Turin, Italy, 1–5 September 2008. [Google Scholar]
- Baltzer, O.; Dehne, F.; Hambrusch, S.; Rau-Chaplin, A. Olap for Trajectories; Technical Report TR-08-11; School of Computer Science, Carleton University: Ottawa, ON, Canada, 2008; Available online: https://carleton.ca/scs/wp-content/uploads/TR-08-11-Dehne.pdf (accessed on 30 September 2024).
- Feng, J.; Shi, Y.Q.; Tang, Z.X.; Rui, C.H. Aggregation index technique of moving objects in road networks. J. Jilin Univ. (Eng. Technol. Ed.) 2014, 44, 1799–1805. [Google Scholar]
- Shi, Y.Q. A Study on the Complete Temporal Probabilistic Aggregate Query Over Moving Objects on Road Networks. Ph.D. Thesis, Hohai University, Nanjing, China, 2015. [Google Scholar]
- Shi, Y.; Huang, S.; Zheng, C.; Ji, H. A Hybrid Aggregate Index Method for Trajectory Data. Math. Probl. Eng. 2019, 2019, 1784864. [Google Scholar] [CrossRef]
- Buchin, K.; Driemel, A.; van de L’Isle, N.; Nusser, A. Center-based clustering of trajectories. In Proceedings of the 27th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Chicago, IL, USA, 5 November–8 December 2019; pp. 496–499. [Google Scholar]
- Aronov, B.; Har-Peled, S.; Knauer, C.; Wang, Y.; Wenk, C. Fréchet distance for curves, revisited. In Algorithms—ESA 2006; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4168, pp. 52–63. [Google Scholar]
- Brankovic, M.; Buchin, K.; Klaren, K.; Nusser, A.; Popov, A.; Wong, S. (k, l)-medians clustering of trajectories using continuous dynamic time warping. In Proceedings of the SIGSPATIAL ‘20: 28th International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 3–6 November 2020; pp. 99–110. [Google Scholar]
- Ghazi, B.; Kamal, N.; Kumar, R.; Manurangsi, P.; Zhang, A. Private Aggregation of Trajectories. Proc. Priv. Enhancing Technol. 2022, 2022, 626–644. [Google Scholar] [CrossRef]
- Duong, T. Using iterated local alignment to aggregate trajectory data into a traffic flow map. arXiv 2024, arXiv:2406.17500. [Google Scholar]
- Tong, A.; Sharma, A.; Veer, S.; Pavone, M.; Yang, H. Online Aggregation of Trajectory Predictors. arXiv 2025, arXiv:2502.07178. [Google Scholar]
- Gómez, L.I.; Kuijpers, B.; Vaisman, A.A. Analytical queries on semantic trajectories using graph databases. Trans. GIS 2019, 23, 1078–1101. [Google Scholar] [CrossRef]



| Reference (Year) | Contribution | Limitation |
|---|---|---|
| [6] (2002) | An efficient method for calculating the presence in a spatio-temporal cell. | - The method may generate inaccurate results. - It only focuses on the presence calculation. |
| [5,7] (2007) | Two efficient methods for calculating the presence in a spatio-temporal cell. | - The methods may generate inaccurate results. - They only focus on the presence calculation. |
| [8,9] 2008 | An extension to the GROUP BY clause of SQL for aggregating trajectories. | - The method aggregates trajectories based only on their spatio-temporal coordinates. - Aggregation based on semantic attributes is not considered. |
| [11,12] 2014–2019 | Probabilistic methods for calculating the presence in road sections in a time interval. | - The methods are specialized for road sections. - The methods focus only on the presence calculation. |
| [13] 2019 | Trajectory clustering based on the Fréchet distance. | - The method creates clusters of trajectories based only on their spatio-temporal coordinates. - Clustering or aggregation based on semantic attributes is not considered. |
| [15] 2020 | Trajectory clustering based on the continuous dynamic time warping distance. | - The method creates clusters of trajectories based only on their spatio-temporal coordinates. - Clustering or aggregation based on semantic attributes is not considered. |
| [16] 2022 | A method for aggregating trajectories in a curve. | - The method generates a curve for a set of trajectories based only on their spatio-temporal coordinates. - Semantic attributes are not considered in this process. |
| [17] 2024 | A model for aggregating multiple trajectory predictors (TPs). | - The method generates a predicted trajectory based on multiple TPs and on spatio-temporal coordinates. - Semantic attributes are not considered in this process. |
| [18] 2025 | A method for aggregating a set of segments from different trajectories into a traffic flow map. | - The method generates flow lines (based only on the spatio-temporal coordinates) from a set of segments of trajectories. - Semantic attributes are not considered in this process. |
| Latitude | Longitude | Datetime | Transportation Mode | Trajectory Identifier |
|---|---|---|---|---|
| 39.963966 | 116.328324 | 7 November 2008 09:02:42 | Bus | 24 |
| 39.964004 | 116.328321 | 7 November 2008 09:02:44 | Bus | 24 |
| 39.964051 | 116.328321 | 7 November 2008 09:02:46 | Bus | 24 |
| 39.964103 | 116.328319 | 7 November 2008 09:02:48 | Bus | 24 |
| 40.0771166 | 116.3288333 | 21 June 2007 12:28:34 | Walk | 117 |
| 40.0696 | 116.3296666 | 22 June 2007 14:55:12 | Train | 117 |
| Time Interval (Hours) | MODE of Transportation_Mode | AVG Edge_ Distance (km) | MIN Edge_ Distance (km) | MAX Edge_ Distance (km) | AVG Temperature (°C) | MIN Temperature (°C) | MAX Temperature (°C) |
|---|---|---|---|---|---|---|---|
| (0–1] | Subway | 2.8 | 0 | 164.87 | 29.95 | 26 | 33.99 |
| (1–2] | Subway | 0.79 | 0 | 118.77 | 29.97 | 26 | 34 |
| (2–3] | Subway | 1.07 | 0 | 118.77 | 29.9 | 26 | 34 |
| (3–4] | Subway | 8.57 | 0 | 71.41 | 30 | 26 | 34 |
| (5–6] | Subway | 1.75 | 0 | 71.41 | 30 | 26 | 33.99 |
| (6–7] | Subway | 0.48 | 0 | 96.9 | 29.99 | 26 | 34 |
| (7–8] | Subway | 0.34 | 0 | 39.66 | 30 | 26.01 | 33.99 |
| (8–9] | Subway | 0.37 | 0 | 29.94 | 29.92 | 26 | 34 |
| (9–10] | Subway | 3.2 | 0 | 29.87 | 29.99 | 26 | 34 |
| (10–11] | Car | 7.81 | 0 | 29.84 | 29.94 | 26 | 34 |
| (11–12] | Subway | 6.78 | 0 | 81.74 | 29.97 | 26 | 33.99 |
| (12–13] | n.d | n.d | n.d | n.d | n.d | n.d | n.d |
| (13–14] | n.d | n.d | n.d | n.d | n.d | n.d | n.d |
| (14–15] | Walk | 7.84 | 7.84 | 7.84 | 29.75 | 29.75 | 29.754 |
| Time Interval (Hours) | MODE of Transportation_ Mode | AVG Edge_ Distance (km) | MIN Edge_ Distance (km) | MAX Edge_ Distance (km) | AVG Temperature (°C) | MIN Temperature (°C) | MAX Temperature (°C) |
|---|---|---|---|---|---|---|---|
| (7–8] | Walk | 8.34 | 1.33 | 23.94 | 30.278 | 26.057 | 33.90 |
| Time Interval (Hours) | MODE of Transportation_ Mode | AVG Edge_ Distance (km) | MIN Edge_ Distance (km) | MAX Edge_ Distance (km) | AVG Temperature (°C) | MIN Temperature (°C) | MAX Temperature (°C) |
|---|---|---|---|---|---|---|---|
| (0–1] | Subway | 2.80 | 0 | 164.87 | 29.49 | 26 | 34 |
| (1–2] | Subway | 0.79 | 0 | 118.76 | 29.98 | 26 | 34 |
| (2–3] | Subway | 1.07 | 0 | 32.13 | 29.9 | 26 | 34 |
| (3–4] | Subway | 8.56 | 0 | 71.42 | 29.97 | 26 | 34 |
| (5–6] | Subway | 1.75 | 0 | 96.9 | 30.01 | 26 | 34 |
| (6–7] | Subway | 0.48 | 0 | 39.66 | 30 | 26 | 34 |
| (7–8] | Subway | 0.34 | 0 | 29.94 | 29.92 | 26 | 34 |
| (8–9] | Subway | 0.37 | 0 | 29.87 | 30 | 26 | 34 |
| (9–10] | Subway | 3.20 | 0 | 29.84 | 30 | 26 | 34 |
| (10–11] | Car | 7.81 | 0 | 71.74 | 29.94 | 26 | 34 |
| (11–12] | Subway | 6.78 | 0 | 78.24 | 29.96 | 26 | 34 |
| (12–13] | n.d | n.d | n.d | n.d | n.d | 26 | 34 |
| (13–14] | n.d | n.d | n.d | n.d | n.d | 26 | 34 |
| (14–15] | Walk | 784.69 | 784.69 | 784.69 | 29.75 | 29.75 | 29.75 |
| Time Interval (Hours) | MODE of Transportation_ Mode | AVG Edge_ Distance (km) | MIN Edge_ Distance (km) | MAX Edge_ Distance (km) | AVG Temperature (°C) | MIN Temperature (°C) | MAX Temperature (°C) |
|---|---|---|---|---|---|---|---|
| (3–4] | Subway | 16.55 | 0 | 33.10 | 30.98 | 29.87 | 32.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arboleda, F.J.M.; Garani, G.; Hoyos, N.A.Á. A Formal Model of Trajectories for the Aggregation of Semantic Attributes. Big Data Cogn. Comput. 2025, 9, 110. https://doi.org/10.3390/bdcc9050110
Arboleda FJM, Garani G, Hoyos NAÁ. A Formal Model of Trajectories for the Aggregation of Semantic Attributes. Big Data and Cognitive Computing. 2025; 9(5):110. https://doi.org/10.3390/bdcc9050110
Chicago/Turabian StyleArboleda, Francisco Javier Moreno, Georgia Garani, and Natalia Andrea Álvarez Hoyos. 2025. "A Formal Model of Trajectories for the Aggregation of Semantic Attributes" Big Data and Cognitive Computing 9, no. 5: 110. https://doi.org/10.3390/bdcc9050110
APA StyleArboleda, F. J. M., Garani, G., & Hoyos, N. A. Á. (2025). A Formal Model of Trajectories for the Aggregation of Semantic Attributes. Big Data and Cognitive Computing, 9(5), 110. https://doi.org/10.3390/bdcc9050110







