PK-Judge: Enhancing IP Protection of Neural Network Models Using an Asymmetric Approach

Abstract

This paper introduces PK-Judge, a novel neural network watermarking framework designed to enhance the intellectual property (IP) protection by incorporating an asymmetric cryptograp hic approach in the verification process. Inspired by the paradigm shift from HTTP to HTTPS in enhancing web security, this work integrates public key infrastructure (PKI) principles to establish a secure and verifiable watermarking system. Unlike symmetric approaches, PK-Judge employs a public key infrastructure (PKI) to decouple ownership validation from the extraction process, significantly increasing its resilience against adversarial attacks. Additionally, it incorporates a robust challenge-response mechanism to mitigate replay attacks and leverages error correction codes (ECC) to achieve an Effective Bit Error Rate (EBER) of zero, ensuring watermark integrity even under conditions such as fine-tuning, pruning, and overwriting. Furthermore, PK-Judge introduces a new requirement based on the principle of separation of privilege, setting a foundation for secure and scalable watermarking mechanisms in machine learning. By addressing these critical challenges, PK-Judge advances the state-of-the-art in neural network IP protection and integrity, paving the way for trust-based AI technologies that prioritize security and verifiability.

1. Introduction

In the expanding vista of technological sectors dominated by deep learning models, the overarching concerns of trustworthiness and ownership validation have gained substantial traction. These models are invaluable assets as their development requires well-designed engineered architectures, large-scale of datasets, substantial computational resources and domain-specific expertise for optimization. These sophisticated architectures, applied to numerous cutting-edge applications and services [1,2,3,4,5,6], accentuate the necessity for robust intellectual property (IP) protection mechanisms. Beyond mere authenticity and traceability, the definitive proof of ownership is an integral component of the trust equation of these networks. This evolving scenario mandates a comprehensive examination and potential re-calibration of current methodologies.

In this context, digital watermarking emerges as a pivotal concept. Digital watermarking is a process that involves embedding imperceptible information, often referred to as a watermark, into digital media such as images, audio, video, and documents [7,8]. Functioning much like a physical watermark on paper, its primary objective is to assert ownership, authenticate, verify the integrity, and manage the rights of the content [8]. The advent of the digital age has made it easier to reproduce and distribute a watermarked content, often leading to unauthorized copying and distribution.

A robust digital watermark should be able to resist various attacks and manipulations, be difficult to remove without degrading the quality of the original content, and be detectable even in modified versions of the content [7,9]. As digital content proliferates across various platforms and channels, the significance of digital watermarking continues to escalate, serving both as a deterrent against misuse and a mechanism for rights management [10]. In the context of deep learning domain, many protocols like  [11,12,13,14,15] adopt a symmetric watermarking scheme by inserting random bits into the model space. Ownership validation is then a matter of extracting this watermark and evaluating it against a response using a “pre-defined acceptable threshold”. If the match exceeds this threshold, the model’s ownership is confirmed. Thus, the determination “valid owner” in current IP protection protocols is attributed to the knowledge of a suitable number of bits that had been watermarked in the model. Such a determination method is weak. One can make this a more challenging task to exploit by increasing the size of the watermark, as well as increasing the percentage of accuracy for acceptance. This alone will introduce challenges due to potential size and nosiness of the embed-extraction process. But our work, see Section 5, does demonstrate we can overcome this. By itself, a system of I-know-the-secret/extract-the-watermark and compare the two is a symmetric scheme. Symmetric schemes used for authentication are prone to abuse. Once one reveals their knowledge of the secret, that secret has been revealed even if this reveal was completed in a secure and private setting, there is a potential for exposure. A solution to overcome the potential for exposure in an application such as IP protection is to embed many secret keys (all of the same size) in multiple places and discard a key once used and in a ’determination’ and then move to the next embedded key, when challenged for ownership. Such a method is impractical, and prone for other types of abuse. Here we introduce a novel approach of proving ownership by embedding a digital signature. Only one public key can validate the digital signature. Knowledge of the watermark does not demonstrate ownership; rather, by verifying the extracted digital signature with the public key, all entities know the owner of the model is the owner of the signing key (which is secret-but tied to the unique public key). In our work we add a challenge-response mechanism to our protocol, which assures all parties this person is the owner of the secret key. In the end, our protocol does not collapse as a symmetric system would if there is partial exposure of the watermark to other parties during the determination of ownership. The contributions of this paper can be summarized as follows:

• Application of public-key digital signatures: PK-Judge embeds cryptographic digital signatures into neural networks, enabling secure ownership validation independent of the watermark extraction process.
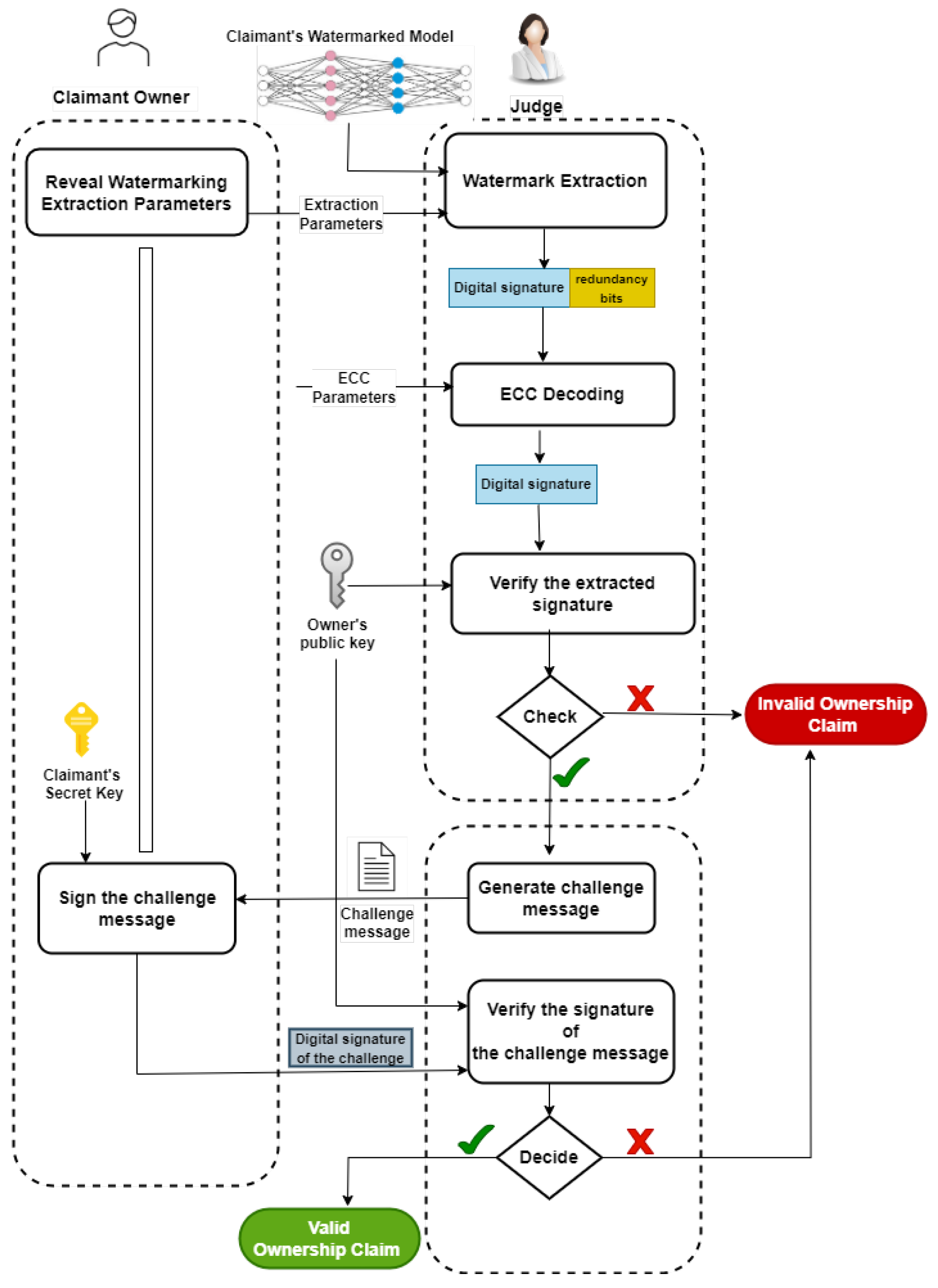
• Challenge-Response Mechanism: A robust challenge-response protocol is incorporated to mitigate the risk of replay attacks, ensuring that ownership claims are trustworthy and resilient to adversarial strategies.
• Error Correction Codes (ECC): By employing ECC, PK-Judge achieves an Effective Bit Error Rate (EBER) of zero, ensuring the integrity of embedded watermarks even under adversarial scenarios, such as model fine-tuning, pruning, or overwriting.
• Ownership Verification: A new requirement for ownership verification is proposed, leveraging the principle of separation of privilege to enhance security and guide future watermarking designs.

The use of a public-key cryptography in watermark verification offers a more secure and reliable method for proving ownership. Asymmetric cryptosystems, when properly employed, have long been recognized for providing greater trust and security. Drawing inspiration from the world of network protocols, such as the transition from HTTP [16] to HTTPS [17] offers valuable insights. HTTPS, beyond its technical attributes, marked a significant change in building user confidence in online interactions. Analogously, in the realm of neural networks, we contend that trust should be rooted in models that unequivocally validate their source and ownership. We anticipate that many of the integrity challenges in neural networks will be effectively addressed by embracing digital signatures. Leveraging robust public-key cryptographic protocols within the design and deployment of deep learning models, digital signatures can offer a transparent and verifiable chain of ownership and authenticity. Advocating for this strict standard, our aim is to shape a future where the neural network approach is marked by a detailed integration of security and trust, leading to a time of neural network solutions that are both verifiable and reliable.

2. Related Work

Model watermarking for a single-owner protection has rapidly advanced with two major trends based on the owner’s verification interface: (i) White-Box watermarking that embeds secret information in model internals (weights, dynamic parameters, or network structures) and (ii) Black Box watermarking that relies on specially crafted inputs (e.g., out-of-distribution or near-boundary samples) for ownership verification.

2.1. White Box Watermarking

Weights-Based Embedding: Several methods embed watermark directly in neural network weights Uchida et al. [11] embedded static watermarks into model weights via regularization. They are utilizing a secret matrix to facilitate both embedding and extraction. Ownership is verified by comparing the extracted watermark with the original using Bit Error Rate (BER). However, the approach is susceptible to statistical attacks due to increased variance in the watermarked layer [18] and vulnerable to fine-tuning. Namba and Sakuma [19] proposed exponential weighting for robust watermarking, while Liu et al. [20] introduced a greedy residual approach to embed watermarks with minimal accuracy loss but their approach lead to increased computational complexity and longer training times due to the greedy residual embedding process. Wang and Kerschbaum [21] presented RIGA, which hides watermarks covertly in weights. Although these approaches preserve fidelity, they can be computation-heavy when verifying across large model weight matrices. DeepiSign [14] embedded cryptographic hashes in the frequency domain. Fan et al. [22] introduced passport layers as a DNN model protection mechanism. Tang  et al. [15] introduced Deep Serial Number (DSN) by training a teacher model, followed by using knowledge distillation to transfer the teacher model’s knowledge to student models. Li et al. [23] integrate license features into models by synchronizing license training with model parameters through gradient optimization and introduce employ random perturbations for data standardization.

Dynamic Parameters: Another method focuses on embedding signals into dynamic parameters, such as batch normalization statistics or activation distributions. Li et al. [24] advocated leveraging external feature embeddings to verify ownership passively. Rouhani et al. [12] (DeepSigns) introduced an activation-distribution watermark. DeepMarks [13] employs a technique where a watermark is embedded within the model’s weight distribution’s probability density function, employing a method akin to that of Uchida et al. for extraction. Ownership is verified by correlating the extracted watermark with the owner’s signature through dot product computation. But, this protocol has a large calculation overhead.

Structure-Level Watermarking: Instead of focusing on weights, some approaches alter or tag the network architecture itself. Chen et al. [25] proposed a lottery-ticket-based watermark that prunes and reconfigures subnetwork structures, while Zhao et al. [26] introduced structure pruning or architectural morphing to encode watermarks. Such methods often demand no extra data and avoid performance drops by carefully adjusting layers or channels. Nevertheless, they lack generalization and flexibility across diverse architectures and are less robust to architectural compression or layer-wise transformations.

2.2. Black-Box Watermarks

Out-of-Distribution Samples. Many single-owner watermarking schemes rely on creating Out-of-Distribution Samples as trigger inputs. Adi et al. [27] utilized backdoor embedding for watermarking with black-box verification. Zhang et al. [28] used pattern-based triggers for black-box watermarking. Jia et al. [29] presented entangled watermarks that embed watermarks into Out-of-Distribution data points, while Jia et al. [30] combined subnetwork partitioning with watermark triggers for verification. Li et al. [31] inject license keys into the model through backdoor learning. Peng et al. [32] generate trigger samples with a distinct data distribution different from the original task, serving as the watermark for black-box watermarking. Fingerprint information is then embedded into a select few of the model’s critical weights through a method that combines fine-tuning and loss-guided techniques. In the context of Large Language Models’ copyright, Xu et al. [33] introduced the Hufu watermark which uses a specific input format as a trigger instead of relying on conventional input triggers. Kim et al. [34] proposed margin-based watermarking to enforce the trigger set to have an excessive margin.

Near-Decision-Boundary Samples: Some methods have crafted triggers close to a model’s decision boundary. Mehta et al. [35] (AIME) leveraged classification errors near boundaries to embed hidden signals, and Yang et al. [36] used bi-level optimization to create boundary-tight watermarks. Such approaches sometimes degrade the model’s overall accuracy if boundary samples are too aggressive, and generating them can be computationally expensive.

Natural Samples with Preset Triggers: Attaching digital patterns or small perturbations to seemingly natural inputs is another query-based strategy. Bansal et al. [37] proposed certified smoothing for watermark embedding, while Li et al. [24] introduced small universal triggers. Nie et al. [38] secured model integrity via compression-resistant triggers, and Szyller et al. [39] (DAWN) dynamically inserted mislabeled data to watermark networks. Although these triggers are easy to inject during training they can negatively affect model usability if the trigger significantly shifts input distributions.

Subnetworks as Watermarks: Lv et al. [40] embed a watermark subnetwork into the task model and design a watermark regularizer. It trains HufuNet, an encoder-decoder model that inputs and then reconstructs trigger samples. Wang et al. [41] trains a watermark branch, namely PTYNet, without modifying the original model. Using a preset rule, the PTYNet is inserted into the protected model and is then fine-tuned for watermark embedding. For verification, PTYNet is injected into the model and tested with trigger samples to exhibit specific behaviors. Pautov et al. [42] proposed probabilistic framework to enhance trigger-set-based watermarking robustness by rigorously analyzing and validating the transferability of trigger sets to both proxy and stolen models. Some approaches verify the model ownership by extracting the model’s intrinsic characteristics as fingerprinting [43,44,45]. The authors in [46] uses trusted hardware and secure multiparty computation techniques but it suffers from high hardware costs, memory limitations, and performance overhead.

3. Watermarking Requirements

To effectively ensure the authenticity and ownership of a neural network model, the watermarking process must adhere to a set of stringent criteria. These requirements, both functional and security-related, dictate the reliability and resilience of the watermark against various adversarial scenarios.

• Fidelity: The watermarked model must retain its accuracy and effectiveness in performing its intended task. The probability of misclassifying a data point x from the dataset D (excluding the trigger dataset T) should be bounded by ${Pr}_{X\in D\setminus T}[\mathtt{mis}-\mathtt{Classify}({\mathcal{M}}_{\mathrm{wm}},X)]\le {ϵ}_0$, where ${ϵ}_0$ is a negligible parameter.
• Robustness: The embedded watermark should remain detectable and correctly extracted even after adversarial attacks such as model tuning, pruning, or overwriting [11,13], ensuring that $Pr[\mathtt{extract}\_\mathtt{watermark}({\mathcal{M}}_{\mathrm{wm}}^{\prime })=\mathtt{True}]=1$, where ${\mathcal{M}}_{\mathrm{wm}}^{\prime }$ is an attacked model.
• Uniqueness: The embedded watermark should be distinct and specific to a particular model ${\mathcal{M}}_{\mathrm{wm}}$ and its owner.
• Integrity: The probability that a non-watermarked model $\mathcal{M}$ is incorrectly identified as watermarked should be bounded by the parameter ${ϵ}_1$, i.e., $Pr[\mathtt{FalsePositive}({\mathcal{M}}_{\mathrm{wm}}|\mathrm{key})]\le {ϵ}_1$. Furthermore, any legal author must be able to prove their ownership with a probability of $1-{ϵ}_2$, specifically $Pr[\mathtt{ownership}\_\mathtt{verify}({\mathcal{M}}_{\mathrm{wm}}|\mathrm{key})=\mathtt{True}]\ge 1-{ϵ}_2$, where ${ϵ}_1$ and ${ϵ}_2$ are negligible parameters.
• Capacity: The watermarking scheme should be designed to embed sufficient information without compromising the fidelity and the integrity of the model [11,14].
• Efficiency: The watermarking process—embedding, extraction, and verification—should be computationally efficient, ensuring minimal overhead in model operation, as highlighted in [11].
• Universality: The watermarking technique should be versatile, making it applicable across various architectures and types of neural network models.

Watermarking systems require robust authentication mechanisms beyond mere watermark extraction. A critical contribution of this work is formalizing the necessity of an independent security verification process, decoupled from watermark extraction, as a fundamental requirement for all watermarking schemes. This addresses inherent vulnerabilities in schemes where extraction alone serves as proof of ownership. To mitigate risks, ownership claims must be validated through a separate security mechanism distinct from the extraction pipeline.

The principle of separation of privilege [47,48], a cornerstone of secure system design, mandates that authorization should depend on multiple independent conditions. For instance, communication systems decouple authentication from message decoding. Similarly, watermark-based ownership verification systems violate this principle if they rely exclusively on watermark extraction. We thus propose the following requirement:

8.

Ownership Verification Requirement: A watermarking scheme must authenticate ownership via a process independent of watermark extraction, ensuring adversarial corruption of extraction does not compromise verification.

This separation reduces susceptibility to attacks that exploit process dependencies. For example, symmetric watermarking schemes using XOR-based comparisons between extracted watermarks and secret keys, coupled with Bit Error Rate (BER) thresholds, inherently fail this criterion. Their verification is tied solely to the extraction, creating a single point of compromise. By enforcing independent verification, systems ensure that corruption of one process (e.g., extraction) does not propagate to the authentication mechanism, thereby enhancing overall security.

4. Background

4.1. Digital Signatures

Digital signatures [49,50] provide cryptographic guarantees of authenticity, integrity, and non-repudiation for digital assets. A signature scheme as illustrated in Figure 1 consists of the following components, where ($sk$: secret key, $pk$: public key, $\sigma$: signature, $\lambda$: security parameter, m: message):

• KeyGen: Generate asymmetric key pair $(sk,pk)\leftarrow \mathtt{KeyGen}(\lambda )$
• Sign: Create signature $\sigma \leftarrow \mathtt{Sign}(sk,\mathrm{hash}(m))$
• Verify: Output $\{\mathrm{TRUE},\mathrm{FALSE}\}\leftarrow \mathtt{Verify}(pk,\mathrm{hash}(m),\sigma )$

A secure signature scheme will satisfy the following two properties: (i) Once a signature generated from a message and the secret key, it can be verified using the associated public key. (ii) It is computationally infeasible to produce a valid signature of any message without the knowledge of the party’s secret key.

Short signature [51] are particularly advantageous due to their compact size, which enables seamless integration within neural network models. Compared to traditional methods such as the RSA signature  [49], short signatures significantly reduce computational overhead during both the signing and verification processes, making them suitable noisy and sensitive capacity systems such as neural network models.

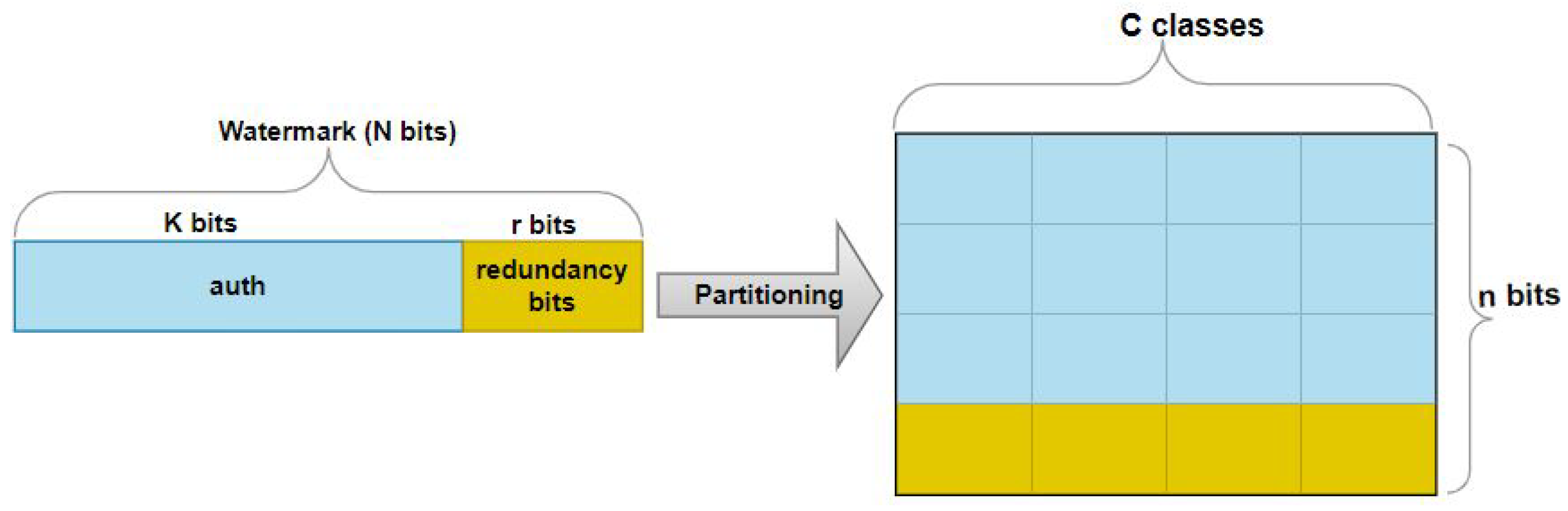
4.2. Error Correction Codes (ECC)

Error Correction Codes (ECC) [52] ensure data integrity under noise or transmission errors through two core operations:

• Encoding: Transforms message $\mathbf{m}$ (k-bit) to codeword $\omega$ (N-bit, $N>k$) via $\omega \leftarrow \mathrm{Encode}(\mathbf{m})$, adding redundancy $r=N-k$ for error resilience.
• Decoding: Recovers original message ${\mathbf{m}}^{\prime }$ from corrupted ${\omega }^{\prime }$ using ${\mathbf{m}}^{\prime }\leftarrow \mathrm{Decode}({\omega }^{\prime })$.

Common ECC types include Hamming codes for single-bit correction [53], Bose-Chaudhuri-Hocquenghem (BCH) codes for multiple random bit errors [54], Turbo codes for high error rates [55], Low-Density Parity-Check (LDPC) codes for large blocks [56], and Reed-Solomon (RS) codes for correcting multiple symbol errors, including bursts [52]. For our study, we selected Reed-Solomon coding due to its robustness against burst errors, efficiency in handling structured errors, and suitability for applications requiring high reliability, such as watermarking deep neural networks. The choice of RS parameters are detailed as detailed in Section 6.

5. Materials and Methods

5.1. Security Model

In any neural network model IP protection scheme, the goal of the scheme is such that model owners should be authenticated as the model owner, and any other user would never be authenticated as the owner. Here, we provide a probabilistic security model that outlines this application. Let $\mathcal{O}$ denote the event the judge has authenticated some entity as the owner; let $o_{ow}$ denote the true model owner. Thus we are interested in the event $\mathcal{O}=o_{ow}$. We will let u denote any party. Let $M_{*}$ denote the public neural network model, the model for which ownership is in question (in the case where one is using watermarking, the model would be the watermarked model). Let $\mathrm{\Sigma }$ represent the IP protection scheme. Now almost all IP protection schemes require an input to $\mathrm{\Sigma }$ as a response by the claimant to the judge, which we denote by $\mathbf{resp}(u)$. We can describe the judge determination as probabilistic, in particular as a conditional probability $Prob(\mathcal{O}=u|\mathrm{\Sigma },M_{*},\mathbf{resp}(u))$. However, there must be one more conditioning factor that takes into account external information, for example, information that may have been leaked via a previous judicial determination (i.e., a previous trial of ownership), we represent this as $\mathrm{\Gamma }$. Then there are non negative security parameters ${ϵ}_1$ and ${ϵ}_2$ for which the necessary security conditions must satisfy Equation (1) as described below.

$$\begin{array}{l}Prob(\mathcal{O}=o_{ow}|\mathrm{\Sigma },M_{*},\mathbf{resp}(o_{ow}),\mathrm{\Gamma })\ge 1-{ϵ}_1\\ Prob(\mathcal{O}=u|\mathrm{\Sigma },M_{*},\mathbf{resp}(u),\mathrm{\Gamma })\le {ϵ}_2\mathrm{where} u\ne o_{ow}\end{array}$$

(1)

Now the adversary $\mathcal{A}$ may search for any advantage to defeat one or both of the above security conditions. In particular, the adversary may attempt to modify $M_{*}$, such as pruning, so that one or both of the above equations is violated. If we represent these modifications as $f(M_{*})$ then they may attempt to achieve $Prob(\mathcal{O}=o_{ow}|\mathrm{\Sigma },f(M_{*}),\mathbf{resp}(o_{ow}),\mathrm{\Gamma })<1-{ϵ}_1$, using $f(M_{*})$. In such cases, it would be noted that $\mathrm{\Sigma }$ is insecure against the attack $f(·)$.

5.2. Neural Network Watermarking as a Noisy Channel

Traditional approaches treat watermarking in neural networks as a data hiding problem, where arbitrary bits are injected into the model space. However, this simplistic view fails to account for the dynamic noise landscape inherent in real-world deployments and the necessary security requirements for a trustworthy verification.

We formulate the watermarking as a noisy communication channel through Shannon’s noisy channel coding theorem [57]. The model parameters $\theta \in {\mathbb{R}}^d$ act as the communication medium, the watermark is the encoded message, and noise arises from both inherent and malicious post-deployment operations. For instance, fine-tuning [27] introduces parameter shifts analogous to signal attenuation, while pruning and quantization induce structured noise akin to packet loss. Additional noise sources arise from the stochastic nature of neural network training, limited training data, the inherent randomness of optimization processes (e.g., stochastic gradient descent) [58], which destabilizes embedded watermarks. Adversarial attacks introduce deliberate distortions to erase ownership signals. This multifaceted noise landscape requires a watermarking framework that integrates robustness at cryptographic levels.

Many watermark verification schemes [11,12] rely on a threshold $\tau$ of bits of the extracted watermark versus what was known by the owner when it was embedded, but this approach of relying on threshold of bits (characterized by Bit Error Rate (BER)) lends itself to several limitations. First, threshold ambiguity arises because different applications impose varying Bit Error Rate (BER) tolerances; for instance, high-security domains may require $\tau <{10}^{-6}$, whereas non-critical applications may tolerate $\tau \approx 0.2$, complicating threshold selection. Second, this threshold dependency enables adversaries to manipulate just enough bits to fall below the required threshold, thus invalidating ownership claims.

The focus on threshold and BER is due to the noise inherent to a watermarking scheme in a neural network, in order to alleviate the concern of noisy watermark processes, some watermarking schemes employ small watermarks ($k\le 32$ bits) this design choice introduces vulnerabilities. First, computational tractability, small key spaces enable brute-force attacks. Second, scalability constraints, these limit the feasibility of multi-stakeholder allocation protocols. Lastly, ambiguity, small-sized watermarks allow for collision, the same bitstring may be the authenticator of ownership of two different (or more) neural networks.

5.3. Increasing Capacity and Reducing the Threshold

To increase capacity within the network, we partitioned the message-to-be-embedded into structured segments (“partitions”) in order to manage the capacity constraints. For example, in our implementation (see Section 6) the partitions mirror the number of classes C in the dataset as illustrated in Figure 2. Our success in increasing the capacity of how much can be embedded-then-successfully extracted does not impact the noisiness of this embed-then-extract process. Without such improvements, one may have a significant BER and have to approach validation using a threshold $\tau$. In such cases, a secret k-bit bitstring $\mathbf{str}$ used has $2^{-k}$ strength (the probability of guessing $\mathbf{str}$). However any string ${\mathit{str}}^{\prime }$ that has at most $\tau$-percentage many errors, will be successful in validating ownership. The security for this setting is no longer near the $2^{-k}$ level of security. For example in the case $k=100$, with a $\tau =0.2$, there are $\left({\displaystyle \genfrac{}{}{0pt}{}{100}{80}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{100}{81}}\right)+\cdots +\left({\displaystyle \genfrac{}{}{0pt}{}{100}{0}}\right)$ many responses ${\mathit{str}}^{\prime }$ that prove ownership, the proportion $(\left({\displaystyle \genfrac{}{}{0pt}{}{100}{80}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{100}{81}}\right)+\cdots +\left({\displaystyle \genfrac{}{}{0pt}{}{100}{0}}\right))/2^{100}\approx 2^{-32.78}$, which is 33 bit security. According to Keylength.com [59], 100 bit symmetric key is secure until 2039 whereas 33 bit security has a security level dating the time period of the 1950’s.

The solution is to use an error-correction-code (ECC), where we encode the authenticator $\mathbf{auth}$ with a ECC encoder, the output of the decoder is the watermark $wm$ and then embed. When extracting the watermark, we decode ${\psi }^{\prime }$ using the ECC decoder which is ${\mathit{auth}}^{\prime }$, which is then the input to the validation scheme. We quantify post-decoding errors via the term Effective Bit Error Rate (EBER), defined as:

$$\mathrm{EBER}={\displaystyle \frac{\mathrm{Hamming}\mathrm{Distance}(\mathbf{auth},{\mathit{auth}}^{\prime })}{k}},$$

where $aut{h}^{\prime }=\mathrm{Decode}({\psi }^{\prime })$ is the recovered authenticator and k is the original bit length of $\mathbf{auth}$. The ECC layer corrects errors before verification, ensuring robust authentication. The goal of EBER equaling 0 removes the need of a threshold $\tau$.

5.4. Why Symmetric Key Schemes Are Not Suitable Authenticators

Although symmetric key schemes (for example, Hash-based message authentication code (HMACs)) [60] could theoretically bind watermarks to a secret key, they introduce critical vulnerabilities absent in asymmetric cryptography. A symmetric verification scheme requires the sharing of the secret key with all verifiers (example judge), creating a single point of failure where a compromised verifier enables undetectable forgery. Even in the case of honest verifiers, there are weaknesses, in any setting for which this ownership determination takes place, some information may be exposed/leak during the determination. This information can then be collected by adversaries and used in subsequent ownership determinations. Applying this to our probabilistic security model, this leaked information would become part of $\mathrm{\Gamma }$. Then the adversary u (where $u\ne o_{ow}$), with the leaked information, can violate one of the security conditions such as $Prob(\mathcal{O}=u|\mathrm{\Sigma },M_{*},\mathbf{resp}(u),\mathrm{\Gamma })\gg {ϵ}_2$.

Some may note that with the improved capacity and the use of error-correction codes, one can embed multiple symmetric keys into the neural network model. Then as a secret key is used in an ownership determination, the owner can now stop using this secret key and utilize the next. But this does not stop the adversary from replaying an old key in situations where they claim the ownership, calling this the current key. There are no parties to guide which keys are relevant.

5.5. Applying Digital Signatures as Authenticators in the Watermark

Traditional neural network watermarking approaches [11,12,13,14] suffer from a fundamental limitation: once a watermark is publicly revealed, its security and evidentiary power are compromised. Such exposure undermines the watermark’s role as a secure and indisputable marker of ownership. This occurs because existing schemes treat watermarks as secret credentials rather than asymmetric verifiable assertions [11,12,13,14]. Once exposed, adversaries can trivially replicate or modify these watermarks, voiding their evidentiary value.

We resolve this fundamental limitation by embedding the digital signature of the owner directly into the model. Digital signatures inherently preserve their evidentiary value even under public scrutiny because, even if an adversary learns the signature, they cannot generate a valid signature without the corresponding secret key. This creates a persistent and verifiable linkage between the model parameters and the owner’s credentials—a binding that cannot be achieved with random or hardcoded bits lacking cryptographic authentication [49,51]. There is no leakage issue as only one public key $pk$ can be used to verify the digital signature that was embedded as a watermark in the neural network. While digital signatures guarantee authenticity, their binary sensitivity poses a critical challenge: even a single bit flip in signature—caused by any source of noise—invalidates the entire ownership claim. An error bit causes an avalanche of bit errors. PK-Judge mitigates this by encoding the signature using an error correction code (ECC) framework [52,53,54]. We highlight how we apply digital signatures in our ownership verification within PK-Judge in the following two paragraphs.

Formally, let ${\mathsf{id}}_{\mathrm{owner}}$ denote the owner identifier and H a collision-resistant hash function. The signature process binds model parameters $\theta$ through: $\mathsf{m}=H(\theta \Vert {\mathsf{id}}_{\mathrm{owner}})$; $\sigma =\mathrm{Sign}(\mathsf{m},s{k}_{\mathrm{owner}})$, where $s{k}_{\mathrm{owner}}$ is the private key. The signature $\sigma$ is embedded via constrained optimization: ${\theta }^{*}={\mathrm{argmin}}_{{\theta }^{\prime }}\mathcal{L}({\theta }^{\prime })+{\lambda }_1{\parallel E({\theta }^{\prime })-\sigma \parallel }_2^2$, with E as the embedding extractor and ${\lambda }_1$ controlling the fidelity-robustness trade-offs. The scheme resists ambiguity attacks [61] by making counterfeit watermarks ${\sigma }_{\mathrm{adv}}$ computationally indistinguishable from random noise unless the adversary possesses $s{k}_{\mathrm{owner}}$.

The public key $pk$ must be made known so that anyone can verify the signature. However, an attacker may acquire both the watermarked model and $pk$, then claim public key as their own. In such a scenario, they might also claim that the embedded watermark is proof of their rights. Simple public-key verification would not immediately distinguish whether $pk$ truly belongs to the model’s original creator or an impersonator who stole the key. The public key $\mathrm{pk}$, commonly tied to the owner’s identity by a public-key certificate in accordance with the X.509 standard [62]. However, this alone does not guarantee that the party now presenting the model is the true owner, as certificates can be compromised in practice. A prominent example is the DigiNotar breach of 2011 [63], which enabled malicious actors to forge or misuse digital certificates, thereby generating signatures that appeared legitimate. PK-Judge mitigates this threat by combining public verification with a challenge-response protocol. The verifier issues a fresh random challenge c, and only the authentic owner who holds the private key $sk$ can produce a valid signature $\zeta =\mathrm{Sign}(c,sk)$ that can be verified using the published public key. Any replay of previous signatures fails because each new challenge has never been signed before. An attacker who merely possesses the public key or has extracted the original signature $\sigma$ for a different message is incapable of forging $\zeta$. Historical accounts and security analyses corroborate that even widely publicized or leaked public keys remain safe if a valid signature on a fresh challenge is mandatory for proof of ownership [51,64]. This mechanism is analogous to authentication in hardware security modules (HSMs) [65], where cryptographic operations are bound to physical hardware.

Using a digital signature and a challenge-response protocol as verification satisfies the separation of privileged and property 8 (Ownership verification requirement) in our watermark requirements (see Section 3). The Separation of Privilege principle, defined by Saltzer and Schroeder [47] as a requirement that no single mechanism or authority holds exclusive control, addresses this need. In the context of PK-Judge, extracting the watermark from the model is an operation that can be performed openly, and verifying ownership through public keys and challenge-response can be conducted by any third party who obtains the necessary information. The model owner, who embeds the cryptographic signature, cannot unilaterally confirm ownership without external scrutiny. Ownership is established only when multiple independent conditions are satisfied, including a valid public certificate, a correct signature extracted through error correction, and the completion of a challenge-response step proving possession of the legitimate private key.

In PK-Judge, we want to utilize short signatures such as BLS signatures. For 512-bit BLS signatures [51], ECC adds only 4.2% redundancy (32 bytes), efficiently managed via class-aligned partitioning (Section 5.3) to maintain scalability. Thus, utilizing digital signatures and a challenge-response protocol, as utilized in PK-Judge, as the verification does not suffer from leakage and/or dishonesty during an ownership determination. That is, there is no information that can be provided to adversaries so that they can violate security conditions like the Equation (1). The information extracted via the watermark is the same digital signature and the challenge is randomly selected every time. Old signatures do not help provide signatures on new messages (challenges). as it is cryptographically infeasible to determine a signing key from a signature.

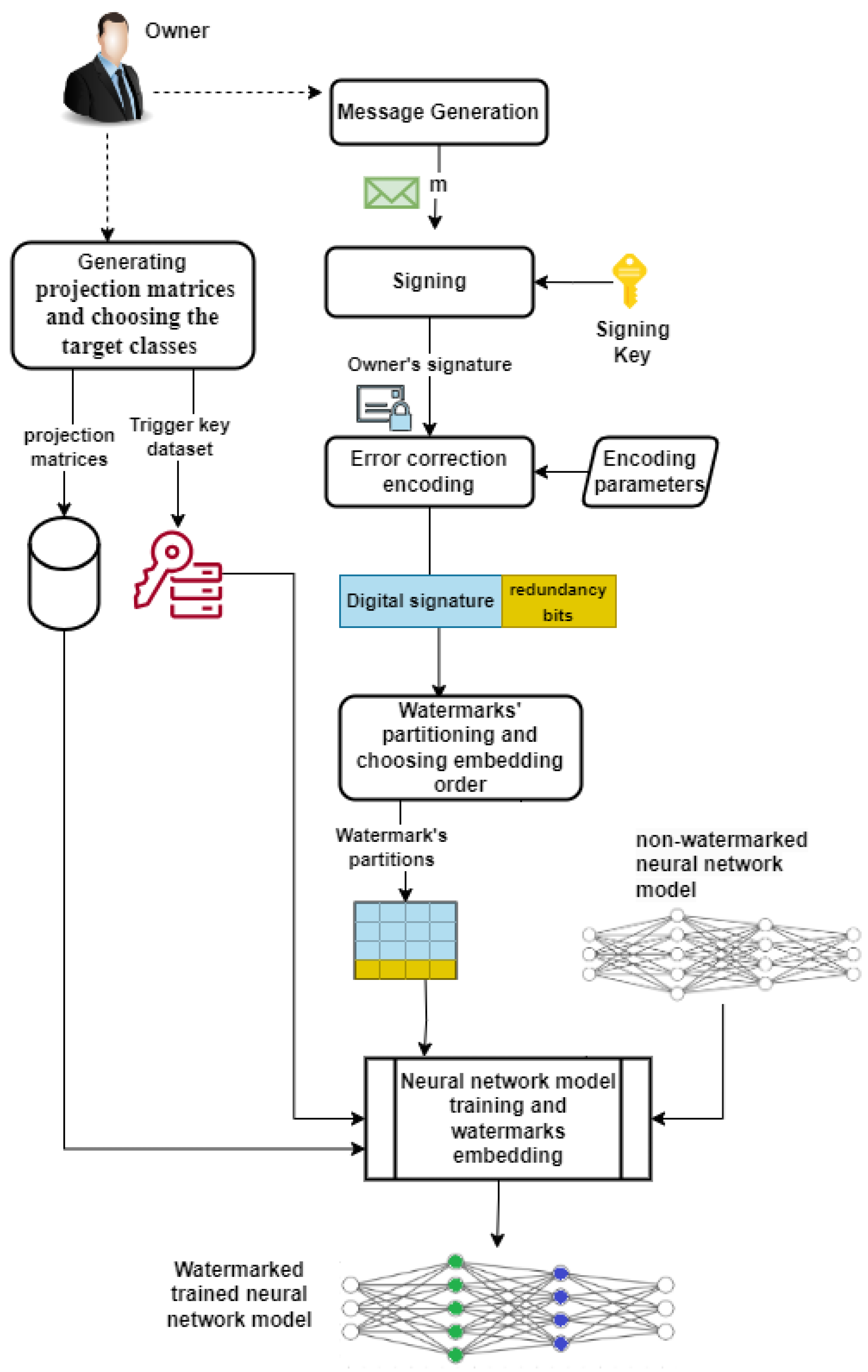
5.6. PK-Judge: Error-Corrected Cryptographic Ownership Verification

PK-Judge integrates digital signatures, error-correcting codes, and a challenge-response protocol to establish cryptographically secure ownership of neural networks. As shown in Figure 3, a digital signature is encoded and embedded in the network parameters, preserving fidelity while ensuring that any bit errors introduced by fine-tuning, pruning, or other transformations are correctable.

Figure 4 illustrates the verification workflow between the claimant owner and a judge evaluating an ownership claim over a watermarked model. First, the claimant reveals the extraction parameters so the judge can extract and ECC-decode the embedded digital signature from the model. If the extracted signature is valid under the public key, the judge proceeds by issuing a challenge message, which the claimant signs with their secret key. Finally, the judge verifies that challenge signature to conclusively confirm (or reject) the claimant’s ownership of the model. Algorithm 1 outlines the entire process, from generating the signed payload to validating ownership claims. The framework’s implementation details, results and discussion are further elaborated in Section 6.

Algorithm 1 PK-Judge: Error-Corrected Digital Signatures for Verifiable Ownership

Input:  m: A designated message for ownership  $sk$: Owner’s private signing key, $pk$: Owner’s public key  t: Error correction code parameters  $Cert$: Certificate associating the owner’s identity with $pk$  $\kappa$: Embedding and extraction hyperparameters  Param: Parameters for challenge-response verification Embedding Phase:  1: $M\leftarrow \mathrm{hash}(m)$  2: $\sigma \leftarrow \mathrm{Sign}(M,sk)$  3: $\psi \leftarrow \mathrm{ECC}\_\mathrm{Encode}(\sigma ,t)$  4: ${\theta }_w\leftarrow \mathrm{Embed}(\theta ,\psi ,\kappa )$ Extraction Phase:  1: $flag\leftarrow \mathrm{VerifyPublicKey}(Cert,pk)$  2: if not $flag$ then  3:   return False, “Invalid Certificate”  4: end if  5: $b^{\prime }\leftarrow \mathrm{Extract}({\theta }_w^{*},\kappa )$  6: ${\sigma }^{\prime }\leftarrow \mathrm{ECC}\_\mathrm{Decode}(b^{\prime },t)$ Ownership Verification Phase:  1: if $\mathrm{VerifySignature}({\sigma }^{\prime },pk)$ then  2:    if $\mathrm{ChallRSPVerify}(\mathrm{PARAM},sk,pk)$ then  3:    return True, “Verification Successful”  4:    else  5:    return False, “Additional Verification Failed”  6:    end if  7: else  8:    return False, “Signature Verification Failed”  9: end if

6. Results and Discussion

6.1. Implementation Across Watermarking Frameworks and Model Architectures

In a white-box setting, PK-Judge has been comprehensively validated by integrating it into three established watermarking frameworks serving as host protocols. These include: (1) DeepSigns [12], which leverages statistical alignment of activation distributions to embed watermarks; (2) RIGA [21], a protocol that uses adversarial training to embed a watermark, jointly training an extractor network to recover encoded bits and a detector network to ensure covertness; and (3) DeepiSign [14], which employs fragile wavelet hashing, transforming CNN layer weights into the frequency domain with wavelet techniques to embed watermarks via scrambling and scaling. In all frameworks, ECC-encoded digital signatures were embedded to ensure robust ownership identification. Ownership verification achieved an effective bit error rate (EBER) of zero under challenge-response protocols, where the framework successfully decodes the embedded signatures without errors even when subjected to adversarial queries. This multi-framework evaluation highlights PK-Judge’s adaptability across diverse embedding strategies, enhancing its efficacy in securing intellectual property.

We implemented PK-Judge using PyTorch [66], enabling the model owner to configure the architecture, specify the training dataset, select a watermarking protocol, and set associated hyperparameters. For our experiments, we utilized ResNet18 [67] trained on CIFAR10 [68] for RIGA. We also employed ResNet18 on CIFAR10 for DeepiSigns. For DeepSigns [12], we conducted experiments on ResNet101 [67] and DenseNet201 [69] (modified with two fully connected layers before the output) using CIFAR10, partitioning the watermark to enhance capacity as described in Section 5.3. For comparative analysis, we extended experiments to MNIST with an MLP (784-512FC-512FC-10FC) and CIFAR10 with a CNN (3×32×32; 32C3(1)-32C3(1)-MP2(1)-64C3(1)-64C3(1)-MP2(1)-512FC-10FC) and a ResNet18, evaluating PK-Judge’s performance across these datasets and architectures to assess its adaptability and fidelity.

DeepSigns Protocol: We focus on the DeepSigns protocol [12] as the primary host watermarking framework for PK-Judge, due to its established robustness against different attacks. Below, we detail the DeepSigns protocol, given its extensive use in our experiments. For the watermarking protocols of other schemes, we refer the reader to their respective papers  [14,21].

Embedding: Select s Gaussians ${\left\{\mathcal{N}({\mu }_i,{\sigma }^2)\right\}}_{i=1}^s$ from S classes. Encode binary vector $b\in {\{0,1\}}^{s\times N}$ via: $G_{\sigma }=\sigma (\mu A)$, $\widehat{b}=\mathbb{I}[G_{\sigma }\ge 0.5]$   with projection matrix $A\sim \mathcal{N}(0,1)$. Train model with loss:

$${\mathcal{L}}_0+{\lambda }_1\left(\parallel {\mu }_{y^{*}}^l-f^l{(x,\theta )\parallel }_2^2-\sum _{i\ne y^{*}}{\parallel {\mu }_i^l-f^l(x,\theta )\parallel }_2^2\right)+{\lambda }_2\sum _{i,j}\left(b_{ij}log{G}_{\sigma ,ij}+(1-b_{ij})log(1-G_{\sigma ,ij})\right).$$

where ${\mathcal{L}}_0$ is the original task loss, ${\lambda }_1$ aligns with the Gaussian mixture prior, and ${\lambda }_2$ ensures watermark fidelity.

Extraction: Compute ${\mu }^{\prime }$ from layer activations using key samples. Recover $b^{\prime }$ via:

$$b^{\prime }=I[\sigma (l{\mu }^{\prime }A)\ge 0.5].\mathrm{where}{\mathbb{I}}_{\left\{·\right\}}\mathrm{is}\mathrm{the}\mathrm{indicator}\mathrm{function}.$$

Verification: $\mathrm{BER}={\displaystyle \frac{1}{sN}}{\sum }_{i,j}\mathbb{I}[b_{ij}\ne b_{ij}^{\prime }].$ If $\mathrm{BER}>\tau$, the watermark is invalid.

6.2. Watermark Generation

The ownership watermark combines BLS signatures [51] with Reed-Solomon coding  [52] (Section 4):

• Generate 32-byte BLS private key $sk$ using BLS12-381 curve and compute the corresponding public key $pk$.
• Compute message digest: $h=\mathrm{SHA}\text{-}256(\theta \Vert {\mathsf{id}}_{\mathrm{owner}})$ While we typically include a nonce to ensure message uniqueness (e.g., by setting $h=\mathrm{SHA}\text{-}256(\theta \Vert {\mathsf{id}}_{\mathrm{owner}}\Vert \mathrm{nonce}$), this is not strictly mandatory since the subsequent challenge–response phase already enforces fresh ownership proofs.)
• Sign digest: ${\sigma }_{\mathrm{BLS}}\leftarrow \mathrm{Sign}(h,sk)\in {\{0,1\}}^{512}$
• Error Correction Code (RS) encode: $\psi =\mathrm{RS}\text{-}\mathrm{Enc}({\sigma }_{\mathrm{BLS}},t=32)\in {\{0,1\}}^{768}$

When using DeepSigns as the host framework, we partitioned the watermark $\psi$ mirroring the number of classes that will carry it as described in Section 5.3.

Embedding and Verification in Real Architectures. PK-Judge seamlessly integrates with larger models (e.g., ResNet101, DenseNet-201) by embedding the encoded BLS signature into selected layers. Ownership is verified by (1) extracting and ECC-decoding the watermark to recover the BLS signature; (2) validating it with the public key; and (3) prompting a fresh challenge–response, ensuring the claimant indeed holds the private key. This process securely confirms ownership without ever exposing the secret key. Unlike one-time watermarks, this scheme provides persistent, publicly verifiable ownership through PKI, leveraging digital signatures’ properties to preserve integrity.

PK-Judge has been implemented via blspy [70] and reedsolo [71] libraries, added 32 bytes (256 bits) of redundancy to the 512 bits signature, resulting in a 768-bit (96-byte) watermark. A detailed evaluation of PK-Judge’s performance across various requirements follows in subsequent sections.

6.3. Fidelity Evaluation

PK-Judge’s watermarking framework must maintain baseline model accuracy while preserving watermark integrity across its host protocols. We evaluated fidelity across DeepSigns, RIGA and DeepiSign through targeted experiments measuring test accuracy, Bit Error Rate (BER), and Effective Bit Error Rate (EBER). For DeepSigns, we conducted detailed experiments to assess different cases and explore single-class and multi-class strategies. Experiment 1, 2 and 3 implemented on DeepSigns as host watermarking protocol. Experiments in Section 6.4 implemented on RIGA and DeepiSign protocols.

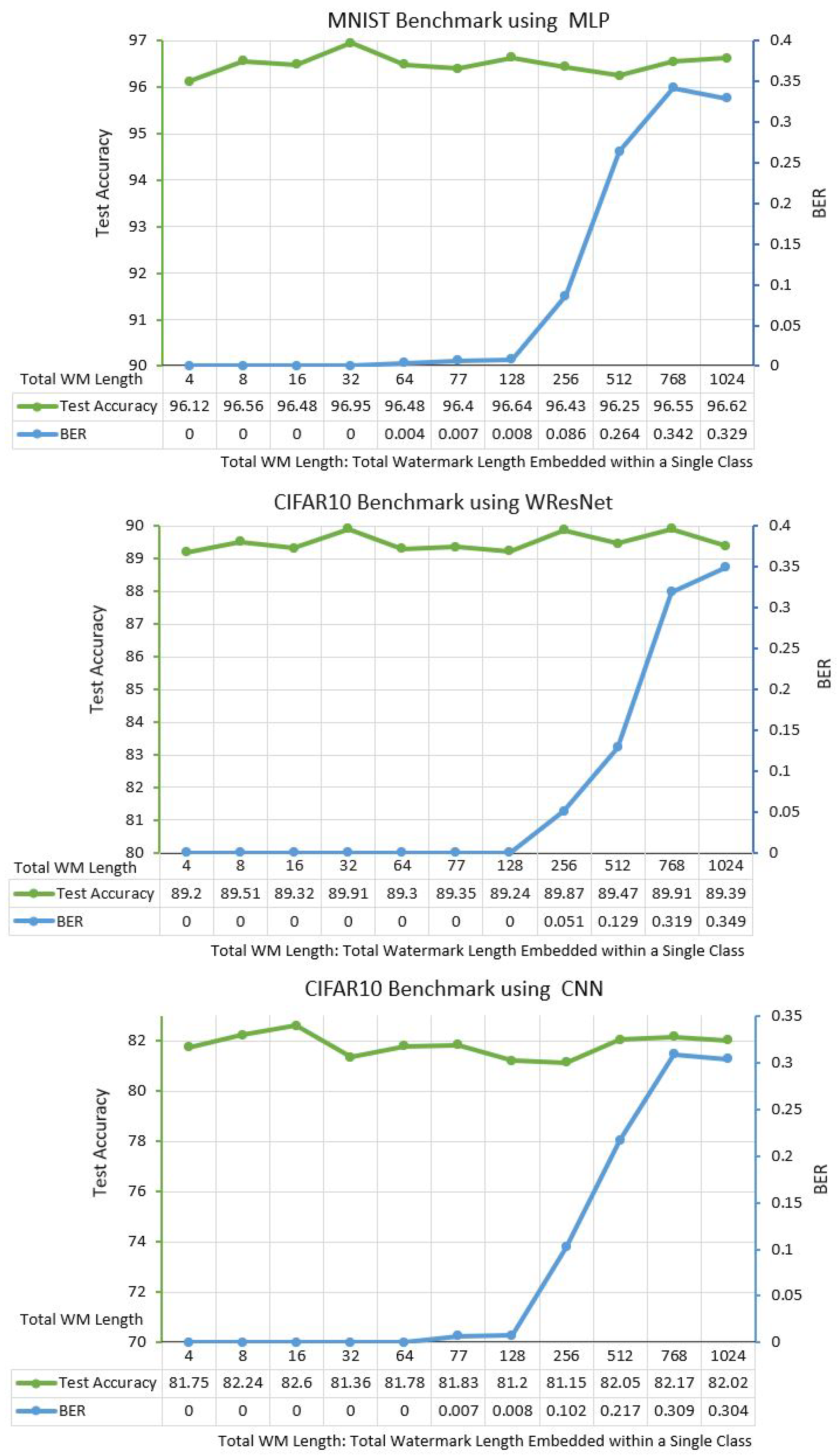
6.3.1. Experiment 1: Single-Class Watermark Capacity

In our first experiment, as illustrated in Figure 5, we focused on understanding the relationship between different watermark lengths for a single class and its corresponding testing accuracy and BER. During our evaluation, watermark sizes ranging from 4 to 1024 bits were tested. Test accuracy remains largely unchanged. However, beyond 64 bits in MLP/CNN (and 128 bits in WResNet), BER grows sharply, indicating a capacity limit. This observation informs our subsequent selection of per-class watermark size to maintain fidelity.

6.3.2. Experiment 2: Multi-Class Watermark Distribution Efficacy

To scale watermark embedding beyond single-class capacity limits, we allocated 77 bits per class across 1–10 classes in different models. We measured test accuracy, BER, and EBER as class count increased (Figure 6, Figure 7 and Figure 8). Test accuracy remained stable across all configurations, with minor improvements at higher class counts due to DeepSigns’ additive loss functions [12]. BER increased with class count confirming distributed embedding’s inherent tradeoff between capacity and integrity. The model with 77 bits carried by 10 classes trained for different epochs. The results shown in

Table 1. Baseline evaluation of test accuracy (Acc),BER, and EBER across architectures with 768-bit watermark across 10 classes.

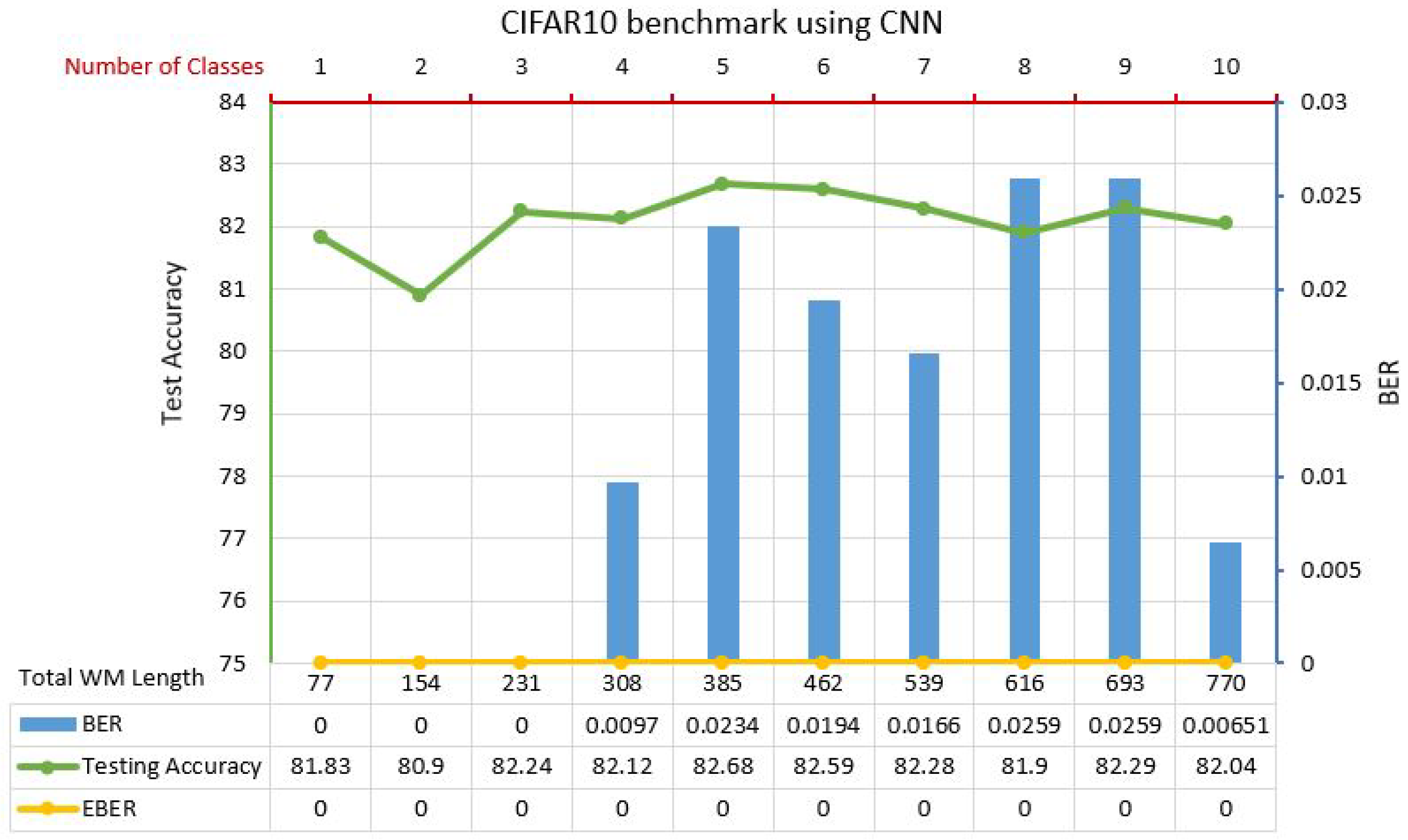
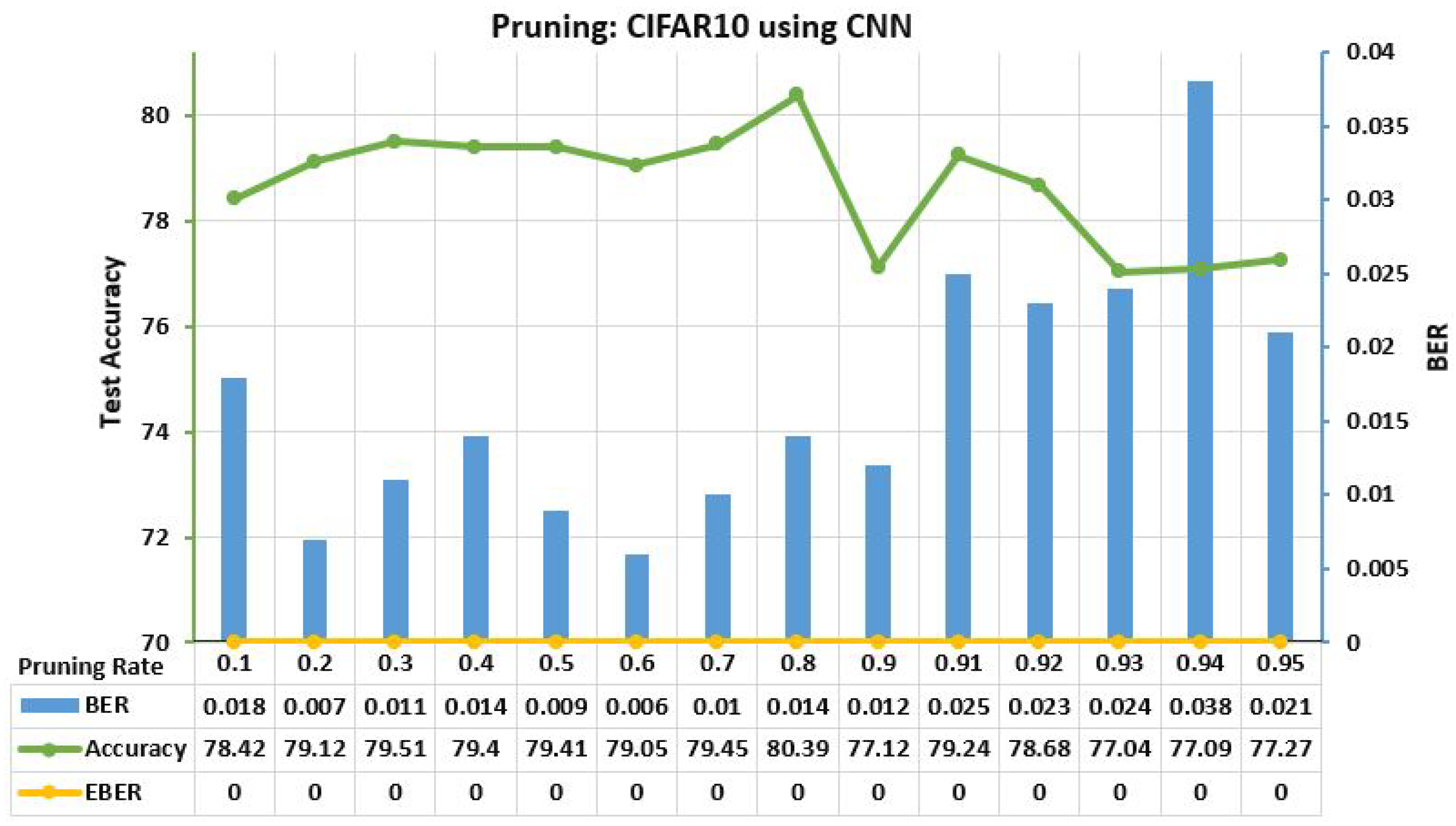
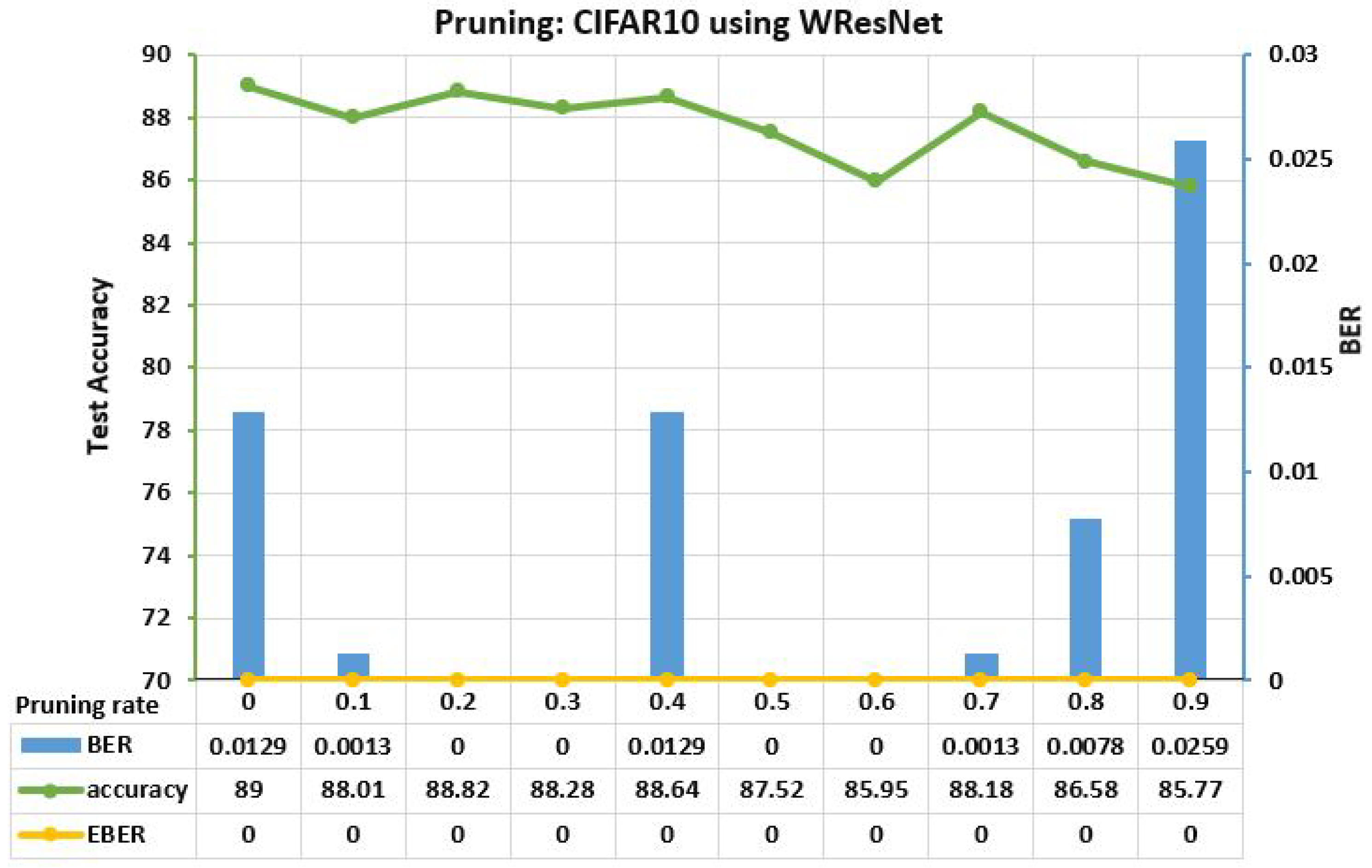
	MNIST MLP				RN18				CNN				RN101				DN201
Epochs	50	100	200	300	50	100	200	300	50	100	200	300	50	100	200	300	50	100	200	300
Acc	96.4	96.1	96.1	96.7	87.5	88.6	87.6	90.1	79.3	79.2	80.9	82.0	84.5	82.1	85.2	83.0	84.1	83.8	83.9	84.2
BER	0.005	0.003	0.004	0.005	0.001	0.004	0.001	0	0.016	0.018	0.027	0.018	0	0	0	0.003	0	0	0	0.013
EBER	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

RN = ResNet, DN = DenseNet. RN18, RN101, CNN and DN201 all using CIFAR10.

. ECC helped achieving zero EBER in all cases. This guarantees precise signature extraction and proving PK-Judge’s capability to preserve model fidility and watermark integrity despite multi-class distribution.

6.3.3. Experiment 3: Watermark Distribution Across Multiple Classes

We further investigated distributing the 768-bit encoded signature watermark across different numbers of classes, starting with ten classes carrying 77 bits each and eventually placing all 768 bits in a single class. Concentrating bits in fewer classes slightly increases BER, while accuracy remains stable. Distributing bits across more classes maintains near-zero BER, balancing watermark integrity and performance.

Table 2. Evaluation of embedding a 768-bit watermark across 1 to 10 classes) for various architectures.

WM	#	MNIST			RN18			CNN			RN101			DN201
Len/Cls	Cls	Acc%	BER	EBER	Acc%	BER	EBER	Acc%	BER	EBER	Acc%	BER	EBER	Acc%	BER	EBER
77	10	96.7	0.005	0	90.1	0	0	82.0	0.018	0	85.0	0	0	84.2	0.013	0
86	9	96.4	0.004	0	87.2	0.003	0	78.3	0.028	0	87.8	0.004	0	84.7	0	0
96	8	96.3	0.003	0	87.6	0.001	0	80.2	0.020	0	82.3	0.019	0	83.0	0.0052	0
110	7	96.7	0.005	0	89.2	0.004	0	80.2	0.023	0	85.0	0	0	83.4	0	0
128	6	96.7	0.014	0	87.1	0.002	0	80.0	0.025	0	79.1	0	0	83.4	0	0
154	5	96.6	0.021	0	88.3	0.003	0	80.0	0.038	NZ	79.6	0	0	82.8	0	0
192	4	96.5	0.043	NZ	85.6	0.018	0	78.2	0.066	NZ	78.7	0	0	82.9	0	0
256	3	96.4	0.068	NZ	88.6	0.047	NZ	79.1	0.055	NZ	86.2	0	0	83.8	0	0
384	2	96.9	0.149	NZ	86.7	0.103	NZ	79.8	0.148	NZ	81.5	0.016	0	82.6	0	0
770	1	96.6	0.342	NZ	89.9	0.319	NZ	80.2	0.314	NZ	80.1	0.020	0	82.6	0.017	0

RN = ResNet, DN = DenseNet, Acc% = Accuracy (%), #Cls = Number of Classes, NZ = Non-Zero.

shows model and dataset choices influence BER, enabling strategic partitioning for zero EBER, supporting robust authentication in PK-Judge.

6.4. Fidelity Experiments with RIGA and DeepiSigns Watermarking Protocols

We evaluated PK-Judge’s fidelity across the RIGA and DeepiSign watermarking protocols, utilizing ResNet18 [67] on CIFAR10 [68] for both, to evaluate model accuracy and watermark integrity with ECC-encoded digital signature as a watermark. Hyperparameters were configured as follows: RIGA was trained for 50 epochs using Adam (learning rate 0.001, batch size 64), while DeepiSign was trained for 50 epochs using SGD (learning rate 0.0001, batch size 100, learning rate multiplier 10). Results, presented in

Table 3. Fidelity Metrics for PK-Judge Across Watermarking Protocols.

Protocol & Model	Acc. Before WM (%)	Acc. After WM (%)	BER	EBER
RIGA (ResNet18, CIFAR10)	97.7	97.53	0.000	0.000
DeepiSigns (ResNet18, CIFAR10)	88.32	87.86	0.018	0.000

, show PK-Judge’s ability to maintain accuracy and watermark integrity, achieving zero EBER post-ECC decoding.

6.5. Robustness Against Adversarial Attack Scenarios

We conducted a thorough assessment of the PK-Judge system’s robustness, where the host framework is DeepSigns. Specifically targeting PK-Judge defenses against three removal attacks: parameter pruning, model fine-tuning, and watermark overwriting. Recall, that the primary indicator of robustness is the successful execution of the Chall-RSP-Verify process, which fundamentally requires an EBER of zero.

6.5.1. Parameter Pruning Attack

Though parameter pruning is often used for genuine optimization purposes [72], in an adversarial setting, it can pose threats to watermarking mechanisms, especially if the watermark is manifested through the model’s parameters. We subjected PK-Judge to various levels of pruning, ranging from low (10%) to severe (90+%), covering a comprehensive scope of conditions that a model might encounter in practical applications. Illustrative results across the tested models shown in Figure 9, Figure 10 and Figure 11 and

Table 4. Performance metrics for pruning at different percentages on ResNet101 (RN101) and DenseNet201 (DN201). All percentages represent pruning percentages.

Metric	Model	10%	20%	30%	40%	50%	60%	70%	80%	90%	91%	92%	93%	94%	95%	96%	97%	98%	99%
Acc%	RN101	81.06	82.02	79.16	78.57	82.64	79.78	81.10	82.13	83.33	82.83	76.84	80.31	83.04	80.66	79.64	79.81	78.98	70.66
BER		0	0	0.021	0.038	0	0	0	0.019	0	0	0.003	0.003	0	0	0	0.019	0.018	0.014
EBER		0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
Acc%	DN201	84.16	84.16	84.16	84.16	84.16	84.16	84.16	84.16	84.18	84.17	84.17	84.26	84.11	83.96	84.02	83.50	83.14	72.60
BER		0	0	0	0	0	0	0	0	0	0	0.001	0.019	0.013	0.013	0.003	0.031	0.031	0.031
EBER		0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

. Notably, PK-Judge has been shown to maintain an EBER of $zero$ consistently across various degrees of pruning. Such an outcome suggests that PK-Judge’s watermarking mechanism is intricately designed to withstand the loss of parameters, thereby ensuring the authenticity of the watermark remains verifiable.

6.5.2. Model Fine-Tuning Attack

To assess PK-Judge’s resilience, we retrained watermarked models on a dataset that has the same features of the original training dataset using standard cross-entropy loss, excluding any watermark-specific losses. This setup simulates an attacker’s attempt to erase the watermark while maintaining model performance [73]. Fine-tuning was performed for 50, 100, and 200 epochs at the learning rate used in the final stage of the original training process. As shown in

Table 5. Evaluation Results after Model Tuning Attack.

Model	Metric	50 Epochs	100 Epochs	200 Epochs
MNIST_MLP	Accuracy	96.67	96.33	96.62
	BER	0.0082	0.0271	0.0293
	EBER	0	0	0
CIFAR10_WideResNet	Accuracy	88.08	87.73	90.44
	BER	0.00311	0.0207	0.0234
	EBER	0	0	0
CIFAR10_CNN	Accuracy	79.39	79.49	81.02
	BER	0.0237	0.0251	0.026
	EBER	0	0	0
ResNet101	Accuracy	84.88	84.66	85.61
	BER	0.0273	0.0273	0.0104
	EBER	0	0	0
DenseNet201	Accuracy	82.5	82.85	82.85
	BER	0.0195	0.0299	0.0299
	EBER	0	0	0

, PK-Judge remains highly robust to fine-tuning attacks. The watermark remains detectable with zero Effective Bit Error Rate (EBER) across all tested epochs, ensuring its persistence even after extensive retraining. Model accuracy is preserved or slightly improved, confirming that the watermark does not interfere with normal learning dynamics. Furthermore, increasing the learning rate in an attempt to disrupt activation maps leads to severe accuracy degradation, making such attacks impractical. These results validate PK-Judge’s ability to withstand fine-tuning attacks, ensuring reliable watermark recovery and ownership verification under adversarial conditions.

6.5.3. Watermark Overwriting Attack

Watermark overwriting refers to the tactic wherein an adversary, aware of the watermarking scheme, attempts to corrupt or replace the original watermark by embedding a new one into the model. Using a new projection matrix, their watermark bits, and input keys, the attacker aims to distort the original watermark and challenge the model’s authentic ownership. In practice, the attacker may not know the embedding protocol and exactly which layers carry the watermark. However, for the purpose of our experiments, we simulate a stronger attack scenario where the adversary can identify the watermarked layers but lacks knowledge of the original watermark, projection matrix, or target classes. The adversary follows the watermark embedding process using their own parameters in an attempt to overwrite the existing watermark. It is shown in

Table 6. PK-Judge Robustness for Overwriting Attack.

Model Name	Detection Success	EBER
MNIST_MLP	Yes	0
CIFAR10_CNN	Yes	0
CIFAR10_ResNet18	Yes	0
CIFAR10_ResNet101	Yes	0
CIFAR10_DenseNet201	Yes	0

, PK-Judge is able to detect the original embedded watermark in the overwritten model successfully and get EBER of $zero$, which proves the robustness of the PK-Judge’ against overwriting attack.

6.6. Evaluation of the Other Watermarking Requirements

Evaluation of Uniqueness: PK-Judge ensures uniqueness by embedding cryptographically generated digital signatures, derived from the owner’s signing key [51,64]. These signatures are mathematically verifiable and inherently unique, transforming each watermark into a definitive identifier tied to the owner. In contrast to methods that embed random bits, which lack intrinsic uniqueness and risk collisions, PK-Judge’s cryptographic approach guarantees that each watermark is distinct and tamper-proof. This eliminates ambiguity in ownership verification and provides a robust, scalable solution for model attribution.

Evaluation of Integrity: PK-Judge’s integrity relies on its challenge-and-response mechanism (Section 5.5), which requires zero EBER for ownership verification. This ensures only the legitimate owner, possessing the secret keys, can verify ownership. Unlike DeepSigns [12], which tolerates errors, PK-Judge enforces perfect watermark retrieval, as demonstrated in Table 2. Additionally, PK-Judge eliminates false positives, preventing incorrect ownership claims in unmarked models. Integrity assessment in unmarked models mirrors fine-tuning, with results detailed in Table 5.

Evaluation of Capacity: PK-Judge maximizes watermark capacity while preserving model performance and watermark integrity. By partitioning the ECC-encoded digital signature (Section 5.3), PK-Judge balances capacity and robustness, leveraging ECC redundancy to ensure zero EBER across architectures (Table 2). For MNIST_MLP, zero EBER is achieved for 77 bits/class (10 classes) up to 154 bits/class (5 classes), with 96.65% accuracy. Similarly, CIFAR10_ResNet18 maintains zero EBER for up to 154 bits/class, while CIFAR10_CNN supports up to 128 bits/class. ResNet101 and DenseNet201 demonstrate exceptional capacity, achieving zero EBER across all class counts, including single-class 768-bit embedding. Beyond these thresholds, non-zero EBER values emerge, defining capacity limits for error-free extraction. PK-Judge’s flexible embedding strategies allow owners to customize watermark density while maintaining zero EBER, meeting stringent capacity requirements for robust ownership verification.

Evaluation of Ownership Verification: PK-Judge is the first framework to implement the principle of separation of privilege in neural network watermarking, establishing a new standard for trust and integrity. Unlike traditional approaches that rely solely on watermark extraction for verification, such as using BER below a threshold, PK-Judge employs a more robust and secure method. Its ownership verification process integrates asymmetric cryptography, signature verification, and a challenge-and-response mechanism, ensuring that claimants not only extract the watermark but also authenticate ownership through independent cryptographic verification. Furthermore, By watermarking all hidden layers of the neural network model, PK-Judge ensures that each layer carries a unique cryptographic signature. Even if attackers attempt to remove or modify certain layers, the remaining watermarked layers retain crucial ownership information, rendering the model’s authenticity detectable.

6.7. Applying Error Correction Codes in DeepSigns

Our work has shown that by applying an error correction code we can achieve an EBER of 0 with the ability to recover a digital signature. Thus, we have shown, via our analysis of PK-Judge, that if one applied an error correction code in DeepSigns, and followed our method of where to embed, one can increase the number of random bits in DeepSigns to a cryptographically secure size. This makes DeepSigns a cryptographically secure watermarking scheme. However, a random bit scheme implies a symmetric key scheme. As we discussed in Section 5.4, security engineers would not design an authentication scheme using symmetric keys. This is due to a variety of reasons, but a primary reason is that symmetric keys are prone to weakening over time due to potential leakage. This is why in protocols like SSH they utilize session keys and create new keys over time. Digital signatures, as an authentication, do not suffer from leakage, as they do not need to be kept private. Further, they can be validated by the public-key. Moreover, by requiring a challenge-response, as PK-Judge does, one knows the party who possesses the signing key, because the response is a signature that is verified by the public-key. And the signing key never leaves the owner’s computing device, the signature output (created due to the challenge-response) does and in the case of PK-Judge this response is verified by the same public-key that verified the embedded watermark(digital signature).

6.8. Comparison with Prior Work

In this section, we compare PK-Judge with several prior neural network watermarking schemes from the literature.

Table 7. Comparison of PK-Judge with Prior Schemes.

Method	Verification Mechanism	Cryptographic Technique	Challenge-Response
PK-Judge	Asymmetric	Digital Signatures	Yes
Hufu [33]	Symmetric	None	No
BlackMark [74]	Symmetric	None	No
Margin-based [34]	Symmetric	None	No
PTYNet [41]	Symmetric	None	No
DeepiSign [14]	Symmetric	Hash Functions	No
AIME [35]	Symmetric	None	No
Entangled [29]	Symmetric	None	No
RIGA [21]	Symmetric	None	No
Puppy [46]	Symmetric	Garbled Circuits	No
DeepIPR [22]	Symmetric	None	No
DeepMarks [13]	Symmetric	None	No
DeepSigns [12]	Symmetric	None	No
Uchida et al. [11]	Symmetric	None	No
Adi et al. [27]	Symmetric	None	No
Namba et al. [19]	Symmetric	None	No
Yang et al. [36]	Symmetric	None	No
Li et al. [24]	Symmetric	None	No

presents a comparison based on verification mechanism, cryptographic technique, separation of privileges and challenge-response capabilities.

Cryptographic Binding and Replay Resistance: Many frameworks [11,12,13,15,33,39] rely on symmetric verification. These methods suffer from replay attacks, where adversaries extract and reuse watermarks to forge ownership (Section 5.4). The lack of cryptographic binding to the owner’s identity enables adversaries to claim ownership without the secret key.Furthermore, the watermarks in these schemes become insecure once exposed, as their secrecy is their primary defense. PK-Judge mitigates these vulnerabilities by embedding a digital signature generated from the owner’s private key, ensuring that only the legitimate owner can produce valid proofs. Even if the watermark is revealed, it remains a valid and verifiable marker of ownership due to its cryptographic foundation, preserving its integrity and security.

Separation of Privilege: Decoupling Extraction and Verification: A foundational advancement in PK-Judge is its adherence to the separation of privilege principle (Section 3, Requirement 8), where watermark extraction is decoupled from ownership verification. Existing frameworks, including protocols in [11,12,13,14,15,21,22,33] conflate these processes. PK-Judge, in contrast, requires two independent proofs: (1) extracting the ECC-corrected signature and (2) cryptographically signing a fresh challenge with the private key. This separation ensures that even if adversaries extract the watermark, they cannot authenticate ownership without the private key.

Challenge-Response Capabilities: PK-Judge supports a dynamic challenge-response protocol, requiring the owner to cryptographically sign fresh challenges with their private key, enhancing security against forgery (Section 3) where as adversaries cannot forge fresh cryptographic proofs. In contrast, most previous schemes [11,12,13,14,15,21,22,23,24,26,27,29,33] lack this capability, relying on static verification that is susceptible to replay or extraction attacks. This feature distinguishes PK-Judge, enabling robust ownership verification under adversarial conditions.

Robustness: PK-Judge’s multi-component design (Section 5) demonstrates superior robustness compared to previous frameworks. PK-Judge achieves a zero Effective Bit Error Rate (EBER) after error-correcting code (ECC) decoding, as demonstrated in our fidelity experiments (Section 6.3). This ensures the integrity of the embedded digital signature against adversarial attacks such as pruning, fine-tuning, and overwriting. After recovering the digital signature through ECC decoding, it is verified using the owner’s public key, enabling the application of a challenge-response mechanism to confirm ownership. In comparison, prior schemes like [11,12,14,21] rely on non-zero BERs under similar conditions and depend on symmetric bit-matching techniques, lacking the cryptographic robustness provided by PK-Judge’s approach.

6.9. Adaptive Error Correction for Verification Challenges

PK-Judge mandates zero EBER for successful signature verification. Owners ensure this by pre-deployment watermark extraction and EBER analysis, enabling proactive adjustment of error correction coding parameters. Adaptive ECC redundancy levels correct errors at the cost of increased watermark size which can be managed by partitioning as illustrated in Section 5.3. This closed-loop adaptation guarantees verification reliability even under adversarial conditions.

7. Conclusions

PK-Judge redefines ownership verification for deep neural networks by bridging cryptographic trust with robust watermarking. Unlike symmetric watermarking schemes that rely on fragile bit-matching thresholds and risk secret exposure, PK-Judge leverages digital signatures and public-key infrastructure to establish irrefutable, non-repudiable ownership. By embedding error-corrected digital signatures into model space, our framework ensures resilience against adversarial tampering while maintaining model fidelity—achieving an Effective Bit Error Rate (EBER) of zero through error correction encoding. Crucially, PK-Judge’s challenge-response protocol eliminates replay attacks by requiring live cryptographic proofs tied to the secret key, a paradigm shift mirroring the trust revolution of HTTPS over HTTP. Our work introduces a separation of privilege principle for ownership verification: knowledge of the watermark alone is insufficient without cryptographic proof of secret key possession. This dual requirement—static signature validation and dynamic challenge fulfillment—sets a new security standard for intellectual property protection in AI. By decoupling watermark extraction from cryptographic verification, PK-Judge ensures that even partial exposure of embedded signatures cannot compromise ownership claims.

PK-Judge’s trust-centric approach potentially sets a new standard for regulatory compliance in AI technologies. This system aligns with evolving global standards for ethical and secure AI deployment, potentially influencing future AI watermarking and ownership verification methods. It paves the way for possible accreditation systems where neural network models are trusted based on verifiable watermarks. Overall, PK-Judge represents a shift towards a more secure, trust-based approach in AI and ML, addressing the critical need for trust and security in these rapidly advancing fields.