Evaluating the Effect of Surrogate Data Generation on Healthcare Data Assessment

Abstract

In healthcare applications, often it is not possible to record sufficient data as required for deep learning or data-driven classification and feature detection systems due to the patient condition, various clinical or experimental limitations, or time constraints. On the other hand, data imbalance invalidates many of the test results crucial for clinical approvals. Generating synthetic (artificial or dummy) data has become a potential solution to address this issue. Such data should possess adequate information, properties, and characteristics to mimic the real-world data recorded in natural circumstances. Several methods have been proposed for this purpose, and results often show that adding surrogates improves the decision-making accuracy. This article evaluates the most recent surrogate data generation and data synthesis methods to investigate the effects of the number of surrogates on improving the classification results. It is shown that the data analysis/classification results improve with an increasing number of surrogates, but this no longer continues after a certain number of surrogates. This achievement helps in deciding on the number of surrogates for each strategy, resulting in the alleviation of the computation cost.

1. Introduction

Both the scarcity and imbalance of clinical data influence the rapid exploitation of new tools and algorithms in medical and patient care environments due to two major reasons: first, clinical approval, which is needed for a robust and high performance of the system, and second, failures in the application of high-performance computational systems such as deep neural networks (DNNs) which, upon receiving appropriately sized data, can provide a perfect outcome, i.e., 100% accuracy, for diagnostic purposes.

In recent years, a solution to the above problems has been achieved by generating supplemental data. One of these methods, surrogate data generation, has become popular and apparently effective in improving the decision-making process and mitigating the impact of imbalanced recorded data.

Data insufficiency refers to the situation where the data in hand do not represent the full diversity of the corresponding problem. It influences the training performance of classifiers by underfitting the classifier model, making the classifications inaccurate. On the other hand, although existing classifiers are somewhat capable of coping with global class imbalance, new methods are needed to address the challenges posed by imbalanced data streams, mainly for data-driven techniques [1].

In the quest for supplemental data, there have been various approaches to their generation. Although no formal definitions exist for the generation type, we note that augmented, synthetic, and surrogate data have emerged as distinct types within their fields of application. Augmented data are generated by various transformations of the original data. Synthetic data are generated from mathematical models of the original data. Surrogate data represent a particular type of supplemental data that can replace the original, where essential properties, generally statistical, are preserved from the original.

The clinical application of surrogate data implies similarity with the real data. This is part of data diversity, which may include their temporal, spectral, spatial, statistical, or probabilistic properties. The aforementioned similarity can occur in any one or more of these domains.

Data augmentation is a well-established technique for generating supplemental data via computer vision [2], where the surrogate data are generated synthetically via bootstrapping by resampling from the distribution of the original signals. This is used as the replacement for a type of Monte Carlo method. Therefore, the standard methods of augmentation preserve some order statistics of the data, such as mean and variance, by simply shuffling the time series (TS) randomly.

In addition to helping recover the nature of the recorded data, the generation process also involves in the model’s generalization capability. It achieves generalization by mitigating overfitting and enhancing the characterization boundaries of the trained models [3]. The majority of data augmentation approaches involve the random alteration of the TS, for example, by adding random noise to the data, scaling the data, or slicing the data in the time (temporal diversity) and frequency (spectral diversity) domains [4]. Such random alterations to the TS mean that while they preserve the data characteristics in one domain, they may negatively affect the data in another domain where the diagnostic information lies. This is because there are a plethora of TSs having different properties and sequential patterns of diversity. For example, single-channel 3-D gait signals recorded using accelerometers are different from multi-channel 1-D electroencephalography (EEG) signals due to their intrinsic behaviors in time and frequency domains as well as the spatial diversity of EEG signals.

A single-channel surrogate may be insensitive to the delays (temporal shifts) of some clinically significant events in the signal, whereas a multi-channel surrogate maybe sensitive to the relative shifts/delays in different channels but more robust due to the correlation between the channels.

Several different surrogate data generation techniques have been proposed in the past two decades. The complexity and flexibility of the surrogate generation techniques have gradually increased and their efficacy improved. Here, we consider the most popular techniques in chronological order and examine how an increase in the number of surrogates can affect the accuracy of data classification and decision making. We also focus on the overlap between surrogate data generation and data synthesis.

An extensive review of surrogate data generation methods was carried out by Lancaster et al. [5].

Generally, data surrogates are a type of synthetic data that use bootstrapping and/or resampling from the original data distribution, often with replacement. Although this may be achieved by shuffling the TS randomly while preserving the mean, variance, or higher-order statistics, to maintain more nuanced temporal trends, correlations, and power spectra, approaches such as that by Theiler et al. [6], namely, amplitude-adjusted Fourier transform (AAFT), or its improved version, the iterated AAFT (IAAFT) proposed by Schreiber and Schmitz [7], may be needed. The basis of these algorithms is to randomly change the phase of the TS in the Fourier domain while maintaining the original amplitude distribution. The fundamental premise of both algorithms is that higher-order correlations can be mitigated through Fourier domain phase randomization, as the power spectrum is invariant under Fourier phase permutations. We will use the term AAFT for this kind of data generation.

There are also two popular methods for augmented data generation by randomizing, namely window distortion methods.

Mathematically, one way of generating surrogates is by dividing the TS into slices (or segments) and considering each slice as a replica of the data before performing classification. This method was introduced for TS in [8]. At the classifier training stage, each slice is assigned to the same class as the TS. The size of the slice is a parameter in this method. For testing, each slice from a test TS is classified using the trained classifier, and a majority vote is applied for decision making. This method is referred to as window slicing (WS) [8].

Another form of WS discards only 10% of data at random starting points of the TS while retaining 90% of the data at random and adjusting the rest of the TS accordingly [9]. Thus, it has the potential to distort the entire TS shape significantly, not just the signal within the window. Window warping (WW) contracts or expands each window randomly by up to 25% [10,11] of the TS. Window warping (WW) is used on windows of TS data of various sizes and time points. The window can be contracted or expanded in various quantities, up to 50% [10] of the window size. The rest of the TS is adjusted to maintain the TS length. Thus, it has the potential to distort the entire TS shape significantly, not just the signal within the window.

A goal of healthcare data assessment is to be able to analyze and predict the underlying causes. Frequently, this is an exercise in classification that the current deep learning neural networks excel in.

Deep learning has been successfully developed and implemented for image annotation, fusion, recognition, super-resolution, transform, etc., as well as speech transcription, with super-human results, surpassing humans in several applications, including games and robotic vision.

The current resurgence of neural networks is attributed to the deep network proposed by Krizhevsky et al. [12] in 2012, namely AlexNet. This reduces the classification error by about 10% for a dataset of 15 million images classified into 1000 categories. The AlexNet convolutional neural network (CNN) exploits the complexity variations in the data through convolutional layers. These networks are successfully used in transfer learning [13], where the earlier layers of the network are trained to recognize general image features using a wide range of image collection methods, and the following, usually fully connected, layers are trained to recognize the images relevant to a particular application. This allows for the tuning of few parameters in the last few layers of the network for a new application instead of retraining the whole network. This allows the transformation of data into images for surrogate data generation, which motivated us previously [14] to transform our 1-D TS data into 2-D images. Therefore, any type of image, including those produced by 1-D-to-2-D transformation, can be processed by transfer learning methods without much training time.

A detailed analysis in [15] compares various 1-D-to-2-D image transforms for classification, and the Gramian angular field (GAF) is cited as the most widely used for this purpose.

Some examples of using CNN for analyses are those by Byeon et al. [16], who used CNN to classify the conditions of subjects using their biomedical data.

Tsai et al. [17] used line graphs (the simple bilevel image of the curve) as the input image for a neural network. This is computationally inexpensive, as no image processing is involved. In another attempt for converting a 1-D TS to an image, the idea of a GAF was proposed by Zhang and Oates [18] to generate images from TS data as polar graphs. In addition, this approach better preserves and displays the temporal correlation between the time points. To construct the GAF, the TS $\mathit{x}$ is first scaled to [−1, +1] as ${\mathit{x}}^{\left(n\right)}$. Then, the phase $\mathit{\phi }$ and radius $\mathit{r}$ of the polar form are defined as [19]

$${\phi }_i={cos}^{-1}{x}_i^{\left(n\right)} for x_i^{\left(n\right)}\in {\mathit{x}}^{\left(n\right)}$$

(1)

and

$$r_i={\displaystyle \raisebox{1ex}{$i$}\!\left/ \!\raisebox{-1ex}{$N$}\right.} for i=1,2,\cdots N$$

(2)

The GAF defines a matrix with the ith and jth elements as $\cos \left({\phi }_i+{\phi }_j\right)$ and the element distance from the center as $\sqrt{r_i^2+r_j^2}$. A sample of such a GAF can be seen in Figure 1.

In the following section, we examine the above fundamental concepts in the generation of surrogates for some important healthcare data, namely, stroke rehabilitative assessment and activity-recognition data.

2. Methods for Surrogate Rehabilitative Data Generation

2.1. Image-Based Methods

In one of our early attempts, we used a GAF for the 1-D-to-2-D transformation of the TS before classification using an advanced cutting-edge neural network framework for data generation, consequently achieving an improvement in the classification results [6]. This demonstrates how scarce TS data can be effectively augmented to enable the successful use of state-of-the-art analytical tools.

In our previous attempts, we generated surrogate rehabilitative assessment data to produce a supplementary time series that can provide the same fidelity as the original TS [20]. For data collection (off-line or online), we inserted sensors into a small cube used in the assessment process. This allowed for sensing fine motion without any need for attaching bodily intrusive sensors [14].

The block diagram for this system, using the action research arm test (ARAT) [20], is shown in Figure 2 [14]. The accelerometer data were segmented, the outliers due to artifacts were compensated for, and the data were used to generate balanced surrogate data.

One of the tests in the ARAT requires grasping a wooden cube (with a built-in triaxial accelerometer) measuring 7.5 cm all around, removing it from a lower shelf, moving it, and placing it on an upper shelf through a simple prescribed trajectory. The sensor readings are sampled at 30 Hz and used without any pre-filtering. A full explanation of the data can be found in [14]. However, the original data are highly imbalanced, as less data are collected from patients with severe disability as the result of stroke.

From a set of imbalanced data, two sets of surrogates, one with 10 and the other 100 times the data volume, were generated to examine the effect of the number of surrogates on the classification results. However, the numbers of surrogates were equal for all four ARAT scores. Then, these data were transformed into three types of images and finally applied to a deep CNN for classification.

The 10-fold and 100-fold surrogate generation results for the two methods for three different TS-to-image transforms and using AlexNet can be found in

Table 1. Image-based surrogate generation/classification accuracy using 2-D AlexNet with execution durations in parentheses—training/validation = 80/20—averaged over three runs [14].

Surrogate Generation Method	# Fold Surrogate Data	Line Graph	GAF	Wavelet Transform (WT)
No surrogate	Original data	60.7% (5 min)	57.6% (5 min)	46.5% (58 min)
AAFT surrogates	10-fold	90.1% (16 min)	86.7% (1:10 h)	84.1% (2:08 h)
	100-fold	100% (5:12 h)	98.9% (18 h)	98.5% (12:11 h)
IAAFT surrogates	10-fold	97.1% (25 min)	86.8% (1.6 h)	82.2% (1:49 h)
	100-fold	99.9% (5:06 h)	99.1% (17 h)	98.5% (10:02 h)

[14]. We used MATLAB R2018a and H/W Dell XPS (3.4 GHz capable) system with 16 RAM running on Windows 10 and Intel UHD graphics 620 for this purpose.

In this table, the image transforms vary greatly in complexity, as shown by the variation in run times. In this case, we note the improvement in test accuracies as the fold number of surrogates increases; the simplest image transform, i.e., the line graph, provided the best run times as well as an improvement in test accuracies.

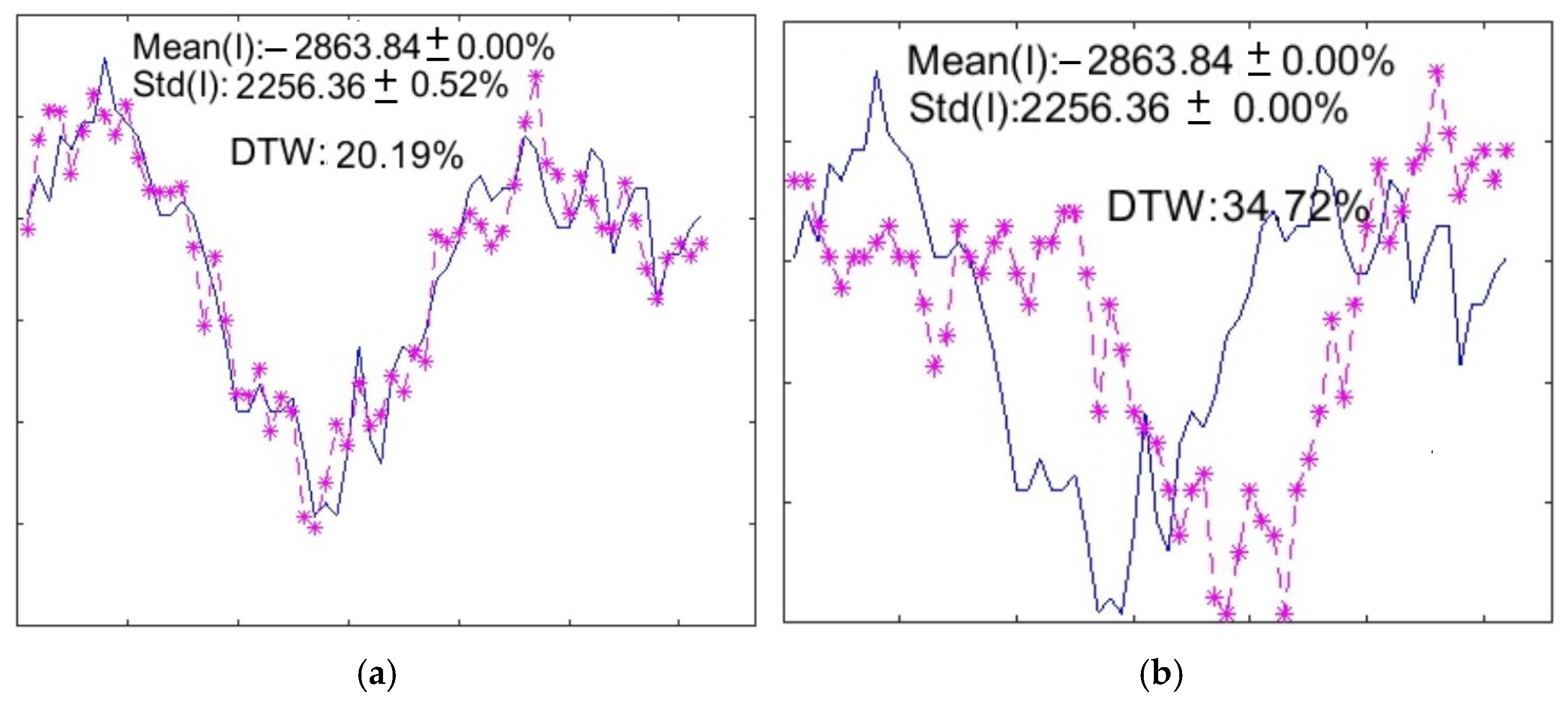
2.2. One-Dimensional Methods

In our next attempt, we generated surrogates for the ARAT data without transforming them to images by applying the 1-D CNN directly to the TS data [19]. We also examined the differences in the performance of various neural networks to enable data analysis from wearables. It is shown that deep learning systems can be trained in the case of data shortages before being deployed into resource-constrained edge systems accessible to patients or clinicians.

Here, surrogate TS generation, which has been successfully used before [5], is employed and proves to be very effective. As demonstrated in the block diagram in Figure 2, in all the cases, AAFT or IAAFT is used for surrogate data generation, and various neural networks are applied for data classification.

In addition to the fully connected neural network and CNN previously used in [14] for image-based approaches, here, both CNNs and long short-term memory networks (LSTM) are examined, too. LSTMs are recurrent neural networks (RNNs) known for exploiting the previous state and output of the data samples for predicting the current data sample or segment. In one work [19], it is demonstrated that 1-D applications, i.e., CNN and LSTM, require approximately five times less computational complexity. Moreover, 1-D approaches are compared with the 2-D ones. The related results are provided in

Table 2. Comparing various neural networks applied to 2-D and 1-D forms of data and their surrogates [19]. There was a 50-fold generation of surrogates.

Model	Input	Number of Parameters	Training Accuracy	Validation Accuracy	Testing Accuracy
2-D AlexNet + transfer learning	Image	62,381,347	99.45%	98.53%	51.6%
2-D CNN	Image	99.851	98.87%	98.20%	39.1%
1-D CNN	Time series	141,735	99.98%	98.86%	90.7%
LSTM	Time series	213,395	98.43%	98.48%	98.7%

. Here, for 2-D inputs, the WT was used, as it has a good theoretical background and offers a better performance than the GAF. We used transfer learning to reduce the training effort. For comparison, we used our own 2-D CNN, which was trained using the surrogate data.

In Table 2, since we are comparing NN architectures, we use the training and validation accuracies for a fixed 50-fold increase in surrogate data. Notably, we test the NN using the original time series only, and the improvement in the testing accuracy shows the generalization ability of the NN trained using surrogates only.

We note that the 1-D NN provided good results with fewer training parameters, with a 50-fold increase in surrogate data.

We used the testing accuracy in Table 1 and Table 2 as a prime indicator of the benefits of surrogate data generation. We did not intend to exhaustively compare all the approaches, but rather we analyzed them to gain an insight into effective surrogate data generation methods. We conclude that the SSA/AAFT approach to surrogate data generation coupled with 1D-CNN offers the best results in terms of training efficiency and classification, and we use this in Section 4.

2.3. Shape-Preserving Technique

A complex-shape TS contains various components that are likely in different subspaces. Methods that can decompose a TS into its constituent subspaces allow for the restoration of the desired components (maintaining the signal shape) and the alteration of those with less clinical significance and are random.

Generally, 1-D signal decomposition is a challenging task and may not be a fully automatic method. One effective 1-D signal separation method is singular spectrum analysis (SSA), which has been applied to several types of clinical data [21].

In SSA, for a signal of length L, the overlapping windows of TS size M (also called the embedding dimension) are ordered as rows of a so-called Hankel matrix X of size (L − M + 1) × M. In the decomposition stage, $\mathbf{C}={\mathbf{X}}^T\mathbf{X}$ is factorized into $\mathbf{C}=\mathbf{U}\mathbf{\Lambda }{\mathbf{U}}^{\mathit{T}}$, where $\mathbf{U}=\left\{{\mathit{u}}_i\right\}$ is the matrix of eigenvectors ${\mathit{u}}_i$, and Λ is an M × M diagonal matrix of eigenvalues ${\lambda }_i$. In the grouping stage, some criteria are employed to select and combine the ${\lambda }_i^{1/2}{\mathit{u}}_i$ components, and finally, in the reconstruction stage, the desired signal is reconstructed by diagonal averaging [21].

Using SSA in [22], it was stressed that by synthesizing the data and involving influential and distinctive features in surrogate generation, we can alleviate the need for large data sizes. Also, in previous methods, attempts have focused on preserving the order statistics of the data without considering the shapes of main data characteristics such as trend, various harmonics, or even physiologically relevant information. This may be particularly difficult when single-channel data such as single accelerometer output are under consideration.

To tackle this problem, before applying 1-D CNN, SSA was used to decompose the TS into trends and cycles to describe the shape of the signal and other components belonging to noise or the less significant information for clinical diagnosis, which may be called low-level components [22]. These low-level components may be changed randomly and recombined with the original trend and cyclic components to form a surrogate TS.

Looking at the pattern of eigenvalues by means of a scree plot (Figure 3), we see that the eigenvalues decrease in order of magnitude, and often only the first few λs are dominant. This identifies the significant λs and eigenvectors that contribute to trend and seasonal data. The cyclic seasonal data with lower amplitudes also manifest themselves as couples of adjacent equal-magnitude λs in the scree plot [21,22,23]. The remaining values belong to the noise or irregular part of the TS, which in many instances is treated as noise. In [22], the dominant eigenvalues were selected based on the relevant dimension estimation (RDE) concept introduced by Braun et al. [24].

Therefore, to generate the surrogates that can preserve the relative shape (morphology) and statistical properties of the signals, SSA is applied to decompose the TS into its constituent eigentriples. Those components with eigenvalue magnitudes greater than an empirical threshold, ${\lambda }_i\ge T_r$, are preserved, and the rest are randomized as many times as the number of required surrogates. The overall process, including 1-D CNN for classification, is illustrated in Figure 4 [22].

Several tests were carried out to demonstrate the efficacy of the method in terms of preserving the statistical properties as well as the signal morphology. The mean, standard deviation, autocorrelation function (ACF) by means of root mean squared difference of both the TS and the surrogates were estimated and compared. In addition, the similarity between the original signal and its surrogates were examined by comparing their dynamic time warping (DTW) measures. Figure 5 demonstrates the surrogate generated by two methods, namely the SSA/AAFT (shape preserving) [22] and AAFT (phase randomization) [25] methods. In both, a smaller number denotes fewer differences.

Each of these methods has its pros and cons. Certainly, the two methods can also be combined to cater for temporal shifts in the clinically important events within the TS. These events can include the overall signal, the trend, the seasonal or cyclic components, or even sparse events within the noise subspace.

Sparse events may be considered anomalies or transients in the clinical data, such as interictal epileptiform discharges in electroencephalographic data [26] or instances when the ARAT cube falls due to disability. Such transients might indicate very significantly abnormal symptoms in medical diagnosis.

Transient events contribute to the nonstationarity of the data and possible nonlinearity in the data-generating or -recording systems. Using SSA or a time-frequency domain method such as STFT or WT, it is possible to search for such events within the noise subspace easily [27,28,29] before going through the surrogate generation process in Figure 4. In [27], the authors derived spike-type anomalies directly from the noise subspace using SSA. In [28], the intrinsic properties of human accelerometer data [30], i.e., linearity and stationarity, were identified. For stationarity, two parametric tests, namely, the augmented Dickey–Fuller (ADF) test [31] and the Kwiatkowski–Phillips–Schmidt–Shin (KPSS) test [32], are employed. The ADF test assumes that the TS ${\mathbf{x}=\{x}_t\}$ is a first-order autoregressive, AR(1), process in the following form:

$$x_t=\rho x_{t-1}+{\epsilon }_t$$

(3)

where $\rho$ is the pole of the corresponding AR filter, and ${\epsilon }_t$ is the residual error at time instant $t$. When $\left|\rho \right|=1$, the system is nonstationary as it converts to instability. The ADF test does not perform sufficiently well, even if the first AR parameter $\left|\rho \right|$ is close to 1, which motivates other test statistics. Conversely, the KPSS test computes a metric for the nonstationarity level $w_{ns}$ using the residual signal as follows:

$$KPSS: w_{ns}={\displaystyle \frac{1}{L^2}}\sum _{t=1}^L{\displaystyle \frac{{\epsilon }_t^2}{{\sigma }^2}}$$

(4)

where L is the signal length, and ${\sigma }^2$ is the estimated variance of the signal. The higher $w_{ns}$, the higher the level of nonstationarity. For a parametric nonlinearity check, there are many simple tests, including the one proposed in [33], where the authors formulated a broadly used parametric test for assessing nonlinearity. They tested for heteroskedacity, which is the inconstancy of the variance over time.

Nonparametric tests do not have any assumption about the data distribution. Therefore, they use, for example, sample autocorrelation to check for spread or cyclostationarity.

In nonparametric linearity tests, a statistic is estimated by considering the original data linearly generated. In estimating the same statistics for the surrogates, if the variation in values is beyond that explainable by normal variance, then the hypothesis is rejected, which suggests that there was possible nonlinearity in data generation. A statistic based on nonlinear predictor errors (NPEs) proposed by Schreiber and Schmitz [7] was shown to be a good indicator for testing for and detecting nonlinearity. The NPE predicts the value of a TS by utilizing an embedded phase space and then compares it with the actual value at the same time instance. The procedure for using the NPE involves the following steps: (i) determining suitable embedding parameters D and τ, (ii) creating a phase-space model of the data, (iii) performing a zero-order prediction of the values in the TS, and (iv) calculating the error between actual and predicted values.

For all the surrogates, these parameters are normalized by dividing them by the standard deviation of the TS values to obtain a distribution of errors. Then, a t-test is run to find the errors between the original TS and its surrogates.

For SSA applications in surrogate data generation, these parameters are considered to set the best embedding dimension, which is an influential and impactful parameter in 1-D signal decomposition.

In [29], the focus is on using the spectrogram of the TS for detecting the transient events prior to decomposing the signal into its constituent components using SSA. The following pseudo-code expresses the processing steps for the spectrogram:

The original signal has its significant transients removed; their values replaced by linearly interpolating the signal between the start and end points of the transient. The difference in values between the interpolated and transient signals is stored. After the surrogate is generated, the differences in step 4 of the algorithm are added back to the surrogate. Figure 6 shows the results of Algorithm 1 for one TS.

Algorithm 1: Detection of Significant Transients for Spectrogram Data

I. Generate spectrogram of zero-mean signal II. For all time points     compute mean and std     cluster the means using k-means III. For all clusters     remove members that are:     < mean threshold % low energy     > std threshold    % energy not evenly spread     remove clusters with few members IV. For valid clusters  % members adjoining time points     find start and end values of time points     linearly interpolate signal between start/end times     subtract from actual signal % transient only     store differences       % to be restored

3. Generative Adversarial Network for Synthetic Clinical Data Generation

In a very recent approach [34] inspired by the work of Allahyani et al. [35], a method for generating heterogeneous multivariate TS data is proposed. Two datasets (both imbalanced) are processed. The first one is the ARAT dataset described previously [14], and the second one is a larger activity-recognition dataset created in late 2019 [36]. The latter dataset includes the records of eighteen various complex daily activities, as shown in

Table 3. Activity recognition dataset including 18 different activities [36].

Types of Activity	Activity Name
Using body	Walking, Jogging, Stair Climbing, Sitting, Standing, Kicking
Eating/Drinking	Soup, Chips, Pasta, Drinking, Eating Sandwich
Using hands only	Typing, Playing Catch, Dribbling, Writing, Clapping, Brushing Teeth, Folding Cloths

. These activities were executed by 51 different participants, each for a duration of three minutes.

Two inertial measurement unit (IMU) sensors, namely, a triaxial accelerometer and a triaxial gyroscope connected to a smartwatch and a smartphone, respectively, were used for collecting the data.

The wearable smartwatch was used by the participants on their dominant hands, and the smartphone was set on the waist. Both sensors collected the gait signals at a sampling frequency of 20 Hz. In the dataset, each row shows three axes of acceleration signals, three axes of gyroscope data, and the executed activities’ abbreviated names. The dataset was partitioned into 10 s segments related to 200 observations through non-overlapping sliding windows. Every data segment was labeled with the most recurring activity name. This led to a dataset structure of size 16,854 × 6 × 200, where 16,854 represents the total number of TS segments, 6 indicates the number of axes (triaxial gyro + triaxial acceleration), and 200 refers to the length of the segments.

At first, a vanilla generative adversarial network (GAN) was used to spawn the multivariate surrogate TS data. The model was then trained separately on each category in the first dataset, as the authors did not see it feasible to predict the label by visual inspection.

For the second dataset, the model was trained using the entire dataset to distinguish between different classes. Although the generated data satisfied the necessary criteria, a thorough examination showed that the generated dataset did not include several segments of the original data. This refers to the mode collapse problem, meaning that it fails to capture the heterogeneity of the actual data distribution. To examine this hypothesis, the longest common subsequence (LCSS) algorithm was employed to assess the similarity between the original data segments and the generated surrogate (or synthetic) data. Therefore, mode collapse happened, as most of the generated data seemed to be parented by a small portion of the dataset. Furthermore, the classifier trained using the synthesized or generated data and assessed by using the real original data for validation performed poorly [34].

To overcome the mode collapse problem, a new structure called the TS Siamese GAN (TS-SGAN) was proposed. This method involves incorporating a layer that learns the differences between diverse input structures and uses this information to represent all the modes, enabling the generator to create more heterogeneous data. This is achieved by adding a Siamese network that first differentiates between the dataset components and then exploits the similarity between the data and the surrogates using a second discriminator in the network. In this design, the mode collapse problem is highly mitigated, and the generated data are heterogeneous, as evidenced by their distribution across both datasets. The new structure led to excellent classification results when the classifier was trained on the newly generated data [34]. However, we should bear in mind that when using TS-SGAN, the generated data are meant to be very similar to the original data. A block diagram of the TS-SGAN surrogate generator is depicted in Figure 7.

To implement the TS-SGAN, the GAN formulation and the block responsible for making the generated data more heterogeneous and consequently alleviating mode collapse need to be merged. The first part follows the conventional GAN equation based on equilibrium. The second part is achieved by changing the GAN’s output using a heterogeneity principle for both the generator G and the second discriminator D2. The latter is used to differentiate between the diversity in the real TS data and the heterogeneity in the generated signals. In a way similar to the Nash equilibrium principle governing the relation between G and D1 for generating realistic TS data, to generate heterogeneous data, we rely on the equilibrium [37] between G and D2.

Hence, it is concluded that for post-stroke rehabilitative assessment using ARAT data, the classifiers based on deep learning require considerably large-size datasets. This data should be both realistic and diverse to enable the development and use of effective classifiers for the identification of various gaits or patients’ actions. By synthesizing multi-fold data similar to the original ones, TS-SGAN improved the classification performance from 63% to 98.2% for the ARAT dataset and from 48.73% to 90.8% for the activity-recognition dataset.

4. Effectiveness of Surrogate Data Generation

There is a wide range of patient assessment data recorded by variety of sensors [38]. The use of accelerometers is very popular since the sensors are externally mounted and can track body movement and gait [30].

The data widely used in our previous works described in Section 2 are ARAT accelerometer signals for the evaluation of post-stroke rehabilitation progress. Other data are related to the WISDM Smartphone and Smartwatch Activity and Biometrics dataset introduced in [36].

The embedded accelerometer generated 3D movement data of variable lengths. The clinical staff scored these data, which can be regarded as a classification task. Overall, 78 sets of data were recorded, where 31 scored 3, 38 scored 2, 6 scored 1, and 3 scored 0. The median length of the data is 91 samples, with 32 samples as the lowest and 231 samples as the highest.

The activity-recognition dataset, created in 2019, includes eighteen different daily activities. The activities were performed by 51 participants each for a duration of three minutes. Two IMU sensors, namely, a triaxial accelerometer and a triaxial gyroscope connected to a smartwatch and a smartphone, respectively, were used to collect the data. The smartwatch was worn on the participant’s dominant hand, while the smartphone was placed on the waist. Both devices sampled data at 20 samples/s.

Both datasets were processed and classified by the TS-SGAN system. The most recent systems introduced here were used to generate different-fold surrogate data and classify them. The classification accuracy is reported for each system and dataset in the corresponding publications.

As the main objective of this article, here, we assess the changes in classification accuracy when the number of surrogates increases. The graph in Figure 8 shows the effect of the number of surrogates on the classification accuracy.

On the other hand, data imbalance occurs when sample sizes of some data classes are different from those of other classes in a dataset. Indeed, the difference in size is not the only cause for data imbalance. Gender, age, the time and environment of data recording, systems used for data recording, and many other possible factors can make the data imbalanced and affect the decision-making results.

The performance of predicted models is highly influenced by any imbalance in the data and increases in the sample size. Overall, using imbalanced data (i.e., those with a large difference between the majority and minority classes) for training or validation deteriorates the model performance. It is, however, expected that during surrogate generation, this shortcoming is resolved.

Machine learning techniques do not perform well when the data are imbalanced. This is mainly because during any optimization, they focus on minimizing the error rate for the majority class while ignoring the minority class. The authors in [39] demonstrated the drawbacks of class imbalance for several classifiers’ accuracies. Mathematically, it is favorable to identify the nature of the relationship between the degree of class imbalance and the corresponding effects on classifier performance accurately to enable researchers to better tackle the problem.

As we believe that the relationship between the class imbalance ratio and the classification accuracy is convex, to this end, we assume that all the techniques used for surrogate data generators also convert the imbalanced data into balanced ones. Hence, a similar number of surrogates is envisaged. Additionally, for the TS-SGAN approach, we overcome the mode collapse problem to ensure that the generated dataset is heterogenous.

5. Conclusions and Recommendations

We have shown here that surrogate data are useful and positively affect analyses of healthcare data. More specifically, they improve the results of their classification, particularly where deep learning is applied. Such applications require the surrogates to retain specific characteristics of the data, such as distribution, shape, and transients, and be less sensitive or insensitive to some data variations such as temporal shifts. These characteristics often involve diagnostic information and need to be maintained and accessible in the surrogates. Any violation of these principles will overfit the classifiers and cause larger error rates in the classification of test data.

In Figure 8, we observe that by using larger number of surrogates, the classification accuracy improves. However, this is not open ended, and the graphs tend to saturate and reach to a steady state when the number of surrogates surpasses a certain level.

It is necessary to understand that that the area of surrogate data generation may overlap with data synthesis. Data synthesis methods do not necessarily consider the data distribution or parametric characteristics of the data such as order statistics. Therefore, shape-preserving methods such as SSA or TS-SGAN by themselves may not fully comply with the surrogate data generation principle. This means that the current surrogate data generators do not comply with all the permissible changes that surrogates can have. Therefore, the use of methods such as TS-SGAN are more appropriate for data synthesis than for surrogate generation methods. In data synthesis, the diversity in the data (warping, anomaly, relation between segments, etc.) is not fully exploited. So, the training, validation, and testing accuracy values rapidly increase with the production of synthesized data (which are in fact very similar to the actual data). On the other hand, when the intention is to classify the data, the classifier may not be robust against the desired changes in data morphology such as amplitude, time warping (i.e., squeezing or stretching the TS), or time shift. Therefore, the comparisons in Figure 8 may be neither fair comparisons nor good indicators of the surrogates’ adequacy.

In addition, we stress that a good surrogate generator for clinical use should not only maintain the diagnostic features but also be coupled with the classifier to ensure that each generated surrogate is classified under the right diagnostic category.

Figure 9 suggests a more reasonable flowchart for a clinical surrogate data generator, which includes SSA for denoising and maintaining trends and seasonal (cyclic) information as well as transients (which can also be detected using WT); then phase randomizing (random time shifting); followed by time warping; and, finally (although this can be in an earlier stage), resampling from the data distribution using lower-order (e.g., mean and variance) to higher-order (e.g., skewness and kurtosis) statistics. The actual clinical diagnostic tests would set the necessary limits on various statistical parameters of the surrogate generators, such as the time shift and time warping parameters. In addition, representative anomalies in the data, which may refer to diagnostic indicators, should be well preserved by the surrogates.

Finally, it is emphasized that the classification result is not a good metric for assessing the quality of surrogate generators unless proper features are utilized or very deep DNNs with millions of parameters are used to exploit a wide range of variations in the data and the surrogates. So far, no inclusive and meaningful testing method has been introduced. Such a metric should consider and preserve data statistics of various orders (mean, variance, skewness, kurtosis) and shapes and be insensitive to and robust against effects such as time shift and warping.