Abstract
Data structures such as sets, lists, and arrays are fundamental in mathematics and computer science, playing a crucial role in numerous real-life applications. These structures represent a variety of entities, including solutions, conditions, and objectives. In scenarios involving large datasets, eliminating duplicate elements is essential to reduce complexity and enhance performance. This paper introduces a novel algorithm that uses logarithmic prime numbers to efficiently sort data structures and remove duplicates. The algorithm is mathematically rigorous, ensuring correctness and providing a thorough analysis of its time complexity. To demonstrate its practicality and effectiveness, we compare our method with existing algorithms, highlighting its superior speed and accuracy. An extensive experimental analysis across one thousand random test problems shows that our approach significantly outperforms two alternative techniques from the literature. By discussing the potential applications of the proposed algorithm in various domains, including computer science, engineering, and data management, we illustrate its adaptability through two practical examples in which our algorithm solves the problem more than and times faster than the existing algorithms in the literature. The results of these examples demonstrate that the superiority of our algorithm becomes increasingly pronounced with larger problem sizes.
1. Introduction
Data structures such as sets, lists, arrays, and graphs are foundational to mathematics and computer science and pivotal in representing and organizing diverse entities, including solutions, conditions, objectives, and other data-centric elements [1,2,3]. Efficient manipulation of these structures is vital for the seamless operation and effectiveness of computational systems, with applications spanning algorithm optimization to complex database management [4,5]. Yet, the presence of duplicate elements within extensive datasets presents significant challenges, resulting in heightened computational complexity, diminished performance, excessive memory consumption, and potential inaccuracies in data analysis [6,7,8,9,10]. For instance, eliminating duplicate solutions in the reliability evaluation of multistate flow networks remains a notable challenge in the literature [8,11,12,13,14,15]. To remove duplicate solutions, a tree structure was used in [2] to compare vector components. Discussing the impact of the processor count on the sorting performance, the author in [4] explains how parallelization techniques can enhance the efficiency of sorting algorithms for large datasets. The authors in [7] developed efficient algorithms for optimally sorting permutations using specific types of transposition trees, namely single brooms, double brooms, and millipede trees, and introduced a new class of millipede trees, while comparing their sorting bounds with existing algorithms. The authors in [8] employed a pairwise comparison test to eliminate duplicates. The authors in [11] developed an improved signal-sorting algorithm based on congruence transform that effectively sorts both staggered and periodic PRI signals, addressing the issue of pseudo-peaks and enhancing sorting accuracy, though with a computational complexity that may require optimization for large-scale data processing. In [15], the authors used a data structure to convert each vector into a unique number and then compared these numbers instead of the vectors to remove duplicates. Although comparing numbers is significantly more efficient than comparing vectors, the data structure proposed in [15] is impractical for larger vector sizes. Thus, eliminating duplicates becomes imperative to streamline operations, enhance efficiency, and uphold data-processing integrity [16,17,18,19]. The authors [19] developed a simulation-based approach for generating synthetic training data to improve the detection of structural defects in parts using acoustic resonance testing (ART), demonstrating enhanced sorting accuracy by integrating eigenfrequency measurements and specific geometric data.
Existing methods to tackle this issue, such as pairwise comparison tests (PCTs) and sequential sort methods (SSMs), encounter notable limitations regarding computational complexity and memory overhead, particularly when handling vast datasets [5,6]. This research gap underscores the necessity for novel algorithms capable of efficiently managing large-scale datasets with intricate structures, while providing scalable solutions for sorting and duplicate removal [4,7,11,20,21,22].
To bridge this gap, we introduce a pioneering algorithm that exploits the mathematical concept of logarithmic prime numbers (LPNs) to efficiently sort data structures and eliminate duplicates with remarkable efficacy. The algorithm’s design, grounded in mathematical rigor, ensures correctness and includes a comprehensive analysis of its time complexity. Leveraging the unique properties of LPNs, this innovative approach offers a fresh perspective on data structure management, distinguishing it from conventional methods. Moreover, the proposed algorithm eliminates the need for pairwise comparisons and set-to-vector conversions, resulting in reduced memory overhead and enhanced simplicity in implementation.
The main contributions of this work are (1) proposing a mathematically rigorous algorithm for sorting data structures and removing duplicates, (2) providing a thorough analysis of the algorithm’s time complexity, and (3) showcasing the algorithm’s practical applicability across various domains. This potential is illustrated through practical examples of duplicate removal in malware analysis and gene sequence analysis. Additionally, we demonstrate the superiority of our proposed algorithm compared to two other methods from the literature using one thousand random test problems and two practical examples. The insights gained have the potential to influence future developments in data-processing algorithms, offering a valuable tool for researchers and practitioners in managing and analyzing large datasets effectively [23,24,25,26,27]. The proposed algorithm marks a significant advancement in the quest for efficient and scalable methods for handling large-scale datasets in an increasingly data-driven world.
The remainder of this paper is structured as follows: Section 2 reviews two well-known algorithms for sorting and duplicate elimination. Section 3 introduces the proposed algorithm, detailing its design and analyzing its time complexity. Section 4 presents extensive experimental results, comparing the performance of the algorithms using one thousand randomly generated test problems and two practical examples of relatively large size. Finally, Section 5 concludes the study with remarks on the findings and suggestions for future research directions.
2. Current Related Methods
Two primary methods are currently employed for sorting and removing duplicates: the pairwise comparison test (PCT) and the sequential sort method (SSM).
2.1. Pairwise Comparison Test
The PCT is an intuitive and straightforward approach that has been used widely in the literature [5,23,25,26,27]. It involves comparing each pair of sets and removing one of the two if they are identical. This process is repeated until all pairs of sets have been compared. Many researchers have used this technique to remove duplicate solutions in different areas [18,22,26].
To illustrate, consider seven sets: s1 = {e1, e5}, s2 = {e1, e4, e6}, s3 = {e2, e3, e5}, s4 = {e1, e4, e6}, s5 = {e1, e6}, s6 = {e2, e6}, and s7 = {e1, e4, e6}. Table 1 demonstrates the procedure for using the PCT to detect and remove duplicates by comparing si with sj for i < j with i = 1, 2, …, 6 and j = i + 1, i + 2, …, 7, provided that sj has not been removed. In Table 1, the notation “≠” denotes the related pair is not equal (e.g., s1 ≠ s2), while the notation “=” indicates that the related pair is identical (e.g., s2 = s4 in the cell at the intersection of the third row and fifth column). When a pair of sets is found to be identical, the set with the larger label is discarded (e.g., s4).

Table 1.
The procedure of the PCT to the example.
The PCT offers a simple and effective means of identifying and eliminating duplicate sets. However, its computational complexity grows quadratically with the number of sets, as each pair must be compared individually. This can lead to inefficiencies when dealing with large datasets. Consequently, researchers have explored alternative methods, such as the sequential sort method (SSM), which aims to reduce the computational burden while maintaining the accuracy of duplicate removal [28,29,30].
The pairwise comparison approach, while effective in eliminating duplicates, falls short when it comes to sorting sets. Its application becomes particularly cumbersome and less efficient compared to the SSM, especially when dealing with numerous sets. The time complexity of the PCT is detailed below.
Lemma 1.
The time complexity of the pairwise comparison test is O(n∙m2) for removing all duplicates, where m represents the number of sets, and n denotes the maximum number of elements in each set.
Proof.
Assuming that all the sets are given as binary vectors, the time complexity of the pairwise comparison of two sets, each with a maximum of n elements, is O(n). Since there are m sets and each set needs to be compared with every other not-processed set, the total number of comparisons required is given by the sum (m − 1) + (m − 2) + … + 1 = m(m − 1)/2. Each of these comparisons is of the order O(n). Therefore, the total time complexity of this approach is as follows:
Thus, the overall time complexity of PCT for removing duplicates from m sets is O(n∙m2). □
2.2. Sequential Sort Method
Compared to PCT, the SSM provides a more streamlined solution for both sorting and duplicate elimination. This method involves transforming all sets into vectors, assigning a value of one to the coordinate if the corresponding element is present in the set and zero otherwise. The sorting process then commences by ordering the values of the first coordinate, followed by the second, and so forth, until all coordinates are sorted.
The efficiency of the SSM is attributed to its ability to concurrently sort and identify duplicates. By arranging the vectors based on their coordinate values, identical sets naturally group together, facilitating the detection and removal of duplicates. This method eliminates the need for explicit pairwise comparisons, enhancing computational efficiency.
To illustrate this method, consider the previous example with seven sets: s1 = {e1, e5}, s2 = {e1, e4, e6}, s3 = {e2, e3, e5}, s4 = {e1, e4, e6}, s5 = {e1, e6}, s6 = {e2, e6}, and s7 = {e1, e4, e6}. After converting these sets into vectors and applying the SSM, the sorted vectors reveal the duplicate sets, such as s2, s4, and s7, which can then be effortlessly removed. Table 2 showcases the outcomes after sequentially sorting all elements.

Table 2.
The results before and after employing the SSM on the example.
The SSM indeed provides a more efficient approach to identifying and removing duplicate sets compared to the PCT. The method’s ability to sort sets while facilitating duplicate removal is a significant advantage, especially when dealing with large datasets. The time complexity of the SSM is discussed below.
Lemma 2.
The time complexity of the sequential sort method is O(n∙m∙log(m)) for sorting all sets and removing all duplicate sets, where m represents the number of sets, and n denotes the maximum number of elements in each set.
Proof.
The time complexity to represent the m sets as binary vectors, where each set has a maximum of n elements, is O(mn). Following this, the method performs sorting operations on each coordinate of these vectors. Efficient sorting algorithms such as quicksort or merge sort, which have an average time complexity of O(m∙log(m)) for sorting m elements, are typically used [7,11]. Since the SSM sorts the vectors based on their coordinate values and there are, at most, n coordinates in each vector, the overall time complexity for sorting all coordinates becomes O(n∙m∙log(m)).
Therefore, the total time complexity of this approach, which includes representing the sets as binary vectors and sorting them, is as follows:
Thus, the SSM has a time complexity of . □
Compared to the PCT, which has a time complexity of O(n∙m2), the SSM offers a significant improvement in efficiency, particularly when the number of sets (m) is large. The logarithmic factor introduced by the sorting algorithm helps to reduce the computational burden, making the SSM more scalable and suitable for handling extensive datasets.
It is worth noting that the SSM’s efficiency can be further enhanced by employing optimized sorting algorithms or parallel processing techniques [4,7,22,28]. These optimizations can help to reduce the constant factors associated with the time complexity and improve the method’s performance in practice. Moreover, the SSM’s ability to sort sets provides an additional benefit beyond duplicate removal. Sorted sets can be useful in various applications, such as set intersection, union, and comparison operations, which can be performed more efficiently on sorted sets.
3. The Proposed Method
In this section, we introduce a novel method for sorting sets and removing duplicates based on the concept of logarithmic prime numbers (LPNs). The proposed method aims to address the limitations of existing approaches, such as the PCT and the SSM, by providing an efficient, simple, and scalable solution.
3.1. Logarithmic Prime Number and Algorithm Description
A logarithmic prime number (LPN) is defined as the logarithm of a prime number, such as log(2) and log(7). The use of LPNs in this context is motivated by their unique properties, which enable the transformation of sets into distinct numbers. Assume that sets s1, s2, …, and sm are given and is the union of all the sets. Let r be the number of elements in and let P = { p1, p2, …, pr} be the set of the first r prime numbers. We define the LPN associated with each element, as , where , for i = 1, 2, …, r. For example, l(e1) = log(2), l(e2) = log(3), l(e3) = log(5), etc. Hence, the LPNs associated with each element are clearly unique. Then, we define the LPN associated with each set as the sum of the LPNs of its elements. Hence, assuming s as a set of elements, we have
where ei is the ith element in , and l(ei) is its LPN. To illustrate, Table 3 shows the procedure of calculating the LPN, L(si) for each set si, where i = 1, 2, …, 7, in the example discussed in Section 2.

Table 3.
The procedure of calculating the LPN for each set in the example.
The fundamental theorem of arithmetic states that every positive integer greater than 1 can be uniquely represented as a product of prime numbers, up to the order of the factors [1]. Accordingly, the following result shows the uniqueness of the corresponding LPNs to each set.
Theorem 1.
Let
,
, …, and
, , …, be two sequences of the prime numbers. We have
if and only if
and
, for
.
Proof.
If and , for , then it is trivial that Now, assume that Hence, , and so . As , , …, and , , …, are prime numbers, and prime factorizations are unique, we conclude that and , for . Hence, the proof is complete. □
According to the definition of LPNs, the theorem above demonstrates the uniqueness of the associated LPNs to each set, and therefore the following result is at hand.
Corollary 1.
The sets si and sj are identical if and only if L(si) = L(sj).
Main properties: The LPN, L(s), has several key properties that make it effective for sorting sets and eliminating duplicates.
- It assigns a unique LPN to each distinct set, ensuring no two different sets share the same number. This is essential for accurately distinguishing between sets and identifying duplicates.
- The LPN, L(s), increases consistently as elements are added to the set s. This property helps maintain the relative order of sets when they are sorted by their LPNs.
- The LPN, L(s), offers a compact representation of the set s, encoding the entire set with just one value. This reduces memory usage and enhances the efficiency of sorting and comparison processes.
By exploiting these properties of LPNs, the proposed method can effectively sort sets and remove duplicates without the need for pairwise comparisons or the conversion of sets into vectors.
The fundamental idea behind the proposed algorithm is to transform each set into a unique number, ensuring that different sets are assigned different numbers. Subsequently, these numbers are sorted to facilitate the identification and removal of duplicates. To optimize runtime efficiency, the LPN of each element is calculated only once at the beginning of the algorithm and then directly utilized in computing the LPNs of the related sets. This approach eliminates the need for repetitive calculations of the LPN for each arc. Furthermore, unlike the SSM, the proposed algorithm does not require the conversion of each set into a vector, streamlining the sorting and duplicate removal process. Once the LPNs for all sets have been computed, any sorting algorithm can be applied to arrange these numbers in ascending or descending order. During the sorting process, duplicate numbers, which correspond to duplicate sets, can be easily identified and eliminated.
3.2. Pseudo-Code
Let S and be the set of the given sets s1, s2, …, and sm for sorting and deduplication, and the union of all sets in S, respectively. One note that the elements of the sets s1, s2, …, and sm are denoted by ej. Let r be the total number of all the elements ej in all the sets, and, accordingly, e1, e2, e3, …, er be all the elements in all the sets, which constitute the set . For instance, in the example with s1 = {e1, e5}, s2 = {e1, e4, e6}, s3 = {e2, e3, e5}, s4 = {e1, e4, e6}, s5 = {e1, e6}, s6 = {e2, e6}, and s7 = {e1, e4, e6}, we have m = 7, S = { s1, s2, …, s7}, { e1, e2, e3, e4, e5, e6}, and, accordingly, r = 6. Let also P be the set of the first r prime numbers and assume that index(e) refers to the index or position of the element e in . The following pseudo-code, Algorithm 1, provides a high-level overview of the proposed algorithm based on LPNs:
| Algorithm 1: Logarithmic Prime Number Approach |
| Input: S = { s1, s2, …, sm} and P = { p1, p2, …, pr}, which means there are a total of r different elements in all the sets. Output: a new S containing the sorted and duplicate-free sets. Step 0:. Let L be an empty map (dictionary) to store the LPNs of elements. Calculate LPNs as l(ei) = log(pi), for i = 1, 2, …, r, and let L(s) = 0 for each set s in S. Step 1: Calculate the LPN for each set s in S using L(s) = L(s) + l(e). Step 2: Sort the sets based on their LPNs. Step 3: Remove duplicate sets in S if their LPNs are equal. |
The best way to understand and illustrate an algorithm is through a simple example. Hence, we use the same example of the sets s1 = {e1, e5}, s2 = {e1, e4, e6}, s3 = {e2, e3, e5}, s4 = {e1, e4, e6}, s5 = {e1, e6}, s6 = {e2, e6}, and s7 = {e1, e4, e6} to detect and remove the duplicates by using Algorithm 1.
Step 0. We have and . Also, we set L(si) = 0, for i = 1, 2, …, 6.
Step 1. We calculate L(s1) = log(2) + log(11) = 1.342423, L(s2) = log(2) + log(7) + log(13) = 2.260071, L(s3) = log(3) + log(5) + log(11) = 2.217484, L(s4) = log(2) + log(7) + log(13) = 2.260071, L(s5) = log(2) + log(13) = 1.414973, L(s6) = log(3) + log(13) = 1.591065, L(s7) = log(2) + log(7) + log(13) = 2.260071.
Step 2. The sorted sets are s1, s5, s6, s3, s2, s4, and s7.
Step 3. As the LPNs for s2, s4, and s7 are equal, s4 and s7 are duplicated and should be removed. Hence, the solution set is {s1, s2, s3, s5, s6}.
This pseudo-code provides a concise representation of the proposed algorithm. The actual implementation may vary based on the programming language and specific requirements of the project. It is noteworthy that the sorting algorithm in Step 2 can be chosen based on the desired time complexity and the characteristics of the dataset [19,28]. The choice of the sorting algorithm does not affect the overall logic of the proposed method. Furthermore, it is worth noting that Euclid’s theorem demonstrates the existence of an infinite number of prime numbers [31]. Consequently, for any sizable set of members, regardless of its length, our proposed method allows for the removal of duplicates by establishing correspondence with LPNs associated with the set’s members.
While the proposed method is efficient for sorting and removing duplicates in sets of a relatively large size, it is important to note that floating-point imprecision can impact its accuracy when dealing with very large sets, such as those containing 10100 distinct elements. The precision required to accurately distinguish between logarithmic values of large prime numbers poses a challenge, which should be considered a limitation of this approach.
3.3. Time Complexity Analysis
We compute the time complexity of our proposed approach based on the pseudo-code provided in Section 3.2. The time complexity of Step 0 to determine the set and calculate the LPNs, l(ei), for I = 1, 2, …, r is of the order of O(r). In Step 1, L(s) for each set, s in S is calculated by iterating through the elements of the set and summing their corresponding LPNs. This operation at worst-case has a time complexity of O(n), where n represents the maximal cardinality of each set in S. Since there are m sets in S, the time complexity of Step 1 is . After obtaining the LPNs for all sets, sorting these numbers using an efficient sorting algorithm, such as quicksort or merge sort, has a time complexity of O(m∙log(m)), where m is the number of sets. Thus, Step 2 is of the order of O(m∙log(m)). The sorting process also facilitates the identification and removal of duplicates, as duplicate sets will have the same LPN.
Therefore, as the steps are executed in parallel, the time complexity of our proposed LPN approach (LPNA) is O(r + m∙n + m∙log(m)). As there are m sets among which the maximum number of elements in a set is n, hence the total number of distinct elements in all the sets is less than m∙n, that is, r < m∙n. As a result, O(r + m∙n + m∙log(m)) = O(m∙n + m∙log(m)), and the following result is at hand.
Lemma 3.
The time complexity of the proposed LPN approach is O(m∙n +m∙log(m)), where m is the number of sets, and n is the maximal number of elements in each set.
Next, we describe briefly the advantages of our proposed method compared to the other two approaches.
3.4. Advantages of the Proposed Algorithm
The analysis of our algorithm, LPNA, and comparison to existing methods, i.e., PCT and SSM, demonstrate several key advantages:
- Efficiency: The LPNA enhances computational efficiency and improves time complexity in processing large datasets. By calculating the LPN of each element only once and directly using it for the related sets, the method reduces redundant computations, which is especially beneficial when the number of sets significantly exceeds the number of elements. Based on the complexity results, Table 4 below provides all the time complexities together to have a more convenient comparison of the algorithms.
 Table 4. The time complexity of approaches.
Table 4. The time complexity of approaches.
The table clearly shows the superiority of our proposed approach compared to the other two available methods in the literature. Moreover, in large enough practical cases, the number of sets, m, can be greater than 10n, and, hence, log(m) > n; accordingly, the time complexity of our proposed algorithm in such cases is O(m∙log(m)), which shows that LPNA outperforms the other approaches more significantly as the problem size increases.
- 2.
- Simplicity: The proposed algorithm streamlines the sorting process and simplifies the overall approach in the following ways. Firstly, by representing sets as LPNs, it reduces the complexity of sorting from handling intricate set structures to merely organizing a list of numbers. This simplification not only makes the sorting operation more efficient but also easier to implement. Secondly, the proposed method avoids the need to convert each set into a vector, thereby simplifying the process of sorting and removing duplicates. This leads to a reduction in memory overhead and enhances the readability and maintainability of the algorithm, making it more straightforward and user-friendly, particularly for large datasets.
- 3.
- Compatibility: The proposed method exhibits high compatibility and flexibility, as it can be integrated with any sorting algorithm. This adaptability allows for tailored implementation and optimization based on specific requirements, making the method suitable for a wide range of applications. Furthermore, this compatibility facilitates the integration of the method with existing systems, enhancing its applicability across various domains.
Although the superiority of our proposed approach to the other discussed methods is clear, in the next section, we provide extensive experimental results to demonstrate the practical efficiency of the proposed method
4. Experimental Results
Here, we first compare all three methods on one thousand randomly generated test problems and use the CPU times to compare the algorithms’ performances. Comparing the final solutions of the algorithms on these test problems is also a practical way to validate the algorithms’ results. Moreover, we discuss several potential applications of our proposed approach in various domains and provide two practical examples of duplicate removal in malware analysis and gene sequence analysis to show how the proposed approach can be adopted in real-world problems.
4.1. Randomly Generated Test Problems
We evaluate our proposed technique, logarithmic prime number approach (LPNA), and the existing methods in the literature outlined in Section 2, pairwise comparison test (PCT) and sequential sort method (SSM), on one thousand test problems to demonstrate the practical efficiency LPNA. All three algorithms are implemented in the MATLAB programming environment. Remembering that m, r, and n denote, respectively, the number of sets, the number of all the different elements in all the sets, and the maximum number of elements in each set, the test problems are generated using the MATLAB command randi ([0 1], m, r), where m (the number of sets in each test problem) and r (the maximum number of elements in each set) are randomly selected integers from the ranges [8000, 10,000] and [20, 25], respectively. Each test problem is represented by a binary matrix with m rows and r columns, where each row is a vector representing a set. A value of 1 in a row indicates that the corresponding element belongs to the set, while a value of 0 indicates that it does not. Hence, the number of nonzero entities in each row, which is less than or equal to r, represents the number of elements in the set associated with that row. This process generates one thousand test problems, each containing m sets with up to r elements. To ensure the presence of duplicate sets in each test problem, we generate a random integer, d, from the range . We then remove d sets from each test problem and replace them with d randomly selected duplicate sets. Moreover, a random number generator with a fixed seed is used to ensure the reproducibility of the results. The numerical computations were conducted on a computer equipped with a 12th Gen Intel(R) Core(TM) i5-12500 processor running at 3.00 GHz and with 32 GB of RAM.
We provide the average times of each algorithm to solve each one-hundred test problem in Table 5 below. The columns in this table are ith (the ith one-hundred test problem), m (the average number of sets in each test problem), r (the average of the maximum number of elements in a set), tPCT (the running time of PCT), tSSM (the running time of SSM), tLPNA (the running time of LPNA), tPCT/tLPNA, and tSSM/tLPNA (the time ratios). The last two columns of this table demonstrate that, on average, our proposed algorithm solved the test problems over 2600 times faster than PCT and more than 220 times faster than SSM. This stark contrast underscores the clear superiority of our proposed algorithm over those from the existing literature.

Table 5.
The results of the comparison of three methods.
While the table provides a clear illustration of the superiority of our proposed algorithm over others, we sought to offer a more intuitive comparison by analyzing the running times of the algorithms across the one thousand random test problems. To achieve this, we utilized the performance profile methodology introduced by Dolan and Moré [32]. This approach considers the ratio of the execution times of each algorithm relative to the best-performing one.
Assuming ti,j for i = 1, 2, 3 represents the running times of PCT, SSM, and LPNA, respectively, for j = 1, 2, …, 1000, the performance ratios are as follows:
for i = 1, 2, 3. The performance of each algorithm is calculated as , where ni is the number of test problems for which ri,j ≤ τ, j = 1, 2, …, 1000.
Figure 1 visually represents the performance profile analysis conducted for the three algorithms. Notably, LPNA emerges as the superior performer, demonstrating faster solution times for all test problems. The horizontal axis highlights instances where LPNA has solved specific problems over 3500 times faster than another algorithm. To facilitate interpretation, four key points, P1, P2, P3, and P4, have been identified on the diagrams. Points P1 and P3 indicate that LPNA solved at least 20% of the test problems more than 481 times faster than SSM and 3442 times faster than PCT, respectively. Similarly, points P2 and P4 demonstrate that LPNA solved at least 50% of the test problems at least 397 times faster than SSM and 3222 times faster than PCT. Overall, in this performance profile, algorithms positioned higher on the diagram are favored over others [32]. This analysis unequivocally highlights the effectiveness of our proposed algorithm compared to others in the literature.
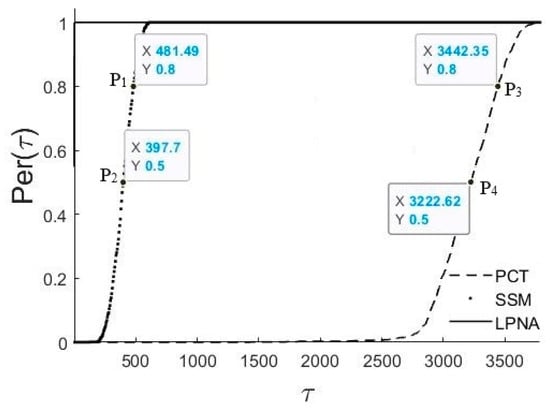
Figure 1.
CPU time–performance profiles for all three approaches.
Next, we explore various potential applications of our proposed method across different fields. We also present two examples, duplicate removal in malware analysis and gene sequence analysis, to demonstrate its practical utility. These examples illustrate how our approach can be effectively applied to real-world challenges.
4.2. Potential Applications and Practical Examples
The proposed method based on LPNs offers a straightforward approach to handling large datasets, enhancing the efficiency of sorting and duplicate removal processes. Its compatibility with various sorting algorithms provides flexibility in implementation and optimization, catering to specific requirements across different domains. This versatility and practicality make the method a valuable asset in fields that require efficient manipulation and analysis of large-scale datasets. Some potential areas of application include the following:
- In cybersecurity, analysts often deal with large datasets of malware samples. Duplicate samples can slow down the analysis and cause redundant work. By removing duplicates, the analysis becomes faster and more efficient, improving detection and mitigation strategies. This way, analysts can quickly identify unique threats. In Example 1, we compare the performance of LPNA and SSM in removing duplicates from malware datasets, showing the effectiveness and efficiency of our proposed algorithm.
- In bioinformatics, researchers frequently work with large datasets of genetic sequences, where duplicates can occur due to sequencing errors or redundant data submissions. Removing these duplicates is essential for accurate comparative analyses, like identifying unique genetic markers or mutations. Duplicates can lead to misleading results when comparing gene sequences to identify disease-related genes. Algorithms are used to filter out redundant sequences, ensuring the integrity of the analysis. In Example 2, we show how our proposed algorithm effectively detects and eliminates duplicate gene sequences, demonstrating its superiority over other algorithms from the literature.
- The method can identify and remove duplicate data entries in large databases, enhancing storage efficiency and data integrity.
- By efficiently sorting and removing duplicate user preferences or item similarities, our proposed method can improve the performance of recommendation algorithms, leading to more precise and relevant suggestions for users.
- The method can be utilized to sort and eliminate duplicate text fragments or documents, supporting tasks like plagiarism detection, document clustering, and information retrieval.
There are several other areas in which a duplicate detection algorithm can be used, such as in experimental evaluation, optimization techniques, machine learning for a dataset preparation, and so forth.
- Example 1. (Duplicate Removal in Malware Analysis)
As an illustration of many applications of the proposed method, let us consider a scenario where a cybersecurity firm specializes in analyzing malware samples to identify new threats and develop appropriate defense mechanisms [33]. Within their analysis pipeline, they amass a significant volume of binary state vectors representing diverse attributes and behaviors of malware, encompassing system calls, file operations, network activities, and memory usage. Recognizing the imperative of streamlining the malware analysis process and enhancing threat detection accuracy, the administration initiates a request for duplicate removal before data-processing ensues. Integral to this process is the extraction of relevant features from the binary state vectors, including the frequency of system calls, file access patterns, network traffic characteristics, and behavioral anomalies. To demonstrate the practicality and efficacy of our proposed approach in real-world applications, we consider the scenario where five hundred thousand 50-tuple binary state vectors are aggregated and subjected to a duplicate removal procedure. Hence, in this example, there are m = 500,000 sets each of which contains at most r = 50 elements.
In our investigation, we apply both our proposed method and the SSM to eliminate duplicates from this dataset, facilitating a comparative analysis to ascertain the correctness and efficacy of each approach. It is noteworthy that, based on experimental findings outlined in Section 4.2, we discern that the PCT is impractical for such large-scale data and would entail significant computational time. Therefore, we exclude this method from our example. The ensuing results are summarized in Table 6 below, with similar columns as in Table 5. Notably, the observed outcomes demonstrate the outstanding superiority of our proposed algorithm compared to the others in a relatively large example. As Table 4 shows, our algorithm solves the example more than 30,000 times faster than SSM.

Table 6.
The final results of Example 1.
- Example 2. (Duplicate Removal in Gene Sequence Analysis)
DNA, or deoxyribonucleic acid, is the hereditary material in almost all living organisms. It is composed of two long strands forming a double helix. Each strand is made up of simpler molecules called nucleotides, which are in turn composed of a sugar, a phosphate group, and a nitrogenous base. The four nitrogenous bases in DNA are adenine (A), cytosine (C), guanine (G), and thymine (T). These bases pair in a specific manner: adenine pairs with thymine (A-T), and cytosine pairs with guanine (C-G). The sequence of these bases encodes genetic information essential for the growth, development, and functioning of living organisms [34,35].
In the area of bioinformatics, researchers often engage in extensive analysis of genetic sequences to identify unique genetic markers or mutations linked to various diseases. Gene sequences are constructed from four nucleotides, represented by the letters A, C, G, and T [34,35]. Imagine a scenario where a genetic research lab is focused on analyzing large datasets of gene sequences to uncover disease-related genes and understand genetic variations. These datasets comprise thousands of gene sequences represented as strings of these four letters.
To ensure the accuracy and efficiency of their comparative analyses, the lab needs to eliminate duplicate sequences that may have arisen due to sequencing errors or redundant data submissions. This duplicate removal process is essential for preventing misleading results and maintaining the integrity of the analysis. They collect one million gene sequences, each represented by a string of 100 nucleotides (letters A, C, G, and T). Hence, in this example, we have m = 1,000,000 sets each with at most r = 100 elements. By applying the duplicate removal algorithm, the lab can streamline its data-processing pipeline, ensuring that unique gene sequences are analyzed.
To simulate such a case, we use the MATLAB function randseq (100) to generate one million random DNA sequences, each consisting of 100 nucleotides. To ensure the presence of duplicate sequences, we remove 15% of the generated sequences and add the same number of randomly selected duplicate sequences. Then, we apply both the LPNA and the SSM to remove the duplicates.
An important note is that these sequences cannot be represented as binary vectors, requiring an adaptation of LPNA for this case. Let e1, e2, …, e100 represent the nucleotides in each sequence, where ei is one of the letters A, C, G, or T for i = 1, 2, …, 100. Define f(ei) as 1, 2, 3, or 4 if ei is A, C, G, or T, respectively. The adapted LPN of element ei is then l(ei) = f(ei)∙log(pi), for i = 1, 2, …, 100, where pi is the ith prime number (e.g., p1 = 2, p2 = 3, p3 = 5, etc.). The LPN for each set (or sequence) remains as given in Equation (1).
We employ both LPNA and SSM in this example, and the final results are presented in Table 7, with similar columns as in Table 5. The table shows that our proposed algorithm can solve such a relatively large-sized example in less than one CPU second, while the SSM needs more than 18 CPU hours to tackle it. It also shows that LPNA solves the example more than 71,000 times faster than SSM. Compared to the previous numerical results, the example vividly illustrates that, as the problem size increases, the performance advantage of our method also grows.

Table 7.
The final results of Example 2.
By showcasing the effectiveness of our proposed approach alongside a conventional method like SSM, we underscore the practical utility and efficiency gains achievable through our method, particularly in the context of large-scale data-processing tasks, such as gene sequence analysis.
5. Conclusions
In this study, we explored various methods for sorting sets and removing duplicates, with a focus on the pairwise comparison test, the sequential sort method, and our newly proposed algorithm based on LPNs. The pairwise comparison test offers a simple approach to duplicate removal but is hindered by high computational complexity, especially in large datasets. The sequential sort method improves efficiency by simultaneously sorting and removing duplicates but requires converting sets into vectors, which can be memory-intensive.
To overcome these challenges, we introduced an innovative algorithm that leverages LPNs to represent each set uniquely, enabling efficient sorting and duplicate removal without the need for pairwise comparisons or set-to-vector conversions. This method utilizes the fundamental theorem of arithmetic to ensure the uniqueness of the LPN representation for each set. We demonstrated the theoretical and practical superiority of our proposed approach compared to the pairwise comparison test and sequential sort method through the complexity analysis results and extensive numerical results obtained on one thousand randomly generated test problems.
The proposed algorithm has the potential to revolutionize the way we handle large-scale datasets across various domains. By providing a more efficient, simple, and compatible approach to sorting and duplicate removal, this method can significantly reduce computational complexity and streamline data-processing pipelines. The impact of this work extends beyond the realm of computer science and mathematics, as it can be applied to diverse fields, such as bioinformatics, recommendation systems, text processing, and more. The algorithm’s ability to efficiently process massive datasets can lead to breakthroughs in data-driven research, enabling faster and more accurate insights that drive innovation and discovery. Moreover, the compatibility of the proposed method with various sorting algorithms opens opportunities for tailored implementation and optimization based on specific domain requirements. This flexibility makes the algorithm a valuable tool for researchers and practitioners seeking to push the boundaries of data-processing and analysis.
Future research will focus on conducting comprehensive experimental evaluations to compare the performance of our method with other advanced techniques, exploring optimization strategies to further enhance its efficiency, investigating extensions to accommodate more complex data structures, and examining its integration with other algorithms for holistic data processing and analysis solutions. By building upon the foundation laid by this work, we aim to contribute to the development of cutting-edge data-processing techniques that can tackle the ever-growing challenges of the big-data era.
Author Contributions
Conceptualization, W.-C.Y. and M.F.-e.; methodology, W.-C.Y.; validation, W.-C.Y. and M.F.-e.; formal analysis, W.-C.Y. and M.F.-e.; investigation, W.-C.Y. and M.F.-e.; resources, W.-C.Y. and M.F.-e.; data curation, W.-C.Y. and M.F.-e.; writing—original draft preparation, W.-C.Y. and M.F.-e.; writing—review and editing, M.F.-e.; visualization, W.-C.Y. and M.F.-e.; project administration, W.-C.Y.; funding acquisition, W.-C.Y. and M.F.-e. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by NTHU under grant 113Q2714E1 titled ‘A Study on Fairness-Constrained Knee Osteoarthritis Severity Classification Model Based on Deep Learning and Swarm Intelligence Optimization’. This research was also funded in part by the Ministry of Science and Technology, R.O.C., grant numbers MOST 102-2221-E-007-086-MY3 and MOST 104-2221-E-007-061-MY3; and in part by FAPESP, grant number 2023/13667-5.
Data Availability Statement
Data sharing does not apply to this article, as no new data were collected or studied in this study.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Selvi, P. An Analysis on Removal of Duplicate Records using Different Types of Data Mining Techniques: A Survey. Int. J. Comput. Sci. Mob. Comput. 2017, 6, 38–42. [Google Scholar]
- Forghani-Elahabad, M.; Francesquini, E. Usage of task and data parallelism for finding the lower boundary vectors in a stochastic-flow network. Reliab. Eng. Syst. Saf. 2023, 238, 109417. [Google Scholar] [CrossRef]
- Andriyanov, N.; Dementev, V.; Tashlinskiy, A.; Vasiliev, K. The Study of Improving the Accuracy of Convolutional Neural Networks in Face Recognition Tasks. In Pattern Recognition; ICPR International Workshops and Challenges. ICPR 2021. Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2021; Volume 12665. [Google Scholar] [CrossRef]
- Marszałek, Z. Parallelization of Modified Merge Sort Algorithm. Symmetry 2017, 9, 176. [Google Scholar] [CrossRef]
- Raj, D.; Remya, R. An Efficient Technique for Removing Duplicates in A Dataset. Int. J. Eng. Res. Technol. 2013, 2, 3889–3893. [Google Scholar]
- Svitov, D.; Alyamkin, S. Margindistillation: Distillation for margin-based softmax. arXiv 2020, arXiv:2003.02586. [Google Scholar]
- Sadanandan, I.T.; Chitturi, B. Optimal Algorithms for Sorting Permutations with Brooms. Algorithms 2022, 15, 220. [Google Scholar] [CrossRef]
- Yeh, W.C. Novel Binary-Addition Tree Algorithm (BAT) for Binary-State Network Reliability Problem. Reliab. Eng. Syst. Saf. 2021, 208, 107448. [Google Scholar] [CrossRef]
- Niu, Y.F.; Shao, F.M. A practical bounding algorithm for computing two-terminal reliability based on decomposition technique. Comput. Math. Appl. 2011, 61, 2241–2246. [Google Scholar] [CrossRef]
- Dhivyabharathi, G.V.; Kumaresan, S. A survey on duplicate record detection in real world data. In Proceedings of the 2016 3rd International Conference on Advanced Computing and Communication Systems (ICACCS), Coimbatore, India, 22–23 January 2016. [Google Scholar] [CrossRef]
- Dong, H.; Ge, Y.; Zhou, R.; Wang, H. An Improved Sorting Algorithm for Periodic PRI Signals Based on Congruence Transform. Symmetry 2024, 16, 398. [Google Scholar] [CrossRef]
- Huang, D.H. An algorithm to generate all d-lower boundary points for a stochastic flow network using dynamic flow constraints. Reliab. Eng. Syst. Saf. 2024, 249, 110217. [Google Scholar] [CrossRef]
- Forghani-elahabad, M.; Alsalami, O.M. Using a Node–Child Matrix to Address the Quickest Path Problem in Multistate Flow Networks under Transmission Cost Constraints. Mathematics 2023, 11, 4889. [Google Scholar] [CrossRef]
- Xu, X.Z.; Niu, Y.F.; Song, Y.F. Computing the reliability of a stochastic distribution network subject to budget constraint. Reliab. Eng. Syst. Saf. 2021, 216, 107947. [Google Scholar] [CrossRef]
- Yeh, W.C. Search for All d-Mincuts of a Limited-Flow Network. Comput. Oper. Res. 2002, 29, 1843–1858. [Google Scholar] [CrossRef]
- Niu, Y.F.; Wei, J.H.; Xu, X.Z. Computing the Reliability of a Multistate Flow Network with Flow Loss Effect. IEEE Trans. Reliab. 2023, 72, 1432–1441. [Google Scholar] [CrossRef]
- Wang, Q.; Jaffres-Runser, K.; Xu, Y.; Scharbarg, J.-L.; An, Z.; Fraboul, C. TDMA Versus CSMA/CA for Wireless Multihop Communications: A Stochastic Worst-Case Delay Analysis. IEEE Trans. Ind. Inform. 2017, 13, 877–887. [Google Scholar] [CrossRef]
- Sosa-Holwerda, A.; Park, O.-H.; Albracht-Schulte, K.; Niraula, S.; Thompson, L.; Oldewage-Theron, W. The Role of Artificial Intelligence in Nutrition Research: A Scoping Review. Nutrients 2024, 16, 2066. [Google Scholar] [CrossRef] [PubMed]
- Heinrich, M.; Valeske, B.; Rabe, U. Efficient Detection of Defective Parts with Acoustic Resonance Testing Using Synthetic Training Data. Appl. Sci. 2022, 12, 7648. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Shu, J.; Wu, C.H.; Zhou, L.-H.; Song, X.R. Island microgrid based on distributed photovoltaic generation. Power Syst. Prot. Control 2014, 42, 55–61. [Google Scholar]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2013, 18, 577–601. [Google Scholar] [CrossRef]
- Narushynska, O.; Teslyuk, V.; Doroshenko, A.; Arzubov, M. Data Sorting Influence on Short Text Manual Labeling Quality for Hierarchical Classification. Big Data Cogn. Comput. 2024, 8, 41. [Google Scholar] [CrossRef]
- Bureš, V.; Cabal, J.; Čech, P.; Mls, K.; Ponce, D. The Influence of Criteria Selection Method on Consistency of Pairwise Comparison. Mathematics 2020, 8, 2200. [Google Scholar] [CrossRef]
- Basheer Ahmed, M.I.; Zaghdoud, R.; Ahmed, M.S.; Sendi, R.; Alsharif, S.; Alabdulkarim, J.; Albin Saad, B.A.; Alsabt, R.; Rahman, A.; Krishnasamy, G. A Real-Time Computer Vision Based Approach to Detection and Classification of Traffic Incidents. Big Data Cogn. Comput. 2023, 7, 22. [Google Scholar] [CrossRef]
- Krivulin, N.; Prinkov, A.; Gladkikh, I. Using Pairwise Comparisons to Determine Consumer Preferences in Hotel Selection. Mathematics 2022, 10, 730. [Google Scholar] [CrossRef]
- Huang, D.-H.; Huang, C.-F.; Lin, Y.-K. Reliability Evaluation for a Stochastic Flow Network Based on Upper and Lower Boundary Vectors. Mathematics 2019, 7, 1115. [Google Scholar] [CrossRef]
- Dodevska, Z.; Radovanović, S.; Petrović, A.; Delibašić, B. When Fairness Meets Consistency in AHP Pairwise Comparisons. Mathematics 2023, 11, 604. [Google Scholar] [CrossRef]
- Cheon, J.; Son, J.; Ahn, Y. Economic and environmental factor-integrated optimal model for plastic-waste sorting. J. Ind. Eng. Chem. 2024; in press. [Google Scholar] [CrossRef]
- Qian, K.; Fachrizal, R.; Munkhammar, J.; Ebel, T.; Adam, R. Large-scale EV charging scheduling considering on-site PV generation by combining an aggregated model and sorting-based methods. Sustain. Cities Soc. 2024, 107, 105453. [Google Scholar] [CrossRef]
- Liu, T.; Chen, X.; Peng, Q.; Peng, J.; Meng, J. An enhanced sorting method for retired battery with feature selection and multiple clustering. J. Energy Storage 2024, 87, 111422. [Google Scholar] [CrossRef]
- Carbó-Dorca, R. On Prime Numbers Generation and Pairing. Int. J. Innov. Res. Sci. Eng. Stud. (IJIRSES) 2023, 3, 12–17. [Google Scholar]
- Dolan, E.D.; Moré, J.J. Benchmarking optimization software with performance profiles. Math. Program. 2002, 91, 201–213. [Google Scholar] [CrossRef]
- Ramamoorthy, J.; Gupta, K.; Shashidhar, N.K.; Varol, C. Linux IoT Malware Variant Classification Using Binary Lifting and Opcode Entropy. Electronics 2024, 13, 2381. [Google Scholar] [CrossRef]
- Brown, T.A. Gene Cloning and DNA Analysis: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Laforgia, A.; Inchingolo, A.D.; Piras, F.; Colonna, V.; Giorgio, R.V.; Carone, C.; Rapone, B.; Malcangi, G.; Inchingolo, A.M.; Inchingolo, F.; et al. Therapeutic Strategies and Genetic Implications for Periodontal Disease Management: A Systematic Review. Int. J. Mol. Sci. 2024, 25, 7217. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).