Improving Machine Learning Predictive Capacity for Supply Chain Optimization through Domain Adversarial Neural Networks
Abstract
1. Introduction
- Implementing DANN for data generalization on small data with high variation.
- Enhancing the capability of the ML model to forecast the sales.
- Utilizing the transfer learning approach on a dataset to predict the sales of different products (different target variables).
- Implication of result for supply chain optimization using the sales prediction.
2. Related Work
2.1. Datasets in Supply Chain
2.2. Models in a High Variable and Limited Data Framework
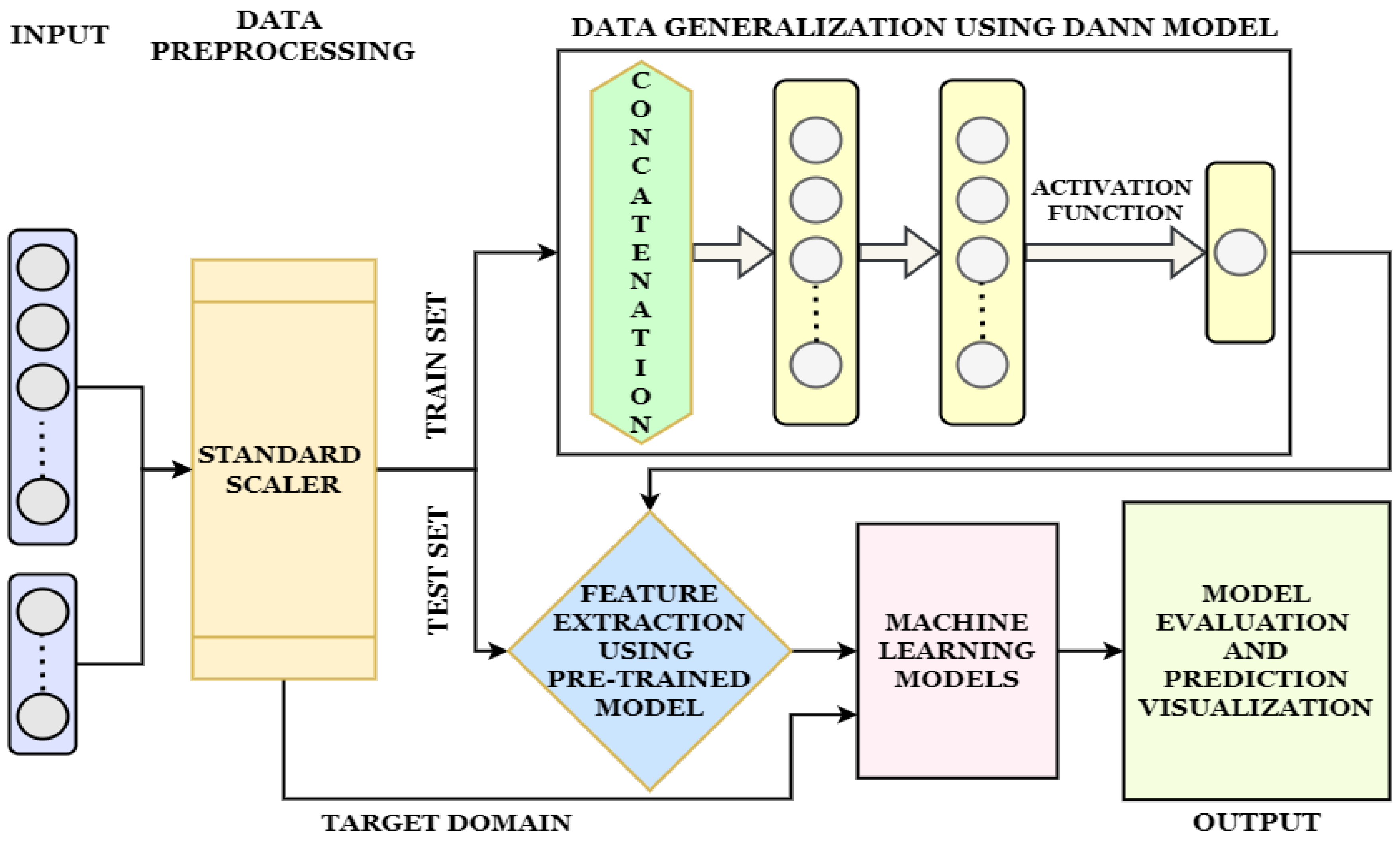
3. Proposed Methodology
| Algorithm 1 Pipeline of Proposed Methodology |
|
3.1. Dataset Description
3.2. Data Handling and Analysis
Non-Stationary Testing of the Dataset
3.3. Data Preprocessing
3.4. Domain Adversarial Neural Network
3.5. Machine Learning Models
3.5.1. Linear Regression Model
3.5.2. Support Vector Regressor Model
3.5.3. Decision Tree Regressor Model
3.5.4. Random Forest Regressor Model
3.5.5. Extreme Gradient Boost XGBoost Regressor Model
3.6. Performance Parameters of Model
4. Results and Discussion
4.1. Results of DANN Model for Data Generalization
4.2. Comparative Study of Outcomes of Various Machine Learning Models
4.3. Sales Prediction for Supply Chain Optimization
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DANN | Domain Adversarial Neural Networks |
| SCO | Supply Chain Optimization |
| SCM | Supply Chain Management |
| FMCG | Fast-Moving Consumer Goods |
| ML | Machine Learning |
| DL | Deep Learning |
| RNN | Recurrent Neural Network |
| SVR | Support Vector Regression |
| RF | Random Forest |
| DTR | Decision Tree Regressor |
| RMSE | Root Mean Square Error |
| MSE | Mean Square Error |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| XGBoost | Extreme Gradient Boosting |
| KPSS | Kwiatkowski–Phillips–Schmidt–Shin |
| ReLU | Rectified Linear Unit |
References
- McCarthy, T.M.; Golicic, S.L. Implementing collaborative forecasting to improve supply chain performance. Int. J. Phys. Distrib. Logist. Manag. 2002, 32, 431–454. [Google Scholar] [CrossRef]
- Bourland, K.E.; Powell, S.G.; Pyke, D.F. Exploiting timely demand information to reduce inventories. Eur. J. Oper. Res. 1996, 92, 239–253. [Google Scholar] [CrossRef]
- Tadayonrad, Y.; Ndiaye, A.B. A new key performance indicator model for demand forecasting in inventory management considering supply chain reliability and seasonality. Supply Chain Anal. 2023, 3, 100026. [Google Scholar] [CrossRef]
- Arunachalam, D.; Kumar, N.; Kawalek, J.P. Understanding big data analytics capabilities in supply chain management: Unravelling the issues, challenges and implications for practice. Transp. Res. Part E Logist. Transp. Rev. 2018, 114, 416–436. [Google Scholar] [CrossRef]
- L’heureux, A.; Grolinger, K.; Elyamany, H.F.; Capretz, M.A. Machine learning with big data: Challenges and approaches. IEEE Access 2017, 5, 7776–7797. [Google Scholar] [CrossRef]
- Zhu, L.; Spachos, P.; Pensini, E.; Plataniotis, K.N. Deep learning and machine vision for food processing: A survey. Curr. Res. Food Sci. 2021, 4, 233–249. [Google Scholar] [CrossRef]
- Al-Sahaf, H.; Bi, Y.; Chen, Q.; Lensen, A.; Mei, Y.; Sun, Y.; Tran, B.; Xue, B.; Zhang, M. A survey on evolutionary machine learning. J. R. Soc. N. Z. 2019, 49, 205–228. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, C.; Liu, F.; Qiu, Z.; He, Y. Application of deep learning in food: A review. Compr. Rev. Food Sci. Food Saf. 2019, 18, 1793–1811. [Google Scholar] [CrossRef]
- Bertolini, M.; Mezzogori, D.; Neroni, M.; Zammori, F. Machine Learning for industrial applications: A comprehensive literature review. Expert Syst. Appl. 2021, 175, 114820. [Google Scholar] [CrossRef]
- Hu, H.; Xu, J.; Liu, M.; Lim, M.K. Vaccine supply chain management: An intelligent system utilizing blockchain, IoT and machine learning. J. Bus. Res. 2023, 156, 113480. [Google Scholar] [CrossRef]
- Guo, H.; Zou, T. Cross-border e-commerce platform logistics and supply chain network optimization based on deep learning. Mob. Inf. Syst. 2022, 2022, 2203322. [Google Scholar] [CrossRef]
- Kaya, S.K.; Yildirim, Ö. A prediction model for automobile sales in Turkey using deep neural networks. Endüstri Mühendisliği 2020, 31, 57–74. [Google Scholar]
- Giri, C.; Chen, Y. Deep learning for demand forecasting in the fashion and apparel retail industry. Forecasting 2022, 4, 565–581. [Google Scholar] [CrossRef]
- Kilimci, Z.H.; Akyuz, A.O.; Uysal, M.; Akyokus, S.; Uysal, M.O.; Atak Bulbul, B.; Ekmis, M.A. An improved demand forecasting model using deep learning approach and proposed decision integration strategy for supply chain. Complexity 2019, 2019, 9067367. [Google Scholar] [CrossRef]
- Chien, C.F.; Lin, Y.S.; Lin, S.K. Deep reinforcement learning for selecting demand forecast models to empower Industry 3.5 and an empirical study for a semiconductor component distributor. Int. J. Prod. Res. 2020, 58, 2784–2804. [Google Scholar] [CrossRef]
- Qi, M.; Shi, Y.; Qi, Y.; Ma, C.; Yuan, R.; Wu, D.; Shen, Z.J. A practical end-to-end inventory management model with deep learning. Manag. Sci. 2023, 69, 759–773. [Google Scholar] [CrossRef]
- Amellal, I.; Amellal, A.; Seghiouer, H.; Ech-Charrat, M. An integrated approach for modern supply chain management: Utilizing advanced machine learning models for sentiment analysis, demand forecasting, and probabilistic price prediction. Decis. Sci. Lett. 2024, 13, 237–248. [Google Scholar] [CrossRef]
- Alshurideh, M.T.; Hamadneh, S.; Alzoubi, H.M.; Al Kurdi, B.; Nuseir, M.T.; Al Hamad, A. Empowering Supply Chain Management System with Machine Learning and Blockchain Technology. In Cyber Security Impact on Digitalization and Business Intelligence: Big Cyber Security for Information Management: Opportunities and Challenges; Alzoubi, H.M., Alshurideh, M.T., Ghazal, T.M., Eds.; Springer International Publishing: Cham, Switzerland, 2024; pp. 335–349. [Google Scholar] [CrossRef]
- Dzalbs, I.; Kalganova, T. Accelerating supply chains with Ant Colony Optimization across a range of hardware solutions. Comput. Ind. Eng. 2020, 147, 106610. [Google Scholar] [CrossRef] [PubMed]
- Constante, F.; Silva, F.; Pereira, A. DataCo smart supply chain for big data analysis. Mendeley Data, 13 March 2019; Version 5. [Google Scholar] [CrossRef]
- Siniosoglou, I.; Xouveroudis, K.; Argyriou, V.; Lagkas, T.; Goudos, S.K.; Psannis, K.E.; Sarigiannidis, P. Evaluating the effect of volatile federated timeseries on modern DNNs: Attention over long/short memory. In Proceedings of the 2023 12th International Conference on Modern Circuits and Systems Technologies (MOCAST), Athens, Greece, 28–30 June 2023; pp. 1–6. [Google Scholar]
- Wasi, A.T.; Islam, M.; Akib, A.R. SupplyGraph: A Benchmark Dataset for Supply Chain Planning using Graph Neural Networks. arXiv 2024, arXiv:2401.15299. [Google Scholar]
- Zhang, X.; Wang, J.; Chen, J.; Liu, Z.; Feng, Y. Retentive multimodal scale-variable anomaly detection framework with limited data groups for liquid rocket engine. Measurement 2022, 205, 112171. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, Z.; Fu, X.; Wei, X.; Liu, T.; Yan, R.; Qin, Z.; Zhang, J. A Viewpoint Adaptation Ensemble Contrastive Learning framework for vessel type recognition with limited data. Expert Syst. Appl. 2024, 238, 122191. [Google Scholar] [CrossRef]
- Deng, S.; Sprangers, O.; Li, M.; Schelter, S.; de Rijke, M. Domain Generalization in Time Series Forecasting. ACM Trans. Knowl. Discov. Data 2024, 18, 1–24. [Google Scholar] [CrossRef]
- Hayashi, S.; Tanimoto, A.; Kashima, H. Long-term prediction of small time-series data using generalized distillation. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; pp. 1–8. [Google Scholar]
- Han, H.; Liu, Z.; Barrios Barrios, M.; Li, J.; Zeng, Z.; Sarhan, N.; Awwad, E.M. Time series forecasting model for non-stationary series pattern extraction using deep learning and GARCH modeling. J. Cloud Comput. 2024, 13, 2. [Google Scholar] [CrossRef]
- Javeri, I.Y.; Toutiaee, M.; Arpinar, I.B.; Miller, J.A.; Miller, T.W. Improving neural networks for time-series forecasting using data augmentation and AutoML. In Proceedings of the 2021 IEEE Seventh International Conference on Big Data Computing Service and Applications (BigDataService), Oxford, UK, 23–26 August 2021; pp. 1–8. [Google Scholar]
- Borovykh, A.; Oosterlee, C.W.; Bohté, S.M. Generalization in fully-connected neural networks for time series forecasting. J. Comput. Sci. 2019, 36, 101020. [Google Scholar] [CrossRef]
- Martínez, F.; Frías, M.P.; Pérez-Godoy, M.D.; Rivera, A.J. Time series forecasting by generalized regression neural networks trained with multiple series. IEEE Access 2022, 10, 3275–3283. [Google Scholar] [CrossRef]
- Shrestha, D.L.; Solomatine, D.P. Machine learning approaches for estimation of prediction interval for the model output. Neural Netw. 2006, 19, 225–235. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R. Efficient Learning Machines: Theories, Concepts, and Applications for Engineers and System Designers; Apress: Berkeley, CA, USA, 2015. [Google Scholar]
- Reddy, P.S.M. Decision tree regressor compared with random forest regressor for house price prediction in mumbai. J. Surv. Fish. Sci. 2023, 10, 2323–2332. [Google Scholar]
- Nevendra, M.; Singh, P. Empirical investigation of hyperparameter optimization for software defect count prediction. Expert Syst. Appl. 2022, 191, 116217. [Google Scholar] [CrossRef]
- Weber, F.; Schütte, R. A domain-oriented analysis of the impact of machine learning—The case of retailing. Big Data Cogn. Comput. 2019, 3, 11. [Google Scholar] [CrossRef]
- Syam, N.; Sharma, A. Waiting for a sales renaissance in the fourth industrial revolution: Machine learning and artificial intelligence in sales research and practice. Ind. Mark. Manag. 2018, 69, 135–146. [Google Scholar] [CrossRef]
- Marr, B. Artificial Intelligence in Practice: How 50 Successful Companies Used AI and Machine Learning to Solve Problems; John Wiley & Sons: Chichester, UK, 2019. [Google Scholar]






| Sr. No. | Product ID | Stationarity | KPSS Result (p-Value) | Sr. No. | Product ID | Stationarity | KPSS Result (p-Value) |
|---|---|---|---|---|---|---|---|
| 1 | AT5X5K | NS | 0.0419 | 16 | POV001L24P | NS | 0.01 |
| 2 | ATN01K24P | S | 0.1 | 17 | POV002L09P | S | 0.1 |
| 3 | ATN02K12P | S | 0.1 | 18 | POV005L04P | S | 0.1 |
| 4 | ATWWP001K24P | NS | 0.046 | 19 | POV500M24P | S | 0.0993 |
| 5 | ATWWP002K12P | S | 0.1 | 20 | SE200G24P | NS | 0.01 |
| 6 | MAR01K24P | S | 0.1 | 21 | SE500G24P | NS | 0.019 |
| 7 | MAR02K12P | NS | 0.049 | 22 | SOP001L12P | NS | 0.025 |
| 8 | MASR025K | S | 0.1 | 23 | SOS001L12P | NS | 0.01 |
| 9 | POP001L12P.1 | S | 0.1 | 24 | SOS002L09P | NS | 0.022 |
| 10 | POP001L12P | S | 0.089 | 25 | SOS003L04P | NS | 0.0254 |
| 11 | POP002L09P | S | 0.074 | 26 | SOS005L04P | NS | 0.01 |
| 12 | POP005L04P | NS | 0.048 | 27 | SOS008L02P | NS | 0.01 |
| 13 | POP500M24P | S | 0.826 | 28 | SOS250M48P | Non-Stationary | 0.025 |
| 14 | POPF01L12P | NS | 0.036 | 29 | SOS500M24P | NS | 0.05 |
| 15 | MAHS025K | NS | 0.029 |
| Sr. No. | Product ID | Score | ||||
|---|---|---|---|---|---|---|
| 1 | AT5X5K | 0.014 | 0.118 | 0.985 | 0.078 | 0.28 |
| 2 | ATN01K24P | 0.01 | 0.102 | 0.989 | 0.077 | 0.24 |
| 3 | ATN02K12P | 0.027 | 0.164 | 0.972 | 0.096 | 0.72 |
| 4 | MAR01K24P | 0.011 | 0.104 | 0.988 | 0.082 | 0.34 |
| 5 | MAR02K12P | 0.012 | 0.109 | 0.987 | 0.076 | 0.24 |
| 6 | POP001L12P.1 | 0.008 | 0.089 | 0.991 | 0.06 | 0.44 |
| 7 | POP001L12P | 0.022 | 0.148 | 0.977 | 0.084 | 0.58 |
| 8 | POP002L09P | 0.016 | 0.126 | 0.983 | 0.094 | 0.345 |
| 9 | POPF01L12P | 0.012 | 0.109 | 0.987 | 0.074 | 0.335 |
| 10 | POV001L24P | 0.028 | 0.167 | 0.971 | 0.107 | 0.32 |
| 11 | SE200G24P | 0.015 | 0.122 | 0.984 | 0.08 | 0.265 |
| 12 | SE500G24P | 0.015 | 0.122 | 0.984 | 0.089 | 0.328 |
| 13 | SOP001L12P | 0.0107 | 0.103 | 0.989 | 0.085 | 0.226 |
| 14 | SOS001L12P | 0.008 | 0.089 | 0.991 | 0.073 | 0.38 |
| 15 | SOS008L02P | 0.011 | 0.105 | 0.988 | 0.078 | 0.24 |
| 16 | SOS002L09P | 0.04 | 0.197 | 0.956 | 0.13 | 0.49 |
| 17 | SOS003L04P | 0.017 | 0.13 | 0.982 | 0.102 | 0.38 |
| 18 | SOS005L04P | 0.008 | 0.089 | 0.991 | 0.073 | 0.18 |
| Model | Product ID | Performance Metrics | ||||
|---|---|---|---|---|---|---|
| Score | ||||||
| Linear Regression | ATWWP001K24P | 0.014 | 0.121 | 0.985 | 0.085 | 0.526 |
| ATWWP002K12P | 0.011 | 0.109 | 0.988 | 0.075 | 0.572 | |
| MAHS025K | 0.012 | 0.11 | 0.987 | 0.072 | 0.253 | |
| MASR025K | 0.036 | 0.18 | 0.963 | 0.143 | 0.41 | |
| POP005L04P | 0.039 | 0.198 | 0.96 | 0.147 | 0.57 | |
| POP500M24P | 0.125 | 0.353 | 0.874 | 0.25 | 0.74 | |
| POV002L09P | 0.042 | 0.205 | 0.957 | 0.161 | 0.72 | |
| POV005L04P | 0.03 | 0.175 | 0.969 | 0.136 | 0.613 | |
| POV500M24P | 0.025 | 0.16 | 0.974 | 0.124 | 0.6 | |
| SOS250M48P | 0.06 | 0.245 | 0.939 | 0.175 | 0.523 | |
| SOS500M24P | 0.081 | 0.284 | 0.918 | 0.223 | 0.575 | |
| SVR (Linear kernel) | ATWWP001K24P | 0.018 | 0.136 | 0.98 | 0.106 | 0.56 |
| ATWWP002K12P | 0.015 | 0.12 | 0.984 | 0.085 | 0.58 | |
| MAHS025K | 0.012 | 0.11 | 0.987 | 0.074 | 0.254 | |
| MASR025K | 0.038 | 0.19 | 0.969 | 0.14 | 0.4 | |
| POP005L04P | 0.04 | 0.2 | 0.959 | 0.147 | 0.52 | |
| POP500M24P | 0.127 | 0.35 | 0.87 | 0.25 | 0.81 | |
| POV002L09P | 0.045 | 0.21 | 0.954 | 0.163 | 0.68 | |
| POV005L04P | 0.032 | 0.17 | 0.967 | 0.135 | 0.54 | |
| POV500M24P | 0.026 | 0.16 | 0.973 | 0.127 | 0.65 | |
| SOS250M48P | 0.061 | 0.24 | 0.938 | 0.16 | 0.55 | |
| SOS500M24P | 0.082 | 0.28 | 0.917 | 0.22 | 0.57 | |
| SVR (RBF kernel) | ATWWP001K24P | 0.023 | 0.152 | 0.976 | 0.11 | 0.69 |
| ATWWP002K12P | 0.112 | 0.335 | 0.887 | 0.11 | 0.55 | |
| MAHS025K | 0.053 | 0.23 | 0.966 | 0.107 | 0.26 | |
| MASR025K | 0.142 | 0.377 | 0.857 | 0.14 | 0.34 | |
| POP005L04P | 0.078 | 0.28 | 0.921 | 0.131 | 0.5 | |
| POP500M24P | 0.06 | 0.26 | 0.932 | 0.17 | 0.76 | |
| POV002L09P | 0.034 | 0.18 | 0.965 | 0.11 | 0.31 | |
| POV005L04P | 0.031 | 0.17 | 0.968 | 0.1 | 0.34 | |
| POV500M24P | 0.029 | 0.17 | 0.97 | 0.1 | 0.64 | |
| SOS250M48P | 0.063 | 0.25 | 0.936 | 0.142 | 0.39 | |
| SOS500M24P | 0.046 | 0.214 | 0.953 | 0.14 | 0.49 | |
| XGBoost Regressor | ATWWP001K24P | 1.17 × | 0.001 | 0.999 | 7.5 × | 0.003 |
| ATWWP002K12P | 9.31 × | 9.6 × | 0.999 | 5.8 × | 0.0031 | |
| MAHS025K | 5.65 × | 7.5 × | 0.999 | 4.8 × | 0.0025 | |
| MASR025K | 1.14 × | 0.001 | 0.999 | 7.32 × | 0.0059 | |
| POP005L04P | 9.17 × | 9.5 × | 0.999 | 6.4 × | 0.0039 | |
| POP500M24P | 1.25 × | 0.0011 | 0.999 | 8 × | 0.017 | |
| POV002L09P | 9.55 × | 9.7 × | 0.999 | 7.1 × | 0.0028 | |
| POV005L04P | 1.59 × | 1.26 × | 0.999 | 8.7 × | 0.0048 | |
| POV500M24P | 1.36 × | 0.0011 | 0.999 | 8.4 × | 0.0044 | |
| SOS250M48P | 1.1 × | 0.001 | 0.999 | 7 × | 0.0027 | |
| SOS500M24P | 9 × | 9.5 × | 0.999 | 6.8 × | 0.0036 | |
| Model | Product ID | Best Hyperparameters 1 | Performance Metrics | ||||
|---|---|---|---|---|---|---|---|
| Score | |||||||
| DTR | ATWWP001K24P | [8; 2; 4] | 0.011 | 0.108 | 0.988 | 0.048 | 0.19 |
| ATWWP002K12P | [7; 3; 4] | 0.014 | 0.12 | 0.985 | 0.045 | 0.283 | |
| MAHS025K | [8; 1; 6] | 0.005 | 0.076 | 0.994 | 0.032 | 0.118 | |
| MASR025K | [5; 1; 2] | 0.015 | 0.123 | 0.984 | 0.087 | 0.55 | |
| POP005L04P | [7; 1; 3] | 0.006 | 0.079 | 0.993 | 0.044 | 0.395 | |
| POP500M24P | [6; 3; 6] | 0.04 | 0.204 | 0.958 | 0.132 | 0.83 | |
| POV002L09P | [6; 2; 4] | 0.016 | 0.129 | 0.983 | 0.094 | 0.59 | |
| POV005L04P | [6; 4; 4] | 0.021 | 0.147 | 0.978 | 0.088 | 0.386 | |
| POV500M24P | [6; 2; 3] | 0.008 | 0.092 | 0.991 | 0.067 | 0.29 | |
| SOS250M48P | [6; 3; 4] | 0.025 | 0.16 | 0.974 | 0.079 | 0.42 | |
| SOS500M24P | [5; 3; 5] | 0.063 | 0.252 | 0.936 | 0.171 | 0.81 | |
| RF | ATWWP001K24P | [8; 1; 2; 100] | 0.005 | 0.072 | 0.994 | 0.03 | 0.13 |
| ATWWP002K12P | [5; 2; 2; 100] | 0.0135 | 0.116 | 0.986 | 0.049 | 0.29 | |
| MAHS025K | [8; 1; 4; 100] | 0.004 | 0.07 | 0.995 | 0.034 | 0.12 | |
| MASR025K | [8; 1; 2; 300] | 0.006 | 0.083 | 0.993 | 0.04 | 0.27 | |
| POP005L04P | [8; 1; 5; 100] | 0.015 | 0.12 | 0.984 | 0.069 | 0.42 | |
| POP500M24P | [8; 1; 3; 100] | 0.023 | 0.153 | 0.976 | 0.108 | 0.69 | |
| POV002L09P | [8; 1; 3; 100] | 0.01 | 0.1 | 0.989 | 0.071 | 0.43 | |
| POV005L04P | [7; 1; 2; 100] | 0.005 | 0.076 | 0.994 | 0.054 | 0.21 | |
| POV500M24P | [8; 1; 3; 300] | 0.004 | 0.069 | 0.995 | 0.051 | 0.19 | |
| SOS250M48P | [7; 1; 3; 100] | 0.011 | 0.107 | 0.988 | 0.057 | 0.27 | |
| SOS500M24P | [6; 2; 5; 100] | 0.038 | 0.195 | 0.961 | 0.133 | 0.77 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sayyad, J.; Attarde, K.; Yilmaz, B. Improving Machine Learning Predictive Capacity for Supply Chain Optimization through Domain Adversarial Neural Networks. Big Data Cogn. Comput. 2024, 8, 81. https://doi.org/10.3390/bdcc8080081
Sayyad J, Attarde K, Yilmaz B. Improving Machine Learning Predictive Capacity for Supply Chain Optimization through Domain Adversarial Neural Networks. Big Data and Cognitive Computing. 2024; 8(8):81. https://doi.org/10.3390/bdcc8080081
Chicago/Turabian StyleSayyad, Javed, Khush Attarde, and Bulent Yilmaz. 2024. "Improving Machine Learning Predictive Capacity for Supply Chain Optimization through Domain Adversarial Neural Networks" Big Data and Cognitive Computing 8, no. 8: 81. https://doi.org/10.3390/bdcc8080081
APA StyleSayyad, J., Attarde, K., & Yilmaz, B. (2024). Improving Machine Learning Predictive Capacity for Supply Chain Optimization through Domain Adversarial Neural Networks. Big Data and Cognitive Computing, 8(8), 81. https://doi.org/10.3390/bdcc8080081








