Abstract
Cardiovascular diseases (CVDs) are highly prevalent, sudden onset, and relatively fatal, posing a significant public health burden. Long-term dynamic electrocardiography, which can continuously record the long-term dynamic ECG activities of individuals in their daily lives, has high research value. However, ECG signals are weak and highly susceptible to external interference, which may lead to false alarms and misdiagnosis, affecting the diagnostic efficiency and the utilization rate of healthcare resources, so research on the quality of dynamic ECG signals is extremely necessary. Aimed at the above problems, this paper proposes a dynamic ECG signal quality assessment method based on CNN and LSTM that divides the signal into three quality categories: the signal of the Q1 category has a lower noise level, which can be used for reliable diagnosis of arrhythmia, etc.; the signal of the Q2 category has a higher noise level, but it still contains information that can be used for heart rate calculation, HRV analysis, etc.; and the signal of the Q3 category has a higher noise level that can interfere with the diagnosis of cardiovascular disease and should be discarded or labeled. In this paper, we use the widely recognized MIT-BIH database, based on which the model is applied to realistically collect exercise experimental data to assess the performance of the model in dealing with real-world situations. The model achieves an accuracy of 98.65% on the test set, a macro-averaged F1 score of 98.5%, and a high F1 score of 99.71% for the prediction of Q3 category signals, which shows that the model has good accuracy and generalization performance.
1. Introduction
Cardiovascular diseases (CVDs) are highly prevalent, sudden onset, and relatively fatal, posing a significant public health burden. According to the World Health Organization (WHO) 2019 statistics, CVD is the largest cause of death globally, with ischaemic heart disease topping the list, accounting for 16% of all deaths in the world [1]. Most chronic diseases such as cardiovascular diseases are not diagnosed until the late stages, when the cost of treatment and rehabilitation has become prohibitive to the general public, especially the poor, and treatment is much more difficult [2]. Early warning in the early stages of the disease would alleviate some of the pressure on the cost of treatment and rehabilitation of the disease and increase the success rate of treatment. The electrocardiogram (ECG) has been widely used in the cardiovascular field due to its non-invasive characteristics [3]. Depending on the time of acquisition, ECG can be categorized into static ECG and dynamic ECG. Conventional static ECG is limited by the length of the acquisition and the physical condition of the patient at the time of acquisition and has a certain degree of serendipity, which makes it difficult to effectively capture the ECG signals during sudden abnormalities or disease episodes, and thus has limitations in the diagnosis of certain diseases. In contrast, a long-term dynamic electrocardiogram (Holter ECG) can continuously record the long-term dynamic ECG activity of an individual in daily life, which is unique for transient arrhythmia capture and the detection of transient myocardial ischemia [4], and it can reduce the frequency and cost of the patient’s trips to the hospital, thus making the study of dynamic electrocardiograms highly valuable.
However, ECG signals are weak and highly susceptible to external interference, and during the actual acquisition process ECG signals may contain a large amount of noise due to improper methods, daily activities, or environmental interference. According to statistics, more than 20 million sets of ECG signals are stored globally each year, of which approximately 5% have signal quality problems [5]. Due to the long duration and the user’s activity, long-term dynamic ECG signals are more susceptible to noise interference. Figure 1 shows the waveforms of long-term dynamic ECG signals disturbed by different degrees of noise. It can be seen that the signal distortion under noise interference is severe and key information is difficult to detect.
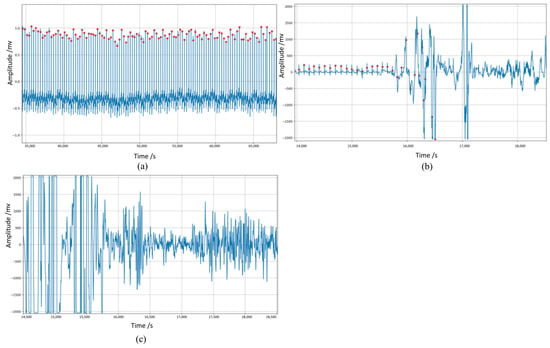
Figure 1.
Waveforms of ECG signals (in blue) disturbed by different degrees of noise. The red dot represents the peak of the R−wave detected by the Pan-Tompkin algorithm. (a) ECG signal with little noise, (b) ECG signal partly disturbed by noise, (c) ECG signal severely disturbed by noise. Poor quality ECG increases the risk of false alarms and misdiagnosis, interfering with correct diagnostic information, so many researchers use noise reduction algorithms. However, research has shown that most denoising methods significantly alter the localization waves of ECG [6]. Therefore, some researchers have used signal quality assessment strategies to address this problem. Signal quality assessment (SQA) is the process of determining the quality and acceptability of a signal [7]. When applied in the field of electrocardiograms, SQA allows researchers to determine the clinical acceptability of ECG signals, reduce the interference of noise in automated disease diagnosis, and improve the accuracy of signal analysis, thus ensuring the reliability of ECG signal analysis [2]. In addition, this evaluation mechanism allows researchers to select different signal segments based on clinical research needs, which is beneficial for the practical application of electrocardiogram signal analysis technology. ECG signal quality assessment plays a vital role in significantly improving the diagnostic accuracy and reliability of unsupervised ECG analysis systems [5].
Some traditional SQA algorithms require the detection of the fiducial features of ECG signals (such as QRS complexes) or unbiased estimation of the signals. The performance of the algorithm depends on the accuracy and reliability of the QRS complex wave detection algorithm or noise estimation algorithm, which remains a challenging problem in long-term dynamic ECG signals. Eigenvalue-based methods often rely on prior knowledge such as expert experience and threshold setting, which makes it difficult to find the optimal threshold parameters in long-term dynamic electrocardiograms with PQRST waveform morphology, heart rate, and various noise changes over time. Therefore, this article proposes a dynamic electrocardiogram signal quality evaluation method based on CNN and LSTM and applies it to actual collected exercise experimental data. This method does not rely on expert experience and traditional feature engineering, nor does it rely on the reliability of R-wave detection algorithms, and it can directly learn features from ECG data. The signal quality evaluation method proposed in this article screens the electrocardiogram signals before conducting heart rate analysis and disease prediction. In this way, signals that are severely interfered with are distinguished to avoid their impact on the analysis or disease prediction results. The signal is split into three categories to accommodate different signal quality requirements for different tasks in forecasting (e.g., cardiac disease prediction and heart rate calculation, HRV analysis, etc.) Through this quality evaluation method, the accuracy and efficiency of dynamic electrocardiogram signal analysis can be improved, and false alarms and misdiagnoses can be reduced.
2. Research Status
Many researchers have explored different methods of ECG signal quality assessment. Some studies [8,9,10,11,12,13,14,15,16,17,18,19,20] have evaluated signal quality based on characteristic parameters extracted from the signal, referred to as signal quality indicators (SQIs). Common SQIs include local waveform morphology (e.g., slope and shape of the QRS waveform), time-domain characteristics (e.g., signal turning points, range of signal amplitude, etc.), frequency-domain characteristics (power spectral distribution, baseline relative power, etc.), and interval characteristics (e.g., R-R interval mean, etc.). (e.g., R-R interval mean vs. standard deviation, etc.). This kind of research based on signal quality metrics usually includes two phases: feature extraction and classification. The classification phase is often based on heuristic rules, such as setting thresholds or criteria.
The most common methods for SQA are based on time or frequency features extracted from the signal. Tat et al. [8] proposed a threshold-based quality assessment method that combines an improved Pan-Tompkins algorithm with a standard deviation of the amplitude of the ECG signals. Smital et al. [9] proposed a method based on continuous signal-to-noise ratio curves. Wang et al. [10] proposed a signal quality measure based on the area difference between consecutive QRS wave clusters, which is predicted using a mismatch metric. Orphanidou et al. [11] proposed a method based on the measurement of signal wavelet entropy. Yuan et al. [12] used discrete wavelet transform (DWT) to capture local abrupt changes in signals and proposed a frequency adaptive method for averaging absolute deviation curves. Falk et al. [13] proposed a method based on modulated spectrum signal representation (MSSR). However, it is worth noting that these methods rely on the reliability and accuracy of QRS wave cluster detection algorithms, which remains a challenging issue in long-term dynamic ECG signals.
With the rise of artificial intelligence techniques, some studies [16,17,18,19,20,21,22,23,24] have employed machine-learning methods or neural-network models for assessing the quality of ECG signals. Zhang et al. [16] used features such as spectral distribution, signal complexity, and horizontal and vertical variations of the wave combined with LSTM for quality assessment. Liu [17] proposed a method based on the signal quality index and machine learning to select an optimized subset of the quality index based on the maximum mean minimum variance criterion. Kłosowski et al. [19] used short-time Fourier transform to extract features and combine them with LSTM for quality assessment. Liu et al. [20] used wavelet scattering to extract features and combined it with Bi-LSTM for wearable ECG quality assessment. Liu et al. [21] used the QRS inter-heartbeat similarity principle combined with Resnet and self-attention mechanisms for quality assessment. However, these methods still require feature engineering of the signal, relying on how good the feature engineering is, and the selection and computation of different features have a large impact on the results. In addition, a single feature or a fixed number of features often reflect only a part of the information of the data, while too many features not only increase the complexity of the model but some of the features will also have an impact on the results. Due to the limited adaptability and flexibility of these methods, it is still challenging to handle the complex ECG signals captured by wearable devices.
Moreover, most studies have only performed a simple binary classification (acceptable, unacceptable) for SQA, which is too imprecise for practical long-term dynamic ECG monitoring scenarios. Categorizing the results into five levels would be too complex and affect the efficiency of the calculations. As in long-term dynamic ECG monitoring, there are data with very good quality where the details of the ECG waveforms are clean and undistorted, there are data that are mildly contaminated but the R-wave of the ECG waveforms can still be detected, and there are data that are completed corrupted by noise, making it impossible to obtain the ECG waveforms. Therefore, for long-term dynamic ECG data, a three-category classification SQA method is more suitable because it can effectively reduce the number of false alarms while improving the efficiency of data utilization.
3. Materials and Methods
In this paper, we proposed a convolutional neural network (CNN) and long short-term memory network (LSTM)-based signal quality assessment method; CNN networks enable automatic feature extraction and capture localized features well. Sequences that have a temporal dependency are usually analyzed using recurrent neural networks, and this is because the neurons in different layers inside are also connected, hence the network can memorize, whereas LSTM is developed based on RNN and can solve the limitations of RNN and has better performance, hence the combination of CNN and LSTM is used.
Figure 2 shows the flowchart of the long-term dynamic ECG SQA system. Dynamic ECG signals were first subjected to signal pre-processing (including high-pass filter, trap filter, etc.) and then predicted and classified by the signal quality assessment model. Signals with the Q1 category have low noise levels and can be used for reliable arrhythmia diagnosis, etc. Signals with the Q2 category have a higher noise level but still contain information and can be used for heart rate calculations, HRV analyses, etc. Signals in category Q3 have a high noise level and can be marked out or discarded.
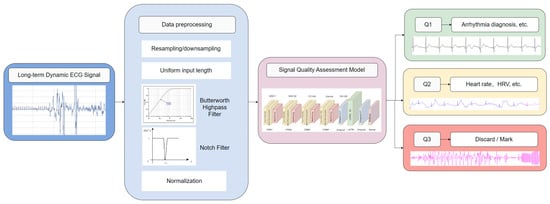
Figure 2.
Flowchart of long-term dynamic ECG SQA system.
3.1. Signal Quality Assessment Rules and Datasets
3.1.1. Signal Quality Assessment Rules
It is necessary to define the three quality classifications before evaluating signal quality. Some articles [9,17,25] have described three quality categories, with Smital [9] proposing to divide signals into three categories: Q1 segments that exhibit such a low noise level that they allow any common type of analysis, including full ECG wave analysis; Q2 segments that contain such a level of noise that they allow reliable QRS complex detection and this basic rhythm analysis; and Q3 segments that contain such levels of noise that they cannot be processed further. Steinberg [25] proposed dividing signals into three categories: dominant, significant, and inadequate. (1) Dominant (excellent signal quality): easy rhythm diagnosis; 75–100% of all beats of the rhythm strip exhibiting distinct and well-defined P, QRS, and T. (2) Significant (acceptable signal quality): rhythm diagnosis can be established for 50–75% of the tracing. (3) Inadequate: accurate ECG morphology present in less than 50% of the tracing-signal quality, not useful for rhythm diagnosis.
On this basis, this article proposes the definition of signal quality evaluation according to the characteristics of dynamic electrocardiogram signals and the input characteristics of the model, as follows:
Q1 (Excellent): The Q1 category ECG signal is free of noise interference, and important waveforms of the ECG signal, such as QRS complex, P waves, etc., can be observed, or there are only 0~3 interfered heartbeats. This grade has a higher signal quality and can be used for arrhythmia disease prediction.
Q2 (Qualified): The noise level of the Q2 category ECG signal is increased, and there is a small amount of noise interference. Important points in the ECG signal are not clear, e.g., the PR interval and/or QRS duration cannot be reliably measured, the P-wave may be distorted, or the start and end points are not sufficiently clear, but the R-wave can still be identified, or there are more than three disturbed beats. Q2 category signals allow for reliable QRS detection and correct measurement of the heart rate.
Q3 (Fail): The Q3 category ECG signal has substantial noise interference. Important features of the ECG signal are difficult to recognize and most of the heartbeats are interfered with by noise. Segments of Q3 category signals cannot be processed further because of unreliable QRS wave cluster detection and basic heart rate analysis. These signals interfere with the diagnosis of cardiovascular disease, and this segment of data should be discarded or labeled in further signal analysis.
Figure 3 shows the ECG signals of the different categories, where (a) shows category Q1, (b) shows category Q2, and (c) shows category Q3.
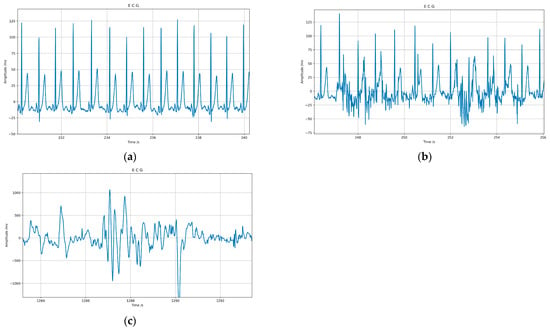
Figure 3.
ECG signals of different categories: (a) shows category Q1, (b) shows category Q2, (c) shows category Q3.
3.1.2. Datasets
In the field of ECG signal quality assessment, the most used dataset is CinC11, and the MIT-BIH arrhythmia database is the most frequently used ECG dataset after CinC11. Next is the NSTDB dataset, which is the only dataset that does not have ECG recordings and contains only the noise commonly found in ECG recordings [26]. The CinC11 dataset classifies ECG signals into acceptable and unacceptable categories only and is therefore not applicable to this paper. Therefore, we have used the MIT-BIH arrhythmia database and NSTDB dataset. In addition to this, we collected the exercise experiment dataset.
Two different datasets were used in this study: one was the noise-stressed MIT-BIH arrhythmia dataset, which consisted of MIT-BIH arrhythmia data with different levels of noise, and the other was a dynamic ECG dataset collected by our team in a non-clinical environment using a single-lead ECG patch.
Noisy ECG Dataset: This dataset was obtained by adding varying degrees of noise to the MIT-BIH arrhythmia database [27]. The MIT-BIH arrhythmia database includes ECG data from 47 subjects with common types of arrhythmia, such as atrial fibrillation, atrial premature beats, and ventricular premature beats. However, the ECG data in this dataset were selected from high-quality signals that contain only a small amount of noise and cannot fully reflect the significant noise interference present in long-term ECG monitoring. Therefore, we synthesized a noisy dataset for the SQA model training.
Noise in ECG signals can usually be classified into four types: baseline drift, industrial frequency interference, EMG interference, and electrode motion artifacts. Among them, the first three types of noise can be filtered or suppressed using digital filters, etc. However, electrode motion artifacts are different from other types of noise in that their spectra are highly overlapped with the ECG signal, and digital filters may lead to changes in the waveforms of the ECG signal, and thus motion artifacts are usually considered to be the most challenging noise. For these reasons, this study focuses on motion artifact noise and superimposes the noise on arrhythmia data based on three different signal-to-noise ratios. The noise used for synthesis was electrode motion artifacts from the MIT-BIH noise stress database (MIT-BIH NS) [28]. In the early experiments, the signal-to-noise ratio was selected in a stepwise manner, and the waveforms of the fused signals were tested under different signal-to-noise ratios, and finally the signal-to-noise ratio settings that complied with the signal quality evaluation rules were found. The specific settings are shown in Table 1. Figure 2 shows typical waveforms for the three categories.

Table 1.
Correspondence between SNR and categories.
The signal-to-noise ratio was calculated according to the formula , and in the actual implementation the energy of the ECG signal was first calculated, and then, based on the specified signal-to-noise ratio, the scaling factor of the noise signal was calculated, the noise signal was scaled, and then added to the ECG signal.
In addition to this, this study used the example noise ECG signals provided by the MIT-BIH noise stress database (recordings “118e_6”, “119e_6”) as the standard signal, and compared the experimentally synthesized data with this standard signal. The results are shown in Figure 4, where (a) and (b) are the waveforms of the standard signal at different deflation scales and (c) and (d) are the waveforms of the synthesized noisy ECG signal. It can be seen that the effect of noise superposition in this study is consistent with the standard signal, which proves that the data processing in this study is reliable.
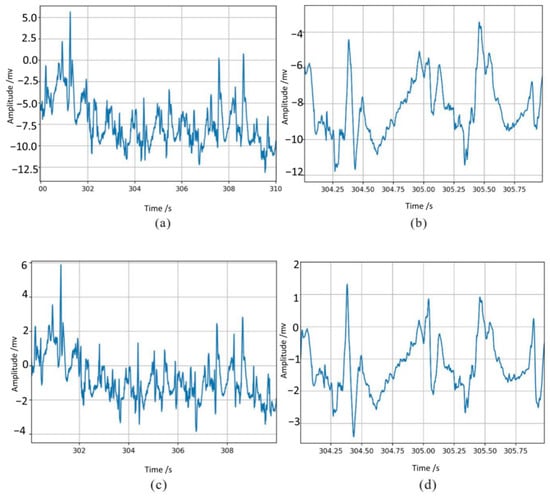
Figure 4.
The effect of noise superimposition compared with the standard signal: (a,b) are the waveforms of the standard signal at different deflation scales, and (c,d) are the waveforms of the synthesized noisy ECG signal.
Dynamic ECG Dataset: To evaluate the performance of our proposed SQA model in a practical ECG monitoring environment, this study specially created a dynamic ECG dataset containing motion artifact interference. This dataset was collected in a non-clinical setting using a wearable single-lead ECG patch from 14 healthy volunteers (5 males and 10 females, aged 20–24). As motion artifacts are the most common and challenging noise to eliminate in long-term ECG monitoring, we have designed eight typical motions to trigger motion artifacts during the ECG signal collection process. The volunteers were asked to perform eight different motions (with short rest between motions) in sequence during a 15-min ECG signal collection process; the details of the experiment are shown in Table 2. Finally, the dataset consists of 15 dynamic ECG recordings, each lasting for 15 min and collected under the interference of eight typical motions. Figure 5 shows an example of the collected dynamic ECG.

Table 2.
The motion details in dynamic ECG data acquisition.
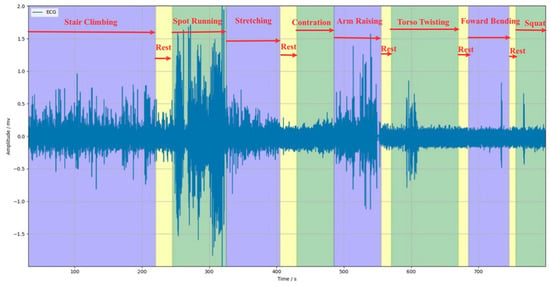
Figure 5.
Example of the collected dynamic ECG.
3.2. Proposed SQA Model
3.2.1. Data Preparation
Pre-processing of the input signals is required to adapt to the model input requirements, reduce disturbances, and improve the accuracy and adaptability of the system analysis.
Since different data sources have different sampling frequencies and different acquisition times, the original data are first downsampled or resampled to unify the sampling frequency of the signal to a fixed value of fs; next, the signal is cropped using a non-overlapping sliding window of 10 s to ensure that the data input to the model are of the same size. Data cropping can improve the adaptability of the model to the data source so that the model can be compatible with data from different acquisition devices and different acquisition times.
The signals that satisfy the input dimensions of the model are filtered by cascading 0.67 Hz Butterworth high-pass filters and 50 Hz trap filters to reduce the impact of easily removable noise, such as baseline drift and industrial frequency interference, on the results.
The filtered signals are normalized for deviation with the following formula:
where max and min are the maximum and minimum values of all samples, so this method is also called min–max normalization. This processing method scales the data into the [−1,1] interval, and adjusting the data distribution can reduce the impact of too large a difference in eigenvalues on the model.
To train the model, the dataset should be divided. The preprocessed and labeled data are randomly disrupted and divided into training sets, validation sets, and testing sets in the ratio of 7:2:1. The division process uses hierarchical division to ensure consistent data distribution on each dataset.
Data preprocessing can accelerate the convergence speed of the model, reduce the gradient disappearance or explosion, improve the generalization ability of the model, and enhance the adaptability of the model. A total of 25,920 valid data are obtained after preprocessing, and the three categories have equal amounts of data, all of which are 8640, which can effectively reduce the impact of data imbalance on the results.
3.2.2. Model Design
This study is based on a one-dimensional convolutional neural network (1D-CNN) implemented with a long short-term memory network (LSTM). The convolutional layer of a CNN network can extract important features, especially local features, directly from the input data without manual intervention such as feature engineering. LSTM can alleviate the problem of gradient vanishing by preserving long-term information through gating units. When applying LSTM to ECG signals, it can capture not only the subtle changes between heartbeats but also the long-term heart rate fluctuations [29]. The network architecture shown in Figure 6 is implemented through the TensorFlow framework and trained and validated for the three-category classification signal quality problem.

Figure 6.
Structure of the model.
Convolutional Layers. 1D-CNN layers are used, configured with 3 × 1 sized convolutional kernels. Immediately following each convolutional layer is the batch normalization layer (BNL). This layer is introduced to reduce internal covariate bias and to further improve the stability and efficiency of the training process by normalizing each small batch of data. This is followed by the pooling layer, and the maximum pooling method is chosen in this study to highlight the most important signal features to reduce the computational burden. Through four iterative combinations of the convolutional layer, batch normalization layer, and pooling layer, the network gradually builds up a feature hierarchy from simple to complex.
LSTM layer and fully connected layer. This is followed by a long short-term memory (LSTM) network layer designed to capture and process long-term dependencies in time-series data. The classification output is obtained through the fully connected layer and the predicted probabilities for each category are output using the Softmax activation function, which ultimately gives the most likely classification result.
We use the Adam optimizer to obtain higher computational performance. Since it is a multi-classification problem we use categorical cross-entropy as a loss function to reduce the risk of overfitting by regularization. A grid search strategy is used to explore the hyperparameter space to find the optimal network configuration. After a series of experiments, the model performs well when the number of convolutional kernels is set to 32, 64, 64, and 128, respectively. To improve the training efficiency and model generalization ability, we use the early stopping strategy; when the performance of the validation set shows no improvement or even starts to decline for consecutive epochs, we stop the training early to prevent overfitting on the training set. After 100 calendar elements of training, the model reaches convergence on the test set.
3.2.3. Assessment Indicators
The common evaluation metrics for evaluating models usually include accuracy, precision, recall, and F1 score [29], and since this paper investigates the three-category classification problem, the macro-averaging metrics are computed based on the confusion matrix to evaluate the algorithm’s performance on the entire test set. The confusion matrix for the three classification problems is shown in Table 3:

Table 3.
Confusion matrix for the three-category classification problem.
From the confusion matrix, the accuracy is calculated as follows:
Macro-averaging is the process of calculating performance metrics (e.g., accuracy, recall, and F1 scores) individually for each category and then averaging the metrics across all categories. Each category is considered equally important, regardless of the sample size of the category. The macro-averaging formula is given below:
, , and are the precision, recall, and F1 score of the category i (i = 1, 2, 3), which can be calculated by the following formula, respectively:
where TP (true positive) is a true positive indicating the number of samples correctly predicted to be in that category, FP (false positive) is a false positive indicating the number of samples incorrectly predicted to be in that category, and FN (false negative) is a false negative indicating that the samples in that category have been incorrectly predicted to be in another category.
3.2.4. Results
The hybrid CNN + LSTM model proposed in this study performs well on the test set, achieving 98.65% accuracy, demonstrating the model’s high efficiency and good generalization ability. This result indicates that the model has high reliability and accuracy in processing ECG signals of different quality levels. The performance of the model was evaluated in detail by the confusion matrix; the relevant evaluation metrics calculated from the confusion matrix are shown in Table 4, and the confusion matrix is visualized in Figure 7 to facilitate the visualization of the model’s prediction effect on different classes.

Table 4.
Prediction results on the test set.
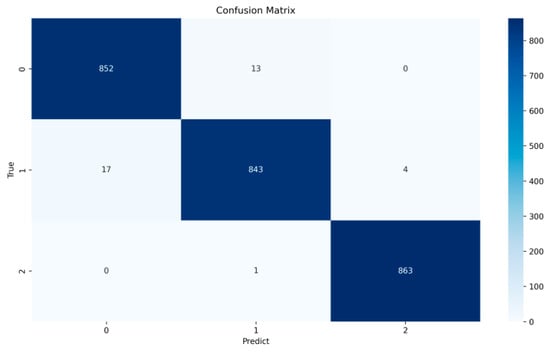
Figure 7.
Confusion matrix.
Compared with precision and recall, the F1 scores can more comprehensively demonstrate the model’s effect, and the macro-averaged F1 score of the model reaches 98.5%, which further proves that the model has a good effect in distinguishing between the different signal quality classes in a detailed way. In particular, the model performs best in the prediction of Q3 category signals with an F1 score of 99.71%. This indicates that the model can efficiently identify and distinguish signals with high noise levels, crucial for reducing misdiagnosis and improving diagnostic efficiency. The results show that 852 Q1 signals are correctly classified by the model, 13 are misclassified as Q2, and none are misclassified as Q3; the precision, recall, and F1 scores for the Q1 category were 98.04%, 98.50%, and 98.27%, respectively. The model correctly classifies 843 Q2 signals, 17 are misclassified as Q1, and 4 are misclassified as Q3; the precision, recall, and F1 scores for the Q2 category were 98.37%, 97.57%, and 97.97%, respectively. For Q3 signals, the model performs particularly well, with 863 signals correctly classified, only 1 misclassified as Q2, and none misclassified as Q1; the precision, recall, and F1 scores for the Q1 category were 99.54%, 99.88%, and 99.71%, respectively.
In addition to this, to assess the effectiveness of the model in dealing with real-world situations, this study likewise tested the actual collected exercise experiment data. To ensure the consistency of the test data with the model training data, the same preprocessing steps as the training dataset were implemented for the data collected in the exercise experiments. These preprocessed data were then used to evaluate the performance of the trained model. Figure 8 illustrates the predicted results of the model when processing the actual noisy ECG data, and Figure 9 provides detailed plots of the signal waveforms with different quality categories to facilitate a more precise view of the model’s classification effect. In these waveform plots, different signal quality classes are distinguished by color backgrounds: green represents Q1 category signals, yellow indicates Q2 category signals, and pink is used to indicate Q3 category signals. The results in Figure 8 and Figure 9 show that the model also performs well in processing ECG signals with noise interference caused by actual exercise. This result further validates the effectiveness and accuracy of the model in practical applications.
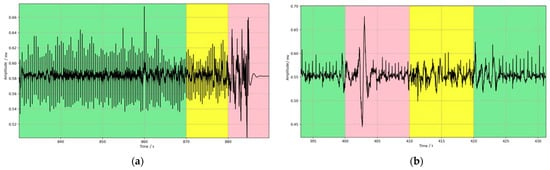
Figure 8.
Predicted results of motion experiment data; the three background colors of green, yellow, and pink represent the data for the Q1, Q2, and Q3 categories, respectively. (a) example 1 (b) example 2.
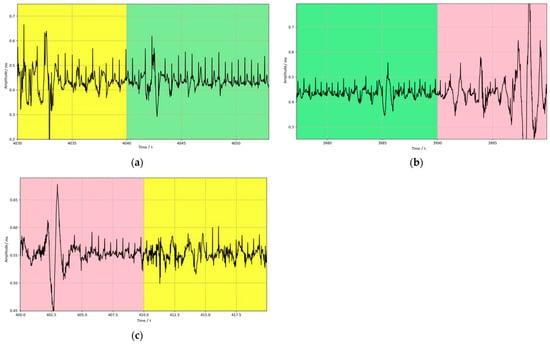
Figure 9.
Waveform details of data with different quality categories; the three background colors of green, yellow, and pink represent the data for the Q1, Q2, and Q3 categories, respectively. (a) example 1, (b) example 2, (c) example 3.
3.3. Model Comparison
3.3.1. Model Introduction
As a controlled experiment, this paper investigates the performance of a variety of commonly used algorithms. In the field of ECG signal quality signal analysis, most studies use feature engineering to extract signal quality metrics combined with heuristic rules or machine-learning methods for classification. The widely used signal quality metrics include the following:
(1) Power spectral distribution of QRS waves (pSQI). The most significant part of the ECG signal is the QRS wave group, whose energy is usually concentrated in a band centered at 10 Hz and with a width of 10 Hz. Therefore, the quality of the signal is assessed by calculating the proportion of the total energy that is accounted for by the energy of the QRS wave, which is calculated by the following formula:
where P(f) is the signal power.
(2) Baseline relative power (basSQI). BasSQI compares the power distribution in the lower frequency bands with the entire frequency range and can assess the denoising effect of baseline drift with the following equation:
(3) Kurtosis (sSQI) and skewness (kSQI). In ECG signal analysis, the shape characteristics of the signal are evaluated using kurtosis (i.e., the fourth-order moments of the signal) and skewness (i.e., the third-order moments of the signal), which can show the signal symmetry and distributional characteristics, and the interference of noise leads to asymmetry in the distribution of the signal, as shown in the following equations:
where µx and σ are the mean and standard deviation of the signal, respectively.
(4) Root mean square (RMS). The RMS (i.e., the second-order moments of the signal) reflects the overall energy level of the signal and helps to capture variations in the signal’s strength, which is calculated using the following formula:
where n is the number of samples and xi is the ith sample.
In the selection of classification algorithms, the most commonly used algorithms for signal quality assessment include k-nearest neighbor (KNN) and support vector machine (SVM). The KNN algorithm classifies the features by measuring the distance between them; however, the performance of the algorithm relies on the selection of k and the distance metric method. In this chapter, the most classical Euclidean distance is used to obtain the optimal k value through the k-fold cross-validation method. This paper uses ten-fold cross-validation, i.e., the training data is divided into 10 subsets; in each fold validation, one of the subsets is used as the validation set, the remaining subsets are used as the training set and repeated 10 times, and the average of the 10 classification results is the final result. SVM algorithms were initially used for binary classification problems, and in this chapter a one-to-many strategy is used and applied to multi-classification problems. The introduction of the kernel trick allows the SVM algorithm to map linearly indistinguishable data into a high-dimensional space to find the optimal separation of hyperparameters. In this paper, the model hyperparameters are tuned for optimal classification performance using a lattice search strategy, i.e., traversing the possible pairs of hyperparameters to find the globally optimal solution among them.
To ensure data consistency, the same preprocessing steps are first performed on the input data, with the only difference being that the datasets for the KNN and SVM models are divided into a 70% training set and a 30% test set to accommodate the algorithms. Next is the feature extraction stage, where the signal quality index of each signal is calculated to form the feature matrices, and then these feature matrices are used as model inputs for training using the KNN and SVM algorithms, respectively.
3.3.2. Results
The experimental results are shown in Table 5, where macro-averages were used for all evaluation metrics. Specifically, the F1 scores of KNN, SVM, and 1D-CNN are 79.68%, 82.78%, and 93.28%, respectively. In contrast, the F1 score of the CNN-LSTM network proposed in this paper is as high as 98.65%, which outperforms the other algorithms. This result proves the efficiency and feasibility of the CNN + LSTM model in ECG signal quality assessment.

Table 5.
Classification performance of different algorithms on the test set.
4. Conclusions
When analyzing long-term dynamic ECG signals, we found that the presence of a large amount of noise in the ECG signal leads to deformation of the ECG waveform, which in turn leads to a decrease in the accuracy of the AI model used for arrhythmia classification, resulting in false alarms of cardiovascular disease. Therefore, this work added a signal quality assessment step to the traditional signal analysis process to classify signal quality according to the level of noise interference. In this way, the influence of noise on the analysis algorithm is reduced, while the utilization of long-term dynamic ECG signals is improved, with a view to playing a role in the field of long-term heart health monitoring.
Some conventional SQA algorithms require the detection of fiducial features of the ECG signal (e.g., QRS complex) or require unbiased estimation of the signal. The algorithmic performance relies on the accuracy and reliability of the QRS complex detection algorithm or the noise estimation algorithm, which remains a challenging problem in long-term ambulatory ECG signals. Eigenvalue-based methods usually rely on a priori knowledge such as expert experience and threshold setting, which makes it difficult to find the optimal threshold parameters in the case of long-range dynamic ECG with PQRST waveform morphology, heart rate, and various noises varying over time.
To address the above issues, this paper proposes a CNN and LSTM-based dynamic ECG signal quality assessment method and applies it to the collected exercise experimental data. This signal quality assessment method divides the signal into three quality levels. Based on the most recognized MIT-BIH dataset, the algorithm achieves 98.65% correctness on the test data, with a macroscopic average F1 score of 98.5% for the model, and performs well in predicting Q3 category signals, with an F1 score as high as 99.71%. It is worth noting that the dataset needs to be further extended for patients with rare arrhythmias or those affected by rare noise types that are not covered.
Author Contributions
Methodology, C.H. and X.A.; software, C.H.; validation, C.H.; investigation, C.H.; resources, X.A.; data curation, C.H., Y.W. (Yuxuan Wei) and Y.W. (Yeru Wei); writing—original draft, C.H.; writing—review and editing, X.A.; project administration, X.A.; funding acquisition, Q.L. and X.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the fund of the Beijing Municipal Education Commission, China, under grant number 22019821001, and the Climbing Program Foundation of the Beijing Institute of Petrochemical Technology (Project No. BIPTAAI-2021-002), and the Zhiyuan Science Foundation of BIPT (No. 2024104).
Data Availability Statement
The datasets involved in this study can be found here: https://github.com/Herccy/SQA/Datasets (accessed on 29 February 2024).
Acknowledgments
Thank you to the individuals and organizations who have contributed to this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- WfsA. Available online: https://www.who.int/news-room/fact-sheets/detail/the-top-10-causes-of-death (accessed on 18 March 2024).
- Silva, I.; Moody, G.; Celi, L. Improving the Quality of ECGs Collected using Mobile Phones: The PhysioNet/Computing in Cardiology Challenge 2011. Comput. Cardiol. 2011, 38, 273–276. [Google Scholar]
- Jekova, I.; Krasteva, V.; Dotsinsky, I.; Christov, I. Recognition of diagnostically useful ECG recordings: Alert for corrupted or interchanged leads. Comput. Cardiol. 2011, 6801, 429–432. [Google Scholar]
- Zaunseder, S.; Huhle, R.; Malberg, H. CinC challenge—Assessing the usability of ECG by ensemble decision trees. In Proceedings of the 2011 Computing in Cardiology, Hangzhou, China, 18–21 September 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 277–280. [Google Scholar]
- Satija, U.; Ramkumar, B.; Manikandan, M.S. A review of signal processing techniques for electrocardiogram signal quality assessment. IEEE Rev. Biomed. Eng. 2018, 11, 36–52. [Google Scholar] [CrossRef]
- Satija, U.; Ramkumar, B.; Manikandan, M.S. A unified sparse signal decomposition and reconstruction framework for elimination of muscle artifacts from ECG signal. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 779–783. [Google Scholar]
- Acharya, U.R.; Fujita, H.; Oh, S.L.; Hagiwara, Y.; Tan, J.H.; Adam, M.; Tan, R.S. Deep convolutional neural network for the automated diagnosis of congestive heart failure using ECG signals. Appl. Intell. 2019, 49, 16–27. [Google Scholar] [CrossRef]
- Tat, T.H.C.; Xiang, C.; Thiam, L.E. Physionet challenge 2011: Improving the quality of electrocardiography data collected using real-time QRS-complex and T-wave detection. In Proceedings of the 2011 Computing in Cardiology, Hangzhou, China, 18–21 September 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 441–444. [Google Scholar]
- Smital, L.; Haider, C.R.; Vitek, M.; Leinveber, P.; Jurak, P.; Nemcova, A.; Smisek, R.; Marsanova, L.; Provaznik, I.; Felton, C.L.; et al. Real-time quality assessment of long-term ECG signals recorded by wearables in free-living conditions. IEEE Trans. Biomed. Eng. 2020, 67, 2721–2734. [Google Scholar] [CrossRef]
- Wang, J.Y. A new method for evaluating ECG signal quality for multi-lead arrhythmia analysis. In Proceedings of the Computers in Cardiology, Memphis, TN, USA, 22–25 September 2002; IEEE: Piscataway, NJ, USA, 2002; pp. 85–88. [Google Scholar]
- Orphanidou, C.; Drobnjak, I. Quality assessment of ambulatory ECG using wavelet entropy of the HRV signal. IEEE J. Biomed. Health Inform. 2016, 21, 1216–1223. [Google Scholar] [CrossRef]
- Yuan, S.; He, Z.; Zhao, J.; Yang, Z.; Yuan, Z. Long-term electrocardiogram signal quality assessment pipeline based on a frequency-adaptive mean absolute deviation curve. Appl. Intell. 2023, 53, 20418–20440. [Google Scholar] [CrossRef]
- Falk, T.H.; Maier, M. MS-QI: A modulation spectrum-based ECG quality index for telehealth applications. IEEE Trans. Biomed. Eng. 2014, 63, 1613–1622. [Google Scholar]
- Behar, J.; Oster, J.; Li, Q.; Clifford, G.D. ECG signal quality during arrhythmia and its application to false alarm reduction. IEEE Trans. Biomed. Eng. 2013, 60, 1660–1666. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, X.; Zhao, L.; Liu, F.; Chen, X.; Yao, Y.; Li, J. Signal quality assessment and lightweight QRS detection for wearable ECG SmartVest system. IEEE Internet Things J. 2018, 6, 1363–1374. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, L.; Zhang, W.; Yao, J. A signal quality assessment method for electrocardiography acquired by a mobile device. In Proceedings of the 2018 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Madrid, Spain, 3–6 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–3. [Google Scholar]
- Liu, S.; Zhong, G.; He, J.; Yang, C. Multi-task cascaded assessment of signal quality for long-term single-lead ECG monitoring. Biomed. Signal Process. Control 2023, 83, 104674. [Google Scholar] [CrossRef]
- Zhang, Y.T.; Liu, C.Y.; Wei, S.S.; Wei, C.Z.; Liu, F.F. ECG quality assessment based on a kernel support vector machine and genetic algorithm with a feature matrix. Front. Inf. Technol. Electron. Eng. 2014, 15, 564–573. [Google Scholar] [CrossRef]
- Kłosowski, G.; Rymarczyk, T.; Wójcik, D.; Skowron, S.; Cieplak, T.; Adamkiewicz, P. The use of time-frequency moments as inputs of lstm network for ecg signal classification. Electronics 2020, 9, 1452. [Google Scholar] [CrossRef]
- Liu, F.; Xia, S.; Wei, S.; Chen, L.; Ren, Y.; Ren, X.; Xu, Z.; Ai, S.; Liu, C. Wearable electrocardiogram quality assessment using wavelet scattering and LSTM. Front. Physiol. 2022, 13, 905447. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhang, H.; Zhao, K.; Liu, H.; Long, F.; Chen, L.; Yang, Y. An Automatic ECG Signal Quality Assessment Method Based on Resnet and Self-Attention. Appl. Sci. 2023, 13, 1313. [Google Scholar] [CrossRef]
- Allam, J.P.; Samantray, S.; Sahoo, S.P.; Ari, S. A deformable CNN architecture for predicting clinical acceptability of ECG signal. Biocybern. Biomed. Eng. 2023, 43, 335–351. [Google Scholar] [CrossRef]
- Naseri, H.; Homaeinezhad, M.R. Electrocardiogram signal quality assessment using an artificially reconstructed target lead. Comput. Methods Biomech. Biomed. Eng. 2015, 18, 1126–1141. [Google Scholar] [CrossRef] [PubMed]
- Reddy, G.N.K.; Manikandan, M.S.; Murty, N.V.L.N. On-device integrated PPG quality assessment and sensor disconnection/saturation detection system for IoT health monitoring. IEEE Trans. Instrum. Meas. 2020, 69, 6351–6361. [Google Scholar] [CrossRef]
- Steinberg, C.; Philippon, F.; Sanchez, M.; Fortier-Poisson, P.; O’Hara, G.; Molin, F.; Sarrazin, J.-F.; Nault, I.; Blier, L.; Roy, K.; et al. A Novel Wearable Device for Continuous Ambulatory ECG Recording: Proof of Concept and Assessment of Signal Quality. Biosensors 2019, 9, 17. [Google Scholar] [CrossRef]
- van der Bijl, K.; Elgendi, M.; Menon, C. Automatic ECG Quality Assessment Techniques: A Systematic Review. Diagnostics 2022, 12, 2578. [Google Scholar] [CrossRef]
- Moody, G.B.; Mark, R.G. The impact of the MIT-BIH Arrhythmia Database. IEEE Eng. Med. Biol. 2001, 20, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Moody, G.B.; Muldrow, W.E.; Mark, R.G. A noise stress test for arrhythmia detectors. Comput. Cardiol. 1984, 11, 381–384. [Google Scholar]
- Chollet, F. Deep Learning with Python; Original work published 2017; Zhang, L., Translator; People’s Posts and Telecommunications Publishing House: Beijing, China, 2018; pp. 172–193. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).