Solar and Wind Data Recognition: Fourier Regression for Robust Recovery
Abstract
1. Introduction
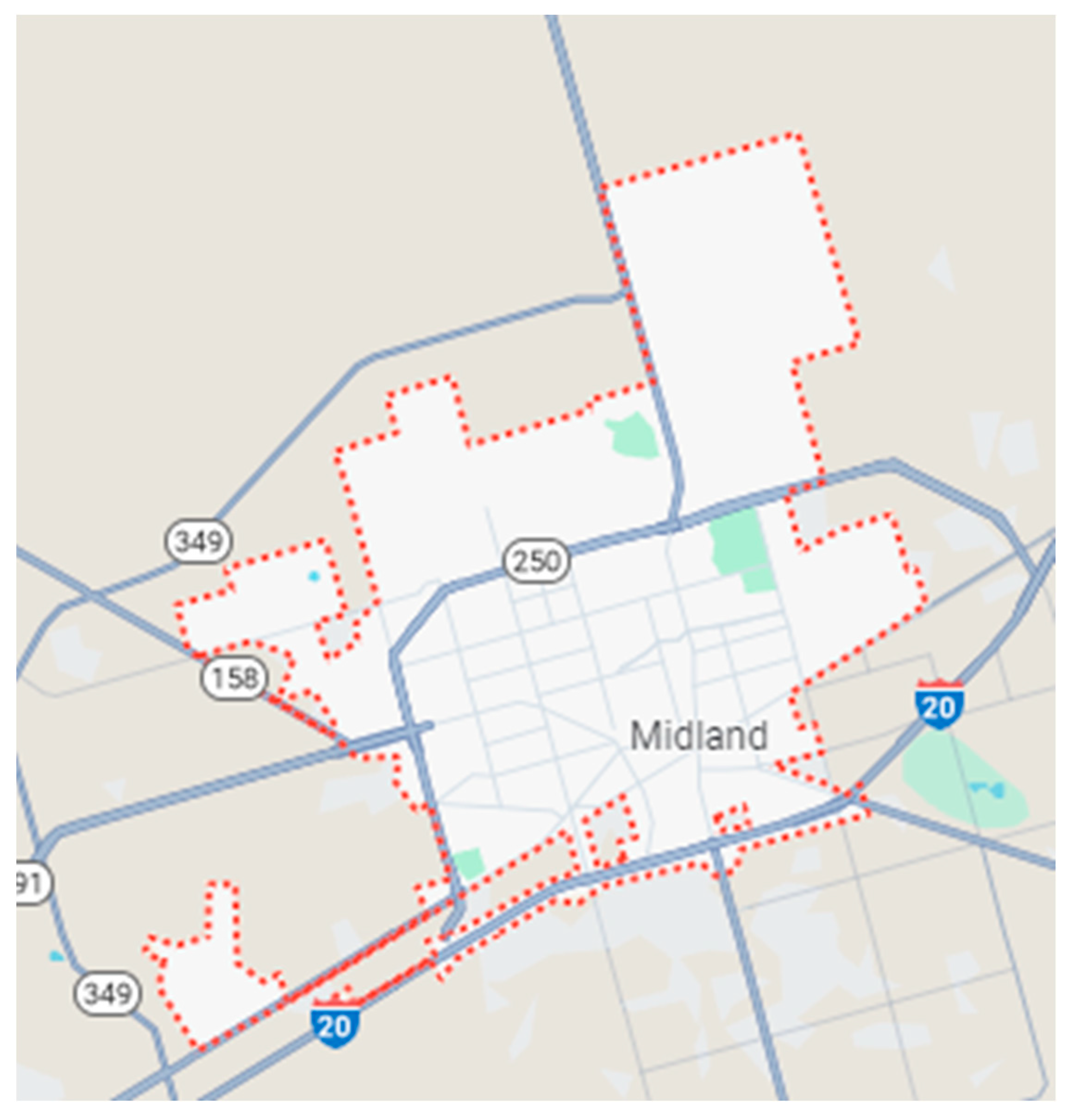
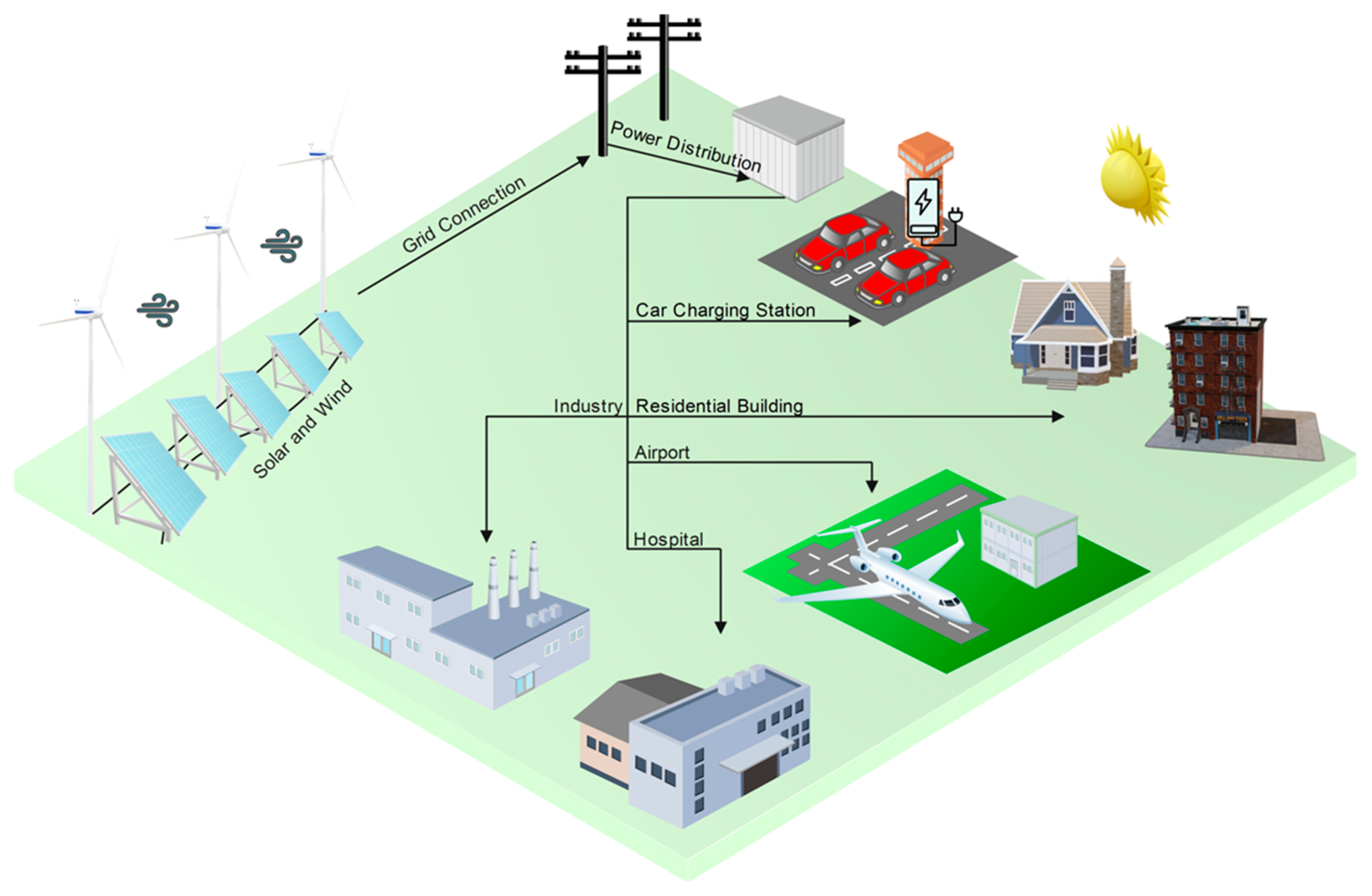
2. Model Site Description and Data Collection
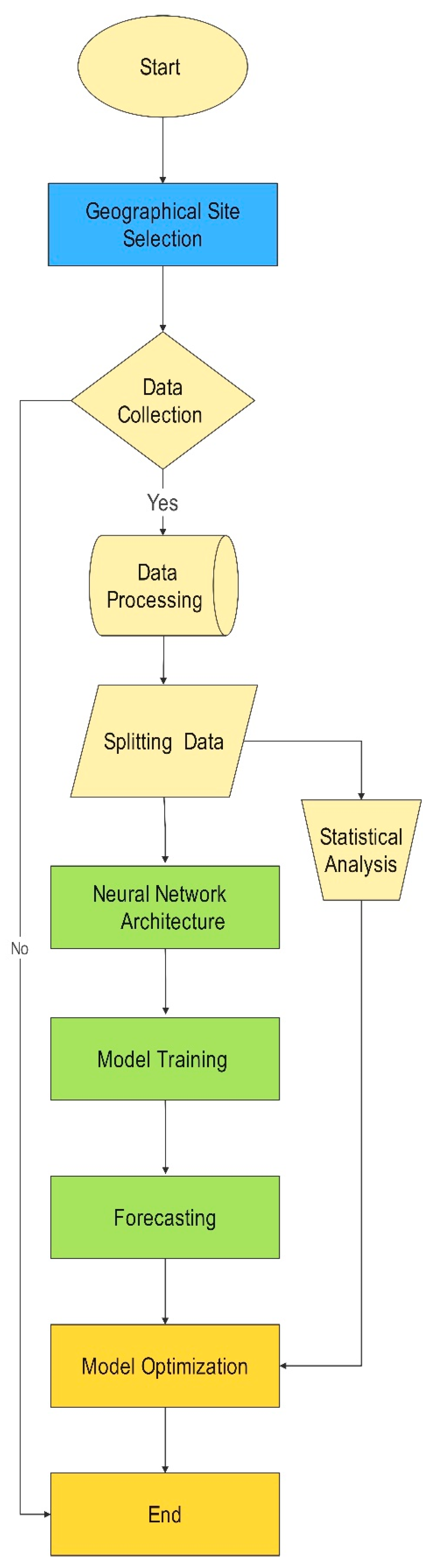
3. Regression-Based Fourier Model and Parameter Estimation
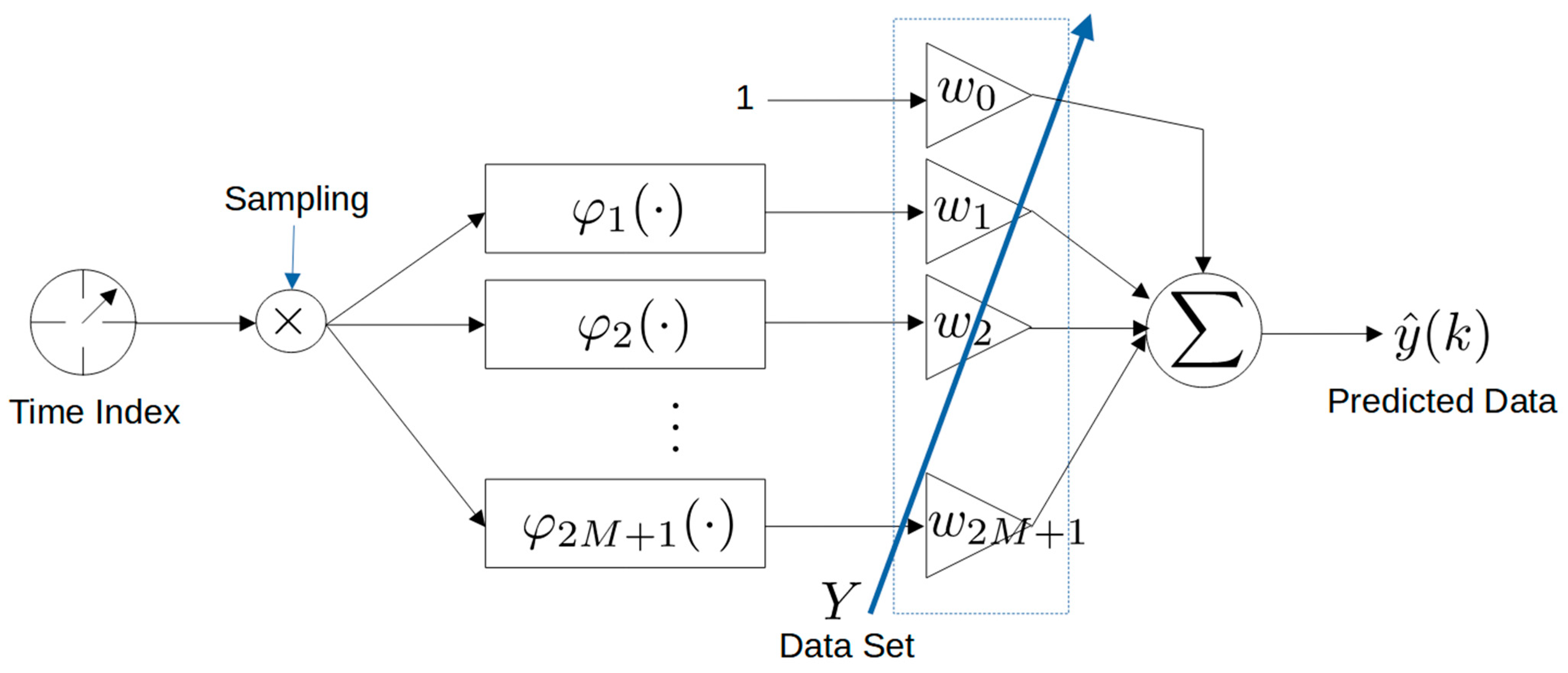
3.1. Regression-Based Fourier Model Formulation
3.2. General Model Description
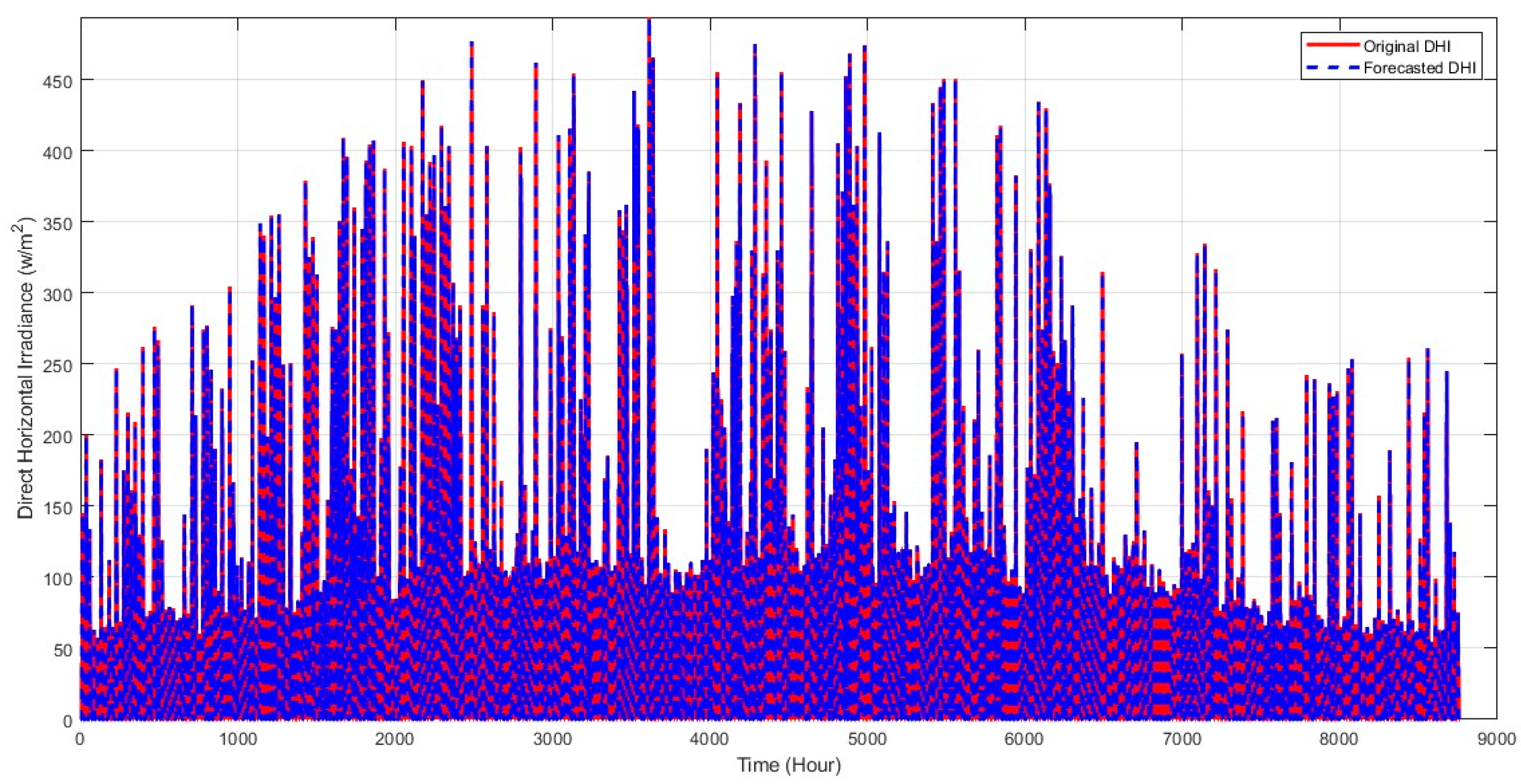
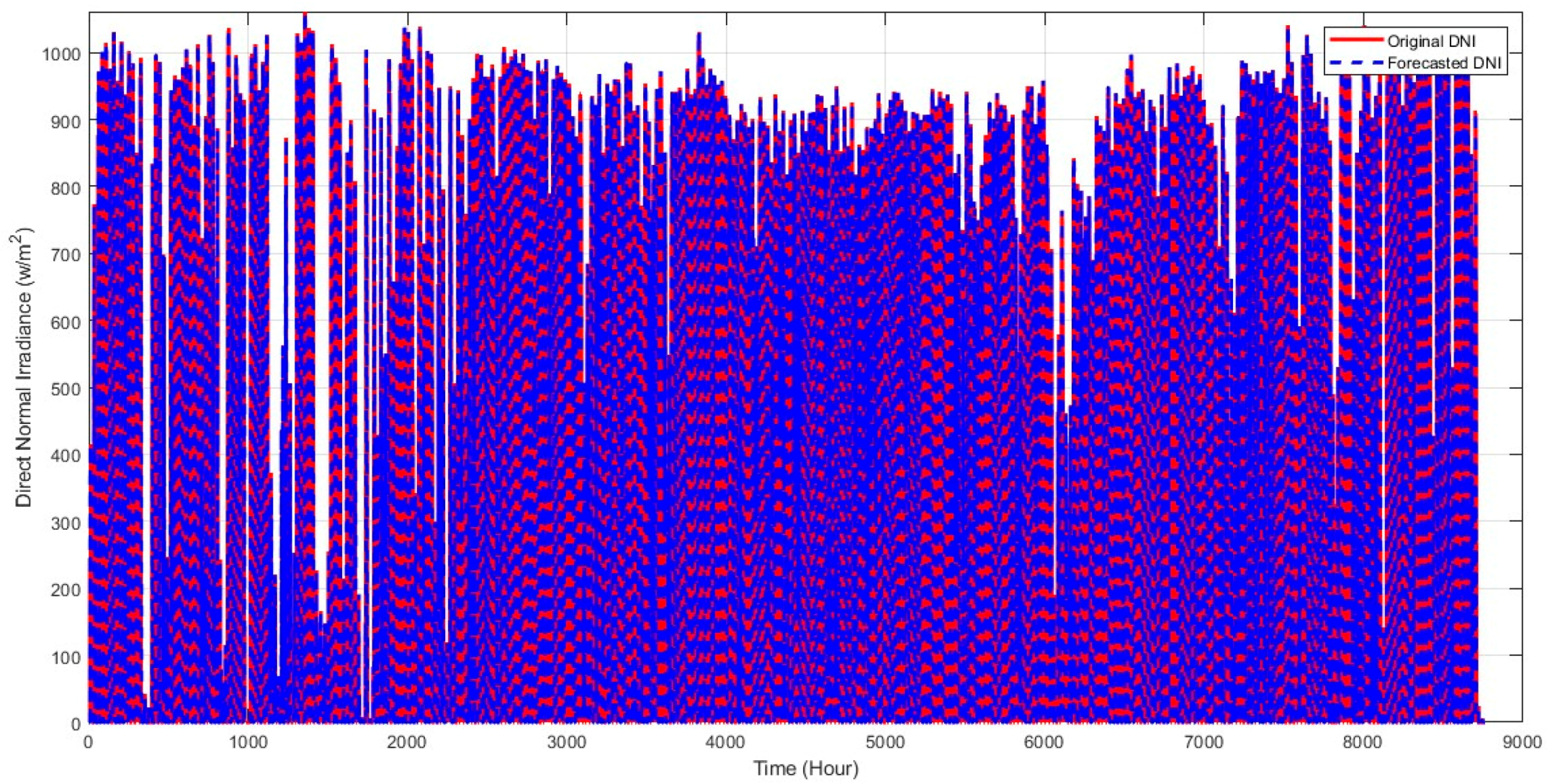
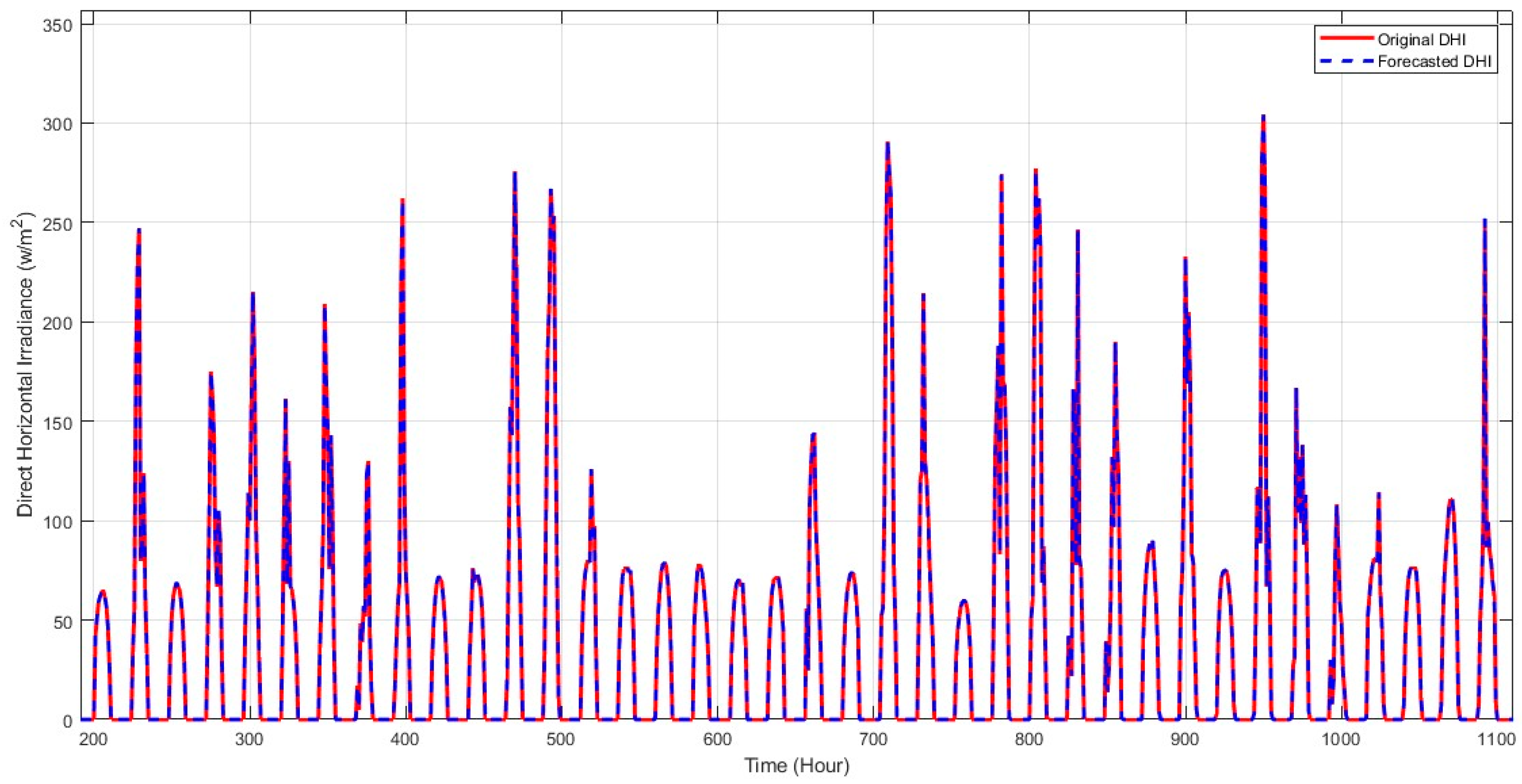
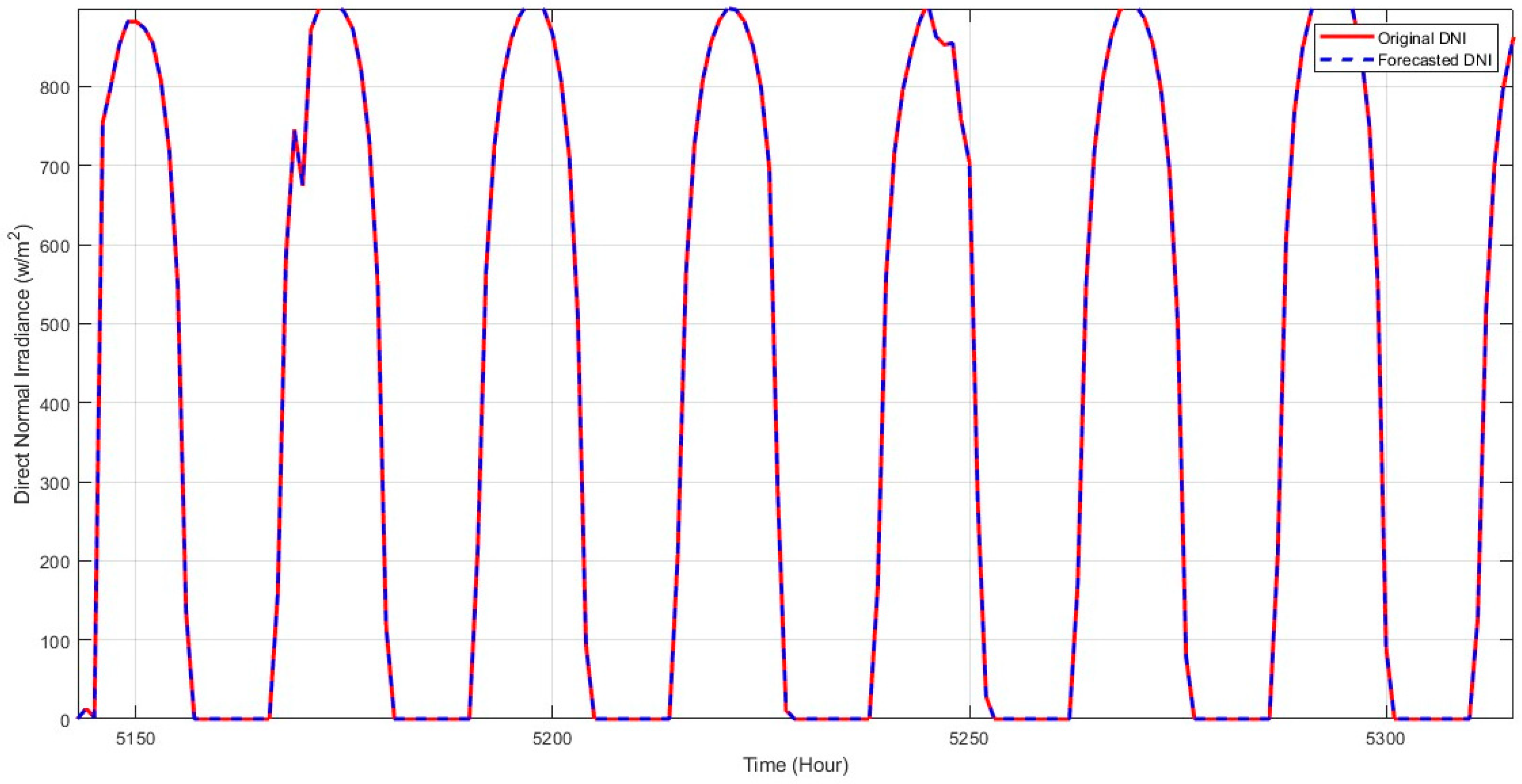
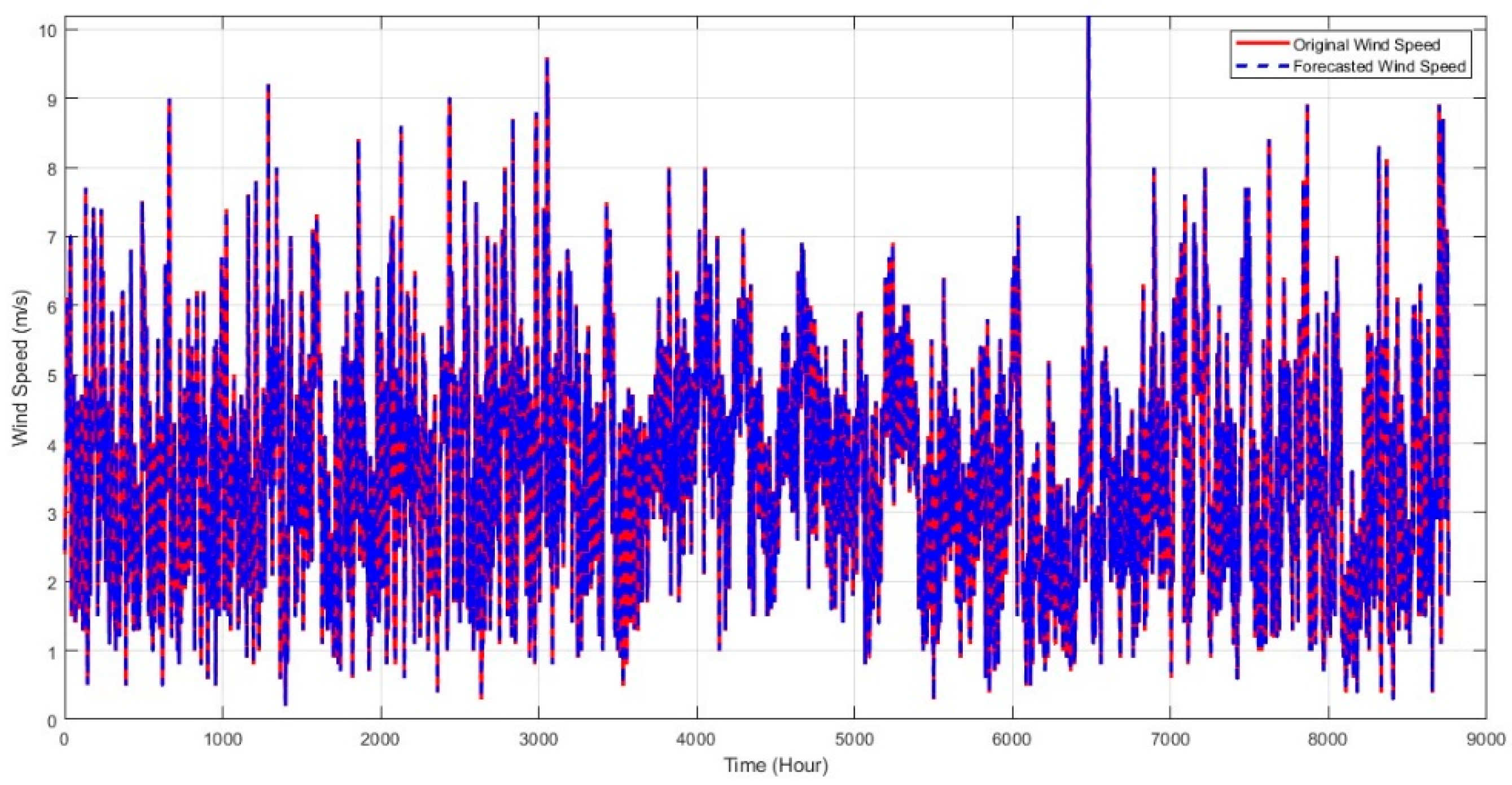
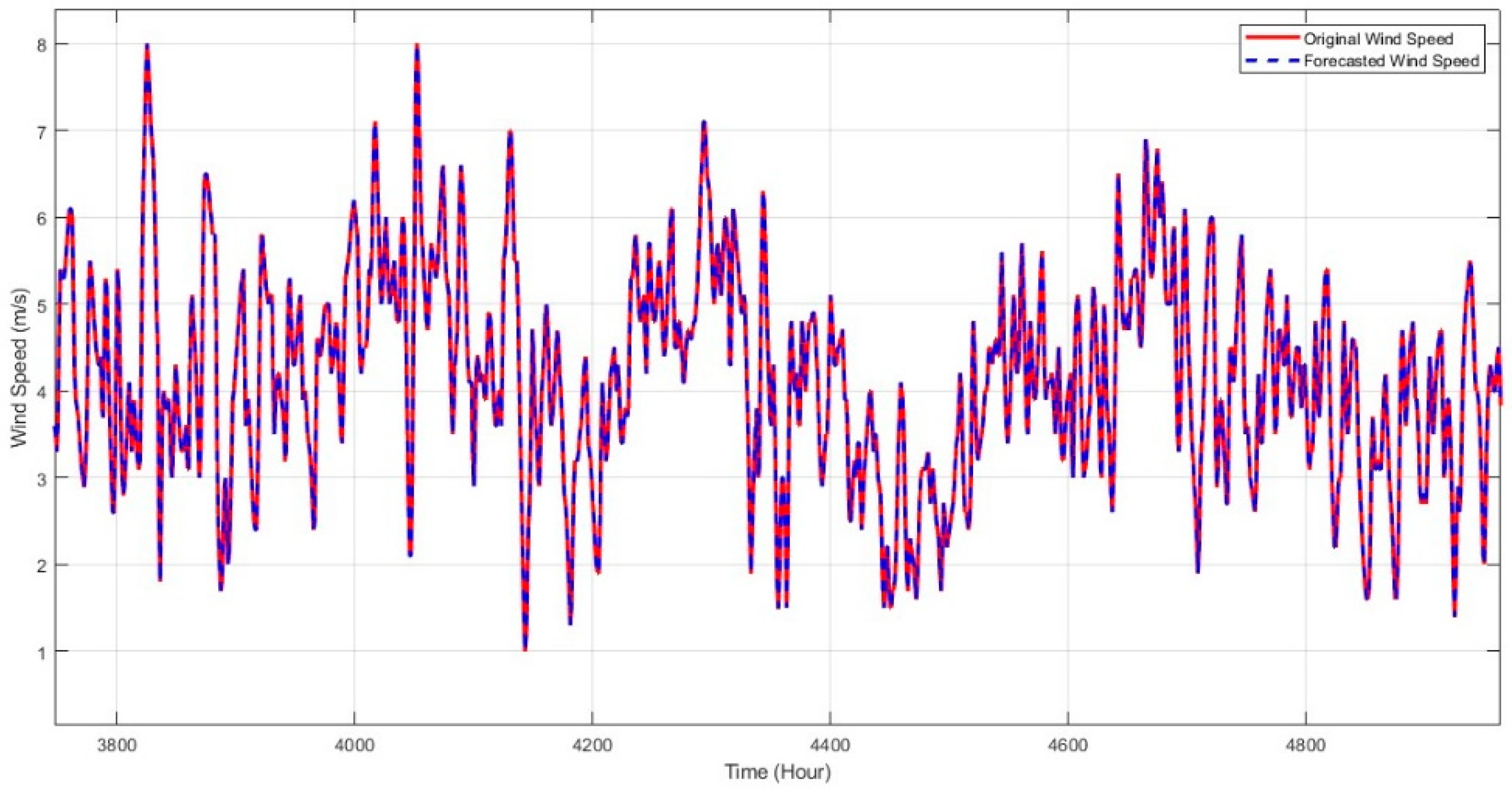
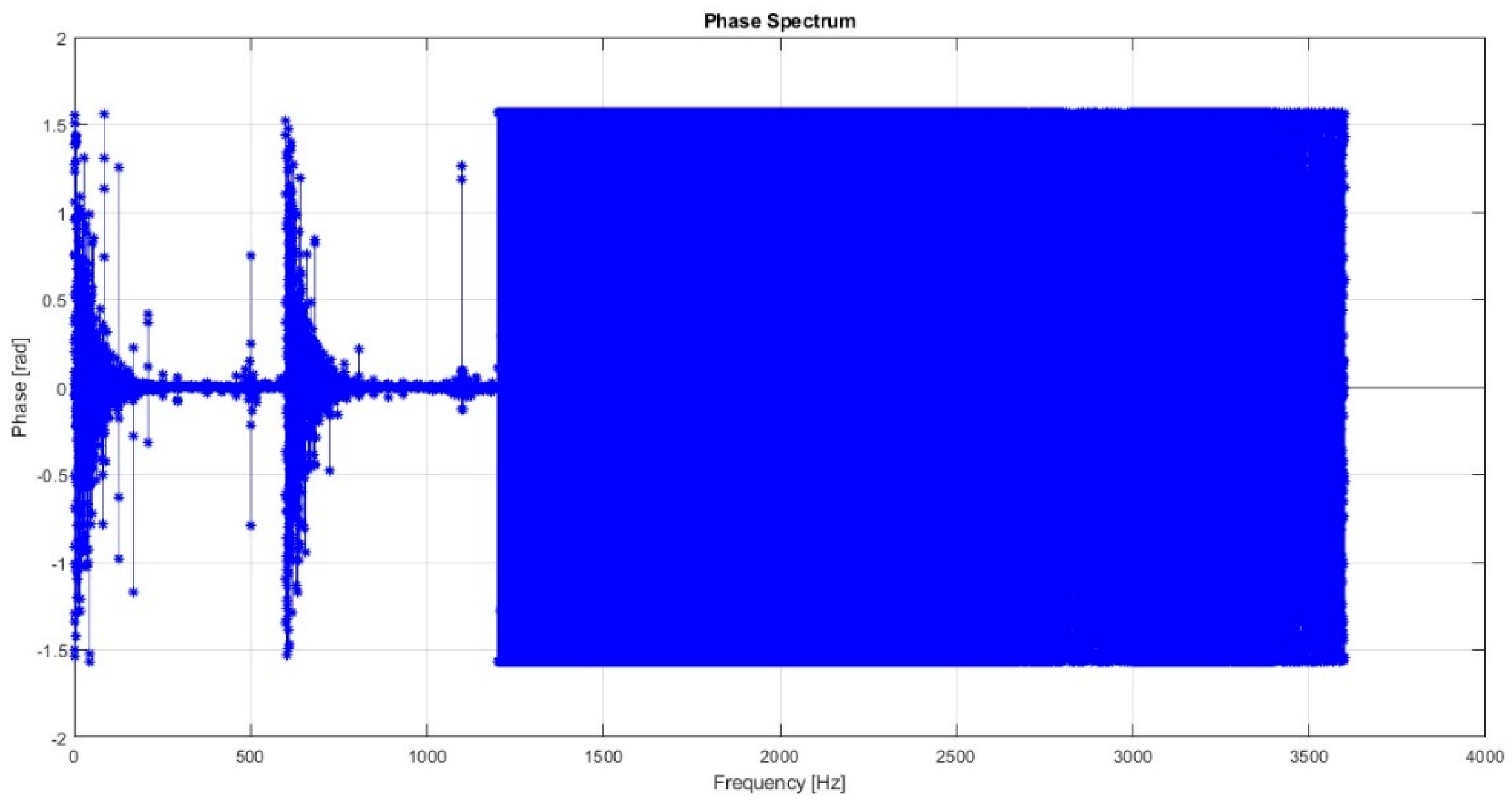
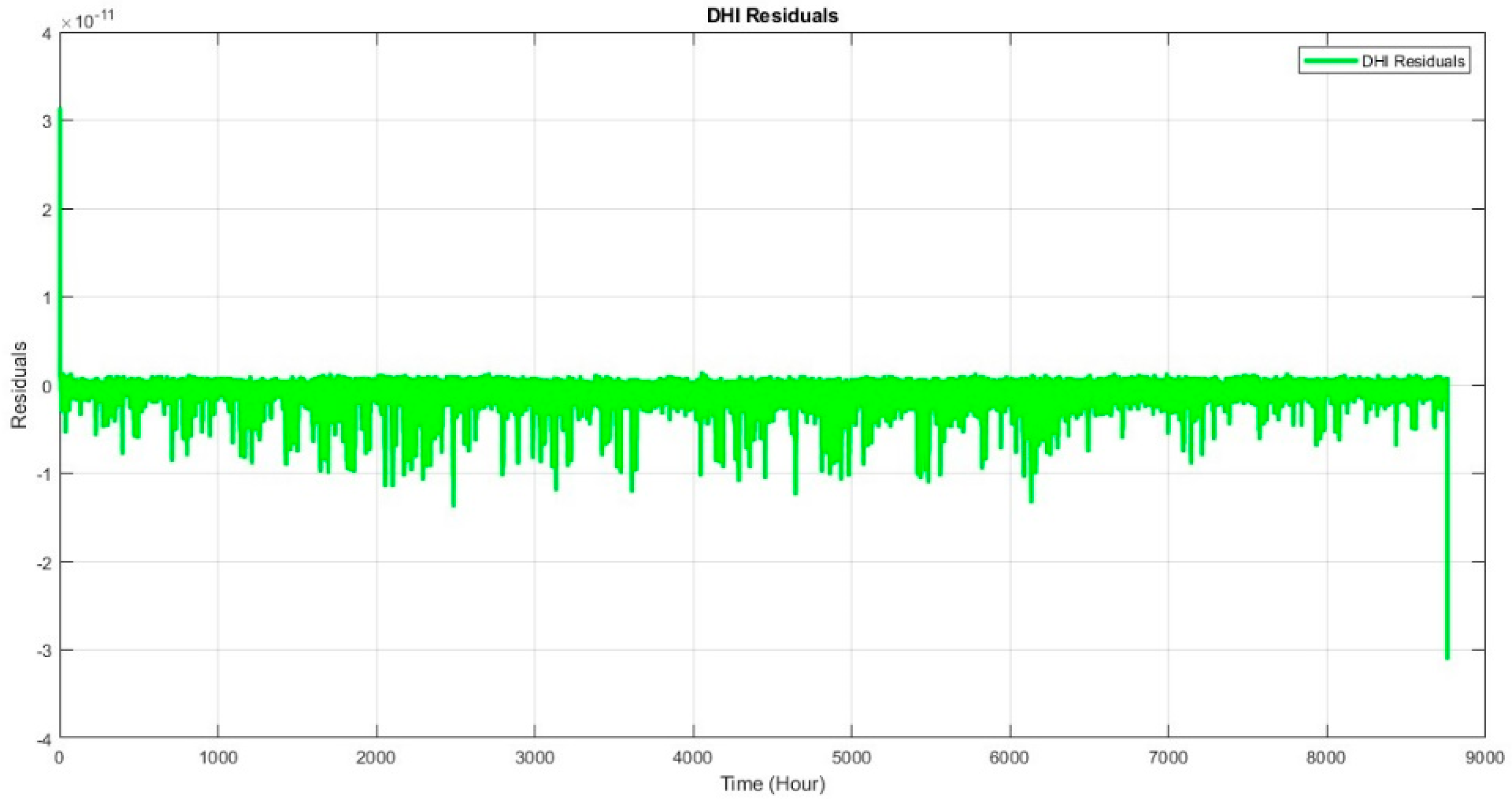
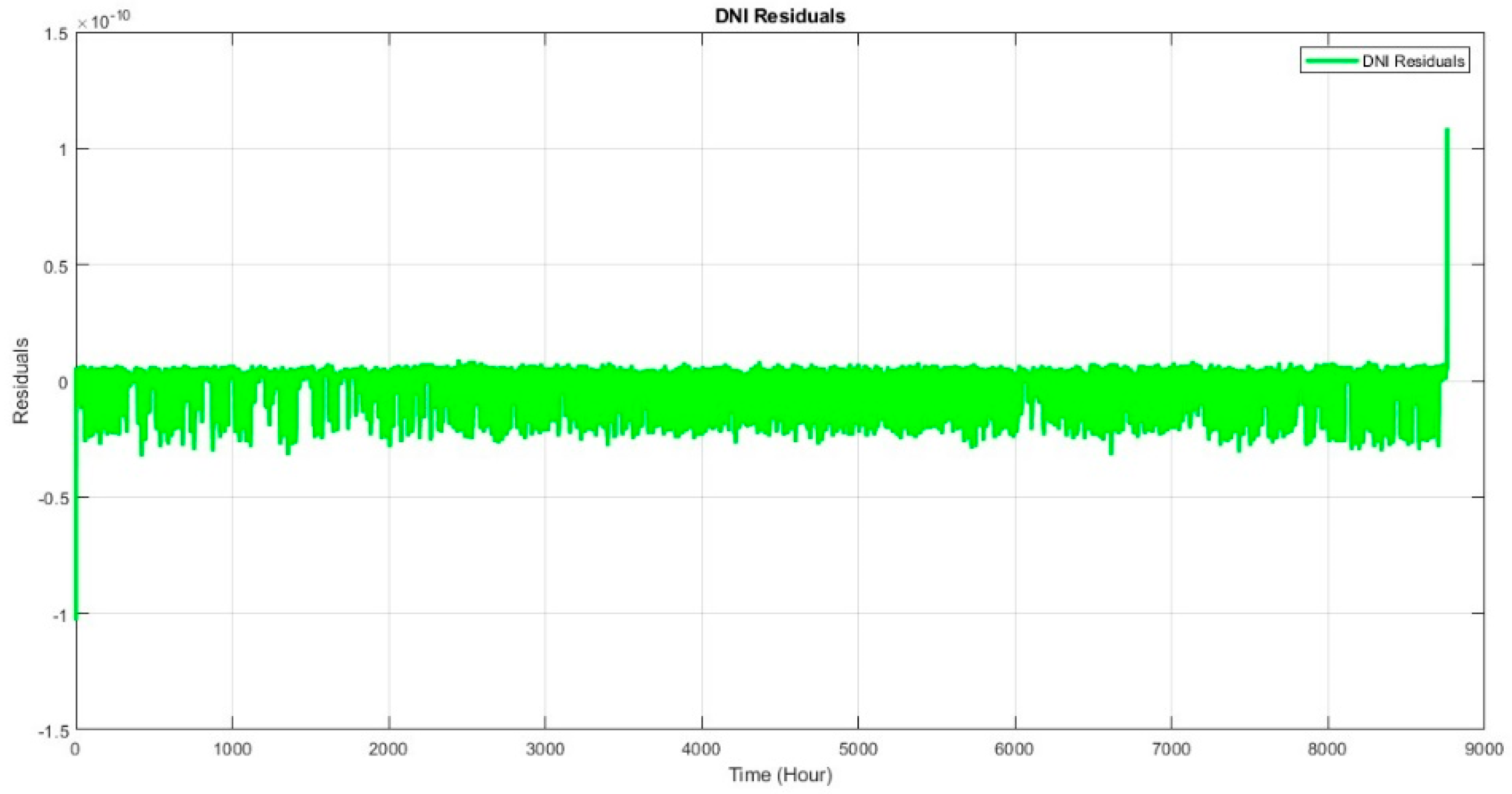
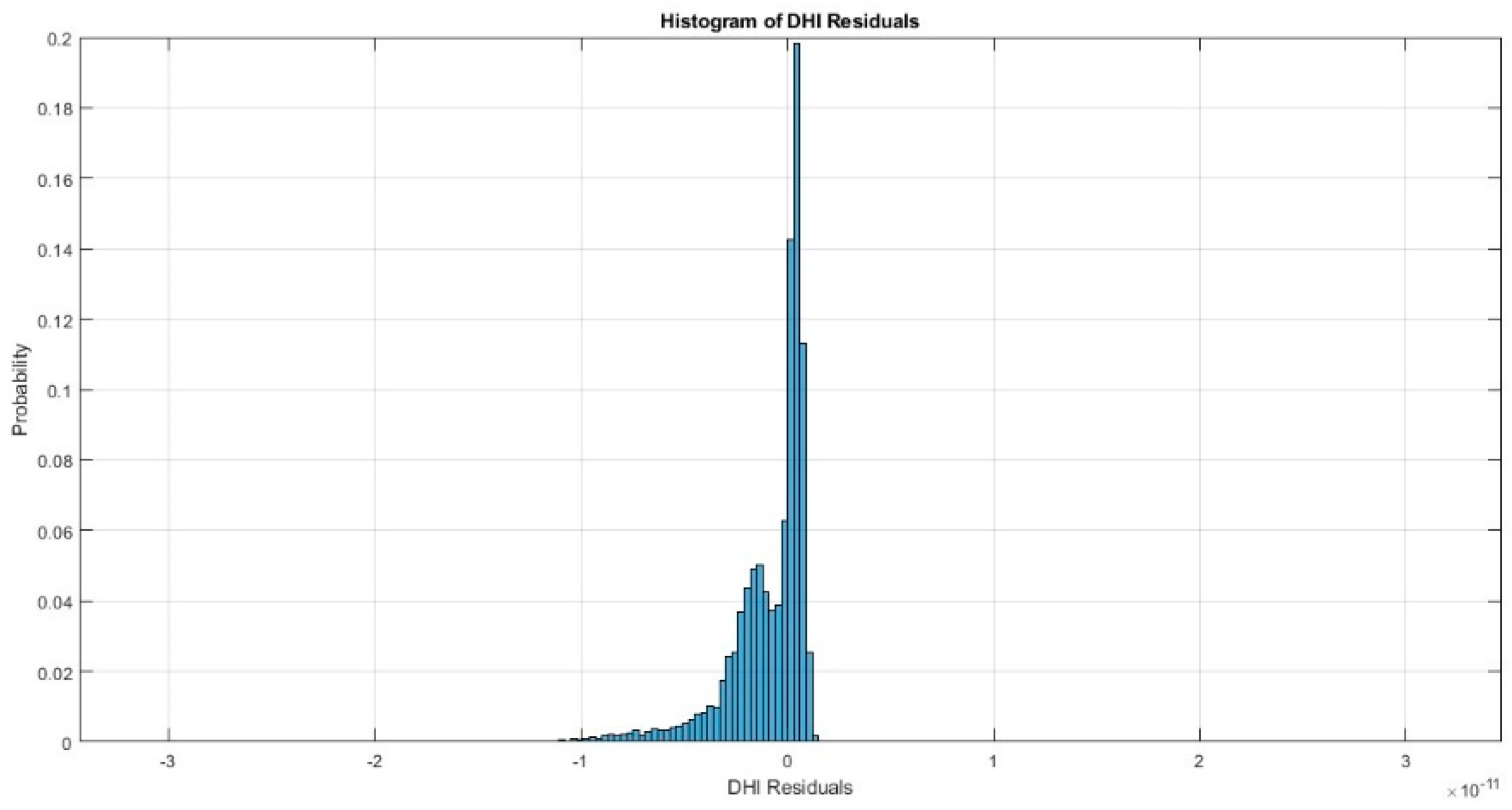
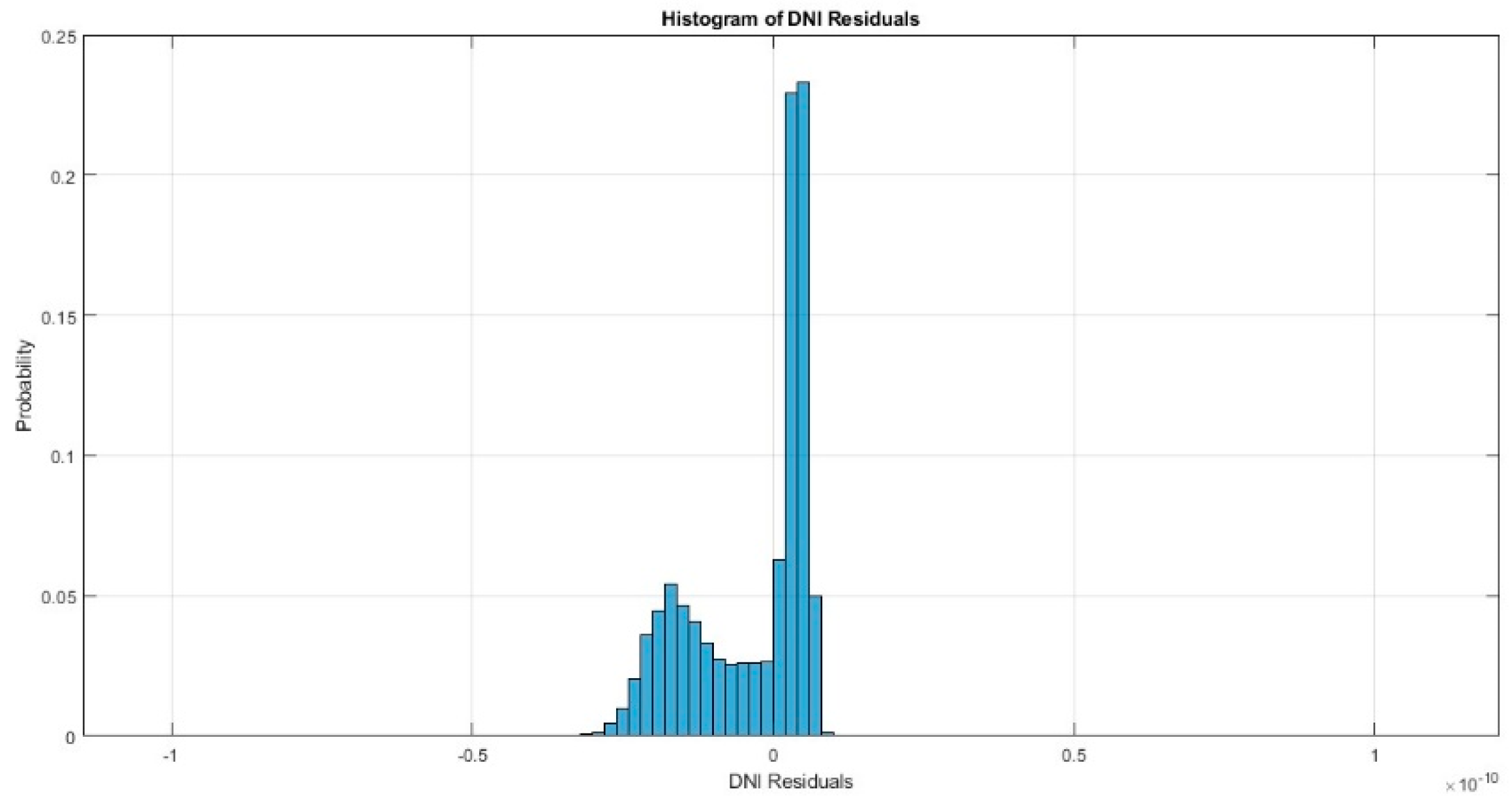
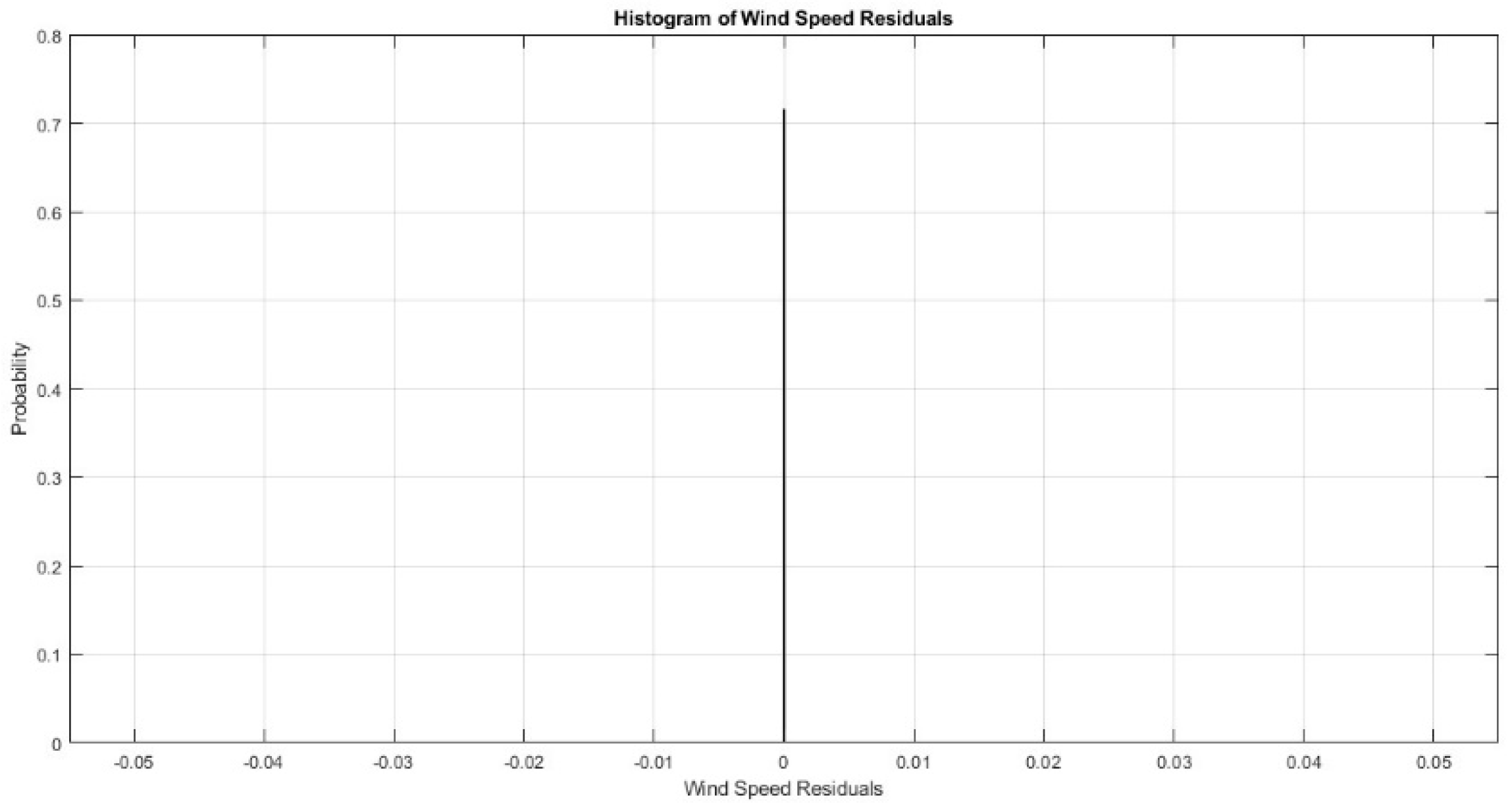
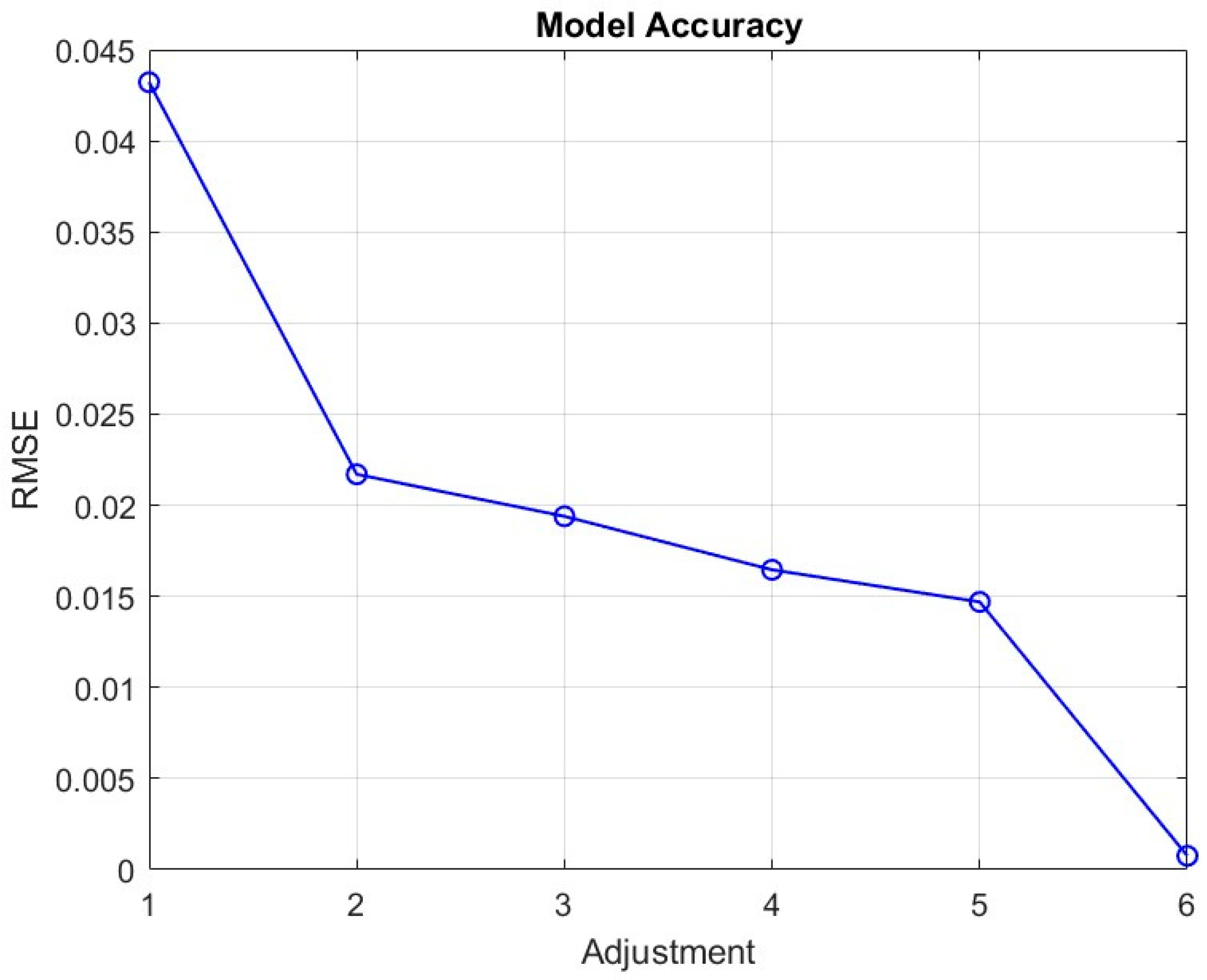
4. Results and Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviation
| Individual data points for variables A and B, respectively. | |
| The means of variables A and B. | |
| y(t) | The signal that changes over time and needs to be predicted. |
| The signal’s total time duration l. | |
| h | The time increment between each signal sample. |
| k | An index representing a specific time instant. |
| Unknown constant coefficients in a mathematical series used for prediction. | |
| The Nyquist frequency, half of the sampling angular frequency . | |
| N | The number of data points in the signal. |
| A vector used in the prediction process. | |
| A vector representing the predicted signal. | |
| ϵ | A small positive constant. |
| T | The fundamental period of the signal. |
| The fundamental angular frequency. | |
| Y | A vector containing all the signal’s sampled data points. |
| The predicted or approximated signal at a specific time instant. | |
| M | A constant term in the mathematical series. |
| The angular frequency at which the signal is sampled. | |
| W | A vector containing coefficients used for prediction. |
| Φ | A matrix of vectors used in the prediction process. |
| A mathematical operation involving the pseudo-inverse matrix. | |
| I | The identity matrix. |
| n | The number of observations in the dataset. |
| The actual values. | |
| The predicted values. |
References
- Strazzabosco, A.; Kenway, S.J.; Lant, P.A. Solar PV adoption in wastewater treatment plants: A review of practice in California. J. Environ. Manag. 2019, 248, 109337. [Google Scholar] [CrossRef] [PubMed]
- Bey, M.; Hamidat, A.; Nacer, T. Eco-energetic feasibility study of using grid-connected photovoltaic system in wastewater treatment plant. Energy 2021, 216, 119217. [Google Scholar] [CrossRef]
- Zhang, Y.; Pinoy, L.; Meesschaert, B.; Van der Bruggen, B. A natural driven membrane process for brackish and wastewater treatment: Photovoltaic powered ED and FO hybrid system. Environ. Sci. Technol. 2013, 47, 10548–10555. [Google Scholar] [CrossRef] [PubMed]
- Al-Aboosi, F.Y.; Al-Aboosi, A.F. Preliminary Evaluation of a Rooftop Grid-Connected Photovoltaic System Installation under the Climatic Conditions of Texas (USA). Energies 2021, 14, 586. [Google Scholar] [CrossRef]
- Al-Aboosi, F.Y. Models and hierarchical methodologies for evaluating solar energy availability under different sky conditions toward enhancing concentrating solar collectors use: Texas as a case study. Int. J. Energy Environ. Eng. 2020, 11, 177–205. [Google Scholar] [CrossRef]
- Yadav, A.K.; Chandel, S. Solar radiation prediction using Artificial Neural Network techniques: A review. Renew. Sustain. Energy Rev. 2014, 33, 772–781. [Google Scholar] [CrossRef]
- Sharma, N.; Sharma, P.; Irwin, D.; Shenoy, P. Predicting solar generation from weather forecasts using machine learning. In Proceedings of the 2011 IEEE International Conference on Smart Grid Communications (SmartGridComm), Brussels, Belgium, 17–20 October 2011. [Google Scholar]
- Jebli, I.; Belouadha, F.-Z.; Kabbaj, M.I.; Tilioua, A. Prediction of solar energy guided by pearson correlation using machine learning. Energy 2021, 224, 120109. [Google Scholar] [CrossRef]
- Torabi, M.; Mosavi, A.; Ozturk, P.; Varkonyi-Koczy, A.; Istvan, V. A hybrid machine learning approach for daily prediction of solar radiation. In Recent Advances in Technology Research and Education: Proceedings of the 17th International Conference on Global Research and Education Inter-Academia–2018, Kaunas, Lithuania, 24–27 September 2018; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Hassan, M.Z.; Ali, M.E.K.; Ali, A.S.; Kumar, J. Forecasting day-ahead solar radiation using machine learning approach. In Proceedings of the 2017 4th Asia-Pacific World Congress on Computer Science and Engineering (APWC on CSE), Mana Island, Fiji, 11–13 December 2017. [Google Scholar]
- González-Plaza, E.; García, D.; Prieto, J.-I. Monthly Global Solar Radiation Model Based on Artificial Neural Network, Temperature Data and Geographical and Topographical Parameters: A Case Study in Spain. Sustainability 2024, 16, 1293. [Google Scholar] [CrossRef]
- Xu, L.; Li, Y.; Wang, X.; Liu, L.; Ma, M.; Yang, J. A Machine Learning Approach to Estimating Solar Radiation Shading Rates in Mountainous Areas. Sustainability 2024, 16, 931. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, W.; Wang, J.; Han, T.; Kong, L. A novel hybrid approach for wind speed prediction. Inf. Sci. 2014, 273, 304–318. [Google Scholar] [CrossRef]
- Chang, W.-Y. A literature review of wind forecasting methods. J. Power Energy Eng. 2014, 2, 161. [Google Scholar] [CrossRef]
- DuVivier, K.; Mooney, B.T. Moat Mentality: Onshore and Offshore Approaches to Wind Waking. Notre Dame J. Emerg. Tech. 2020, 1, 1. [Google Scholar]
- Hemami, A. Wind Turbine Technology; Cengage Learning: Clifton Park, NY, USA, 2012. [Google Scholar]
- Delgado, I.; Fahim, M. Wind turbine data analysis and LSTM-based prediction in SCADA system. Energies 2020, 14, 125. [Google Scholar] [CrossRef]
- He, Y.; Kusiak, A. Performance assessment of wind turbines: Data-derived quantitative metrics. IEEE Trans. Sustain. Energy 2017, 9, 65–73. [Google Scholar] [CrossRef]
- Becker, R.; Thrän, D. Completion of wind turbine data sets for wind integration studies applying random forests and k-nearest neighbors. Appl. Energy 2017, 208, 252–262. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, S.; Li, T. Review of evaluation criteria and main methods of wind power forecasting. Energy Procedia 2011, 12, 761–769. [Google Scholar] [CrossRef]
- Wu, Y.-K.; Hong, J.-S. A literature review of wind forecasting technology in the world. In Proceedings of the 2007 IEEE Lausanne Power Tech, Lausanne, Switzerland, 1–5 July 2007; pp. 504–509. [Google Scholar]
- Lei, M.; Shiyan, L.; Chuanwen, J.; Hongling, L.; Yan, Z. A review on the forecasting of wind speed and generated power. Renew. Sustain. Energy Rev. 2009, 13, 915–920. [Google Scholar] [CrossRef]
- Firat, U.; Engin, S.N.; Saraclar, M.; Ertuzun, A.B. Wind speed forecasting based on second order blind identification and autoregressive model. In Proceedings of the 2010 Ninth International Conference on Machine Learning and Applications, Washington, DC, USA, 12–14 December 2010. [Google Scholar]
- Guo, Z.-h.; Wu, J.; Lu, H.-y.; Wang, J.-z. A case study on a hybrid wind speed forecasting method using BP neural network. Knowl. Based Syst. 2011, 24, 1048–1056. [Google Scholar] [CrossRef]
- Faria, D.L.; Castro, R.; Philippart, C.; Gusmao, A. Wavelets pre-filtering in wind speed prediction. In Proceedings of the 2009 International Conference on Power Engineering, Energy and Electrical Drives, Lisbon, Portugal, 18–20 March 2009. [Google Scholar]
- Che, G.; Zhou, D.; Wang, R.; Zhou, L.; Zhang, H.; Yu, S. Wind Energy Assessment in Forested Regions Based on the Combination of WRF and LSTM-Attention Models. Sustainability 2024, 16, 898. [Google Scholar] [CrossRef]
- Rueda-Bayona, J.G.; Cabello Eras, J.J.; Sagastume, A. Modeling Wind Speed with a Long-Term Horizon and High-Time Interval with a Hybrid Fourier-Neural Network Mode. Available online: https://www.iieta.org/journals/mmep/paper/10.18280/mmep.080313 (accessed on 2 January 2024).
- Laboratory, S.E. National Solar Radiation Data Base Sites for Texas. 2024. Available online: http://www.me.utexa (accessed on 2 January 2024).
- Midland Map. 2023. Available online: https://www.google.com/maps (accessed on 3 December 2023).
- EIA—U.S. Energy Information Administration. Use of Energy in Homes.Energy Explained. Available online: https://www.eia.gov/energyexplained/use-of-energy/homes.php (accessed on 12 February 2024).
- Lee, M.H.L.; Ser, Y.C.; Selvachandran, G.; Thong, P.H.; Cuong, L.; Son, L.H.; Tuan, N.T.; Gerogiannis, V.C. A Comparative Study of Forecasting Electricity Consumption Using Machine Learning Models. Mathematics 2022, 10, 1329. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Aboosi, A.F.; Muñoz Vazquez, A.J.; Al-Aboosi, F.Y.; El-Halwagi, M.; Zhan, W. Solar and Wind Data Recognition: Fourier Regression for Robust Recovery. Big Data Cogn. Comput. 2024, 8, 23. https://doi.org/10.3390/bdcc8030023
Al-Aboosi AF, Muñoz Vazquez AJ, Al-Aboosi FY, El-Halwagi M, Zhan W. Solar and Wind Data Recognition: Fourier Regression for Robust Recovery. Big Data and Cognitive Computing. 2024; 8(3):23. https://doi.org/10.3390/bdcc8030023
Chicago/Turabian StyleAl-Aboosi, Abdullah F., Aldo Jonathan Muñoz Vazquez, Fadhil Y. Al-Aboosi, Mahmoud El-Halwagi, and Wei Zhan. 2024. "Solar and Wind Data Recognition: Fourier Regression for Robust Recovery" Big Data and Cognitive Computing 8, no. 3: 23. https://doi.org/10.3390/bdcc8030023
APA StyleAl-Aboosi, A. F., Muñoz Vazquez, A. J., Al-Aboosi, F. Y., El-Halwagi, M., & Zhan, W. (2024). Solar and Wind Data Recognition: Fourier Regression for Robust Recovery. Big Data and Cognitive Computing, 8(3), 23. https://doi.org/10.3390/bdcc8030023






