Forecasting Human Core and Skin Temperatures: A Long-Term Series Approach
Abstract
1. Introduction
2. Materials and Methods
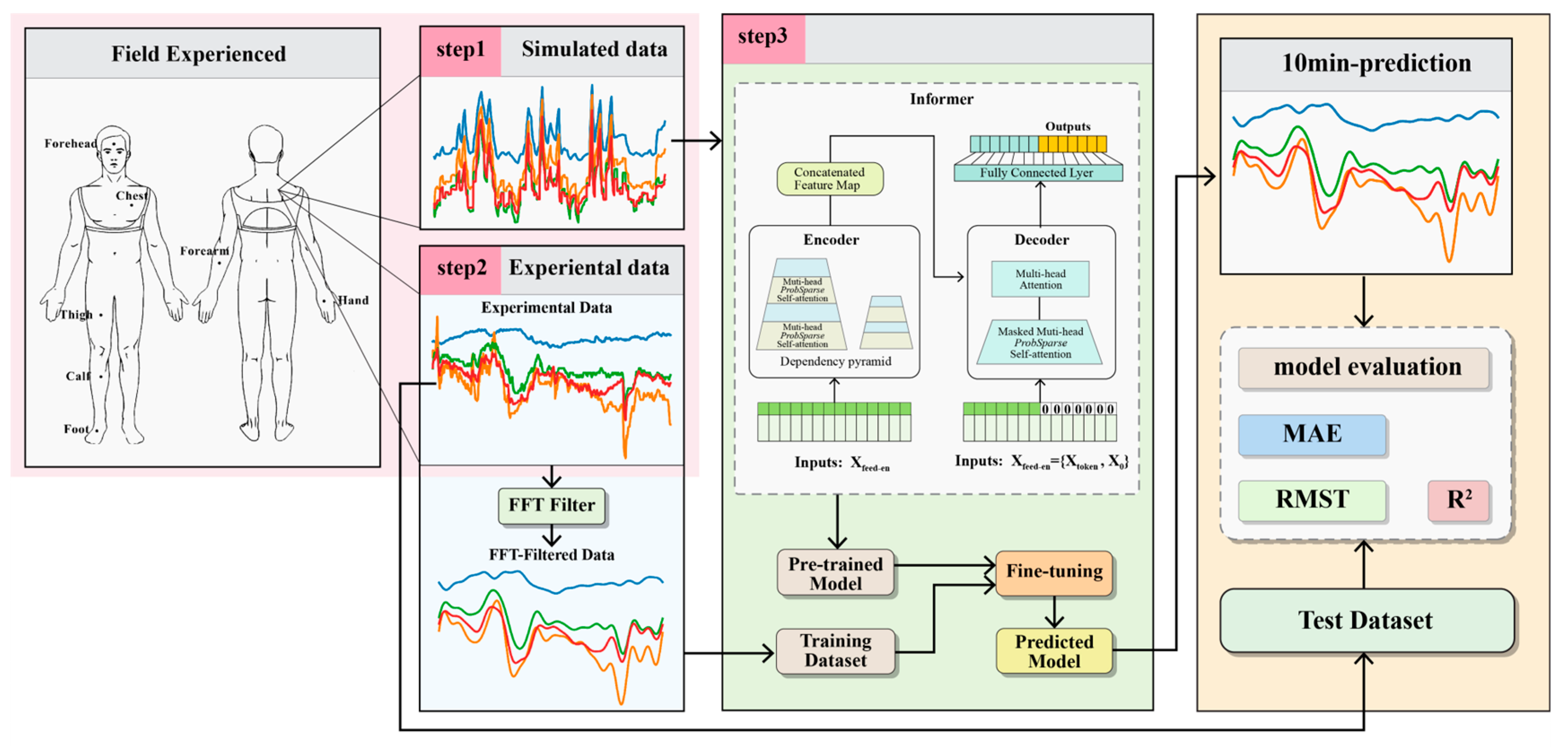
2.1. Methods
2.1.1. Thermo-Physiological Model
2.1.2. Informer
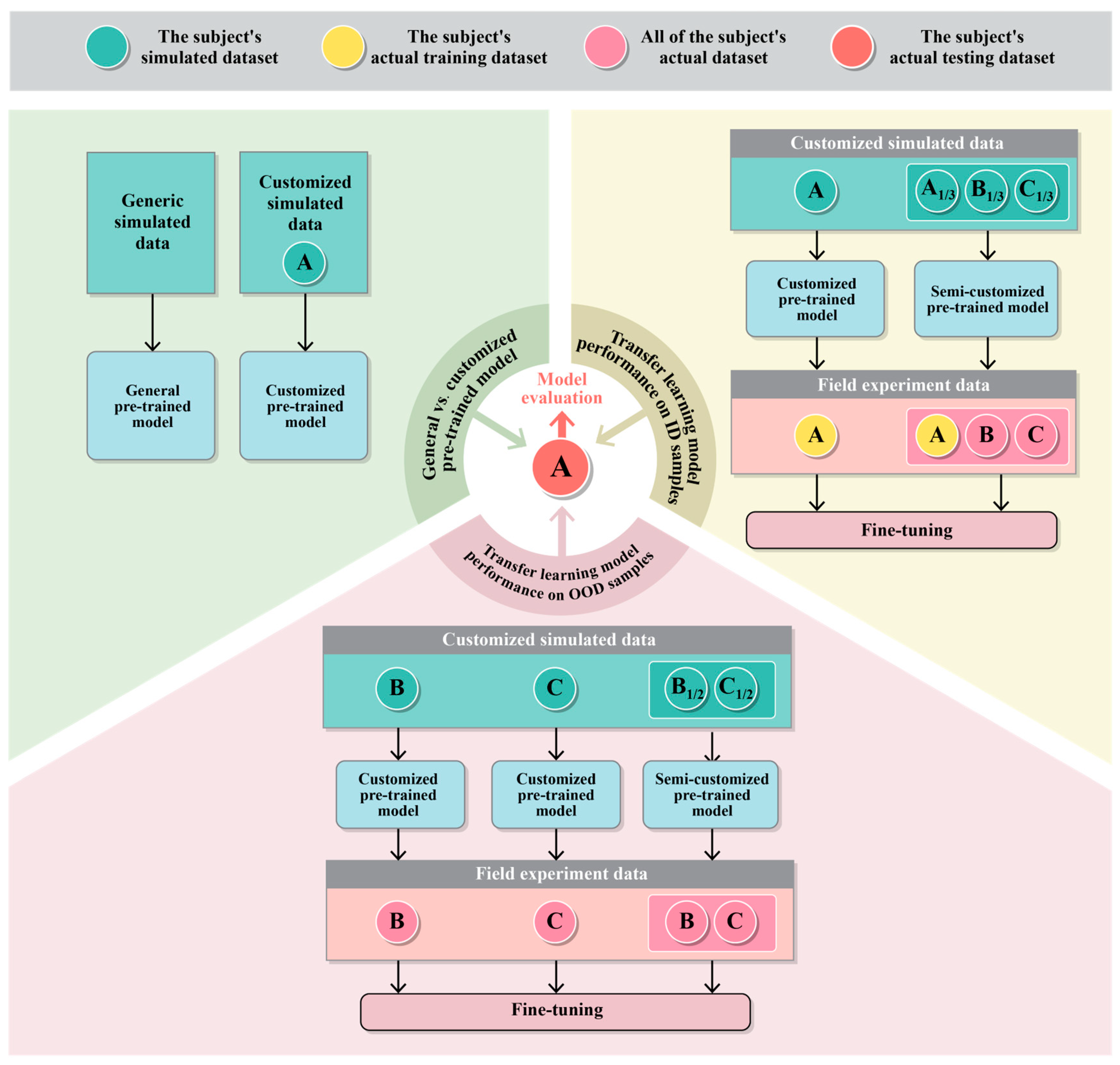
2.1.3. Transfer Learning
2.1.4. Evaluation of the Model Performance
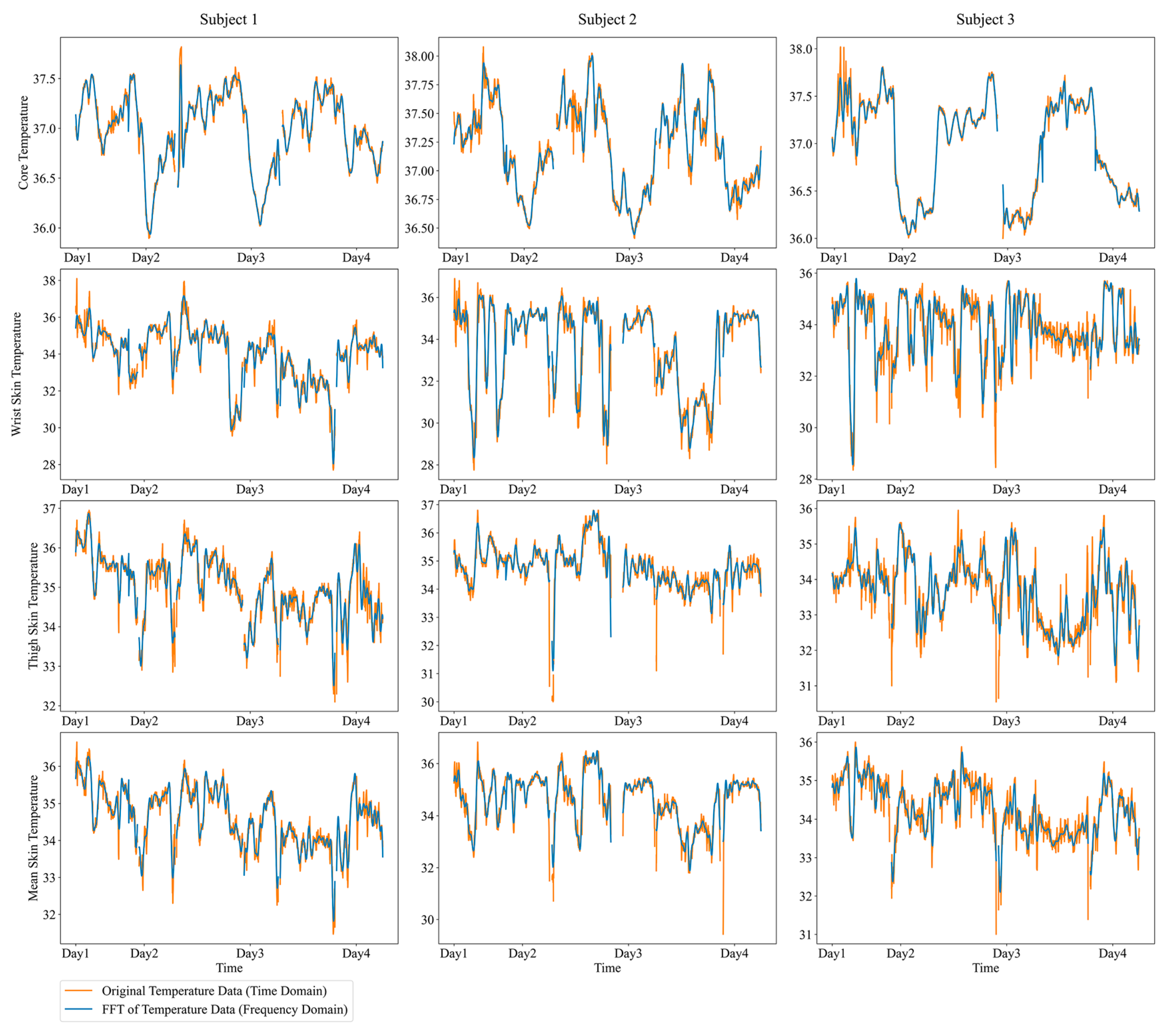
2.2. Dataset
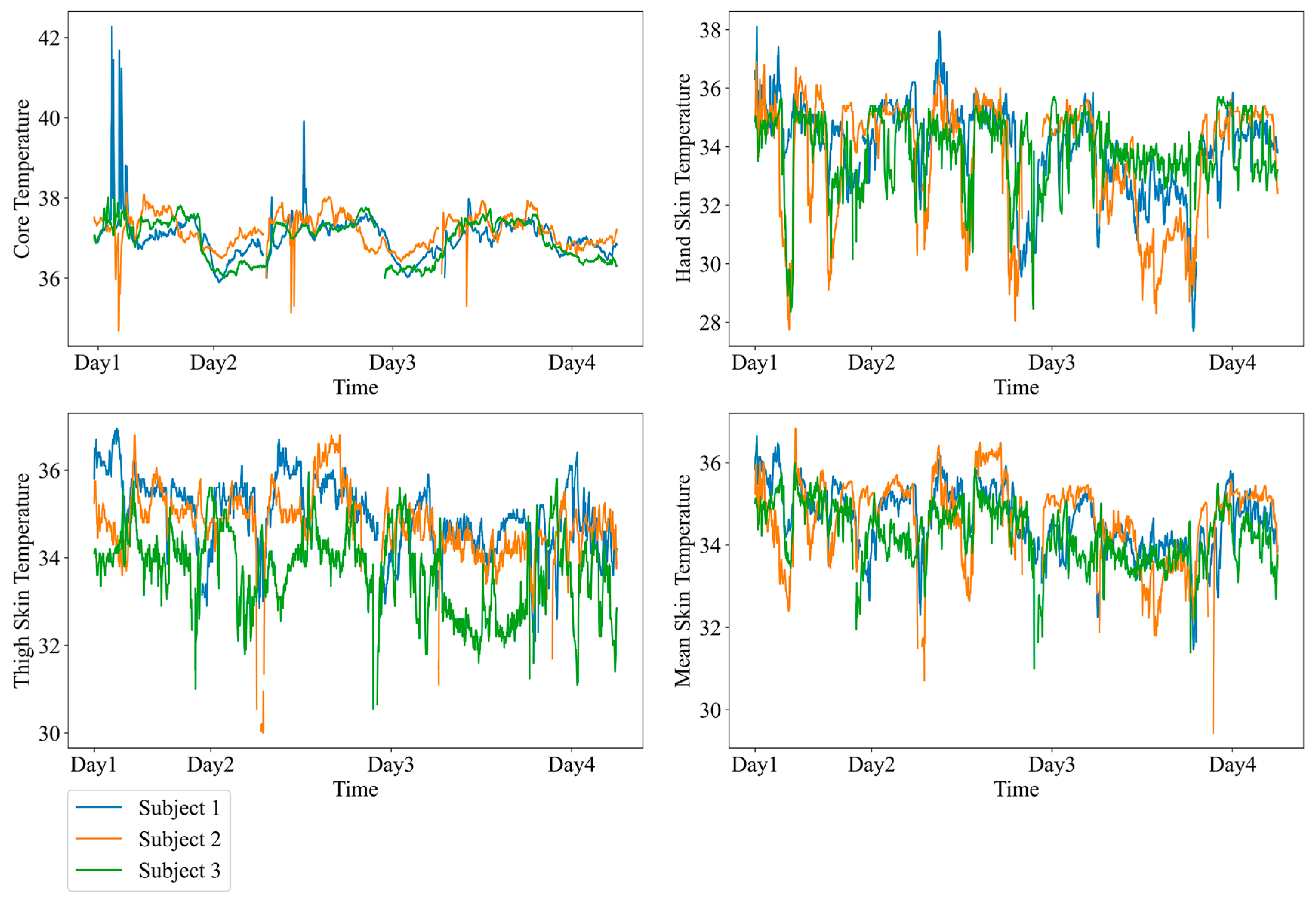
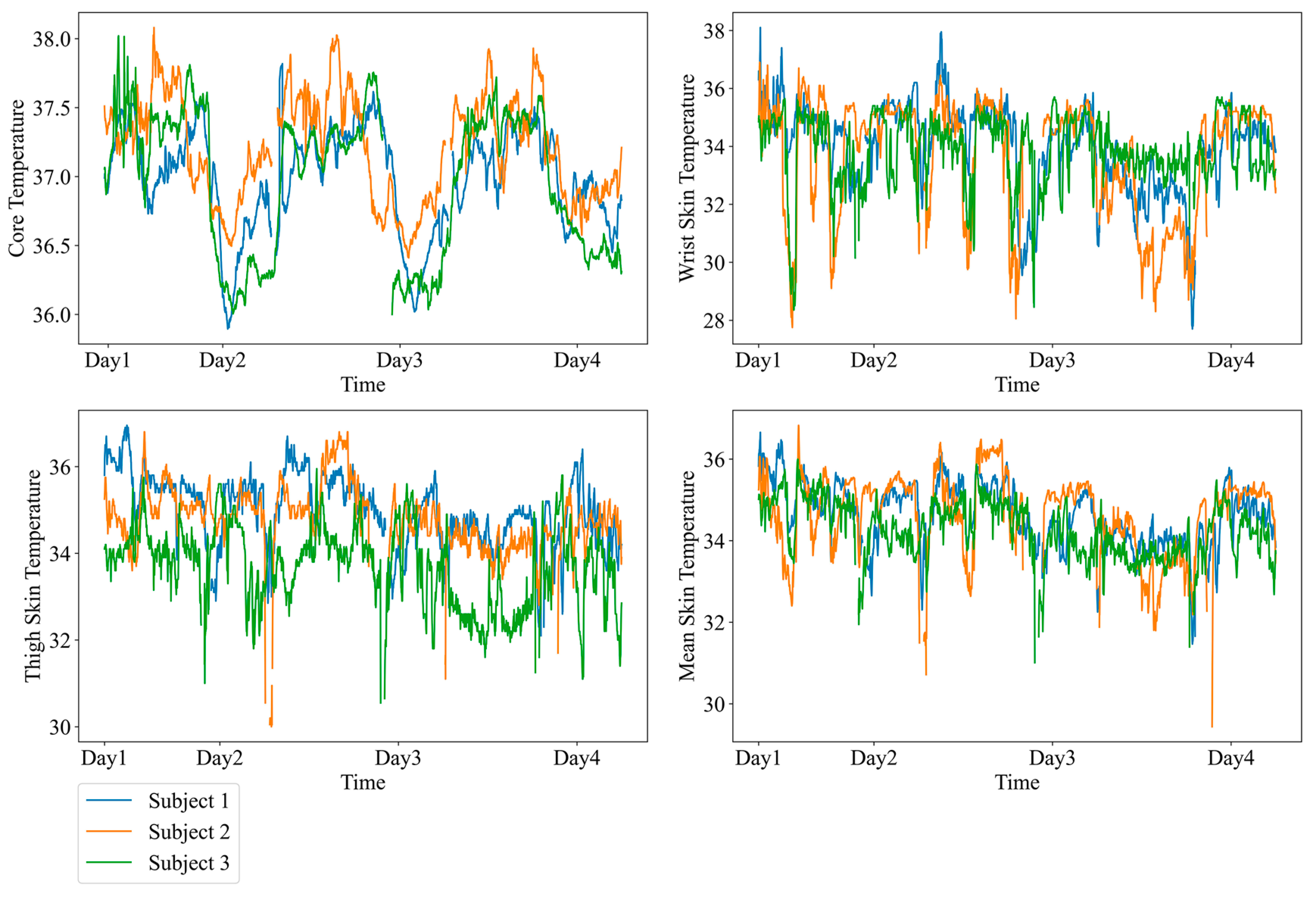
2.2.1. Experimental Dataset
2.2.2. Simulated Dataset
2.3. Model Training and Testing
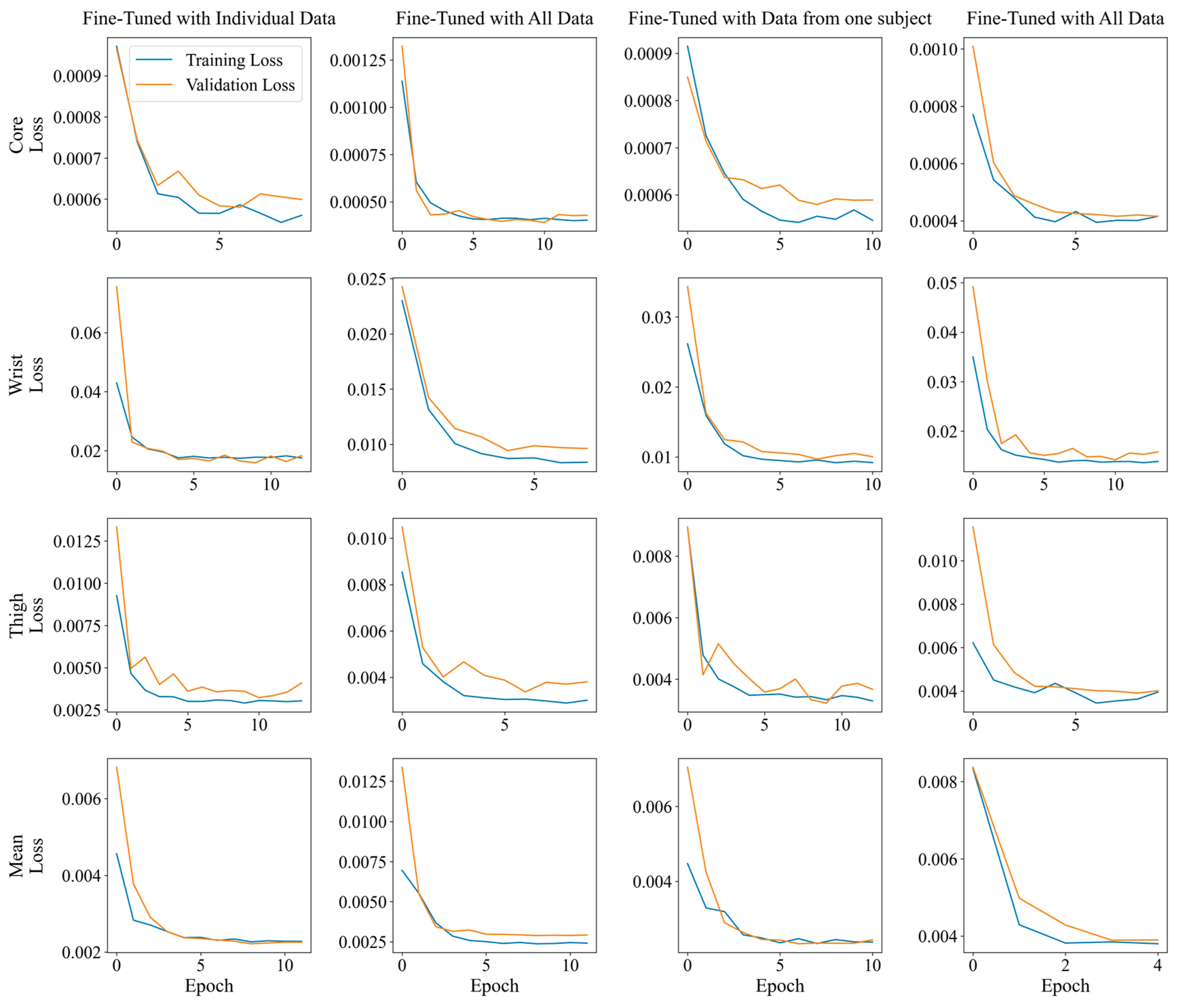
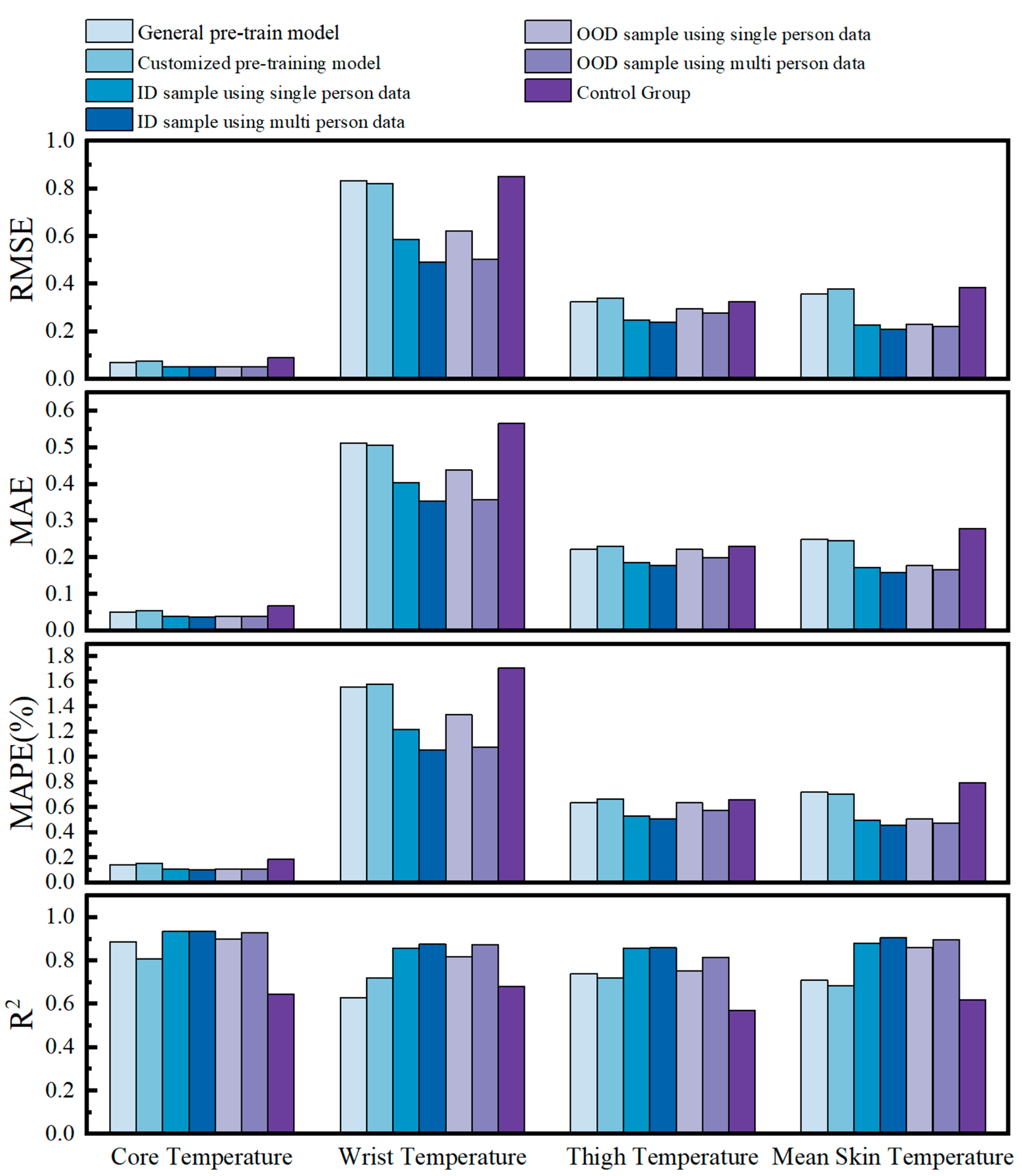
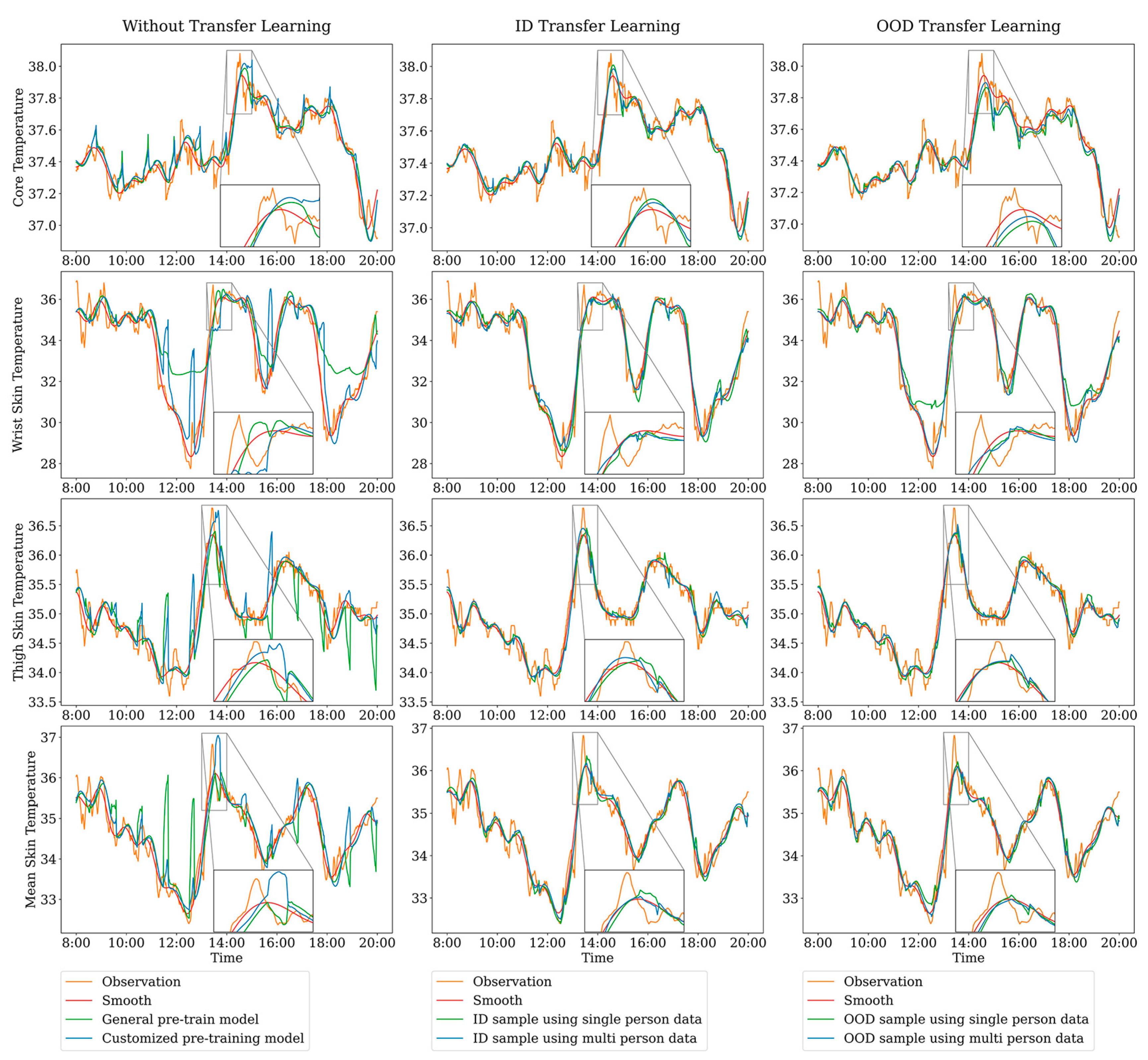
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Hyperparameter | Value |
|---|---|
| Prediction Task | Univariate Forecasting Univariate |
| Max Epoch | 20 |
| Patience | 3 |
| Activation Function | GELU |
| Initial Learning Rate | 0.00001 |
| Dropout Rate | 0.05 |
| Loss Function | Mean Squared Error (MSE) |
| Token Length | Same as Prediction Sequence Length |
| Input Sequence Length | Twice the Prediction Sequence Length |
| Attention Sampling Number | 5 |
| Model Dimension | 512 |
| Number of Heads in Multi-Head Attention | 8 |
| Number of Encoder Layers | 2 |
| Number of Decoder Layers | 1 |
| Subject ID | Age | Height (m) | Weight (kg) | Work Environment |
|---|---|---|---|---|
| 1 | 51 | 1.7 | 65 | Semi-indoor/Semi-outdoor |
| 2 | 61 | 1.68 | 61 | Outdoor |
| 3 | 33 | 1.72 | 73 | Indoor |
| Subjects | Time (h) | Temperature Level | Humidity Level | Wind Speed Level | Labor Intensity Level | Posture |
|---|---|---|---|---|---|---|
| Subject 1 | 0–7 | 1 | 2 | 0 | 0 | Lying |
| 7–8 | 2 | 2 | 0/1 | 0 | Standing | |
| 8–10 | 2/3 | 1 | 0 | 1/2 | Standing | |
| 10–12 | 2/3/4 | 1 | 0 | 1/2 | Standing | |
| 12–13 | 1 | 1 | 0 | 0 | Sitting | |
| 13–14 | 1 | 1 | 0 | 1/2 | Sitting | |
| 14–17 | 2/3/4 | 1 | 0 | 1/2 | Standing | |
| 17–18 | 2/3 | 1 | 0 | 1/2 | Standing | |
| 18–19 | 1/2 | 1 | 0 | 1/2 | Sitting | |
| 19–20 | 2/3 | 1 | 0 | 1/2 | Standing | |
| 20–21 | 2/3 | 1 | 0/1 | 1/2 | Standing | |
| 21–24 | 1 | 1 | 0 | 0 | Sitting | |
| Subject 2 | 0–7 | 1 | 2 | 0 | 0 | Lying |
| 7–8 | 2 | 2 | 0/1 | 1/2 | Standing | |
| 8–10 | 2/3 | 1 | 0 | 1/2 | Standing | |
| 10–12 | 2/3/4 | 1 | 0 | 1/2 | Standing | |
| 12–13 | 1 | 1 | 0/1 | 0 | Sitting | |
| 13–14 | 1 | 1 | 0/1 | 1/2 | Sitting | |
| 14–17 | 2/3/4 | 1 | 0/1 | 1/2 | Standing | |
| 17–18 | 2/3 | 1 | 0/1 | 1/2 | Standing | |
| 18–19 | 1/2 | 1 | 0/1 | 0/1 | Sitting | |
| 19–21 | 1/2 | 1 | 0/1 | 0 | Sitting | |
| 21–24 | 1 | 1 | 0 | 0 | Lying | |
| Subject 3 | 0–7 | 1 | 2 | 0 | 0 | Lying |
| 7–8 | 1/2 | 2 | 0 | 0 | Standing | |
| 8–10 | 1/2 | 1 | 0 | 1/2 | Standing | |
| 10–12 | 2 | 1 | 0 | 1/2 | Standing | |
| 12–13 | 1 | 1 | 0 | 0 | Sitting | |
| 13–14 | 1 | 1 | 0 | 1/2 | Sitting | |
| 14–17 | 2/3 | 1 | 0 | 1/2 | Standing | |
| 17–18 | 1/2 | 1 | 0 | 1/2 | Standing | |
| 18–19 | 1 | 1 | 0 | 1/2 | Sitting | |
| 19–20 | 1/2 | 1 | 0 | 1/2 | Standing | |
| 20–21 | 1/2 | 1 | 0 | 1/2 | Standing | |
| 21–24 | 1 | 1 | 0 | 0 | Sitting |
| Parameters | Level | Range |
|---|---|---|
| Air Temperature | 0 | 23–26 (°C) |
| 1 | 27–30 (°C) | |
| 2 | 31–33 (°C) | |
| 3 | 34–37 (°C) | |
| 4 | 38–42(°C) | |
| Air Humidity | 0 | 0–30 (%) |
| 1 | 31–60 (%) | |
| 2 | 61–95 (%) | |
| Wind Speed | 0 | 0–1.5 (m/s) |
| 1 | 1.6–3.3 (m/s) | |
| 2 | 3.4–5.4 (m/s) | |
| 3 | 5.5–7.9 (m/s) | |
| 4 | 8.0–10.7 (m/s) | |
| PAR [54] | 0 | 1–2.5 |
| 1 | 2.6–3.9 | |
| 2 | 4.0–7.0 |
| Simulated Environment | Time (h) | Temperature Level | Humidity Level | Wind Speed Level | Labor Intensity Level | Posture |
|---|---|---|---|---|---|---|
| Daily Outdoor Work | 0–7 | 0 | 1 | 0 | 0 | Lying |
| 7–9 | 0 | 1 | 0 | 0 | Sitting | |
| 9–10 | 1 | 2 | 3 | 2 | Standing | |
| 10–12 | 2 | 2 | 2 | 2 | Standing | |
| 12–13 | 1 | 1 | 0 | 0 | Sitting | |
| 13–16 | 3 | 2 | 1 | 1 | Standing | |
| 16–18 | 2 | 2 | 3 | 2 | Standing | |
| 18–20 | 2 | 1 | 2 | 1 | Sitting | |
| 20–24 | 0 | 1 | 0 | 0 | Sitting | |
| Extreme Outdoor Work | 0–7 | 0 | 1 | 0 | 0 | Lying |
| 7–9 | 0 | 1 | 0 | 0 | Sitting | |
| 9–10 | 2 | 2 | 3 | 2 | Standing | |
| 10–12 | 3 | 2 | 4 | 2 | Standing | |
| 12–13 | 1 | 1 | 0 | 0 | Sitting | |
| 13–16 | 4 | 2 | 1 | 1 | Standing | |
| 16–18 | 3 | 2 | 3 | 2 | Standing | |
| 18–20 | 2 | 1 | 2 | 1 | Sitting | |
| 20–24 | 0 | 1 | 0 | 0 | Sitting | |
| Indoor Work | 0–7 | 0 | 1 | 0 | 0 | Lying |
| 7–9 | 0 | 1 | 0 | 0 | Sitting | |
| 9–10 | 1 | 2 | 0 | 2 | Sitting | |
| 10–12 | 1 | 2 | 0 | 2 | Sitting | |
| 12–13 | 2 | 1 | 0 | 0 | Sitting | |
| 13–16 | 1 | 2 | 0 | 1 | Sitting | |
| 16–18 | 1 | 2 | 0 | 2 | Sitting | |
| 18–20 | 2 | 1 | 0 | 1 | Sitting | |
| 20–24 | 0 | 1 | 0 | 0 | Sitting |


References
- Heikens, M.J.; Gorbach, A.M.; Eden, H.S.; Savastano, D.M.; Chen, K.Y.; Skarulis, M.C.; Yanovski, J.A. Core Body Temperature in Obesity. Am. J. Clin. Nutr. 2011, 93, 963–967. [Google Scholar] [CrossRef] [PubMed]
- Pascoe, D.D.; Mercer, J.B.; de Weerd, L. Physiology of Thermal Signals. In Medical Devices and Systems; CRC Press: Boca Raton, FL, USA, 2006; pp. 447–466. ISBN 0429123043. [Google Scholar]
- Joshi, A.; Wang, F.; Kang, Z.; Yang, B.; Zhao, D. A Three-Dimensional Thermoregulatory Model for Predicting Human Thermophysiological Responses in Various Thermal Environments. Build. Environ. 2022, 207, 108506. [Google Scholar] [CrossRef]
- Fiala, D.; Lomas, K.J.; Stohrer, M. Computer Prediction of Human Thermoregulatory and Temperature Responses to a Wide Range of Environmental Conditions. Int. J. Biometeorol. 2001, 45, 143–159. [Google Scholar] [CrossRef] [PubMed]
- Tanabe, S.; Kobayashi, K.; Nakano, J.; Ozeki, Y.; Konishi, M. Evaluation of Thermal Comfort Using Combined Multi-Node Thermoregulation (65MN) and Radiation Models and Computational Fluid Dynamics (CFD). Energy Build. 2002, 34, 637–646. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Tanabe, S. Development of JOS-2 Human Thermoregulation Model with Detailed Vascular System. Build. Environ. 2013, 66, 1–10. [Google Scholar] [CrossRef]
- Huizenga, C.; Hui, Z.; Arens, E. A Model of Human Physiology and Comfort for Assessing Complex Thermal Environments. Build. Environ. 2001, 36, 691–699. [Google Scholar] [CrossRef]
- Gulati, T.; Hatwar, R.; Unnikrishnan, G.; Rubio, J.E.; Reifman, J. A 3-D Virtual Human Model for Simulating Heat and Cold Stress. J. Appl. Physiol. 2022, 133, 288–310. [Google Scholar] [CrossRef] [PubMed]
- Unnikrishnan, G.; Hatwar, R.; Hornby, S.; Laxminarayan, S.; Gulati, T.; Belval, L.N.; Giersch, G.E.W.; Kazman, J.B.; Casa, D.J.; Reifman, J. A 3-D Virtual Human Thermoregulatory Model to Predict Whole-Body and Organ-Specific Heat-Stress Responses. Eur. J. Appl. Physiol. 2021, 121, 2543–2562. [Google Scholar] [CrossRef]
- Wu, Z.; Yang, R.; Qian, X.; Yang, L.; Lin, M. A Multi-Segmented Human Bioheat Model under Immersed Conditions. Int. J. Therm. Sci. 2023, 185, 108029. [Google Scholar] [CrossRef]
- Salloum, M.; Ghaddar, N.; Ghali, K. A New Transient Bioheat Model of the Human Body and Its Integration to Clothing Models. Int. J. Therm. Sci. 2007, 46, 371–384. [Google Scholar] [CrossRef]
- Younes, J.; Chen, M.; Ghali, K.; Kosonen, R.; Melikov, A.K.; Ghaddar, N. A Thermal Sensation Model for Elderly under Steady and Transient Uniform Conditions. Build. Environ. 2023, 227, 109797. [Google Scholar] [CrossRef]
- Davoodi, F.; Hassanzadeh, H.; Zolfaghari, S.A.; Havenith, G.; Maerefat, M. A New Individualized Thermoregulatory Bio-Heat Model for Evaluating the Effects of Personal Characteristics on Human Body Thermal Response. Build. Environ. 2018, 136, 62–76. [Google Scholar] [CrossRef]
- Fu, M.; Weng, W.; Chen, W.; Luo, N. Review on Modeling Heat Transfer and Thermoregulatory Responses in Human Body. J. Therm. Biol. 2016, 62, 189–200. [Google Scholar] [CrossRef] [PubMed]
- Petersson, J.; Kuklane, K.; Gao, C. Is There a Need to Integrate Human Thermal Models with Weather Forecasts to Predict Thermal Stress? Int. J. Environ. Res. Public. Health 2019, 16, 4586. [Google Scholar] [CrossRef]
- Makhlouf, K.; Hmidi, Z.; Kahloul, L.; Benhrazallah, S.; Ababsa, T. On the Forecasting of Body Temperature Using Iot and Machine Learning Techniques. In Proceedings of the 2021 International Conference on Theoretical and Applicative Aspects of Computer Science (ICTAACS), Skikda, Algeria, 15–16 December 2021; pp. 1–6. [Google Scholar]
- Staffini, A.; Svensson, T.; Chung, U.; Svensson, A.K. Heart Rate Modeling and Prediction Using Autoregressive Models and Deep Learning. Sensors 2021, 22, 34. [Google Scholar] [CrossRef] [PubMed]
- Nazarian, N.; Liu, S.; Kohler, M.; Lee, J.K.W.; Miller, C.; Chow, W.T.L.; Alhadad, S.B.; Martilli, A.; Quintana, M.; Sunden, L. Project Coolbit: Can Your Watch Predict Heat Stress and Thermal Comfort Sensation? Environ. Res. Lett. 2021, 16, 034031. [Google Scholar] [CrossRef]
- Boudreault, J.; Campagna, C.; Chebana, F. Machine and Deep Learning for Modelling Heat-Health Relationships. Sci. Total Environ. 2023, 892, 164660. [Google Scholar] [CrossRef] [PubMed]
- Dasari, A.; Revanur, A.; Jeni, L.A.; Tucker, C.S. Video-Based Elevated Skin Temperature Detection. IEEE Trans. Biomed. Eng. 2023, 70, 2430–2444. [Google Scholar] [CrossRef] [PubMed]
- Carluccio, G.; Erricolo, D.; Oh, S.; Collins, C.M. An Approach to Rapid Calculation of Temperature Change in Tissue Using Spatial Filters to Approximate Effects of Thermal Conduction. IEEE Trans. Biomed. Eng. 2013, 60, 1735–1741. [Google Scholar] [CrossRef]
- Zhong, W.; Mallick, T.; Meidani, H.; Macfarlane, J.; Balaprakash, P. Explainable Graph Pyramid Autoformer for Long-Term Traffic Forecasting. arXiv 2022, arXiv:2209.13123. [Google Scholar] [CrossRef]
- Pan, G.; Wu, Q.; Ding, G.; Wang, W.; Li, J.; Zhou, B. An Autoformer-CSA Approach for Long-Term Spectrum Prediction. IEEE Wirel. Commun. Lett. 2023, 12, 1647–1651. [Google Scholar] [CrossRef]
- Jiang, Y.; Gao, T.; Dai, Y.; Si, R.; Hao, J.; Zhang, J.; Gao, D.W. Very Short-Term Residential Load Forecasting Based on Deep-Autoformer. Appl. Energy 2022, 328, 120120. [Google Scholar] [CrossRef]
- Gong, M.; Zhao, Y.; Sun, J.; Han, C.; Sun, G.; Yan, B. Load Forecasting of District Heating System Based on Informer. Energy 2022, 253, 124179. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, L.; Li, N.; Tian, J. Time Series Forecasting of Motor Bearing Vibration Based on Informer. Sensors 2022, 22, 5858. [Google Scholar] [CrossRef]
- Wang, C.; Mahadevan, S. Heterogeneous Domain Adaptation Using Manifold Alignment. IJCAI Proc.-Int. Jt. Conf. Artif. Intell. 2011, 22, 1541. [Google Scholar]
- Duan, L.; Xu, D.; Tsang, I. Learning with Augmented Features for Heterogeneous Domain Adaptation. arXiv 2012, arXiv:1206.4660. [Google Scholar] [CrossRef]
- Kulis, B.; Saenko, K.; Darrell, T. What You Saw Is Not What You Get: Domain Adaptation Using Asymmetric Kernel Transforms. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; pp. 1785–1792. [Google Scholar]
- Zhu, Y.; Chen, Y.; Lu, Z.; Pan, S.; Xue, G.-R.; Yu, Y.; Yang, Q. Heterogeneous Transfer Learning for Image Classification. AAAI Conf. Artif. Intell. 2011, 25, 1304–1309. [Google Scholar] [CrossRef]
- Radočaj, P.; Radočaj, D.; Martinović, G. Image-Based Leaf Disease Recognition Using Transfer Deep Learning with a Novel Versatile Optimization Module. Big Data Cogn. Comput. 2024, 8, 52. [Google Scholar] [CrossRef]
- Harel, M.; Mannor, S. Learning from Multiple Outlooks. arXiv 2010, arXiv:1005.0027. [Google Scholar] [CrossRef]
- Shu, Z.; Zhou, Y.; Zhang, J.; Jin, J.; Wang, L.; Cui, N.; Wang, G.; Zhang, J.; Wu, H.; Wu, Z.; et al. Parameter Regionalization Based on Machine Learning Optimizes the Estimation of Reference Evapotranspiration in Data Deficient Area. Sci. Total Environ. 2022, 844, 157034. [Google Scholar] [CrossRef]
- Nam, J.; Kim, S. Heterogeneous Defect Prediction. In Proceedings of the 2015 10th Joint Meeting on Foundations of Software Engineering, Bergamo Italy, 30 August–4 September 2015; pp. 508–519. [Google Scholar]
- Zhang, W.; Wang, Z.; Li, X. Blockchain-Based Decentralized Federated Transfer Learning Methodology for Collaborative Machinery Fault Diagnosis. Reliab. Eng. Syst. Saf. 2023, 229, 108885. [Google Scholar] [CrossRef]
- Mao, W.; Zhang, W.; Feng, K.; Beer, M.; Yang, C. Tensor Representation-Based Transferability Analytics and Selective Transfer Learning of Prognostic Knowledge for Remaining Useful Life Prediction across Machines. Reliab. Eng. Syst. Saf. 2024, 242, 109695. [Google Scholar] [CrossRef]
- Abdelhamid, S.; Hegazy, I.; Aref, M.; Roushdy, M. Attention-Driven Transfer Learning Model for Improved IoT Intrusion Detection. Big Data Cogn. Comput. 2024, 8, 116. [Google Scholar] [CrossRef]
- Prettenhofer, P.; Stein, B. Cross-Language Text Classification Using Structural Correspondence Learning. In Proceedings of the 48th Annual Meeting of the Association for Computational Linguistics, Uppsala, Sweden, 11–16 July 2010; pp. 1118–1127. [Google Scholar]
- Zhou, J.T.; Tsang, I.W.; Pan, S.J.; Tan, M. Heterogeneous Domain Adaptation for Multiple Classes. Artif. Intell. Stat. PMLR 2014, 33, 1095–1103. [Google Scholar]
- Zhou, J.; Pan, S.; Tsang, I.; Yan, Y. Hybrid Heterogeneous Transfer Learning through Deep Learning. AAAI Conf. Artif. Intell. 2014, 28, 2213–2219. [Google Scholar] [CrossRef]
- Takahashi, Y.; Nomoto, A.; Yoda, S.; Hisayama, R.; Ogata, M.; Ozeki, Y.; Tanabe, S. Thermoregulation Model JOS-3 with New Open Source Code. Energy Build. 2021, 231, 110575. [Google Scholar] [CrossRef]
- Stolwijk, J.A.J. A Mathematical Model of Physiological Temperature Regulation in Man; NASA, Yale University: New Haven, CT, USA, 1971. [Google Scholar]
- Oyama, T.; Fujii, M.; Nakajima, K.; Takakura, J.; Hijioka, Y. Validation of Upper Thermal Thresholds for Outdoor Sports Using Thermal Physiology Modelling. Temperature 2023, 11, 92–106. [Google Scholar] [CrossRef]
- Choudhary, B. Udayraj Validity of the JOS-3 Model for Male Tropical Population and Analysis of Their Thermal Comfort. Sādhanā 2023, 48, 208. [Google Scholar] [CrossRef]
- Jia, X.; Li, S.; Zhu, Y.; Ji, W.; Cao, B. Transient Thermal Comfort and Physiological Responses Following a Step Change in Activity Status under Summer Indoor Environments. Energy Build. 2023, 285, 112918. [Google Scholar] [CrossRef]
- Liang, H.; Tanabe, S.; Niu, J. Coupled Simulation of CFD and Human Thermoregulation Model in Outdoor Wind Environment. E3S Web Conf. 2023, 396, 05008. [Google Scholar] [CrossRef]
- d’Ambrosio Alfano, F.R.; Palella, B.I.; Riccio, G. THERMODE 2023: Formulation and Validation of a New Thermo-Physiological Model for Moderate Environments. Build. Environ. 2024, 252, 111272. [Google Scholar] [CrossRef]
- Choudhary, B. A Coupled CFD-Thermoregulation Model for Air Ventilation Clothing. Energy Build. 2022, 268, 112206. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. AAAI Conf. Artif. Intell. 2021, 35, 11106–11115. [Google Scholar] [CrossRef]
- Wang, G.; Bai, H. Study on the Climate Changes in Cangzhou in Recent 38 Years. Meteorol. Environ. Res. 2012, 3, 16–17+23. [Google Scholar]
- Service, T.W.; Junker, K.; Service, B.; Coehoorn, C.J.; Harrington, M.; Martin, S.; Stuart-Hill, L.A. An Assessment of the Validity and Reliability of the P022–P Version of e-Celsius Core Temperature Capsules. J. Therm. Biol. 2023, 112, 103486. [Google Scholar] [CrossRef] [PubMed]
- Hardy, J.D.; Du Bois, E.F.; Soderstrom, G.F. The Technic of Measuring Radiation and Convection: One Figure. J. Nutr. 1938, 15, 461–475. [Google Scholar] [CrossRef]
- Buller, M.J.; Tharion, W.J.; Cheuvront, S.N.; Montain, S.J.; Kenefick, R.W.; Castellani, J.; Latzka, W.A.; Roberts, W.S.; Richter, M.; Jenkins, O.C. Estimation of Human Core Temperature from Sequential Heart Rate Observations. Physiol. Meas. 2013, 34, 781. [Google Scholar] [CrossRef] [PubMed]
- Joint FAO/WHO/UNU. Human Energy Requirements: Report of a Joint FAO/WHO/UNU Expert Consultation, Rome, 17–24 October 2001; UNU/WHO/FAO: Rome, Italy, 2004. [Google Scholar]
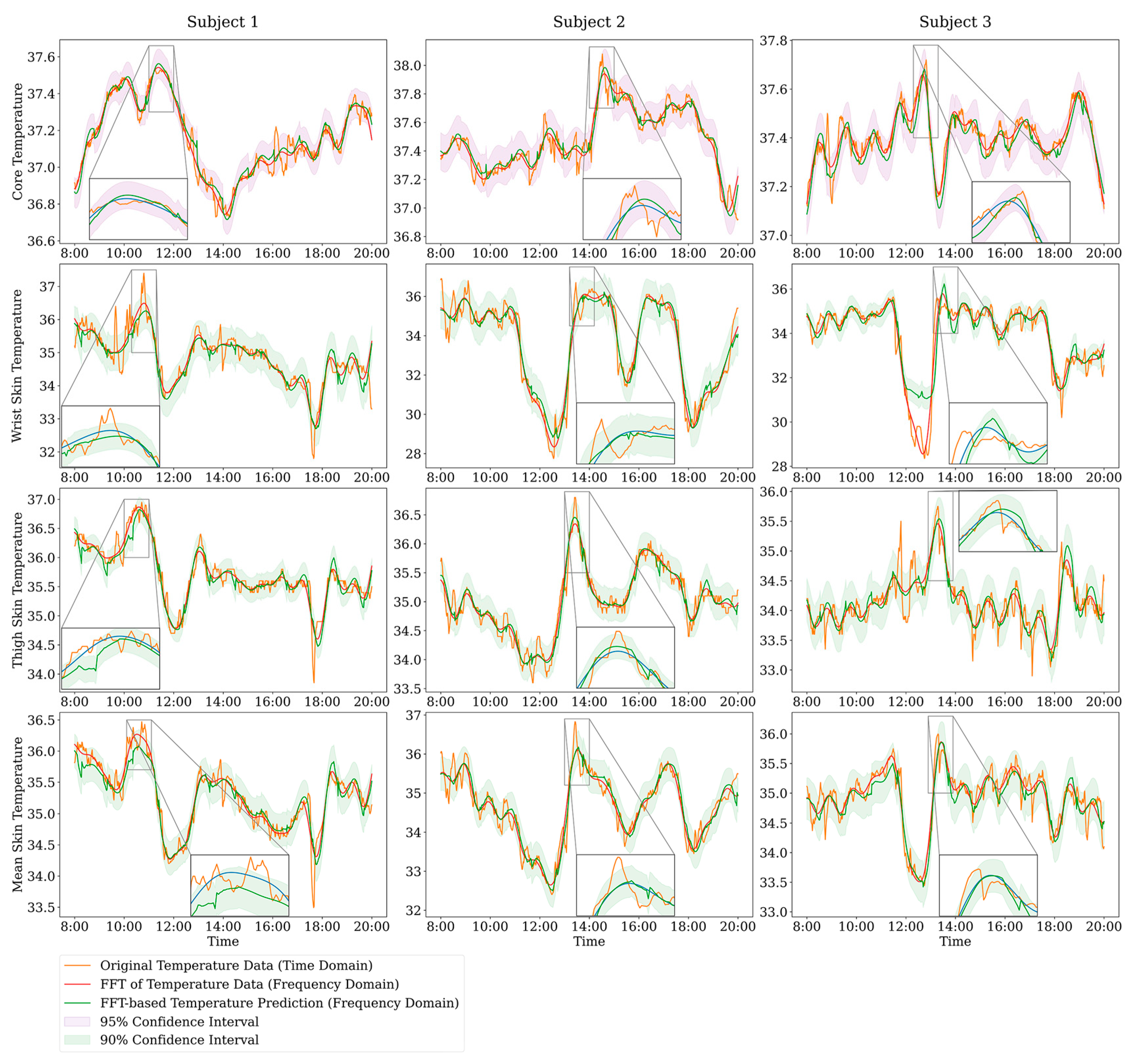
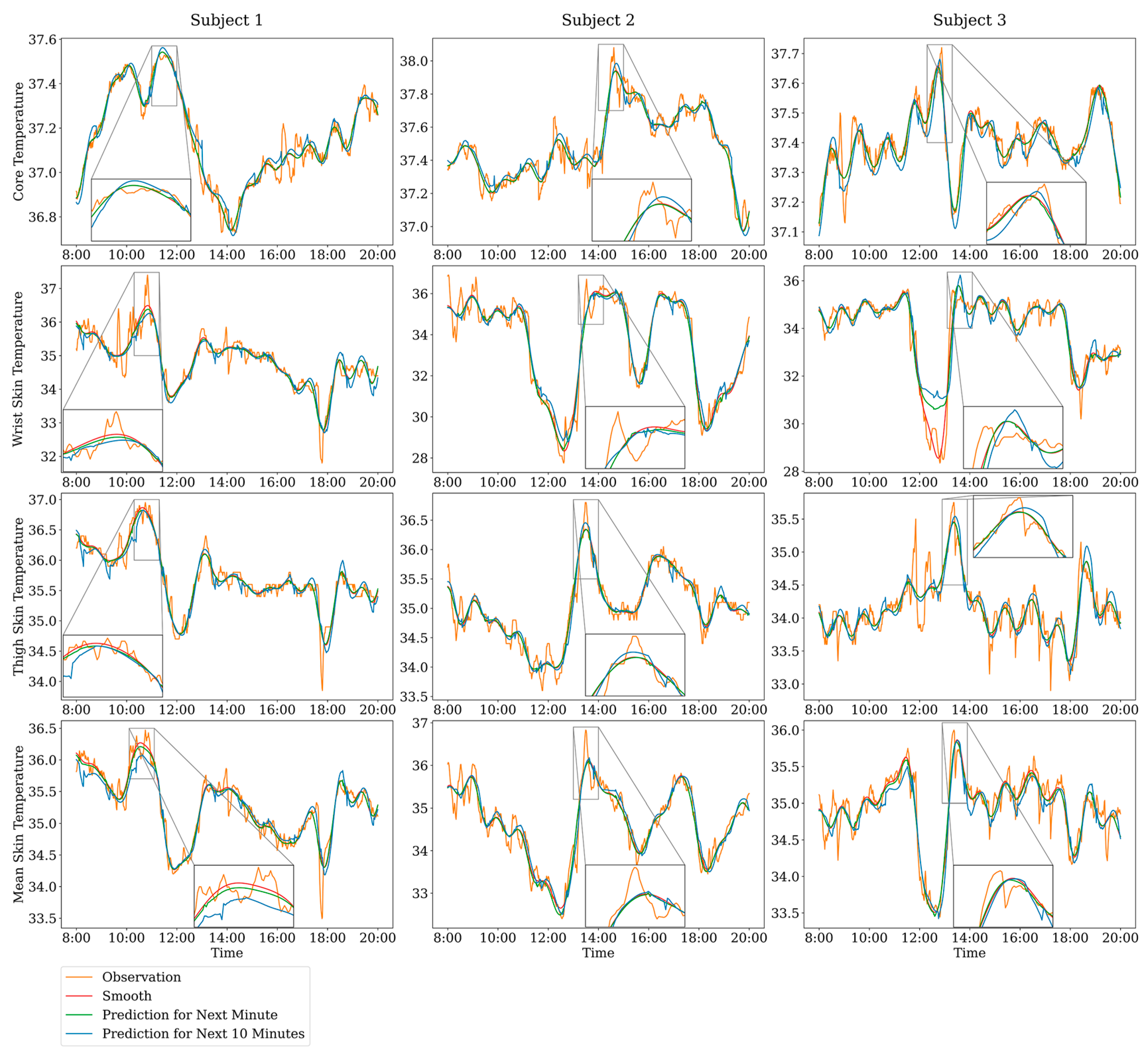
| Participant ID | Amount of Tcr Data | Amount of Tsk Data |
|---|---|---|
| 1 | 4168 | 4108 |
| 2 | 4123 | 3952 |
| 3 | 4158 | 4133 |
| Predicted Part | Evaluation Metric | Customized Pretrained Model | Generic Pretrained Model | Control Group | ||
|---|---|---|---|---|---|---|
| Training Set | Test Set | Training Set | Test Set | |||
| Tcr | RMSE | 0.056 | 0.069 | 0.060 | 0.077 | 0.09 |
| MAE | 0.028 | 0.052 | 0.030 | 0.056 | 0.068 | |
| MAPE (%) | 0.075 | 0.138 | 0.080 | 0.149 | 0.183 | |
| R2 | 0.996 | 0.889 | 0.993 | 0.808 | 0.644 | |
| Thand | RMSE | 0.186 | 0.832 | 0.349 | 0.820 | 0.851 |
| MAE | 0.079 | 0.512 | 0.155 | 0.505 | 0.565 | |
| MAPE (%) | 0.240 | 1.558 | 0.485 | 1.580 | 1.708 | |
| R2 | 0.939 | 0.628 | 0.983 | 0.719 | 0.680 | |
| Tthigh | RMSE | 0.164 | 0.325 | 0.322 | 0.341 | 0.324 |
| MAE | 0.073 | 0.222 | 0.149 | 0.231 | 0.230 | |
| MAPE (%) | 0.209 | 0.636 | 0.429 | 0.664 | 0.660 | |
| R2 | 0.969 | 0.741 | 0.983 | 0.719 | 0.569 | |
| Tsk,mean | RMSE | 0.165 | 0.359 | 0.303 | 0.379 | 0.385 |
| MAE | 0.072 | 0.250 | 0.137 | 0.246 | 0.278 | |
| MAPE (%) | 0.207 | 0.720 | 0.393 | 0.706 | 0.795 | |
| R2 | 0.965 | 0.709 | 0.984 | 0.685 | 0.618 | |
| Predicted Part | Evaluation Metric | Fine-Tuned with Individual Data | Fine-Tuned with All Data | Control Group | ||
|---|---|---|---|---|---|---|
| Training Set | Test Set | Training Set | Test Set | |||
| Tcr | RMSE | 0.048 | 0.052 | 0.050 | 0.051 | 0.09 |
| MAE | 0.033 | 0.039 | 0.032 | 0.037 | 0.068 | |
| MAPE (%) | 0.089 | 0.106 | 0.086 | 0.100 | 0.183 | |
| R2 | 0.991 | 0.934 | 0.989 | 0.936 | 0.644 | |
| Thand | RMSE | 0.509 | 0.585 | 0.448 | 0.491 | 0.851 |
| MAE | 0.362 | 0.403 | 0.333 | 0.353 | 0.565 | |
| MAPE (%) | 1.095 | 1.220 | 0.992 | 1.051 | 1.708 | |
| R2 | 0.926 | 0.858 | 0.953 | 0.876 | 0.680 | |
| Tthigh | RMSE | 0.196 | 0.247 | 0.181 | 0.240 | 0.324 |
| MAE | 0.146 | 0.185 | 0.135 | 0.177 | 0.230 | |
| MAPE (%) | 0.419 | 0.531 | 0.386 | 0.507 | 0.660 | |
| R2 | 0.896 | 0.858 | 0.916 | 0.860 | 0.569 | |
| Tsk,mean | RMSE | 0.220 | 0.228 | 0.220 | 0.209 | 0.385 |
| MAE | 0.171 | 0.173 | 0.170 | 0.159 | 0.278 | |
| MAPE (%) | 0.489 | 0.495 | 0.486 | 0.455 | 0.795 | |
| R2 | 0.924 | 0.879 | 0.922 | 0.905 | 0.618 | |
| Predicted Part | Evaluation Metric | Fine-Tuned with Data from One Subject | Fine-Tuned with All Data | Control Group | ||
|---|---|---|---|---|---|---|
| Training Set | Test Set | Training Set | Test Set | |||
| Tcr | RMSE | 0.052 | 0.054 | 0.052 | 0.052 | 0.09 |
| MAE | 0.039 | 0.040 | 0.037 | 0.039 | 0.068 | |
| MAPE (%) | 0.104 | 0.107 | 0.100 | 0.105 | 0.183 | |
| R2 | 0.984 | 0.901 | 0.987 | 0.928 | 0.644 | |
| Thand | RMSE | 0.568 | 0.623 | 0.469 | 0.502 | 0.851 |
| MAE | 0.407 | 0.438 | 0.341 | 0.357 | 0.565 | |
| MAPE (%) | 1.240 | 1.335 | 1.031 | 1.079 | 1.708 | |
| R2 | 0.867 | 0.820 | 0.945 | 0.873 | 0.680 | |
| Tthigh | RMSE | 0.215 | 0.296 | 0.192 | 0.277 | 0.324 |
| MAE | 0.163 | 0.222 | 0.144 | 0.200 | 0.230 | |
| MAPE (%) | 0.466 | 0.635 | 0.413 | 0.574 | 0.660 | |
| R2 | 0.817 | 0.752 | 0.896 | 0.816 | 0.569 | |
| Tsk,mean | RMSE | 0.243 | 0.231 | 0.226 | 0.220 | 0.385 |
| MAE | 0.193 | 0.177 | 0.176 | 0.166 | 0.278 | |
| MAPE (%) | 0.553 | 0.507 | 0.503 | 0.475 | 0.795 | |
| R2 | 0.870 | 0.860 | 0.911 | 0.898 | 0.618 | |
| Predicted Part | Confidence Interval | Participant 1 | Participant 2 | Participant 3 |
|---|---|---|---|---|
| Tcr | 95% | ±0.08 | ±0.13 | ±0.08 |
| Thand | 90% | ±0.53 | ±0.96 | ±0.48 |
| Tthigh | 90% | ±0.21 | ±0.28 | ±0.36 |
| Tsk,mean | 90% | ±0.27 | ±0.43 | ±0.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, X.; Wu, J.; Hu, Z.; Li, C.; Sun, B. Forecasting Human Core and Skin Temperatures: A Long-Term Series Approach. Big Data Cogn. Comput. 2024, 8, 197. https://doi.org/10.3390/bdcc8120197
Han X, Wu J, Hu Z, Li C, Sun B. Forecasting Human Core and Skin Temperatures: A Long-Term Series Approach. Big Data and Cognitive Computing. 2024; 8(12):197. https://doi.org/10.3390/bdcc8120197
Chicago/Turabian StyleHan, Xinge, Jiansong Wu, Zhuqiang Hu, Chuan Li, and Boyang Sun. 2024. "Forecasting Human Core and Skin Temperatures: A Long-Term Series Approach" Big Data and Cognitive Computing 8, no. 12: 197. https://doi.org/10.3390/bdcc8120197
APA StyleHan, X., Wu, J., Hu, Z., Li, C., & Sun, B. (2024). Forecasting Human Core and Skin Temperatures: A Long-Term Series Approach. Big Data and Cognitive Computing, 8(12), 197. https://doi.org/10.3390/bdcc8120197






