A Comparative Study of Secure Outsourced Matrix Multiplication Based on Homomorphic Encryption
Abstract
1. Introduction
- We provide a detailed analysis of the state of the art in HE matrix multiplication algorithms with fixed-point numbers.
- We evaluate the impact of different operating systems and libraries on their performance.
- We apply curve fitting to derive high-precision extrapolation formulas for homomorphic multiplication of larger matrices.
2. Related Work
2.1. Privacy-Preservation in Deep Learning
2.2. Matrix Multiplication in Privacy-Preserving Neural Networks
3. Homomorphic Encryption Libraries
| Library | Numbers with Fixed-Point | Integer Numbers | Language | OS | CPU | GPU | Ref. | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CKKS | TFHE | BFV | BGV | LTV | DHS | FHEW | YASHE | Windows | Linux | |||||
| Microsoft SEAL | ● | ● | C++ | ● | ● | ● | [48] | |||||||
| PALISADE | ● | ● | ● | ● | ● | C++ | ● | ● | ● | [49] | ||||
| HEAAN | ● | C++ | ● | ● | [58] | |||||||||
| cuYASHE | ● | C++ | ● | ● | [85] | |||||||||
| HElib | ● | ● | C++ | ● | ● | [69] | ||||||||
| FHEW | ● | C++ | ● | ● | [75] | |||||||||
| TFHE | ● | C++ | ● | ● | [77] | |||||||||
| NuFHE | ● | Python | ● | ● | ● | [78] | ||||||||
| Lattigo | ● | ● | Go | ● | ● | ● | [79] | |||||||
| ● | Haskell | ● | ● | ● | ● | [80] | ||||||||
| cuHE | ● | ● | C++ | ● | ● | ● | [81] | |||||||
| Concrete | ● | Rust | ● | ● | [83] | |||||||||
| cuFHE | ● | C++ | ● | ● | [84] | |||||||||
| node-seal | ● | ● | TypeScript | ● | ● | ● | [86] | |||||||
| Pyfhel | ● | ● | Python | ● | ● | ● | [87] | |||||||
| SEAL-python | ● | ● | Python | ● | ● | ● | [88] | |||||||
4. Secure Matrix Multiplication
- .
- .
- .
- .
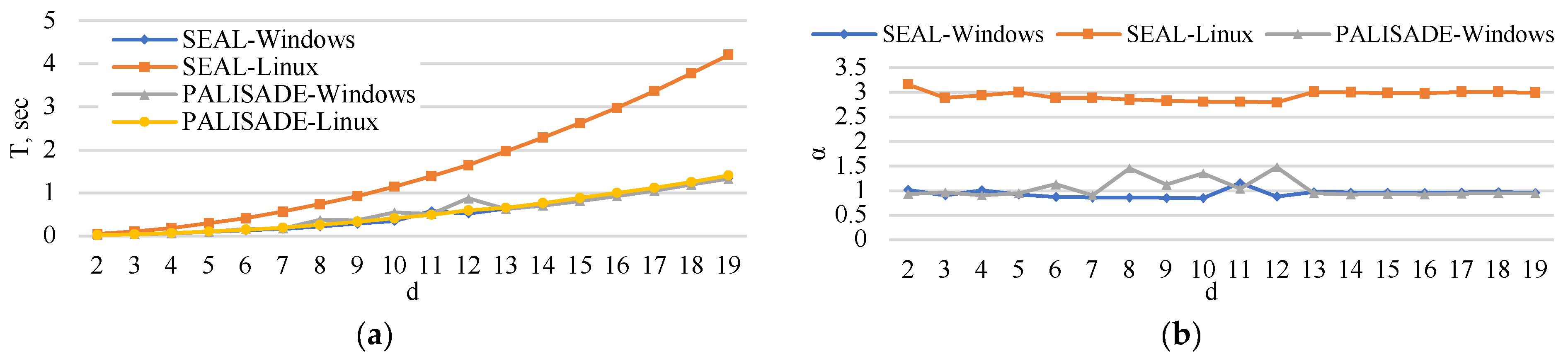
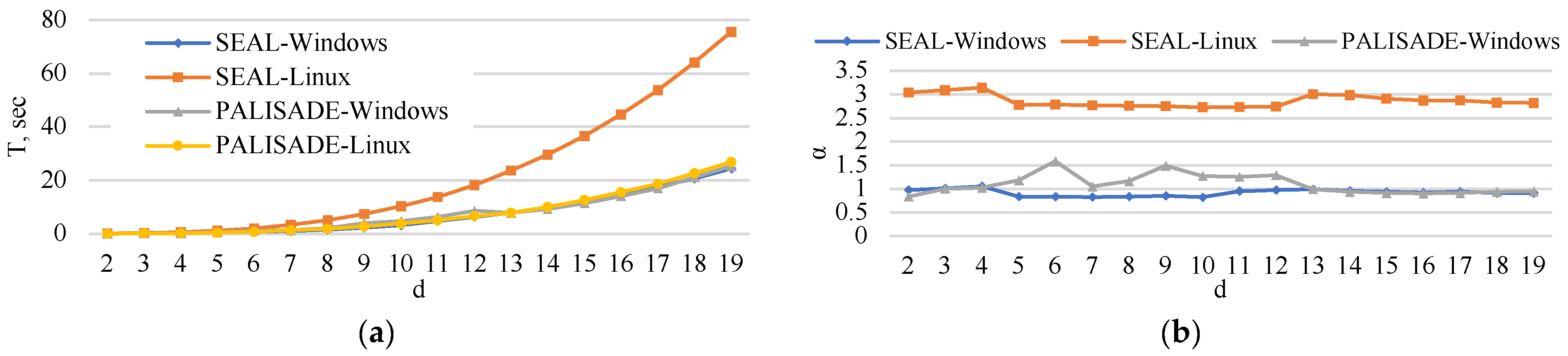
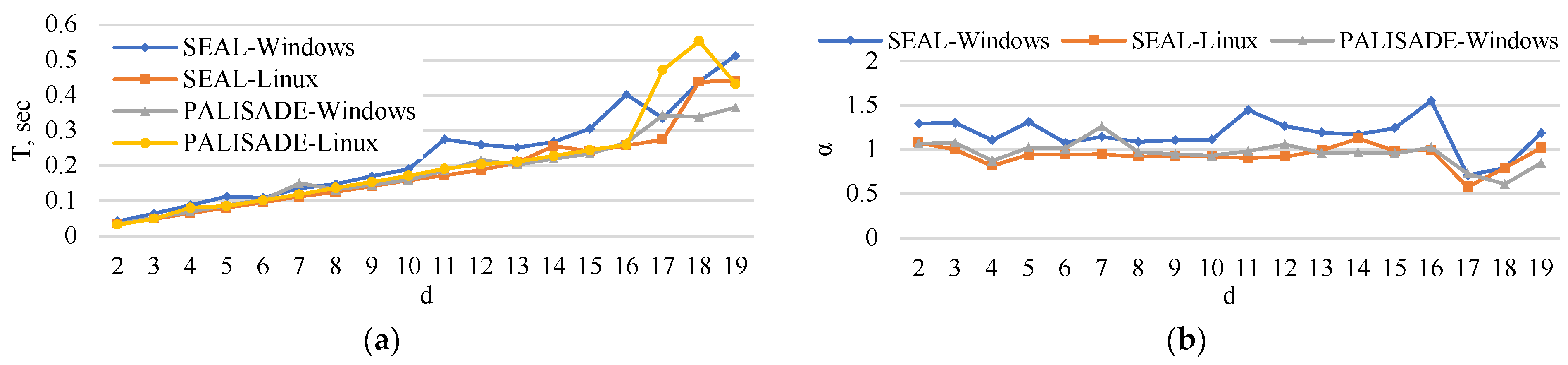
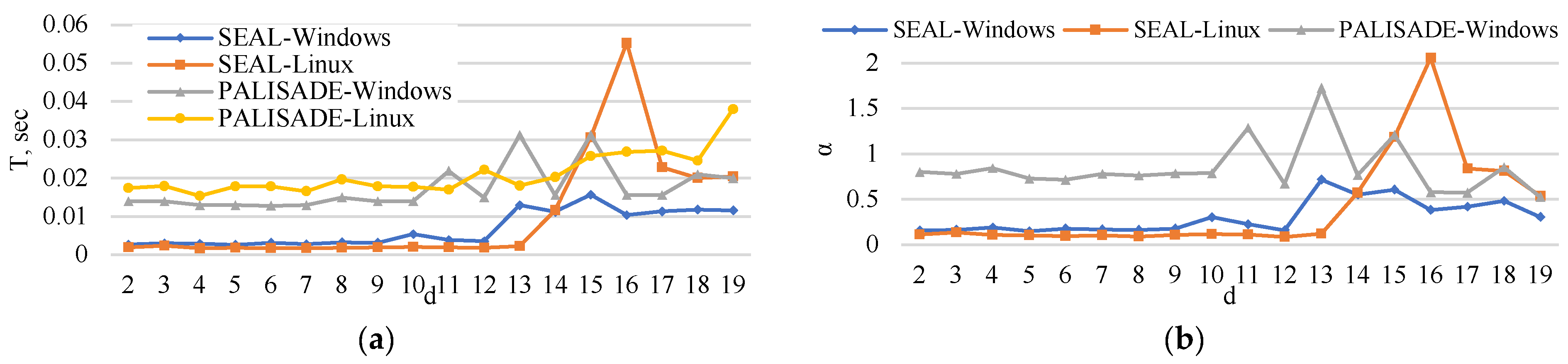
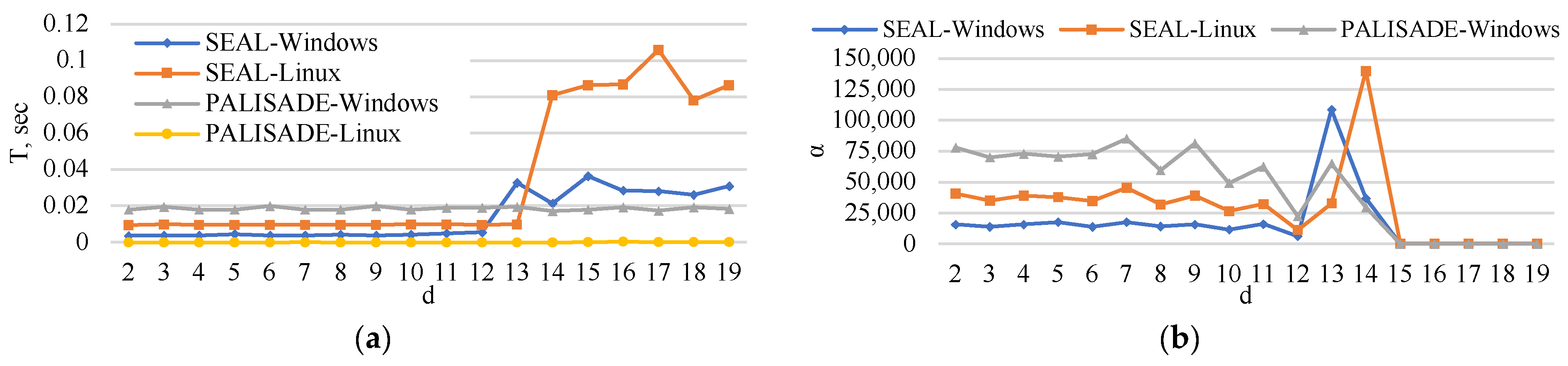
5. Experimental Analysis
5.1. Encoding Time
5.2. Encryption Time
5.3. Matrix Multiplication Time
5.4. Decryption Time
5.5. Decoding Time
5.6. Execution Time
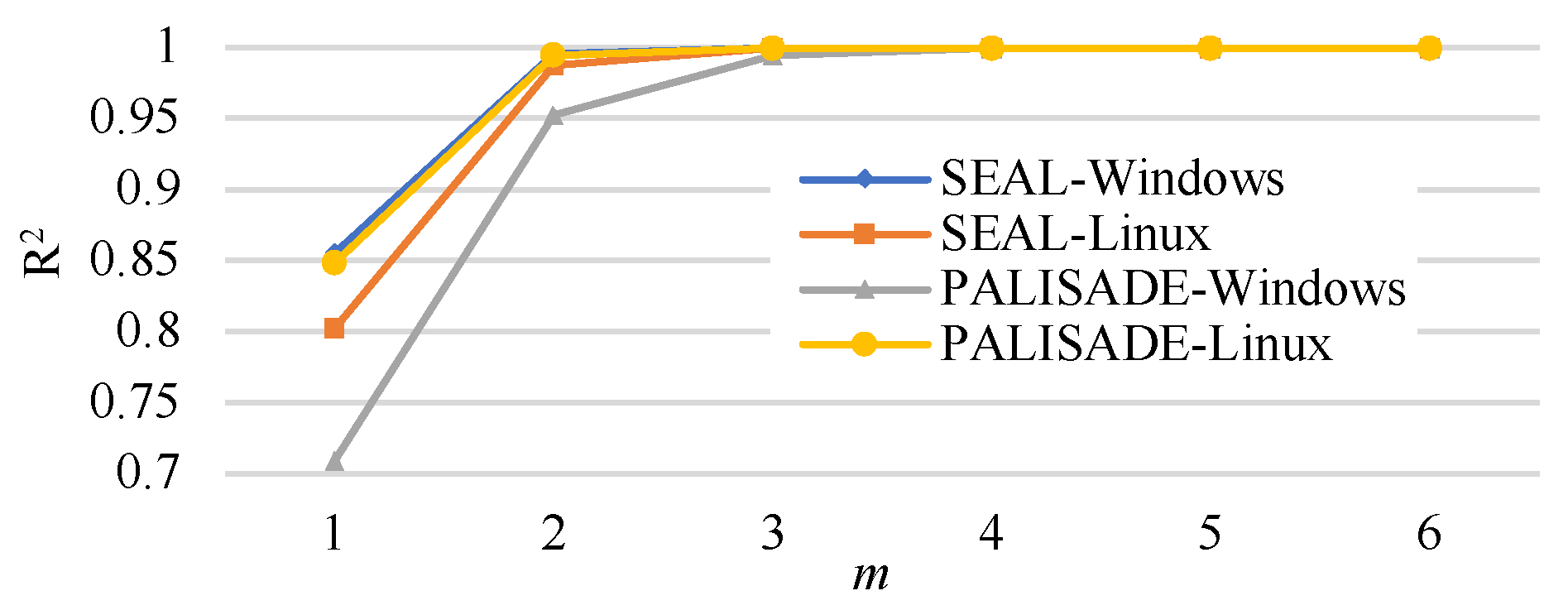
6. Extrapolation
- SEAL-Windows
- SEAL-Linux:
- PALISADE-Windows:
- PALISADE-Linux:
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- CKKS.Setup(): Setting a ring of dimension , a ciphertext modulus , a modulus coprimal to , a key and error distribution and over , correspondingly.
- SymEnc (, ): is an input plaintext and is a secret key. and are randomly picked from and error distributions, i.e., and . , where is a word-sized prime number. It returns the ciphertext .
- CKKS.KeyGen(): Secret key , where is drawn from key distribution , i.e., , and public key .
- CKKS.Dec (ct, sk): Converts ciphertext ct to plaintext. Given is a ciphertext at the -th level, the plaintext is returned.
- : Adds two ciphertexts and . The result is ciphertext .
- : Multiplies two ciphertexts and . The result is ciphertext .
- : Multiplies ciphertext with some scalar .
- : Transforms an encryption of into an encryption of .
References
- Kamara, S.; Lauter, K. Cryptographic Cloud Storage. In Proceedings of the International Conference on Financial Cryptography and Data Security, Tenerife, Spain, 25–28 January 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 136–149. [Google Scholar]
- Alabdulatif, A.; Kumarage, H.; Khalil, I.; Atiquzzaman, M.; Yi, X. Privacy-Preserving Cloud-Based Billing with Lightweight Homomorphic Encryption for Sensor-Enabled Smart Grid Infrastructure. IET Wirel. Sens. Syst. 2017, 7, 182–190. [Google Scholar] [CrossRef]
- Borrego, C.; Amadeo, M.; Molinaro, A.; Jhaveri, R.H. Privacy-Preserving Forwarding Using Homomorphic Encryption for Information-Centric Wireless Ad Hoc Networks. IEEE Commun. Lett. 2019, 23, 1708–1711. [Google Scholar] [CrossRef]
- Bouti, A.; Keller, J. Towards Practical Homomorphic Encryption in Cloud Computing. In Proceedings of the 2015 IEEE Fourth Symposium on Network Cloud Computing and Applications (NCCA), Munich, Germany, 11–12 June 2015; pp. 67–74. [Google Scholar]
- Brakerski, Z. Fully Homomorphic Encryption without Modulus Switching from Classical GapSVP. In Proceedings of the Annual Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 868–886. [Google Scholar]
- Brakerski, Z.; Gentry, C.; Vaikuntanathan, V. (Leveled) Fully Homomorphic Encryption without Bootstrapping. ACM Trans. Comput. Theory (TOCT) 2014, 6, 1–36. [Google Scholar] [CrossRef]
- dos Santos, L.C.; Bilar, G.R.; Pereira, F.D. Implementation of the Fully Homomorphic Encryption Scheme over Integers with Shorter Keys. In Proceedings of the 2015 7th IEEE International Conference on New Technologies, Mobility and Security (NTMS), Paris, France, 27–29 July 2015; pp. 1–5. [Google Scholar]
- Chauhan, K.K.; Sanger, A.K.; Verma, A. Homomorphic Encryption for Data Security in Cloud Computing. In Proceedings of the 2015 IEEE International Conference on Information Technology (ICIT), Bhubaneswar, India, 21–23 December 2015; pp. 206–209. [Google Scholar]
- Chen, J. Cloud Storage Third-Party Data Security Scheme Based on Fully Homomorphic Encryption. In Proceedings of the 2016 IEEE International Conference on Network and Information Systems for Computers (ICNISC), Wuhan, China, 15–17 April 2016; pp. 155–159. [Google Scholar]
- Derfouf, M.; Eleuldj, M. Cloud Secured Protocol Based on Partial Homomorphic Encryptions. In Proceedings of the 2018 4th IEEE International Conference on Cloud Computing Technologies and Applications (Cloudtech), Brussels, Belgium, 26–28 November 2018; pp. 1–6. [Google Scholar]
- El Makkaoui, K.; Ezzati, A.; Hssane, A.B. Challenges of Using Homomorphic Encryption to Secure Cloud Computing. In Proceedings of the 2015 IEEE International Conference on Cloud Technologies and Applications (CloudTech), Marrakech, Morocco, 2–4 June 2015; pp. 1–7. [Google Scholar]
- El-Yahyaoui, A.; El Kettani, M.D.E.-C. A Verifiable Fully Homomorphic Encryption Scheme to Secure Big Data in Cloud Computing. In Proceedings of the 2017 IEEE International Conference on Wireless Networks and Mobile Communications (WINCOM), Rabat, Morocco, 1–4 November 2017; pp. 1–5. [Google Scholar]
- Felipe, M.R.; Aung, K.M.M.; Ye, X.; Yonggang, W. Stealthycrm: A Secure Cloud Crm System Application That Supports Fully Homomorphic Database Encryption. In Proceedings of the 2015 IEEE International Conference on Cloud Computing Research and Innovation (ICCCRI), Singapore, 26–27 October 2015; pp. 97–105. [Google Scholar]
- Kim, J.; Koo, D.; Kim, Y.; Yoon, H.; Shin, J.; Kim, S. Efficient Privacy-Preserving Matrix Factorization for Recommendation via Fully Homomorphic Encryption. ACM Trans. Priv. Secur. (TOPS) 2018, 21, 1–30. [Google Scholar] [CrossRef]
- Peng, H.-T.; Hsu, W.W.; Ho, J.-M.; Yu, M.-R. Homomorphic Encryption Application on FinancialCloud Framework. In Proceedings of the 2016 IEEE Symposium Series on Computational Intelligence (SSCI), Athens, Greece, 6–9 December 2016; pp. 1–5. [Google Scholar]
- Hrestak, D.; Picek, S. Homomorphic Encryption in the Cloud. In Proceedings of the 2014 37th IEEE International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 26–30 May 2014; pp. 1400–1404. [Google Scholar]
- Jubrin, A.M.; Izegbu, I.; Adebayo, O.S. Fully Homomorphic Encryption: An Antidote to Cloud Data Security and Privacy Concems. In Proceedings of the 2019 15th IEEE International Conference on Electronics, Computer and Computation (ICECCO), Abuja, Nigeria, 10–12 December 2019; pp. 1–6. [Google Scholar]
- Kangavalli, R.; Vagdevi, S. A Mixed Homomorphic Encryption Scheme for Secure Data Storage in Cloud. In Proceedings of the 2015 IEEE International Advance Computing Conference (IACC), Banglore, India, 12–13 June 2015; pp. 1062–1066. [Google Scholar]
- Kavya, A.; Acharva, S. A Comparative Study on Homomorphic Encryption Schemes in Cloud Computing. In Proceedings of the 2018 3rd IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), Bangalore, India, 18–19 May 2018; pp. 112–116. [Google Scholar]
- Ghanem, S.M.; Moursy, I.A. Secure Multiparty Computation via Homomorphic Encryption Library. In Proceedings of the 2019 Ninth IEEE International Conference on Intelligent Computing and Information Systems (ICICIS), Cairo, Egypt, 8–10 December 2019; pp. 227–232. [Google Scholar]
- Kocabas, O.; Soyata, T. Utilizing Homomorphic Encryption to Implement Secure and Private Medical Cloud Computing. In Proceedings of the 2015 IEEE 8th International Conference on Cloud Computing, New York, NY, USA, 27 June–2 July 2015; pp. 540–547. [Google Scholar]
- Kocabas, O.; Soyata, T.; Couderc, J.-P.; Aktas, M.; Xia, J.; Huang, M. Assessment of Cloud-Based Health Monitoring Using Homomorphic Encryption. In Proceedings of the 2013 IEEE 31st International Conference on Computer Design (ICCD), Asheville, NC, USA, 6–9 October 2013; pp. 443–446. [Google Scholar]
- Lupascu, C.; Togan, M.; Patriciu, V.-V. Acceleration Techniques for Fully-Homomorphic Encryption Schemes. In Proceedings of the 2019 22nd IEEE International Conference on Control Systems and Computer Science (CSCS), Bucharest, Romania, 28–30 May 2019; pp. 118–122. [Google Scholar]
- Babenko, M.; Tchernykh, A.; Chervyakov, N.; Kuchukov, V.; Miranda-López, V.; Rivera-Rodriguez, R.; Du, Z.; Talbi, E.-G. Positional Characteristics for Efficient Number Comparison over the Homomorphic Encryption. Program. Comput. Softw. 2019, 45, 532–543. [Google Scholar] [CrossRef]
- Marwan, M.; Kartit, A.; Ouahmane, H. Applying Homomorphic Encryption for Securing Cloud Database. In Proceedings of the 2016 4th IEEE International Colloquium on Information Science and Technology (CiSt), Tangier, Morocco, 24–26 October 2016; pp. 658–664. [Google Scholar]
- Murthy, S.; Kavitha, C.R. Preserving Data Privacy in Cloud Using Homomorphic Encryption. In Proceedings of the 2019 3rd IEEE International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 12–14 June 2019; pp. 1131–1135. [Google Scholar]
- Hoffstein, J.; Pipher, J.; Silverman, J.H. NTRU: A Ring-Based Public Key Cryptosystem. In Proceedings of the International Algorithmic Number Theory Symposium, Portland, OR, USA, 21–25 June 1998; Springer: Berlin/Heidelberg, Germany, 1998; pp. 267–288. [Google Scholar]
- Sun, X.; Zhang, P.; Sookhak, M.; Yu, J.; Xie, W. Utilizing Fully Homomorphic Encryption to Implement Secure Medical Computation in Smart Cities. Pers. Ubiquitous Comput. 2017, 21, 831–839. [Google Scholar] [CrossRef]
- Tebaa, M.; El Hajji, S.; El Ghazi, A. Homomorphic Encryption Method Applied to Cloud Computing. In Proceedings of the 2012 IEEE National Days of Network Security and Systems, Marrakech, Morocco, 20–21 April 2012; pp. 86–89. [Google Scholar]
- Van Dijk, M.; Gentry, C.; Halevi, S.; Vaikuntanathan, V. Fully Homomorphic Encryption over the Integers. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, French Riviera, France, 30 May–3 June 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 24–43. [Google Scholar]
- Zhao, F.; Li, C.; Liu, C.F. A Cloud Computing Security Solution Based on Fully Homomorphic Encryption. In Proceedings of the 16th IEEE International Conference on Advanced Communication Technology, Pyeongchang, Republic of Korea, 16–19 February 2014; pp. 485–488. [Google Scholar]
- Ni, Z.; Kundi, D.-e.-S.; O’Neill, M.; Liu, W. A High-Performance SIKE Hardware Accelerator. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2022, 30, 803–815. [Google Scholar] [CrossRef]
- Cintas Canto, A.; Mozaffari Kermani, M.; Azarderakhsh, R. Reliable architectures for finite field multipliers using cyclic codes on FPGA utilized in classic and post-quantum cryptography. IEEE Trans. Circuits Syst. I 2023, 1, 157–161. [Google Scholar] [CrossRef]
- Tian, J.; Wu, B.; Wang, Z. High-Speed FPGA Implementation of SIKE Based on an Ultra-Low-Latency Modular Multiplier. IEEE Trans. Circuits Syst. I 2021, 68, 3719–3731. [Google Scholar] [CrossRef]
- Ogburn, M.; Turner, C.; Dahal, P. Homomorphic Encryption. Procedia Comput. Sci. 2013, 20, 502–509. [Google Scholar] [CrossRef]
- Lu, W.; Sakuma, J. More Practical Privacy-Preserving Machine Learning as a Service via Efficient Secure Matrix Multiplication. In Proceedings of the 6th Workshop on Encrypted Computing & Applied Homomorphic Cryptography, Toronto, ON, Canada, 19 October 2018; pp. 25–36. [Google Scholar]
- Armknecht, F.; Boyd, C.; Carr, C.; Gjøsteen, K.; Jäschke, A.; Reuter, C.A.; Strand, M. A Guide to Fully Homomorphic Encryption. Available online: https://eprint.iacr.org/2015/1192 (accessed on 8 April 2023).
- Kim, S.; Lee, K.; Cho, W.; Cheon, J.H.; Rutenbar, R.A. FPGA-Based Accelerators of Fully Pipelined Modular Multipliers for Homomorphic Encryption. In Proceedings of the 2019 IEEE International Conference on ReConFigurable Computing and FPGAs (ReConFig), Cancun, Mexico, 9–11 December 2019; pp. 1–8. [Google Scholar]
- Kuang, L.; Yang, L.T.; Feng, J.; Dong, M. Secure Tensor Decomposition Using Fully Homomorphic Encryption Scheme. IEEE Trans. Cloud Comput. 2015, 6, 868–878. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, J.-W.; Kim, Y.-S.; No, J.-S. Near-Optimal Polynomial for Modulus Reduction Using L2-Norm for Approximate Homomorphic Encryption. IEEE Access 2020, 8, 144321–144330. [Google Scholar] [CrossRef]
- Mert, A.C.; Öztürk, E.; Savaş, E. Design and Implementation of Encryption/Decryption Architectures for BFV Homomorphic Encryption Scheme. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2019, 28, 353–362. [Google Scholar] [CrossRef]
- Al Badawi, A.; Chao, J.; Lin, J.; Fook Mun, C.; Jie Sim, J.; Meng Tan, B.H.; Nan, X.; Aung, K.M.M.; Ramaseshan Chandrasekhar, V. Towards the AlexNet Moment for Homomorphic Encryption: HCNN, TheFirst Homomorphic CNN on Encrypted Data with GPUs. arXiv 2018, arXiv:1811. [Google Scholar] [CrossRef]
- Cheon, J.H.; Kim, D.; Kim, Y.; Song, Y. Ensemble Method for Privacy-Preserving Logistic Regression Based on Homomorphic Encryption. IEEE Access 2018, 6, 46938–46948. [Google Scholar] [CrossRef]
- Ciocan, A.; Costea, S.; Ţăpuş, N. Implementation and Optimization of a Somewhat Homomorphic Encryption Scheme. In Proceedings of the 2015 14th IEEE RoEduNet International Conference-Networking in Education and Research (RoEduNet NER), Craiova, Romania, 24–26 September 2015; pp. 198–202. [Google Scholar]
- Foster, M.J.; Lukowiak, M.; Radziszowski, S. Flexible HLS-Based Implementation of the Karatsuba Multiplier Targeting Homomorphic Encryption Schemes. In Proceedings of the 2019 MIXDES-26th IEEE International Conference “Mixed Design of Integrated Circuits and Systems”, Rzeszow, Poland, 27–29 June 2019; pp. 215–220. [Google Scholar]
- Crainic, T.G.; Perboli, G.; Tadei, R. Recent advances in multi-dimensional packing problems. New Technol. Trends Innov. Res. 2012, 1, 91–110. [Google Scholar]
- Cheon, J.H.; Kim, A.; Yhee, D. Multi-dimensional packing for heaan for approximate matrix arithmetics. Available online: https://eprint.iacr.org/2018/1245 (accessed on 8 April 2023).
- Microsoft SEAL 2022. Available online: https://github.com/Microsoft/SEAL (accessed on 8 April 2023).
- Files Master·PALISADE/PALISADE Release GitLab. Available online: https://gitlab.com/palisade/palisade-release/-/tree/master (accessed on 8 April 2023).
- Abadi, M.; Chu, A.; Goodfellow, I.; McMahan, H.B.; Mironov, I.; Talwar, K.; Zhang, L. Deep learning with differential privacy. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 308–318. [Google Scholar]
- Li, L.; Fan, Y.; Tse, M.; Lin, K.Y. A review of applications in federated learning. Comput. Ind. Eng. 2020, 149, 106854. [Google Scholar] [CrossRef]
- Du, W.; Atallah, M.J. Secure multi-party computation problems and their applications: A review and open problems. In Proceedings of the 2001 Workshop on New Security Paradigms, Cloudcroft, NM, USA, 10–13 September 2001; pp. 13–22. [Google Scholar]
- Hirasawa, K.; Ohbayashi, M.; Koga, M.; Harada, M. Forward propagation universal learning network. In Proceedings of the IEEE International Conference on Neural Networks (ICNN′96), Washington, DC, USA, 3–6 June 1996; Volume 1, pp. 353–358. [Google Scholar]
- Rumelhart, D.E.; Durbin, R.; Golden, R.; Chauvin, Y. Backpropagation: The basic theory. In Backpropagation: Theory, Architectures and Applications; Psychology Press: East Sussex, UK, 1995; pp. 1–34. [Google Scholar]
- Bottou, L. Stochastic gradient descent tricks. In Neural Networks: Tricks of the Trade, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 421–436. [Google Scholar]
- Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a convolutional neural network. In Proceedings of the 2017 IEEE International Conference on Engineering and Technology (ICET), Antalya, Turkey, 21–23 August 2017; pp. 1–6. [Google Scholar]
- Rivest, R.L.; Adleman, L.; Dertouzos, M.L. On Data Banks and Privacy Homomorphisms. Found. Secur. Comput. 1978, 4, 169–180. [Google Scholar]
- Cheon, J.H.; Kim, A.; Kim, M.; Song, Y. Homomorphic Encryption for Arithmetic of Approximate Numbers. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security (ASIACRYPT 2017), Hong Kong, China, 3–7 December 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 409–437. [Google Scholar]
- Gentry, C. A Fully Homomorphic Encryption Scheme; Stanford University. 2009. Available online: https://crypto.stanford.edu/craig/craig-thesis.pdf (accessed on 8 April 2023).
- Homomorphic Encryption Standardization. Available online: https://homomorphicencryption.org/ (accessed on 8 April 2023).
- López-Alt, A.; Tromer, E.; Vaikuntanathan, V. On-the-Fly Multiparty Computation on the Cloud via Multikey Fully Homomorphic Encryption. In Proceedings of the Forty-Fourth Annual ACM Symposium on Theory of Computing, New York, NY, USA, 20–22 May 2012; pp. 1219–1234. [Google Scholar]
- Fan, J.; Vercauteren, F. Somewhat Practical Fully Homomorphic Encryption. Available online: https://eprint.iacr.org/2012/144 (accessed on 8 April 2023).
- Gentry, C.; Sahai, A.; Waters, B. Homomorphic Encryption from Learning with Errors: Conceptually-Simpler, Asymptotically-Faster, Attribute-Based. In Proceedings of the Annual Cryptology Conference (CRYPTO 2013), Santa Barbara, CA, USA, 18–22 August 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 75–92. [Google Scholar]
- Bos, J.W.; Lauter, K.; Loftus, J.; Naehrig, M. Improved Security for a Ring-Based Fully Homomorphic Encryption Scheme. In Proceedings of the IMA International Conference on Cryptography and Coding (IMACC 2013), Oxford, UK, 17–19 December 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 45–64. [Google Scholar]
- Hariss, K.; Chamoun, M.; Samhat, A.E. Cloud Assisted Privacy Preserving Using Homomorphic Encryption. In Proceedings of the 2020 4th IEEE Cyber Security in Networking Conference (CSNet), Lausanne, Switzerland, 21–23 October 2020; pp. 1–8. [Google Scholar]
- Kee, R.; Sie, J.; Wong, R.; Yap, C.N. Arithmetic Circuit Homomorphic Encryption and Multiprocessing Enhancements. In Proceedings of the 2019 IEEE International Conference on Cyber Security and Protection of Digital Services (Cyber Security), Oxford, UK, 3–4 June 2019; pp. 1–5. [Google Scholar]
- Oppermann, A.; Grasso-Toro, F.; Yurchenko, A.; Seifert, J.-P. Secure Cloud Computing: Communication Protocol for Multithreaded Fully Homomorphic Encryption for Remote Data Processing. In Proceedings of the 2017 IEEE International Symposium on Parallel and Distributed Processing with Applications and 2017 IEEE International Conference on Ubiquitous Computing and Communications (ISPA/IUCC), Guangzhou, China, 12–15 December 2017; pp. 503–510. [Google Scholar]
- Silva, E.A.; Correia, M. Leveraging an Homomorphic Encryption Library to Implement a Coordination Service. In Proceedings of the 2016 IEEE 15th International Symposium on Network Computing and Applications (NCA), Cambridge, MA, USA, 31 October–2 November 2016; pp. 39–42. [Google Scholar]
- Halevi, S.; Shoup, V. Algorithms in Helib. In Proceedings of the Annual Cryptology Conference, Santa Barbara, CA, USA, 17–21 August 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 554–571. [Google Scholar]
- Jiang, X.; Kim, M.; Lauter, K.; Song, Y. Secure Outsourced Matrix Computation and Application to Neural Networks. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, Toronto, ON, Canada, 15–19 October 2018; pp. 1209–1222. [Google Scholar]
- Kim, M.; Song, Y.; Wang, S.; Xia, Y.; Jiang, X. Secure Logistic Regression Based on Homomorphic Encryption: Design and Evaluation. JMIR Med. Inform. 2018, 6, e8805. [Google Scholar] [CrossRef]
- Pulido-Gaytan, B.; Tchernykh, A.; Cortés-Mendoza, J.M.; Babenko, M.; Radchenko, G.; Avetisyan, A.; Drozdov, A.Y. Privacy-Preserving Neural Networks with Homomorphic Encryption: Challenges and Opportunities. Peer-to-Peer Netw. Appl. 2021, 14, 1666–1691. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, P.; Liu, J.K.; Yu, J.; Xie, W. Private Machine Learning Classification Based on Fully Homomorphic Encryption. IEEE Trans. Emerg. Top. Comput. 2018, 8, 352–364. [Google Scholar] [CrossRef]
- Yamada, Y.; Rohloff, K.; Oguchi, M. Homomorphic Encryption for Privacy-Preserving Genome Sequences Search. In Proceedings of the 2019 IEEE International Conference on Smart Computing (SMARTCOMP), Washington, DC, USA, 12–15 June 2019; pp. 7–12. [Google Scholar]
- Ducas, L.; Micciancio, D. FHEW: Bootstrapping Homomorphic Encryption in Less than a Second. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Sofia, Bulgaria, 26–30 April 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 617–640. [Google Scholar]
- FFTW. Available online: http://www.fftw.org/ (accessed on 10 December 2022).
- TFHE. Available online: https://tfhe.github.io/tfhe/ (accessed on 10 December 2022).
- A GPU Implementation of Fully Homomorphic Encryption on Torus. Available online: https://github.com/nucypher/nufhe (accessed on 10 December 2022).
- Lattigo: Lattice-Based Multiparty Homomorphic Encryption Library in Go 2022. Available online: https://github.com/tuneinsight/lattigo (accessed on 10 December 2022).
- Crockett, E.; Peikert, C. Λoλ: Functional Lattice Cryptography. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 993–1005. [Google Scholar]
- Dai, W.; Sunar, B. CuHE: A Homomorphic Encryption Accelerator Library. In Proceedings of the International Conference on Cryptography and Information Security in the Balkans, Koper, Slovenia, 3–4 September 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 169–186. [Google Scholar]
- Doröz, Y.; Shahverdi, A.; Eisenbarth, T.; Sunar, B. Toward Practical Homomorphic Evaluation of Block Ciphers Using Prince. In Proceedings of the International Conference on Financial Cryptography and Data Security (FC 2014), Christ Church, Barbados, 3–7 March 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 208–220. [Google Scholar]
- Concrete. Available online: https://github.com/zama-ai/concrete-core (accessed on 10 December 2022).
- CuFHE. Available online: https://github.com/vernamlab/cuFHE (accessed on 10 December 2022).
- Alves, P.; Aranha, D. Efficient GPGPU Implementation of the Leveled Fully Homomorphic Encryption Scheme YASHE. Available online: https://www.ic.unicamp.br/~ra085994/reports_and_papers/outros/drafts/efficient_gpgpu_implementation_of_yashe-draft.pdf (accessed on 8 April 2023).
- Angelou, N. Node-Seal, A Homomorphic Encryption Library for TypeScript or JavaScript Using Microsoft SEAL. 2022. Available online: https://github.com/s0l0ist/node-seal (accessed on 8 April 2023).
- Pyfhel. Available online: https://github.com/ibarrond/Pyfhel (accessed on 10 December 2022).
- SEAL-Python. Available online: https://github.com/Huelse/SEAL-Python (accessed on 10 December 2022).
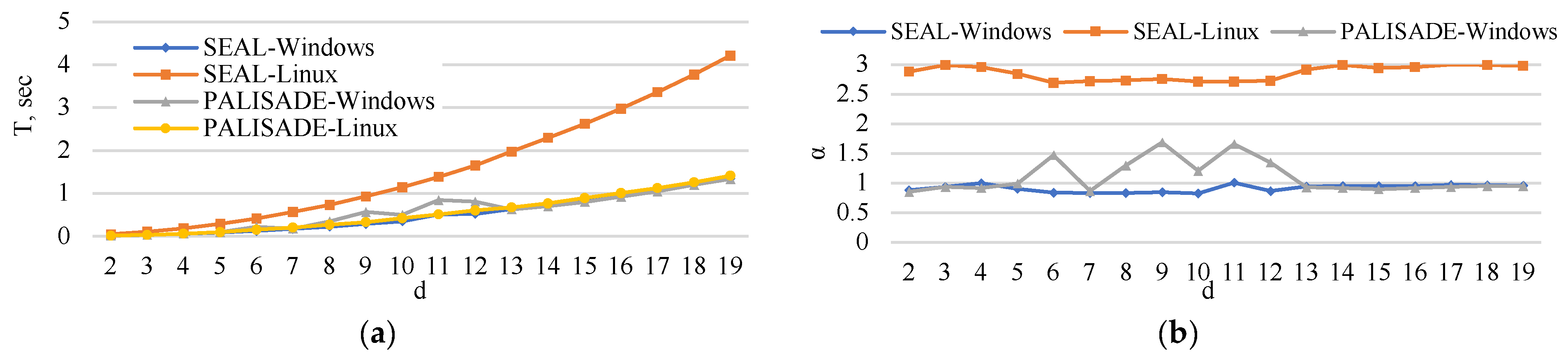




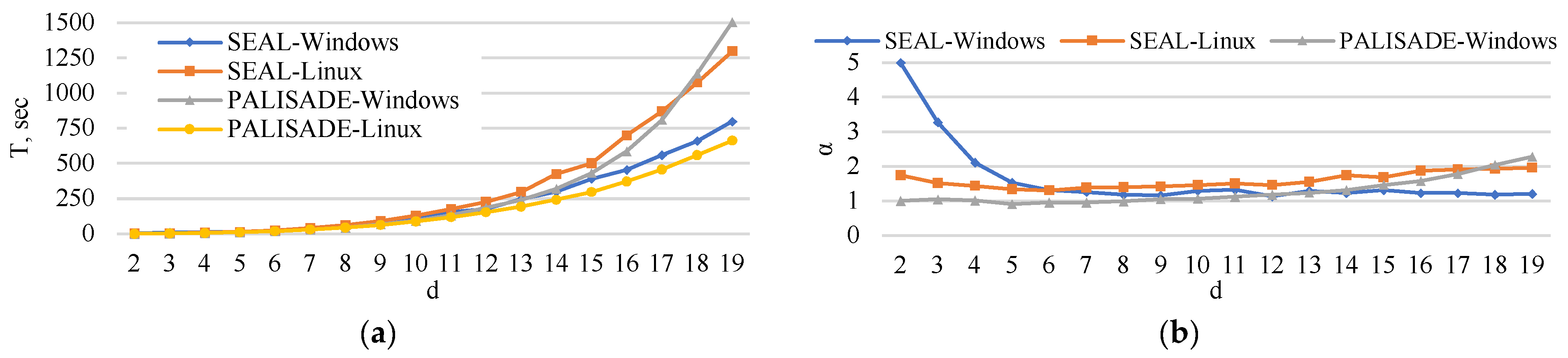
| Ref. | Number of Ciphertexts | Complexity | Required Depth | Library | OS | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| HElib | HEAAN | Microsoft SEAL | PALISADE | Windows | Linux | Mac OS | ||||
| [69] | 1 Mult | ● | ● | |||||||
| [79] | 1 | 1 Mult + 2 CMult | ● | ● | ||||||
| new | 1 | 1 Mult + 2 CMult | ● | ● | ● | ● | ||||
| Parameter | Security Level | |||
|---|---|---|---|---|
| Value | 128 | 8,192 | 220 | 3.2 |
| Notation | Meaning |
|---|---|
| SEAL-Linux | Implementation of the algorithm using the SEAL library compiled in OS Linux Ubuntu |
| SEAL-Windows | Implementation of the algorithm using the SEAL library compiled in OS Windows 10 |
| PALISADE- Linux | Implementation of the algorithm using the PALISADE Library compiled in OS Linux Ubuntu |
| PALISADE-Windows | Implementation of the algorithm using the PALISADE Library compiled in OS Windows 10 |
| T, s | Time to complete the operation/algorithm in seconds. |
| d | The matrix order |
| α | Degradation over PALISADE-Linux (times) |
| Name | Library | OS | ||
|---|---|---|---|---|
| SEAL | PALISADE | Windows | Linux | |
| SEAL-Linux | ● | ● | ||
| SEAL-Windows | ● | ● | ||
| PALISADE- Linux | ● | ● | ||
| PALISADE-Windows | ● | ● | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Babenko, M.; Golimblevskaia, E.; Tchernykh, A.; Shiriaev, E.; Ermakova, T.; Pulido-Gaytan, L.B.; Valuev, G.; Avetisyan, A.; Gagloeva, L.A. A Comparative Study of Secure Outsourced Matrix Multiplication Based on Homomorphic Encryption. Big Data Cogn. Comput. 2023, 7, 84. https://doi.org/10.3390/bdcc7020084
Babenko M, Golimblevskaia E, Tchernykh A, Shiriaev E, Ermakova T, Pulido-Gaytan LB, Valuev G, Avetisyan A, Gagloeva LA. A Comparative Study of Secure Outsourced Matrix Multiplication Based on Homomorphic Encryption. Big Data and Cognitive Computing. 2023; 7(2):84. https://doi.org/10.3390/bdcc7020084
Chicago/Turabian StyleBabenko, Mikhail, Elena Golimblevskaia, Andrei Tchernykh, Egor Shiriaev, Tatiana Ermakova, Luis Bernardo Pulido-Gaytan, Georgii Valuev, Arutyun Avetisyan, and Lana A. Gagloeva. 2023. "A Comparative Study of Secure Outsourced Matrix Multiplication Based on Homomorphic Encryption" Big Data and Cognitive Computing 7, no. 2: 84. https://doi.org/10.3390/bdcc7020084
APA StyleBabenko, M., Golimblevskaia, E., Tchernykh, A., Shiriaev, E., Ermakova, T., Pulido-Gaytan, L. B., Valuev, G., Avetisyan, A., & Gagloeva, L. A. (2023). A Comparative Study of Secure Outsourced Matrix Multiplication Based on Homomorphic Encryption. Big Data and Cognitive Computing, 7(2), 84. https://doi.org/10.3390/bdcc7020084










