Rating Prediction Quality Enhancement in Low-Density Collaborative Filtering Datasets

Abstract

Collaborative filtering has proved to be one of the most popular and successful rating prediction techniques over the last few years. In collaborative filtering, each rating prediction, concerning a product or a service, is based on the rating values that users that are considered “close” to the user for whom the prediction is being generated have given to the same product or service. In general, “close” users for some user u correspond to users that have rated items similarly to u and these users are termed as “near neighbors”. As a result, the more reliable these near neighbors are, the more successful predictions the collaborative filtering system will compute and ultimately, the more successful recommendations the recommender system will generate. However, when the dataset’s density is relatively low, it is hard to find reliable near neighbors and hence many predictions fail, resulting in low recommender system reliability. In this work, we present a method that enhances rating prediction quality in low-density collaborative filtering datasets, by considering predictions whose features are associated with high prediction accuracy as additional ratings. The presented method’s efficacy and applicability are substantiated through an extensive multi-parameter evaluation process, using widely acceptable low-density collaborative filtering datasets.

1. Introduction

The ultimate goal of a recommender system is to produce personalized recommendations of products and services for its clients/users. Typically, a recommender system aims at generating rating predictions for the goods and services the users have not rated yet and then recommends the ones achieving the higher rating prediction score for each user [1,2,3].

One of the most successful and popular rating prediction techniques, over the last years, is collaborative filtering (CF). CF algorithms initially compute the vicinity between each pair of users (user₁, user₂) in the dataset, based on a user similarity function metric which considers the products or services that both user₁ and user₂ have rated: the more resemblant ratings entered by user₁ and user₂ for commonly rated items are, the higher the similarity these two users share. For each dataset user u, the users having the larger similarity with them create u’s neighborhood and hence are termed u’s near neighbors (NNs). Then, for each product-service x that user u has not yet evaluated, the ratings of u’s NNs to x are used, in order to predict the rating value that u would give to x, based on a rating prediction formula [4,5,6]. This setting follows the reasoning that humans trust the people who consider close to them when seeking recommendations for services and products in the real world, regardless of the service or product category [7,8].

Typically, the success of the CF rating prediction procedure is based on the reliability of the users’ neighborhood. As expected, users with a small number of NNs, as well as users having many NNs with low similarity values, tend to obtain inferior quality predictions more frequently [9,10,11]. The key factor of having users with a small number of NNs, which leads to reduced rating prediction quality in CF, is the density of the dataset, i.e., the number of user ratings within the dataset, when compared with the total numbers of both the users and the products or services. Typically, the less density a CF dataset has, the lower the overall rating prediction quality observed for this dataset is [12,13].

More specifically, the aforementioned low rating prediction quality results in (a) demoted rating prediction accuracy (i.e., the closeness between the rating prediction value and the user’s real rating value to the products or services) and (b) low rating prediction coverage (i.e., the percentage of the products not already rated by a user u, for which a prediction can be computed, based on the CF procedure). The first of these root causes leads to situations where the recommender system may recommend products that the user–client will not like, whereas the second root cause implies that the recommender system may never recommend products that the user or client would actually like. The first consequence is deemed more severe than the second one, in the sense that when failing to recommend some specific products/items that the user would like, the recommender system may still formulate a successful recommendation including some other products/items that the user would rate highly. Nevertheless, both root causes negatively affect the reliability of the recommender system [14,15]. Addressing both root causes would therefore enhance the recommendation quality of a recommender system, including the aspects of reliability, accuracy, and coverage.

Previous and state-of-the-art work explored, in a broader context, the rating prediction accuracy of related factors in low-density CF datasets [16]. This work showed that three factors are correlated with rating prediction accuracy reduction. These factors are (a) the number of NNs taking part in the formulation of the rating prediction, (b) the mean rating value the item for which the prediction is calculated has, and (c) the mean rating value the user for whom the prediction is being calculated has.

The present work incorporates the aforementioned knowledge into a technique for enhancing rating prediction quality in low-density CF datasets. More specifically, the proposed technique entails a preprocessing step that computes predictions for all unrated items, for each user. Subsequently, the rating predictions, which are deemed of high accuracy (considering the factors identified in Margaris et al. [16]), are added to the low-density rating dataset as additional ratings, effectively increasing the dataset density. Once this density enrichment step has concluded, any algorithm, either memory-based or model-based, can be applied to the updated dataset to generate rating predictions and recommendations. Figure 1 outlines the proposed approach. The present paper focuses on the computation of the high-accuracy prediction phase, which effectively constitutes a preprocessing step that is applied to the user–item rating matrix.

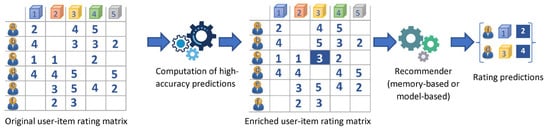
Figure 1. Proposed approach.

In Figure 1 we can observe that (i) the prediction regarding the rating of user c for item 3 is based on four near neighbors of c, namely a, b, d, and e (n.b. for the sake of example we consider as NNs users that have at least two common ratings with the target user), (ii) the average of the ratings for item 3 is close to the high end of the rating scale, and (iii) the average of the ratings for user c is close to the low end of the rating scale; therefore, this rating prediction is deemed of high accuracy and is inserted into the user–item rating matrix producing the enriched user–item rating matrix. Considering the enriched user–item rating matrix, user c now has two items rated in common with user f; hence, user c can contribute to the formulation of a rating prediction on item 1 for user f. Additionally, the incorporated rating will be taken into account for the formulation of the prediction on item 3 for user d.

In order to substantiate both the efficacy and the applicability of the presented method, an extensive multi-parameter evaluation has been conducted, using three types of recommenders (memory-based, model-based, and implicit trust-based), eight widely acceptable low-density datasets, two user similarity metrics, as well as two error/deviation metrics for rating prediction.

The contribution of the present work to the state-of-the-art comprises (a) an algorithm that enriches the user–item rating matrix with rating predictions that are deemed of high confidence, allowing recommendation algorithms to operate on the enriched dataset (which is denser) and thus produce better recommendations, (b) an extensive evaluation of the efficiency of the proposed approach under a wide set of parameters, and using both memory-based and model-based recommendation algorithms, which substantiates that the proposed approach significantly enhances the rating prediction quality in low-density CF datasets, and (c) an evaluation of using the proposed approach in combination with implicit trust-based techniques, which also aim to improve rating prediction quality and coverage, where the results show that additional gains may be reaped from this combination.

The rest of the paper is structured as follows: in Section 2, the related work is overviewed, whereas in Section 3 and Section 4 the presented algorithm is analyzed and evaluated, respectively. Section 5 discusses the results and compares them with the results of state-of-the-art algorithms sourced from the literature, and Section 6 concludes the paper, and outlines future work.

2. Related Work

Rating prediction quality is one of the CF research fields that has attracted considerable research attention during the last 20 years. Two main categories of this research field exist. The first one comprises works that take into account supplementary information sources, such as social user relations or characteristics of the products and services or user reviews concerning products and services; correspondingly, the second category comprises research works that are exclusively based on the information stored in the user–item rating matrix.

Regarding the first category, Chen et al. [17] present an algorithm that enhances rating prediction quality in memory-based CF. This algorithm incorporates genre information concerning the items, in order to predict whether each user would like a specific item. Furthermore, by combining user and item categorical features, this algorithm represents relations between users and items in the user–item–weight matrix. Gao et al. [18] present a technique that contains a context-aware neural CF model and a fuzzy clustering algorithm. In order to produce service and user clusters, the proposed algorithm uses contextual information and fuzzy c-means. Lastly, it presents a new prediction model, namely context-aware neural CF, which is able to discover latent cluster features as well as latent features in historical QoS data. A clustering-based algorithm is also presented by Zhang et al. [19], which aims at reducing the data sparsity importance. In this algorithm, user groups are used in order to distinguish users with different preferences and then, based on the preference of the active user, it obtains the NN set from the corresponding group of users. Furthermore, this work introduces a new user similarity metric that takes into account user preference in the global and local perspectives.

Nilashi et al. [20] introduce a new machine learning technique based on soft computing, which considers multiple quality factors in the TripAdvisor accommodation service, and exploits this information to retrieve eco-friendly hotels that match the search criteria. This technique is developed using prediction machine learning algorithms, as well as reduction of dimensionality, and aims to enhance the rating prediction scalability of the user ratings’ values. Jiang et al. [21] introduce a modified hypertext-induced topic search algorithm-based user interest filtering and the Latent Dirichlet Allocation-based interest detection model, which distills high-influence users and emerging interests. This algorithm decreases the adverse impact of user interests not related to the current context, as well as forms the target user’s NN set and recommends the results according to NN rating data. Furthermore, it introduces a label propagation and CF-based algorithm user interest community detection algorithm, which assigns, to each post, an individual tag, and then updates its label until stable user interest communities are obtained. Marin et al. [22] examine the variations in users’ rating practices and employ the concept of “rating proximity” and a tensor-based workflow to create a smoother representation of users’ preferences, that is more resilient to variations of users’ rating practices and produces more accurate recommendations.

Zhang et al. [23] introduce a location-aware deep CF algorithm that integrates a similarity adaptive corrector with a multilayer perceptron, which is able to learn the location correlation, as well as the nonlinear and the high-dimensional interactions between services and users. Yang et al. [24] introduce a model-based algorithm that enhances the quality of CF recommendations by first identifying users whose rating data are sparse, and then sourcing from social networks user-to-user trust information for these users, in order to generate more informed recommendations. This algorithm adopts matrix factorization methods which utilize trust relationships to map users into low-dimensional latent feature spaces. It targets the learning of the preference patterns of users with high-quality recommendations, as well as reflecting the mutual influence between users on their impressions’ formulation. Nassar et al. [25] present a multi-criteria deep learning CF technique, which enhances CF performance. Initially, this technique receives the items’ and users’ characteristics and inserts them into a deep neural network (DNN) which computes predictions on the ratings of the criteria. Then, a second DNN is used which takes as input the aforementioned criteria and produces the overall ratings.

The algorithms presented in [26,27,28] fuse the rating prediction matrix with semantic information to enhance rating prediction quality. More specifically, Nguyen et al. [26] compute the cognitive similarity of the user about similar movies, and subsequently process the cognitive similarity-enhanced input using a three-layered architecture comprising (a) the item layer (which encompasses the network between items), (b) the cognition layer (which pertains to the network between the cognitive similarity of users), and (c) the user layer (which entails the network between users occurring in their cognitive similarity), achieving thus improvements in rating prediction accuracy. Alaa El-deen Ahmed et al. [27] introduce a hybrid recommendation system that combines (a) knowledge-driven recommendations generated with the use of a customized ontology and (b) recommendations created using classifiers and neural network-based collaborative filtering. This approach enables the flow of semantic information toward the machine learning component and, inversely, statistical information toward the ontology, resulting in improved rating prediction accuracy. Nguyen et al. [28] employ word embedding to first understand the plot of movies, and subsequently use this additional knowledge to compute more accurate movie-to-movie similarity measures, which are then utilized in the rating prediction generation process.

The approaches listed above fall into three general categories, each exhibiting its own merits: (a) the memory-based approach, which is easier to implement and better supports recommendation explainability, being additionally independent of the content on which the algorithm is applied; (b) the model-based approach, which offers higher accuracy, performs better with sparse user–item rating matrixes and being more scalable, and (c) the hybrid approach, which is more complex to create and apply, but on the other hand, offers additional performance gains and successfully tackles the issues of information loss and sparsity [29,30].

Although the aforementioned research works achieve considerable performance improvements, the supplementary information, which they all require, cannot be found in every CF dataset. Hence, a CF algorithm that is based only on the essential CF information, i.e., the {user, item, rating, timestamp} tuple may be more useful, since such an algorithm that operates solely on the user–item rating matrix can be applied to any CF dataset.

Towards this direction, Valdiviezo-Diaz et al. [31] present a rating prediction Bayesian model that produces justified recommendations. This model is based on both item-based and user-based CF approaches, and recommends items by using similar items’ and users’ information, respectively. Neysiani et al. [32] present a method that uses genetic algorithms, which are efficient when searching in very large spaces, in order to identify association rules in CF. This method can work without a minimum support threshold, set by the users, as well as a fitness function that identifies only the most interesting rules. Cui et al. [33] introduce a CF technique based on time cuckoo search K-means and correlation coefficient. In order to separate big data into smaller problems, this technique uses the cuckoo search K-means. Furthermore, in order for this technique to achieve accurate and quick recommendations, it uses a user clustering pre-processing algorithm. Wang et al. [34] present a hybrid model, which evaluates user similarity in an objective and comprehensive manner. This model contains an item similarity metric, which is based on the Kullback–Leibler divergence and adjusts the adjusted Proximity–Significance–Singularity model output. Furthermore, the model takes into account user asymmetric and user preference factors, which improve the reliability of the model output, by distinguishing the rating preference between different users. Jiang et al. [35] introduce a slope one algorithm that aims at the problems of untrusted ratings as well as the low accuracy in recommender systems. This algorithm is based on user similarity and the fusion of trusted data. In this algorithm, the trusted data are initially selected and then the user similarity is calculated. Finally, the computed similarity is added to the importance of the enhanced slope one algorithm and the final recommendation is produced. Margaris et al. [36] introduce the CF_VR (standing for CF Virtual Ratings), which aims to enhance the rating prediction coverage at sparse CF datasets. In this algorithm, for every NN not being able to contribute to the computation of the rating prediction, with a real rating, a virtual rating (VR) is produced and used instead. As a result, the density of the rating matrix is effectively increased, and hence the “grey sheep” problem is reduced.

Still, none of the aforementioned research works targets rating prediction quality enhancement in low-density CF datasets by considering predictions with specific characteristics as additional ratings.

Recently, Margaris et al. [16] and Margaris et al. [37] explore the factors associated with the accuracy of rating predictions in sparse and dense CF datasets, respectively.

The present work contributes to the state-of-the-art research on rating prediction accuracy in sparse CF datasets, by presenting an algorithm that enhances the rating prediction quality in sparse datasets, through the introduction of a preprocessing step, which calculates rating predictions for all cases that satisfy the conditions set in previous state-of-the-art research work, and subsequently adds these predictions in the original dataset as additional ratings producing an enhanced dataset. Then, any rating prediction algorithm can be applied to the enriched dataset, including memory-based algorithms, model-based algorithms, and algorithms exploiting additional features. The proposed algorithm is multi-parametrically evaluated and has been found to significantly enhance the rating prediction quality in low-density CF datasets.

3. The Proposed Algorithm

The typical process of a CF rating prediction algorithm consists of two basic steps:

(a)

Compute the similarity between all pairs of users in the dataset, using a similarity metric (such as the Cosine Similarity (CS) and the Pearson Correlation Coefficient (PCC), which are the ones used in the majority of the CF algorithms [38,39]). Once all user-user similarities are computed, the NNs for each user are determined.

(b)

For each user, U predict the rating values for the items they have not already rated, based on the rating values their NNs gave to the same items. To this end, a CF rating prediction formula is employed, where a typical formula choice is:

$$p_{U,i}=\overline{r_U}+\frac{{{\displaystyle \sum }}_{V\in N{N}_U}sim\left(U,V\right)* \left(r_{V,i}-\overline{r_V}\right)}{{{\displaystyle \sum }}_{V\in N{N}_U}sim\left(U,V\right)},$$

(1)

where U and i denote the user and the item, respectively, for whom the rating prediction is computed, $\overline{r_U}$ denotes the average value of U’s ratings, V iterates over the U’s NNs, and sim(U, V) signifies the similarity value between the pair of users U and V (calculated in the first CF step).

The proposed algorithm includes a preprocessing step, which computes predictions for all unrated items for each user, and the rating predictions, which satisfy the “rating prediction reliability” criteria identified in Margaris et al. [16] are added in the low-density rating dataset as additional ratings.

More specifically, the rating prediction reliability criteria identified by Margaris et al. [16] are as follows:

(i)

The number of NNs considered for the rating prediction formulation is at least four of the user’s NNs have rated the item and have thus contributed to the calculations of Equation (1).

(ii)

The active user’s average rating value is close to the lower or the higher end of the rating scale. In more detail, Ref. [16] asserts that for users having average rating values in the lower 10% of the rating scale, or in the higher 10% of the rating scale, rating predictions are considerably more accurate compared to predictions for users having average rating values close to the middle of the rating scale. Consequently, in this paper, we adopt the condition $(\overline{r_U}\le user\_threshold\_min \vee \overline{r_U}\ge user\_threshold\_max$) for utilizing a prediction to increase the density of the user–item rating matrix, where:

$$user\_threshold\_min=rating\_scale\_low\_bound+\frac{rating\_scale\_high\_bound-rating\_scale\_low\_bound}{10 },$$

(2)

and similarly

$$user\_threshold\_max=rating\_scale\_low\_bound-\frac{rating\_scale\_high\_bound-rating\_scale\_low\_bound}{10 },$$

(3)

(iii)

The average rating of the prediction item is close to the bounds of the rating scale. Similarly to the case of the user’s average rating, Ref. [16] asserts that for items having average rating values in the lower 10% of the rating scale, or in the higher 10% of the rating scale, rating predictions are considerably more accurate as compared to the rating predictions for items whose average rating values are close to the middle of the rating scale. Therefore, in this research, we adopt the condition (${\mathrm{i}}_{\mathrm{avg}}\le item\_threshold\_min \vee$ ${\mathrm{i}}_{\mathrm{avg}}\ge user\_threshold\_max$) for utilizing a prediction to increase the density of the user–item rating matrix, where:

$$item\_threshold\_min=rating\_scale\_low\_bound+\frac{rating\_scale\_high\_bound-rating\_scale\_low\_bound}{10 },$$

(4)

and similarly:

$$item\_threshold\_max=rating\_scale\_high\_bound-\frac{rating\_scale\_high\_bound-rating\_scale\_low\_bound}{10 }$$

(5)

As stated above, in this work, for a prediction to be added to the low-density rating dataset as an additional rating, we require that it meets all three criteria, since this has been experimentally found to deliver the maximum rating prediction enhancement. Algorithm 1 presents the pseudo-code of the algorithm for executing the proposed preprocessing step of the rating prediction enhancement in detail.

Algorithm 1: Preprocessing step of the rating prediction enhancement algorithm

Input: the original sparse CF dataset D Output: the updated CF dataset containing both the original and the additional ratings, D_enriched 1: function ENRICH_DATASET (CF_Dataset D) 2: credible_predictions ← ∅ 3: for each U ∈ D.users do 4:  for each i ∈ D.items do 5:   NNs_ratings_on_i = {r ∈ D.ratings: r.user ∈ user_NNs[U] and r.item = i and r.value != NULL} 6:   if D.ratings[U,i] = NULL and (avg_user_ratings[U] ≤ user_threshold_min or avg_user_ratings[U] ≥ user_threshold_max) and (avg_item_ratings[i] ≤ item_threshold_min or avg_item_ratings[i] ≥ item_threshold_max) then 7:      $prediction\leftarrow \mathrm{avg}\_\mathrm{user}\_\mathrm{ratings}\left[\mathrm{U}\right]+$          $\frac{{{\displaystyle \sum }}_{\mathrm{r}\in \mathrm{NNs}\_\mathrm{ratings}\_\mathrm{on}\_\mathrm{i} }user\_sim\left[\mathrm{U},\mathrm{r}.\mathrm{user}\right]* \left(\mathrm{r}.\mathrm{value}-\mathrm{avg}\_\mathrm{user}\_\mathrm{ratings}\left[\mathrm{r}.\mathrm{user}\right]\right)}{{{\displaystyle \sum }}_{\mathrm{r}\in \mathrm{NNs}\_\mathrm{ratings}\_\mathrm{on}\_\mathrm{i} }user\_sim\left[\mathrm{U},\mathrm{r}.\mathrm{user}\right]}$ 8:      credible_predictions $\leftarrow$ credible_predictions ∪ (user: U, item: i, value: prediction) 9:   end if 10:  end for 11: end for 12: D_Enriched.users ← D.users  // Formulate and return result 13: D_Enriched.items ←D.items 14: D_Enriched.ratings ← D.ratings ∪ credible_predictions 15: return (D_Enriched) 16: end function

After the preprocessing step has concluded, the typical CF procedure (steps (a) and (b)) is applied to the updated dataset. It has to be mentioned that although all user-to-user similarities have been computed in the preprocessing step, they need to be computed anew since the enriched dataset contains now more elements, which affect the similarity values. This applies also to rating predictions.

4. Experimental Evaluation

In order to assess the efficacy of the presented algorithm, a set of experiments is conducted, considering two rating prediction aspects, widely used in CF research, (a) the rating prediction accuracy, measured using two prediction error metrics, the mean average error (MAE) and the root-mean-square error (RMSE) and (b) the rating prediction coverage, i.e., the percentage of the prediction cases where the CF system can produce a numeric prediction. Additionally, to ascertain result reliability and generalizability, we explore the benefits of the proposed algorithm both on memory-based recommendation algorithms and model-based algorithms. Furthermore, in memory-based algorithms, we take into account the two most widespread user similarity measures in CF research, i.e., the PCC and the CS ([38,40,41]).

In our experiments, we utilize eight open-access sparse datasets, which are widely used in CF research. More specifically, we use the Ciao dataset [42], the Epinions Dataset [43], as well as six Amazon datasets [44,45,46,47]. As far as the six Amazon datasets are concerned, the five-core ones are used, in order to ensure that for each prediction case, at least four other ratings concerning the exact same item exist, so that we can produce valid results when applying the CF algorithm. These eight datasets vary in terms of involved product categories as well as in the number of items and users; however, all eight are considered sparse since all densities <<1%. Table 1 summarizes the features of the datasets.

Table 1. Dataset detailed information.

Dataset #	Dataset Title	Density	#Users (in K)	#Items (in K)	#Ratings (in K)	Avg. Ratings per User
1	Amazon Movies & TV	0.019%	298	60	3400	11.4
2	Amazon CDs and Vinyl	0.017%	112	74	1440	12.9
3	Amazon Grocery and Gourmet Food	0.075%	28	11	231	8.3
4	Amazon Videogames	0.006%	55	17	498	9.1
5	Amazon Office Products	0.03%	102	28	800	7.8
6	Amazon Digital Music	0.08%	17	12	170	10
7	CiaoDVD	0.073%	30	73	1600	53.3
8	Epinions	0.012%	40	140	665	16.6

In order to quantify the outcome of our experiments, we apply the typical “leave-one-out cross-validation” (or “hide one technique” for short), where each time the CF system predicts the rating value of one hidden user rating of the dataset [48,49,50]. In particular, we executed two sets of experiments, where for the first one, for each user, one of the user’s ratings, randomly, is predicted, whereas for the second one, for each user, the user’s last rating value (using the timestamp each rating has) is predicted. These two experiments are found to be in close convergence (their difference is less than 3%) and, for conciseness, in the following subsections we present only the results of the first one.

As stated above, in order to assess the improvements obtained through the introduction of the proposed approach, we employ two measures, the rating prediction error reduction, and the rating prediction coverage enhancement, which are formally defined as follows:

• Let D be a dataset, train(D) be a subset of D used for training, and test(D) = D − train(D) the subset of D used for testing.
• Let E(train(D)) be the enriched training dataset, formulated by applying the preprocessing step described in Section 3 on train(D).
• Let RP be a rating prediction algorithm.
• We apply RP(train(D)) on test(D), obtaining two sets, namely predictions(RP, train(D), test(D)) and failures(RP, train(D), test(D)), where failures(RP, train(D), test(D)) contains the cases for which a rating prediction could not be formulated (e.g., due to the absence of near neighbors), whereas predictions(RP, train(D), test(D)) contains the predictions that could actually be computed. Using the above, we can compute the rating prediction coverage RPC of algorithm RP on dataset D, which is defined as

  $$RPC\left(RP, train\left(D\right), test\left(D\right)\right)=\frac{\left|predictions\left(RP, train\left(D\right), test\left(D\right)\right)\right|}{\left|test\left(D\right)\right|},$$

  (6)

  whereas the rating prediction error can be quantified using either the MAE or the RMSE error metric, as shown in Equations (7) and (8), respectively:

  $$MAE\left(RP, train\left(D\right), test\left(D\right)\right)=\frac{{{\displaystyle \sum }}_{r\in predictions\left(RP, train\left(D\right), test\left(D\right)\right)}\left|r.value-r.realRating\right|}{\left|predictions\left(RP, train\left(D\right), test\left(D\right)\right)\right|}$$

  (7)

  $$RMSE\left(RP, train\left(D\right), test\left(D\right)\right)=\sqrt{\frac{{{\displaystyle \sum }}_{r\in predictions\left(RP, train\left(D\right), test\left(D\right)\right)}^{}{\left(r.value-r.realRating\right)}^2}{\left|predictions\left(RP, train\left(D\right), test\left(D\right)\right)\right|}}$$

  (8)
  It is important to note here that model-based algorithms typically compute a prediction for every case in the test dataset; when the model is not able to provide specific latent variables for the (user, item) pair for which the prediction is formulated, the prediction value degenerates to a dataset-dependent constant value [51]. Due to this fact, for model-based algorithms, the rating prediction coverage is ignored, and the evaluation is only based on the rating prediction error.
• Correspondingly, we apply RP(train(E(D))) on test(D), i.e., we obtain predictions using the enhanced dataset as input to the rating prediction algorithm, obtaining two sets, namely predictions(RP, train(E(D)), test(D)) and failures(RP, train(E(D)), test(D)), and we compute $RPC\left(RP, train\left(E\left(D\right)\right), test\left(D\right)\right)$, $MAE\left(RP, train\left(E\left(D\right)\right), test\left(D\right)\right)$ and $RMSE\left(RP, train\left(E\left(D\right)\right), test\left(D\right)\right)$, applying the Equations (1)–(3).
• Then, the rating prediction coverage enhancement (RPCE) for the rating prediction algorithm RP on dataset D is defined as

  $$RPCE\left(RP, train\left(D\right),test\left(D\right)\right)=\frac{RPC\left(RP, train\left(E\left(D\right)\right), test\left(D\right)\right)-RPC\left(RP, train\left(D\right), test\left(D\right)\right)}{RPC\left(RP, train\left(D\right), test\left(D\right)\right)}$$

  (9)

  whereas the rating prediction error reduction (RPER) considering the MAE and RMSE error metrics is computed as shown in Equations (5) and (6), respectively:

  $$RPE{R}_{MAE}\left(RP,train\left(D\right),test\left(D\right)\right)=\frac{MAE\left(RP, train\left(D\right), test\left(D\right)\right)-MAE\left(RP, train\left(E\left(D\right)\right), test\left(D\right)\right)}{MAE\left(RP, train\left(D\right), test\left(D\right)\right)}$$

  (10)

  $$RPE{R}_{RMSE}\left(RP, train\left(D\right),test\left(D\right)\right)=\frac{RMSE\left(RP, train\left(D\right), test\left(D\right)\right)-RMSE\left(RP, train\left(E\left(D\right)\right), test\left(D\right)\right)}{RMSE\left(RP, train\left(D\right), test\left(D\right)\right)}$$

  (11)

4.1. Using the Preprocessing Step with Memory-Based Rating Prediction Algorithms

In this subsection we report on our findings from using the proposed approach in combination with memory-based prediction algorithms, i.e., the preprocessing step is applied to the original dataset producing an enhanced dataset, and afterward a memory-based rating prediction algorithm is applied to the enhanced dataset, to generate additional rating predictions. Section 4.1.1 and Section 4.1.2 report on the findings considering rating prediction accuracy and coverage, respectively.

4.1.1. Rating Prediction Accuracy Evaluation

In this paragraph, we present the outcomes of the evaluation, in terms of rating prediction error reduction. Figure 2 depicts the rating prediction accuracy gains obtained, as quantified by the MAE and the RMSE deviation measures, when the user–user similarity metric applied is the PCC.

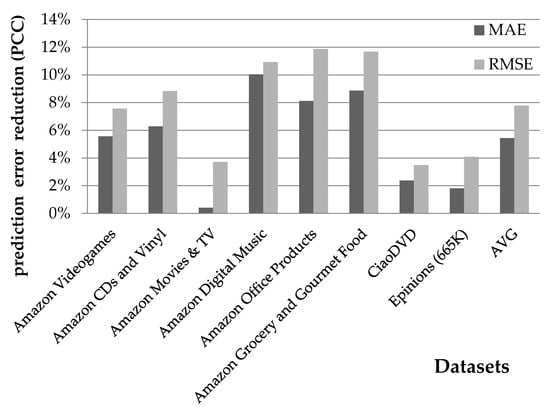
Figure 2. Rating prediction error reduction attained by the presented algorithm, when using the PCC user vicinity metric.

The presented algorithm achieves an average rating prediction error reduction of 5.4% and 7.8%, in terms of the MAE and RMSE deviation metrics, respectively, under the PCC user–user similarity metric. MAE reductions range from 0.41% (for Amazon Movies & TV) to 10.04% (for Amazon Digital Music). Correspondingly, the RMSE reductions range from 3.49% (for the CiaoDVD) to 11.87% (for the Amazon Office Products). In general, we can observe that RMSE reductions are higher than the improvements in MAE, signifying that the proposed method corrects large prediction errors.

Figure 3 depicts the respective rating prediction accuracy gains, as quantified by the MAE and the RMSE measures, when the user-user similarity is quantified by the CS metric. The average rating prediction error reduction considering the MAE metric under the CS user similarity metric is 2.4%. The corresponding reduction considering the RMSE metric is 6%. These MAE reductions range from 1% (observed for Amazon Movies & TV as well as for Amazon CDs and Vinyl) to 4.1% (for Amazon Office Products). Correspondingly, RMSE reductions range from 1.4% (for Amazon Movies & TV) to 9.5% (for Amazon Digital Music). The RMSE reductions are again higher than the respective improvements in the MAE, signifying that the proposed method corrects large prediction errors.

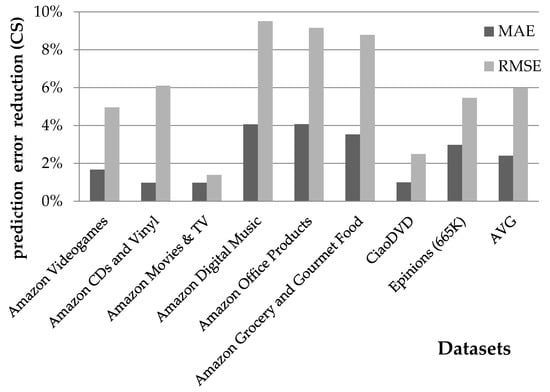
Figure 3. Rating prediction error reduction attained by the presented algorithm, when using the CS user vicinity metric.

4.1.2. Rating Prediction Coverage Evaluation

In this paragraph, the outcomes of the performance evaluation of the proposed algorithm are presented, in terms of rating prediction coverage enhancement.

Figure 4 depicts the rating prediction coverage gains when user similarity is calculated through the PCC metric.

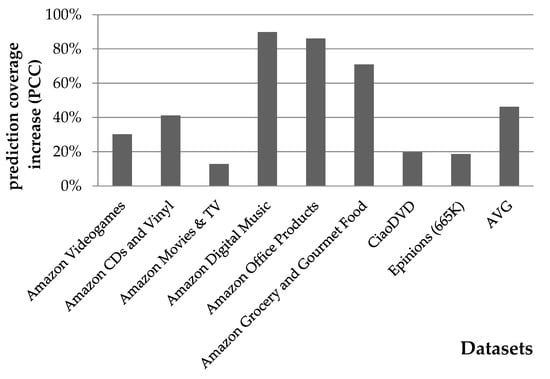
Figure 4. Rating prediction coverage enhancement attained by the presented algorithm, when using the PCC user vicinity metric.

The presented algorithm achieves an average rating prediction coverage enhancement of 46.2% when the user similarity metric applied is the PCC, ranging from 12.8% for the case of the Amazon Movies & TV dataset to 89.8% for the case of the Amazon Digital Music dataset. At this point, it is worth noting that the initial coverage of Amazon Digital Music was less than 20%; hence, the improvement margin for this dataset was considerable, whereas the initial coverage for the Amazon Movies & TV dataset was >65%, leading to reduced improvement margins. It is worth noting that for the Amazon datasets, smaller initial coverage was found to be directly associated with the coverage increase achieved, whereas the CiaoDVD and Epinions datasets deviate from the pattern, exhibiting lower coverage improvement compared to Amazon datasets with similar initial coverage. A more detailed analysis of this observation will be conducted in the context of our future work.

Similarly, Figure 5 depicts the respective rating prediction coverage gains when the user–user similarity metric applied is the CS. The proposed algorithm, under the CS metric, achieves an average rating prediction coverage enhancement of 35.3%, ranging from 9.1% for the case of the Amazon Movies & TV dataset, to 60.8% for the case of the Amazon Office Products dataset. Analogously to the previous case (when the PCC metric is used), for the Amazon datasets, the rating coverage increase achieved by the proposed algorithm was found to be monotonically decreasing with the datasets’ initial coverage. In particular, the Amazon Movies & TV dataset had the highest initial coverage (90.8%), whereas the Amazon Office Products dataset had the smallest initial coverage (59.8%). Nevertheless, the CiaoDVD and Epinions datasets exhibit reduced coverage improvement, compared to Amazon datasets with similar initial coverage, an issue that will be explored in our future work.

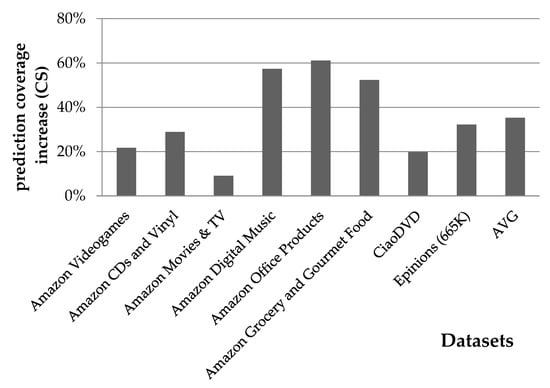
Figure 5. Rating prediction coverage enhancement attained by the presented algorithm, when using the CS user vicinity metric.

4.2. Using the Preprocessing Step with Model-Based Rating Prediction Algorithms

In this subsection, we report on our experiments, which aim to validate the applicability of the proposed approach in conjunction with model-based recommendation algorithms. In particular, we followed the process depicted in Figure 1, first applying the preprocessing step presented in Section 3, and subsequently using the enriched user–item rating matrix as input to a model-based rating prediction algorithm. To ensure the generalizability of the results, we tested two different model-based rating prediction algorithms and more specifically (a) the item-based algorithm [52,53] and (b) the matrix factorization algorithm [54,55].

Figure 6 illustrates the improvements obtained in rating prediction accuracy through the application of the proposed algorithm in three Amazon product datasets [47] when rating predictions were computed using the item-based algorithm. In Figure 6 we can observe that the average MAE improvement is 1.8%, ranging from 1.3% for the Videogames datasets to 2.1% for the Digital music dataset, whereas the corresponding average improvement for the RMSE metric is 1.7%, ranging from 1.6% for the Videogames dataset to 1.8% for the Digital Music and the Office products datasets.

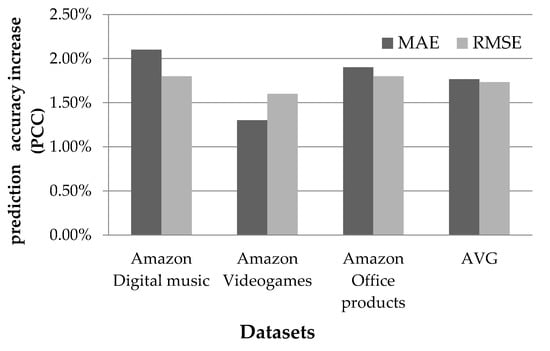
Figure 6. Rating prediction accuracy enhancement achieved by the proposed approach, when rating predictions are computed using the item-based algorithm.

Figure 7 illustrates the improvements obtained in rating prediction accuracy through the application of the proposed algorithm in the same three Amazon product datasets shown in Figure 7 [47] when rating predictions are computed using the matrix factorization algorithm. In Figure 8 we can observe that the average MAE improvement is 4.1%, ranging from 3.5% for the Videogames dataset to 4.7% for the Office products dataset, whereas the corresponding average improvement for the RMSE metric is 2.5%, ranging from 1.1% for the Digital Music dataset to 4.7% for the Videogames dataset.

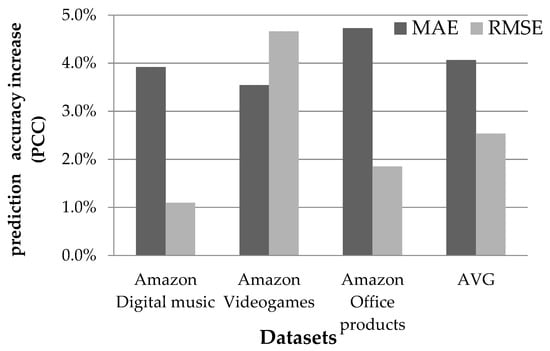
Figure 7. Rating prediction accuracy enhancement achieved by the proposed approach, when rating predictions are computed using the matrix factorization algorithm.

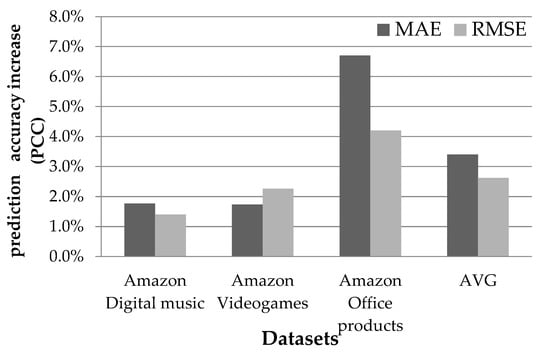
Figure 8. Rating prediction accuracy enhancement achieved by the proposed approach, when rating prediction computation is performed using the TrustSVD algorithm, which computes and exploits implicit trust.

The experiments presented in this section, therefore, demonstrate that the proposed approach can be employed in combination with model-based algorithms, with the rating accuracy prediction benefits ranging from fair to substantial, depending on the dataset.

4.3. Using the Preprocessing Step with Implicit Trust Rating Prediction Algorithms

In this subsection, we report on our experiments aimed to validate the applicability of the proposed approach in conjunction with recommendation algorithms that compute and exploit implicit trust. Similarly to the practice described in the previous section, we followed the process depicted in Figure 1, first applying the preprocessing step presented in Section 3, and subsequently using the enriched user–item rating matrix as input to an implicit trust-based rating prediction algorithm. The algorithm used for this validation is TrustSVD [56], which was tuned to only exploit the implicit trust; explicit trust relationships that could be accommodated by the algorithm were not provided.

Figure 9 illustrates the improvements obtained in rating prediction accuracy through the application of the proposed algorithm in the same three Amazon product datasets depicted in Figure 6 and Figure 7 [47], in combination with the TrustSVD rating prediction algorithm [56]. In Figure 8 we can observe that the average MAE improvement is 3.4%, ranging from 1.7% for the Videogames dataset to 6.7% for the Office products dataset, whereas the corresponding average improvement for the RMSE metric is 2.6%, ranging from 1.4% for the Digital Music dataset to 4.2% for the Office products dataset.

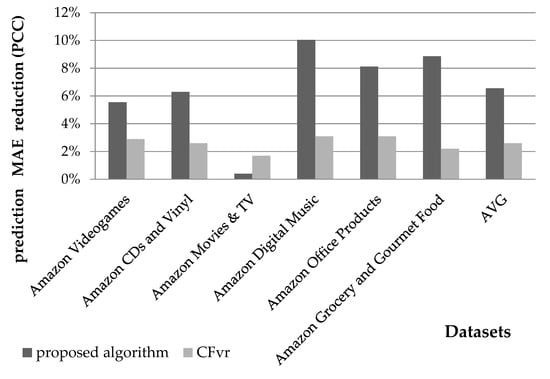
Figure 9. Comparison of rating prediction MAE reduction attained by the presented algorithm and the CF_VR algorithm.

5. Discussion of the Results and Comparison with Previous Work

The results of the experimental evaluation presented above, substantiate that the algorithm proposed effectively enhances rating prediction quality in low-density CF datasets, regardless of their item domain (we have used datasets having a wide range of item domains, from Movies and Music to Office Products and Food), the number of items and the number of users contained therein, as well as the density level of the dataset. The behavior has been also found to be exhibited under both user similarity metrics utilized in the experiment (PCC and CS). Moreover, the proposed preprocessing step can be combined with model-based algorithms with the corresponding benefits ranging from fair to substantial, as demonstrated in Section 4.2. It is also worth noting that improvements are demonstrated for both aspects of rating prediction quality, i.e., rating prediction accuracy and coverage, and these improvements are observed not only on an average level, but also in every individual dataset examined.

Furthermore, we compare the performance of this algorithm against the performance of the CF_VR algorithm proposed by Margaris et al. [36], which has been found to surpass the performance of other CF rating prediction algorithms (e.g., [57,58]). In this comparison, only the Amazon Datasets Videogames, CDs and Vinyl, Movies & TV, Digital Music, Office Products, and Grocery and Gourmet Food will be considered, since they constitute the intersection of the datasets utilized for performance evaluation in [36] and the current paper.

Considering the aspect of rating prediction accuracy, the presented algorithm achieves an average MAE reduction of 6.6%, whereas the CF_VR achieves an MAE reduction of 2.6%, i.e., the presented algorithm exceeds the performance of CF_VR over 2.5 times. The respective RMSE reductions these algorithms achieve are 9.1% and 3.4%, respectively (for both metrics, the plain CF algorithm is considered as the performance baseline against which error reductions are calculated). Figure 9 and Figure 10 depict the comparison between the two aforementioned algorithms at both average and individual dataset levels; the proposed algorithm consistently outperforms CF_VR in all cases, except for the case of the MAE metric on the Amazon Movies & TV dataset. However, we notice that in this dataset the presented algorithm achieves a higher reduction in the RMSE metric than CF_VR, due to the fact that the proposed algorithm corrects a number of large prediction errors, which are more severely penalized when using the RMSE metric. For conciseness, only figures concerning the algorithms’ performance when using the PCC metric are listed; however, similar observations hold for the results obtained when the CS metric is used instead.

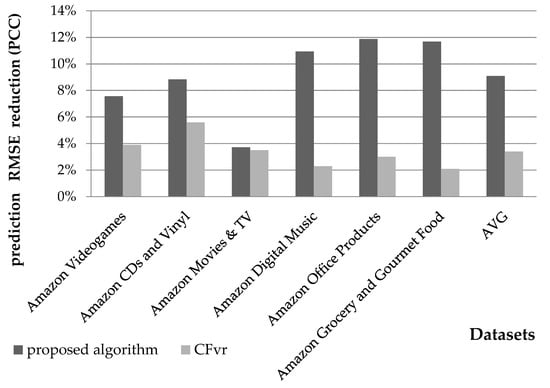
Figure 10. Comparison of rating prediction RMSE reduction attained by the proposed algorithm and the CF_VR algorithm.

Regarding the aspect of coverage increase, the proposed algorithm achieves a coverage increase of 35.6% on average over the datasets considered in the comparison, whereas the improvement attained by the CF_VR algorithm is 30.1%. Figure 11 depicts the comparison results at both average and dataset-level. We can notice that the CF_VR algorithm achieves a better coverage increase in four cases, whereas the presented algorithm achieves a higher coverage increase for two datasets; however, two of the CF_VR’s leads are by a relatively small margin (less than 7.5%). Each of the algorithms ensures two “clear” performance leads at dataset level.

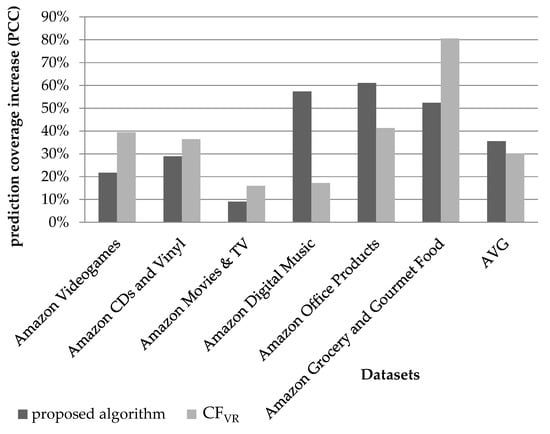
Figure 11. Comparison of increases in coverage attained by the proposed algorithm and the CF_VR algorithm.

Considering recommender systems that exploit implicit trust relationships, Ref. [59] reports on a state-of-the-art algorithm that improves rating prediction coverage against the classic user–user CF algorithm by a ratio varying from 2% to 4.5%. At the same time, the algorithm proposed by Li et al. [59] improves rating prediction accuracy by a margin ranging from 5% to 8.3% considering the MAE, whereas the rating prediction accuracy improvement gains considering the RMSE metric range from 4.86% to 7.59%. The proposed approach on the other hand achieves a coverage prediction increase of 35.6% on average, whereas the improvement in accuracy it attains is 5.43% on average regarding the MAE metric and 7.77% regarding the RMSE metric. Overall, the approach proposed in this paper has a clear performance edge considering rating coverage, although, on average, it has slightly inferior performance, as compared to the implicit trust algorithm proposed in [59]. Finally, as demonstrated in Section 4.3, the proposed algorithm can be combined with implicit trust algorithms, reaping considerable benefits.

6. Conclusions and Future Work

In this work, we presented an algorithm that can effectively enhance rating prediction quality in low-density CF datasets. This algorithm introduces a preprocessing step that determines which rating predictions can be deemed to be reliable, and then computes these rating predictions and incorporates them into the user–item rating matrix, increasing thus the dataset density. The criteria used to characterize rating predictions as “reliable” are sourced from the state-of-the-art research work reported by Margaris et al. [16]. Afterward, the typical CF procedure is applied to the updated dataset, with both memory-based and model-based CF approaches being applicable at the step of the recommendation generation. The presented algorithm was multi-parametrically evaluated, using 8 widely accepted sparse CF datasets, and was found to substantially enhance the rating prediction quality in low-density CF datasets, in terms of both rating prediction coverage and accuracy. The proposed algorithm has also been demonstrated to be applicable in combination with model-based and implicit trust-aware algorithms, resulting in additional performance improvements.

The presented algorithm successfully reduces the CF rating prediction error and it also enhances the rating prediction coverage, in all datasets tested. This behavior was found to be consistent under both user–user similarity metrics utilized in the evaluation (PCC and CS). Furthermore, we also compared the presented algorithm against the CF_VR algorithm (a state-of-the-art CF algorithm, which also targets CF datasets with low density and is based exclusively on the user–item–rating CF tuples), in terms of rating prediction enhancement. The algorithm presented in this work has been demonstrated to perform better than the CF_VR algorithm, in terms of rating prediction accuracy, under both of the user similarity metrics considered. Regarding the aspect of coverage increase, the proposed algorithm achieves better overall performance, despite the fact that in some datasets the CF_VR exhibits a higher coverage increase than the proposed algorithm.

In our future work, we plan to investigate the application of the presented algorithm in dense CF datasets. Adaptation of the proposed algorithm to consider additional information, such as item (sub-)categories, user and item social media information, and user emotions and characteristics, will also be investigated [60,61,62]. The integration of the proposed algorithm with additional accuracy enhancement techniques, including algorithms for fraudulent rating detection and removal [35] will also be considered. Finally, the performance of the proposed algorithm when applying additional user–user similarity metrics, such as the adjusted mutual information, the adjusted Rand index, and the Spearman correlation [63,64,65,66,67], as well as the novel hybrid user similarity model presented in [34] will be also considered.