Physics-Informed Neural Network (PINN) Evolution and Beyond: A Systematic Literature Review and Bibliometric Analysis
Abstract
1. Introduction
2. Background
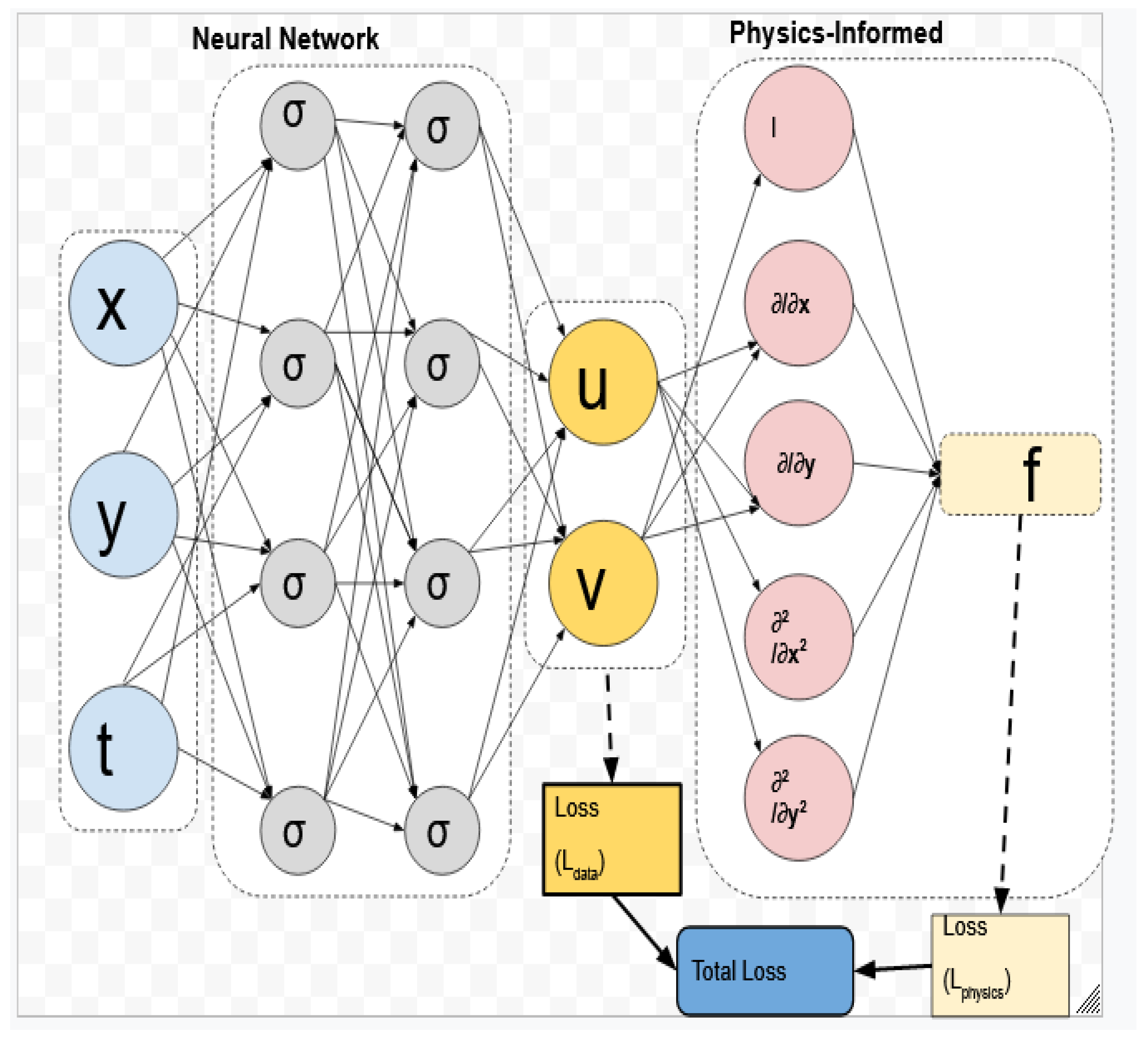
2.1. Physics-Informed Neural Networks
2.2. Modeling and Computation
- Data-driven solutions.
- Data-driven discovery.
- Data-Driven solutions of Partial Differential Equations
- Data Discovery of Partial Differential Equations
3. Methodology
3.1. Quality Assessment
3.2. Qualitative Synthesis Used in the Literature Review
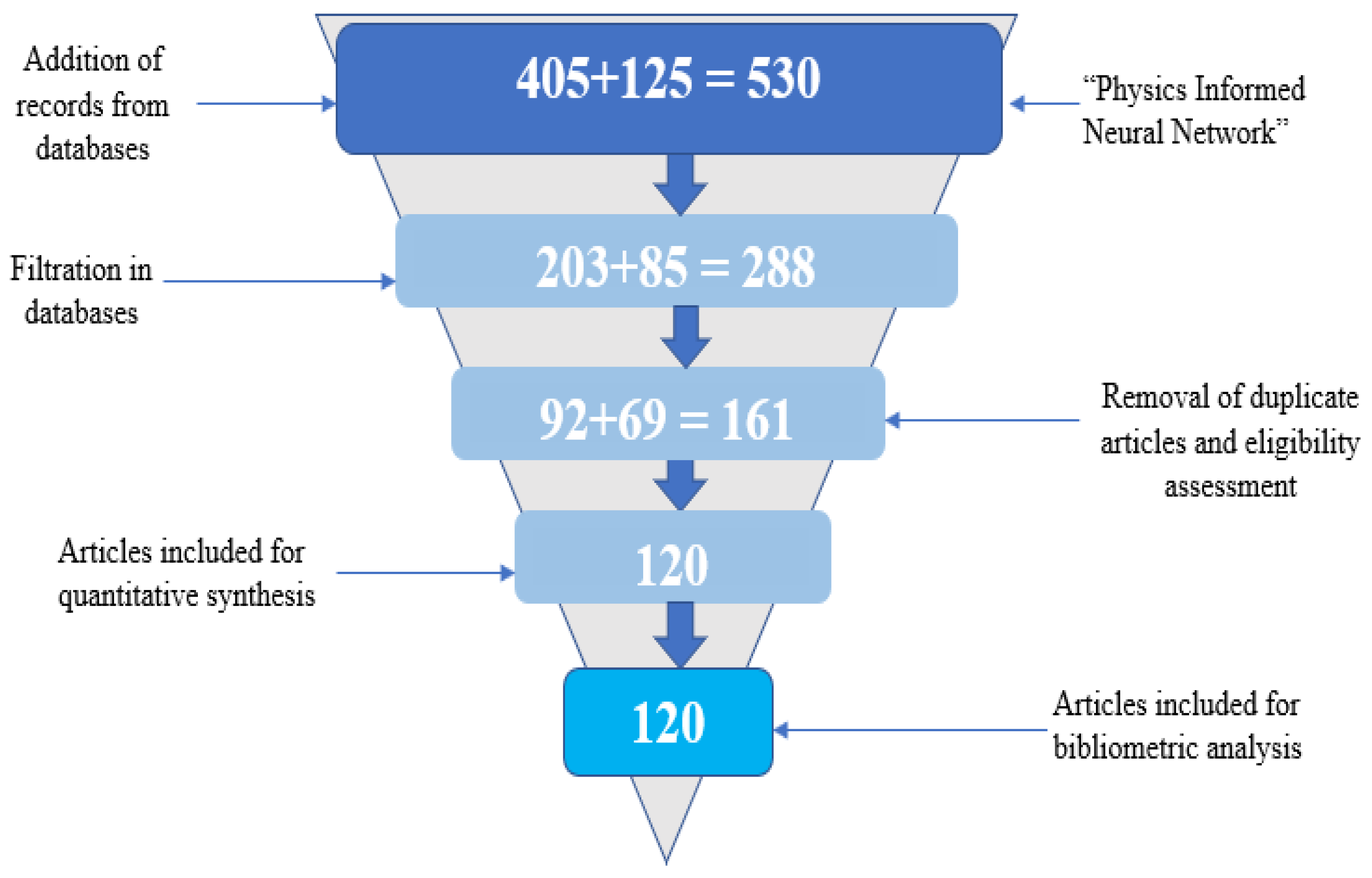
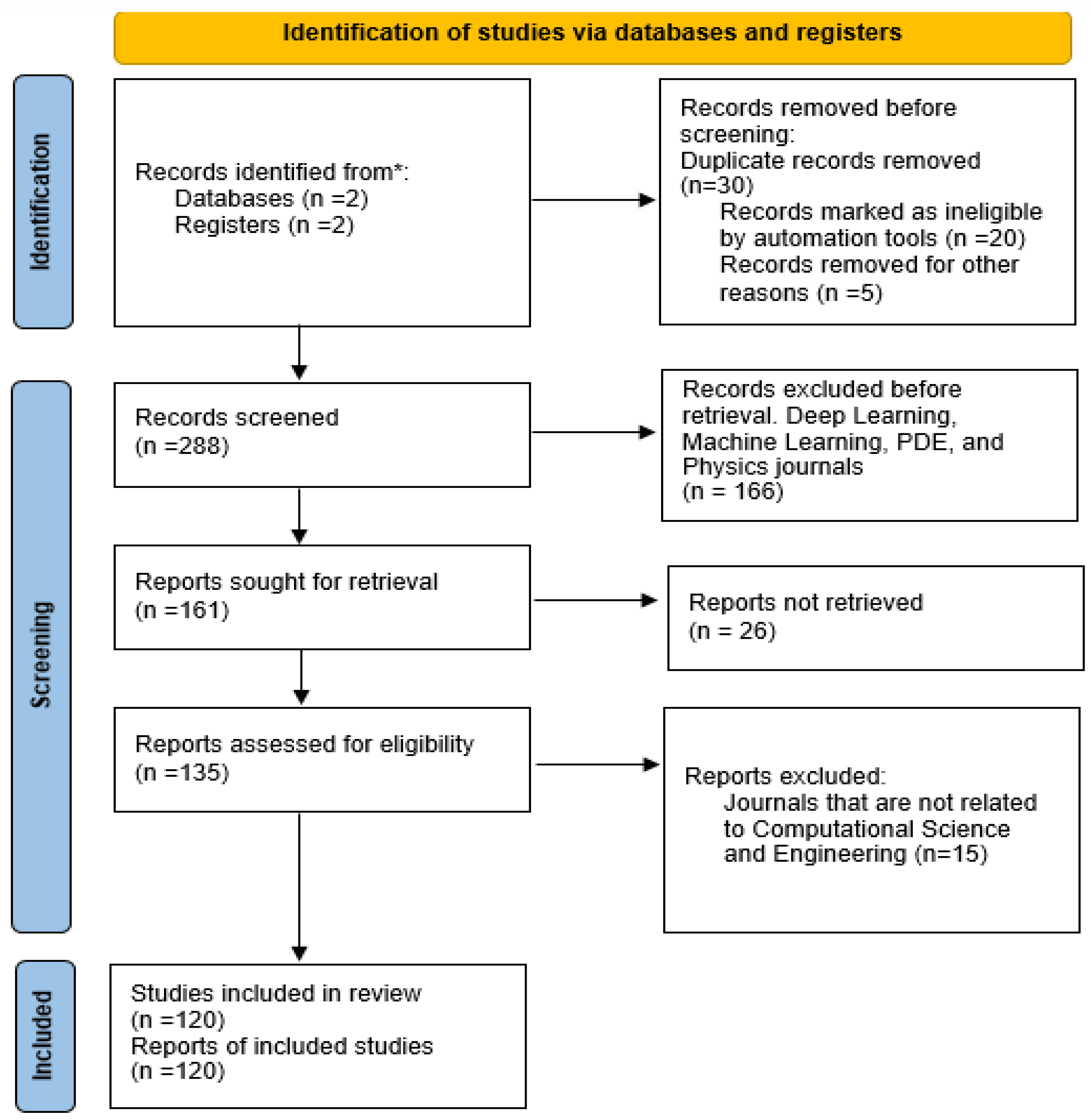
3.3. Quantitative Synthesis (Meta-Analysis)
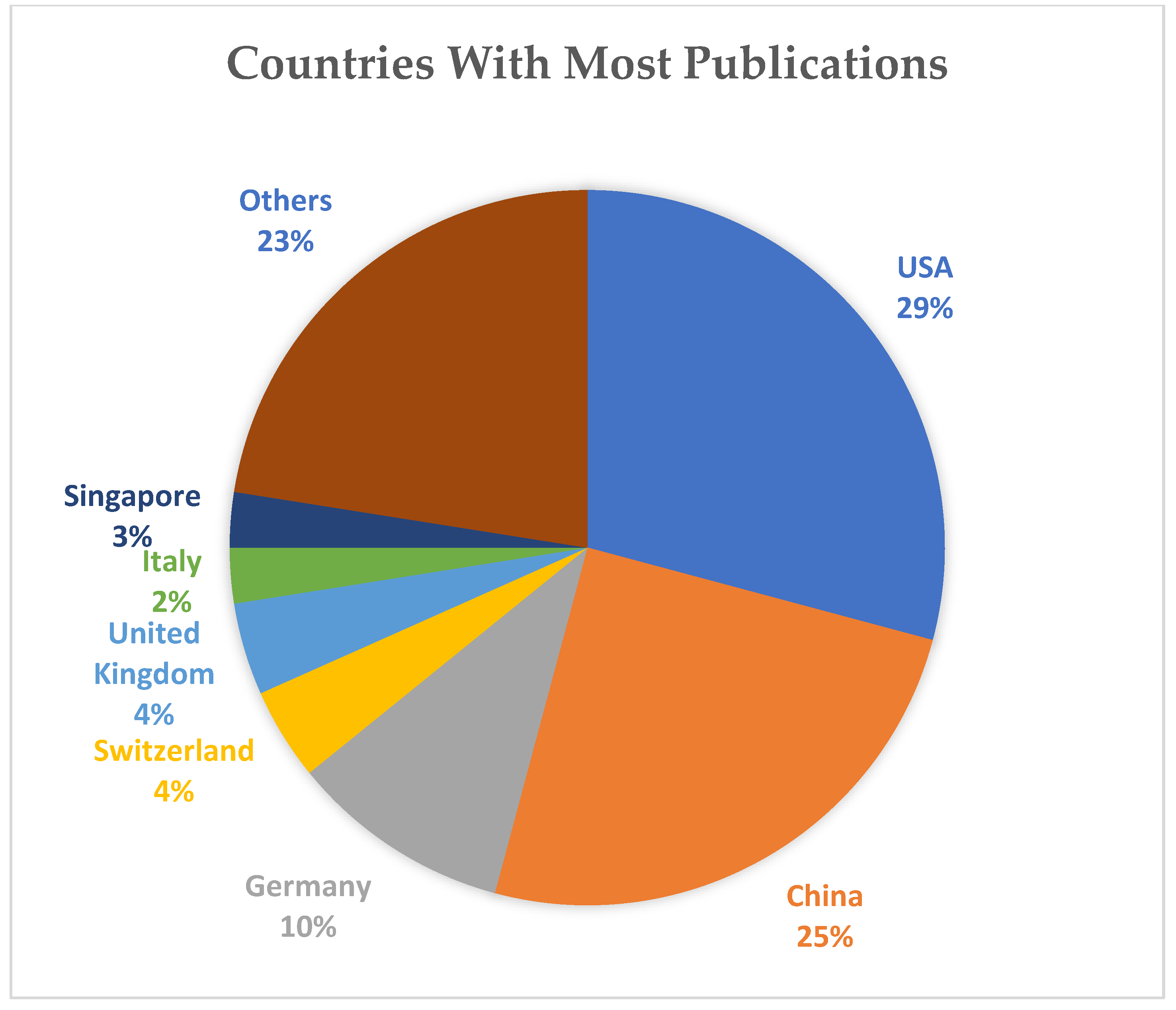
4. Result of Bibliometric Analyses
4.1. Newly Proposed PINN Methods
4.1.1. Extended PINNs
4.1.2. Hybrid PINNs
4.1.3. Minimized Loss Techniques
5. Future Research Direction
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Hu, Z.; Jagtap, A.D.; Karniadakis, G.E.; Kawaguchi, K. When Do Extended Physics-Informed Neural Networks (XPINNs) Improve Generalization? arXiv 2021, arXiv:2109.09444. [Google Scholar] [CrossRef]
- Shukla, K.; Jagtap, A.D.; Karniadakis, G.E. Parallel physics-informed neural networks via domain decomposition. J. Comput. Phys. 2021, 447, 110683. [Google Scholar] [CrossRef]
- Ang, E.; Ng, B.F. Physics-Informed Neural Networks for Flow Around Airfoil. In AIAA SCITECH 2022 Forum; American Institute of Aeronautics and Astronautics: Fairfax, VA, USA, 2021. [Google Scholar] [CrossRef]
- Gnanasambandam, R.; Shen, B.; Chung, J.; Yue, X. Self-scalable Tanh (Stan): Faster Convergence and Better Generalization in Physics-informed Neural Networks. arXiv 2022, arXiv:2204.12589. [Google Scholar]
- Cai, S.; Wang, Z.; Wang, S.; Perdikaris, P.; Karniadakis, G.E. Physics-Informed Neural Networks for Heat Transfer Problems. J. Heat Transf. 2021, 143, 060801. [Google Scholar] [CrossRef]
- Chiu, P.-H.; Wong, J.C.; Ooi, C.; Dao, M.H.; Ong, Y.-S. CAN-PINN: A fast physics-informed neural network based on coupled-automatic–numerical differentiation method. Comput. Methods Appl. Mech. Eng. 2022, 395, 114909. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, X.; Peng, W.; Zhou, W.; Yao, W. A novel meta-learning initialization method for physics-informed neural networks. arXiv 2022, arXiv:2107.10991. [Google Scholar] [CrossRef]
- Yang, S.; Chen, H.-C.; Wu, C.-H.; Wu, M.-N.; Yang, C.-H. Forecasting of the Prevalence of Dementia Using the LSTM Neural Network in Taiwan. Mathematics 2021, 9, 488. [Google Scholar] [CrossRef]
- Huang, B.; Wang, J. Applications of Physics-Informed Neural Networks in Power Systems—A Review. IEEE Trans. Power Syst. 2022, 1. [Google Scholar] [CrossRef]
- Chen, W.; Wang, Q.; Hesthaven, J.S.; Zhang, C. Physics-informed machine learning for reduced-order modeling of nonlinear problems. J. Comput. Phys. 2021, 446, 110666. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, Y.; Sun, H. Physics-informed learning of governing equations from scarce data. Nat. Commun. 2021, 12, 6136. [Google Scholar] [CrossRef]
- Karakusak, M.Z.; Kivrak, H.; Ates, H.F.; Ozdemir, M.K. RSS-Based Wireless LAN Indoor Localization and Tracking Using Deep Architectures. Big Data Cogn. Comput. 2022, 6, 84. [Google Scholar] [CrossRef]
- De Ryck, T.; Jagtap, A.D.; Mishra, S. Error estimates for physics informed neural networks approximating the Navier-Stokes equations. arXiv 2022, arXiv:2203.09346. [Google Scholar]
- Zhai, H.; Sands, T. Controlling Chaos in Van Der Pol Dynamics Using Signal-Encoded Deep Learning. Mathematics 2022, 10, 453. [Google Scholar] [CrossRef]
- Zhang, T.; Xu, H.; Guo, L.; Feng, X. A non-intrusive neural network model order reduction algorithm for parameterized parabolic PDEs. Comput. Math. Appl. 2022, 119, 59–67. [Google Scholar] [CrossRef]
- Ankita; Rani, S.; Singh, A.; Elkamchouchi, D.H.; Noya, I.D. Lightweight Hybrid Deep Learning Architecture and Model for Security in IIOT. Appl. Sci. 2022, 12, 6442. [Google Scholar] [CrossRef]
- Wight, C.L.; Zhao, J. Solving Allen-Cahn and Cahn-Hilliard Equations using the Adaptive Physics Informed Neural Networks. arXiv 2020, arXiv:2007.04542. [Google Scholar]
- Rasht-Behesht, M.; Huber, C.; Shukla, K.; Karniadakis, G.E. Physics-Informed Neural Networks (PINNs) for Wave Propagation and Full Waveform Inversions. J. Geophys. Res. Solid Earth 2022, 127, e2021JB023120. [Google Scholar] [CrossRef]
- Nasiri, P.; Dargazany, R. Reduced-PINN: An Integration-Based Physics-Informed Neural Networks for Stiff ODEs. arXiv 2020, arXiv:2208.12045. [Google Scholar]
- Schiassi, E.; De Florio, M.; D’Ambrosio, A.; Mortari, D.; Furfaro, R. Physics-Informed Neural Networks and Functional Interpolation for Data-Driven Parameters Discovery of Epidemiological Compartmental Models. Mathematics 2021, 9, 2069. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Y.; Zhou, W.; Chen, X.; Yao, W.; Zhao, Y. TONR: An exploration for a novel way combining neural network with topology optimization. Comput. Methods Appl. Mech. Eng. 2021, 386, 114083. [Google Scholar] [CrossRef]
- Wang, S.; Teng, Y.; Perdikaris, P. Understanding and mitigating gradient pathologies in physics-informed neural networks. arXiv 2020, arXiv:2001.04536. [Google Scholar] [CrossRef]
- Fujita, K. Physics-Informed Neural Network Method for Space Charge Effect in Particle Accelerators. IEEE Access 2021, 9, 164017–164025. [Google Scholar] [CrossRef]
- Yu, J.; de Antonio, A.; Villalba-Mora, E. Deep Learning (CNN, RNN) Applications for Smart Homes: A Systematic Review. Computers 2022, 11, 26. [Google Scholar] [CrossRef]
- Dwivedi, V.; Srinivasan, B. A Normal Equation-Based Extreme Learning Machine for Solving Linear Partial Differential Equations. J. Comput. Inf. Sci. Eng. 2021, 22, 014502. [Google Scholar] [CrossRef]
- Haghighat, E.; Amini, D.; Juanes, R. Physics-informed neural network simulation of multiphase poroelasticity using stress-split sequential training. Comput. Methods Appl. Mech. Eng. 2021, 397, 115141. [Google Scholar] [CrossRef]
- Berg, J.; Nyström, K. A unified deep artificial neural network approach to partial differential equations in complex geometries. Neurocomputing 2018, 317, 28–41. [Google Scholar] [CrossRef]
- Mahesh, R.B.; Leandro, J.; Lin, Q. Physics informed neural network for spatial-temporal flood forecasting. In Climate Change and Water Security; Lecture Notes in Civil Engineering; Springer Nature Singapore Pte Ltd.: Singapore, 2022; Volume 178. [Google Scholar] [CrossRef]
- Ngo, P.; Tejedor, M.; Tayefi, M.; Chomutare, T.; Godtliebsen, F. Risk-Averse Food Recommendation Using Bayesian Feedforward Neural Networks for Patients with Type 1 Diabetes Doing Physical Activities. Appl. Sci. 2020, 10, 8037. [Google Scholar] [CrossRef]
- Henkes, A.; Wessels, H.; Mahnken, R. Physics informed neural networks for continuum micromechanics. Comput. Methods Appl. Mech. Eng. 2022, 393, 114790. [Google Scholar] [CrossRef]
- Patel, R.G.; Manickam, I.; Trask, N.A.; Wood, M.A.; Lee, M.; Tomas, I.; Cyr, E.C. Thermodynamically consistent physics-informed neural networks for hyperbolic systems. J. Comput. Phys. 2020, 449, 110754. [Google Scholar] [CrossRef]
- Fang, Z. A High-Efficient Hybrid Physics-Informed Neural Networks Based on Convolutional Neural Network. IEEE Trans. Neural Networks Learn. Syst. 2021, 33, 5514–5526. [Google Scholar] [CrossRef]
- Lawal, Z.K.; Yassin, H.; Zakari, R.Y. Flood Prediction Using Machine Learning Models: A Case Study of Kebbi State Nigeria. In Proceedings of the 2021 IEEE Asia-Pacific Conference on Computer Science and Data Engineering (CSDE), Brisbane, Australia, 8–10 December 2021. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Kharazmi, E.; Karniadakis, G.E. Conservative physics-informed neural networks on discrete domains for conservation laws: Applications to forward and inverse problems. Comput. Methods Appl. Mech. Eng. 2020, 365, 113028. [Google Scholar] [CrossRef]
- Mao, Z.; Jagtap, A.D.; Karniadakis, G.E. Physics-informed neural networks for high-speed flows. Comput. Methods Appl. Mech. Eng. 2020, 360, 112789. [Google Scholar] [CrossRef]
- Bihlo, A.; Popovych, R.O. Physics-informed neural networks for the shallow-water equations on the sphere. J. Comput. Phys. 2022, 456, 111024. [Google Scholar] [CrossRef]
- Lagaris, I.; Likas, A.; Fotiadis, D. Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans. Neural Networks 1998, 9, 987–1000. [Google Scholar] [CrossRef]
- Zjavka, L. Construction and adjustment of differential polynomial neural network. J. Eng. Comput. Innov. 2011, 2, 40–50. [Google Scholar]
- Zjavka, L. Approximation of multi-parametric functions using the differential polynomial neural network. Math. Sci. 2013, 7, 33. [Google Scholar] [CrossRef]
- Zjavka, L.; Snasel, V. Composing and Solving General Differential Equations Using Extended Polynomial Networks. In Proceedings of the 2015 International Conference on Intelligent Networking and Collaborative Systems, IEEE INCoS 2015, Taipei, Taiwan, 2–4 September 2015; pp. 110–115. [Google Scholar] [CrossRef]
- Raissi, M.; Karniadakis, G.E. Hidden physics models: Machine learning of nonlinear partial differential equations. J. Comput. Phys. 2018, 357, 125–141. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics Informed Deep Learning (Part I): Data-driven Solutions of Nonlinear Partial Differential Equations. arXiv 2017, arXiv:1711.10561. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Multistep Neural Networks for Data-driven Discovery of Nonlinear Dynamical Systems. arXiv 2018, arXiv:1801.01236. [Google Scholar]
- Raissi, M. Deep Hidden Physics Models: Deep Learning of Nonlinear Partial Differential Equations. 2018. Available online: http://jmlr.org/papers/v19/18-046.html (accessed on 3 June 2022).
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Numerical Gaussian Processes for Time-dependent and Non-linear Partial Differential Equations. arXiv 2017, arXiv:1703.10230. [Google Scholar]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Lazovskaya, T.; Malykhina, G.; Tarkhov, D. Physics-Based Neural Network Methods for Solving Parameterized Singular Perturbation Problem. Computation 2021, 9, 97. [Google Scholar] [CrossRef]
- Bati, G.F.; Singh, V.K. Nadal: A neighbor-aware deep learning approach for inferring interpersonal trust using smartphone data. Computers 2021, 10, 3. [Google Scholar] [CrossRef]
- Klyuchinskiy, D.; Novikov, N.; Shishlenin, M. A Modification of Gradient Descent Method for Solving Coefficient Inverse Problem for Acoustics Equations. Computation 2020, 8, 73. [Google Scholar] [CrossRef]
- Li, J.; Zheng, L. DEEPWAVE: Deep Learning based Real-time Water Wave Simulation. Available online: https://jinningli.cn/cv/DeepWavePaper.pdf (accessed on 25 May 2022).
- Nascimento, R.G.; Fricke, K.; Viana, F.A. A tutorial on solving ordinary differential equations using Python and hybrid physics-informed neural network. Eng. Appl. Artif. Intell. 2020, 96, 103996. [Google Scholar] [CrossRef]
- Cheng, Y.; Huang, Y.; Pang, B.; Zhang, W. ThermalNet: A deep reinforcement learning-based combustion optimization system for coal-fired boiler. Eng. Appl. Artif. Intell. 2018, 74, 303–311. [Google Scholar] [CrossRef]
- D’Ambrosio, A.; Schiassi, E.; Curti, F.; Furfaro, R. Pontryagin Neural Networks with Functional Interpolation for Optimal Intercept Problems. Mathematics 2021, 9, 996. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Inferring solutions of differential equations using noisy multi-fidelity data. J. Comput. Phys. 2017, 335, 736–746. [Google Scholar] [CrossRef]
- Lawal, Z.K.; Yassin, H.; Zakari, R.Y. Stock Market Prediction using Supervised Machine Learning Techniques: An Overview. In Proceedings of the 2020 IEEE Asia-Pacific Conference on Computer Science and Data Engineering (CSDE), Gold Coast, Australia, 16–18 December 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Deng, R.; Duzhin, F. Topological Data Analysis Helps to Improve Accuracy of Deep Learning Models for Fake News Detection Trained on Very Small Training Sets. Big Data Cogn. Comput. 2022, 6, 74. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Dong, S.; Li, Z. Local extreme learning machines and domain decomposition for solving linear and nonlinear partial differential equations. Comput. Methods Appl. Mech. Eng. 2021, 387, 114129. [Google Scholar] [CrossRef]
- Alavizadeh, H.; Alavizadeh, H.; Jang-Jaccard, J. Deep Q-Learning Based Reinforcement Learning Approach for Network Intrusion Detection. Computers 2022, 11, 41. [Google Scholar] [CrossRef]
- Arzani, A.; Dawson, S.T.M. Data-driven cardiovascular flow modelling: Examples and opportunities. J. R. Soc. Interface 2020, 18, 20200802. [Google Scholar] [CrossRef]
- SBerrone, S.; Della Santa, F.; Mastropietro, A.; Pieraccini, S.; Vaccarino, F. Graph-Informed Neural Networks for Regressions on Graph-Structured Data. Mathematics 2022, 10, 786. [Google Scholar] [CrossRef]
- Gutiérrez-Muñoz, M.; Coto-Jiménez, M. An Experimental Study on Speech Enhancement Based on a Combination of Wavelets and Deep Learning. Computation 2022, 10, 102. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Ghasemi, M.; Dehghan Manshadi, M.; Mosavi, A. Deep Learning for Wave Energy Converter Modeling Using Long Short-Term Memory. Mathematics 2021, 9, 871. [Google Scholar] [CrossRef]
- Viana, F.A.; Nascimento, R.G.; Dourado, A.; Yucesan, Y.A. Estimating model inadequacy in ordinary differential equations with physics-informed neural networks. Comput. Struct. 2021, 245, 106458. [Google Scholar] [CrossRef]
- Li, W.; Bazant, M.Z.; Zhu, J. A physics-guided neural network framework for elastic plates: Comparison of governing equations-based and energy-based approaches. Comput. Methods Appl. Mech. Eng. 2021, 383, 113933. [Google Scholar] [CrossRef]
- Reyes, B.; Howard, A.A.; Perdikaris, P.; Tartakovsky, A.M. Learning unknown physics of non-Newtonian fluids. Phys. Rev. Fluids 2020, 6, 073301. [Google Scholar] [CrossRef]
- Zhu, J.-A.; Jia, Y.; Lei, J.; Liu, Z. Deep Learning Approach to Mechanical Property Prediction of Single-Network Hydrogel. Mathematics 2021, 9, 2804. [Google Scholar] [CrossRef]
- Rodrigues, P.J.; Gomes, W.; Pinto, M.A. DeepWings©: Automatic Wing Geometric Morphometrics Classification of Honey Bee (Apis mellifera) Subspecies Using Deep Learning for Detecting Landmarks. Big Data Cogn. Comput. 2022, 6, 70. [Google Scholar] [CrossRef]
- Ji, W.; Qiu, W.; Shi, Z.; Pan, S.; Deng, S. Stiff-PINN: Physics-Informed Neural Network for Stiff Chemical Kinetics. J. Phys. Chem. A 2021, 125, 8098–8106. [Google Scholar] [CrossRef] [PubMed]
- James, S.C.; Zhang, Y.; O’Donncha, F. A machine learning framework to forecast wave conditions. Coast. Eng. 2018, 137, 1–10. [Google Scholar] [CrossRef]
- Hu, X.; Buris, N.E. A Deep Learning Framework for Solving Rectangular Waveguide Problems. In Proceedings of the Asia-Pacific Microwave Conference Proceedings, APMC, Hong Kong, 8–11 December 2020; pp. 409–411. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; The MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Lim, S.; Shin, J. Application of a Deep Neural Network to Phase Retrieval in Inverse Medium Scattering Problems. Computation 2021, 9, 56. [Google Scholar] [CrossRef]
- Wang, D.-L.; Sun, Q.-Y.; Li, Y.-Y.; Liu, X.-R. Optimal Energy Routing Design in Energy Internet with Multiple Energy Routing Centers Using Artificial Neural Network-Based Reinforcement Learning Method. Appl. Sci. 2019, 9, 520. [Google Scholar] [CrossRef]
- Su, B.; Xu, C.; Li, J. A Deep Neural Network Approach to Solving for Seal’s Type Partial Integro-Differential Equation. Mathematics 2022, 10, 1504. [Google Scholar] [CrossRef]
- Seo, J.-K. A pretraining domain decomposition method using artificial neural networks to solve elliptic PDE boundary value problems. Sci. Rep. 2022, 12, 13939. [Google Scholar] [CrossRef]
- Mishra, S.; Molinaro, R. Estimates on the generalization error of Physics Informed Neural Networks (PINNs) for approximating a class of inverse problems for PDEs. arXiv 2020, arXiv:2007.01138. [Google Scholar]
- Li, Y.; Wang, J.; Huang, Z.; Gao, R.X. Physics-informed meta learning for machining tool wear prediction. J. Manuf. Syst. 2022, 62, 17–27. [Google Scholar] [CrossRef]
- Arzani, A.; Wang, J.-X.; D’Souza, R.M. Uncovering near-wall blood flow from sparse data with physics-informed neural networks. Phys. Fluids 2021, 33, 071905. [Google Scholar] [CrossRef]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; Volume 9, pp. 249–256. Available online: https://proceedings.mlr.press/v9/glorot10a.html (accessed on 17 June 2022).
- Doan, N.; Polifke, W.; Magri, L. Physics-informed echo state networks. J. Comput. Sci. 2020, 47, 101237. [Google Scholar] [CrossRef]
- Falas, S.; Konstantinou, C.; Michael, M.K. Special Session: Physics-Informed Neural Networks for Securing Water Distribution Systems. In Proceedings of the IEEE International Conference on Computer Design: VLSI in Computers and Processors, Hartford, CT, USA, 18–21 October 2020; pp. 37–40. [Google Scholar] [CrossRef]
- Filgöz, A.; Demirezen, G.; Demirezen, M.U. Applying Novel Adaptive Activation Function Theory for Launch Acceptability Region Estimation with Neural Networks in Constrained Hardware Environments: Performance Comparison. In Proceedings of the 2021 IEEE/AIAA 40th Digital Avionics Systems Conference (DASC), San Antonio, TX, USA, 3–7 October 2021; pp. 1–10. [Google Scholar] [CrossRef]
- Fülöp, A.; Horváth, A. End-to-End Training of Deep Neural Networks in the Fourier Domain. Mathematics 2022, 10, 2132. [Google Scholar] [CrossRef]
- Fang, Z.; Zhan, J. A Physics-Informed Neural Network Framework for PDEs on 3D Surfaces: Time Independent Problems. IEEE Access 2020, 8, 26328–26335. [Google Scholar] [CrossRef]
- Markidis, S. The Old and the New: Can Physics-Informed Deep-Learning Replace Traditional Linear Solvers? arXiv 2021, arXiv:2103.09655. [Google Scholar] [CrossRef]
- Baydin, A.G.; Pearlmutter, B.A.; Radul, A.A.; Siskind, J.M. Automatic differentiation in machine learning: A survey. arXiv 2015, arXiv:1502.05767. [Google Scholar]
- Niaki, S.A.; Haghighat, E.; Campbell, T.; Poursartip, A.; Vaziri, R. Physics-informed neural network for modelling the thermochemical curing process of composite-tool systems during manufacture. Comput. Methods Appl. Mech. Eng. 2021, 384, 113959. [Google Scholar] [CrossRef]
- Li, Y.; Xu, L.; Ying, S. DWNN: Deep Wavelet Neural Network for Solving Partial Differential Equations. Mathematics 2022, 10, 1976. [Google Scholar] [CrossRef]
- De Wolff, T.; Carrillo, H.; Martí, L.; Sanchez-Pi, N. Assessing Physics Informed Neural Networks in Ocean Modelling and Climate Change Applications. In Proceedings of the AI: Modeling Oceans and Climate Change Workshop at ICLR 2021, Santiago, Chile, 7 May 2021; Available online: https://hal.inria.fr/hal-03262684 (accessed on 17 June 2022).
- Rao, C.; Sun, H.; Liu, Y. Physics informed deep learning for computational elastodynamics without labeled data. arXiv 2020, arXiv:2006.08472. [Google Scholar] [CrossRef]
- Liu, X.; Almekkawy, M. Ultrasound Computed Tomography using physical-informed Neural Network. In Proceedings of the 2021 IEEE International Ultrasonics Symposium (IUS), Xi’an, China, 11–16 September 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Vitanov, N.K.; Dimitrova, Z.I.; Vitanov, K.N. On the Use of Composite Functions in the Simple Equations Method to Obtain Exact Solutions of Nonlinear Differential Equations. Computation 2021, 9, 104. [Google Scholar] [CrossRef]
- Guo, Y.; Cao, X.; Liu, B.; Gao, M. Solving Partial Differential Equations Using Deep Learning and Physical Constraints. Appl. Sci. 2020, 10, 5917. [Google Scholar] [CrossRef]
- Li, J.; Tartakovsky, A.M. Physics-informed Karhunen-Loéve and neural network approximations for solving inverse differential equation problems. J. Comput. Phys. 2022, 462, 111230. [Google Scholar] [CrossRef]
- Qureshi, M.; Khan, N.; Qayyum, S.; Malik, S.; Sanil, H.; Ramayah, T. Classifications of Sustainable Manufacturing Practices in ASEAN Region: A Systematic Review and Bibliometric Analysis of the Past Decade of Research. Sustainability 2020, 12, 8950. [Google Scholar] [CrossRef]
- Keathley-Herring, H.; Van Aken, E.; Gonzalez-Aleu, F.; Deschamps, F.; Letens, G.; Orlandini, P.C. Assessing the maturity of a research area: Bibliometric review and proposed framework. Scientometrics 2016, 109, 927–951. [Google Scholar] [CrossRef]
- Zaccaria, V.; Rahman, M.; Aslanidou, I.; Kyprianidis, K. A Review of Information Fusion Methods for Gas Turbine Diagnostics. Sustainability 2019, 11, 6202. [Google Scholar] [CrossRef]
- Shu, F.; Julien, C.-A.; Zhang, L.; Qiu, J.; Zhang, J.; Larivière, V. Comparing journal and paper level classifications of science. J. Inf. 2019, 13, 202–225. [Google Scholar] [CrossRef]
- Leiva, M.A.; García, A.J.; Shakarian, P.; Simari, G.I. Argumentation-Based Query Answering under Uncertainty with Application to Cybersecurity. Big Data Cogn. Comput. 2022, 6, 91. [Google Scholar] [CrossRef]
- Yang, L.; Meng, X.; Karniadakis, G.E. B-PINNs: Bayesian physics-informed neural networks for forward and inverse PDE problems with noisy data. J. Comput. Phys. 2021, 425, 109913. [Google Scholar] [CrossRef]
- Goswami, S.; Anitescu, C.; Rabczuk, T. Adaptive fourth-order phase field analysis using deep energy minimization. Theor. Appl. Fract. Mech. 2020, 107, 102527. [Google Scholar] [CrossRef]
- Costabal, F.S.; Yang, Y.; Perdikaris, P.; Hurtado, D.E.; Kuhl, E. Physics-Informed Neural Networks for Cardiac Activation Mapping. Front. Phys. 2020, 8, 42. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Mao, Z.; Adams, N.; Karniadakis, G.E. Physics-informed neural networks for inverse problems in supersonic flows. arXiv 2022, arXiv:2202.11821. [Google Scholar]
- Meng, X.; Li, Z.; Zhang, D.; Karniadakis, G.E. PPINN: Parareal physics-informed neural network for time-dependent PDEs. Comput. Methods Appl. Mech. Eng. 2020, 370, 113250. [Google Scholar] [CrossRef]
- Haghighat, E.; Raissi, M.; Moure, A.; Gomez, H.; Juanes, R. A physics-informed deep learning framework for inversion and surrogate modeling in solid mechanics. Comput. Methods Appl. Mech. Eng. 2021, 379, 113741. [Google Scholar] [CrossRef]
- Kharazmi, E.; Zhang, Z.; Karniadakis, G.E. hp-VPINNs: Variational physics-informed neural networks with domain decomposition. Comput. Methods Appl. Mech. Eng. 2021, 374, 113547. [Google Scholar] [CrossRef]
- Fang, Y.; Wu, G.Z.; Wang, Y.Y.; Dai, C.Q. Data-driven femtosecond optical soliton excitations and parameters discovery of the high-order NLSE using the PINN. Nonlinear Dyn. 2021, 105, 603–616. [Google Scholar] [CrossRef]
- Dourado, A.; Viana, F.A.C. Physics-Informed Neural Networks for Missing Physics Estimation in Cumulative Damage Models: A Case Study in Corrosion Fatigue. J. Comput. Inf. Sci. Eng. 2020, 20, 061007. [Google Scholar] [CrossRef]
- Shin, Y.; Darbon, J.; Karniadakis, G.E. On the convergence of physics informed neural networks for linear second-order elliptic and parabolic type PDEs. arXiv 2020, arXiv:2004.01806. [Google Scholar] [CrossRef]
- Zobeiry, N.; Humfeld, K.D. A physics-informed machine learning approach for solving heat transfer equation in advanced manufacturing and engineering applications. Eng. Appl. Artif. Intell. 2021, 101, 104232. [Google Scholar] [CrossRef]
- Mehta, P.P.; Pang, G.; Song, F.; Karniadakis, G.E. Discovering a universal variable-order fractional model for turbulent Couette flow using a physics-informed neural network. Fract. Calc. Appl. Anal. 2019, 22, 1675–1688. [Google Scholar] [CrossRef]
- Liu, M.; Liang, L.; Sun, W. A generic physics-informed neural network-based constitutive model for soft biological tissues. Comput. Methods Appl. Mech. Eng. 2020, 372, 113402. [Google Scholar] [CrossRef]
- Pu, J.; Li, J.; Chen, Y. Solving localized wave solutions of the derivative nonlinear Schrodinger equation using an improved PINN method. arXiv 2021, arXiv:2101.08593. [Google Scholar] [CrossRef]
- Meng, X.; Babaee, H.; Karniadakis, G.E. Multi-fidelity Bayesian neural networks: Algorithms and applications. J. Comput. Phys. 2021, 438, 110361. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Karniadakis, G.E. Extended physics-informed neural networks (XPINNs): A generalized space-time domain decomposition based deep learning framework for nonlinear partial differential equations. Commun. Comput. Phys. 2020, 28, 2002–2041. [Google Scholar] [CrossRef]
- Pang, G.; D’Elia, M.; Parks, M.; Karniadakis, G. nPINNs: Nonlocal physics-informed neural networks for a parametrized nonlocal universal Laplacian operator. Algorithms and applications. J. Comput. Phys. 2020, 422, 109760. [Google Scholar] [CrossRef]
- Rafiq, M.; Rafiq, G.; Choi, G.S. DSFA-PINN: Deep Spectral Feature Aggregation Physics Informed Neural Network. IEEE Access 2022, 10, 22247–22259. [Google Scholar] [CrossRef]
- Raynaud, G.; Houde, S.; Gosselin, F.P. ModalPINN: An extension of physics-informed Neural Networks with enforced truncated Fourier decomposition for periodic flow reconstruction using a limited number of imperfect sensors. J. Comput. Phys. 2022, 464, 111271. [Google Scholar] [CrossRef]
- Haitsiukevich, K.; Ilin, A. Improved Training of Physics-Informed Neural Networks with Model Ensembles. arXiv 2022, arXiv:2204.05108. [Google Scholar]
- Lahariya, M.; Karami, F.; Develder, C.; Crevecoeur, G. Physics-informed Recurrent Neural Networks for The Identification of a Generic Energy Buffer System. In Proceedings of the 2021 IEEE 10th Data Driven Control and Learning Systems Conference (DDCLS), Suzhou, China, 14–16 May 2021; pp. 1044–1049. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, Y.; Wang, J.; Ju, L.; Qian, Y.; Ye, M.; Yang, J. GW-PINN: A deep learning algorithm for solving groundwater flow equations. Adv. Water Resour. 2022, 165, 104243. [Google Scholar] [CrossRef]
- Yang, M.; Foster, J.T. Multi-output physics-informed neural networks for forward and inverse PDE problems with uncertainties. Comput. Methods Appl. Mech. Eng. 2022, 115041. [Google Scholar] [CrossRef]
- Psaros, A.F.; Kawaguchi, K.; Karniadakis, G.E. Meta-learning PINN loss functions. J. Comput. 2022, 458, 111121. [Google Scholar] [CrossRef]
- Habib, A.; Yildirim, U. Developing a physics-informed and physics-penalized neural network model for preliminary design of multi-stage friction pendulum bearings. Eng. Appl. Artif. Intell. 2022, 113, 104953. [Google Scholar] [CrossRef]
- Xiang, Z.; Peng, W.; Liu, X.; Yao, W. Self-adaptive loss balanced Physics-informed neural networks. Neurocomputing 2022, 496, 11–34. [Google Scholar] [CrossRef]
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, K.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; et al. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. BMJ 2021, 372, n71. [Google Scholar] [CrossRef]

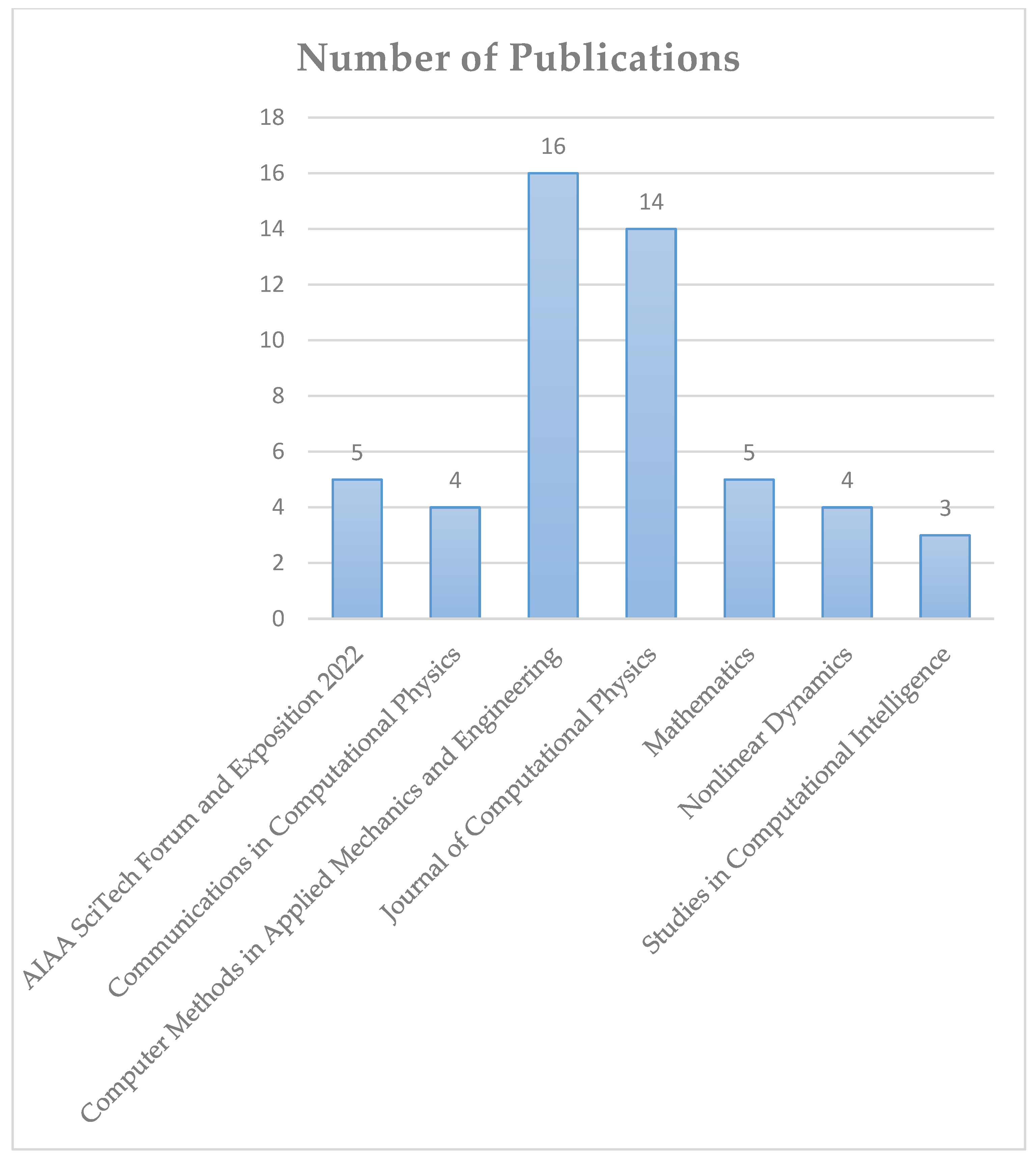
| Group | Population | Percentage (%) |
|---|---|---|
| Journal by Specialization | ||
| 1. Computer Science | 29 | 24.167 |
| 2. Engineering | 31 | 25.833 |
| 3. Mathematic | 35 | 29.166 |
| 4. Physics | 25 | 20.833 |
| Journal by Type | ||
| 1. Conference Article | 21 | 17.500 |
| 2. Journal Article | 99 | 82.500 |
| Journal by Methods | ||
| 1. Conventional PINNs | 97 | 80.833 |
| 2. Extended PINNs | 12 | 10.000 |
| 3. Hybrid PINNs | 7 | 5.833 |
| 4. Minimized Loss PINNs | 4 | 3.333 |
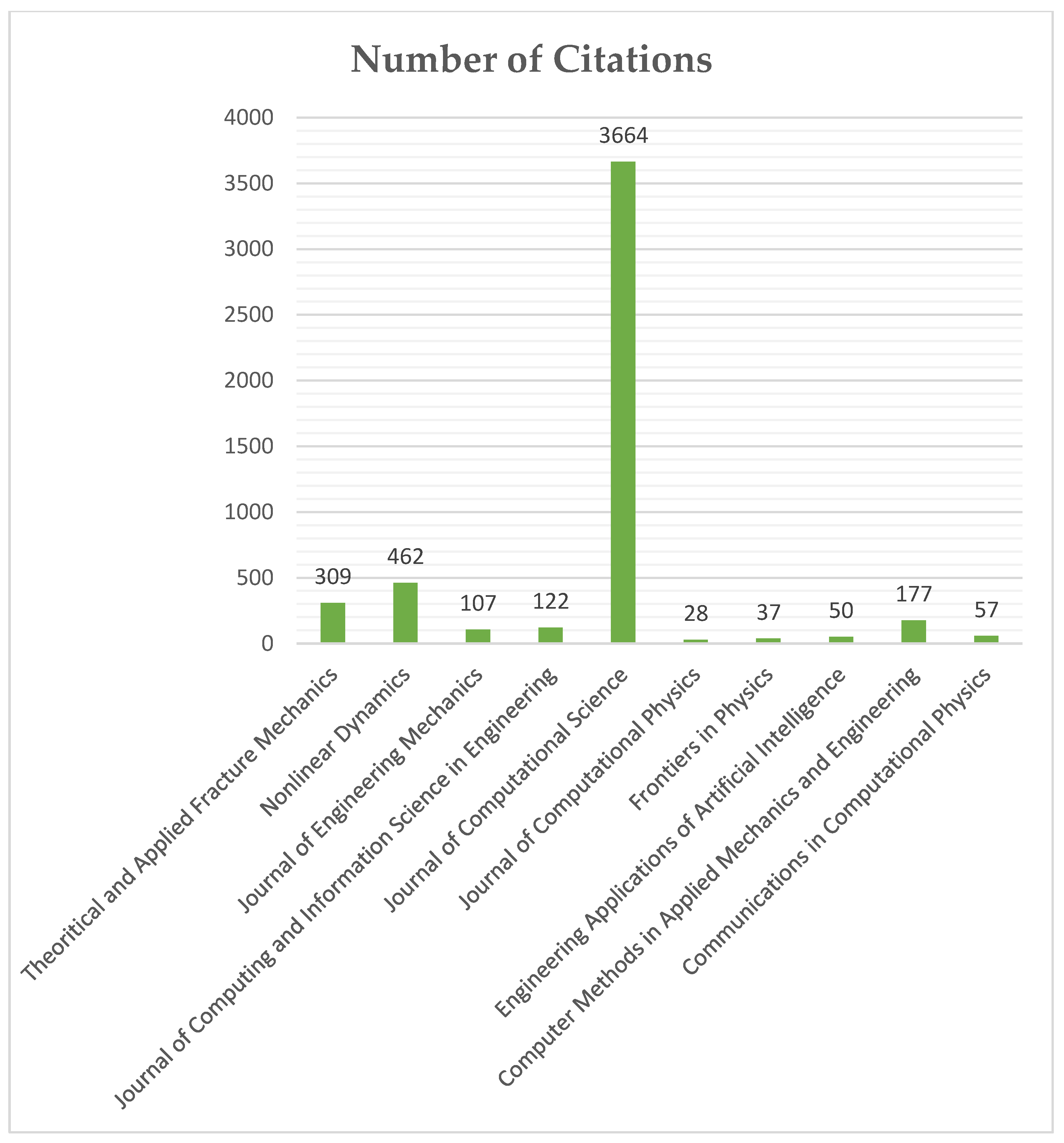
| Authors | Source Title | Number of Citations |
|---|---|---|
| Raissi et al. [1] | Journal of Computational Physics | 3442 |
| Costabal et al. [104] | Frontiers in Physics | 122 |
| Jagtap A.D. et al. [105] | Communications in Computational Physics | 118 |
| Meng, Xuhui et al. [106] | Computer Methods in Applied Mechanics and Engineering | 143 |
| Yang, Liu et al. [102] | Journal of Computational Physics | 183 |
| Haghighat E. et al. [107] | Computer Methods in Applied Mechanics and Engineering | 161 |
| Kharazmi E. et al. [108] | Computer Methods in Applied Mechanics and Engineering | 111 |
| Fang, Yin et al. [109] | Nonlinear Dynamics | 29 |
| Dourado A. et al. [110] | Journal of Computing and Information Science in Engineering | 37 |
| Shin Y. et al. [111] | Communications in Computational Physics | 137 |
| Zobeiry N. et al. [112] | Engineering Applications of Artificial Intelligence | 52 |
| Goswami et al. [103] | Theoretical And Applied Fracture Mechanics | 177 |
| Mehta, Pavan et al. [113] | Fractional Calculus and Applied Analysis | 25 |
| Colby et al. [18] | Communications in Computational Physics | 54 |
| Liu, Minliang et al. [114] | Computer Methods in Applied Mechanics and Engineering | 26 |
| Doan N.A.K. et al. [82] | Journal of Computational Science | 28 |
| Rao, Chengping et al. [92] | Journal of Engineering Mechanics | 57 |
| Pu, Juncai et al. [115] | Nonlinear Dynamics | 21 |
| Meng, Xuhui et al. [116] | Journal of Computational Physics | 31 |
| Li W. et al. [66] | Computer Methods in Applied Mechanics and Engineering | 21 |
| Author | Objective(s) | Technique | Limitation(s) |
|---|---|---|---|
| Jagtap A.D. et al. [35] | The main goal of this study was to develop a unique conservative physics-informed neural network (cPINN) for solving complicated problems. | Conservative physics-informed neural network (cPINN) | Despite the parallelization of the cPINN, it cannot be used for parallel computation. |
| Jagtap A.D. et al. [117] | The main objective of this study was to introduce an XPINN model that improved the generalization capabilities of PINNs. | Extended physics-informed neural networks (XPINNs) | XPINNs enhance generalization in exceptional conditions. Decomposition results in less training data, which makes the model more likely to overfit and lose generalizability. |
| De Ryck et al. [14] | The main goal of this study was to precisely constrain the errors arising from the use of XPINNs to approximate incompressible Navier–Stokes equations. | PINN error estimates | The authors’ estimates in their experiment gave no indication of training errors. |
| G. Pang et al. [118] | This study aimed to extend PINNs to the inference of parameters and functions for integral equations, such as nonlocal Poisson and nonlocal turbulence models (nPINNs). A wide range of datasets must be adaptable to fit the nPINNs. | Nonlocal physics-informed neural networks (nPINNs) | nPINNs require more residual points. Increasing the number of discretization points, on the other hand, makes optimization more challenging and ineffective, and causes error stagnation. |
| Liu Yang et al. [102] | The aim of this study was to introduce a novel method that was designed for solving both forward and inverse nonlinear problems outlined by PDEs with noisy data, which aimed to be more accurate and much faster than a simple PINN. | Bayesian physics-informed neural networks (B-PINNs) | The proposed B-PINNs in this work were only tested in scenarios where data size was up to several hundreds, and no tests were performed with large datasets. |
| Ehsan Kharazmi et al. [108] | The purpose of this research was to bring together current developments in deep learning techniques for PDEs based on residuals of least-squares equations using a newly developed method. | Variational physics-informed neural networks (hp-VPINNs) | Although VPINN performance on inverse problems is encouraging, no comparison was made to classical approaches. |
| Juncai Pu et al. [115] | The goal of the study was to provide an improved PINN approach for localized wave solutions of the derivative nonlinear Schrödinger equation in complex space with faster convergence and optimum simulation performance. | Improved PINN method | Complex integrable equations were not really considered in this study. |
| Enrico Schiassi et al. [21] | The main objective of this study was to propose a novel model for providing solutions to problems with parametric differential equations (DEs) that is more accurate and robust. | Physics-informed neural network theory of functional connections (PINN-TFC) | The proposed technique cannot be applied to data-driven discovery of problems when solving ODEs using both a deterministic and probabilistic approach. |
| Rafiq et al. [119] | The main goal of this experiment was to propose a unique deep Fourier neural network that expands information using spectral feature combination and a Fourier neural operator as the principal component. | Deep spectral feature aggregation physics-informed neural network (DSFA-PINN) | Other mathematical functions, such as the Laplace transform coupled with a Fourier transform, as well as the conventional CNN, cannot be used to generalize models using this method. |
| Gaétan et al. [120] | The major objective of this experiment was to design a robust model architecture for reconstructing periodic flows with a small number of imperfect sensors by extending PINNs with forced truncated Fourier decomposition. | Modal physics-informed neural networks (ModalPINNs) | The application of ModalPINNs is restricted to fluid mechanics only. |
| Colby et al. [18] | The primary objective of this study was to present an Extended PINN method which is more effective and accurate in solving larger PDE problems. | Adaptive physics informed neural networks | This study focused primarily on the problem of solving differential equations. |
| Katsiaryna et al. [121] | The objective of this experiment was to determine an acceptable time window for expanding the solution interval using an ensemble of PINNs. | PINNs with ensemble models | The ensemble algorithm seems to be more computationally intensive than the standard PINN and is not applicable to complex systems. |
| Author | Objective(s) | Technique | Limitation(s) |
|---|---|---|---|
| Meng et al. [106] | The main goal of this research was to introduce a new a hybrid technique that can exploit the high-level computational efficacy of training a neural network with small datasets to significantly speed up the time taken to find solutions to challenging physical problems. | Parareal physics-informed neural network (PPINN) | Domain decomposition of fundamental problems with huge spatial databases cannot be solved with PPINNs. |
| Zhiwei Fang et al. [33] | This paper aimed to present a Hybrid PINN for PDEs and a differential operator approximation for solving the PDEs using a convolutional neural network (CNN). | Hybrid physics-informed neural network (Hybrid PINN) | This Hybrid PINN is not applicable to nonlinear operators. |
| Lahariya M. [122] | The goal of this research was to propose a physics-informed neural network based on grey-box modeling methods for identifying energy buffers using a recurrent neural network. | Physics-informed recurrent neural networks | The proposed model was not validated with real-world industrial processes. |
| Wenqian Chen et al. [11] | The main goal of this research was to develop a reduced-order model that uses high-accuracy snapshots to generate reduced basis information from the accurate network while reducing the weighted sum of residual losses from the reduced-order equation. | Physics-reinforced neural network (PRNN) | The reduced basis set must be small to outperform the Proper Orthogonal Decomposition–Galerkin (POD–G) method in terms of accuracy, as the numerical results of the experiment showed. |
| Xiaoping Zhang [123] | The main objective of this study was to develop a novel method for solving groundwater flow equations using deep learning techniques. | Ground Water-PINN (GW-PINN) | The proposed model cannot be used to predict groundwater flow in more complex and larger areas. |
| Dourado et al. [110] | The major goal of this experiment was to develop a hybrid technique for missing physics estimates in cumulative damage models by combining data-driven and physics-informed layers in deep neural networks. | PINNs for missing physics | Even if the proposed additional levels are used to initialize the neural network, suboptimal setting of these parameters may lead to the failure of the training. |
| Mingyuan Yang [124] | The goal of this experiment was to develop a new hybrid model for uncertain forward and inverse PDE problems. | Multi-Output physics-informed neural network (MO-PINN) | The proposed method cannot be used to solve problems involving multi-fidelity data. |
| Author | Objective(s) | Technique | Limitation(s) |
|---|---|---|---|
| Apostolos F. et al. [125] | The main goal of this study was to provide a gradient-based meta-learning method for offline discovery that uses data from task distributions created using parameterized PDEs with numerous benchmarks to meta-learn PINN loss functions. | Meta-learning PINN loss functions | Optimizing the performance of methods such as RMSProp and Adam for handling inner optimizers with memory was not considered in this experiment. |
| Liu X. et al. [8] | The major objective of this experiment was to use multiple sample tasks from parameterized PDEs and modify the loss penalty term to introduce a novel method that depends on labeled data. | New reptile initialization-based physics-informed neural network (NRPINN) | NRPINNs cannot be used to solve problems in the absence of prior knowledge. |
| Habib et al. [126] | The main goal of this experiment was to develop a model that expresses physical constraints and integrates the regulating physical laws into its loss function (physics-informed), which the model penalizes when they are violated (physics-penalized). | Physics-informed and physics-penalized neural network model (PI-PP-NN) | The proposed model can only be used to create friction pendulum bearings. For any other isolation system, the theoretical basis must be adapted accordingly before it can be used for design. |
| Zixue Xiang [127] | The main goal of this experiment was to develop a technique that allows PINNs to perfectly and efficiently learn PDEs using Gaussian probabilistic models. | Loss-balanced physics-informed neural networks (lbPINNs) | In this experiment, the adaptive weight of PDE loss gradually decreased. Therefore, a theoretical investigation of this paradigm is necessary to increase the robustness and scalability of the technique. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lawal, Z.K.; Yassin, H.; Lai, D.T.C.; Che Idris, A. Physics-Informed Neural Network (PINN) Evolution and Beyond: A Systematic Literature Review and Bibliometric Analysis. Big Data Cogn. Comput. 2022, 6, 140. https://doi.org/10.3390/bdcc6040140
Lawal ZK, Yassin H, Lai DTC, Che Idris A. Physics-Informed Neural Network (PINN) Evolution and Beyond: A Systematic Literature Review and Bibliometric Analysis. Big Data and Cognitive Computing. 2022; 6(4):140. https://doi.org/10.3390/bdcc6040140
Chicago/Turabian StyleLawal, Zaharaddeen Karami, Hayati Yassin, Daphne Teck Ching Lai, and Azam Che Idris. 2022. "Physics-Informed Neural Network (PINN) Evolution and Beyond: A Systematic Literature Review and Bibliometric Analysis" Big Data and Cognitive Computing 6, no. 4: 140. https://doi.org/10.3390/bdcc6040140
APA StyleLawal, Z. K., Yassin, H., Lai, D. T. C., & Che Idris, A. (2022). Physics-Informed Neural Network (PINN) Evolution and Beyond: A Systematic Literature Review and Bibliometric Analysis. Big Data and Cognitive Computing, 6(4), 140. https://doi.org/10.3390/bdcc6040140






