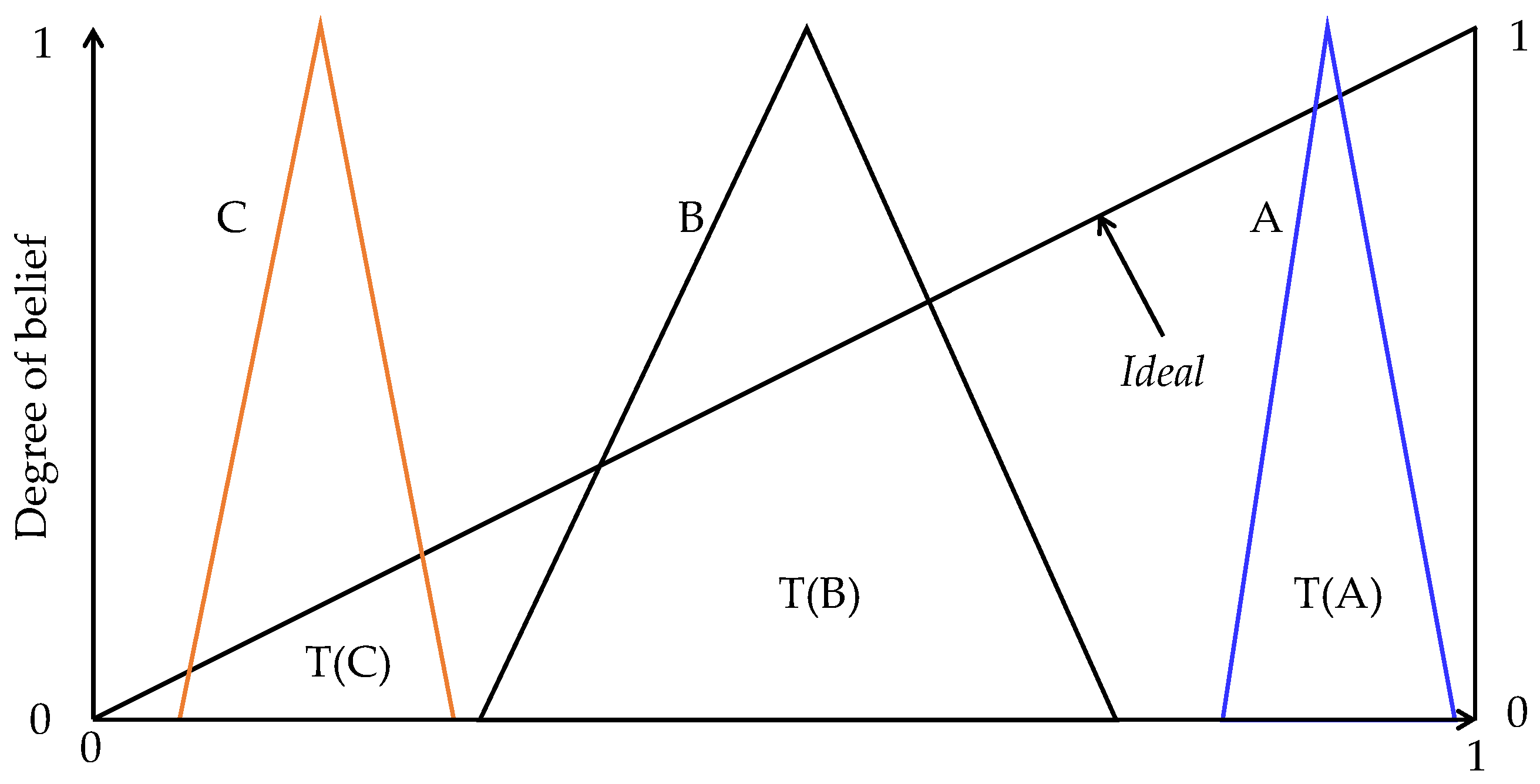1. Introduction
According to the United Nations, sustainability means meeting current needs without jeopardizing the potentials of fulfilling future needs [
1]. This is a broad mission. The UN has divided this mission into seventeen goals known as Sustainable Development Goals (SDGs), which are as follows [
2]: (1) No Poverty, (2) Zero Hunger, (3) Good Health and Well-being, (4) Quality Education, (5) Gender Equality, (6) Clean Water and Sanitation, (7) Affordable and Clean Energy, (8) Decent Work and Economic Growth, (9) Industry, Innovation, and Infrastructure, (10) Reduced Inequality, (11) Sustainable Cities and Communities, (12) Responsible Consumption and Production, (13) Climate Action, (14) Life Below Water, (15) Life on Land, (16) Peace and Justice Strong Institutions, and (17) Partnerships to achieve the Goal. These goals can be achieved by meeting preset targets and indicators [
3]. The activities associated with the targets and indicators generate an information silo consisting of a vast array of unstructured, semi-structured, and structured datasets distributed all around the globe. This information silo is often referred to as big data.
However, big data means horizontally networked yet independent data systems containing a vast number of datasets [
4,
5]. It requires a scalable architecture for efficient storage, manipulation, and analysis. Apart from its volume, its major characteristics are veracity, value, volatility, and validity. Veracity means the accuracy of the datasets. Value deals with generating economic or social wealth from any dataset. Volatility means the tendency for data structures to change over time. Validity means the appropriateness of the datasets for their intended use. The concerned national and international organizations (e.g., International Organizations for Standardization (ISO) and the National Institute of Standards and Technology (NIST)) have been offering vendor-neutral conceptual definitions [
6,
7], taxonomies [
7], requirements and usages [
8,
9], security and privacy [
10], reference architectures [
11,
12], standardization roadmaps [
13], and adoption and modernization schemes [
14] for big data so that it benefits its stakeholders without causing the phenomena of big data equalities [
15]. Some of the relevant articles that deal with the interplay of big data and SDGs are briefly described in the next section.
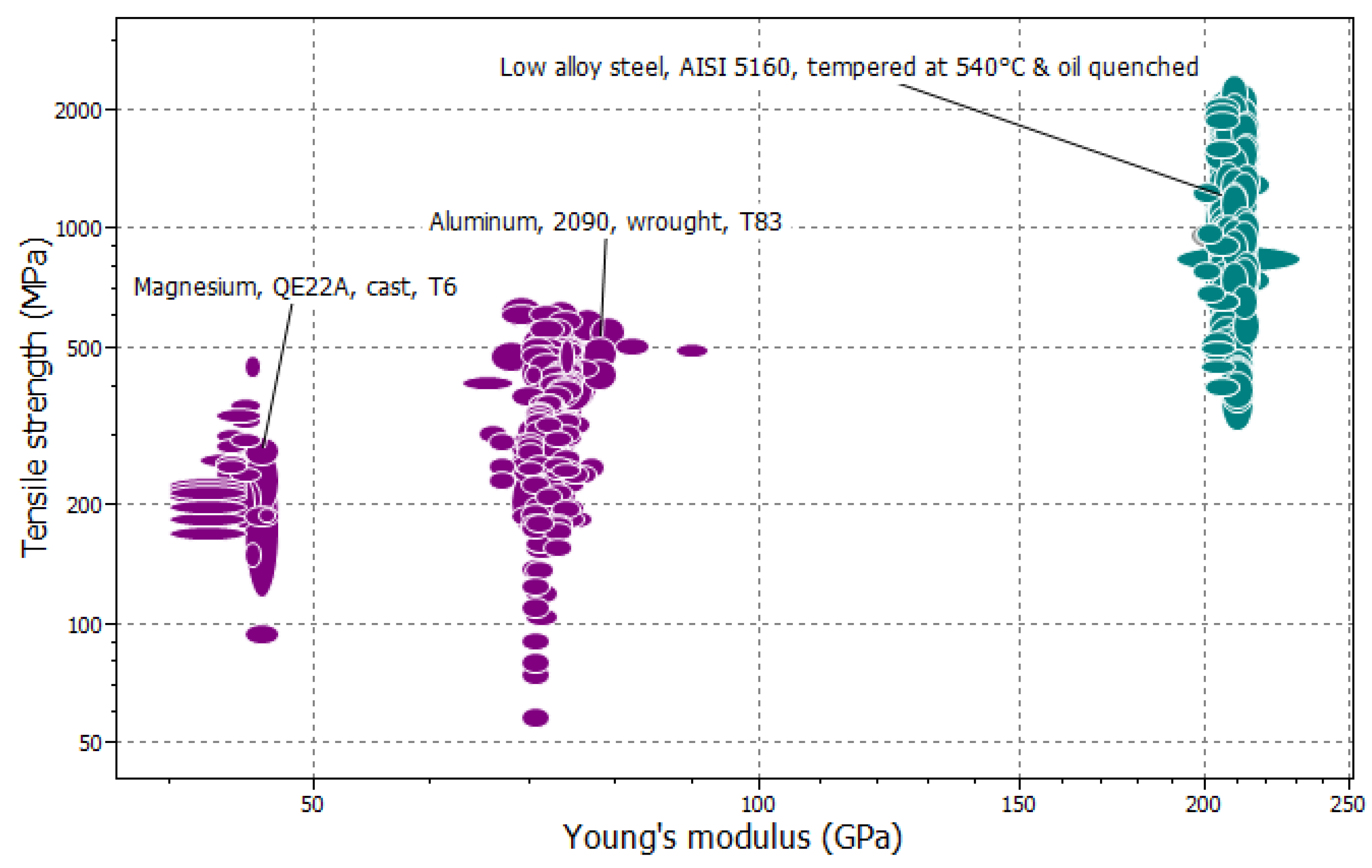
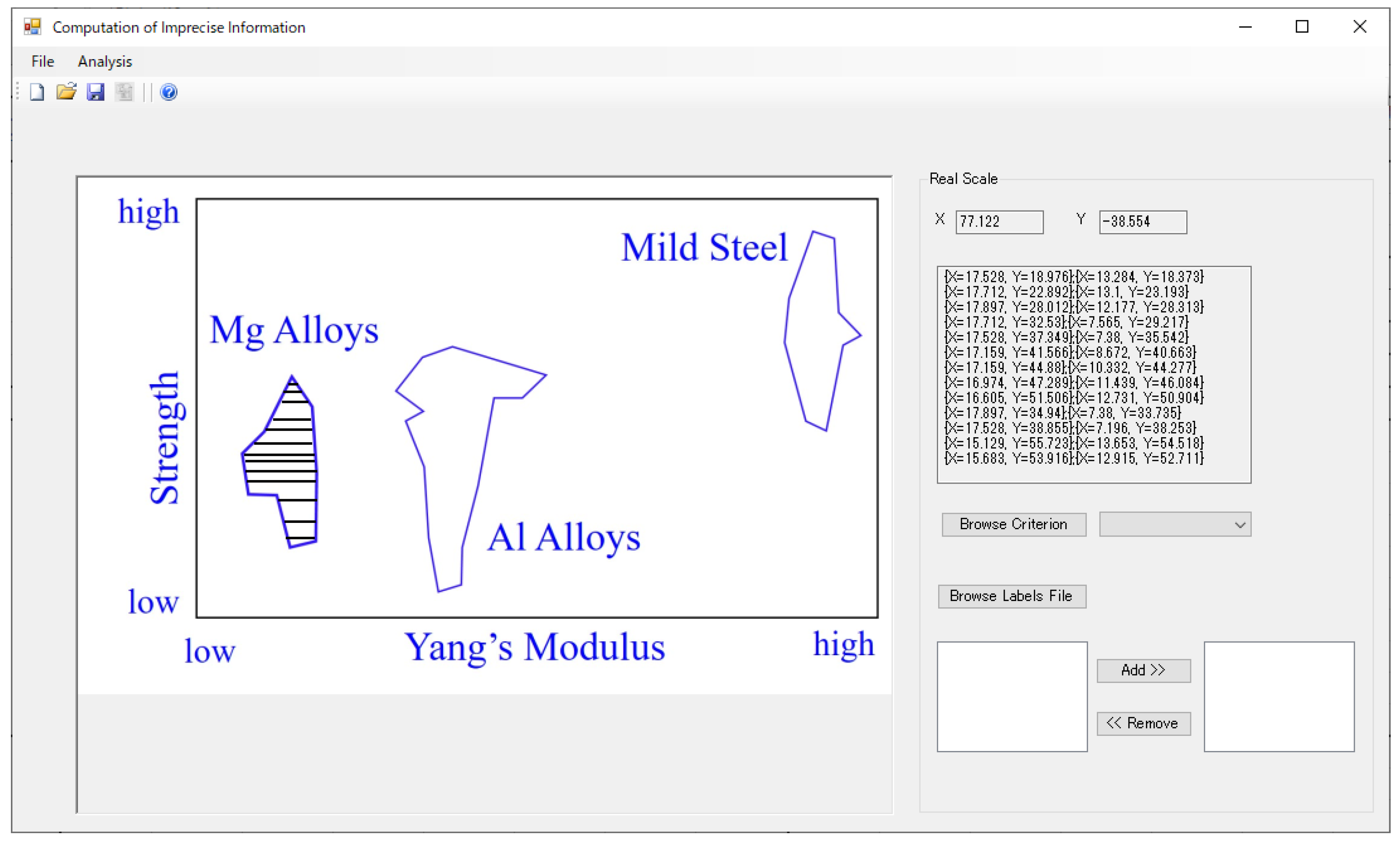
As far as big data-driven value creation is concerned, the relevant datasets must help make decisions. In this case, data analytics are used. In most cases, the analytics help visualize the relevant datasets using some two-dimensional plots. These plots are then used to decide a course of action for achieving predefined objectives. For a better understanding, consider the two-dimensional plot shown in
Figure 1. This plot (a segment of big data of engineering materials) shows the relative positions of three types of materials (mild steels, aluminum alloys, and magnesium alloys) in terms of two material properties (tensile strength and Yang’s modulus). A visual inspection of the plot reveals that mild steels outperform aluminum and magnesium alloys in terms of strength and Yang’s modulus. Therefore, if materials with high strength and Yang’s modulus are needed, mild steels should be chosen out of the three types of materials. This argument is valid if tensile strength and Yang’s modulus are equally important. However, this kind of decision-making may not always be as easy as described above. For example, if the strength and bending ability of a material are not equally important, then how do we compare the aluminum and magnesium alloys?
Thus, a formal decision-making approach must be employed to ensure a fair and rational comparison where the decision-relevant information is graphical information (e.g., a set of two-dimensional plots). A general outline of the said decision-making approach is as follows:
The first step is to set the criteria-based objective functions (e.g., maximize tensile strength, minimize Yang’s modulus, minimize CO
2 emission, and alike). Naturally, this step depends on the underlying situation. The second step is to compute the compliances of the alternatives with respect to criteria-based objective functions. The final step is to consider the importance or weight of each criterion and aggregate compliances so that each alternative receives a decision score for the final decision-making. Remarkably, while performing the second step—while computing compliances—the decision-making approach must be able to compute the graphical information (e.g., two-dimension plots similar to that shown in
Figure 1) rather than numerical data. Consequently, conventional decision-making approaches where the primary decision-relevant information is numerical data are not applicable here. This necessitates a new breed of methods and tools for making rational decisions wherein the graphical information, instead of numerical information, is formally computed. This article is written based on this consideration. There is a particular focus on decision-making aspects centering SDG 12 (responsible consumption and production).
The rest of this article is organized as follows.
Section 2 presents a literature review showing the interplay of big data and SDGs.
Section 3 presents the proposed decision-making framework, mathematical entities, and decision-making tool.
Section 4 presents two case studies showing the efficacy of the proposed decision-making method and tool. The case studies are relevant to SDG 12 (responsible consumption and production). The first case study is conducted to confirm whether or not the proposed decision-making method and tool produce reliable results. The datasets regarding two eco-indicators (CO
2 footprint and water usage) of two types of materials (wooden materials and polymers) are used in this case study. For the other case study, three types of materials (mild steel, aluminum alloys, and magnesium alloys) are ranked using six criteria (strength, modulus of elasticity, cost, density, CO
2 footprint, and water usage) and their relative weights.
Section 5 discusses the implication of the decision-scoring mechanism of the presented decision-making approach. Finally,
Section 6 provides the concluding remarks of this study.
2. Literature Review
This section presents a literature review to understand the interplay of big data and SDGs as elaborately as possible.
For monitoring sustainability, Mihaly et al. [
16] studied the interplay of (a) national sustainability policy, (b) international partnerships, domestic activities, and achievements, (c) status of professional education, (d) spatial databases and services to support implementation of the sustainable development, (e) a case study on the internationally recognized soil geoinformation system, and (f) national earth observation information system and perspectives of its applications. They found that big data regarding earth observations and geospatial data must be enacted to decide the right set of policies for implementing SDGs at a national level.
Li et al. [
17] showed how to benefit from big data in satisfying SDG 16. In particular, they used big data available in the social networks (six million tweets) on corruption and identified that the bribery of law enforcing authority and corruption in the healthcare sector put obstacles in the way of achieving SDG Target 16.5. Furthermore, they utilized unsupervised machine learning methods to make sense of tweets expressed in natural language.
Ryan et al. [
18] studied the ethical issues regarding artificial intelligence and big data while meeting SDGs. They conducted six empirical case studies to see how smart information systems can meet the challenges of six SDGs (2, 3, 7, 8, 11, and 12). They showed that smart information systems are insufficient and may exacerbate or create new issues for community development.
Ryan and Anya [
19] studied the ethical implications of artificial intelligence and big data for implementing SDG in smart cities with a large population. They found that dealing with privacy, ensuring accurate datasets, reducing costs, and building general stakeholders’ trust are the main concerns of implementing big data to achieve SDGs.
MacFeely [
20] reported that out of 232 SDG indicators, only 93 are classified as Tier 1, i.e., the indicators are clearly defined, and data are compiled by internationally accepted standards from at least 50 percent of the countries. The remaining indicators are Tier 2 (72 indicators) or Tier 3 (62 indicators). Tier 2 indicators are clearly defined, but countries do not regularly produce the data. Tier 3 indicators are conceptually clear, but no internationally accepted standards are yet available. Some data sources are used for estimating multiple SDGs. For example, utility bills are used to estimate economic well-being, and well-being is directly related to SDG 1, 8, 10, and 11. Mobile phone utilization datasets are used to estimate public health and disaster, and public health and disaster are directly related to SDG 2, 3, 8, 11, 15, and 16. Nevertheless, web scraping, scanners, mobile phones, social media, satellite images, smart meters, credit cards, road sensors, health records, ship identification, and criminal records are now SDG-related big data sources.
Global assessment of institutional readiness for using big data in official statistics is presented in [
21]. The following points have been raised: (a) from a strategic coordination viewpoint, big data must be exchanged from all regions through the United Nations Global Platform, where national statistics organizations must play a vital role. (b) Legal frameworks must be revised to materialize data sharing between national statistics organizations, private sector data owners, and other stakeholders without violating data privacy and protection laws. (c) Human resource initiatives must be taken overarching competency for big data skills development. Thus, partnerships with higher education institutes to allow up-skilling of big data competency must take place. (d) Required IT infrastructure (cloud storage facilities) in all countries with necessary pre-requisites must be maintained to benefit from big data.
Mwitondi et al. [
22] performed data segmentation considering each SDG a node of a big data source. In doing so they elucidated the complex overlap of the SDGs by using data from different sources, as described in [
23,
24,
25], regarding SDG indicators. The complexity of the data (data randomness, variation in sample size, and socio-economic, cultural, and geopolitical factors) necessitates new data handling algorithms. Big data analytics help understand the interplay of the SDG indicators and open new paths to interdisciplinary research.
Ferreira et al. [
26] showed that big data consisting of satellite images of earth observation can be used to address SDG indicators. However, innovative methods and tools to process ever-growing earth observation data are needed. In this respect, data analytics techniques can help make sense of the enormous quantity of earth observation data available in various formats and collected from numerous sources.
Kashyap and Verkroost [
27] analyzed big data available in social networks (LinkedIn™) to understand gender gaps using regression analysis. They found that the LinkedIn Gender Gap Index (GGI) strongly correlates with International Labor Organization (ILO) ground truth professional gender gaps. This study thus shows the efficacy of social networks being a source of big data for sustainability analysis.
Hassani et al. [
28] studied the up-to-date connections between the SDGs and big data using global Google trends. They summarized the impact of big data on SDGs, showing the current state and challenges to overcome in the foreseeable future. They reported that SDG 1 attracted the most attention to big data projects among all SDGs. In this respect, data silos collected from mobile phones and satellite images and geodata were identified as the top two data sources by which poverty has been combated. For example, satellite image big data processed by artificial intelligence can help evaluate building, car counts, road density, pavement, road width, and roof materials. This information helps stakeholders to match skilled labor with suitable employment or local products with buyers worldwide. As far as SDG 2 is concerned, big data generated from IoT-driven smart sensor networks and geological surveys contribute to smart farming and precision agriculture. Big data generated while monitoring infectious diseases and mental health can contribute to SDG 3. SDG 4 needs prediction and estimation of early school dropouts, which can be performed accurately using big data. In terms of SDG 9 and SDG 12, to the best of our knowledge, big data has just started to earn a great deal of attention. The reason for this is that, without big data, it is not possible to ensure a sustainable supply chain, product life cycle management toward greenhouse gas reduction, consumer behavior assessment, or e-commerce.
Allen et al. [
29] presented a comprehensive literature review showing which big data sources estimate SDGs. They reported that datasets generated by satellite data acquisition systems, surveys, tracking systems, sensors, administrative practices, and opinions are big data sources for sustainability assessment. However, regarding SDG 12, there were no reported data sources.
The above literature review reveals that the interplay of big data and SDGs is highly complex. Big data’s utilization in assessing the degree of fulfillment of SDGs or making necessary arrangements at the global or local level is still in its infancy. Therefore, more research should be conducted to develop more pragmatic methods for mitigating the uncertainty and computational complexity associated with big data associated with sustainability.
3. Decision-Making Method and Tool
This section presents a decision-making method where the decision-relevant information comprises two-dimensional plots rather than numerical data. The relevant mathematical entities, as well as the computing tool, are also presented in this section. This method and tool are collectively referred to as the decision-making approach.
Figure 2 schematically illustrates the proposed decision-making method. It consists of six modules. The first module is denoted as SDG-driven activities, where numerous stakeholders perform activities to achieve SDGs. The second module is denoted as big data, where a vast array of unstructured, semi-structured, and structured datasets collected from the SDG-driven activities are stored for making informed decisions. The third module is denoted as big data analytics. The analytics search big data and help visualize the relevant datasets. The fourth module is denoted as decision formulation, where the decision-maker sets the criteria and their importance. Each criterion is set either in the maximization or minimization format. For example, if social security is a target or indicator of sustainability, then its decision criterion can be “maximize social security”. If CO
2 emission is a target or indicator of sustainability, then its decision criterion can be “minimize CO
2 emission”. In addition to setting the criteria, the importance of the criteria is set either in numerical form (setting relative weights of the criteria) or in linguistic form (e.g., criterion x is more important than criterion y). The last module is denoted as decision computation. In this module, decision-relevant information (in this case, two-dimensional plots) is computed to see how well the alternatives comply with the decision criteria. The values of the compliances are then further processed using the importance of the criteria, which results in a ranking list of the alternatives. Finally, a decision is made using the ranking list. It is worth mentioning that Ullah and Noor-E-Alam [
30] provided a framework and tool for making decisions using graphical information. The method shown in
Figure 2 resembles their work as far as data visualization is concerned.
In order to perform decision computation, the concept of compliance can be used. The mathematical settings for calculating compliance of a numerical range with a given fuzzy number are described in [
31]. In this article, a simplified formulation of the compliance analysis is considered based on the formulation shown in [
31].
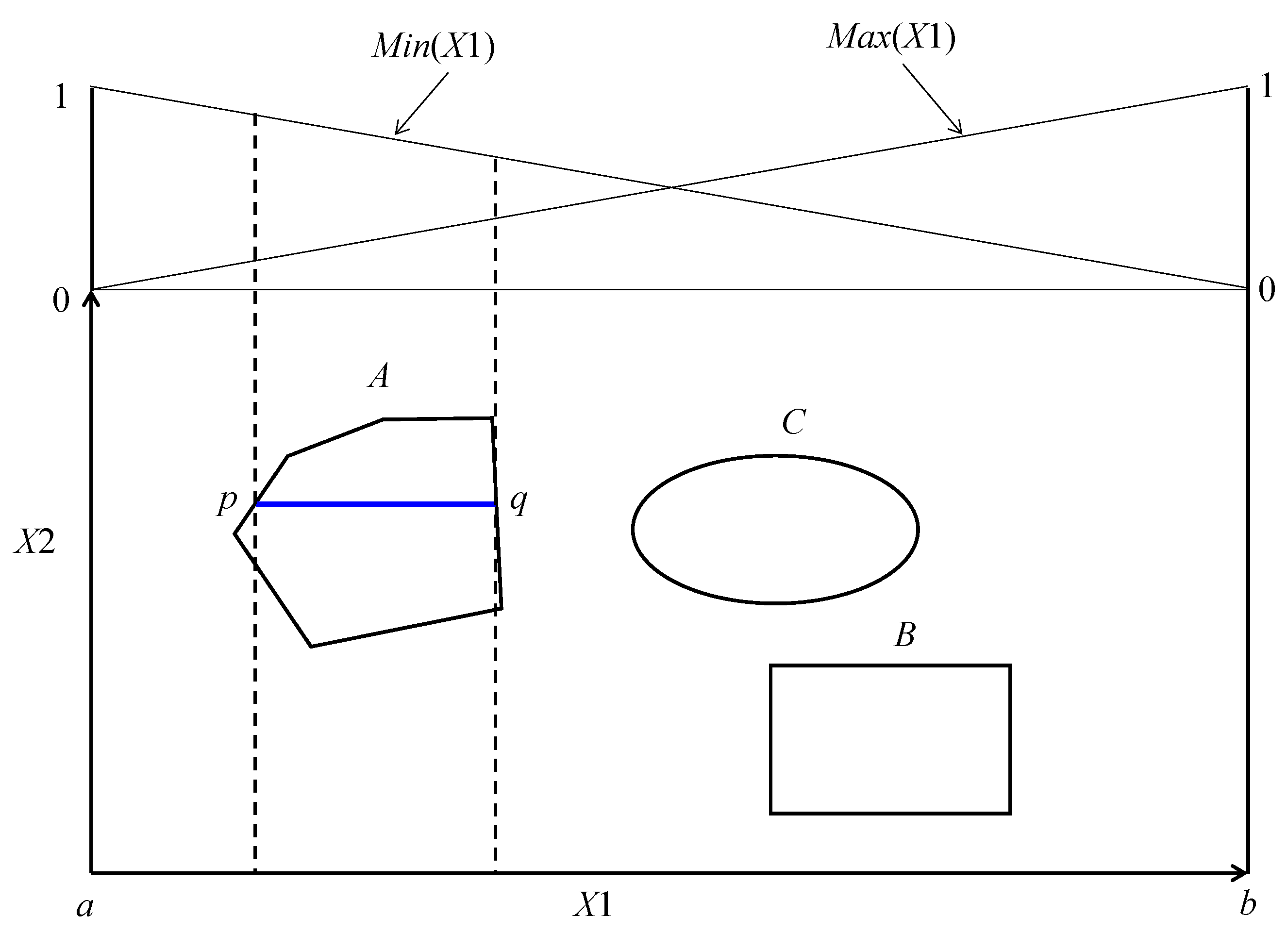
For better understanding, consider an arbitrary two-dimensional plot, as shown in
Figure 3. Let
X1 and
X2 be two parameters associated with the decision-making process and A, B, and C be the alternatives, as schematically illustrated in
Figure 3. The relative positions of the alternatives are shown by a two-dimensional plot where the abscissa is
X1, and the ordinate is
X2. Each alternative can be represented by some intervals in the
X1 and
X2 directions. Each interval complies with the maximization and minimization functions. For example, let [
a,
b] ∈ ℜ be the scale of
X1, as shown in
Figure 3. Here,
x1 ∈ [
a,
b]. The corresponding minimization and maximization functions, denoted as
Min(
X1) and
Max(
X1), are as follows.
For example, consider the case shown in
Figure 3, where one of the possible intervals underlying A is given as [
p,
q]. In order to calculate the compliance, the following functions for maximization and minimization can be defined:
For example, consider that [
a,
b] = [0, 100] and [
p,
q] = [30, 70]. In this case,
Cmax =
Cmin = 0.5. This means that the interval [30, 70] equally complies with maximization and minimization functions defined in the universe of discourse [0, 100]. Consider that [
a,
b] = [0, 100] and [
p,
q] = [20, 50]. In this case,
Cmax = 0.35 and
Cmin = 0.7. This means that [20, 50] complies with minimization more than it complies with maximization in the universe of discourse [0, 100]. Out of
Cmax and
Cmin, one is considered for the decision-making purpose. The explanation is as follows. For example, if
X1 represents CO
2 emission, then it (CO
2 emission) must be minimized. As a result, the criterion becomes “minimize CO
2 emission”. As such, the value of
Cmin, not
Cmax is considered for the decision-making purpose. Similarly, if
X1 represents productivity, then it (productivity) must be minimized. As such, the value of
Cmax, not
Cmin, is considered for the decision-making purpose. Thus, if a given criterion refers to maximization, then its compliance
C is equal to
Cmax. Alternatively, if a given criterion refers to minimization, then its compliance
C is equal to
Cmin. This way, each alternative returns a set of compliances,
C1, …,
Cn ∈ [0, 1], because each alternative entails multiple intervals. A set of compliances can induce a possibility distribution in the form of a triangular fuzzy number. The mathematical procedure to induce fuzzy number from a given set of numerical values is presented in [
32]. For a lucid description of the induction process, refer to Appendix A in [
33].
Let [
t1,
t3] be the support and
t2 be the core of the induced fuzzy number denoted as
T. The compliance of
T with the idealistic possibility distribution of compliances is the compliance of an alternative with respect to the criterion. This aggregated compliance is thus the decision score (denoted as
D) of the alternative with respect to the criterion. Now, the idealistic possibility distribution can be defined in numerous ways. One of the obvious ways is to define it by a function that ensures the maximization of the possibility of compliance in the universe of discourse of [0, 1] as marked by “Ideal” in
Figure 4. As such, the decision score is calculated as follows:
The parameters
r and
s in Equation (5) are defined as follows:
For example, consider that
t1 = 0.2,
t2 = 0.4,
t3 = 0.7. This results in
r = 0.7/1.4 = 0.5,
s = 0.2/0.8 = 0.25,
D = (0.35−0.05)/0.5 = 0.6. If
t1 = 0,
t2 =
t3 = 1, then
r = 1,
s = 0,
D = 1. This means that when the induced possibility distribution (aggregated compliance) takes the shape of the idealistic possibility distribution (
Figure 3), the decision score becomes unit; otherwise, it is less than unit.
The abovementioned decision computation needs a special computing tool. The tool must be able to extract the intervals for an alternative from a given two-dimensional plot [
18]. The pseudocodes of the tool are represented by Algorithm 1 as follows:
| Algorithm 1: Decision-making computation. |
| Step 1: | Start |
| Step 2: | Upload a two-dimensional plot |
| Step 3: | Set the scales for the abscissa and ordinate of the uploaded plot (i.e., minimum and maximum values defining the scales of the abscissa and ordinate of the plot) |
| Step 4: | Select one of the directions (either abscissa or ordinate) for extracting intervals |
| Step 5: | Select one of the alternatives for extracting intervals |
| Step 6: | Drag mouse in the selected direction and extract several intervals covering the region of the selection alternative and direction |
| Step 7: | Repeat Step 5 for all other alternatives |
| Step 8: | Go to Step 3 and select the other direction |
| Step 9: | Repeat Steps 4, …, 6 |
| Step 10: | Output all intervals extracted in the above steps |
| Step 11: | End |
Based on the above pseudocodes, a decision tool is developed that runs on Windows™ operating systems.
Figure 5 and
Figure 6 show two of the user interfaces of the tool developed. Accordingly, a decision-maker first uploads a two-dimensional plot. After that, the decision-maker sets the scale of the abscissa and ordinate. The scale may not have to be the scale of the plot. For example, the arbitrary case shown in
Figure 4 shows that the decision-maker uploaded a two-dimensional plot (stiffness versus cost) of engineering materials. This plot shows the relative positions of five types of materials, namely, aluminum, cast iron, stainless steel, and two types of composites (glass fiber reinforced polymers (GFRP) and carbon fiber reinforced polymers (CFRP)). Thus, these five types of materials are the alternatives for this particular case. Each alternative can be represented by some intervals in the abscissa and ordinate directions. The instance shown in
Figure 5 is a scenario when the decision-maker extracts the intervals in the abscissa direction to represent the cost of cast iron.
4. Case Studies
This section presents two case studies. The first case study is conducted to see whether or not the proposed decision-making approach produces reliable results even though the relevant datasets presented by two-dimensional plots exhibit a great deal of uncertainty. The other is conducted to see whether or not the proposed decision-making approach can be used for multiple-criteria decision-making even though the relevant datasets presented by several two-dimensional plots exhibit a great deal of uncertainty. Both case studies focus on SDG 12 (responsible production and consumption). For assessing the fulfillment of SDG 12, big data relevant to engineering materials becomes an important issue. The description is as follows.
Fulfilling SDG 12 means scanning the whole product life cycle to identify the harmful factors (carbon emissions and resource depletion) and eliminate them. As such, SDG 12 is highly correlated to the notion of material efficiency. It (material efficiency) deals with yield improvement, downsizing and lightening, cost reduction, and reduction of CO
2 footprint of primary material production [
34,
35,
36,
37]. Remarkably, material efficiency is more effective than energy efficiency (energy efficiency deals with the direct energy consumption while manufacturing products [
34,
35,
36,
37]). As a result, tacking all information regarding the characteristics and properties of a vast array of engineering materials has become an important factor for ensuring SDG 12 and beyond. For this, a new concept called materials passport has been introduced. The explanation is as follows.
Since a product includes metals (including precious and rare earths), ceramics, polymers, and natural materials, myriad material processes are entailed in the fabrication of the parts of a product. Furthermore, the reasons and requirements behind using specific materials and their circularity must be known beforehand. Otherwise, the sustainability assessment cannot be performed as expected. In order to deal with material efficiency in a more global context (e.g., circular economy), a concept known as a material passport has been introduced [
38,
39,
40,
41,
42,
43,
44,
45]. The material passport needs material-centric information collected from upstream activities (mining, trade, smelting/refining) and downstream activities (trade, component manufacturing, contract manufacturing and assembly, and end-using). While improving the sustainability of a product, its constituent materials and percentages, and the relevant manufacturing and assembly/service processes-relevant datasets stored in its material passport can be used. Furthermore, the eco-indicators of materials (CO
2 emission of primary production of constituent materials, resource depletion) and other governance issues (whether or not forced labor is used in the upstream and downstream activities) populate material passports. Therefore, material-centric big data extracted from the material passports of various products become essential information for ensuring SDG 12 and other SDGs.
Nevertheless, in most cases, a relevant subset of big data is visualized using two-dimensional (scatter) plots. These plots dominate the underlying decision-making processes ensuring better fulfillment of SDG 12. In such cases, the decision-making method and tool presented in the previous section become instrumental.
4.1. Case Study 1
This case study was conducted to confirm whether or not the proposed decision-making method and tool produce reliable results. In particular, the datasets regarding two eco-indicators (CO2 footprint and water usage) of two types of materials (wooden materials and polymers) were considered.
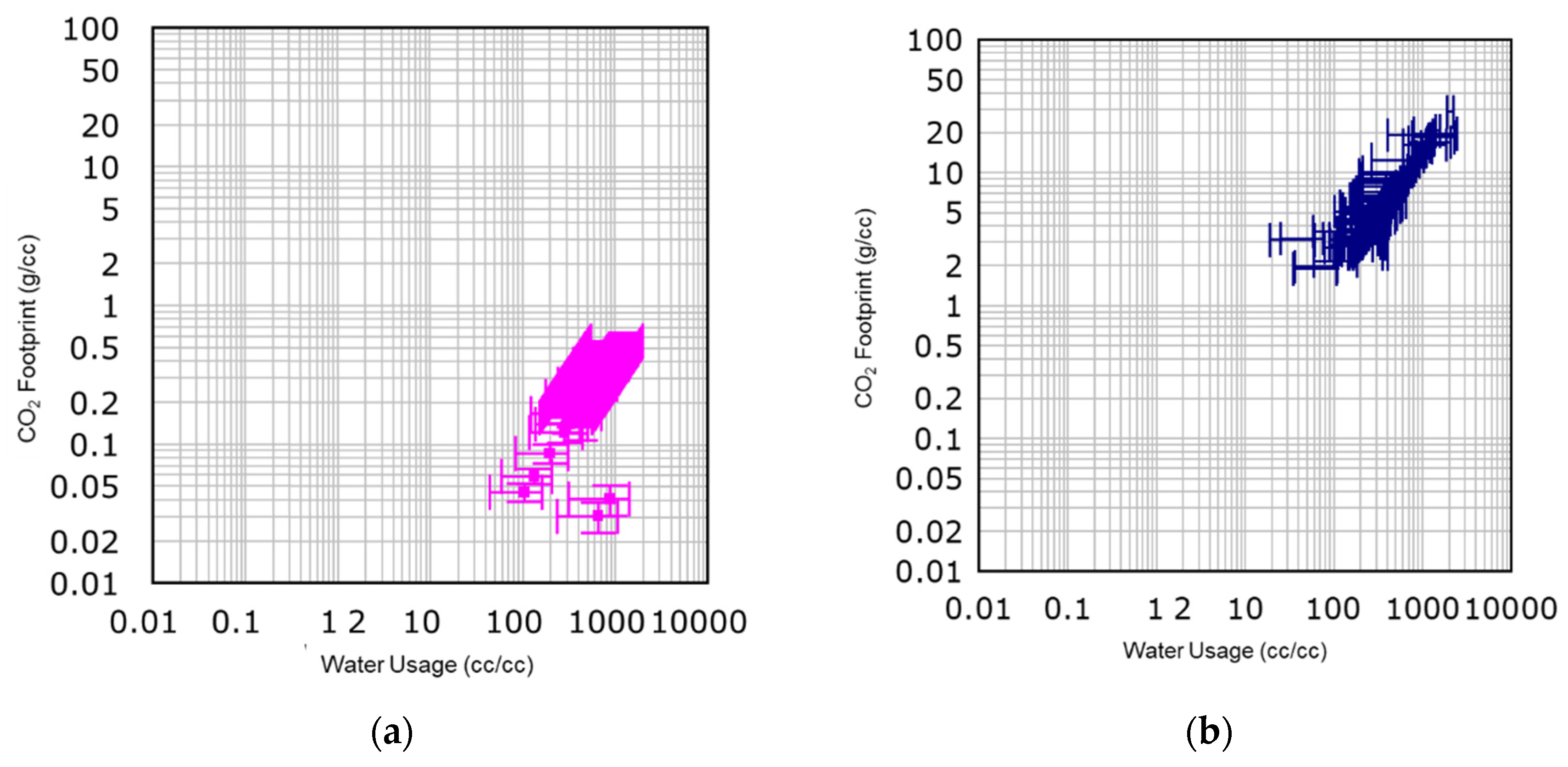
From the big data of engineering materials, the datasets regarding CO
2 footprint and water usage of 447 wooden materials and 244 polymers are shown using two two-dimensional plots in
Figure 6. See [
36] for more details. The datasets are presented in
Figure 7 using two scatter plots where the ordinates present water usages (cc of water/cc of material) and the abscissas present CO
2 emission (grams of CO
2/cc of material) of the primary production of the respective materials. To be more specific, consider the following case where two families of materials, namely, polymers and wooden materials, are ranked in terms of CO
2 footprint and water usage. As shown in
Figure 6, as far as water usage (as a measure of resource depletion) is concerned, both materials can be ranked equally. However, as far as CO
2 footprint is concerned, wooden materials are far better than polymers.
Figure 8 shows the user interface of the decision tool (
Figure 5 and
Figure 6) when the decision-maker extracts the ranges representing uncertainty in water usage. Even though the water usage is plotted using a logarithmic scale starting from 0.01 cc of water/cc of material to 10000 cc of water/cc of material, the range extraction process rescales the plot to [0, 100] (Here, “cc” means cubic centimeter). Therefore, each extracted range becomes a segment of [0, 100]. If preferred, the decision-maker can use other scaling schemes. For example,
Figure 9 shows the extracted ranges representing the uncertainty in water usage of wooden materials. Similarly, water usage and CO
2 footprint ranges are also collected for the rest of the cases.
Table 1 and
Table 2 list the values of the decision-making parameters relevant to decision computation. As seen in
Table 1 and
Table 2, the decision score (
D) values concerning the criterion “minimize water usage” for both groups of materials are comparable (0.395 and 0.410). This means that both natural materials and polymers are equally unsustainable in terms of water usage. This is consistent with the visual inspection of the big data (
Figure 7). On the other hand, the decision score (
D) value concerning CO
2 footprint is very high (0.904) for the natural materials compared to that of polymers (0.449).
The above results imply that the presented decision-making approach is reliable, and it can successfully process the uncertainty underlying big data.
4.2. Case Study 2
Upon confirming the presented decision-making approach’s reliability, it is time to apply it in multiple-criteria decision-making, as described below.
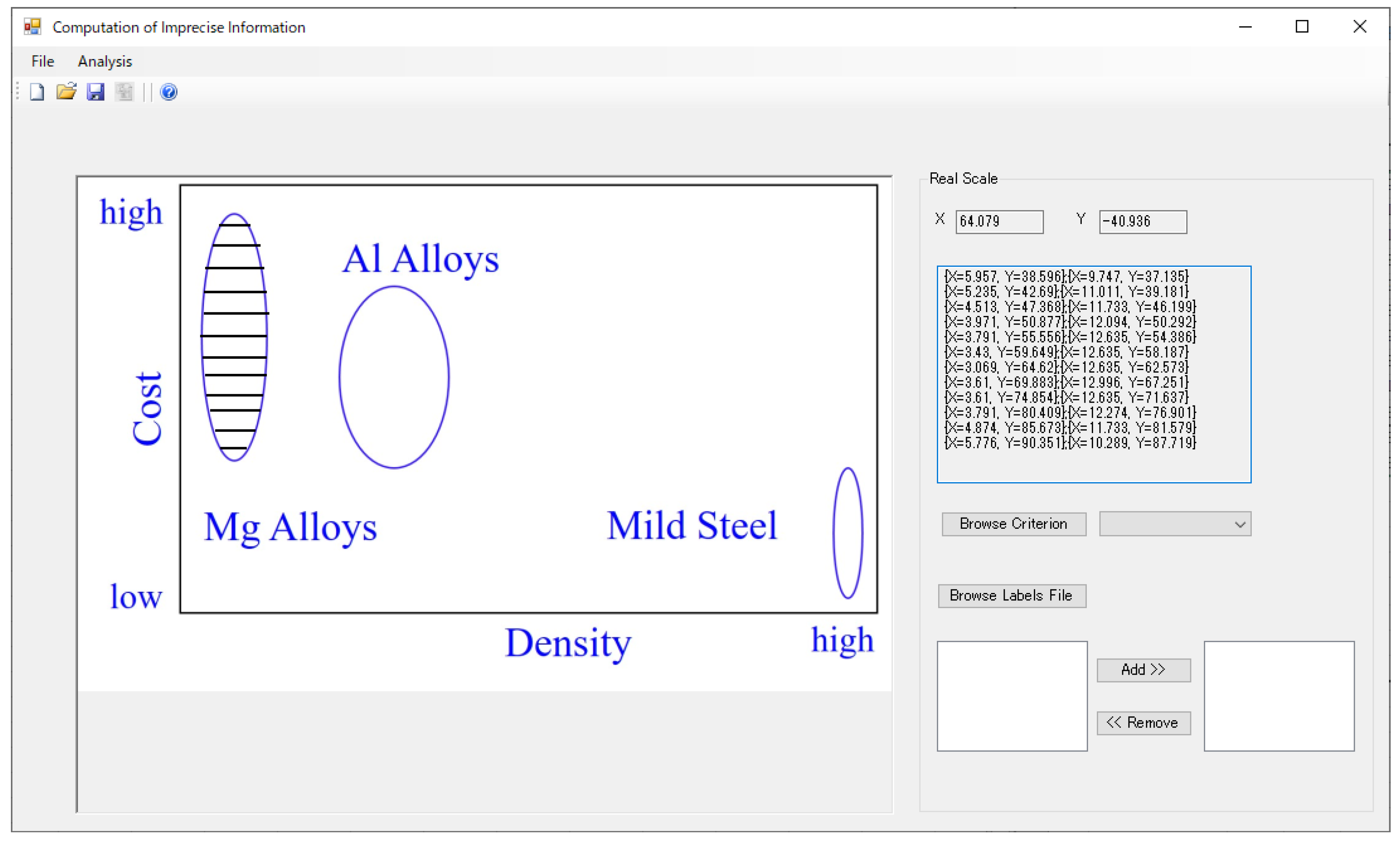
In particular, this case study shows how to rank the three most frequently used metallic materials: mild steel, aluminum alloys, and magnesium alloys, using graphical information generated from big data associated with engineering materials. Six criteria were considered: (1) strength, (2) Yang’s modulus, (3) destiny, (4) CO
2 footprint, (5) water usage, and (6) cost. As such, three two-dimensional plots—strength versus Yang’s modulus, cost versus density, and water usage versus CO
2 footprint—were used showing the relative positions of the mild steel, aluminum alloys, and magnesium alloys on each plot.
Figure 10 shows a scenario where all possible ranges of Yang’s modulus of magnesium alloys are extracted.
Figure 11 shows a scenario where all possible cost ranges of magnesium alloys are extracted.
Figure 12 shows a scenario where all possible ranges of the CO
2 footprint of magnesium alloys are extracted. The same is done for all combinations of criteria and alternatives. In order to ensure sustainability, the strength and Yang’s modulus must be maximized, whereas the density, cost, CO
2 footprint, and water usage must be minimized. The decision scores (
Ds) of the alternatives respective to the respective criteria are listed in
Table 3. The alternatives can be ranked using values of the scores listed in
Table 3. The ranking process is described as follows.
The ranking score denoted as
Rj of the
j-th alternative with respective to all criteria is given as follows:
In Equation (6), Dij is the decision score of the j-th alternative with respect to the i-th criterion, wi is the weight or importance of the i-th criterion, and n is the number of criteria.
In a multi-criteria decision-making process, the decision-makers can set the values of wi as they prefer and see the corresponding rank of the alternatives. For example, if the environmental issues are prioritized over others, the values of the weights of CO2 emission and water usage can be set much higher than that of the others. However, some of the possible weight setting scenarios are presented below for better understanding.
As shown in
Table 4, if the CO
2 footprint, cost, and water usage are prioritized twice as much as others, then mild steels become the best alternative. Aluminum alloys are the second-best, whereas magnesium alloys remain the last choice.
A similar result is found in the case shown in
Table 5, where the strength, Yang’s modulus, and cost are prioritized twice as much as the others. In this case, mild steel becomes the best alternative. Aluminum alloys are the second-best, whereas magnesium alloys remain the last choice.
However, if the density is about 3.5 times more important than others, all alternatives become indifferent (see
Table 6). This means that magnesium alloys are the best alternatives when destiny receives very high importance compared to all other criteria.
The above examples show how an informed decision can easily be made using the presented decision-making approach, even though the relevant datasets presented using two-dimensional plots exhibit uncertainty. Remarkably, the subjectivity or preference of the decision-makers can be documented by reporting the weights, as shown in
Table 4,
Table 5 and
Table 6.
5. Discussions
The presented decision-making approach can be studied further in different directions. One of the directions is discussed in this section, as follows.
Calculating the decision score (
D) is a critical issue in the proposed decision-making approach. As defined above (
Section 3), the decision score is calculated using Equations (5)–(7). Nevertheless, the central theme of the decision score is to see whether or not an induced fuzzy number denoted as T matches the ideal one (denoted “Ideal” in
Figure 4). Further, the induced fuzzy number (T) captures the uncertainty in the compliances calculated using the graphical information. To garner more insight into this issue, consider three arbitrary alternatives, A, B, and C, and their induced fuzzy numbers denoted as T(A), T(B), and T(C), as schematically illustrated in
Figure 13.
Alternative A is very close to the maximum compliance (unit). On the other hand, alternative C is very far from the maximum compliance (unit). The other alternative (B) stays between A and C. Compared to A and C, B entails a large amount of uncertainty, i.e., it is widely spread. Therefore, both distance of the induced fuzzy number from the maximum compliance and its degree of uncertainty must be quantified simultaneously to develop a more insightful decision score. Consequently, the following functions can be used to calculate the components of decision score.
Here,
D1 ∈ [0, 1] quantifies the distance of the centroid of an induced triangular fuzzy number from the maximum compliance (unit), whereas
D2 ∈ [0, 1] quantifies the degree of uncertainty of an induced fuzzy number, which is equal to its area divided by the largest possible area. The less the value of
D1, the better the alternative because the less the value of
D1, the closer the alternative to the maximum compliance. The less the value of
D2, the better the alternative because the less the value of
D2, the less the degree of uncertainty. As a result, a new decision score (
E) can be calculated as follows.
Thus, the more the value of
E, the better the alternative. Based on this new decision scoring approach, the arbitrary alternative shown in
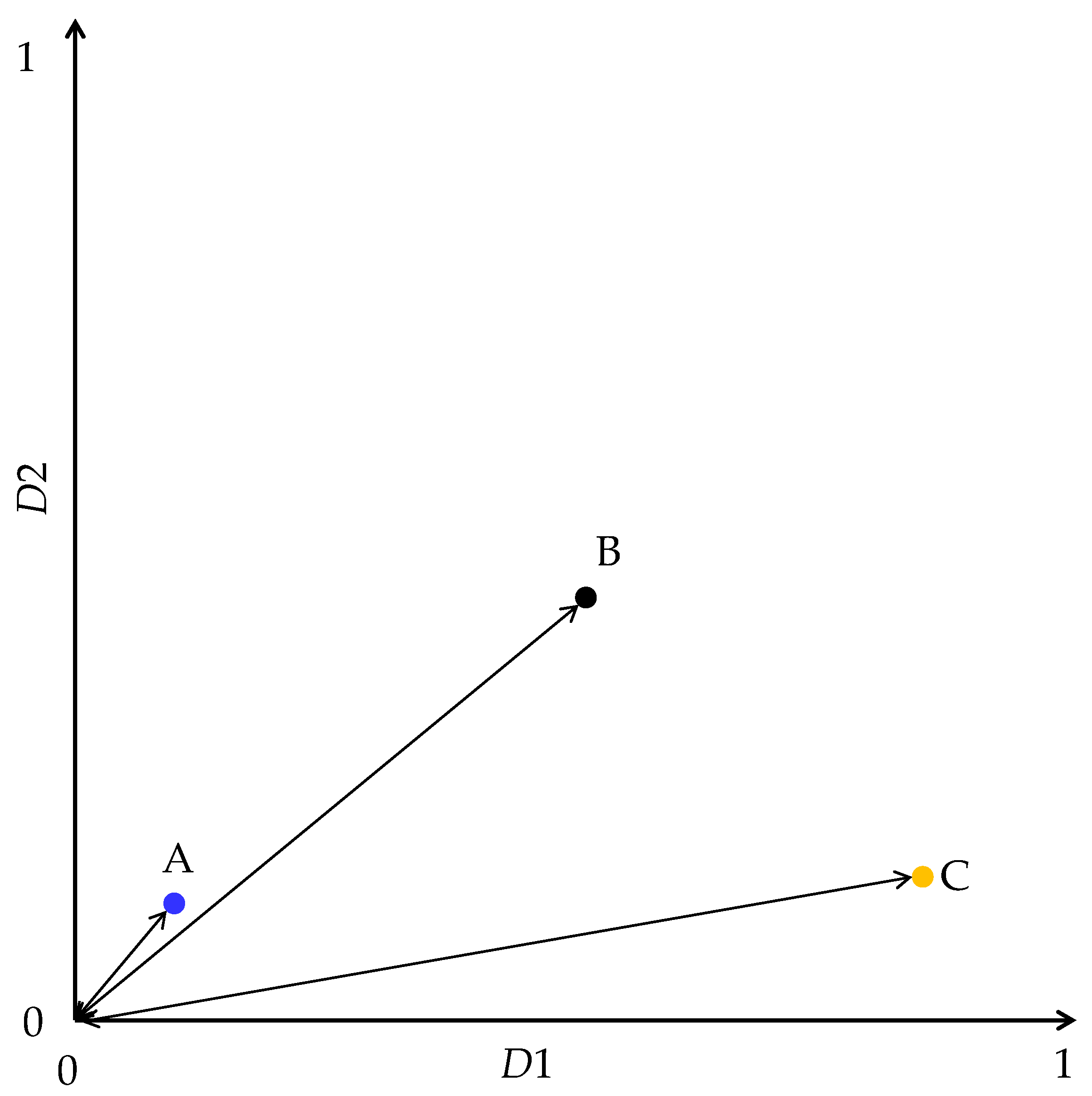
Figure 13 can be shown in the
D2 versus
D1 plot as shown in
Figure 14.
The wooden and polymeric materials (case study 1) were reassessed using the new decision score. The results are shown in
Table 7 and
Table 8 for wooden and polymeric materials, respectively. As seen in
Table 7 and
Table 8, the new decision score (
E) concerning the criterion “minimize water usage” for both groups of materials are comparable (0.44 and 0.43). This means that both natural materials and polymers are equally unsustainable in terms of water usage. This is consistent with the visual inspection of the plot (
Figure 7). On the other hand, the new decision score (
E) concerning CO
2 footprint is very high (0.70) for the natural materials compared to that of polymers (0.45). The above results are consistent with results reported in case study 1. Thus, the decision scores given by
D and
E can serve the purpose of making the right decision. It is worth mentioning that
E is perhaps a better decision score compared to
D because it considers uncertainty as well as the compliances.
6. Concluding Remarks
The information regarding indicators of SDGs and product life-cycle-based arrangements (e.g., material passport) create a vast information silo of big data. Therefore, making the right decisions using such big data will play a pivotal role in achieving sustainability. Since big data is “big”, the relevant datasets, presented in a visual form (a set of two-dimensional plots), become the decision-relevant information. This necessitates novel decision-making methods and tools capable of handling two-dimensional plots rather than numerical data. Furthermore, the methods and tools must accommodate the decision maker’s preferences. Accordingly, this article presents a decision-making method and a tool to formally compute the two-dimensional plots of numerical data. The proposed method and tool can directly extract the decision-relevant information from two-dimensional plots (generated from big data) and compute the decision scores based on the maximization or minimization principle (e.g., minimize CO2 emission).
The efficacy of the presented method and tool are shown using two case studies. The first case study shows that the proposed decision-making method and tool produce reliable results even though the relevant datasets presented using two-dimensional plots exhibit uncertainty. In this case study, the datasets regarding two eco-indicators (CO2 footprint and water usage) of two types of materials (wooden materials and polymers) were plotted using two scatter plots. The datasets regarding CO2 footprint and water usage of 447 wooden materials and 244 polymers are presented. As the plots show, both wooden materials and polymers can be ranked equally regarding water usage. However, as far as CO2 footprint is concerned, wooden materials are far better than polymers. The parameter of the proposed decision-making approach, denoted as the decision score, arrives at the same decision (wooden materials and polymers are indifferent in terms of water usage, but wooden materials are better than polymers in terms of CO2 emission).
The other case study applies the method and tool for multiple-criteria decision-making. In particular, this case ranks the three most frequently used metallic materials—mild steel, aluminum alloys, and magnesium alloys—using graphical information generated from big data on engineering materials. Six criteria were considered: (1) strength, (2) Yang’s modulus, (3) destiny, (4) CO2 footprint, (5) water usage, and (6) cost. In this case study, a parameter denoted as the raking parameter is introduced that aggregates the decision scores of all criteria for an alternative by considering each criterion’s importance or weight. It is shown that weight is instrumental in exercising the decision makers’ preferences.
Numerous policymakers, practitioners, and researchers have been acting in a coordinated manner, while remaining independent, to achieve SDGs. SDG-centric activities, particularly 93 Tier 1, 72 Tier 2, and 62 Tier 3—indicator-centric activities all around the globe, manifest big data. Making sense of such a huge data silo is essential for ensuring the degree of fulfillment of SDGs or putting forward the right set of solutions if the fulfillment is not satisfactory. In such cases, it is most likely that decisions are made from the visualized big data rather than numerical datasets. Therefore, the presented decision-making method and tool can contribute to the advancement of big data-related research for achieving SDGs.
In the next phase of this study, a decision support system can be developed to automate the decision-making approach presented in the previous sections.