A Framework for Content-Based Search in Large Music Collections †
Abstract
1. Introduction
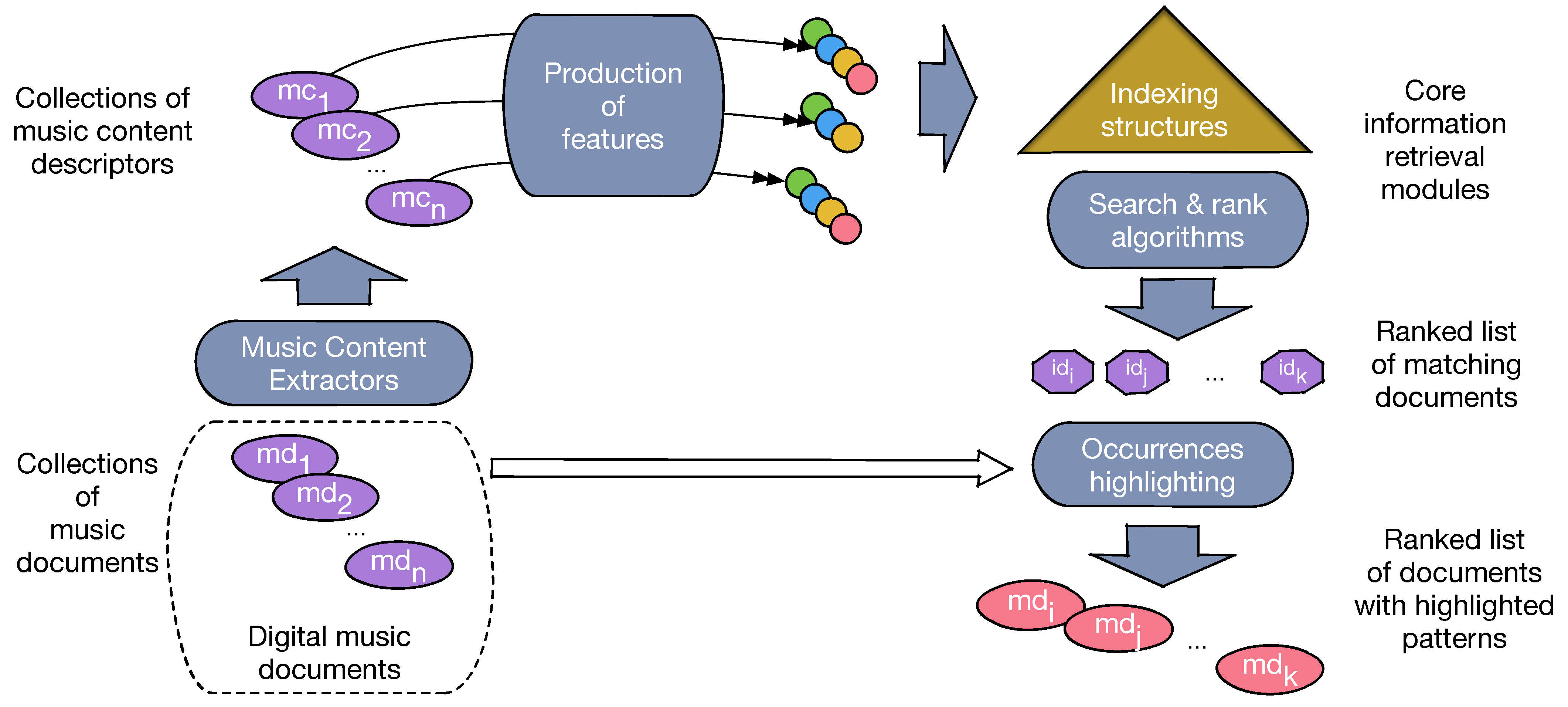
- A Music Content Model, or MCM (Section 3). It borrows from the principles of music notation, reduced to the aspects that are independent from presentation purposes (i.e., ignoring staves, clefs, or other elements that relate to the layout of music scores). Although strongly influenced by the Western music tradition, we believe that this model is general enough to represent a large part of the currently digitized music. We call a Music Content Descriptor (MCD) a description of a music document according to this model. The model supports some major functionalities of a search engine, namely transformations corresponding to the classical linguistic operations in text-based search engines and ranking.
- A set of features that can be obtained from an MCD thanks to the above-mentioned transformations. The features set presented in the current work (Section 4) is by no way intended to constitute a final list, and the framework design is open to the addition of other features like harmony, texture, or timbre.
- The design of the core modules of a search engine, based on these features and dedicated to music retrieval (Section 5). They consist in indexing, searching, ranking, and on-line identification of fragments that match the query pattern.
- An actual implementation (Section 6), dedicated to XML-encoded musical score collections shows how to integrate these modules in a standard information retrieval system, with two main benefits: reduction of implementation efforts and horizontal scalability.
2. Related Work
3. The Music Content Model
3.1. The Domain of Sounds: Pitches and Intervals
- (1)
- The set of pitch symbols , ,
- (2)
- The rest symbol, noted r,
- (3)
- The continuation symbol, noted _.
- A chromatic interval is the number of steps, negative (descending) or positive (ascending), in the chromatic scale, between two pitches.
- A diatonic interval is a nominal distance measuring the number of steps, descending or ascending, in the diatonic scale, between two pitches.
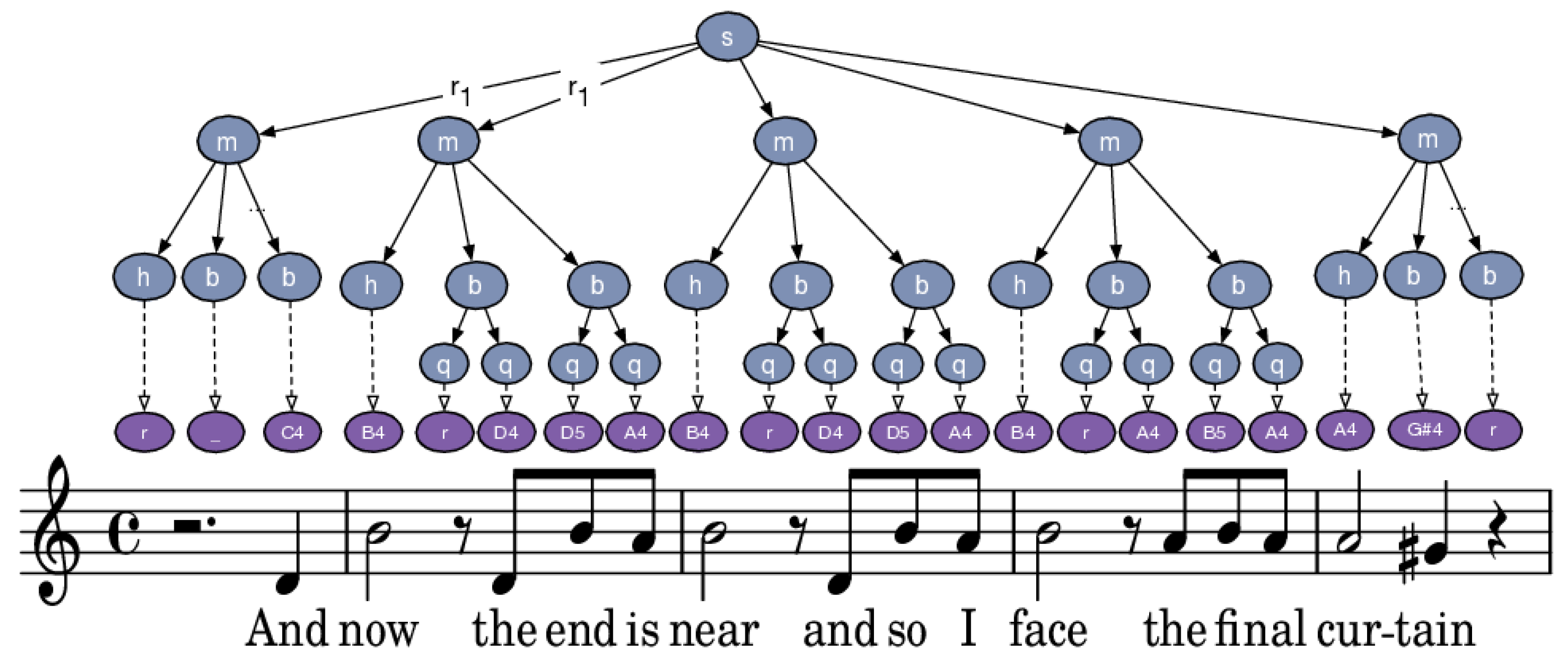
3.2. Music Content Descriptors
- (1)
- (a piece of music is a sequence of measures),
- (2)
- (a measure is decomposed in four quarter notes/beats),
- (3)
- (a beat is decomposed in two quavers/eighth note),
- (4)
- A set of rules where is a musical symbol.
- (1)
- If N has no children,
- (2)
- If N is of the form , I is partitioned in n sub-intervals of equal size each: with
3.3. Non-Musical Domains
3.4. Polyphonic Music
4. Offline Operations: Features and Text-Based Indexing
- There exists an analyzer that takes a content descriptor as input and produces a feature as output.
- There must exist a serialization of a feature as a character string, which makes possible the transposition of queries to standard text-based search supported by the engine.
- Finally, each feature type must be equipped with a scoring function that can be incorporated into the search engine for ranking purposes.
4.1. Chromatic Interval Feature
- (1)
- All repeated values from are merged in a single one.
- (2)
- Rest and continuation symbols are removed.
4.2. Diatonic Interval Feature
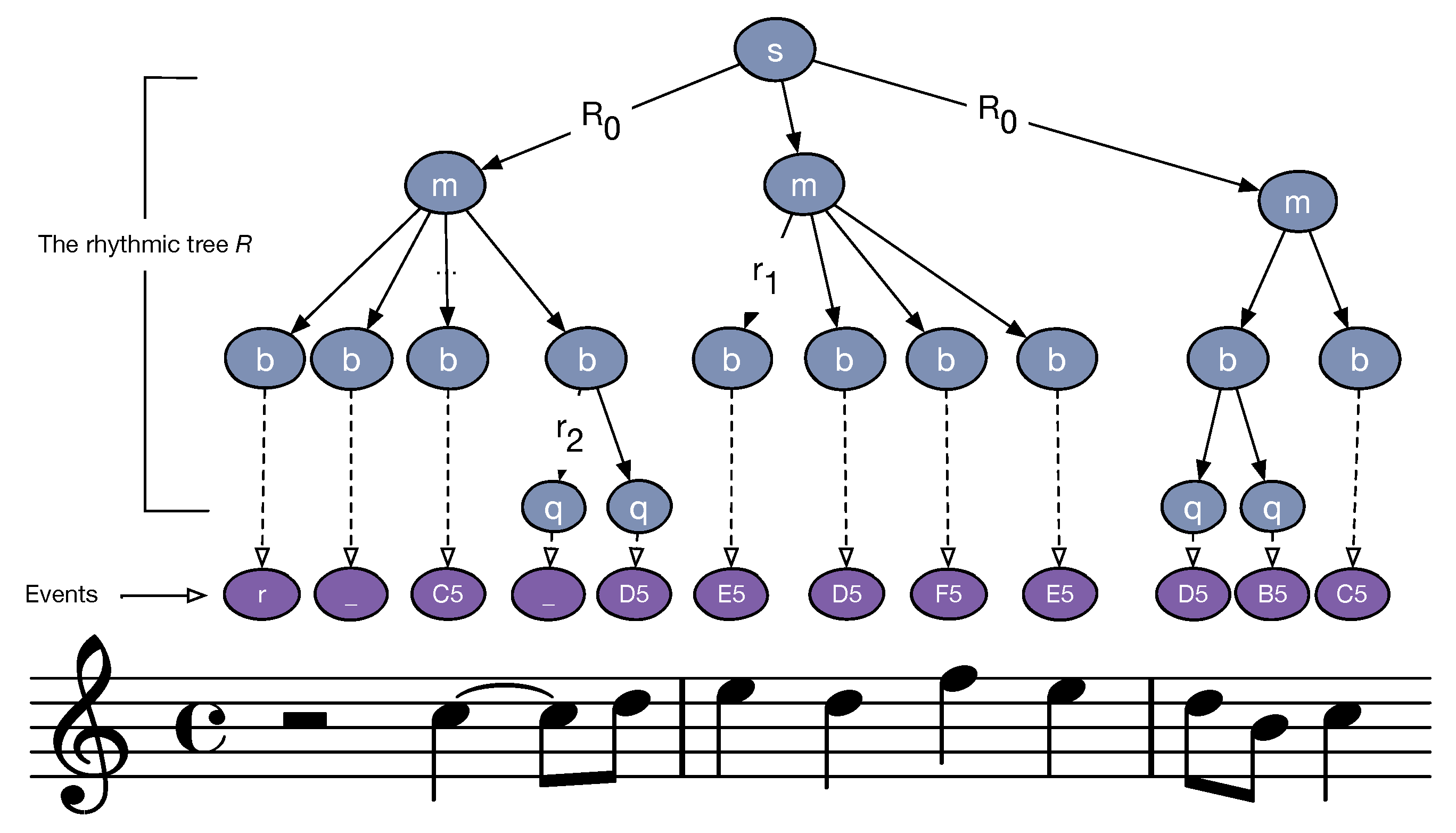
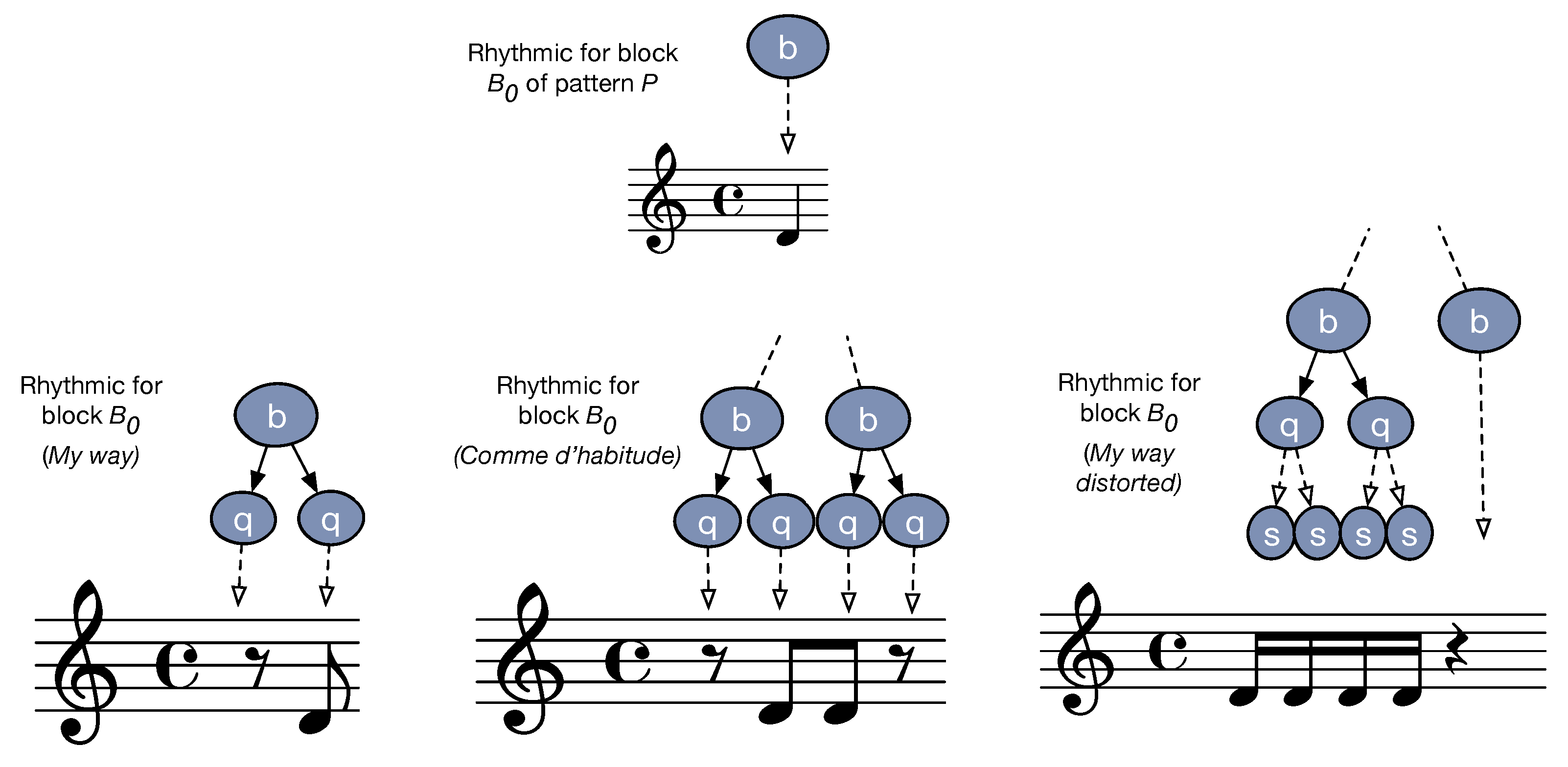
4.3. Rhythmic Feature
- Rhythmic perception is essentially invariant to homomorphic transformations: doubling both the note durations and the tempo results in the same music being played.
- The rhythmic tree provides a very elaborated representation of the rhythmic organization: putting all this information in a feature would favor a very high precision but a very low recall.
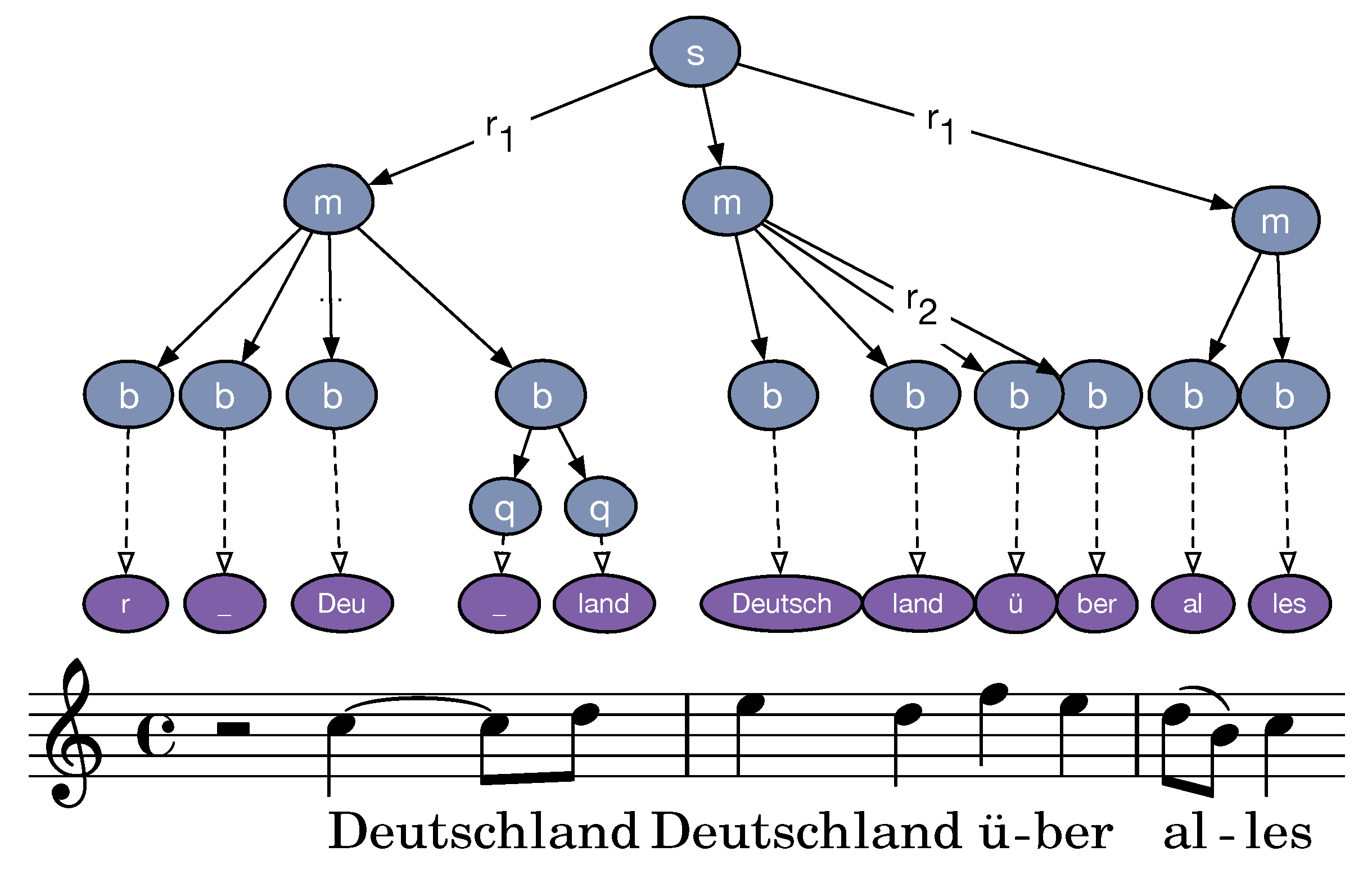
4.4. Lyrics Feature
4.5. Text-Based Indexing
4.6. A Short Discussion
5. Online Operations: (Scalable) Searching, Ranking, Highlighting
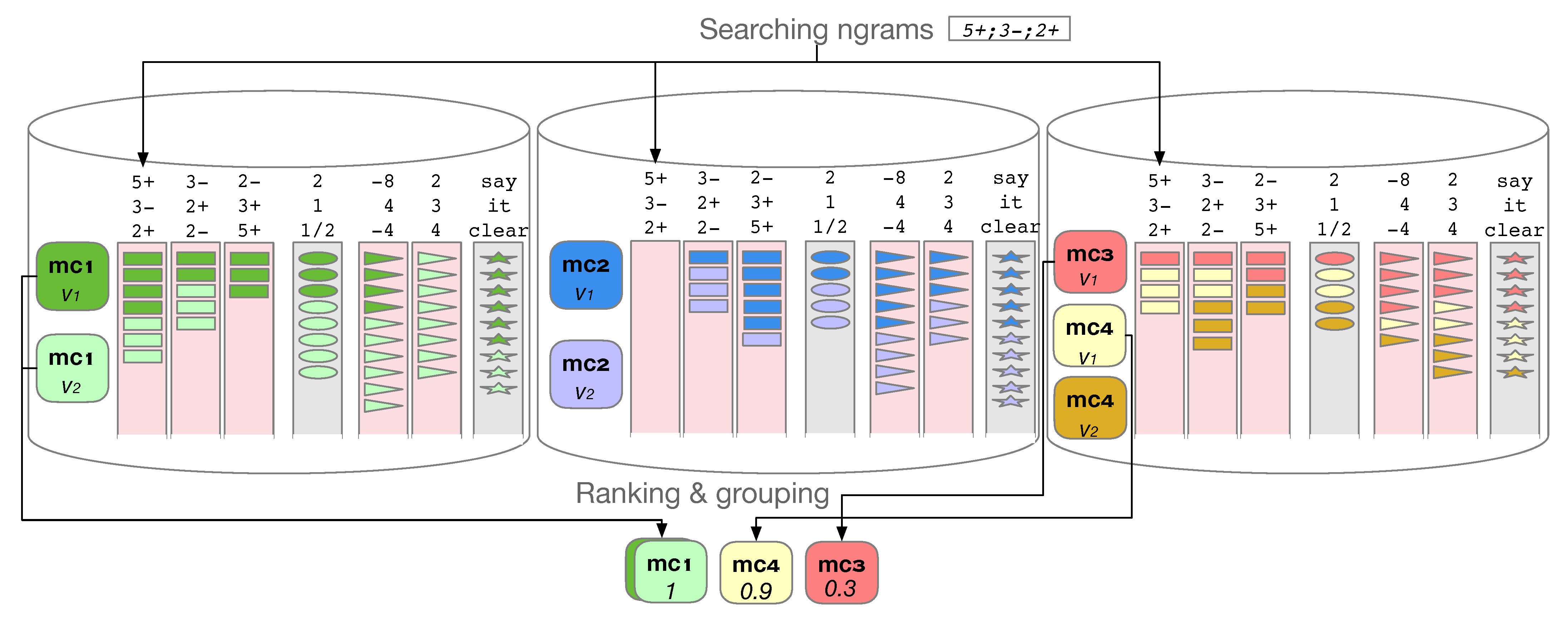
5.1. Searching
5.2. Scalability
5.3. Ranking for Interval-Based Search
- and are two distinct non-rest values, and
- each is either a rest, or a pitch such that
- (1)
- For children of the root: insert/delete/replace a measure.
- (2)
- For all other nodes N: either insert a subtree by applying a rule from to the non-terminal symbol N, or delete the subtree rooted at N.
| Algorithm 1 Rhythmic Ranking |
|
| Algorithm 2 Simplified Rhythmic Ranking |
|
5.4. Ranking for Rhythmic-Based Search
| Algorithm 3 Interval-Based Ranking |
|
5.5. Finding Matching Occurrences
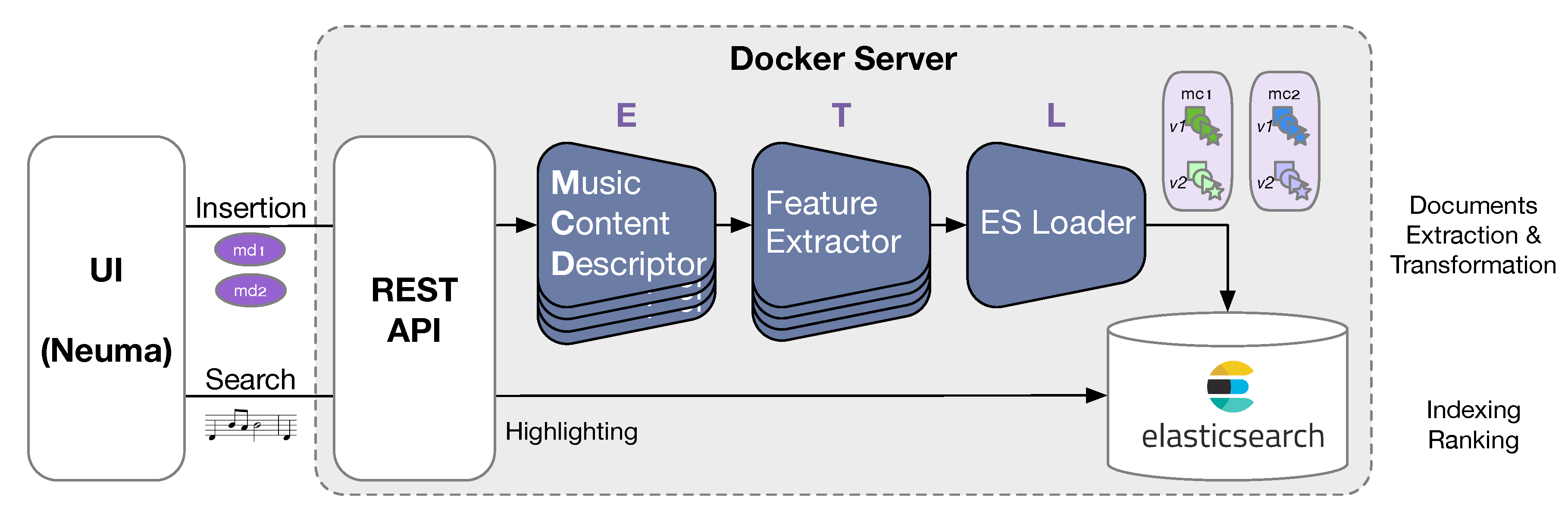
6. Implementation
6.1. Global Architecture

6.2. Query Processing


6.3. Distribution and Aggregation

6.4. Highlighting

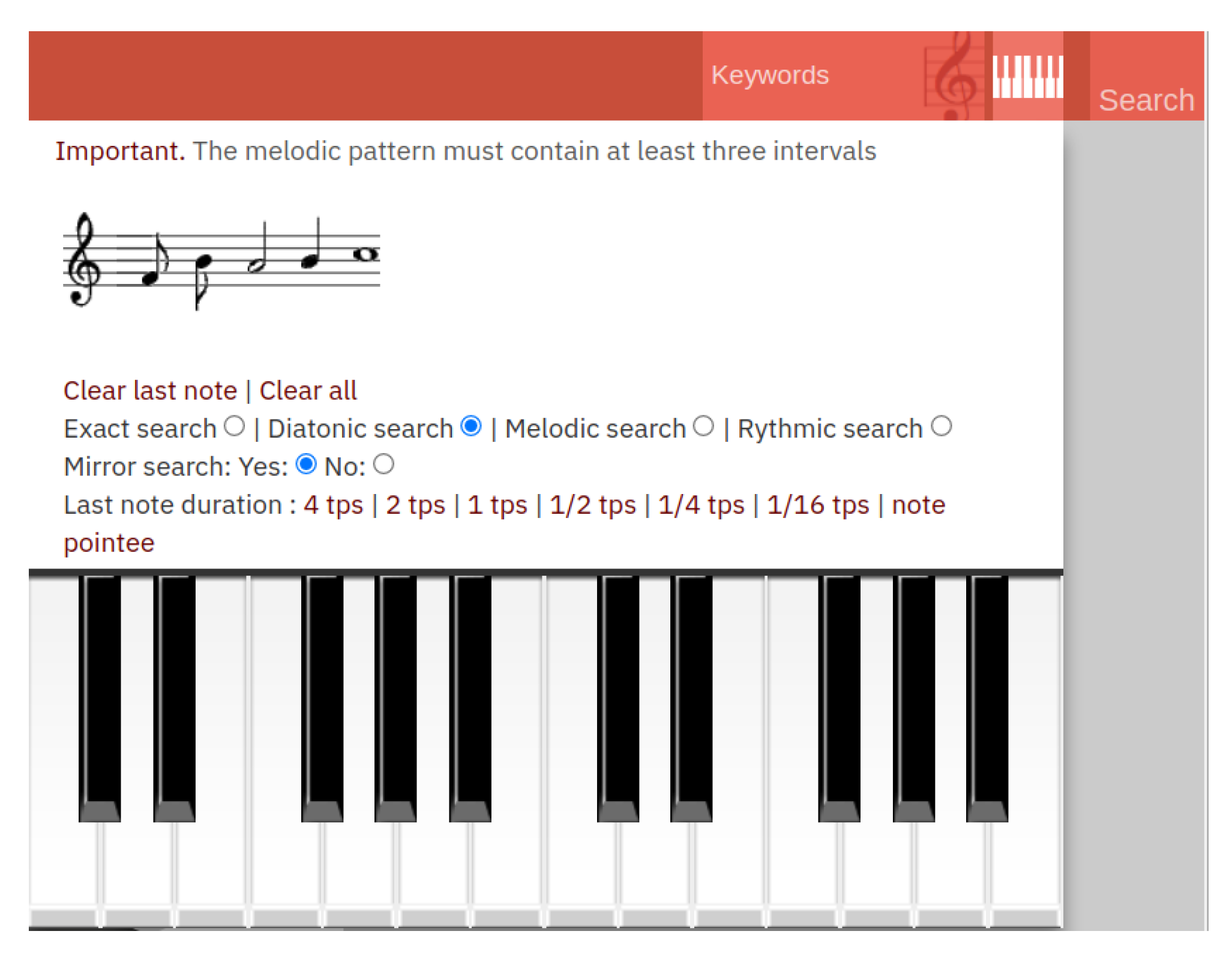
6.5. Interacting with the Server
6.6. Data and Performance Evaluation
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Manning, C.D.; Raghavan, P.; Schutze, H. Introduction to Information Retrieval; Cambridge University Press: Cambridge, UK, 2008; Available online: http://informationretrieval.org/ (accessed on 17 January 2022).
- Samet, H. Foundations of Multidimensional and Metric Data Structures; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2006; Available online: https://www.elsevier.com/books/foundations-of-multidimensional-and-metric-data-structures/samet/978-0-12-369446-1 (accessed on 17 January 2022).
- Zhou, W.; Li, H.; Tian, Q. Recent advance in content-based image retrieval: A literature survey. arXiv 2017, arXiv:1706.06064. [Google Scholar]
- Chen, W.; Liu, Y.; Wang, W.; Bakker, E.; Georgiou, T.; Fieguth, P.; Liu, L.; Lew, M.S. Deep Image Retrieval: A Survey. arXiv 2021, arXiv:cs.CV/2101.11282. [Google Scholar]
- Rothstein, J. MIDI: A Comprehensive Introduction; Computer Music and Digital Audio Series; A-R Editions: 1995; Available online: https://www.areditions.com/publications/computer-music-and-digital-audio/rothstein-midi-a-comprehensive-introduction-2nd-ed-das007.html (accessed on 17 January 2022).
- Apel, W. The Notation of Polyphonic Music, 900–1600; The Medieval Academy of America: Cambridge, MA, USA, 1961; Available online: http://link.sandiego.edu/portal/The-notation-of-polyphonic-music/Qrs0lSyuz7Q/ (accessed on 17 January 2022).
- Gould, E. Behind Bars; Faber Music: Freehold, NJ, USA, 2011; p. 676. Available online: https://www.alfred.com/behind-bars/p/12-0571514561/ (accessed on 17 January 2022).
- Huron, D. The Humdrum Toolkit: Software for Music Research; 1994; Available online: https://www.humdrum.org/Humdrum/ (accessed on 17 January 2022).
- Good, M. MusicXML for Notation and Analysis. In The Virtual Score: Representation, Retrieval, Restoration; Hewlett, W.B., Selfridge-Field, E., Eds.; MIT Press: Cambridge, MA, USA, 2001; pp. 113–124. [Google Scholar]
- MNX 1.0 Draft Specification. 2021. Available online: https://github.com/w3c/mnx (accessed on 15 November 2021).
- Rolland, P. The Music Encoding Initiative (MEI). In Proceedings of the International Conference on Musical Applications Using XML, Milan, Italy, 19–20 September 2002; pp. 55–59. [Google Scholar]
- Music Encoding Initiative. 2015. Available online: http://www.music-encoding.org (accessed on 17 January 2022).
- Huron, D. Music Information Processing Using the Humdrum Toolkit: Concepts, Examples, and Lessons. Comput. Music. J. 2002, 26, 11–26. [Google Scholar] [CrossRef]
- Sapp, C.S. Online Database of Scores in the Humdrum File Format. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), London, UK, 11–15 September 2005. [Google Scholar]
- Rigaux, P.; Abrouk, L.; Audéon, H.; Cullot, N.; Davy-Rigaux, C.; Faget, Z.; Gavignet, E.; Gross-Amblard, D.; Tacaille, A.; Thion-Goasdoué, V. The design and implementation of Neuma, a collaborative Digital Scores Library—Requirements, architecture, and models. Int. J. Digit. Libr. 2012, 12, 73–88. [Google Scholar] [CrossRef]
- MuseScore. Available online: https://musescore.org/ (accessed on 3 December 2021).
- Carterette, B.; Jones, R.; Jones, G.F.; Eskevich, M.; Reddy, S.; Clifton, A.; Yu, Y.; Karlgren, J.; Soboroff, I. Podcast Metadata and Content: Episode Relevance and Attractiveness in Ad Hoc Search. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, Canada, 11–15 July 2021. [Google Scholar] [CrossRef]
- Discogs: Music Database and Marketplace. Available online: https://www.discogs.com/ (accessed on 29 September 2021).
- AllMusic. Available online: https://www.allmusic.com/ (accessed on 3 December 2021).
- Musixmatch. Available online: https://www.musixmatch.com/ (accessed on 3 December 2021).
- Wang, A. The Shazam music recognition service. Commun. ACM 2006, 49, 44–48. [Google Scholar] [CrossRef]
- SoundHound. Available online: https://www.soundhound.com/ (accessed on 29 September 2021).
- Kotsifakos, A.; Papapetrou, P.; Hollmén, J.; Gunopulos, D.; Athitsos, V. A Survey of Query-by-Humming Similarity Methods. In Proceedings of the PETRA’12: The 5th International Conference on Pervasive Technologies Related to Assistive Environments, Heraklion, Crete, Greece, 6–8 June 2012; Association for Computing Machinery: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Cuthbert, M.E.A. Music21. 2006. Available online: http://web.mit.edu/music21/ (accessed on 17 January 2022).
- Foscarin, F.; Jacquemard, F.; Rigaux, P.; Sakai, M. A Parse-based Framework for Coupled Rhythm Quantization and Score Structuring. In MCM 2019—Mathematics and Computation in Music, Proceedings of the Seventh International Conference on Mathematics and Computation in Music (MCM 2019), Madrid, Spain, 18–21 June 2019; Lecture Notes in Computer Science; Springer: Madrid, Spain, 2019. [Google Scholar] [CrossRef]
- Foscarin, F.; Fournier-S’niehotta, R.; Jacquemard, F. A diff procedure for music score files. In Proceedings of the 6th International Conference on Digital Libraries for Musicology (DLfM), The Hague, The Netherlands, 9 November 2019; ACM: The Hague, The Netherlands, 2019; pp. 7–11. [Google Scholar]
- Antila, C.; Treviño, J.; Weaver, G. A hierarchic diff algorithm for collaborative music document editing. In Proceedings of the Third International Conference on Technologies for Music Notation and Representation (TENOR), A Coruña, Spain, 24–26 May 2017. [Google Scholar]
- Simonetta, F.; Carnovalini, F.; Orio, N.; Rodà, A. Symbolic music similarity through a graph-based representation. In Proceedings of the Audio Mostly 2018 on Sound in Immersion and Emotion, Wrexham, UK, 12–14 September 2018; Association for Computing Machinery: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Salamon, J.; Gomez, E. Melody Extraction From Polyphonic Music Signals Using Pitch Contour Characteristics. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 1759–1770. [Google Scholar] [CrossRef]
- Kim, J.W.; Salamon, J.; Li, P.; Bello, J.P. Crepe: A Convolutional Representation for Pitch Estimation. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 161–165. [Google Scholar] [CrossRef]
- Bainbridge, D.; Bell, T. The Challenge of Optical Music Recognition. Comput. Humanit. 2001, 35, 95–121. [Google Scholar] [CrossRef]
- Rebelo, A.; Fujinaga, I.; Paszkiewicz, F.; Marçal, A.R.S.; Guedes, C.; Cardoso, J.S. Optical music recognition: State-of-the-art and open issues. Int. J. Multimed. Inf. Retr. 2012, 1, 173–190. [Google Scholar] [CrossRef]
- Choi, K.Y.; Coüasnon, B.; Ricquebourg, Y.; Zanibbi, R. Music Symbol Detection with Faster R-CNN Using Synthetic Annotations. In Proceedings of the First International Workshop on Reading Music Systems, Paris, France, 20 September 2018. [Google Scholar]
- Ríos Vila, A.; Rizo, D.; Calvo-Zaragoza, J. Complete Optical Music Recognition via Agnostic Transcription and Machine Translation. In Proceedings of the International Conference on Document Analysis and Recognition (ICDAR 2021), Lausanne, Switzerland, 5–10 September 2021; pp. 661–675. [Google Scholar] [CrossRef]
- Knopke, I. The Perlhumdrum and Perllilypond Toolkits for Symbolic Music Information Retrieval. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Philadelphia, PA, USA, 14–18 September 2008; pp. 147–152. [Google Scholar]
- Kornstaedt, A. Themefinder: A Web-based Melodic Search Tool. Comput. Musicol. 1998, 11, 231–236. [Google Scholar]
- Stuart, C.; Liu, Y.W.; Selfridge-Field, E. Search-effectiveness measures for symbolic music queries in very large databases. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Barcelona, Spain, 10–14 October 2004. [Google Scholar]
- Prechelt, L.; Typke, R. An Interface for Melody Input. ACM Trans.-Comput.-Hum. Interact. (TOCHI) 2001, 8, 133–149. [Google Scholar] [CrossRef]
- Fournier-S’niehotta, R.; Rigaux, P.; Travers, N. Is There a Data Model in Music Notation? In Proceedings of the International Conference on Technologies for Music Notation and Representation (TENOR’16), Cambridge, UK, 27–29 May 2016; Anglia Ruskin University: Cambridge, UK, 2016; pp. 85–91. [Google Scholar]
- Fournier-S’niehotta, R.; Rigaux, P.; Travers, N. Querying XML Score Databases: XQuery is not Enough! In Proceedings of the International Conference on Music Information Retrieval (ISMIR), New York, NY, USA, 7–11 August 2016. [Google Scholar]
- Fournier-S’niehotta, R.; Rigaux, P.; Travers, N. Modeling Music as Synchronized Time Series: Application to Music Score Collections. Inf. Syst. 2018, 73, 35–49. [Google Scholar] [CrossRef]
- Casey, M.; Veltkamp, R.; Goto, M.; Leman, M.; Rhodes, C.; Slaney, M. Content-based music information retrieval: Current directions and future challenges. Proc. IEEE 2008, 96, 668–696. [Google Scholar] [CrossRef]
- Jones, M.C.; Downie, J.S.; Ehmann, A.F. Human Similarity Judgments: Implications for the Design of Formal Evaluations. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Vienna, Austria, 23–27 September 2007; pp. 539–542. [Google Scholar]
- Ens, J.; Riecke, B.E.; Pasquier, P. The Significance of the Low Complexity Dimension in Music Similarity Judgements. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Suzhou, China, 23–27 October 2017; pp. 31–38. [Google Scholar]
- Velardo, V.; Vallati, M.; Jan, S. Symbolic Melodic Similarity: State of the Art and Future Challenges. Comput. Music J. 2016, 40, 70–83. [Google Scholar] [CrossRef]
- Typke, R.; Wiering, F.; Veltkamp, R.C. A survey of music information retrieval systems. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), London, UK, 11–15 September 2005; pp. 153–160. [Google Scholar]
- Nanopoulos, A.; Rafailidis, D.; Ruxanda, M.M.; Manolopoulos, Y. Music search engines: Specifications and challenges. Inf. Process. Manag. 2009, 45, 392–396. [Google Scholar] [CrossRef]
- Viro, V. Peachnote: Music Score Search and Analysis Platform. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Miami, FL, USA, 24–28 October 2011; pp. 359–362. [Google Scholar]
- Downie, J.S. Evaluating a Simple Approach to Music Information Retrieval: Conceiving Melodic n-Grams as Text. Ph.D. Thesis, University Western Ontario, London, ON, Canada, 1999. [Google Scholar]
- Neve, G.; Orio, N. Indexing and Retrieval of Music Documents through Pattern Analysis and Data Fusion Techniques. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Barcelona, Spain, 10–14 October 2004; pp. 216–223. [Google Scholar]
- Doraisamy, S.; Rüger, S.M. A Polyphonic Music Retrieval System Using N-Grams. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Barcelona, Spain, 10–14 October 2004; pp. 204–209. [Google Scholar]
- Chang, C.W.; Jiau, H.C. An Efficient Numeric Indexing Technique for Music Retrieval System. In Proceedings of the IEEE International Conference on Multimedia and Expo (ICME), Toronto, ON, Canada, 9–12 July 2006; pp. 1981–1984. [Google Scholar]
- Sanyal, A. Modulo7: A Full Stack Music Information Retrieval and Structured Querying Engine. Ph.D. Thesis, Johns Hopkins University, Baltimore, MD, USA, 2016. [Google Scholar]
- Constantin, C.; du Mouza, C.; Faget, Z.; Rigaux, P. The Melodic Signature Index for Fast Content-based Retrieval of Symbolic Scores Camelia Constantin. In Proceedings of the 12th International Society for Music Information Retrieval Conference, Miami, FL, USA, 24–28 October 2011; pp. 363–368. [Google Scholar]
- Rigaux, P.; Travers, N. Scalable Searching and Ranking for Melodic Pattern Queries. In Proceedings of the International Conference of the International Society for Music Information Retrieval (ISMIR), Delft, The Netherlands, 4–8 November 2019. [Google Scholar]
- Haydn, J. Das Lied der Deutschen. Lyrics by August Heinrich Hoffmann von Fallersleben. 1797. Available online: https://archive.org/details/das-lied-der-deutschen_202102 (accessed on 17 January 2022).
- Taylor, C.; Campbell, M. Sound. Grove Music Online. 2001. Available online: https://doi.org/10.1093/gmo/9781561592630.article.26289 (accessed on 17 January 2022).
- Haynes, B.; Cooke, P. Pitch. Grove Music Online. 2001. Available online: https://doi.org/10.1093/gmo/9781561592630.article.40883 (accessed on 17 January 2022).
- Roeder, J. Pitch Class. Grove Music Online. 2001. Available online: https://doi.org/10.1093/gmo/9781561592630.article.21855 (accessed on 17 January 2022).
- Lindley, M. Interval. Grove Music Online. (Revised by Murray Campbell and Clive Greated). 2001. Available online: https://doi.org/10.1093/gmo/9781561592630.article.13865 (accessed on 17 January 2022).
- Drabkin, W. Diatonic. Grove Music Online. 2001. Available online: https://doi.org/10.1093/gmo/9781561592630.article.07727 (accessed on 17 January 2022).
- Mullally, R. Measure. Grove Music Online. 2001. Available online: https://doi.org/10.1093/gmo/9781561592630.article.18226 (accessed on 17 January 2022).
- Greated, C. Beats. Grove Music Online. 2001. Available online: https://doi.org/10.1093/gmo/9781561592630.article.02424 (accessed on 17 January 2022).
- Campbell, M. Timbre. Grove Music Online. 2001. Available online: https://doi.org/10.1093/gmo/9781561592630.article.27973 (accessed on 17 January 2022).
- Texture. Grove Music Online. 2001. Available online: https://doi.org/10.1093/gmo/9781561592630.article.27758 (accessed on 17 January 2022).
- Anka, P. My Way. Interpret: Frank Sinatra. 1969. Available online: https://www.discogs.com/release/9365438-Frank-Sinatra-My-Way (accessed on 17 January 2022).
- Revaux, J.; François, C. Comme d’Habitude; 1967; Available online: https://www.discogs.com/fr/release/1068588-Claude-Fran%C3%A7ois-Comme-Dhabitude (accessed on 17 January 2022).
- Orpen, K.; Huron, D. Measurement of Similarity in Music: A Quantitative Approach for Non-Parametric Representations. Comput. Music. Res. 1992, 4, 1–44. [Google Scholar]
- Toussaint, G. A comparison of rhythmic similarity measures. In Proceedings of the ISMIR’04: International Conference on Music Information Retrieval (ISMIR), Barcelona, Spain, 10–14 October 2004; pp. 242–245. [Google Scholar]
- Beltran, J.; Liu, X.; Mohanchandra, N.; Toussaint, G. Measuring Musical Rhythm Similarity: Statistical Features versus Transformation Methods. J. Pattern Recognit. Artif. Intell. 2015, 29, 1–23. [Google Scholar] [CrossRef]
- Post, O.; Toussaint, G. The Edit Distance as a Measure of Perceived Rhythmic Similarity. Empir. Musicol. Rev. 2011, 6, 164–179. [Google Scholar] [CrossRef][Green Version]
- Demaine, E.D.; Mozes, S.; Rossman, B.; Weimann, O. An optimal decomposition algorithm for tree edit distance. ACM Trans. Algorithms 2009, 6, 1–19. [Google Scholar] [CrossRef]
- Zhang, K.; Shasha, D. Simple Fast Algorithms for the Editing Distance between Trees and Related Problems. J. Comput. 1989, 18, 1245–1262. [Google Scholar] [CrossRef]
- Ristad, E.; Yianilos, P. Learning string-edit distance. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 522–532. [Google Scholar] [CrossRef]
- Habrard, A.; Iñesta, J.M.; Rizo, D.; Sebban, M. Melody Recognition with Learned Edit Distances. In Structural, Syntactic, and Statistical Pattern Recognition; da Vitoria Lobo, N., Kasparis, T., Roli, F., Kwok, J.T., Georgiopoulos, M., Anagnostopoulos, G.C., Loog, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 86–96. [Google Scholar]
- Cnam. Neuma On-Line Digital Library. 2009. Available online: http://neuma.huma-num.fr/ (accessed on 17 January 2022).
- ElasticSearch. The Elastic Search Engine. Available online: https://www.elastic.co/ (accessed on 3 December 2021).
- Solr. The Apache Solr Search Engine. Available online: https://solr.apache.org/ (accessed on 3 December 2021).
- Sphinx. The Sphinx Search Engine. Available online: https://sphinxsearch.com/ (accessed on 3 December 2021).
- Cuthbert, M.S.; Ariza, C. Music21: A Toolkit for Computer-Aided Musicology and Symbolic Music Data. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Utrecht, The Netherlands, 9–13 August 2010; pp. 637–642. [Google Scholar]
- Benetos, E.; Dixon, S.; Giannoulis, D.; Kirchhoff, H.; Klapuri, A. Automatic music transcription: Challenges and future directions. J. Intell. Inf. Syst. 2013, 41, 407–434. [Google Scholar] [CrossRef]
- Aloupis, G.; Fevens, T.; Langerman, S.; Matsui, T.; Mesa, A.; Rodríguez, Y.; Rappaport, D.; Toussaint, G. Algorithms for Computing Geometric Measures of Melodic Similarity. Comput. Music. J. 2006, 30, 67–76. [Google Scholar] [CrossRef][Green Version]
- Veltkamp, R.; Typke, R.; Giannopoulos, P.; Wiering, F.; Oostrum, R. Using Transportation Distances for Measuring Melodic Similarity. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Baltimore, MD, USA, 26–30 October 2003. [Google Scholar]
- Keogh, E.J.; Ratanamahatana, C.A. Exact Indexing of Dynamic Time Warping. Knowl. Inf. Syst. 2005, 7, 358–386. [Google Scholar] [CrossRef]
- Frieler, K.; Höger, F.; Pfleiderer, M.; Dixon, S. Two web applications for exploring melodic patterns in jazz solos. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Paris, France, 23–27 September 2018; pp. 777–783. [Google Scholar]







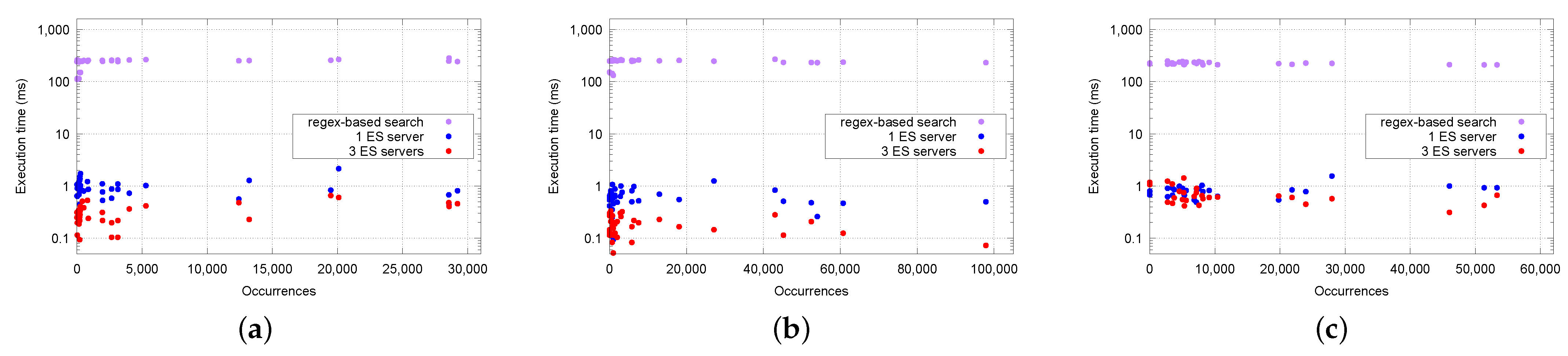
| Feature | Mean Time | Standard Deviation | |
|---|---|---|---|
| Regex-based search | Chromatic | 246 ms | 41 ms |
| Diatonic | 250 ms | 21 ms | |
| Rhythmic | 219 ms | 10 ms | |
| 1 server | Chromatic | 0.869 ms | 0.269 ms |
| Diatonic | 0.583 ms | 0.194 ms | |
| Rhythmic | 0.804 ms | 0.136 ms | |
| 3 servers | Chromatic | 0.312 ms | 0.110 ms |
| Diatonic | 0.166 ms | 0.064 ms | |
| Rhythmic | 0.700 ms | 0.216 ms |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, T.; Fournier-S’niehotta, R.; Rigaux, P.; Travers, N. A Framework for Content-Based Search in Large Music Collections. Big Data Cogn. Comput. 2022, 6, 23. https://doi.org/10.3390/bdcc6010023
Zhu T, Fournier-S’niehotta R, Rigaux P, Travers N. A Framework for Content-Based Search in Large Music Collections. Big Data and Cognitive Computing. 2022; 6(1):23. https://doi.org/10.3390/bdcc6010023
Chicago/Turabian StyleZhu, Tiange, Raphaël Fournier-S’niehotta, Philippe Rigaux, and Nicolas Travers. 2022. "A Framework for Content-Based Search in Large Music Collections" Big Data and Cognitive Computing 6, no. 1: 23. https://doi.org/10.3390/bdcc6010023
APA StyleZhu, T., Fournier-S’niehotta, R., Rigaux, P., & Travers, N. (2022). A Framework for Content-Based Search in Large Music Collections. Big Data and Cognitive Computing, 6(1), 23. https://doi.org/10.3390/bdcc6010023







