Exploring Ensemble-Based Class Imbalance Learners for Intrusion Detection in Industrial Control Networks
Abstract
:1. Introduction
- To evaluate the effectiveness of class imbalance learners over a range of imbalance ratios.
- To provide an informed choice in choosing best-performing methods for identifying attacks in terms of performance accuracy and computational complexity.
2. Related Work
3. Material and Methods
3.1. Datasets
3.2. Methods
- Cost-sensitive tree learner.We apply a pruning procedure and a minimum number of samples for splitting is 2. Additionally, cost ratio is determined by the IR of each dataset.
- -
- Cost-sensitive decision tree (CSC4.5) [6]. It is a cost associated with misclassifying minority occurrences and is used to alter the training set’s class distribution in order to coerce cost-sensitive trees. This mechanism often results in a reduction in the overall misclassification cost, high-cost misclassification, and the size of the tree in a binary prediction task. When training datasets contain a reasonably skewed distribution of classes, smaller trees are a logical byproduct of the tree induction technique.
- Cost-sensitive bagging.For the following bagging-based ensemble techniques, we used decision tree (e.g., J48) as a base classifier and set the number of bags to 100. Parallel technique is used to accelerate the training process.
- -
- RBBagging [7]. Compared to conventional bagging-based approaches for imbalanced data, which employ the same amount of dominant and less dominant samples for each training subset, individual models in RBBagging exhibit a greater degree of diversity, which is one of the essential characteristics of ensemble models. Additionally, the suggested strategy fully utilizes all minority examples through under-sampling, which is accomplished quickly through the use of negative binomial distributions.
- -
- ROSBagging and RUSBagging [8]. Each subset is constructed in ROSBagging by randomly oversampling minority classes in order to form the k-th classifiers. Similarly, RUSBagging creates each subset by randomly under-sampling majority classes. A majority vote is applied when a new instance occurs after construction and each classifier votes. The class with the most votes ends up making the final decision.
- -
- SMOTEBagging [8]. It entails the production of synthetic instances as part of the subset formation process. According to SMOTE, two components must be determined: the number of nearest neighbors k and the extent to which the less majority class is over-sampled.
- Cost-sensitive boosting.A large number of trees (100) is employed as a base learner, and the decision tree method is applied. The cost ratio is varied according to the IR of each dataset.
- -
- RUSBoosting [9]. It combines the Adaboost algorithm and random undersampling technique, which reduces examples from the dominant class at random intervals once that sufficient balance is attained.
- -
- SMOTEBoosting [10]. It incorporates SMOTE into the Adaboost algorithm. SMOTE creates new minority samples by extrapolating previous samples. SMOTEBoosting exacerbates higher model training time limitation as SMOTE is a more sophisticated and time-consuming data sampling strategy.
- -
- AdaC2 [11]. Introducing the cost items into the AdaBoost by incorporating the cost items into the weights update approach, AdaC2 directs the learning towards instances of the marginalized class. It thus increases the effectiveness of the learning framework. The resampling strategy of AdaC2 is based on the principle that false negatives gain more weight than false positives, whereas true positives lose more weight than true negatives.
- Cost-sensitive hybrid ensemble.Similarly, 100 decision trees were used to construct the ensemble, while the cost ratio varies depending on the dataset’s IR.
- -
- EasyEnsemble [12]. It employs a two-stage ensemble technique that incorporates random undersampling during bagging iterations and trains the base classifier using AdaBoost. It trains the base classifier by doing bagging in an unsupervised manner.
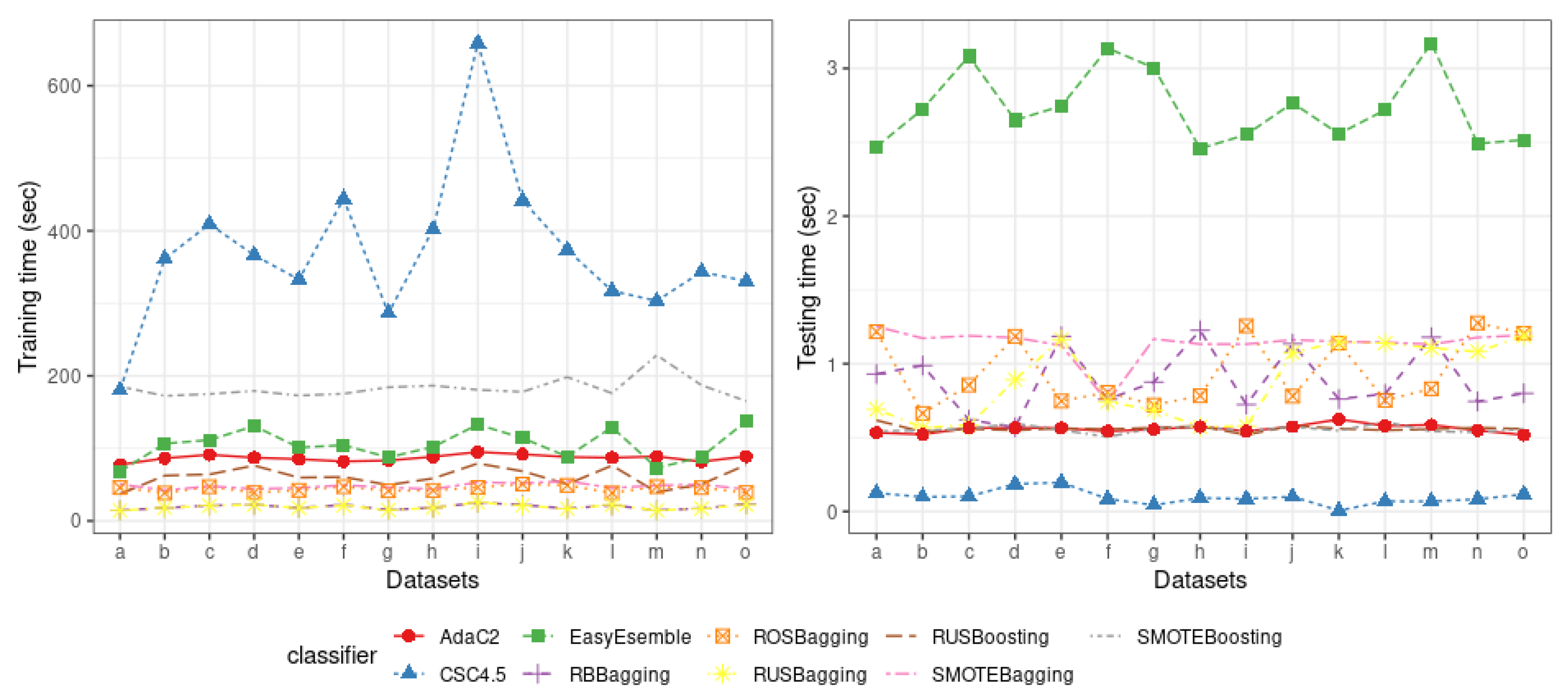
4. Result and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, Z.H. Ensemble Methods: Foundations and Algorithms; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Rokach, L. Taxonomy for characterizing ensemble methods in classification tasks: A review and annotated bibliography. Comput. Stat. Data Anal. 2009, 53, 4046–4072. [Google Scholar] [CrossRef] [Green Version]
- Kuncheva, L.I. Combining Pattern Classifiers: Methods and Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Tama, B.A.; Lim, S. Ensemble learning for intrusion detection systems: A systematic mapping study and cross-benchmark evaluation. Comput. Sci. Rev. 2021, 39, 100357. [Google Scholar] [CrossRef]
- Tama, B.A.; Rhee, K.H. HFSTE: Hybrid feature selections and tree-based classifiers ensemble for intrusion detection system. IEICE Trans. Inf. Syst. 2017, 100, 1729–1737. [Google Scholar] [CrossRef] [Green Version]
- Ting, K.M. An instance-weighting method to induce cost-sensitive trees. IEEE Trans. Knowl. Data Eng. 2002, 14, 659–665. [Google Scholar] [CrossRef] [Green Version]
- Hido, S.; Kashima, H.; Takahashi, Y. Roughly balanced bagging for imbalanced data. Stat. Anal. Data Min. Asa Data Sci. J. 2009, 2, 412–426. [Google Scholar] [CrossRef]
- Wang, S.; Yao, X. Diversity analysis on imbalanced data sets by using ensemble models. In Proceedings of the 2009 IEEE Symposium on Computational Intelligence and Data Mining, Paris, France, 11–15 April 2009; pp. 324–331. [Google Scholar]
- Seiffert, C.; Khoshgoftaar, T.M.; Van Hulse, J.; Napolitano, A. RUSBoost: A hybrid approach to alleviating class imbalance. IEEE Trans. Syst. Man Cybern.-Part A Syst. Hum. 2009, 40, 185–197. [Google Scholar] [CrossRef]
- Chawla, N.V.; Lazarevic, A.; Hall, L.O.; Bowyer, K.W. SMOTEBoost: Improving prediction of the minority class in boosting. In Proceedings of the European Conference on Principles of Data Mining and Knowledge Discovery, Cavtat-Dubrovnik, Croatia, 22–26 September 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 107–119. [Google Scholar]
- Sun, Y.; Kamel, M.S.; Wong, A.K.; Wang, Y. Cost-sensitive boosting for classification of imbalanced data. Pattern Recognit. 2007, 40, 3358–3378. [Google Scholar] [CrossRef]
- Liu, X.Y.; Wu, J.; Zhou, Z.H. Exploratory undersampling for class-imbalance learning. IEEE Trans. Syst. Man Cybern. Part B 2008, 39, 539–550. [Google Scholar]
- Alimi, O.A.; Ouahada, K.; Abu-Mahfouz, A.M.; Rimer, S.; Alimi, K.O.A. A Review of Research Works on Supervised Learning Algorithms for SCADA Intrusion Detection and Classification. Sustainability 2021, 13, 9597. [Google Scholar] [CrossRef]
- Shahraki, A.; Abbasi, M.; Haugen, Ø. Boosting algorithms for network intrusion detection: A comparative evaluation of Real AdaBoost, Gentle AdaBoost and Modest AdaBoost. Eng. Appl. Artif. Intell. 2020, 94, 103770. [Google Scholar] [CrossRef]
- Anton, S.D.D.; Sinha, S.; Schotten, H.D. Anomaly-based intrusion detection in industrial data with SVM and random forests. In Proceedings of the 2019 International Conference on Software, Telecommunications and Computer Networks (SoftCOM), Split, Croatia, 19–21 September 2019; pp. 1–6. [Google Scholar]
- Khan, I.A.; Pi, D.; Khan, Z.U.; Hussain, Y.; Nawaz, A. HML-IDS: A hybrid-multilevel anomaly prediction approach for intrusion detection in SCADA systems. IEEE Access 2019, 7, 89507–89521. [Google Scholar] [CrossRef]
- Upadhyay, D.; Manero, J.; Zaman, M.; Sampalli, S. Intrusion Detection in SCADA Based Power Grids: Recursive Feature Elimination Model with Majority Vote Ensemble Algorithm. IEEE Trans. Netw. Sci. Eng. 2021, 8, 2559–2574. [Google Scholar] [CrossRef]
- Zhu, B.; Gao, Z.; Zhao, J.; vanden Broucke, S.K. IRIC: An R library for binary imbalanced classification. SoftwareX 2019, 10, 100341. [Google Scholar] [CrossRef]
- Lomax, S.; Vadera, S. An empirical comparison of cost-sensitive decision tree induction algorithms. Expert Syst. 2011, 28, 227–268. [Google Scholar] [CrossRef]
- Jeni, L.A.; Cohn, J.F.; De La Torre, F. Facing imbalanced data–recommendations for the use of performance metrics. In Proceedings of the 2013 Humaine Association Conference on Affective Computing and Intelligent Interaction, Geneva, Switzerland, 2–5 September 2013; pp. 245–251. [Google Scholar]
- Luque, A.; Carrasco, A.; Martín, A.; de las Heras, A. The impact of class imbalance in classification performance metrics based on the binary confusion matrix. Pattern Recognit. 2019, 91, 216–231. [Google Scholar] [CrossRef]

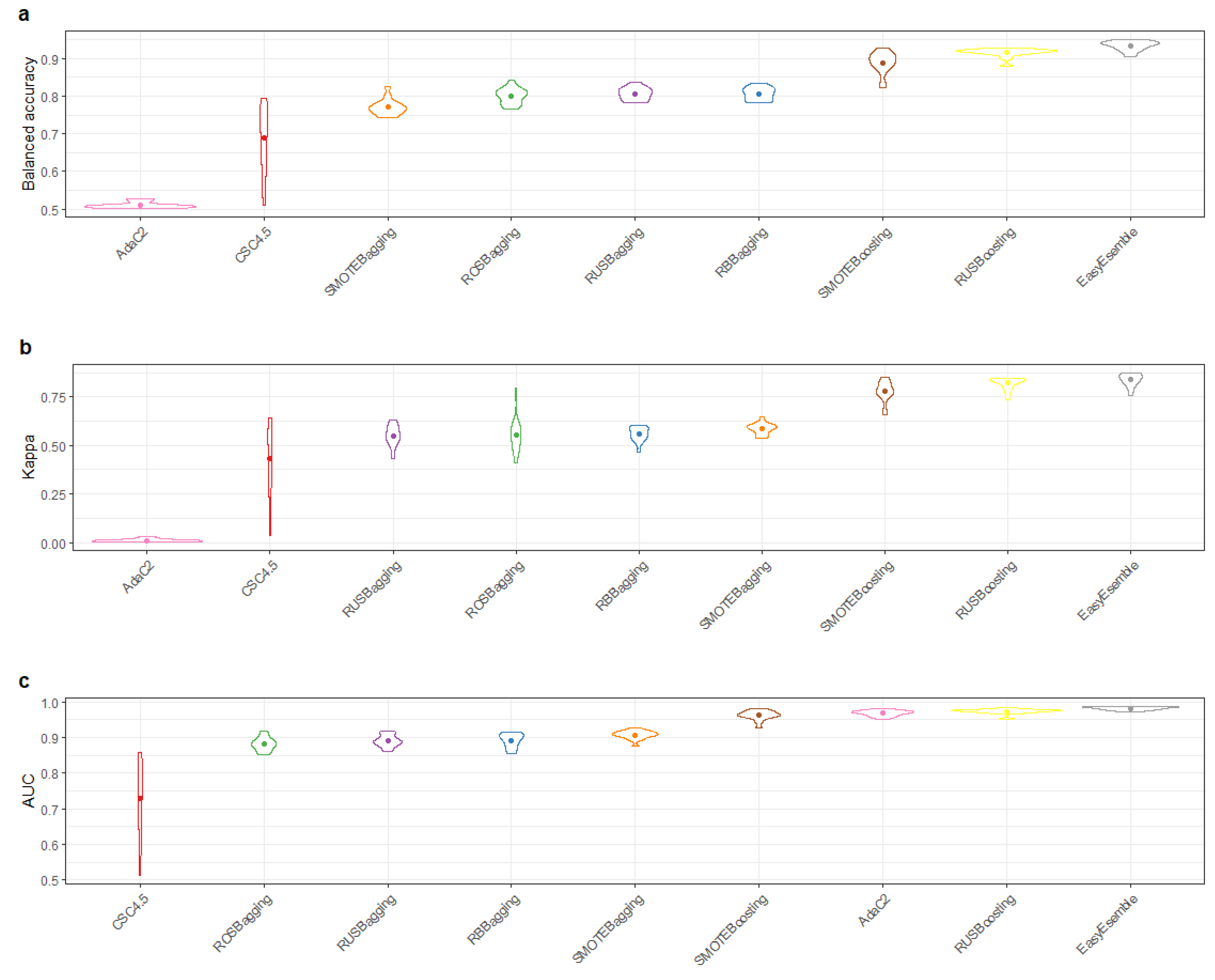
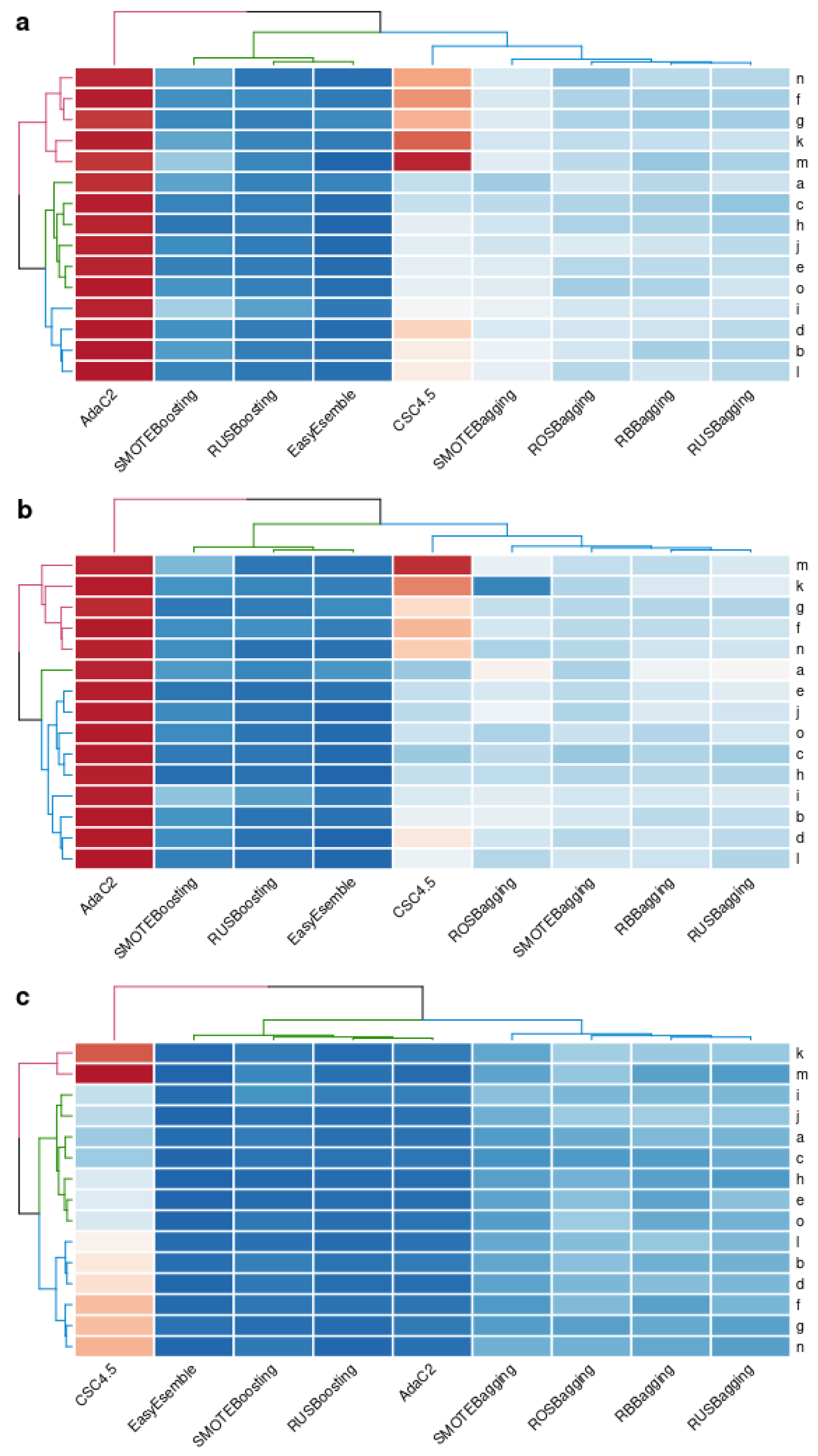
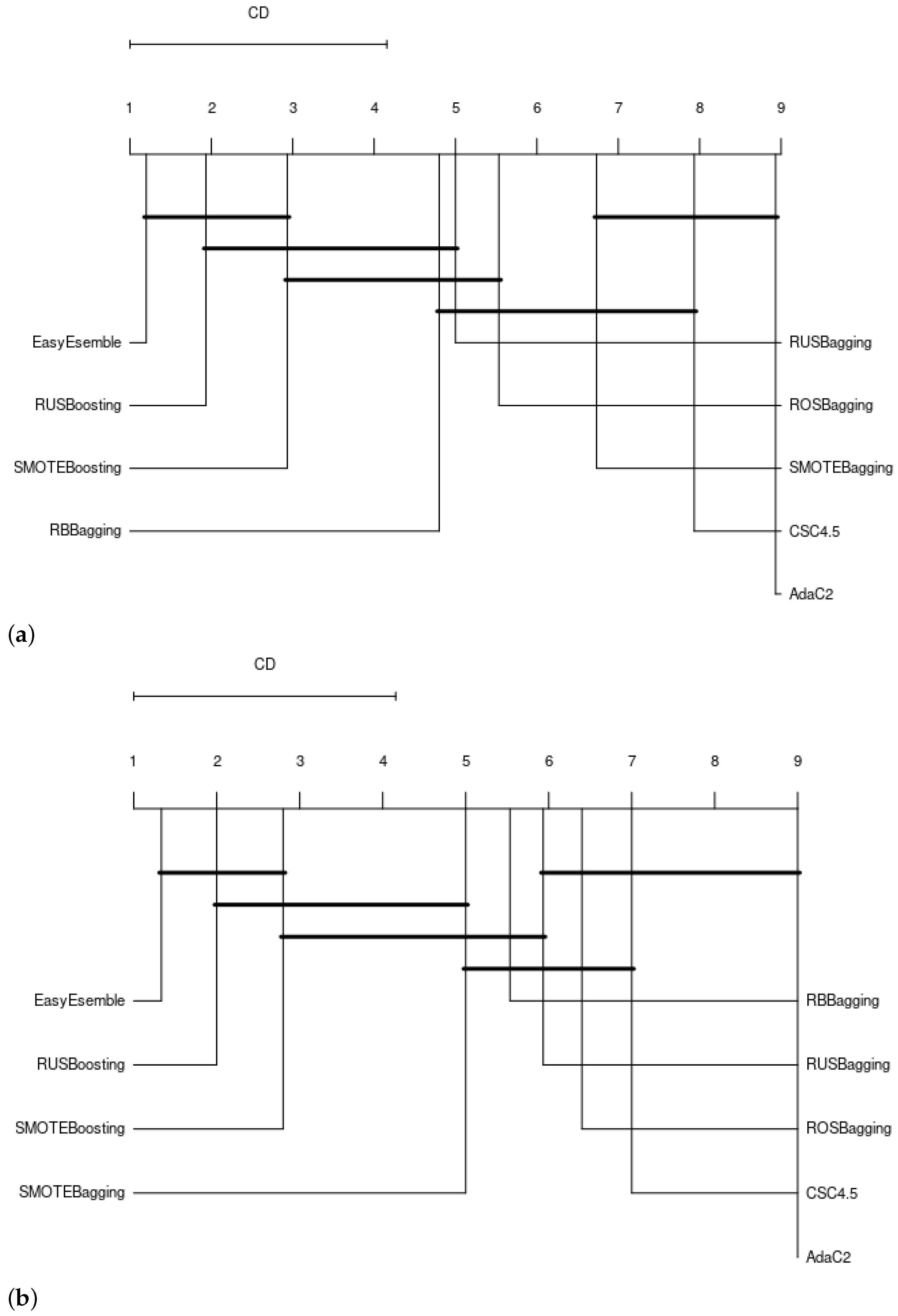

| Datasets | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Class | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o |
| # of natural examples | 1100 | 1544 | 1604 | 1800 | 1481 | 1477 | 1326 | 1544 | 1770 | 1648 | 1282 | 1771 | 1153 | 1353 | 1861 |
| # of attack examples | 3866 | 3525 | 3811 | 3402 | 3680 | 3490 | 3910 | 3771 | 3570 | 3921 | 3969 | 3453 | 4118 | 3762 | 3415 |
| Algorithm | Training Time | Testing Time |
|---|---|---|
| CSC4.5 | 370.09 | 0.097 |
| RBBagging | 19.39 | 0.887 |
| ROSBagging | 44.06 | 0.948 |
| RUSBagging | 19.16 | 0.881 |
| SMOTEBagging | 47.88 | 1.137 |
| RUSBoosting | 60.74 | 0.562 |
| SMOTEBoosting | 183.01 | 0.557 |
| AdaC2 | 86.92 | 0.560 |
| EasyEnsemble | 105.10 | 2.736 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Louk, M.H.L.; Tama, B.A. Exploring Ensemble-Based Class Imbalance Learners for Intrusion Detection in Industrial Control Networks. Big Data Cogn. Comput. 2021, 5, 72. https://doi.org/10.3390/bdcc5040072
Louk MHL, Tama BA. Exploring Ensemble-Based Class Imbalance Learners for Intrusion Detection in Industrial Control Networks. Big Data and Cognitive Computing. 2021; 5(4):72. https://doi.org/10.3390/bdcc5040072
Chicago/Turabian StyleLouk, Maya Hilda Lestari, and Bayu Adhi Tama. 2021. "Exploring Ensemble-Based Class Imbalance Learners for Intrusion Detection in Industrial Control Networks" Big Data and Cognitive Computing 5, no. 4: 72. https://doi.org/10.3390/bdcc5040072
APA StyleLouk, M. H. L., & Tama, B. A. (2021). Exploring Ensemble-Based Class Imbalance Learners for Intrusion Detection in Industrial Control Networks. Big Data and Cognitive Computing, 5(4), 72. https://doi.org/10.3390/bdcc5040072







