1. Introduction
SF6 electrical equipment refers to electrical equipment that uses sulphur hexafluoride (SF6) as insulation or arc extinguishing. SF6 electrical equipment has the advantages of small size, small maintenance, long life and good insulation. With the extensive popularization of intelligent substation, there are more and more power equipment [
1]. The traditional oil-filled equipment is being replaced gradually by SF6 electrical equipment which have unique advantages and account for an increasing proportion of new equipment. With the increasing number of SF6 electrical equipment, the reliability requirements have also increased [
2]. The internal discharge of SF6 electrical equipment leads to the decomposition of internal SF6 gas molecules. The chemical properties of its derivatives are very active. The derivatives can corrode the equipment, which can easily cause a decline in the insulation performance and cause serious damage to the safe and stable operation of the equipment [
3,
4].
In the literature [
5], the phenomenon that the decision tree model or the radial basis function (RBF) neural network model is not used when the diagnosis is not high is firstly described. Then the RBF neural network and the decision tree model are used to diagnose the SF6 electrical equipment. This method requires two diagnostics for all data, which will take a lot of time.
The continuous creation of data has posed new research challenges due to its complexity, diversity and volume. Consequently, Big Data has increasingly become a fully recognized scientific field [
6]. Now big data analytics are increasingly being used to solve real-world problems in life [
7]. And the cloud platform provides an open architecture for big data analytics, which can improve the utilization of data resources [
8].
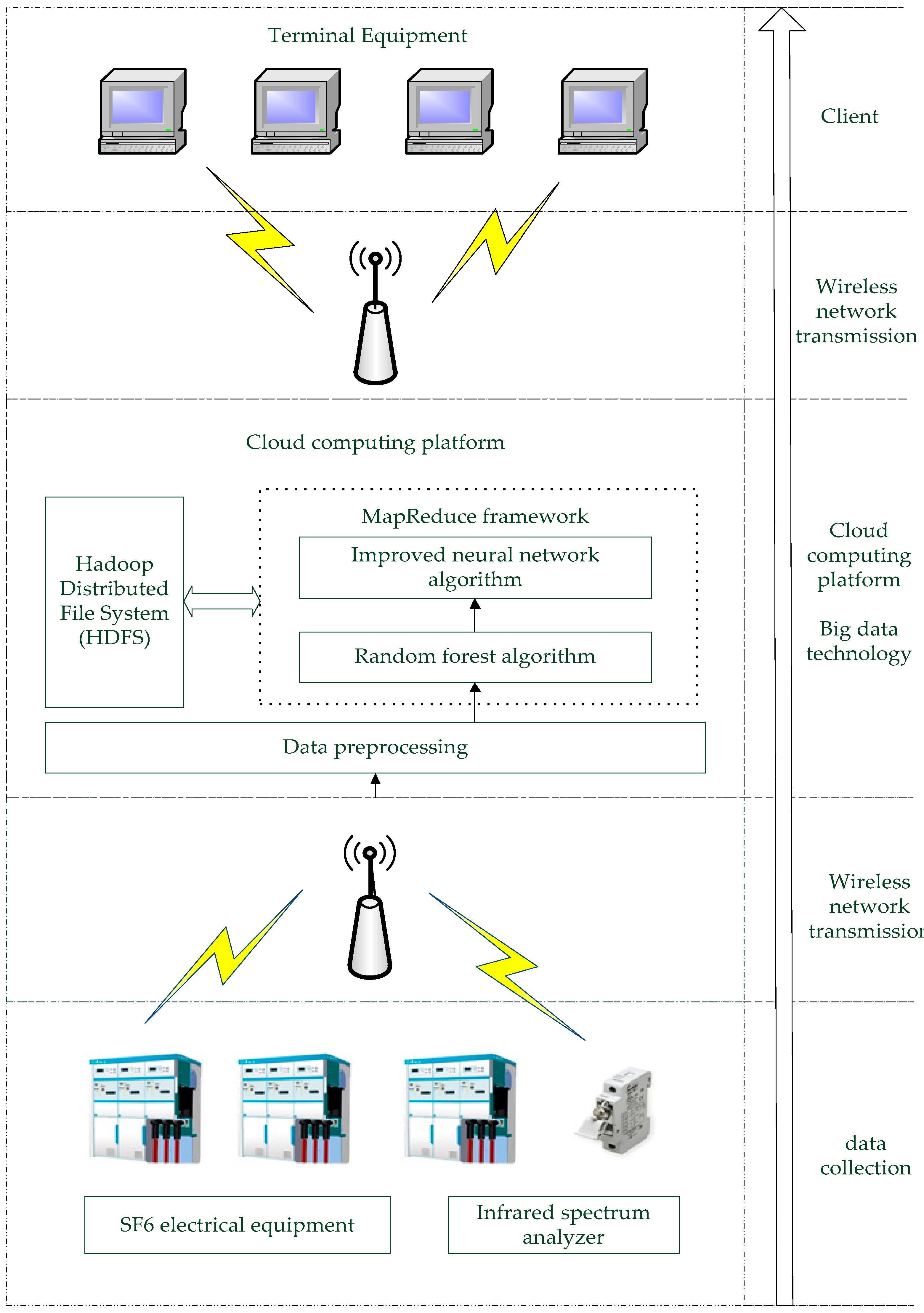
The arrival of the era of big data is accompanied by massive data, which makes the screening of valuable information a core step in the widespread application of big data. Hadoop is an open source distributed computing platform, its distributed file system HDFS and distributed computing framework MapReduce solved the problem of data storage and programming [
9]. Hadoop’s ability to store and process data in bits is trusted. The backup mechanism is used in HDFS to maintain multiple copies of data. The task monitoring mechanism is used in MapReduce. Hadoop is able to dynamically move data between nodes and ensure the dynamic balance of each node, so processing is very fast [
10].
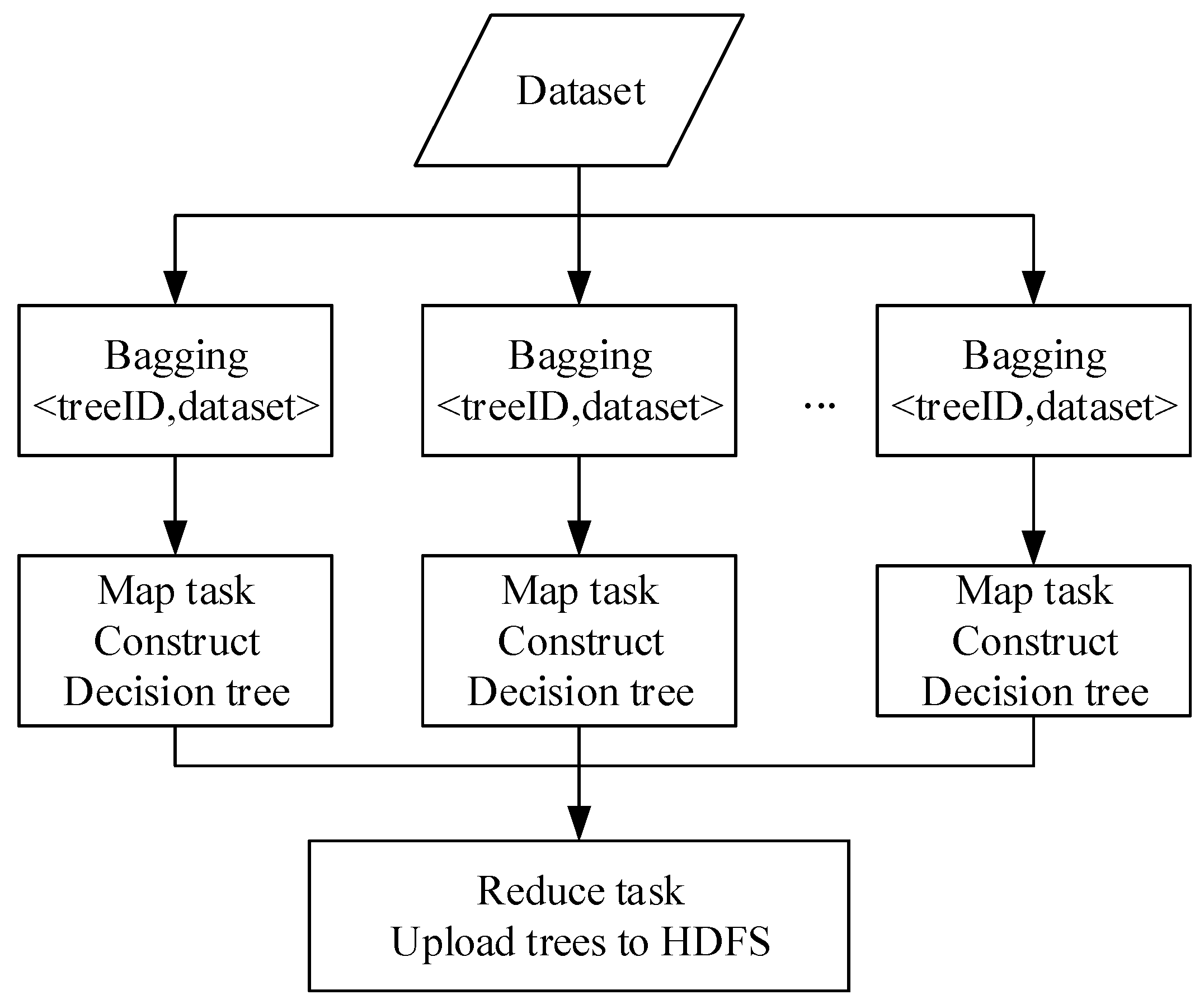
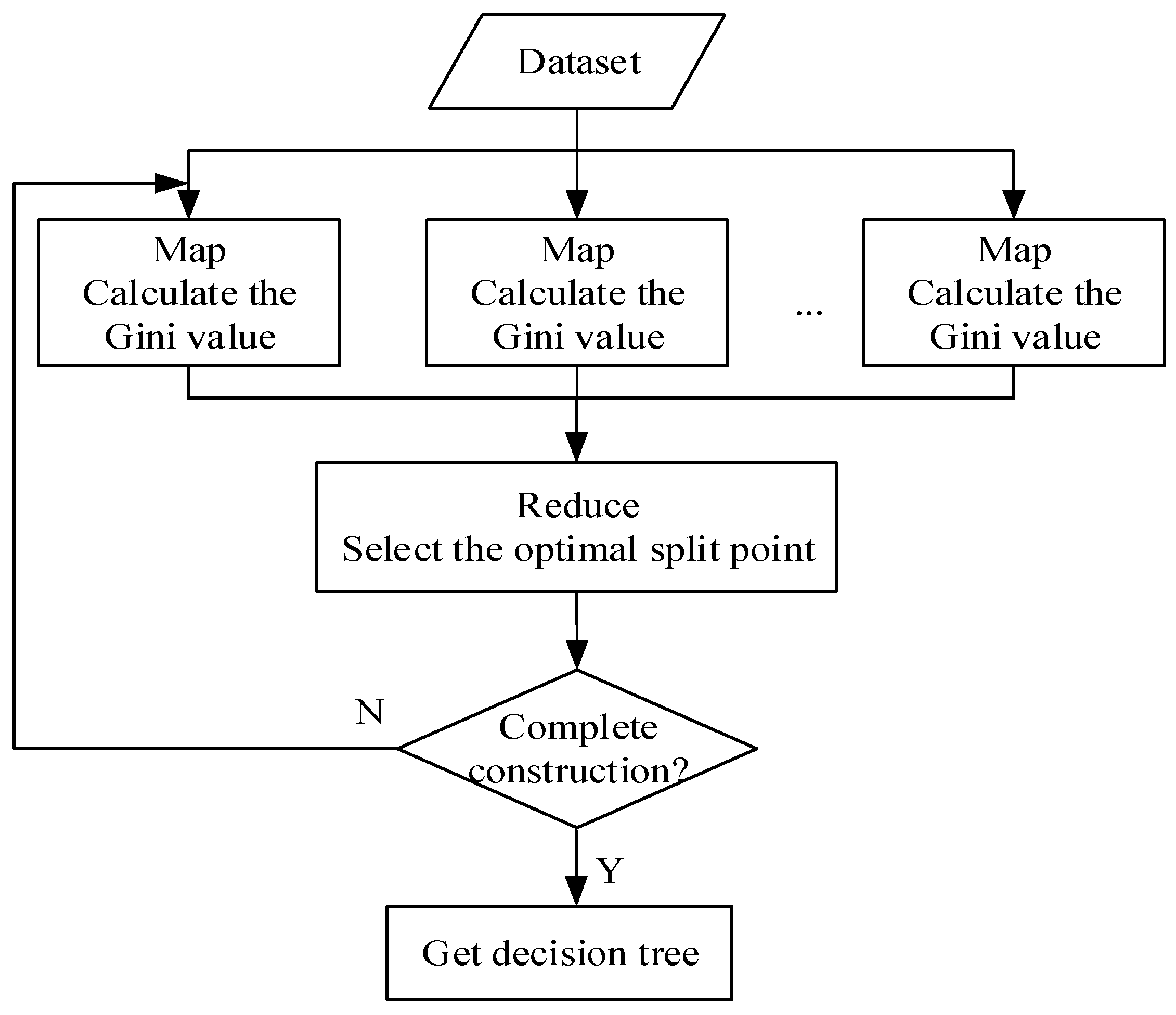
MapReduce is a programming model and related implementation for processing and generating large data sets that are suitable for a wide variety of practical tasks [
11]. MapReduce advantages over parallel databases include storage-system independence and fine-grain fault tolerance for large jobs [
12]. At the same time, MapReduce can realize parallel processing of data and greatly improve the processing efficiency of monitoring data of SF6 electrical equipment [
13].
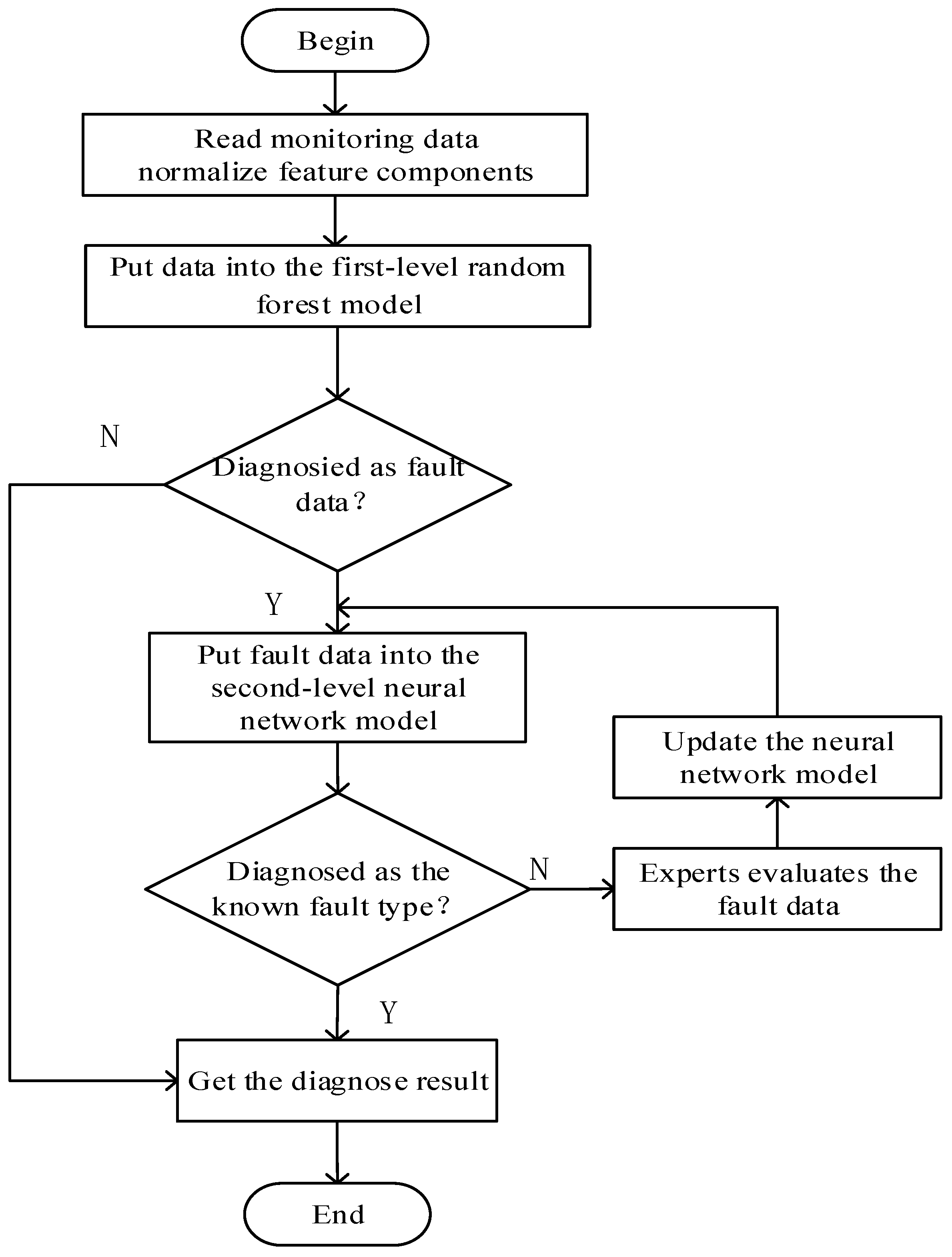
In order to solve the above problems, the two-level fault diagnosis model of SF6 electrical equipment based on the content of SF6 gas derivative as the input for the monitoring data of SF6 electrical equipment was proposed in this paper. The first level fault diagnosis model is first used to determine whether the data is fault data. If yes, it enters the second level fault diagnosis model to identify the specific fault category. If not, the judgment is no longer performed, thereby improving the diagnostic efficiency. In order to quickly realize the fault diagnosis of SF6 electrical equipment for the massive SF6 electrical equipment condition monitoring data, this paper implements the fault diagnosis of SF6 electrical equipment on Hadoop platform and realizes the parallelization of SF6 electrical equipment fault diagnosis algorithm.
3. Monitoring Data Preprocessing
The fault diagnosis of SF6 electrical equipment is one of the methods to verify the operation status of the equipment, but the detection model of the equipment is mostly based on an ideal data set [
22]. In the actual collection process, data redundancy, data loss, and data inconsistency will inevitably occur due to issues such as collection equipment, external environmental disturbances, and human’s misoperation. This will eventually affect later data mining. Therefore, before the fault diagnosis of SF6 electrical equipment, this section fills in the missing values in the monitoring data to implement data pre-processing, and then implements the algorithm.
There are currently few data preprocessing studies on SF6 gas derivative monitoring data. In this section, the SF6 gas derivative content data is used as the processing object. Through the analysis of the data, it is found that there may be three cases of the missing monitoring data. A single approach cannot be fully applied to all situations. Therefore, the data missing values are classified, and different processing methods are adopted for each case.
There are three possible missing values for SF6 gas derivative content monitoring data. These three conditions are described as follows.
- (1)
The missing value is in the same range as the monitoring value recorded before and after it. There are two cases. Case 1: Monitoring data including missing values over a period of time is within normal limits. Case 2: Due to equipment failure, the monitored data including missing values over a period of time is in an abnormal range.
- (2)
The missing value is not in the same range as the monitoring value recorded before and after it. There are also two cases. Case 1: The device just fails and the SF6 gas derivative content rises from the normal range to the abnormal range. Case 2: The equipment was repaired and the content of SF6 gas derivatives dropped from the abnormal range to the normal range.
- (3)
The monitoring values are lost over a period of time.
For the above three cases, the process is as follows.
(1) The weighted interpolation method is used to deal with the case where the first type of data is missing, that is, the weighting factor is introduced for the mean interpolation method.
The basic mean interpolation method takes the arithmetic mean of the n numbers before and after the missing value as a substitute value, as shown in Equation (1).
The weighting factor is introduced for the mean interpolation method, as shown in Equation (2), wherein the record closer to the missing value time has a larger weight.
where
is the weight, the closer to the missing value, the greater the weight of the record.
There are six kinds of SF6 gas derivatives selected in this paper, and SOF2 is used as an example for pretreatment. In order to verify the validity of the algorithm, some SOF2 historical data was read from the database and created some missing cases. In the experiment, four monitoring values were chosen to estimate missing values. When SF6 electrical equipment is in normal condition, its SOF2 content does not exceed 10 .
In this section, multiple sets of experiments were performed for each type of data loss. For reasons of space, only a part of the content was selected as the result.
Experiment 1: The historical data of SOF2 are within the normal range. The experimental data is shown in
Table 1. The numerical values of the serial numbers 3, 4, and 5 are removed in turn, and the interpolation results of SOF2 are shown in
Table 2.
Using the weighted interpolation method to calculate the missing values as follow:
where
,
.
According to
Table 2, the average error of the mean interpolation method is 5.3%, and the average error of the weighted interpolation method is 4.8%. In this case, the weighted interpolation method works well.
Experiment 2: The historical data of SOF2 are within the abnormal range. The experimental data are shown in
Table 3. The numerical values of the Nos. 3, 4, and 5 are removed in turn, and the interpolation results of SOF2 are shown in
Table 4.
According to
Table 4, the average error of the mean interpolation method is 4.12%, and the average error of the weighted interpolation method is 3.86%. The weighted interpolation method works well.
(2) Reading the SOF2 monitoring data from the database for a period of time. The missing value is not in the same range as the monitoring value recorded before and after it.
Experiment 3: When the content of the previous monitoring data of SOF2 missing value is within 10
, and the content of the latter monitoring data is greater than 10
, it indicates that the content of SOF2 fluctuates from the normal range to the abnormal range. The experimental data is shown in
Table 5. If the experiment is continued using the weighted interpolation method and the mean interpolation method, the numerical values of the serial numbers 3 and 4 are sequentially removed, and the experimental results are shown in
Table 6.
It can be seen from
Table 6 that although the error of the interpolation can be reduced by adjusting the weight, it is necessary to find a suitable weight. For sequence number 3, the method of linear interpolation is not suitable.
(3) When the SOF2 monitoring data is read from the database for a period of time, there is a continuous lack of data, and the linear interpolation method cannot be used at this time.
Considering case 2 and case 3, this paper uses the gray correlation degree to interpolate the data. The SF6 gas derivative content data complementing method based on gray correlation is to perform gray scale processing on other component data except the missing value attribute, and to find the closest set of data with the missing value tuple by calculating the correlation degree to make up the complement treatment. The main process is shown in
Figure 4.
The specific steps are follows:
Step 1: Determining the main sequence and subsequence.
A tuple containing missing values is taken as the main sequence. A tuple, in the historical record, with at least one attribute value that is not within the normal range of the safety work is taken as a subsequence. Mark them as and .
Step 2: The matrix formed by the main sequence and subsequences is standardized to obtain a normalized matrix X.
Step 3: Calculate correlation coefficient.
The formula for calculating the correlation coefficient
of
for
is:
where
is the absolute difference sequence of
and
,
and
are the minimum and maximum of
,
is the resolution coefficient and
.
Step 4: Calculate relevance.
The formula for calculating relevance
of
for
is:
where
w is the weight of each SF6 gas derivate. There are six kinds of derivatives, so the
w is set to 1/6.
Step 5: Interpolated missing values.
Sorting the relevance obtained above, and extracting the first 10 sets of tuples those relevance are greater than 0.9 are taken to interpolate the missing values. If less than 10 sets, all the tuples satisfying the condition will be taken. The formula for interpolating missing values
is:
where
j is the column of the missing value in the tuple,
n is the number of tuples taken.
Experiment 3 was re-examined using the gray correlation degree. The experimental results are shown in
Table 7.
From
Table 7, it can be seen that the interpolated values for Nos. 3 and 4 are 8.51 and 13.32, the errors are 0.01 and 0.033 respectively. Therefore, the use of gray correlation can effectively solve the problem of missing data mutations.
The method of grey correlation is to find the closest tuples in the previous record to interpolate missing data. Therefore, when this method is used, there is no case of continuous lack of data.
After pre-processing the monitoring data of the SF6 electrical equipment, a two-level fault diagnosis model of the SF6 electrical equipment can be constructed. First, we train the model on the Hadoop platform. Second, we implemented parallelization of diagnostic algorithms on the Hadoop platform.