Interference Effect of Shock Wave on Tip Leakage Vortex in a Transonic Variable Nozzle Turbine
Abstract
1. Introduction
2. Research Object and Numerical Method
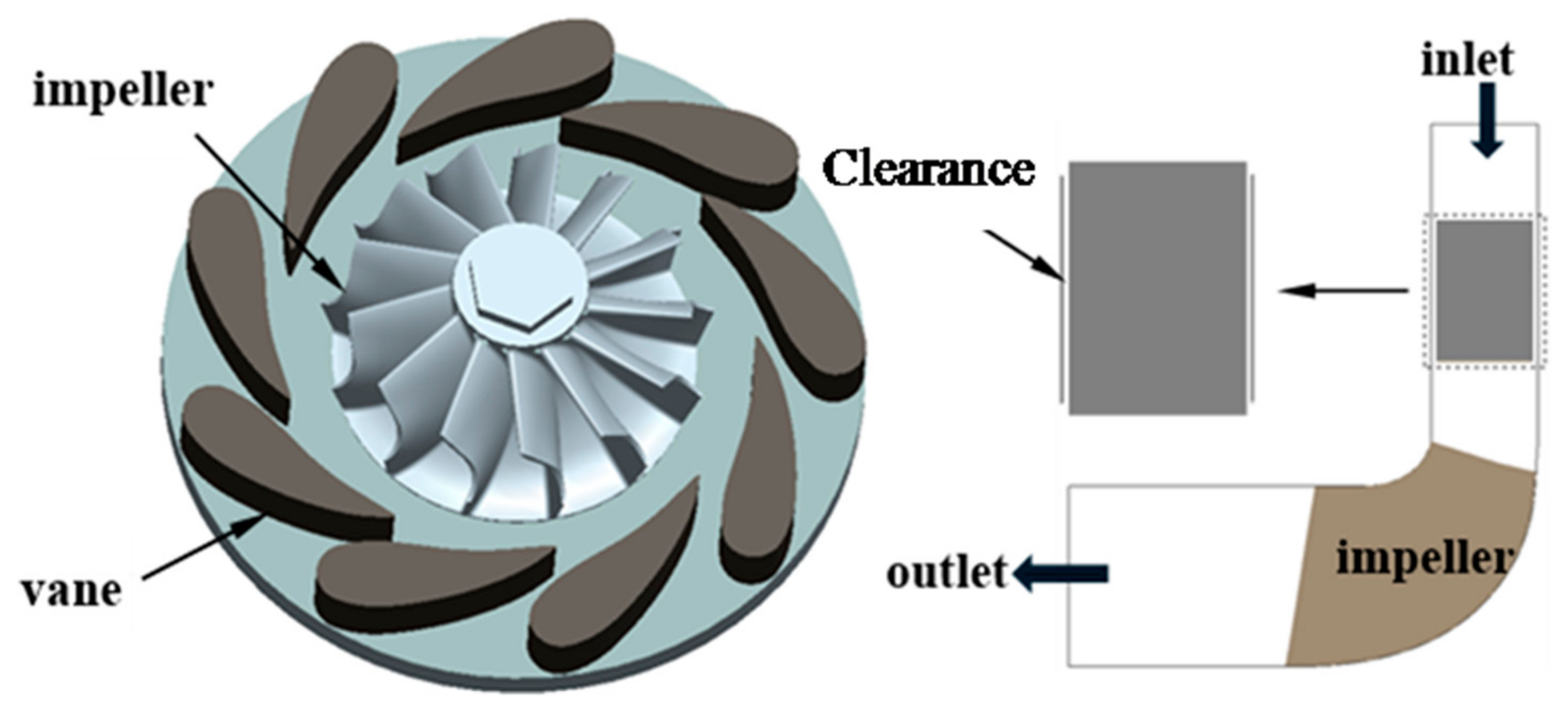
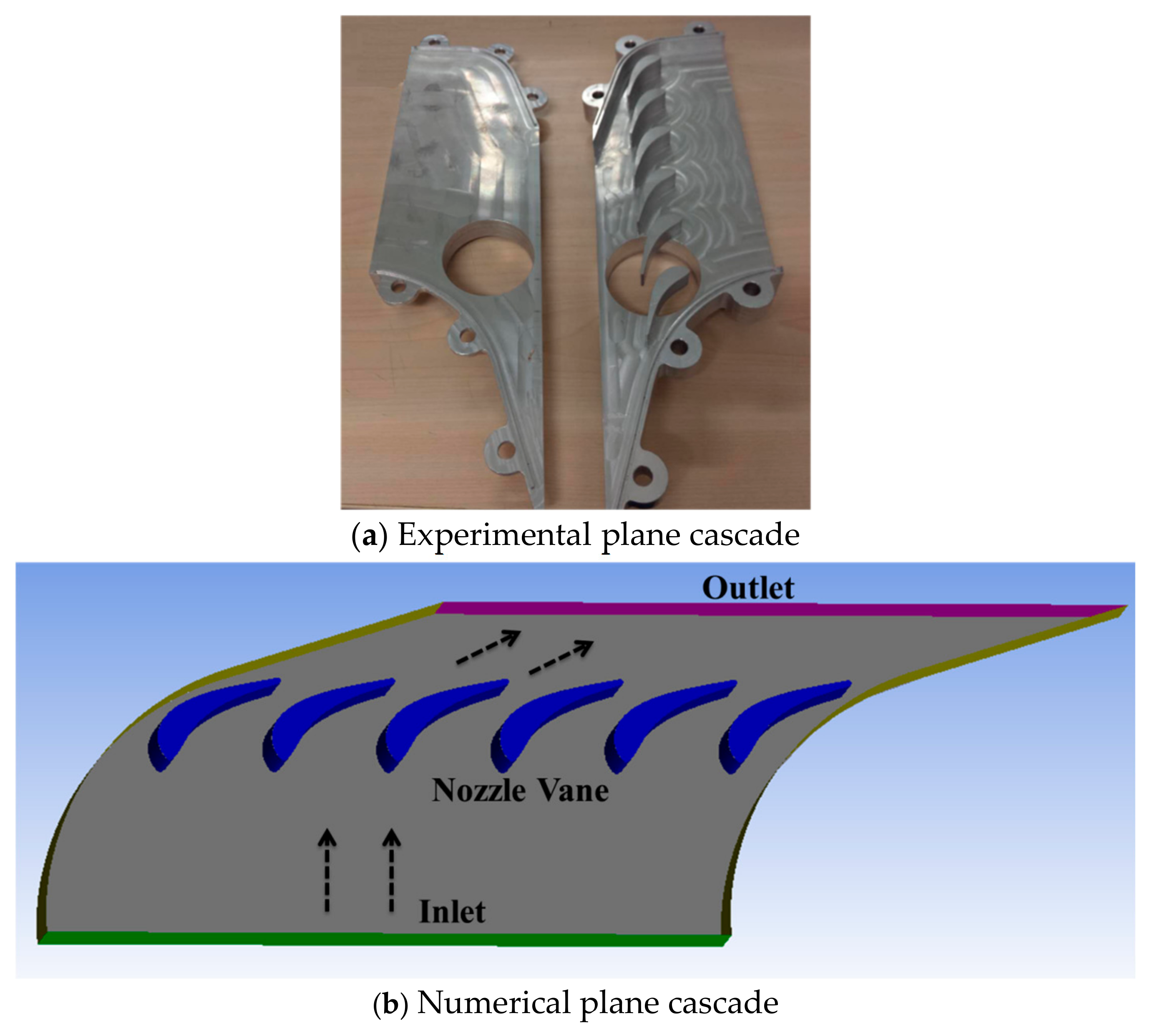
2.1. Geometric Models
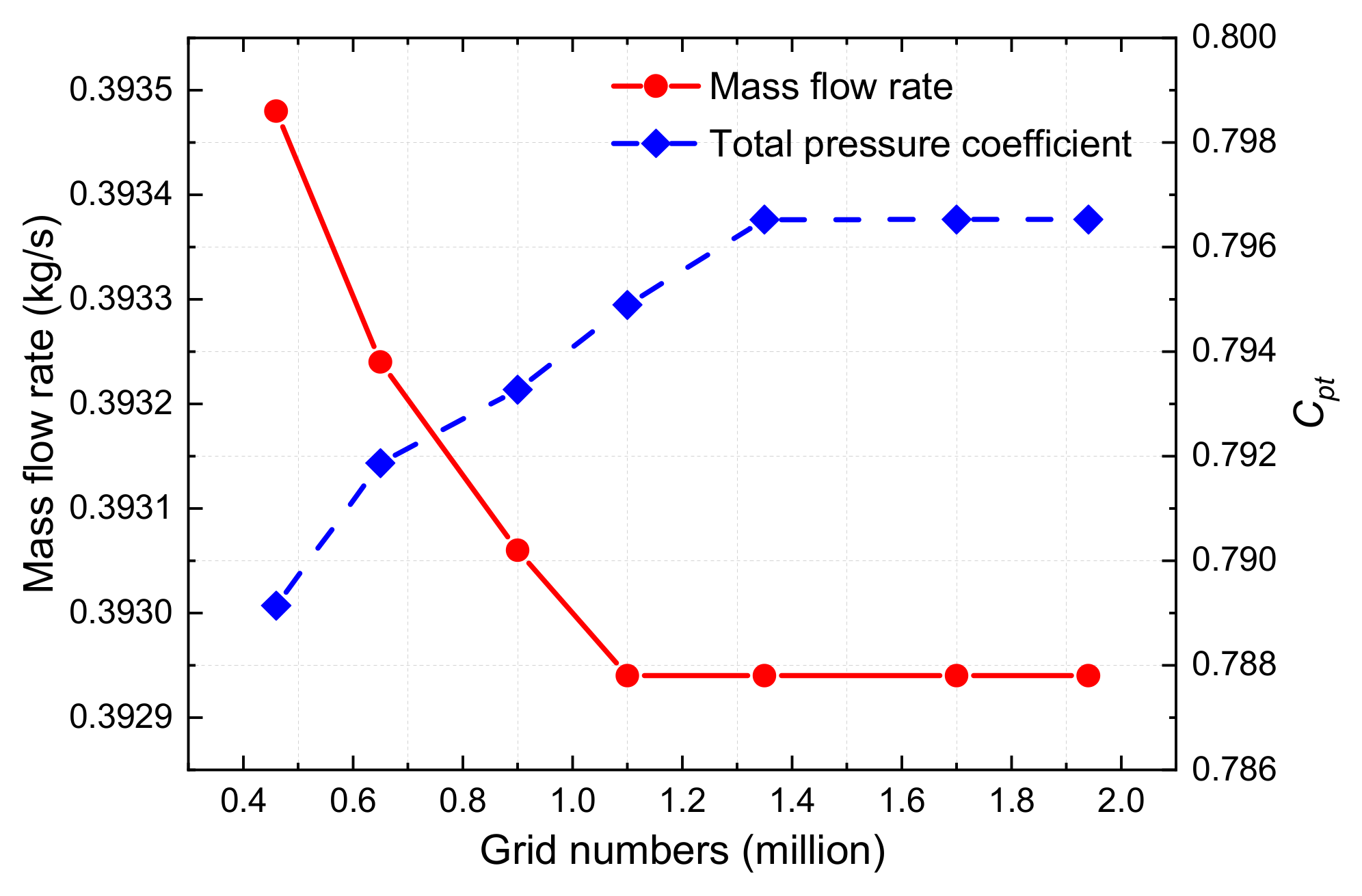
2.2. Numerical Method
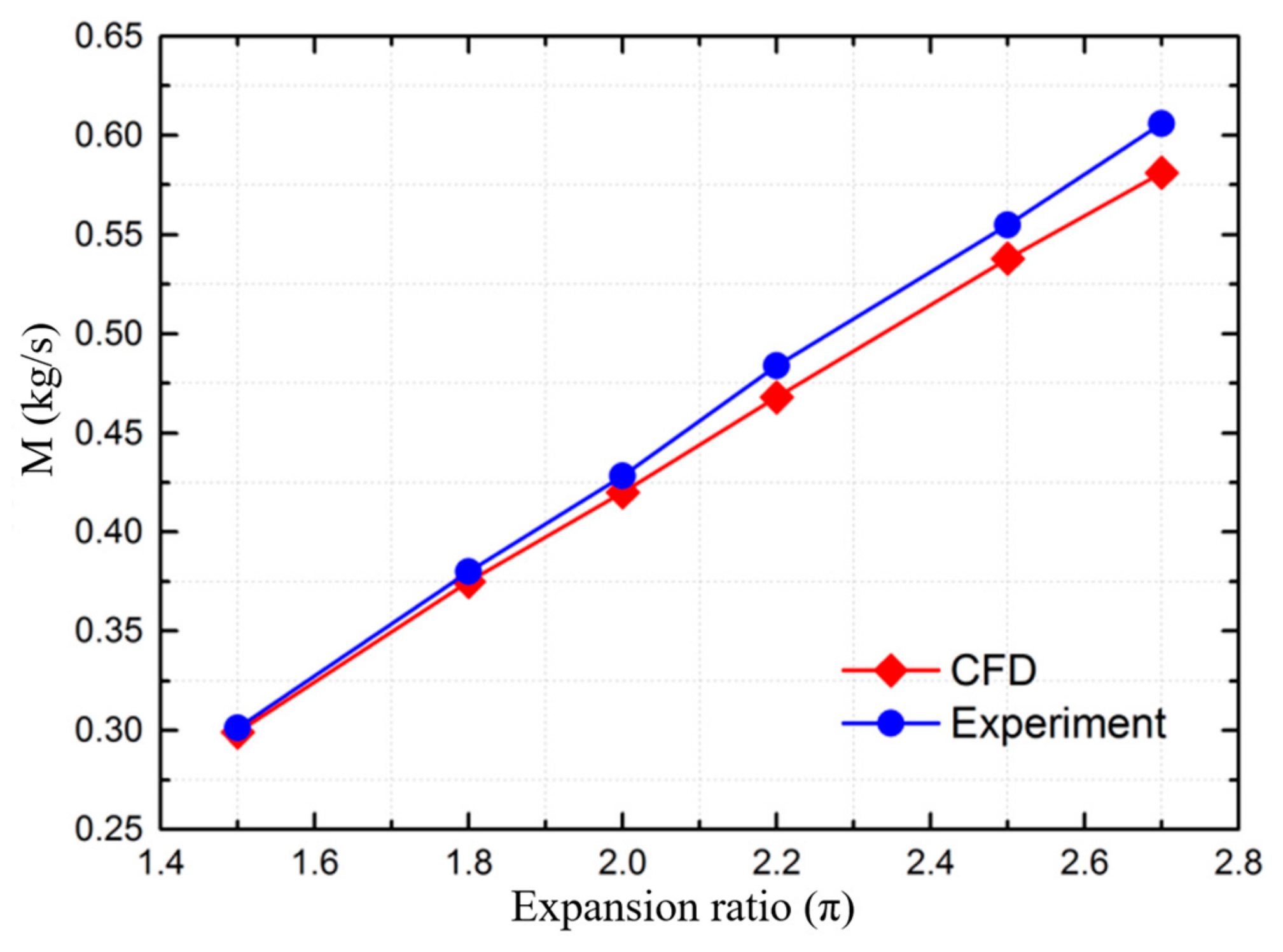
2.3. Boundary Condition and Validation
3. Results and Discussion
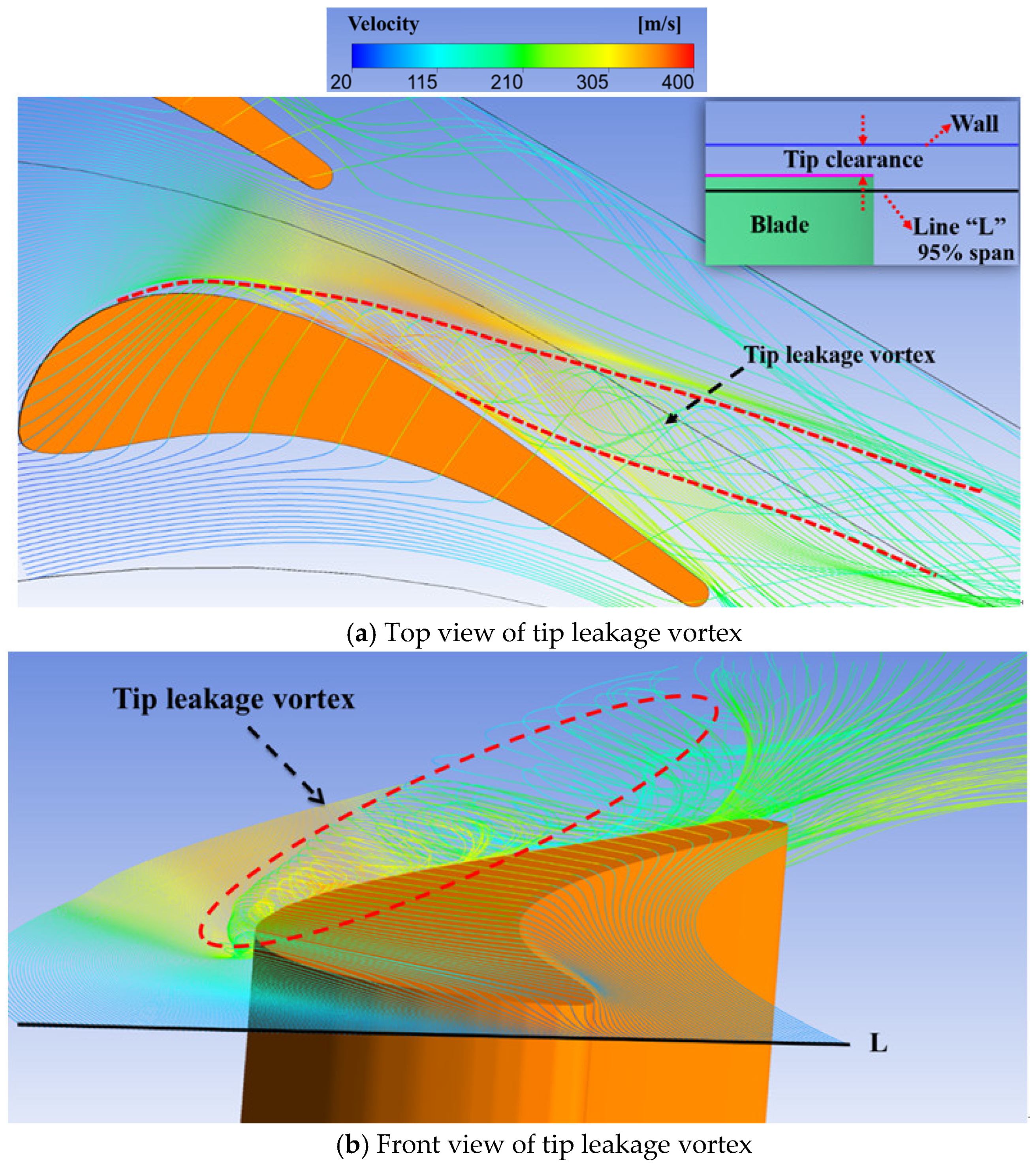
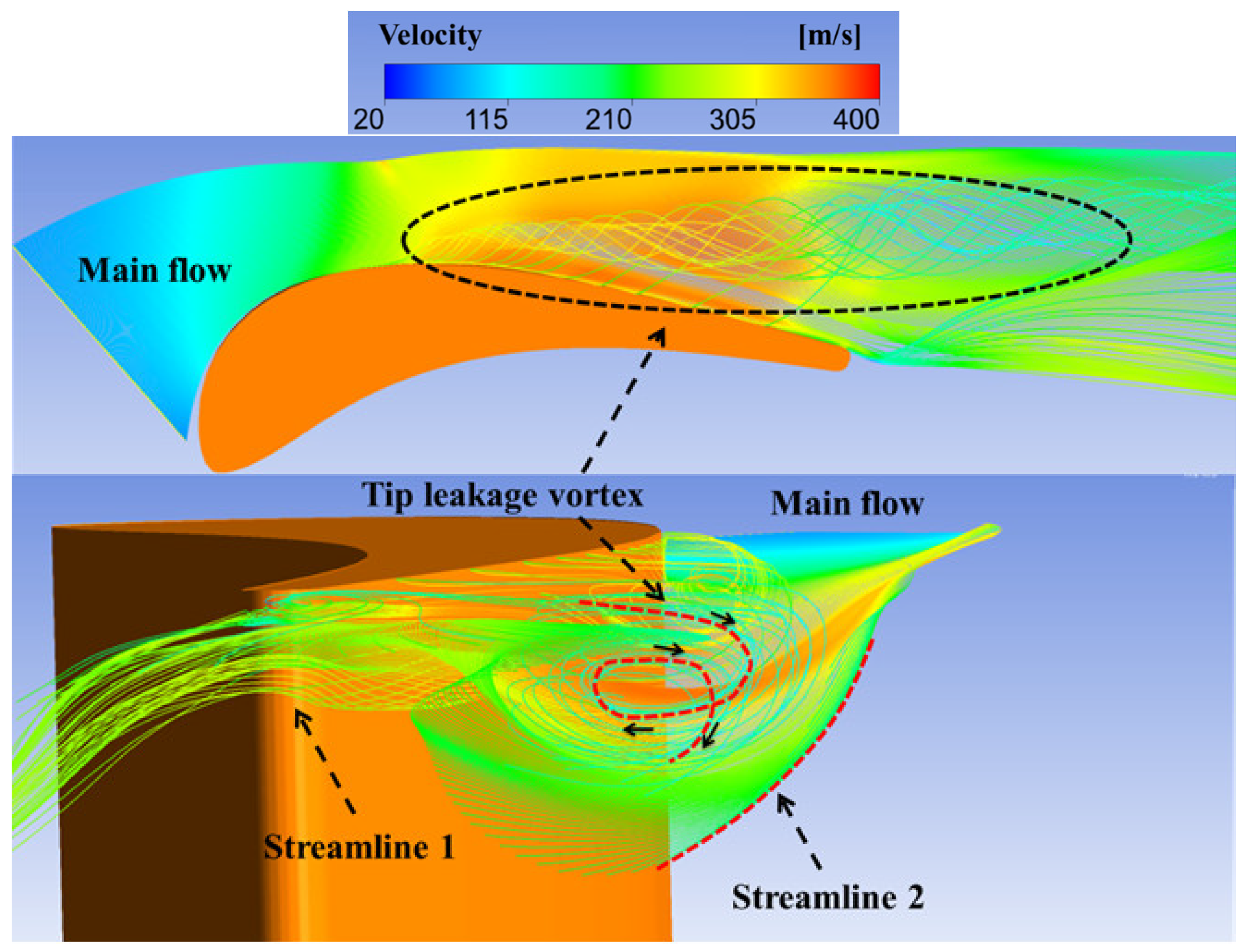
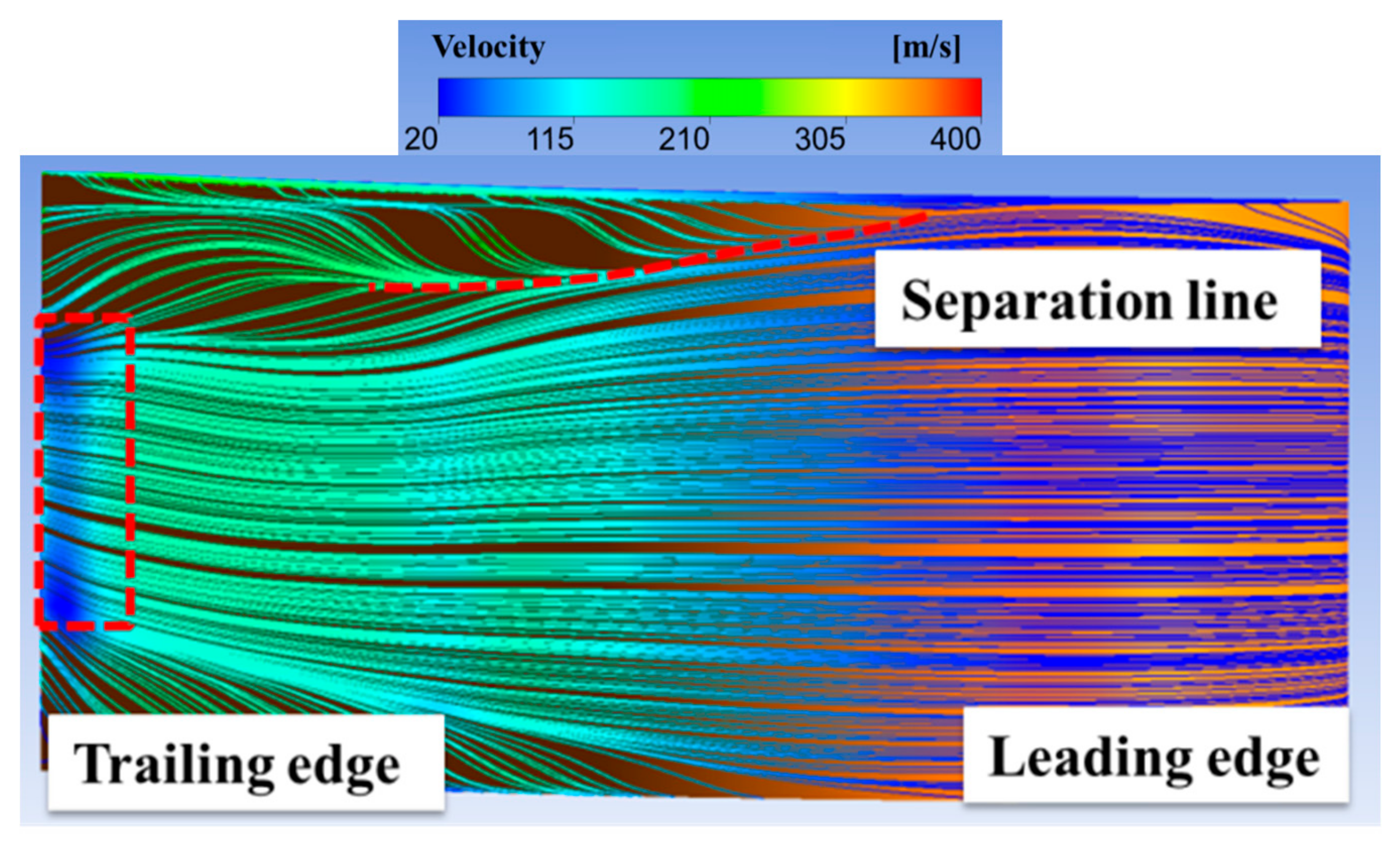
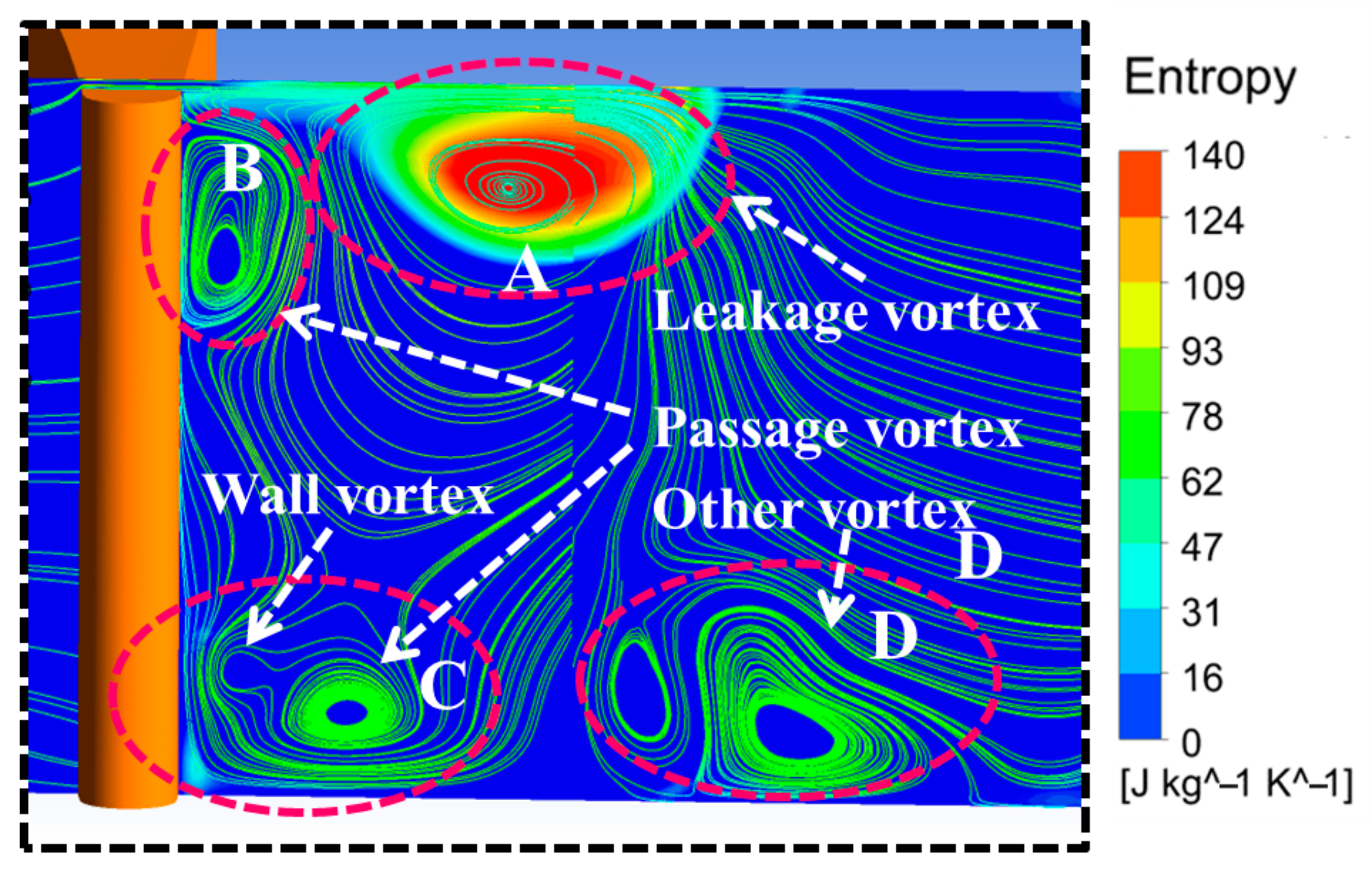
3.1. The Flow Structure of Tip Leakage Flow Without the Effect of Shock Wave
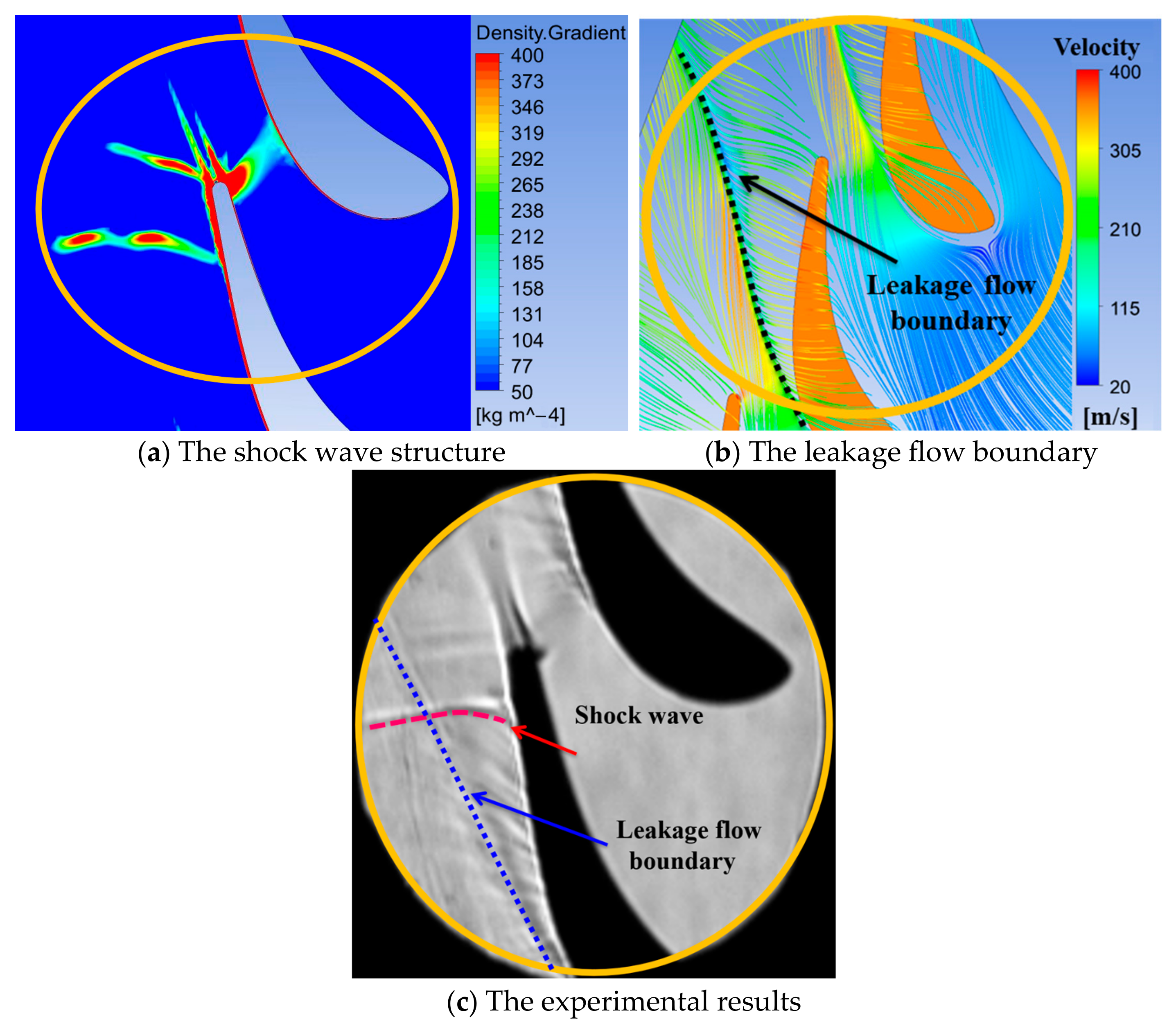
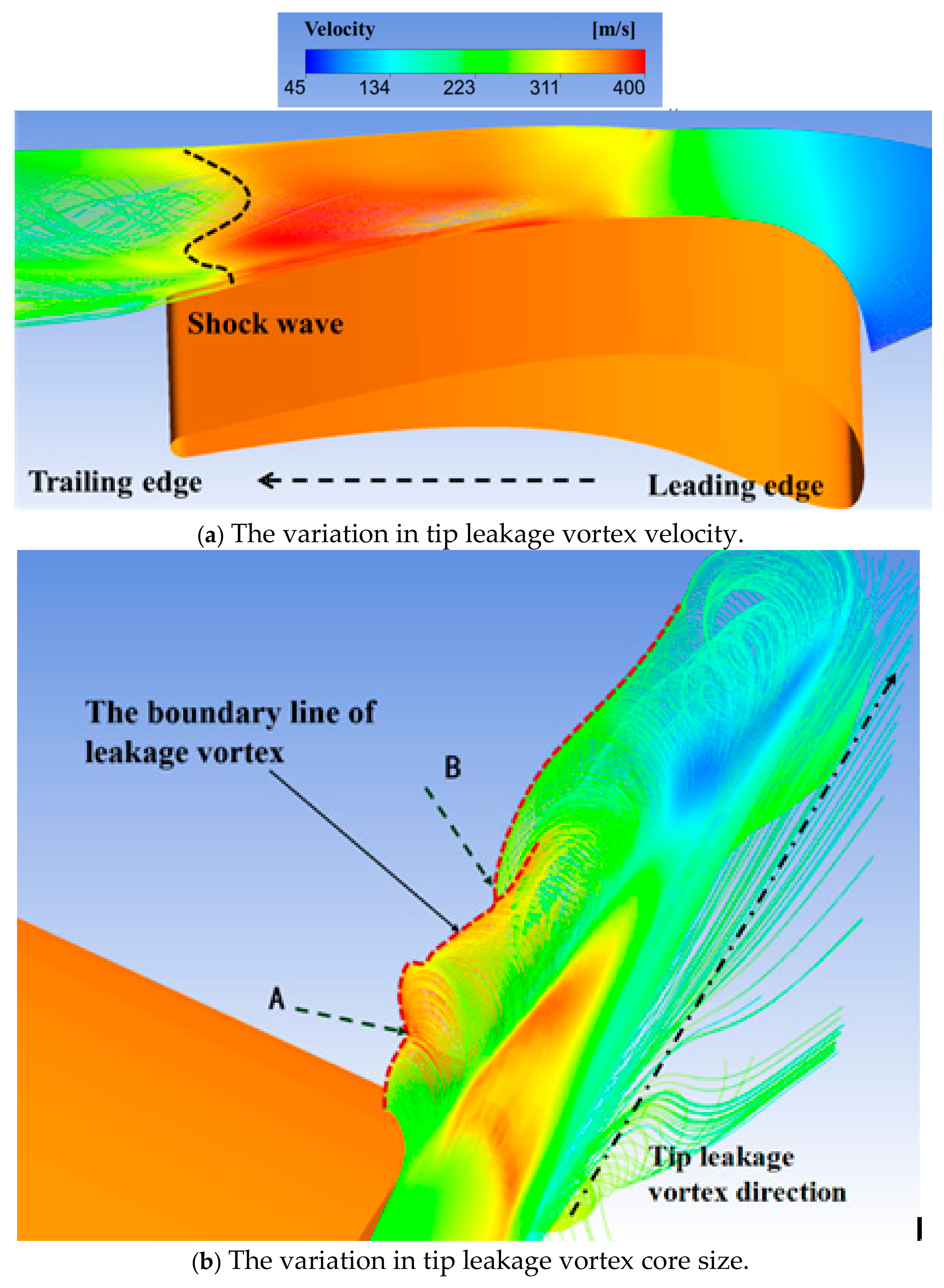
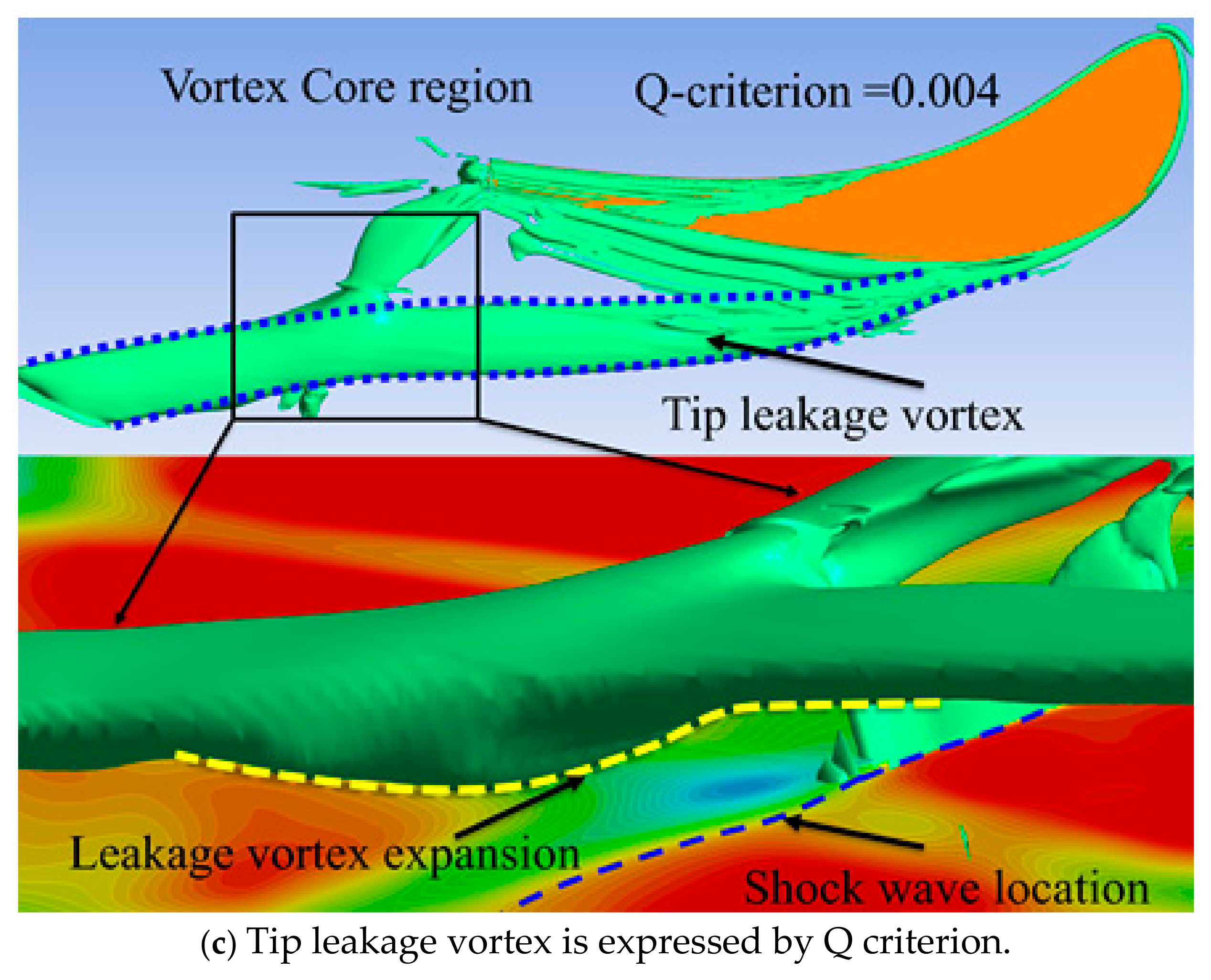
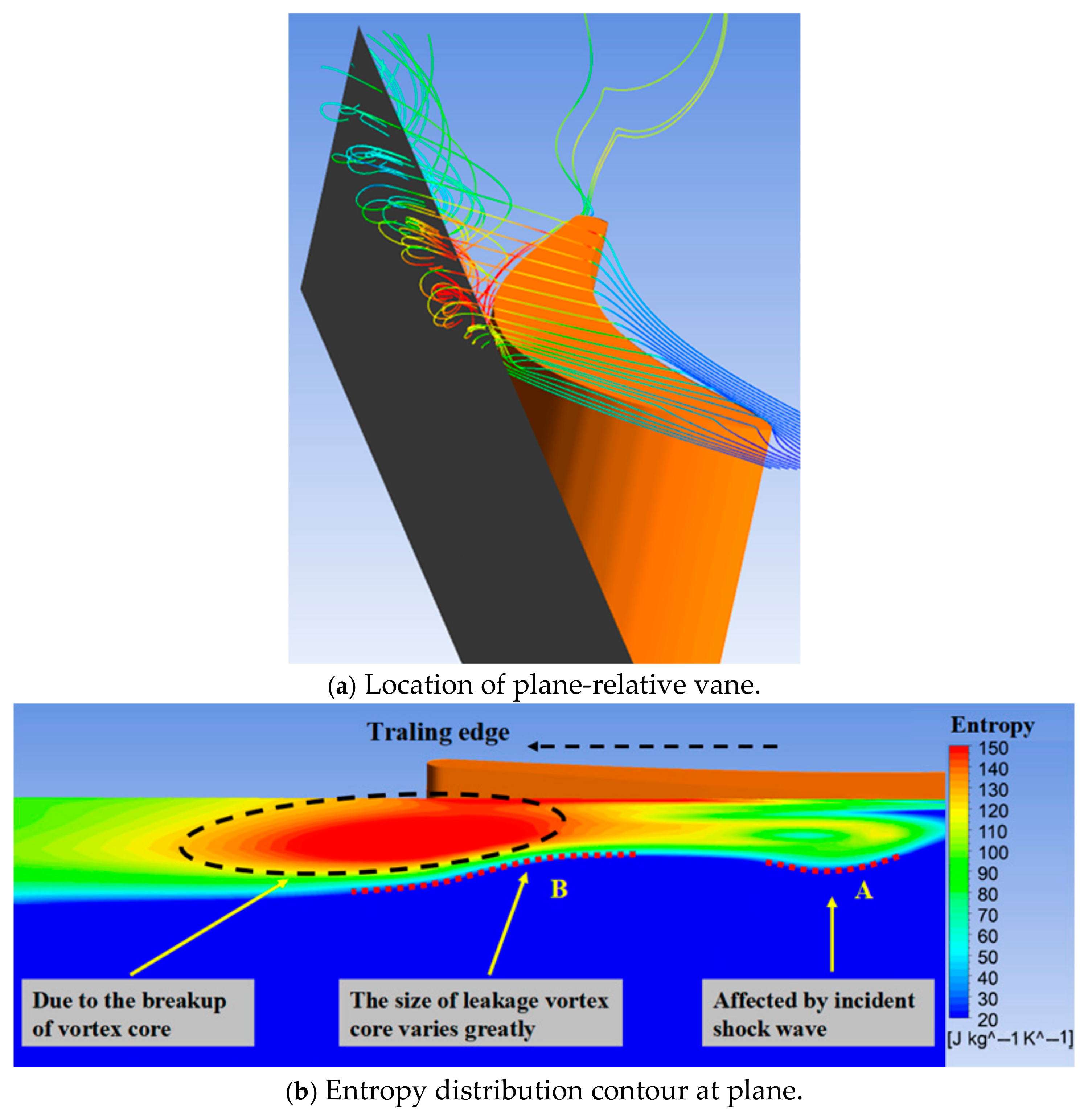
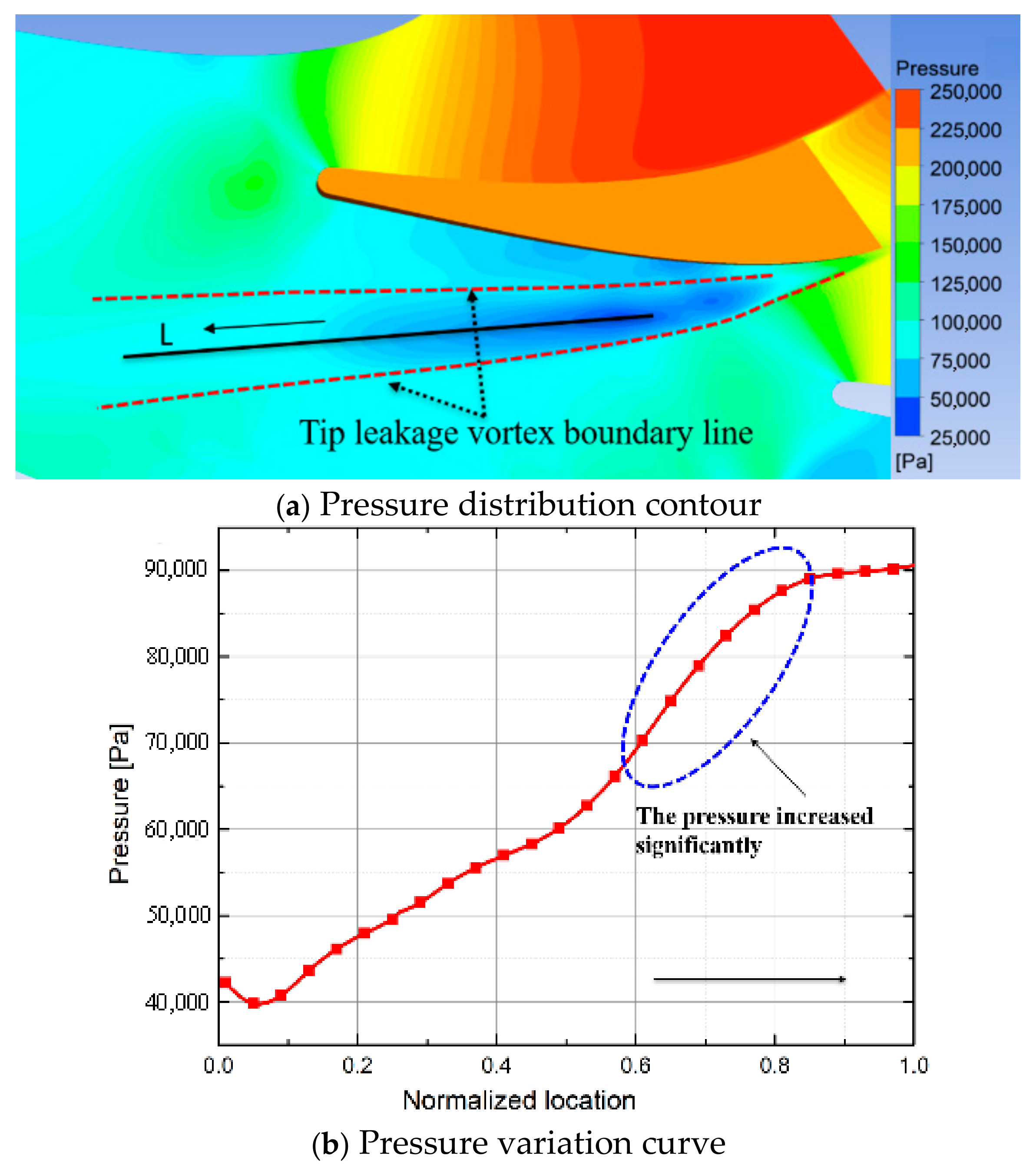
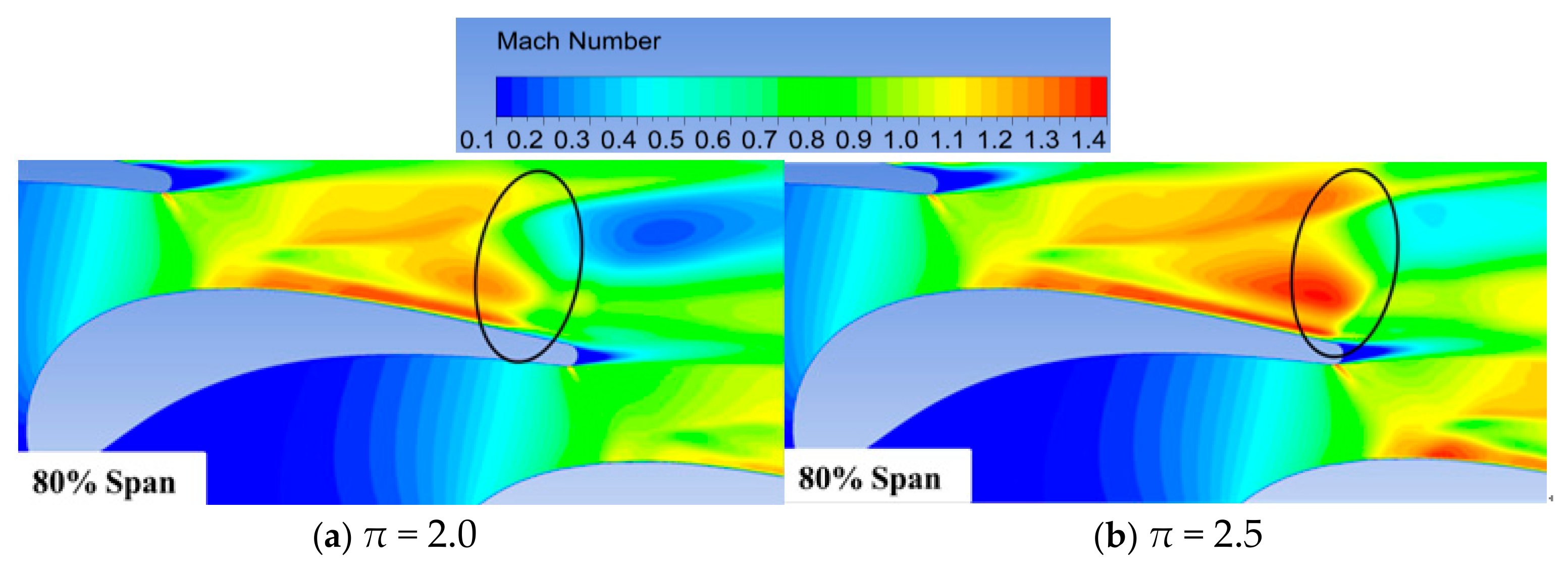
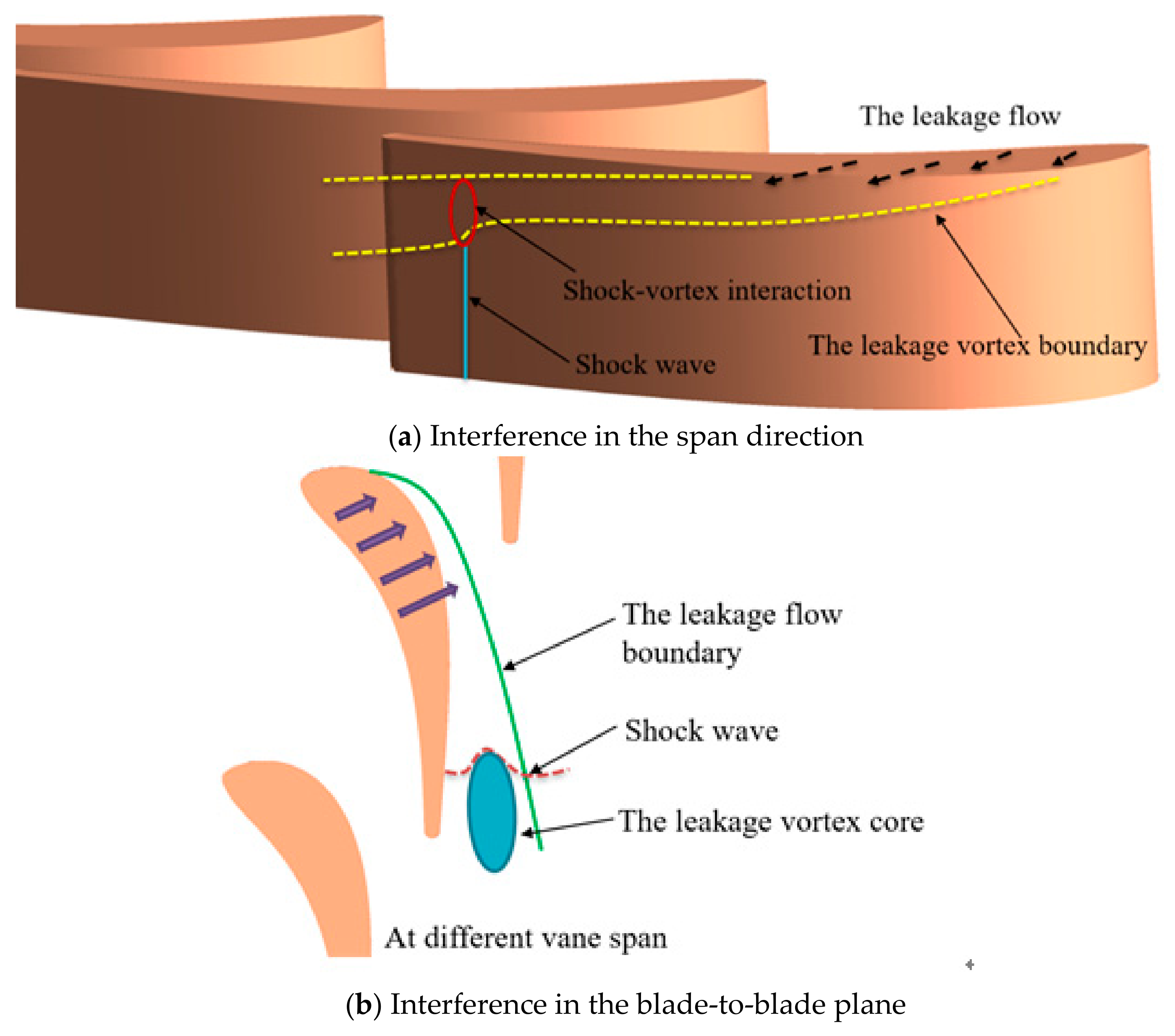
3.2. The Interference of Shock Wave on Tip Leakage Vortex
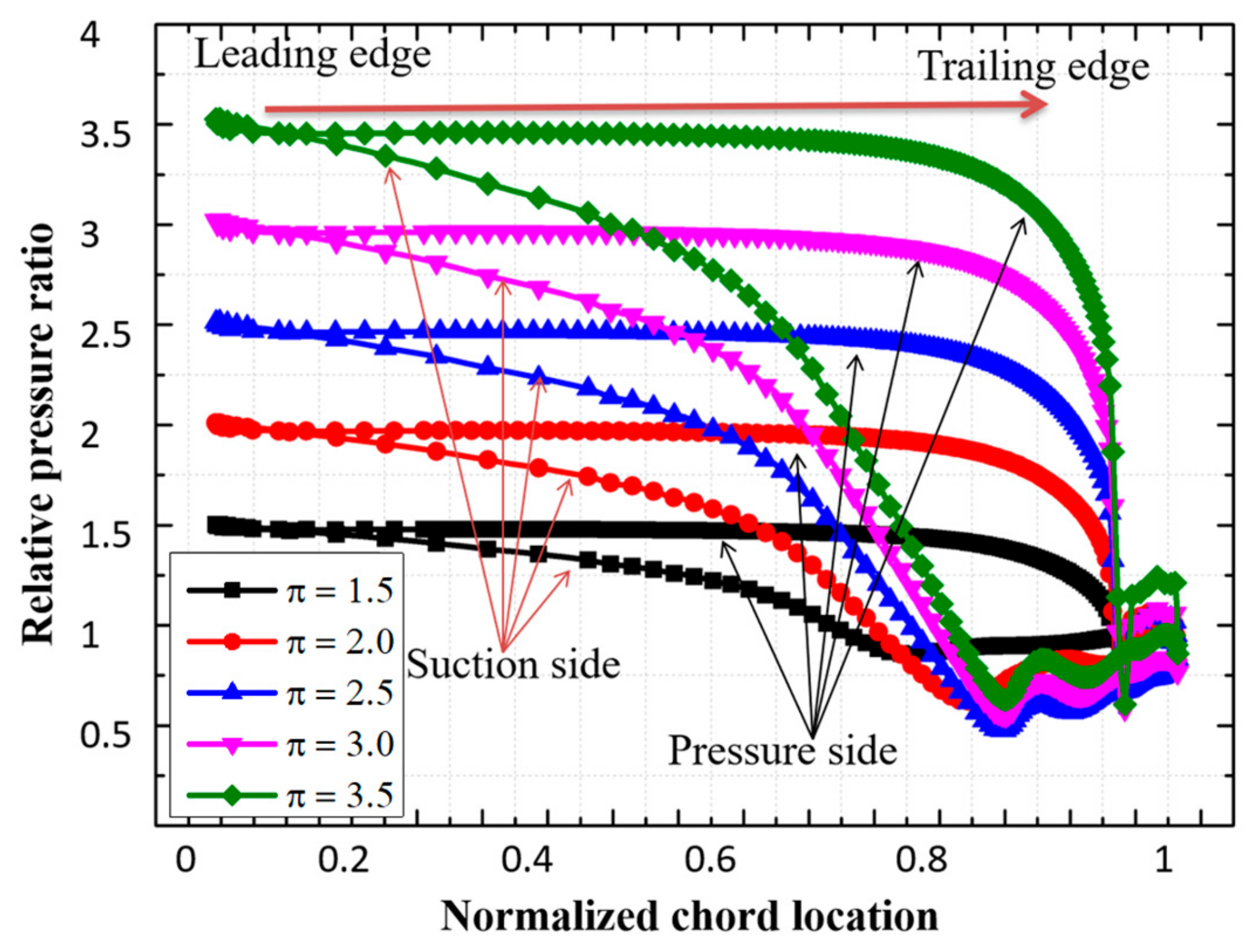
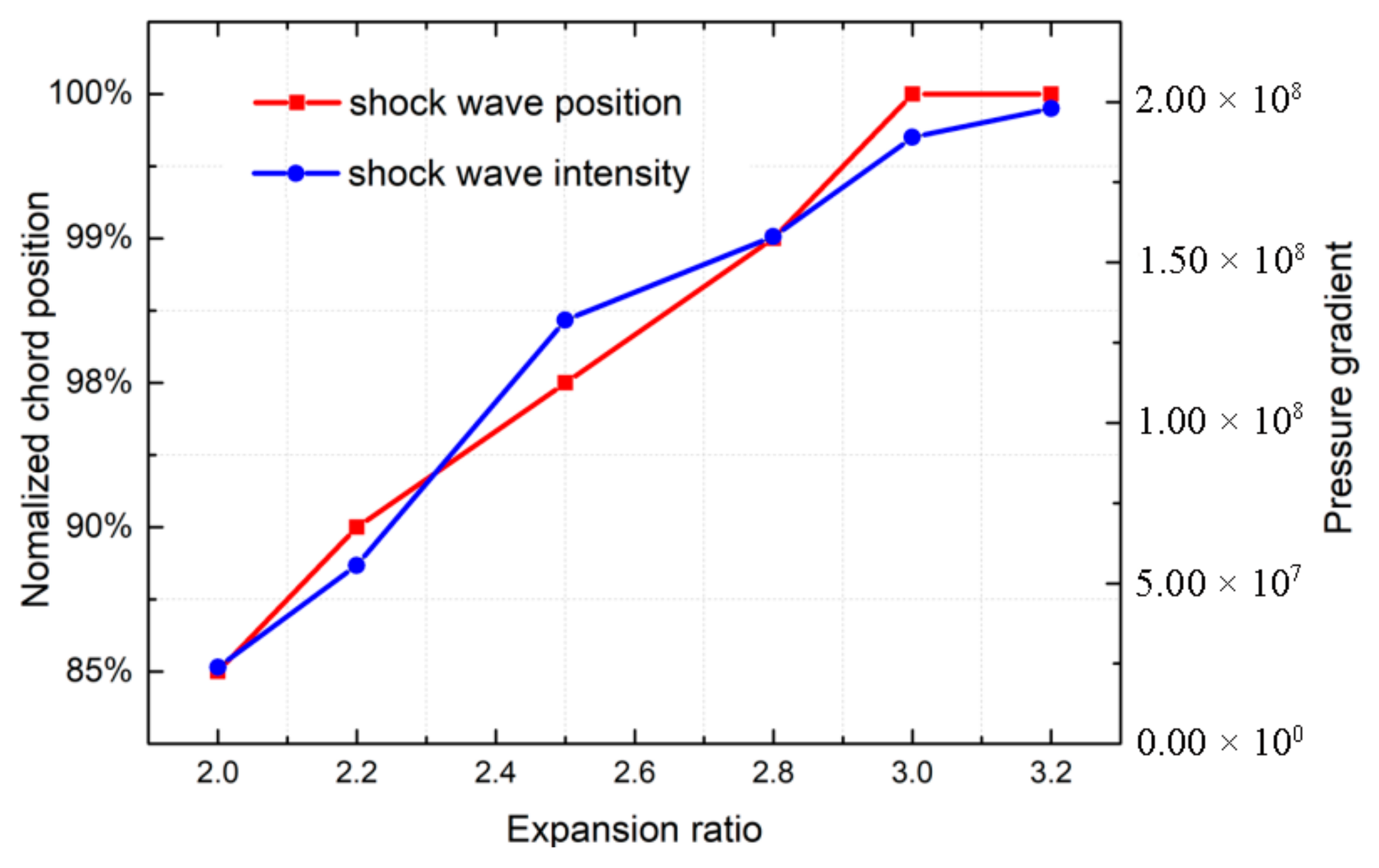
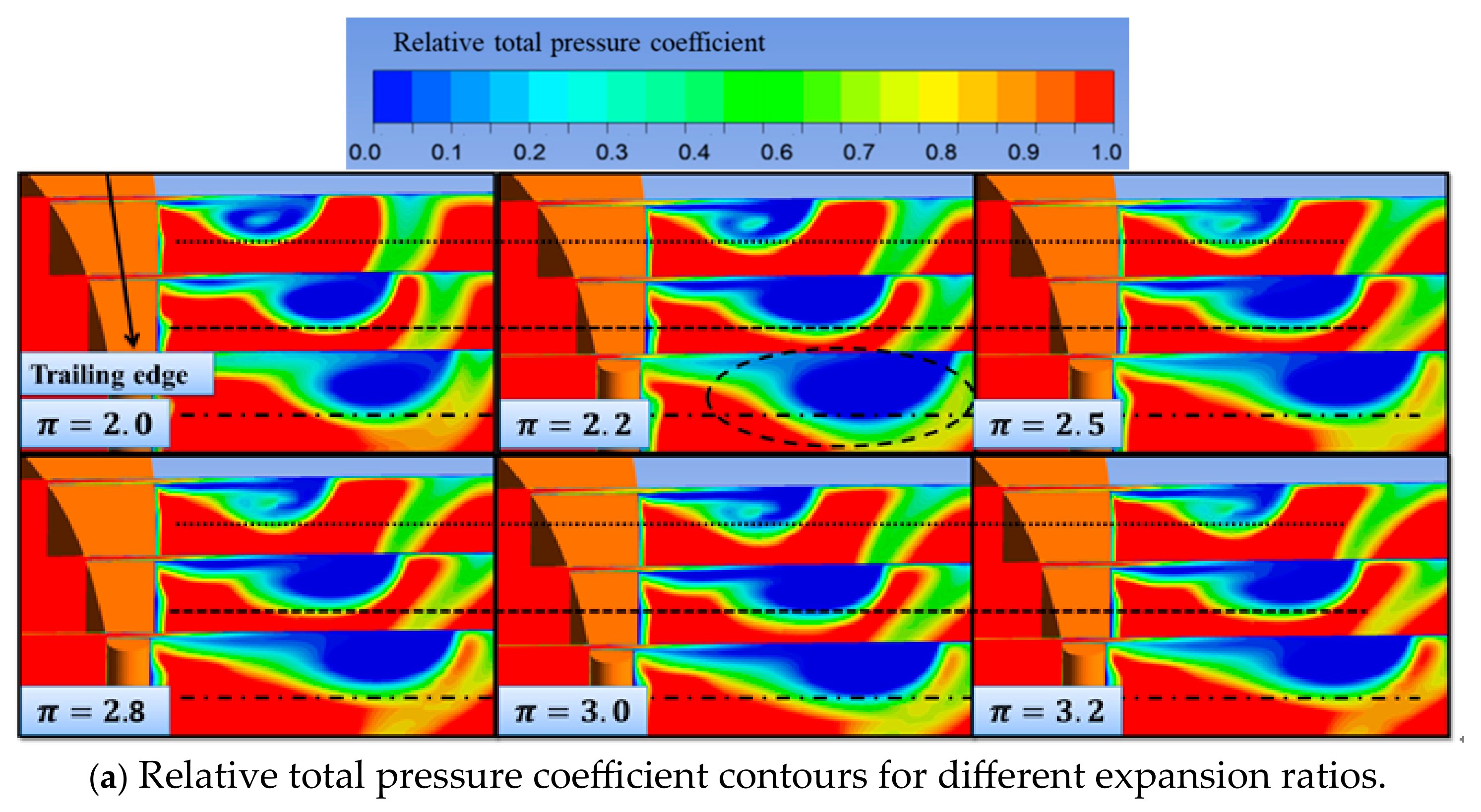
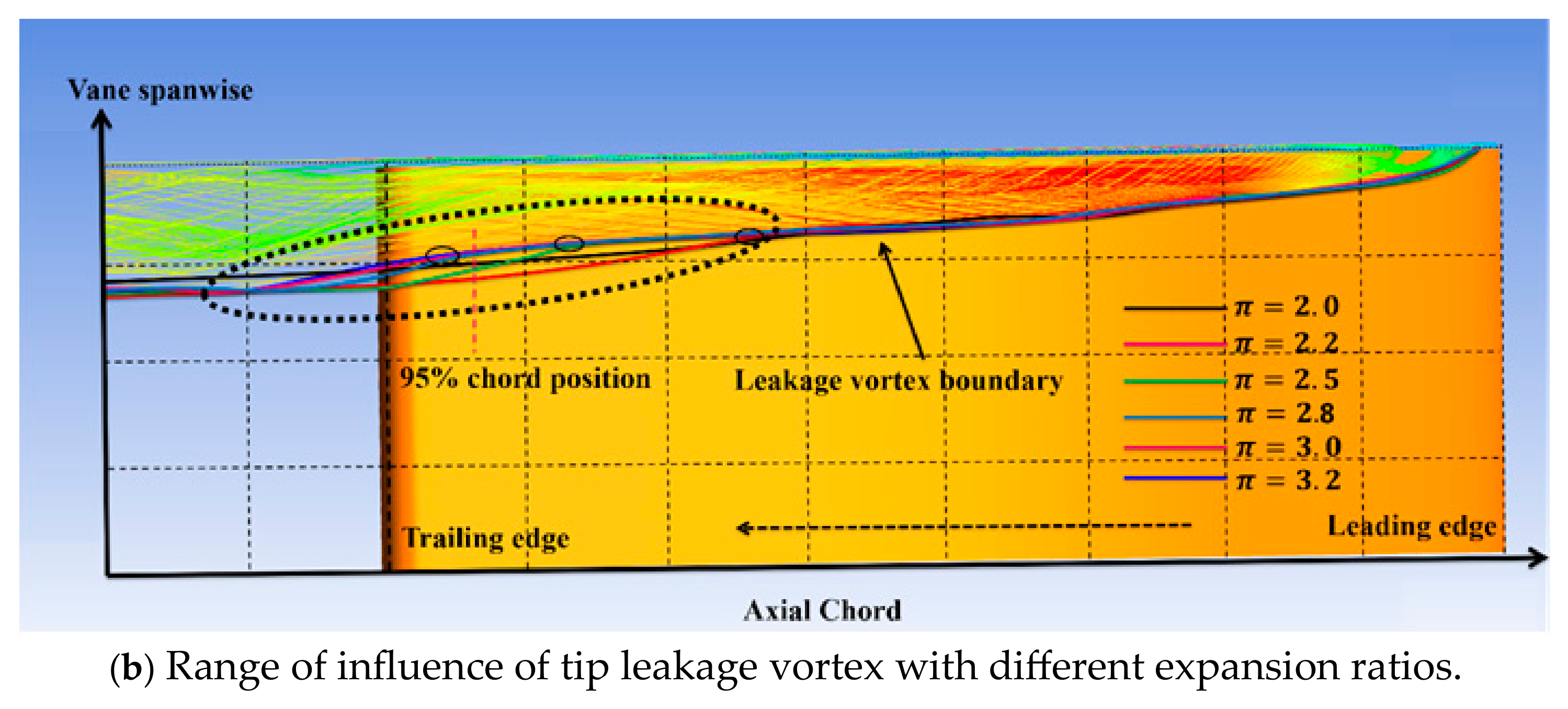
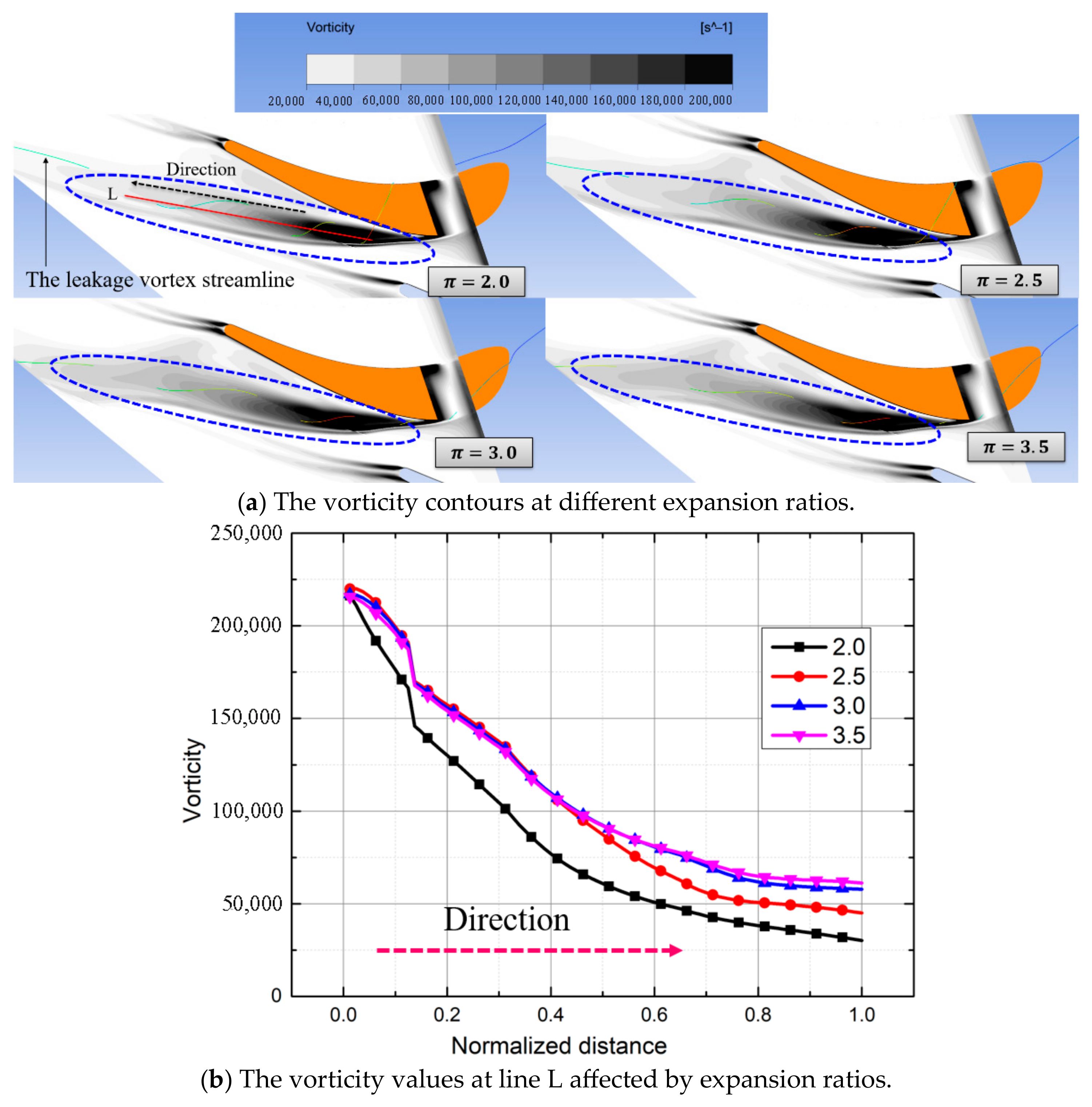
3.3. Influence of Expansion Ratio on the Interference Effect
4. Conclusions
- The mainstream streamline near the suction side is convoluted by the tip leakage vortex at the 40% axial chord location, which enlarges the influence range of the tip leakage vortex. Under the influence of the shock wave, the tip leakage vortex core size was enlarged, and this vortex was finally broken, resulting in a significant increase in flow losses.
- With an increase in the expansion ratio, the expansion position of the tip leakage vortex is shifted to the trailing edge, and the vortex size is first significantly increased and then remains unchanged under the action of the shock wave. In addition, the interference intensity between the shock wave and the leakage vortex increased due to both the intensities of the shock wave and leakage vortex increasing gradually with the increase in the expansion ratio.
- A schematic diagram of the interference model between the shock wave and the leakage vortex is presented. Due to the interference, the shock wave bent against the flow direction, and its strength was weakened by the extrusion of the leakage vortex core. This interference not only leads to significant changes in the flow-field structure but also increases the flow loss. In addition, this interference can lead to an inhomogeneous distribution of the temperature load, which causes thermal stress concentration in the vane and impeller. Therefore, the effect of interference between the shock wave and leakage vortex on the thermal transfer characteristics under different influencing factors should be studied in detail in the future.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| VNT | Variable Nozzle Turbine |
| M | Mass flow ratio |
| RANS | Reynolds-averaged Navier–Stokes |
| Cpt | Total pressure coefficient |
| Expansion ratio | |
| Pt,exit | The total pressure of outlet |
| Ps,exit | The static pressure of outlet |
| Pt,inlet | The total pressure of inlet |
References
- Lauriau, P.-T.; Binder, N.; Cros, S.; Roumeas, M.; Carbonneau, X. Preliminary Design Considerations for Variable Geometry Radial Turbines with Multi-Points Specifications. Int. J. Turbomach. Propuls. Power 2018, 3, 22. [Google Scholar] [CrossRef]
- Novak, O.; Bobcik, M.; Luxa, M.; Fort, J.; Rudas, B.; Synac, J.; Simurda, D.; Furst, J.; Halama, J.; Hric, V.; et al. Turbine Cascades of Last Stage Blades for Wide Range of Operating Conditions. Int. J. Turbomach. Propuls. Power 2019, 4, 33. [Google Scholar] [CrossRef]
- Łuczyński, P.; Giesen, M.; Gier, T.-S.; Wirsum, M. Uncoupled CFD-FEA Methods for the Thermo-Structural Analysis of Turbochargers. Int. J. Turbomach. Propuls. Power 2019, 4, 39. [Google Scholar] [CrossRef]
- Walkingshaw, J.R.; Spence, S.W.T.; Ehrard, J.; Thornhill, D. A Numerical Study of the Flow Fields in a Highly Off-Design Variable Geometry Turbine. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010. [Google Scholar] [CrossRef]
- Putra, M.A.; Joss, F. Investigation of Secondary Flow Behavior in a Radial Turbine Nozzle. J. Turbomach. 2013, 135, 061003. [Google Scholar] [CrossRef]
- Sailesh, C.; Dahlhaug, O.G.; Neopane, H.P. Numerical investigation of the effect of leakage flow through erosion-induced clearance gaps of guide vanes on the performance of Francis turbines. Eng. Appl. Comput. Fluid. Mech. 2018, 12, 662–678. [Google Scholar]
- Zhao, B.; Qi, M.; Zhang, H.; Shi, X. Investigation on effects of shock wave on vortical wake flow in a turbine nozzle cascade. Aerosp. Sci. Technol. 2020, 98, 105690. [Google Scholar] [CrossRef]
- Yamamoto, A.; Minmura, F. Interaction mechanisms between Tip Leakage Flow and the Passage vortex in a linear turbine rotor cascade. J. Turbomach. 1988, 110, 329–338. [Google Scholar] [CrossRef]
- Zhao, B.; Yang, C.; Hu, L.; Sun, H.; Yi, J.; Eric, C.; Shi, X.; Engeda, A. Understanding of the interaction between clearance leakage flow and main passage flow in a VGT turbine. Adv. Mech. Eng. 2015, 7, 652769. [Google Scholar] [CrossRef]
- Roumeas, M.; Cros, S. Aerodynamic Investigation of a Nozzle Clearance Effect on Radial Turbine Performance. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012. [Google Scholar] [CrossRef]
- Li, D.; Lu, H.; Yang, Z.; Pan, T.; Li, Q. Optimization of a transonic axial-flow compressor under inlet total pressure distortion to enhance aerodynamic performance. Eng. Appl. Comput. Fluid. Mech. 2020, 14, 1002–1022. [Google Scholar] [CrossRef]
- Rao, N.M.; Camci, C. Axial Turbine Tip Desensitization by Injection from a Tip Trench: Part 1—Effect of Injection Mass Flow Rate. In Proceedings of the ASME Turbo Expo 2004: Power for Land, Sea, and Air, Vienna, Austria, 14–17 June 2004. [Google Scholar] [CrossRef]
- Rao, N.M.; Camci, C. Axial Turbine Tip Desensitization by Injection from a Tip Trench: Part 2—Leakage Flow Sensitivity to Injection Location. In Proceedings of the ASME Turbo Expo 2004: Power for Land, Sea, and Air, Vienna, Austria, 14–17 June 2004. [Google Scholar] [CrossRef]
- Bindon, J.P. The Measurement and formation of tip clearance loss. J. Turbomach. 1989, 111, 257–263. [Google Scholar] [CrossRef]
- Han, W.J.; Yang, Q.H.; Huang, H.Y.; Jia, L. Topology and Vortex Structures of Turbine Cascade with Different Tip Clearances. Chin. J. Aeronaut. 2002, 15, 18–26. [Google Scholar] [CrossRef]
- Tamaki, H.; Goto, S.; Unno, M.; Iwakami, A. The Effect of Clearance Flow of Variable Area Nozzles on Radial Turbine Performance. In Proceedings of the ASME Turbo Expo 2008: Power for Land, Sea, and Air, Berlin, Germany, 9–13 June 2008. [Google Scholar] [CrossRef]
- Hayami, H.; Senoo, Y.; Hyun, Y.I.; Yamaguchi, M. Effects of tip clearance of nozzle vanes on performance of radial turbine rotor. J. Turbomach. 1990, 112, 58–63. [Google Scholar] [CrossRef]
- Hu, L.; Sun, H.; Yi, J.; Curtis Eric, W.; Morelli, A.; Zhang, J.; Zhao, B.; Yang, C.; Shi, X.; Liu, S. Investigation of Nozzle Clearance Effects on a Radial Turbine: Aerodynamic Performance and Forced Response; SAE Technical Paper; SAE International: Detroit, MI, USA, 2013. [Google Scholar] [CrossRef]
- Rao, N.M.; Camci, C. Visualization of Rotor End-Wall, Tip Clearance, and Outer Casing Surface Flows in a Rotating Axial Turbine Rig. In Proceedings of the ASME Turbo Expo 2005: Power for Land, Sea, and Air, Reno, NV, USA, 6–9 June 2005. [Google Scholar] [CrossRef]
- Tallman, J.; Lakshminarayana, B. Numerical simulation of tip leakage flows in axial flow turbines, with emphasis on flow physics: Part 1: Effect of tip clearance height. J. Turbomach. 2001, 123, 314–323. [Google Scholar] [CrossRef]
- Tallman, J.; Lakshminarayana, B. Numerical simulation of tip leakage flows in axial flow turbines, with emphasis on flow physics: Part II: Effect of out casing relative motion. J. Turbomach. 2001, 123, 324–333. [Google Scholar] [CrossRef]
- Spence, S.W.T.; O’neill, J.W.; Cunningham, G. An investigation of the flow field through a variable geometry turbine stator with Vane end-wall clearance. J. Power Energy 2006, 220, 899–910. [Google Scholar] [CrossRef]
- Hideaki, T.; Masaru, U. Study on flow fields in variable area nozzles for radial turbines. Int. J. Fluid Mach. Syst. 2008, 1, 47–56. [Google Scholar] [CrossRef]
- Kawakubo, T. Unsteady Rotor-Stator Interaction of a Radial-Inflow Turbine with Variable Nozzle Vanes. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010. [Google Scholar] [CrossRef]
- Ramakrishna, P.V.; Govardhan, M. Aerodynamic Performance of Low Speed Axial Flow Compressor Rotors with Sweep and Tip Clearance. Eng. Appl. Comput. Fluid. Mech. 2019, 3, 195–206. [Google Scholar] [CrossRef]
- Guo, Y.; Mao, X.; Gao, L.; Yu, Y. Numerical study on the stability enhancement mechanism of self-recirculating casing treatment in a counter-rotating axial-flow compressor. Eng. Appl. Comput. Fluid. Mech. 2022, 16, 1111–1130. [Google Scholar] [CrossRef]
- Lu, H.; Li, Q. Cantilevered stator hub leakage flow control and loss reduction using non-uniform clearances. Aerosp. Sci. Technol. 2016, 51, 1–10. [Google Scholar] [CrossRef]
- Yang, Y.; Ma, H.; Xiao, A.; Shi, L. Shock wave structures and vortex unsteadiness in the tip region of a transonic turbine cascade under different conditions. Phys. Fluids 2024, 36, 106117. [Google Scholar] [CrossRef]
- Wei, Z.; Ren, G.; Gan, X.; Ni, M.; Chen, W. Influence of shock wave on loss and breakdown of tip-leakage vortex in turbine rotor with varying backpressure. Appl. Sci. 2021, 11, 4991. [Google Scholar] [CrossRef]
- Chen, H. Turbine wheel design for Garrett advanced variable geometry turbines for commercial vehicle applications. In Proceedings of the 8th International Conference of Turbochargers and Turbocharging, London, UK, 12 May 2006; Woodhead Publishing: Cambridge, UK, 2006. [Google Scholar] [CrossRef]
- Saavedra, J.; Paniagua, G.; Saracoglu, B.H. Experimental characterization of the vane heat flux under pulsating trailing-edge blowing. J. Turbomach. 2016, 139, 061004. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, C.; Qi, M.; Zhang, H.; Zhao, B. Shock, Leakage Flow and Wake Interactions in a Radial Turbine with Variable Guide Vanes. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. [Google Scholar] [CrossRef]
- Qi, M.; Lei, X.; Wang, Z.; Ma, C. Investigation on the flow characteristics of a VNT turbine under pulsating flow conditions. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 396–412. [Google Scholar] [CrossRef]
- Lei, X.; Qi, M.; Sun, H.; Hu, L. Study on the Interaction of Clearance Flow and Shock Wave in a Turbine Nozzle; SAE Technical Paper; SAE International: Detroit, MI, USA, 2017. [Google Scholar] [CrossRef]
- Lei, X.; Qi, M.; Sun, H.; Hu, L. Investigation on the Shock Control Using Grooved Surface in a Linear Turbine Nozzle. J. Turbomach. 2017, 139, 121008. [Google Scholar] [CrossRef]
- Lei, X.; Li, R.; Xi, Z.; Yang, C. Study on the effect of nozzle vane and rotor clearance on the performance of variable nozzle turbine. J. Therm. Sci. 2022, 31, 1745–1758. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation Eddy-viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Jun, L.; Sun, H.; Wang, J.; Feng, Z. Numerical investigations on the steady and unsteady leakage flow and heat transfer characteristics of rotor blade squealer tip. J. Therm. Sci. 2011, 20, 304–311. [Google Scholar] [CrossRef]
- Gao, J.; Zheng, Q.; Niu, X.; Yue, G. Aerothermal characteristics of a transonic tip flow in a turbine cascade with tip clearance variations. Appl. Therm. Eng. 2016, 107, 271–283. [Google Scholar] [CrossRef]

| Parameters | Value |
|---|---|
| Cascade solidity | 1.25 |
| Cascade aspect ratio (The ratio of span to chord) | 0.3 |
| Axial chord (mm) | 50 |
| Throat opening (mm) | 9.6 |
| Inlet vane angle (degree) | 0 |
| Outlet vane angle (degree) | 77 |
| Designed attack angle (degree) | 0 |
| Setup angle (degree) | 34.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the EUROTURBO. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Lei, X.; Luo, Q.; Zhang, H. Interference Effect of Shock Wave on Tip Leakage Vortex in a Transonic Variable Nozzle Turbine. Int. J. Turbomach. Propuls. Power 2025, 10, 49. https://doi.org/10.3390/ijtpp10040049
Lei X, Luo Q, Zhang H. Interference Effect of Shock Wave on Tip Leakage Vortex in a Transonic Variable Nozzle Turbine. International Journal of Turbomachinery, Propulsion and Power. 2025; 10(4):49. https://doi.org/10.3390/ijtpp10040049
Chicago/Turabian StyleLei, Xinguo, Qin Luo, and Hanzhi Zhang. 2025. "Interference Effect of Shock Wave on Tip Leakage Vortex in a Transonic Variable Nozzle Turbine" International Journal of Turbomachinery, Propulsion and Power 10, no. 4: 49. https://doi.org/10.3390/ijtpp10040049
APA StyleLei, X., Luo, Q., & Zhang, H. (2025). Interference Effect of Shock Wave on Tip Leakage Vortex in a Transonic Variable Nozzle Turbine. International Journal of Turbomachinery, Propulsion and Power, 10(4), 49. https://doi.org/10.3390/ijtpp10040049




