Heat Load Development and Heat Map Sensitivity Analysis for Civil Aero-Engines
Abstract
1. Introduction
2. Methodology and Approach
2.1. Aero-Engine Heat Sources and Sinks
2.2. Modeling Procedure
3. Results
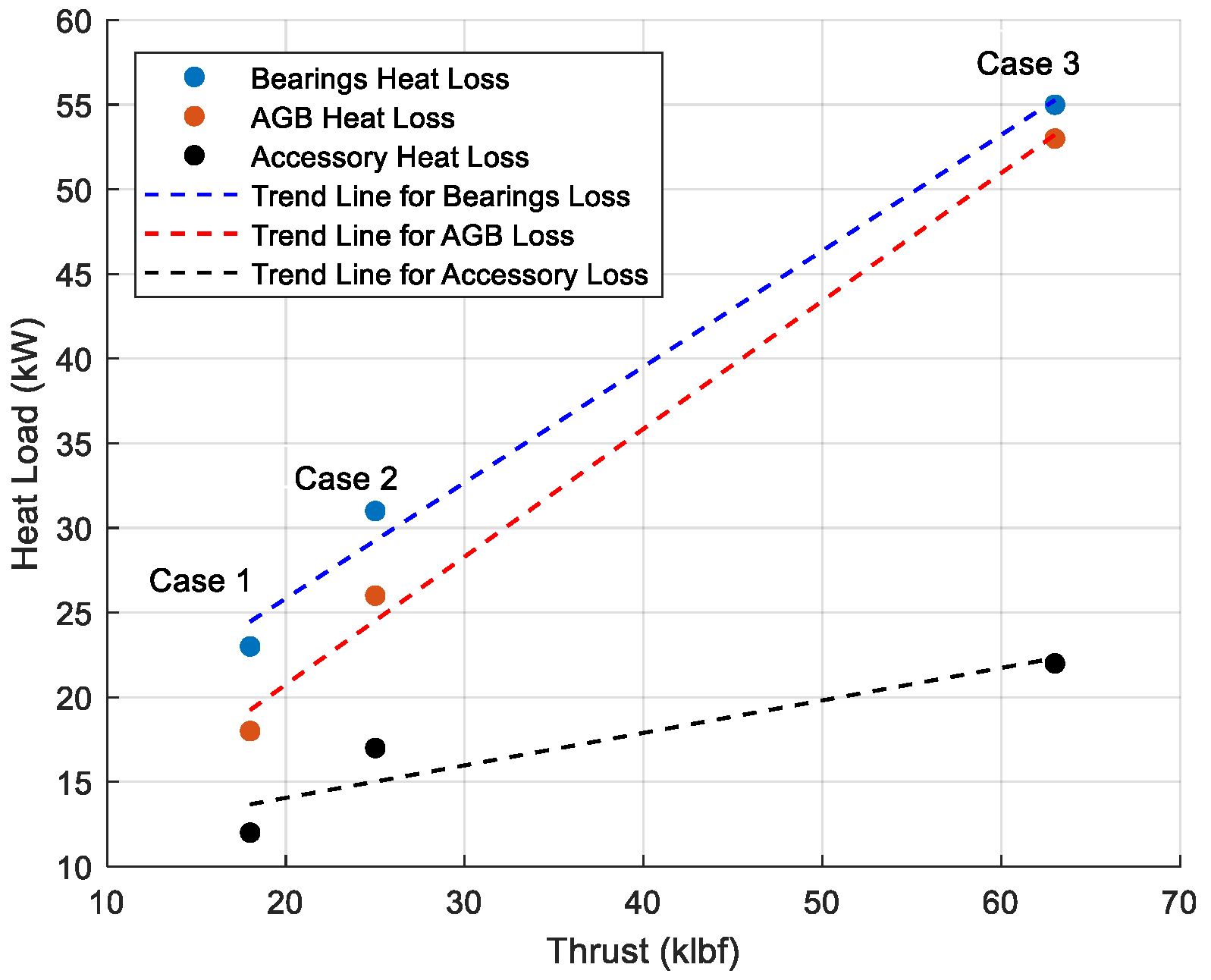
- The first case is a CFM-56 size engine with a take-off thrust of 18 klbf (80 kN). The simulation results obtained by Cranfield’s in-house developed toolbox show that 53 kW of heat load should be transferred to the engine oil at take-off condition, including 18 kW from the accessory gearbox, 23 kW from the engine shaft bearings, and another 12 kW from the engine pumps, seals, etc. The validity of the results is verified through the MTU paper, which validated the heat loads of different components with experimental data (Figure 3 in reference [27]).
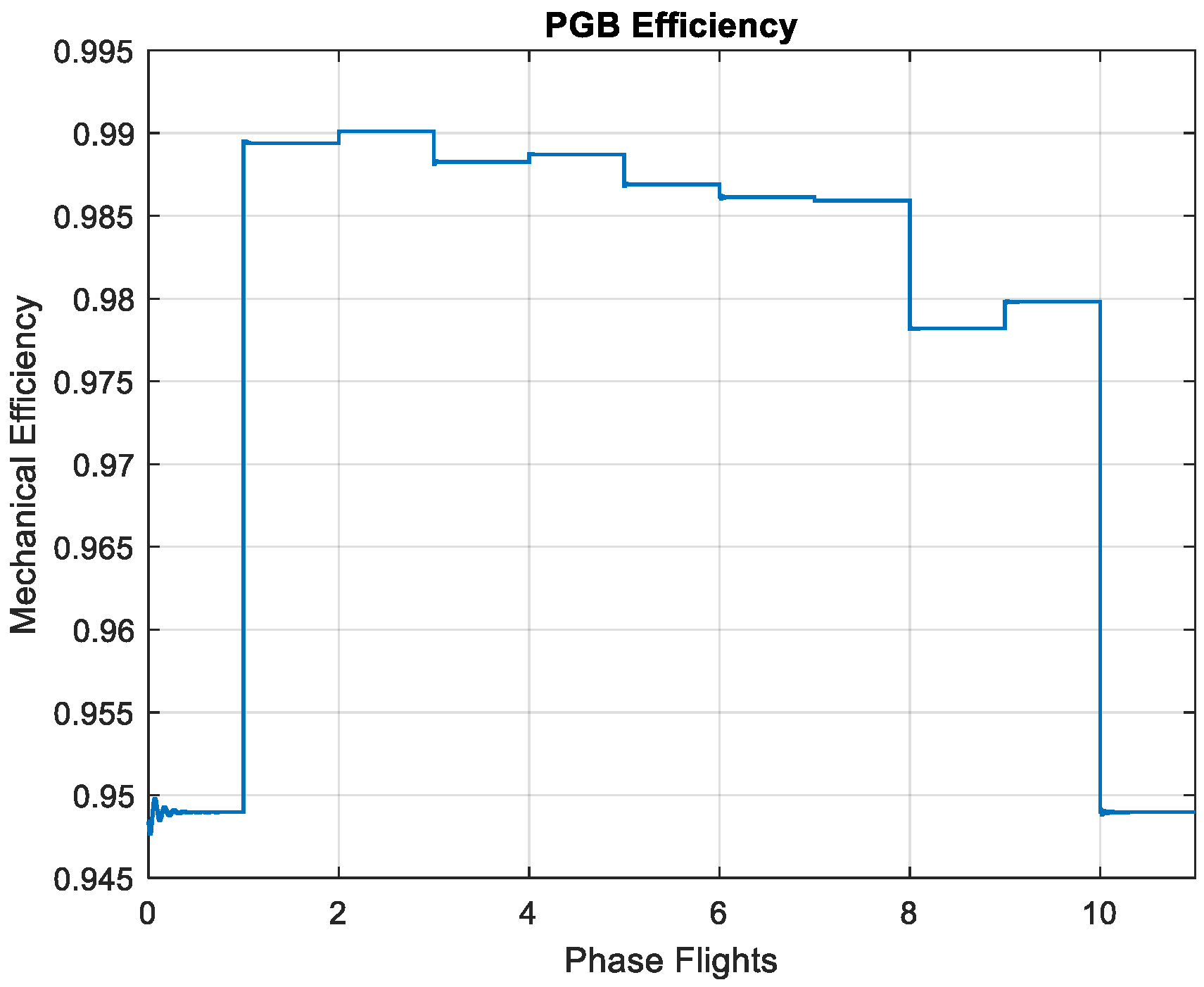
- The second case study demonstrated that increasing the engine size from a conventional turbofan to a geared turbofan, such as the PW1100G with a take-off thrust of 112 kN (25 klbf), dramatically increases the total heat to oil. The physics-based model developed for this engine’s TMS system showed that the power gearbox is the primary source of heat loads in geared turbofan engines. Despite the high efficiency of planetary gearboxes (above 97%), significant heat is generated due to the large amount of power transferred by this component [17].
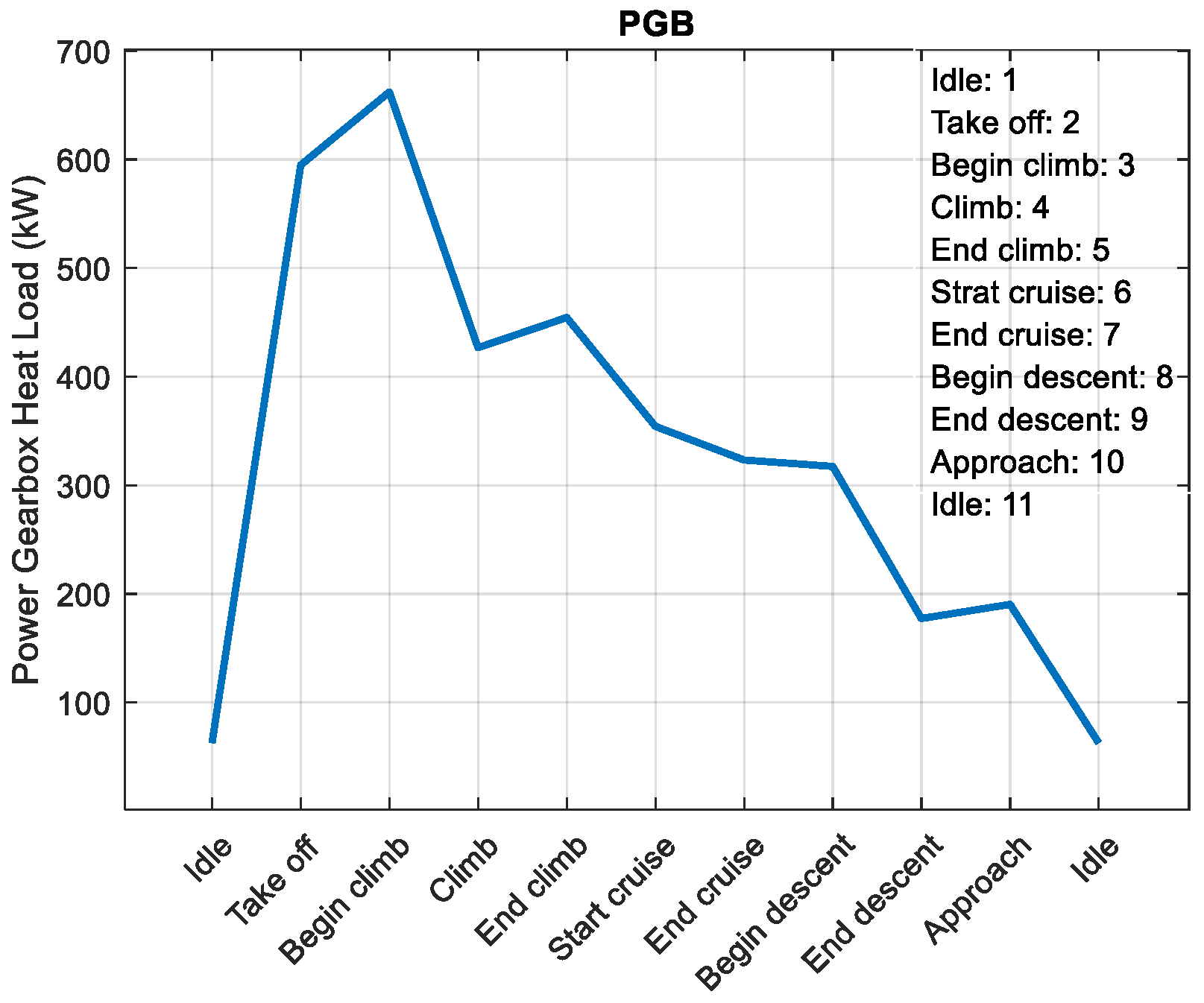
- For the third case study, one version of the UltraFan engine, an Ultra-High Bypass Turbofan with a take-off thrust of 280 kN, is simulated. The results showed that even with state-of-the-art PGB technology boasting over 99% efficiency, 592 kW of heat load is generated during take-off (the engine’s low-pressure shaft power is around 64 MW [28]). Additionally, the heat load values in the bearings and accessory gearbox increase proportionally to the engine’s thrust.
3.1. Sensitivity Analysis of Heat Sources
- Overall, increasing the thrust leads to higher heat loads.
- In low thrust values, the level of thrust (in klbf) is well correlated with the value of AGB heat load (case studies 1 and 2).
- By increasing the thrust value, the correlation is more obvious with the bearing heat loads rather than those of the accessories.
- The slope of the bearing heat load values is slightly higher than those of the AGB in the low thrust ranges. However, at higher thrust levels, the slope for AGBs is higher than that of the bearing heat load.
- The thermal management system architecture design procedure is more sensitive to bearings and AGB characteristics than to accessories characteristics. This should be taken into account in the TMS design and development steps as well as in the definition of degradation management strategies.
- As a rule of thumb, a linear relationship could be fitted to the values of heat loads generated in bearings and the accessory gearbox as a function of thrust value. A more accurate curve-fitting procedure could be carried out by adding more case studies and experimental data.
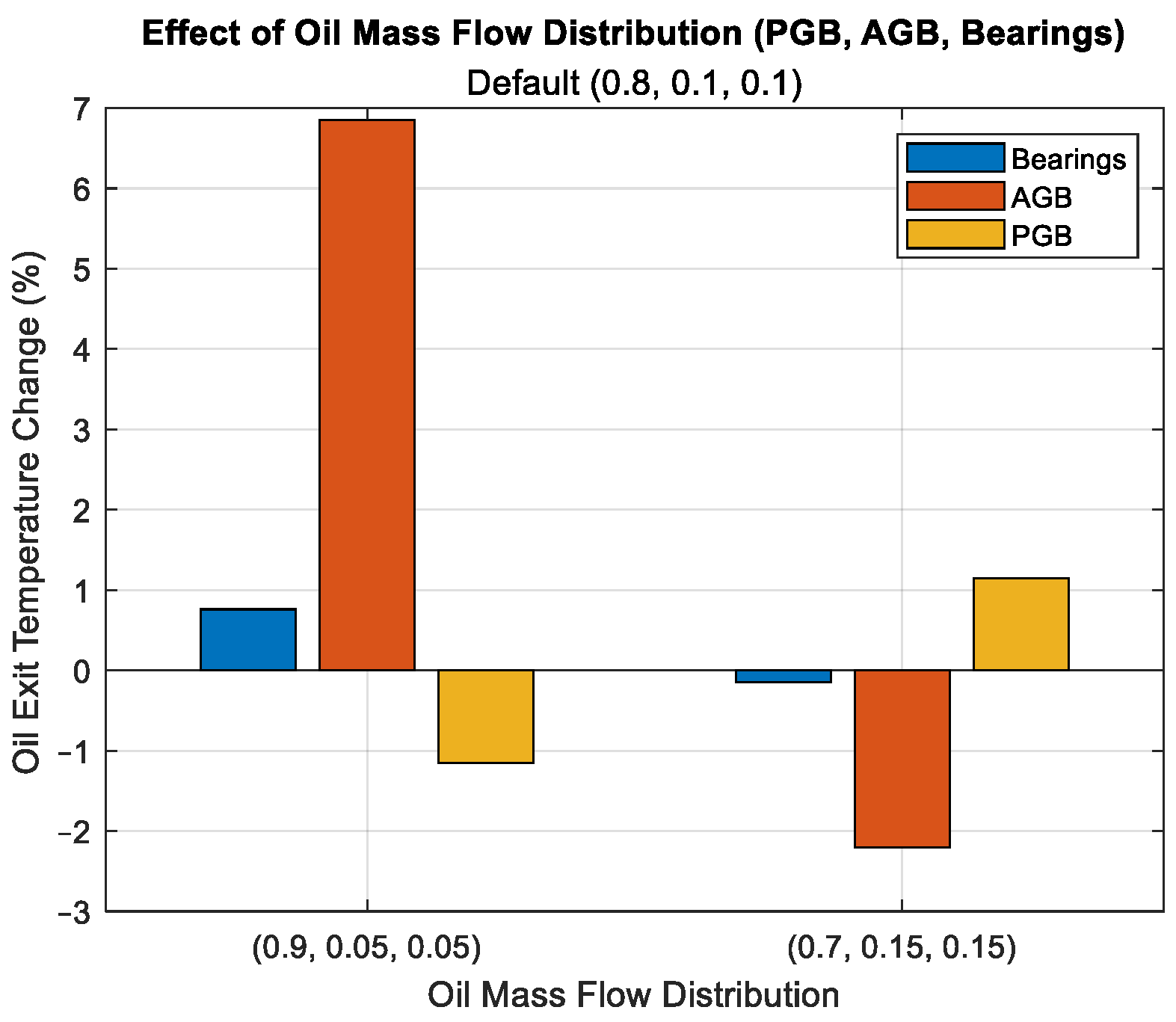
3.2. Sensitivity Analysis of Heat Sinks
- Scenario I: Increase/decrease the oil mass flow rate in all components (changing the size of the oil pump and the oil tanks accordingly).
- Scenario II: Changing the distribution of the oil flow rate in the components (in this scenario, the size of the oil pump and other TMS components is fixed, but the characteristics of the 3-way valve that distributes the oil flow rate to the bearing, AGB, and PGB compartments will be changed).
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Unit | Meaning |
| Ai | m2 | Immersion surface area |
| AOHE | Air Oil Heat Exchanger | |
| b | m | Tooth face width |
| d | mm | Bearing bore diameter |
| D | m | Diameter of the rotating element |
| D1 | inch | Bearing bore diameter |
| D2 | inch | Outside diameter |
| DI | m | Planet bearing bore diameter |
| di | m | Shaft diameter |
| dm | mm | Pitch circle diameter |
| f | - | Friction coefficient |
| f0 | - | Bearing coefficient of loss |
| FA | N | Axial load |
| fe | - | External mesh coefficient of friction |
| FOHE | Fuel Oil Heat Exchanger | |
| Fr | - | Froude number |
| FR | N | Radial load |
| h | m | Immersion depth |
| HEX | Heat exchanger | |
| Hν | - | Gear loss factor |
| M | N.mm | Friction moment |
| M0 | Nm | No-load torque planet bearing |
| Me | - | External mesh mechanical advantage |
| n | rpm | Shaft rotational speed |
| nB | rpm | Planet bearing rotational speed |
| P | N | Load of the bearing |
| PBL | kW | Bearing power loss |
| Pin | kW | Power input |
| PLB | kW | Power loss in bearings |
| PLB0 | kW | Bearing churning loss |
| PLG | kW | Power loss in meshing gear |
| PLG0 | kW | Gear churning power loss |
| PMLE | kW | Friction power loss at the sun/planet mesh |
| PMLI | kW | Friction power loss at the planet/ring mesh |
| PSeal | kW | Seals churning loss |
| Pw | kW | Power loss due to windage |
| Q | kW | Thermal load |
| Re | - | Reynolds number |
| t | m | Disk thickness |
| TBL | Nm | Torque loss per bearing |
| TP | Nm | Planet gear torque |
| Voil | m3 | Oil volume |
| W | lb | Equivalent total load |
| βe | degree | Sun/planet angle |
| ϑ | mm2/s | Operating viscosity |
| μ | - | Friction coefficient |
| μ | Pa s | Lubricant dynamic viscosity |
| μm | - | Mean friction coefficient |
| ν | m2/s | Lubricant kinematic viscosity |
| ρ | kg/m3 | Lubricant density |
| ω | inch | Bearing width |
| Ω | rad/s | Rotational speed |
References
- Jafari, S.; Nikolaidis, T. Thermal Management Systems for Civil Aircraft Engines: Review, Challenges and Exploring the Future. Appl. Sci. 2018, 8, 2044. [Google Scholar] [CrossRef]
- Chapman, J.W.; Hasseeb, H.; Schnulo, S. Thermal management system design for electrified aircraft propulsion concepts. In Proceedings of the AIAA Propulsion and Energy 2020 Forum, New Orleans, LA, USA, 26–28 August 2020; pp. 1–23. [Google Scholar] [CrossRef]
- Kennedy, D.; Bellamy, O.; Combes, B.; Corner, E.; Pittini, M.; Smith, S.; Stern, J. Meeting the UK Aviation Target-Options for Reducing Emissions to 2050 Committee on Climate Change. 2009. Available online: www.theccc.org.uk (accessed on 30 July 2022).
- Directorate-General for Mobility and Transport (European Commission); Directorate-General for Research and Innovation (European Commission). Flightpath 2050: Europe’s Vision for Aviation: Maintaining Global Leadership and Serving Society’s Needs; Publications Office: Luxembourg, 2011. [Google Scholar] [CrossRef]
- van Heerden, A.S.J.; Judt, D.M.; Jafari, S.; Lawson, C.P.; Nikolaidis, T.; Bosak, D. Aircraft thermal management: Practices, technology, system architectures, future challenges, and opportunities. Prog. Aerosp. Sci. 2022, 128, 100767. [Google Scholar] [CrossRef]
- Srinath, A.N.; Pena López, Á.; Miran Fashandi, S.A.; Lechat, S.; di Legge, G.; Nabavi, S.A.; Nikolaidis, T.; Jafari, S. Thermal Management System Architecture for Hydrogen-Powered Propulsion Technologies: Practices, Thematic Clusters, System Architectures, Future Challenges, and Opportunities. Energies 2022, 15, 304. [Google Scholar] [CrossRef]
- Corchero, G.; Montañés, J.L. An approach to the use of hydrogen for commercial aircraft engines. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2005, 219, 35–44. [Google Scholar] [CrossRef]
- Donovan, A.; Roberts, R.A.; Wolff, M. Enhanced ECS/Generator Models in an Integrated Air Vehicle Platform. In Proceedings of the 14th International Energy Conversion Engineering Conference, Salt Lake City, UT, USA, 25–27 July 2016; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2016. [Google Scholar] [CrossRef]
- Lents, C.; Hardin, L.; Rheaume, J.; Kohlman, L. Parallel hybrid gas-electric geared turbofan engine conceptual design and benefits analysis. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference, Salt Lake City, UT, USA, 25–27 July 2016. [Google Scholar] [CrossRef]
- Nikolaidis, T.; Jafari, S.; Bosak, D.; Pilidis, P. Exchange Rate Analysis for Ultra High Bypass Ratio Geared Turbofan Engines. Appl. Sci. 2020, 10, 7945. [Google Scholar] [CrossRef]
- Hudson, W.A.; Levin, M.L.; Hudson, W.A.; Levin, M.L. Integrated Aircraft Fuel Thermal Management; SAE Technical Papers; SAE International: Warrendale, PA, USA, 1986. [Google Scholar] [CrossRef]
- Capitao; Xisto, C.; Jonsson, I.; Lundbladh, A. ENABLEH2 D2.4-Final Report on Heat Management System Deliverable Lead Beneficiary: GKN. Available online: https://ec.europa.eu/research/participants/documents/downloadPublic?documentIds=080166e5f6b47829&appId=PPGMS (accessed on 6 May 2024).
- Scopus Preview-Scopus-Welcome to Scopus. Available online: https://www.scopus.com/home.uri (accessed on 2 May 2024).
- Pal, D.; Severson, M. Liquid cooled system for aircraft power electronics cooling. In Proceedings of the 16th InterSociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), Orlando, FL, USA, 30 May–2 June 2017; pp. 800–805. [Google Scholar] [CrossRef]
- Enable H2, Heat Management System Conceptual Design Tools Report ENABLEH2 PUBLIC REPORT ENABLing cryogEnic Hydrogen-Based CO2-Free Air Transport Deliverable 2.1. Available online: https://ec.europa.eu/research/participants/documents/downloadPublic?documentIds=080166e5eb3948d6&appId=PPGMS (accessed on 6 May 2024).
- Prashanth, P.; Speth, R.L.; Eastham, S.D.; Sabnis, J.S.; Barrett, S.R.H. Post-combustion emissions control in aero-gas turbine engines. Energy Environ. Sci. 2021, 14, 916–930. [Google Scholar] [CrossRef]
- Jafari, S.; Nikolaidis, T.; Van Heerden, A.S.J.; Lawson, C.P.; Bosak, D. Physics-Based Thermal Model for Power Gearboxes in Geared Turbofan Engines. In Proceedings of the ASME Turbo Expo 2020: Turbomachinery Technical Conference and Exposition, Virtual, 21–25 September 2020; Volume 1. [Google Scholar] [CrossRef]
- Jafari, S.; Nikolaidis, T.; Sureddi, R. Physics-Based Thermal Management System Components Design for All-Electric Propulsion Systems. In Proceedings of the ASME Turbo Expo 2021: Turbomachinery Technical Conference and Exposition, Virtual, 7–11 June 2021; Volume 5B. [Google Scholar] [CrossRef]
- Jafari, S.; Bouchareb, A.; Nikolaidis, T. Thermal Performance Evaluation in Gas Turbine Aero Engines Accessory Gearbox. Int. J. Turbomach. Propuls. Power 2020, 5, 21. [Google Scholar] [CrossRef]
- Martins, R.C.; Cardoso, N.F.R.; Bock, H.; Igartua, A.; Seabra, J.H.O. Power loss performance of high pressure nitrided steel gears. Tribol. Int. 2009, 42, 1807–1815. [Google Scholar] [CrossRef]
- Palmgren, A. Ball and Roller Bearing Engineering; S.H. Burbank & Company, Incorporated: Burbank, CA, USA, 1959. [Google Scholar]
- Eschmann, P.; Brändlein, J.; Hasbargen, L.; Weigand, K.; Brändlein, J.; Hasbargen, L.; Weigand, K. Ball and Roller Bearings—Theory, Design and Applications; Wiley: Hoboken, NJ, USA, 1999; 492p. [Google Scholar]
- Friction and Temperature Rise. Available online: https://www.ntnglobal.com/en/products/catalog/pdf/2203E_a10.pdf (accessed on 18 June 2023).
- Estimating Bearing Operating Temperature|SKF. Available online: https://www.skf.com/group/products/rolling-bearings/principles-of-rolling-bearing-selection/bearing-selection-process/operating-temperature-and-speed/estimating-bearing-operating-temperature (accessed on 20 May 2023).
- Harris, T.A.; Kotzalas, M.N. Essential Concepts of Bearing Technology; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar] [CrossRef]
- Adams, M.L. Bearings: Basic Concepts and Design Applications; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar] [CrossRef]
- Streifinger, H. Fuel/Oil System Thermal Management in Aircraft Turbine Engines. In Proceedings of the RTO Meeting Proceedings, Symposium, Design Principles and Methods for Aircraft Gas Turbine Engines, Toulouse, France, 11–15 May 1998; NATO, 1999. p. 12. Available online: https://apps.dtic.mil/sti/tr/pdf/ADA361702.pdf (accessed on 17 May 2022).
- Press Releases|Rolls-Royce-Rolls-Royce UltraFan Power Gearbox Tops World Aerospace Record. Available online: https://www.rolls-royce.com/media/press-releases/2021/31-08-2021-rr-ultrafan-power-gearbox-tops-world-aerospace-record.aspx (accessed on 28 March 2023).
- Autiero, M.; Cirelli, M.; Paoli, G.; Valentini, P.P. A Data-Driven Approach to Estimate the Power Loss and Thermal Behaviour of Cylindrical Gearboxes under Transient Operating Conditions. Lubricants 2023, 11, 303. [Google Scholar] [CrossRef]
- Handschuh, R.U.S. Army, Experimental Study of the Influence of Speed and Load on Thermal Behavior of High-Speed Helical Gear Trains. 2005. Available online: https://ntrs.nasa.gov/citations/20050207440 (accessed on 17 June 2023).
- Neurouth, A.; Changenet, C.; Ville, F.; Burnet, C.; Octrue, M. Influence of Ball Bearings Modeling on the Predicted Thermal Behavior of a High-speed Gear Unit. In Proceedings of the STLE 70th Annual Meeting & Exhibition, Dallas, TX, USA, 17–21 May 2015. [Google Scholar]

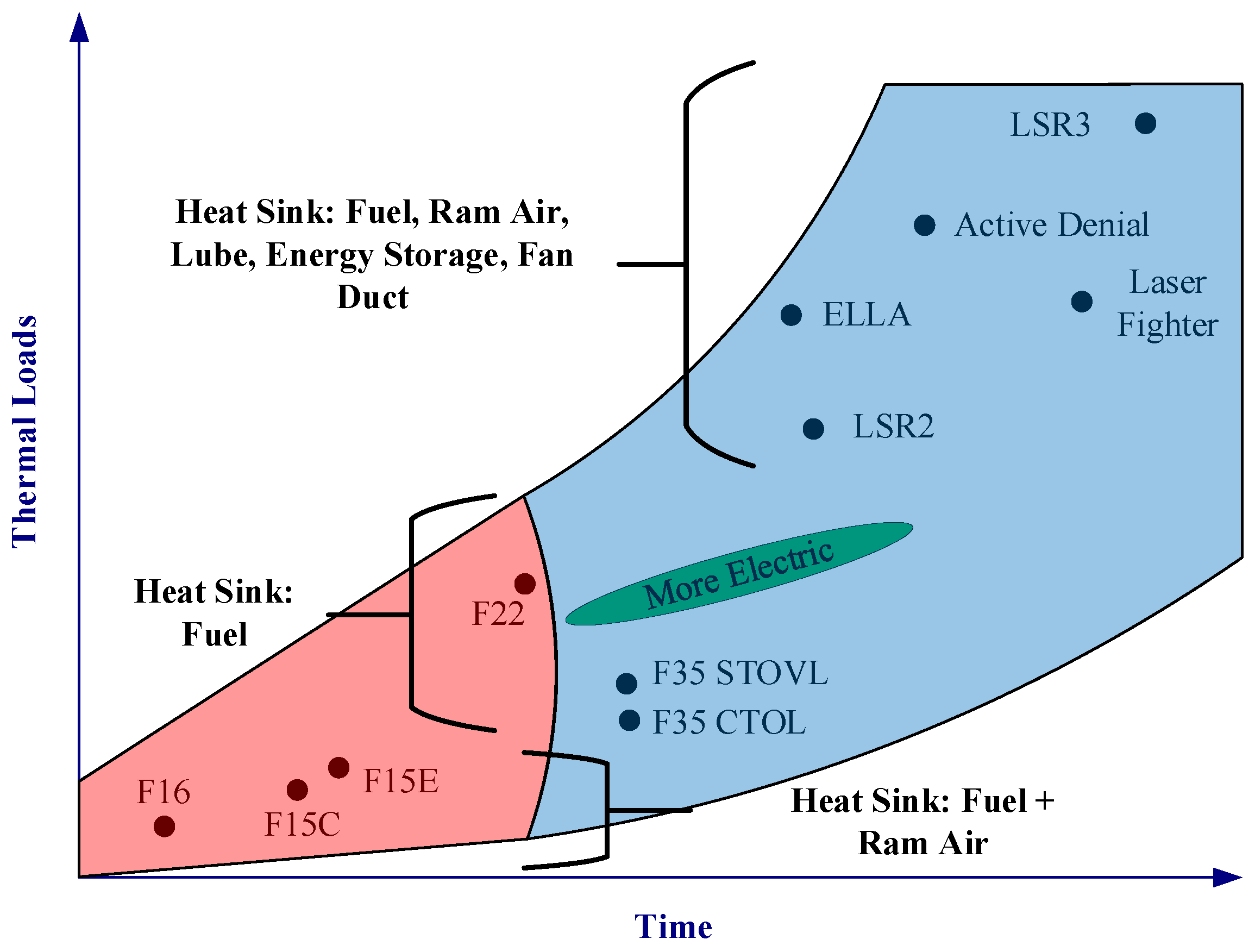


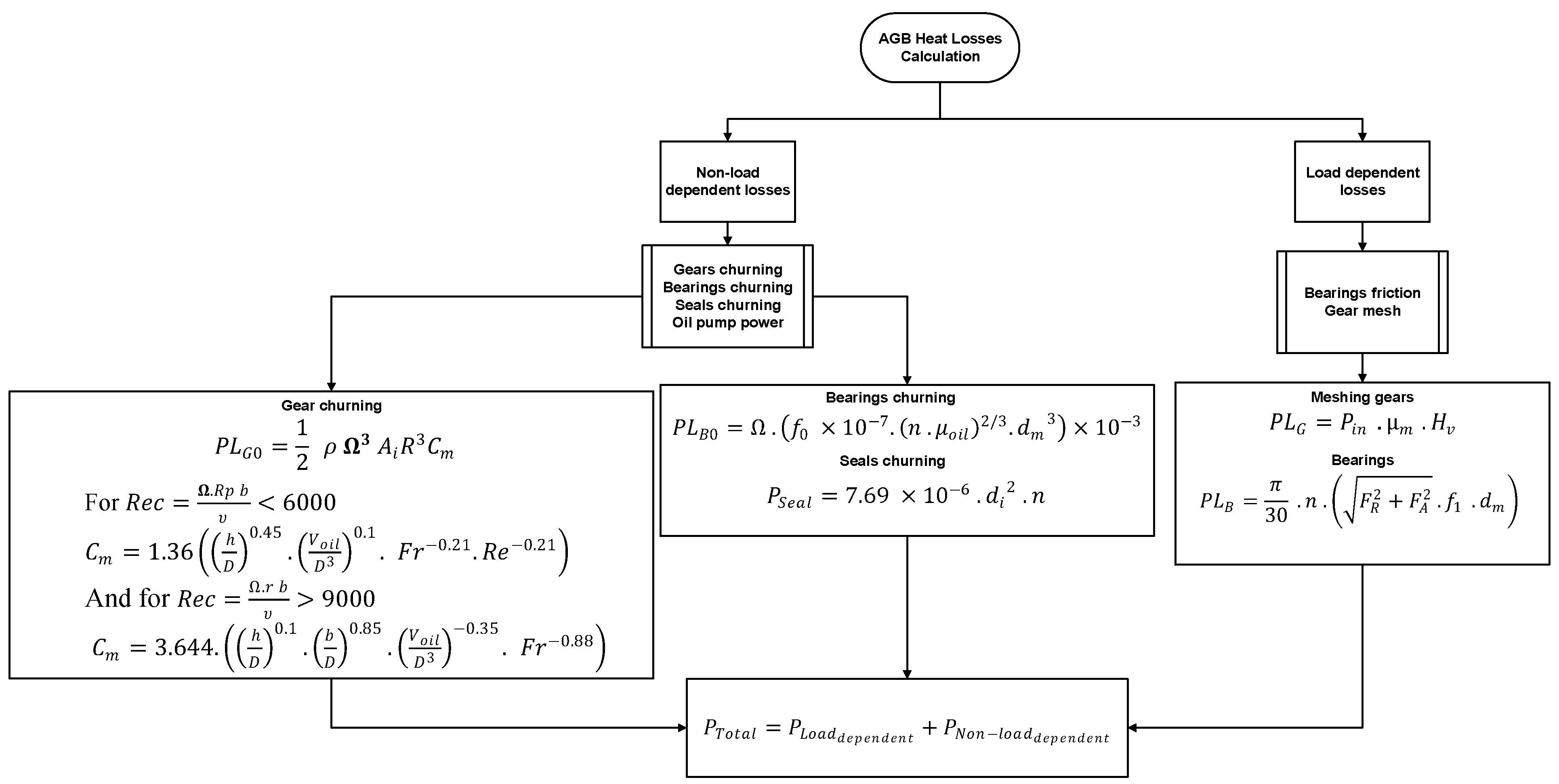
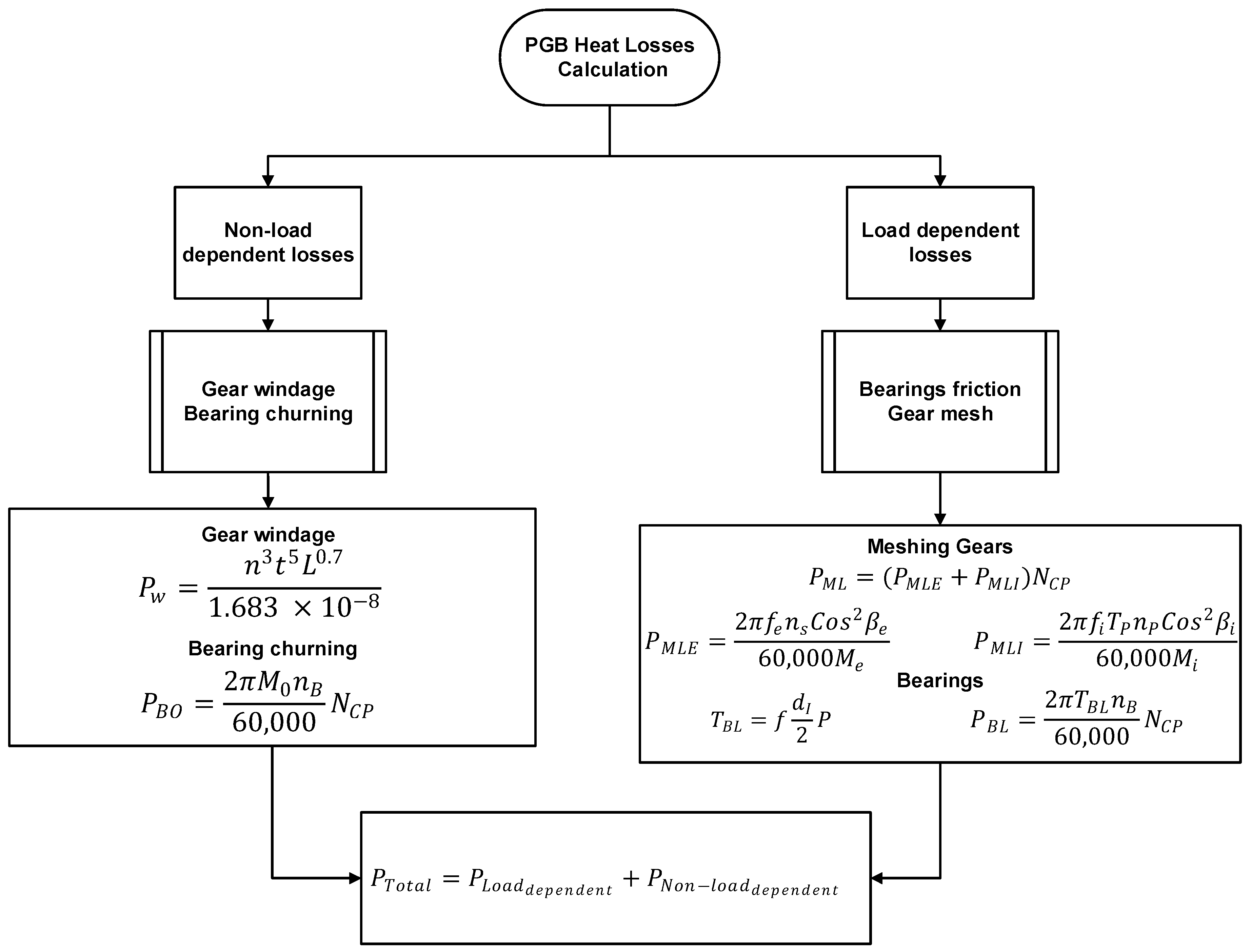
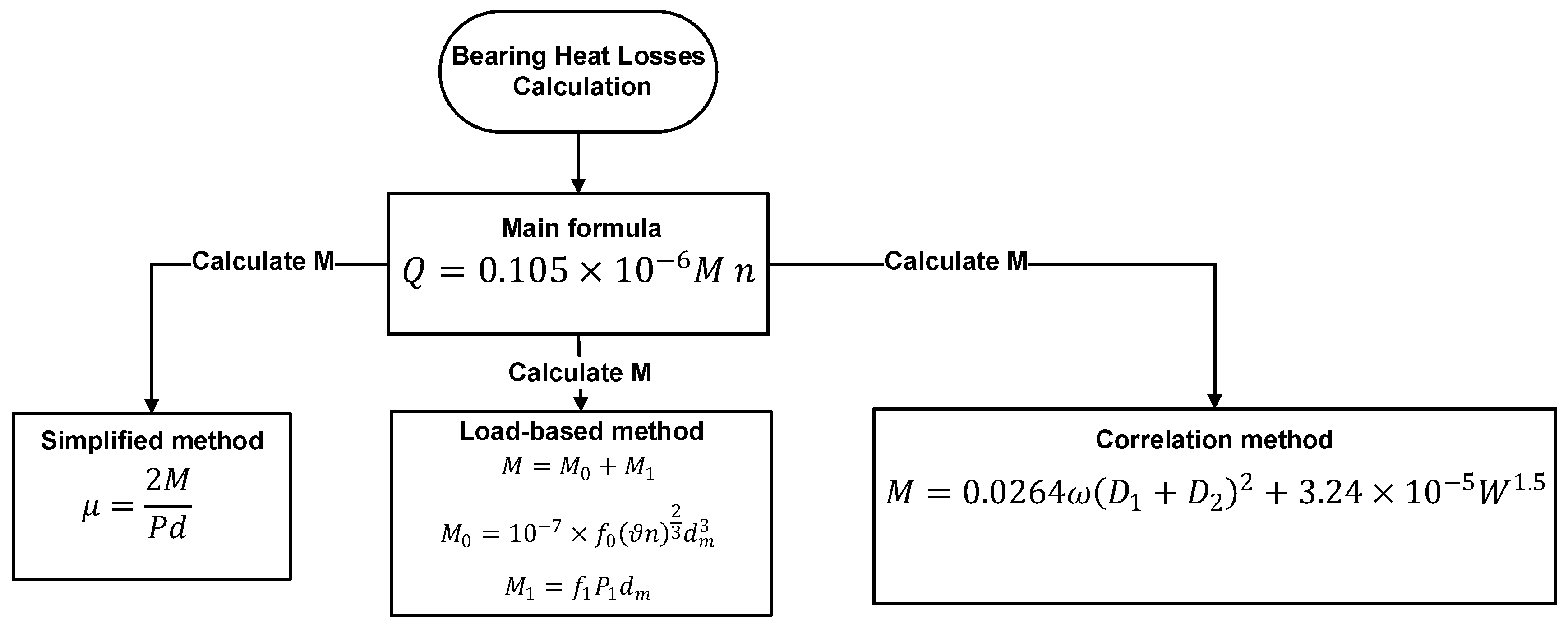
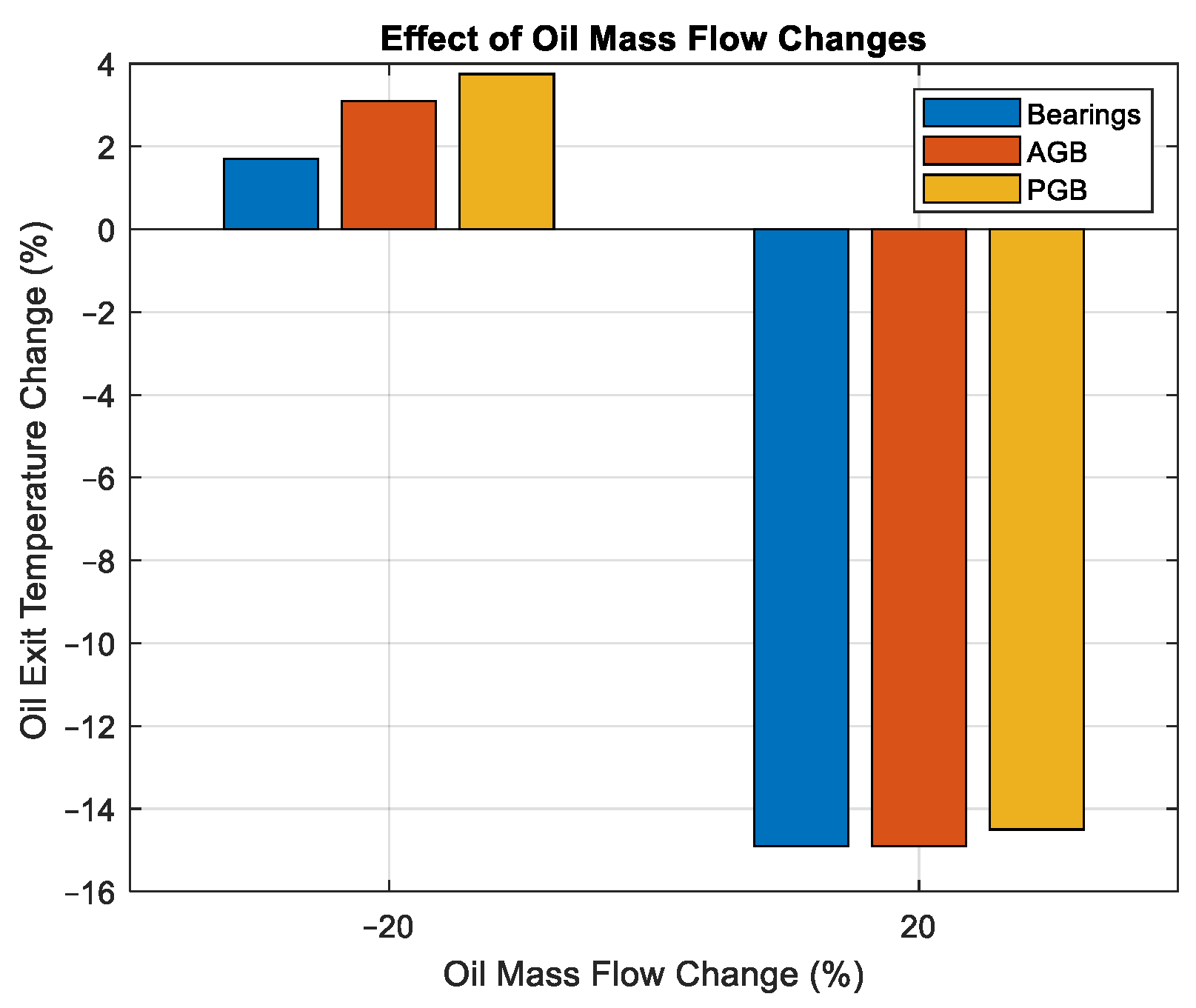
| Heat Sources | Coolant | Heat Sinks |
|---|---|---|
|
|
|
| Method | Formulation | Reference | |
|---|---|---|---|
| I | (3) | [23] | |
| II | (4) | [22] | |
| III | (5) | [25] | |
| Case Study | Take-Off Thrust (klbf) | Bearing’s Heat Load (kW) | AGB (kW) | PGB (kW) | Pumps, Seals, etc. (kW) | Total Heat (kW) |
|---|---|---|---|---|---|---|
| CFM56 size | 18 | 23 | 18 | - | 12 | 53 |
| PW1100G size | 25 | 31 | 26 | 223 | 17 | 297 |
| UltraFan size | 63 | 55 | 53 | 592 | 23 | 722 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Ebrahimi, A.; Jafari, S.; Nikolaidis, T. Heat Load Development and Heat Map Sensitivity Analysis for Civil Aero-Engines. Int. J. Turbomach. Propuls. Power 2024, 9, 25. https://doi.org/10.3390/ijtpp9030025
Ebrahimi A, Jafari S, Nikolaidis T. Heat Load Development and Heat Map Sensitivity Analysis for Civil Aero-Engines. International Journal of Turbomachinery, Propulsion and Power. 2024; 9(3):25. https://doi.org/10.3390/ijtpp9030025
Chicago/Turabian StyleEbrahimi, Alireza, Soheil Jafari, and Theoklis Nikolaidis. 2024. "Heat Load Development and Heat Map Sensitivity Analysis for Civil Aero-Engines" International Journal of Turbomachinery, Propulsion and Power 9, no. 3: 25. https://doi.org/10.3390/ijtpp9030025
APA StyleEbrahimi, A., Jafari, S., & Nikolaidis, T. (2024). Heat Load Development and Heat Map Sensitivity Analysis for Civil Aero-Engines. International Journal of Turbomachinery, Propulsion and Power, 9(3), 25. https://doi.org/10.3390/ijtpp9030025










