Wall-Proximity Effects on Five-Hole Probe Measurements †
Abstract
1. Introduction
2. Materials and Methods
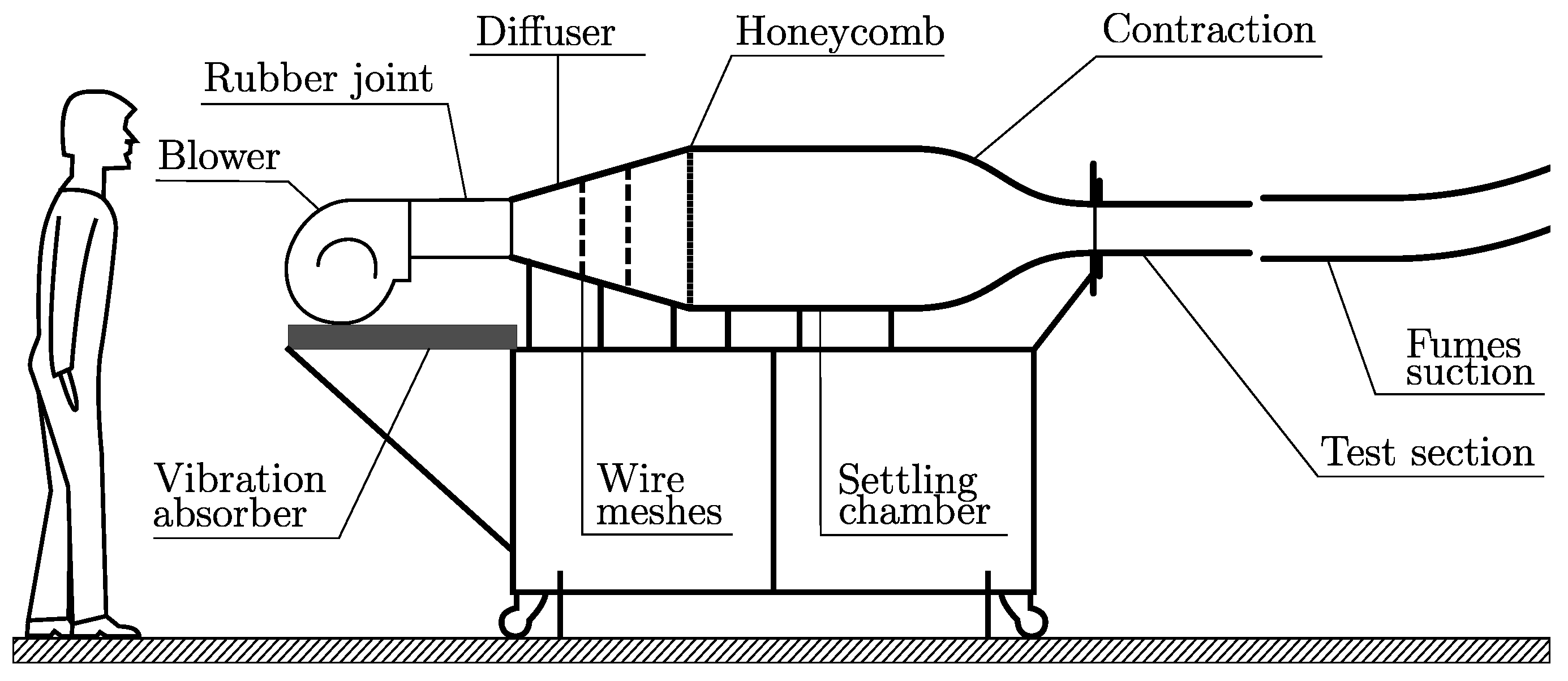
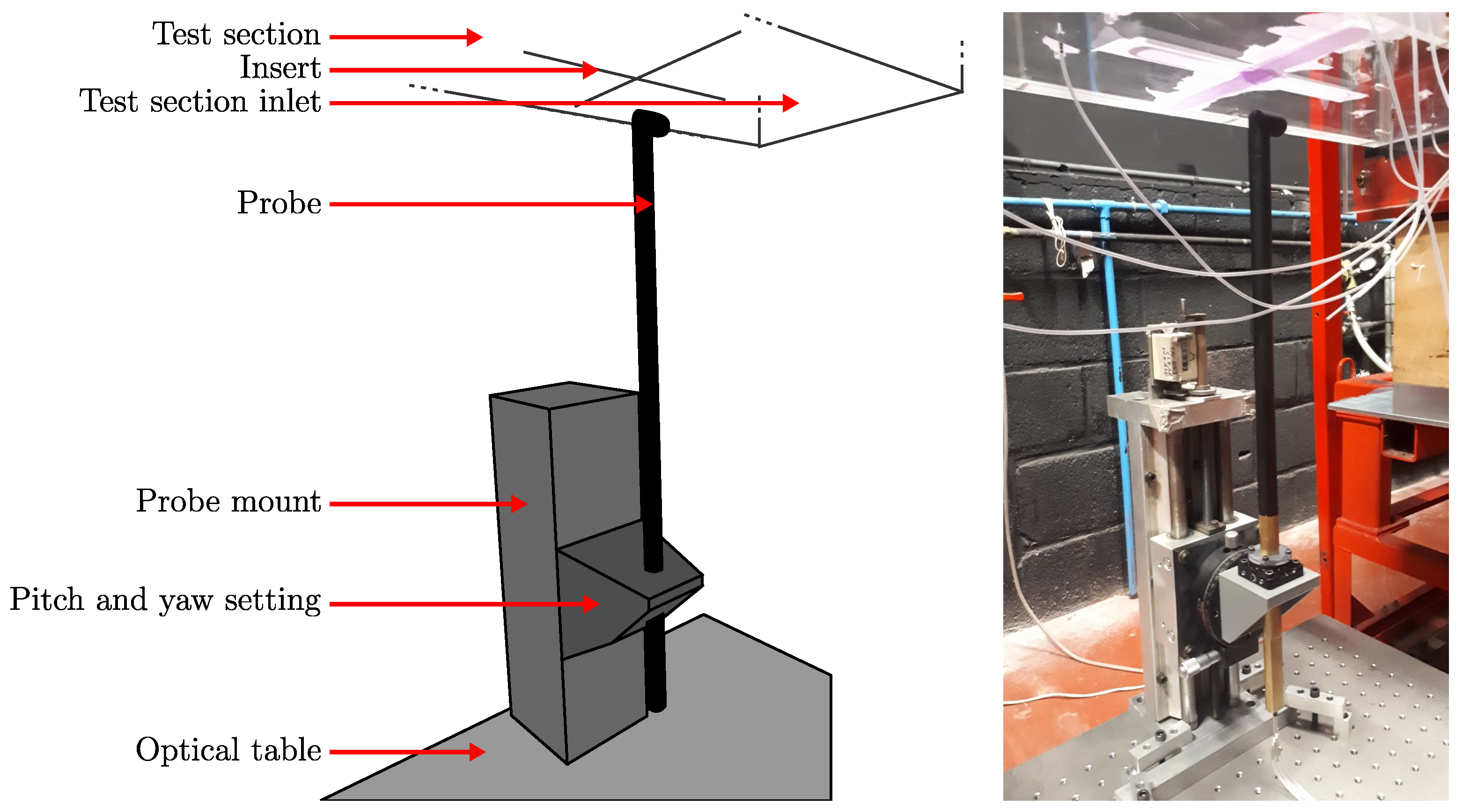
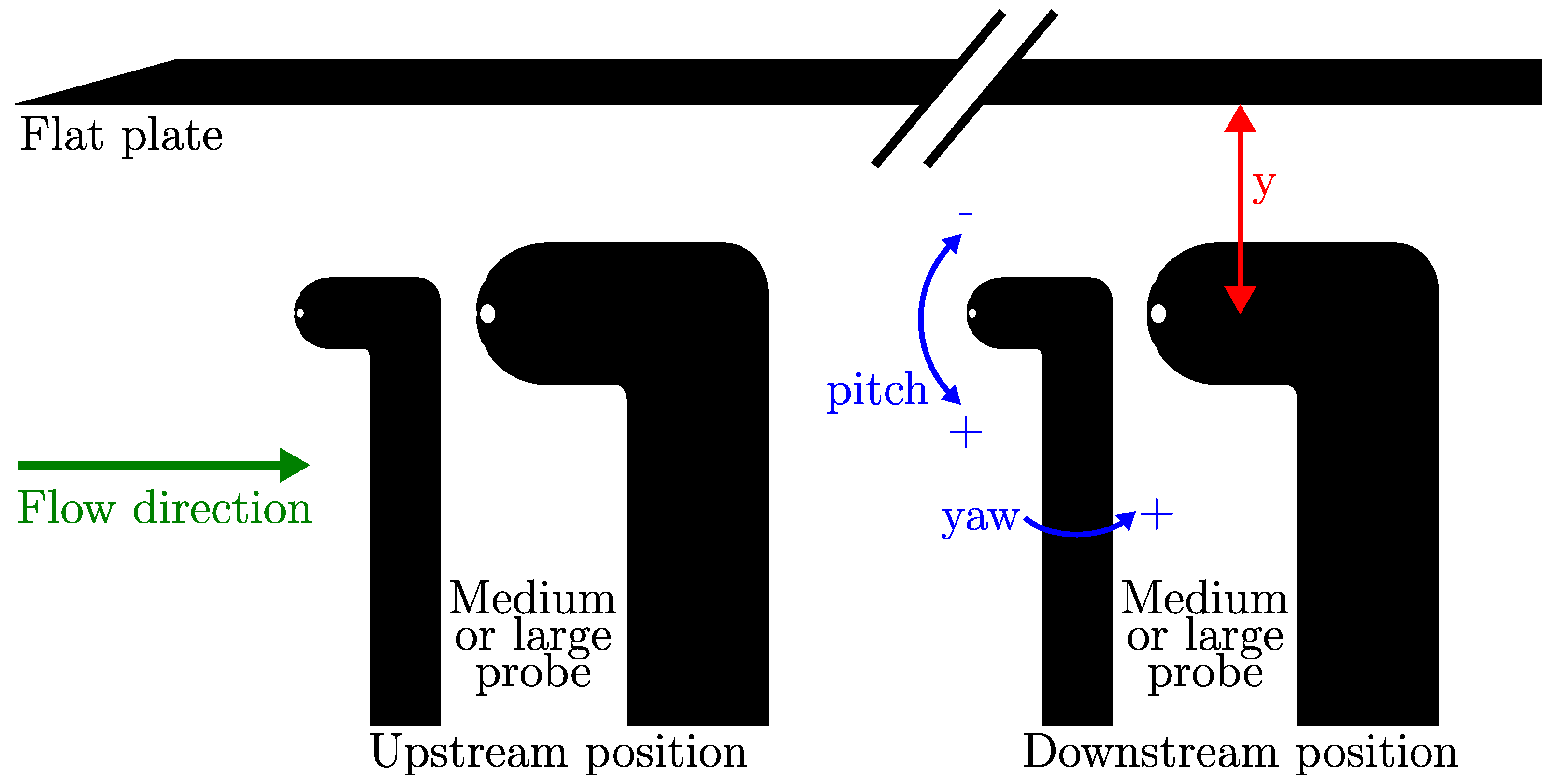
2.1. Setup
2.2. Methodology
- To provide information about the undisturbed flow field to use as a reference of what the probes should measure;
- To provide information about the local flow around the probe to help understand the changes in pressure coefficient due to the wall proximity.
- 2 to 3 pixels of particle size on the camera sensor;
- 8 pixels displacement between each frame in the free stream;
- 10 particles per 32 × 32-pixel window.
- adaptative PIV;
- 64 pixels maximum window size;
- 8 pixels minimum window size;
- 4 pixels grid step size;
- 1.3 minimum peak height ratio;
- outlier detection.
2.3. Data Quality
3. Results
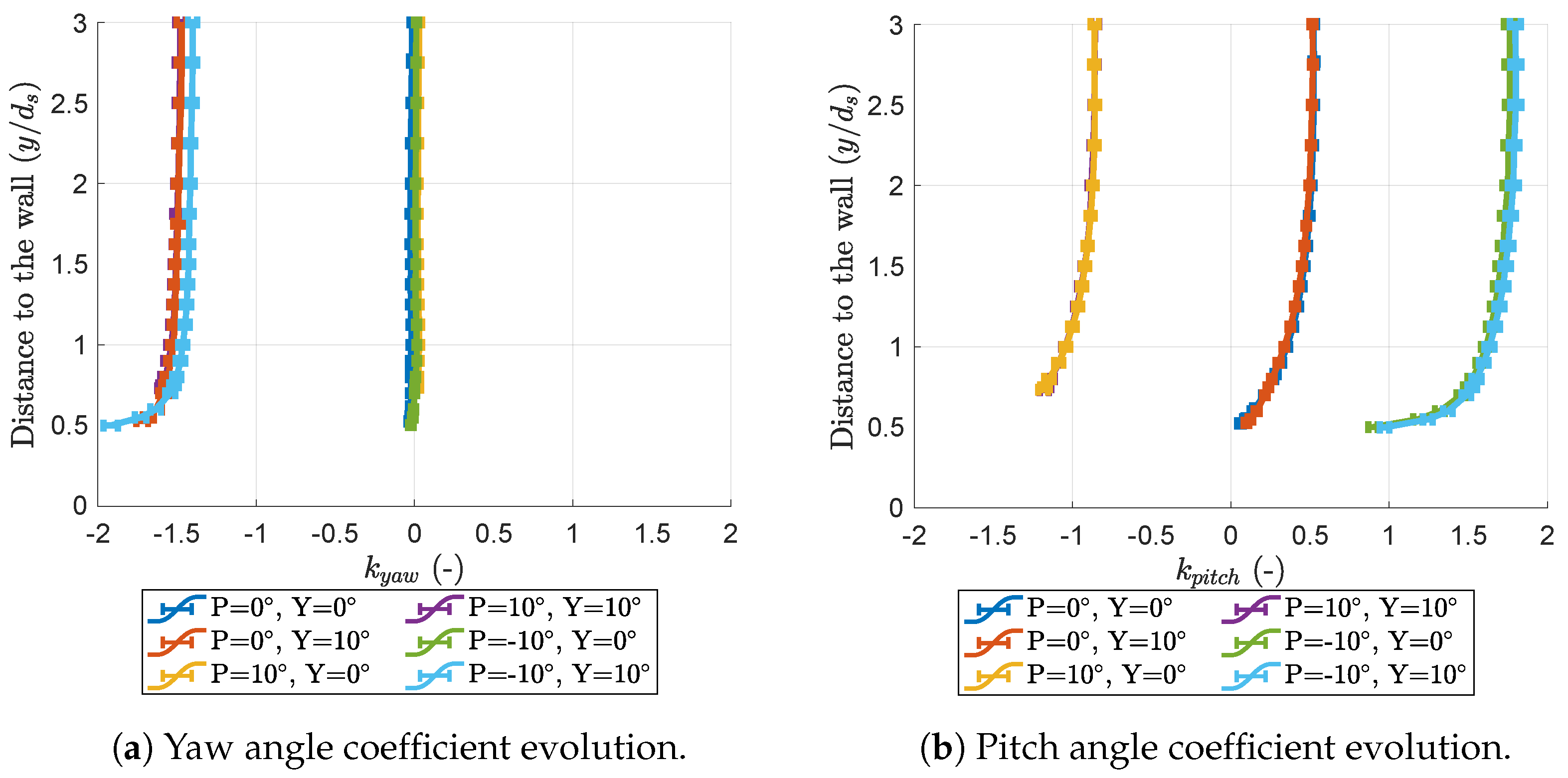
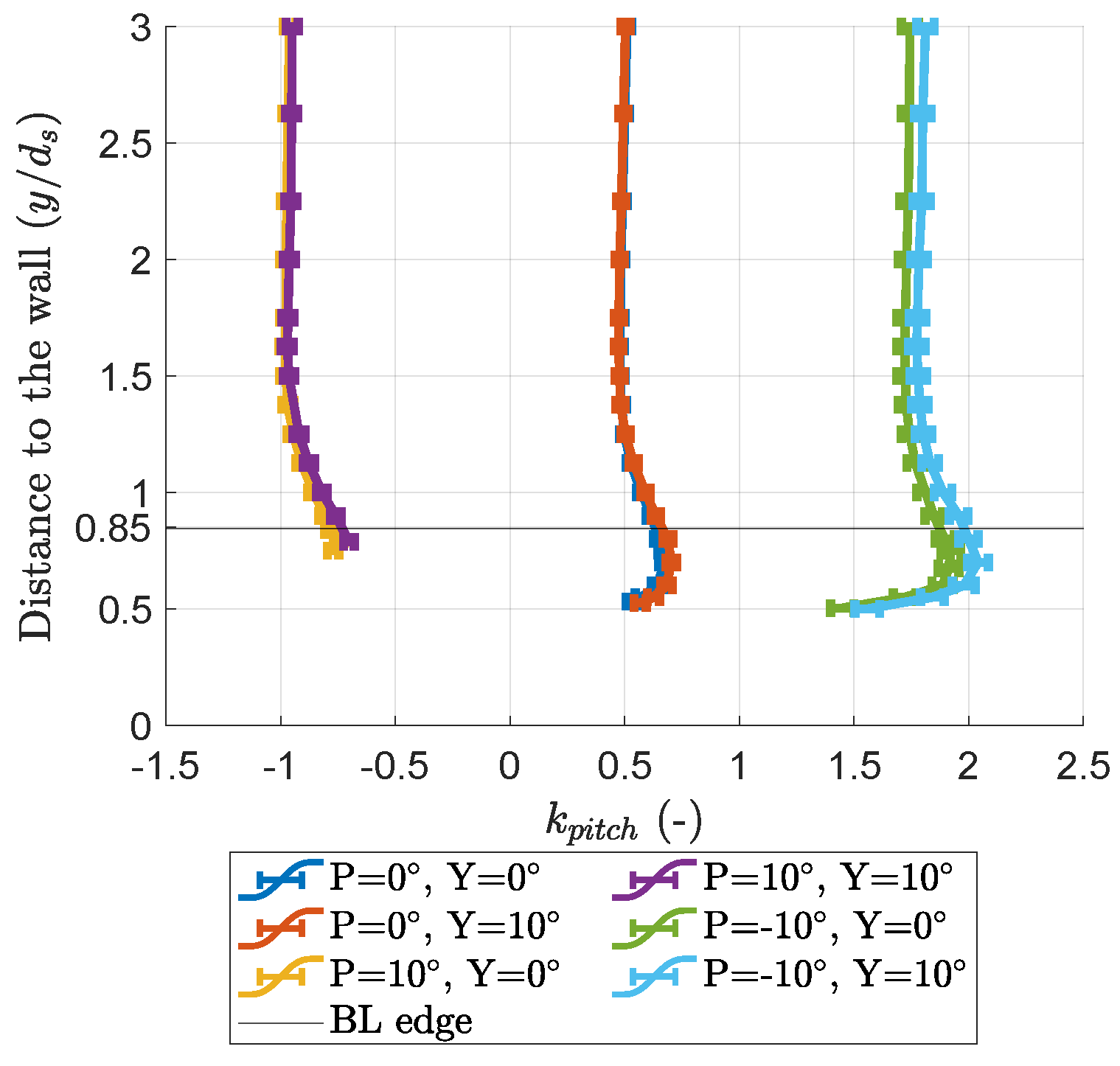
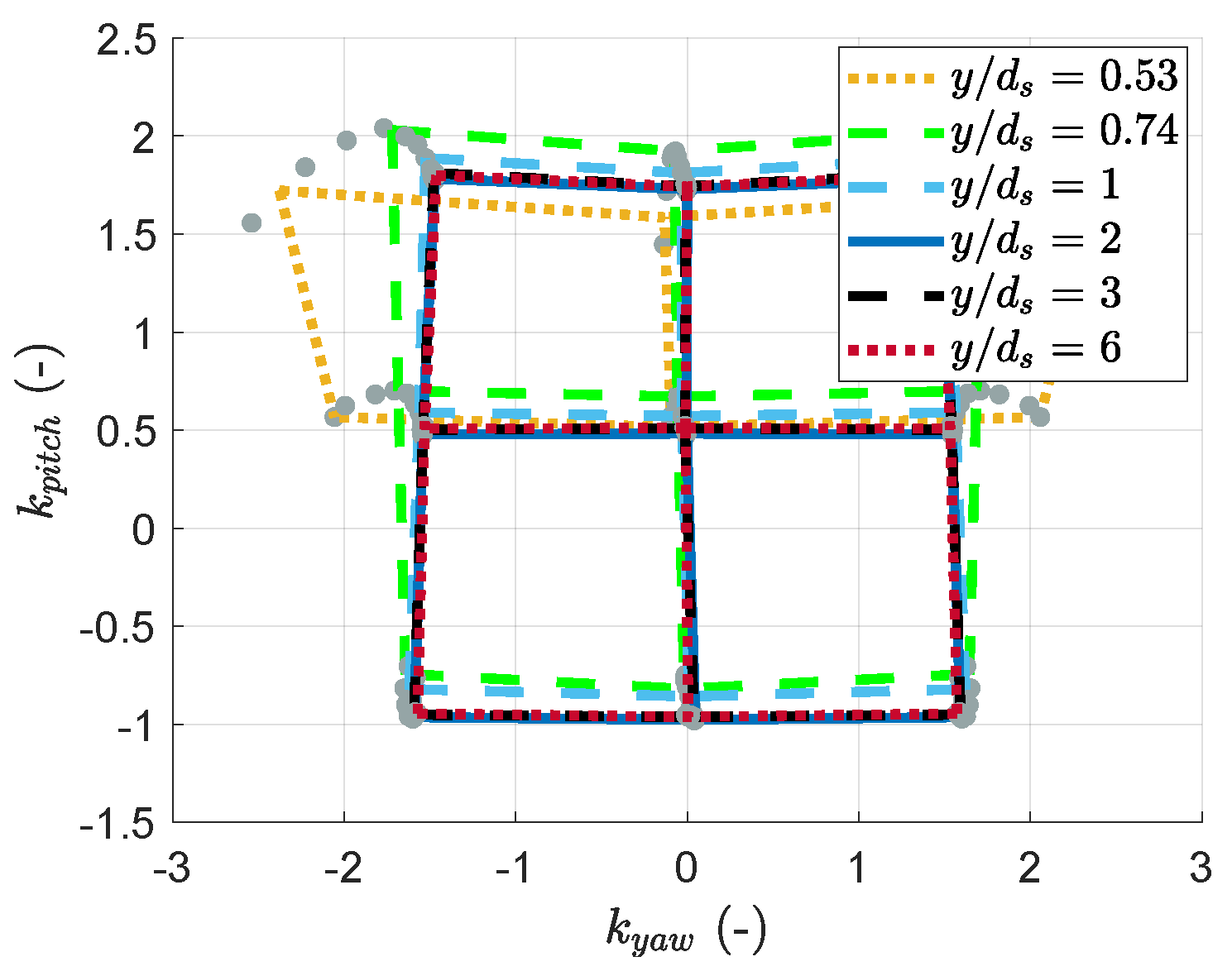
3.1. Wall-Proximity Effect
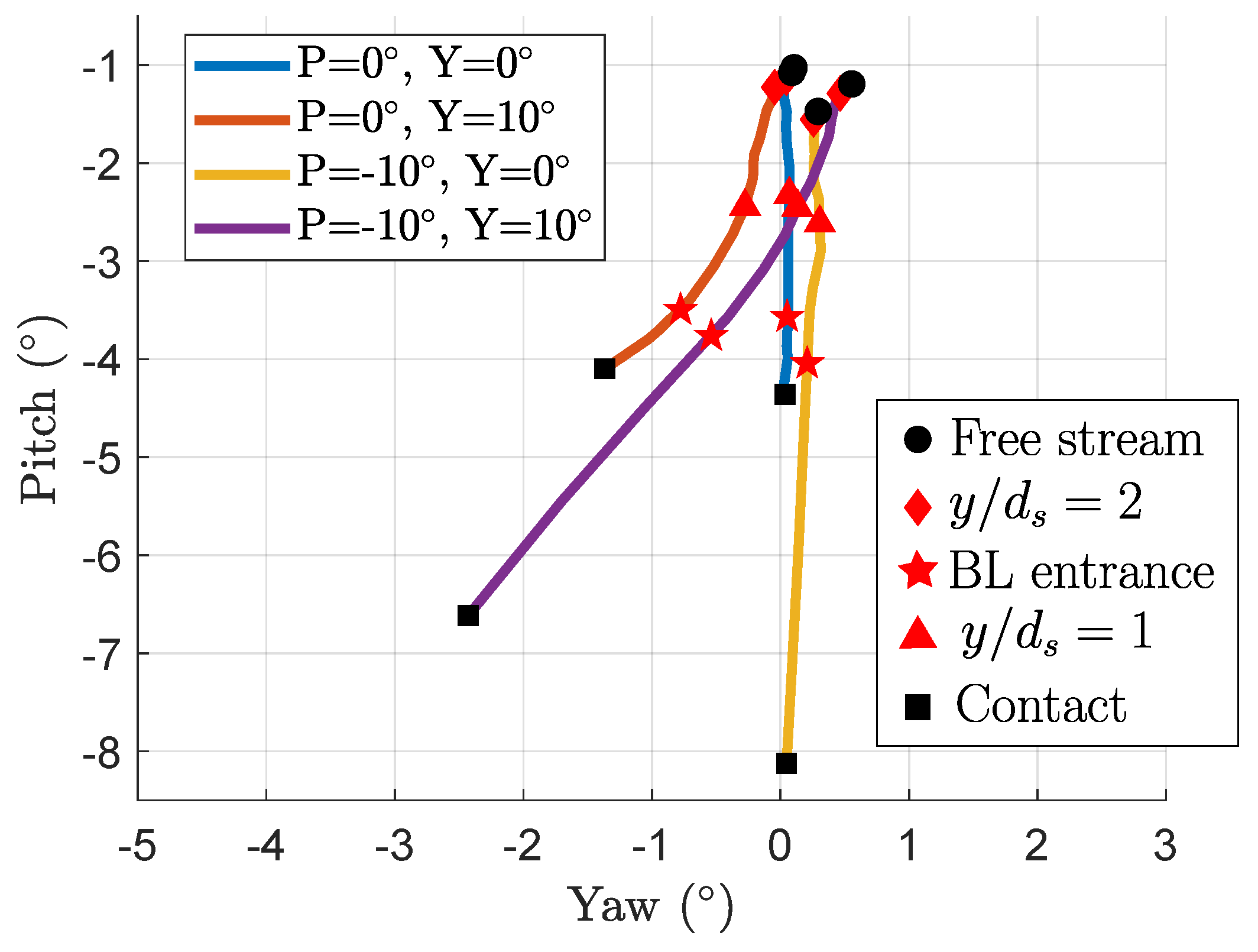
- This experiment has a pitch coefficient definition opposite to the one from [15];
- This experiment uses a different positive yaw direction.
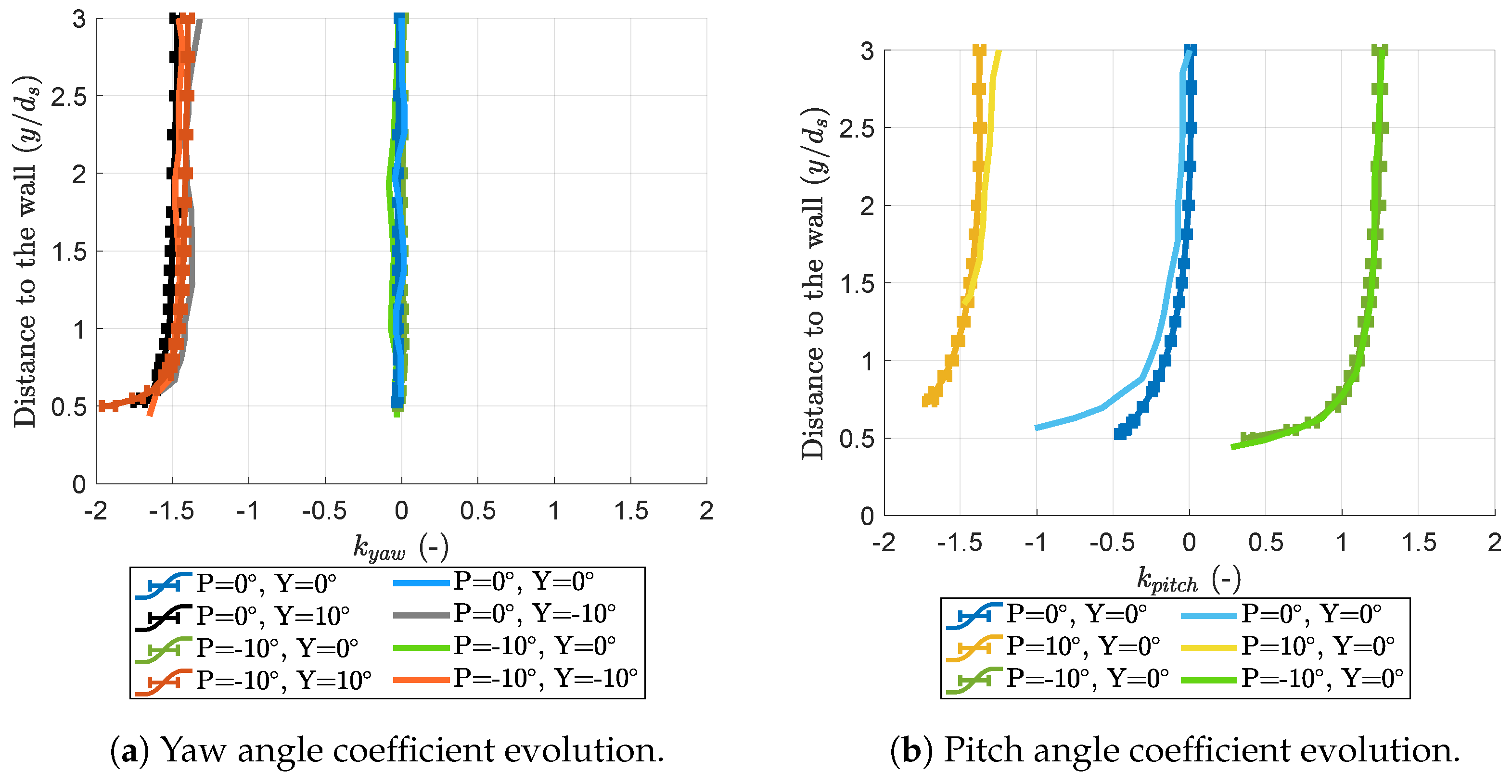
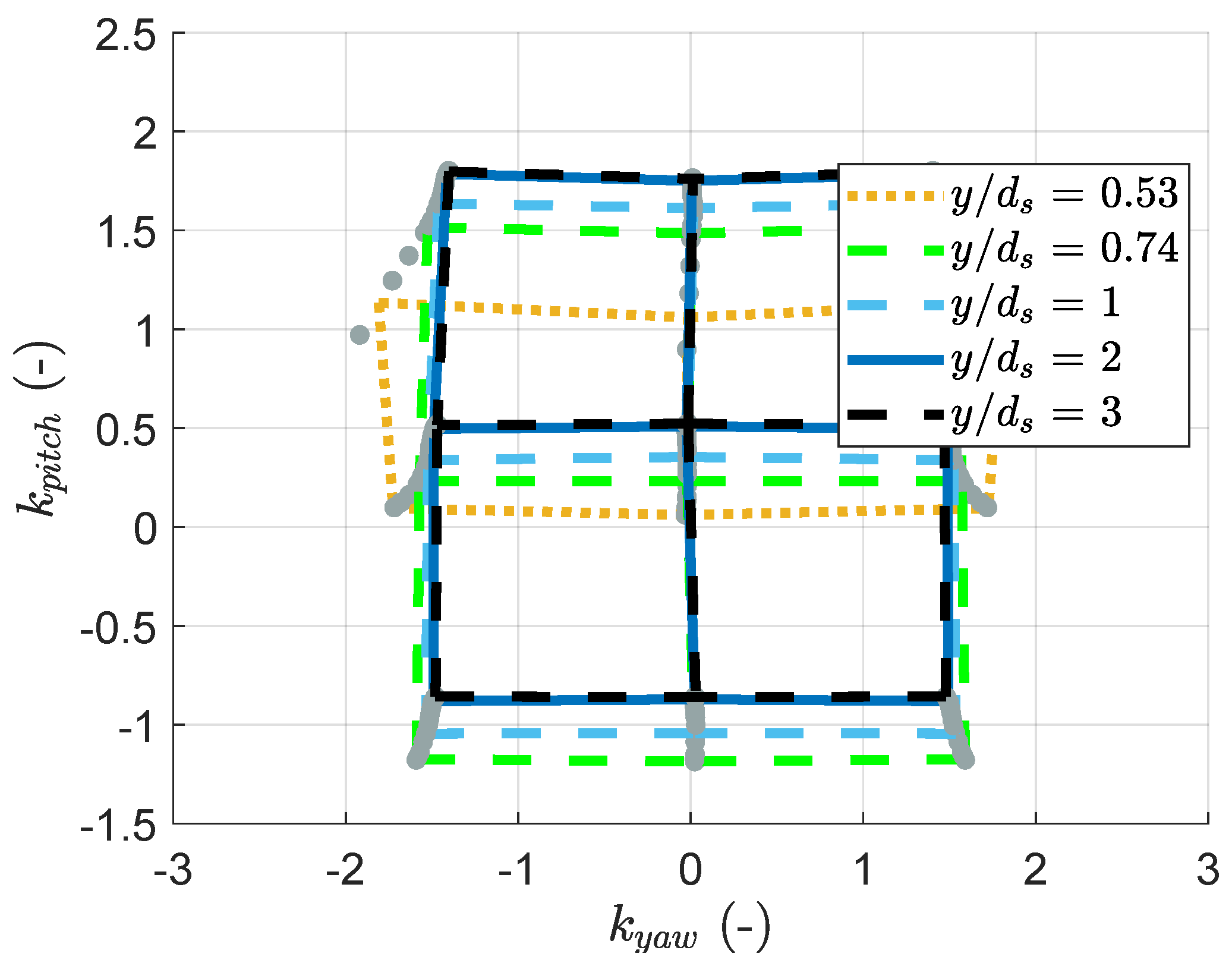
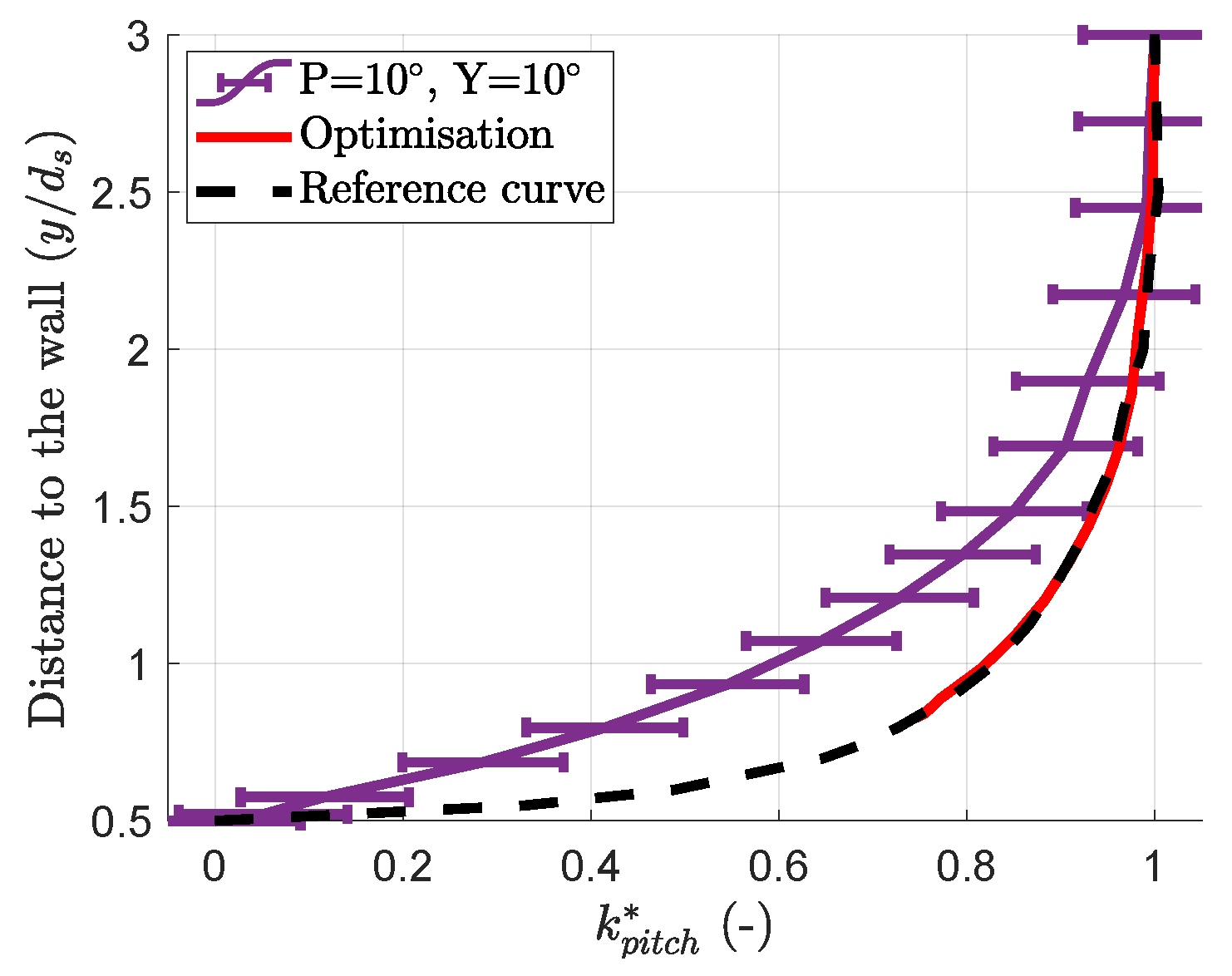
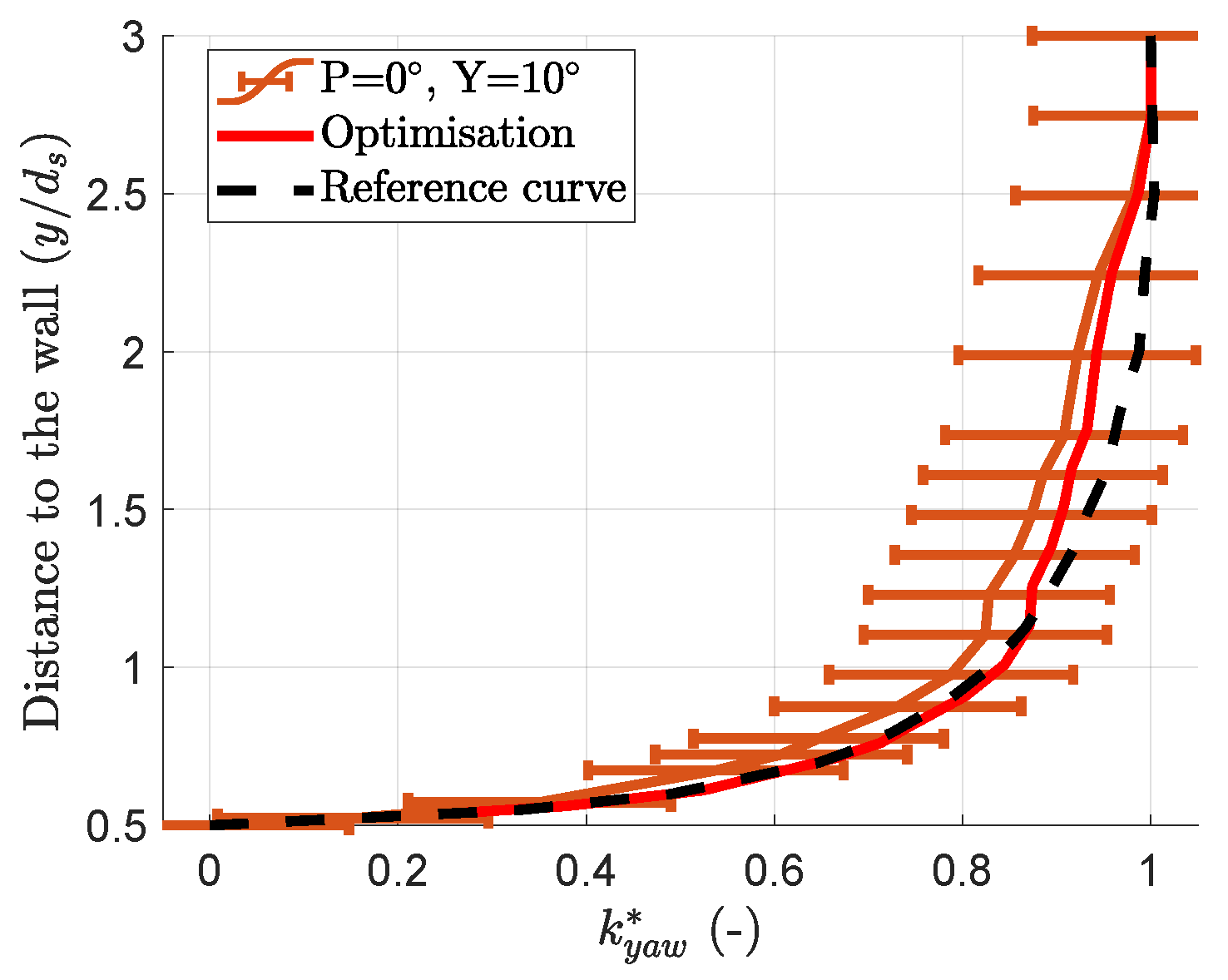
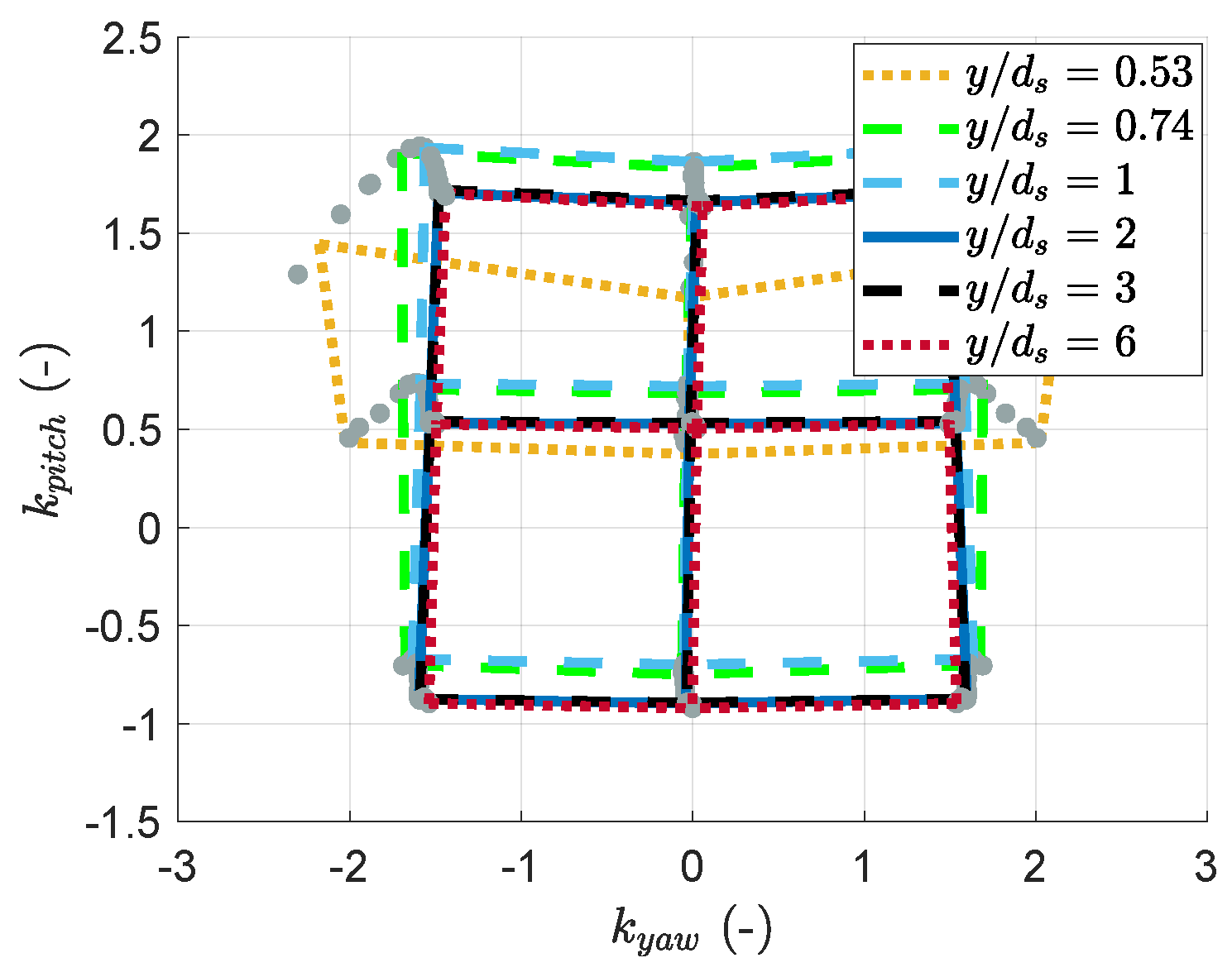
3.2. Similarities in the Evolution of the Coefficients
- the free-stream value is set equal to at ;
- the distance or “error” between the measured curve and the reference curve is computed;
- the curve is linearly scaled in the and directions until the error is minimised.
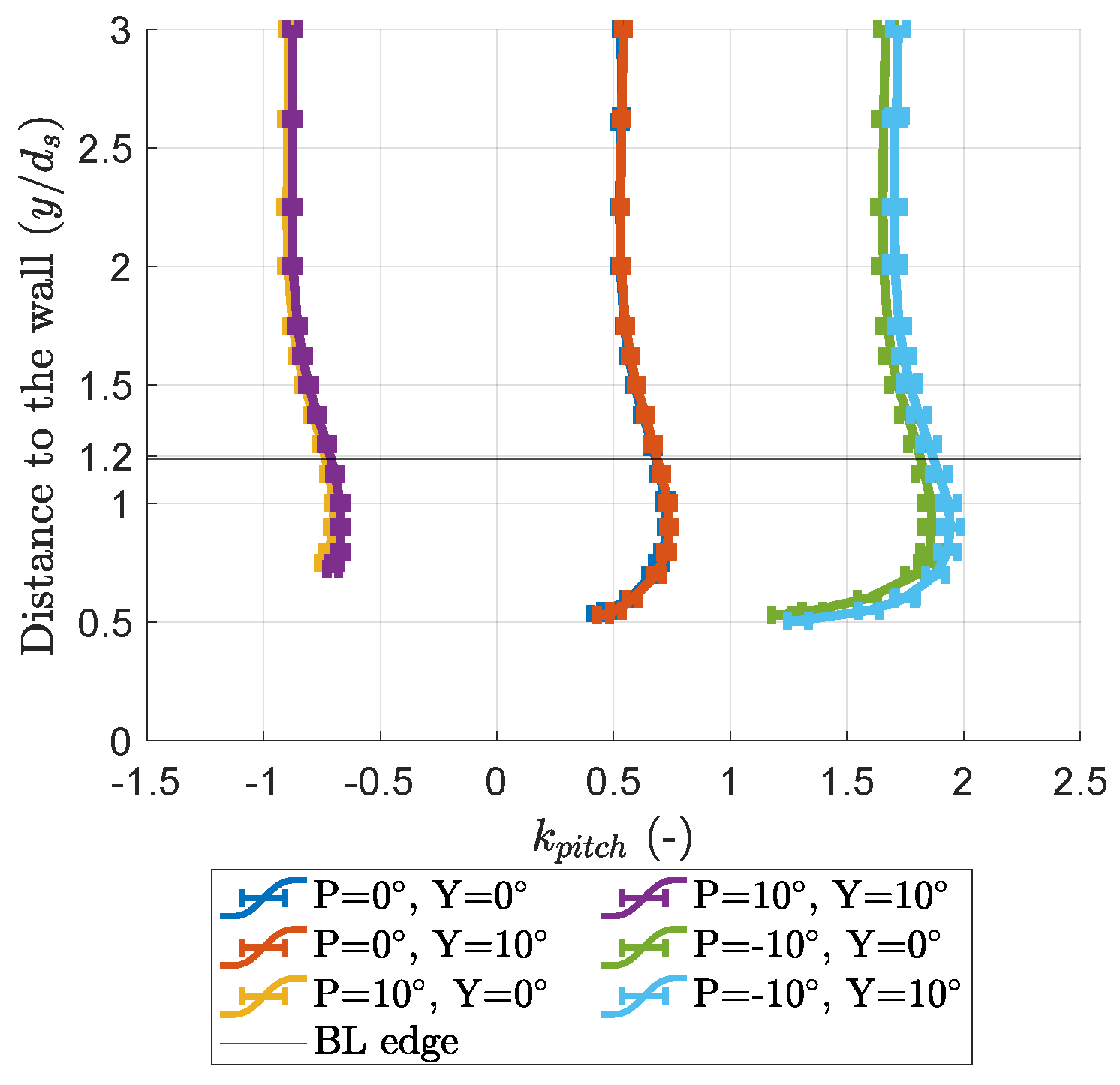
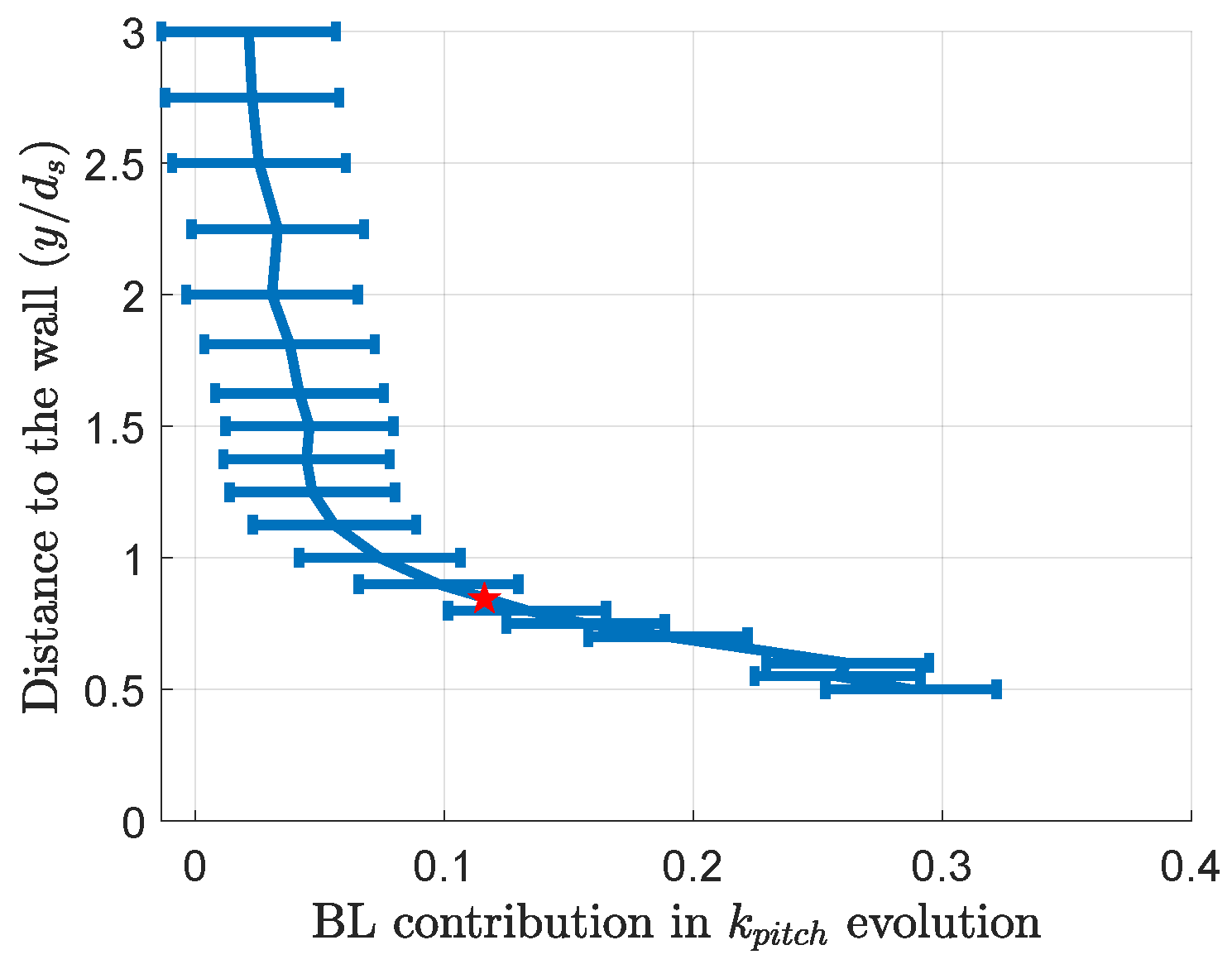
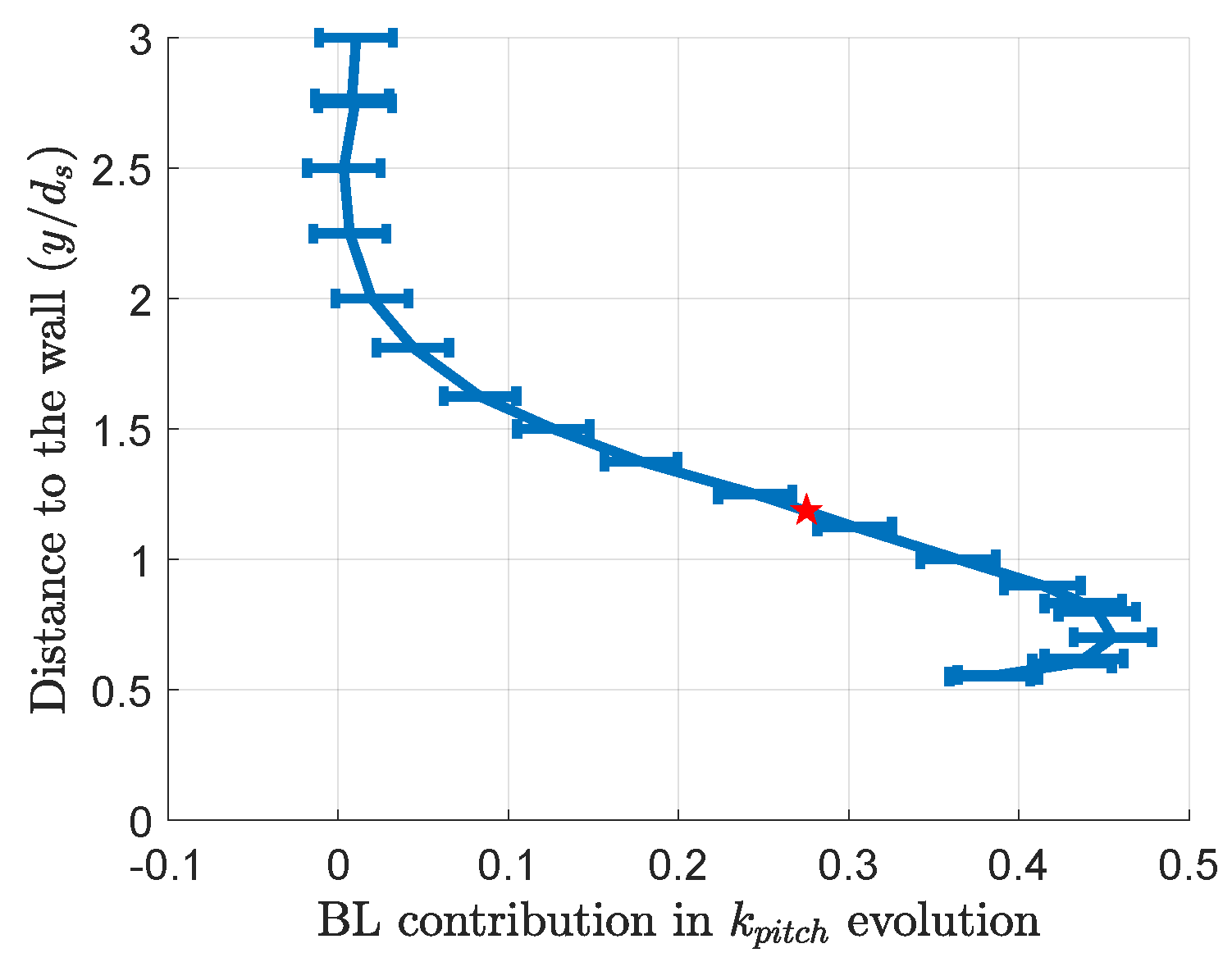
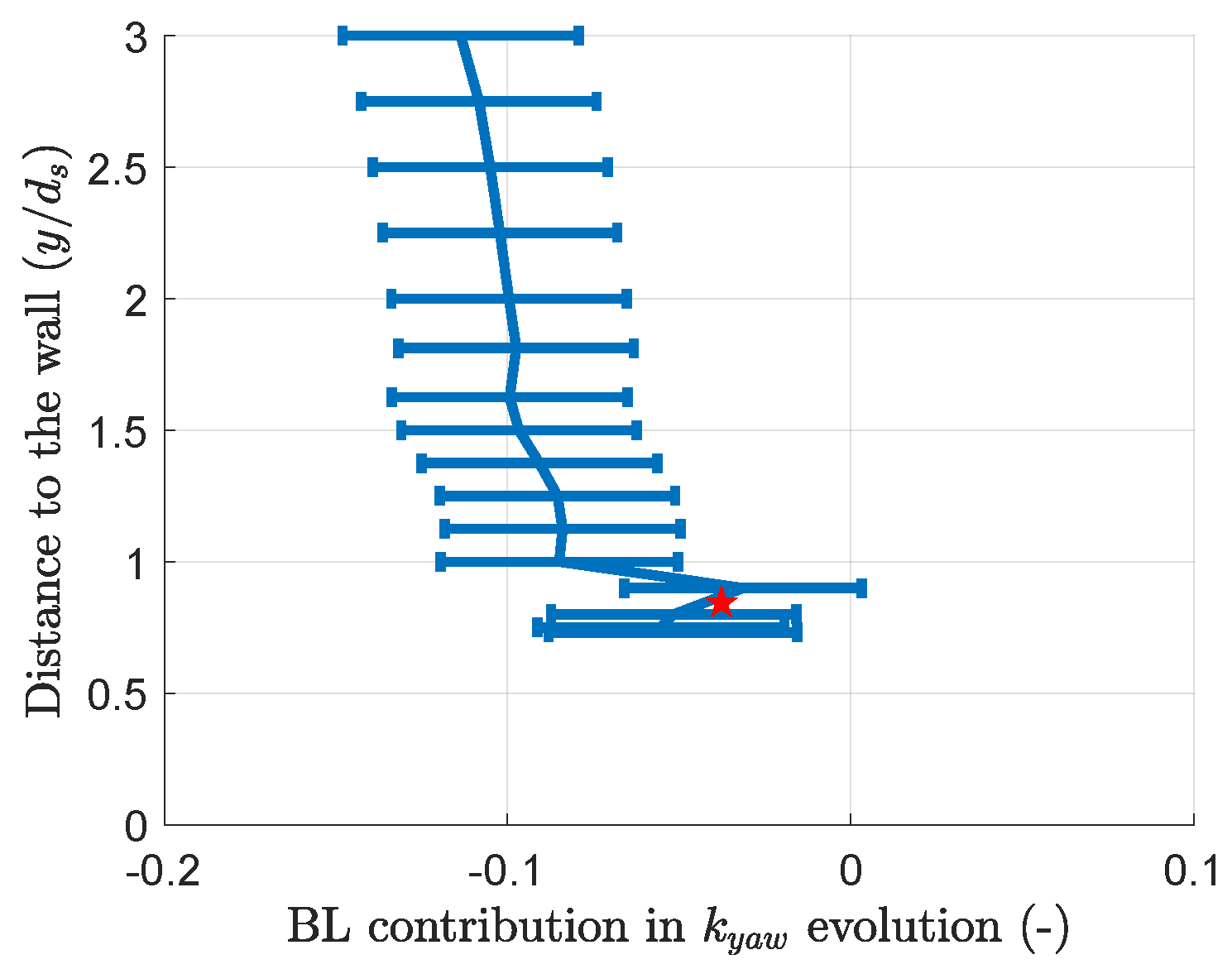
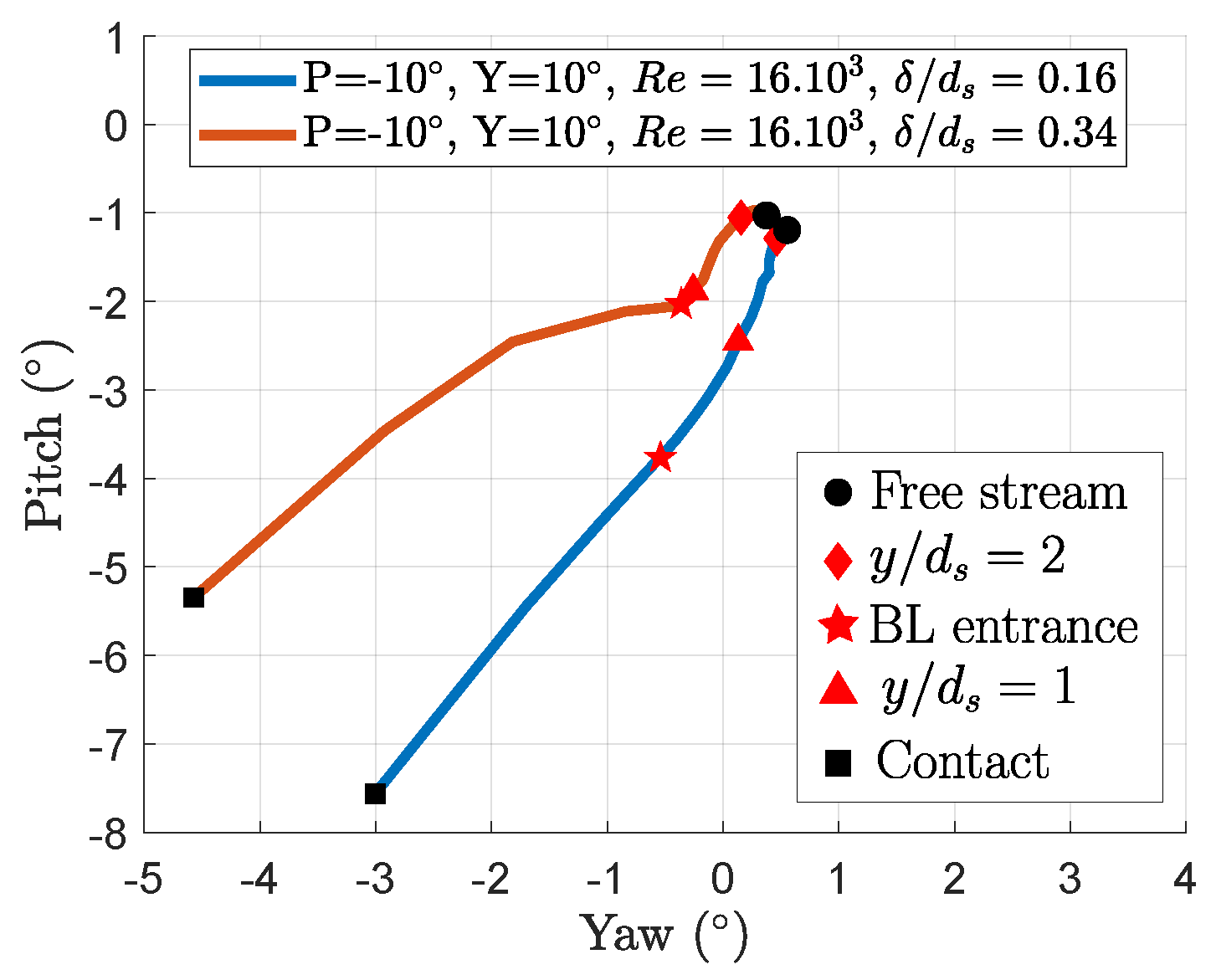
3.3. Boundary Layer Influence
- The assumption is made that the boundary layer and wall-proximity effect are independent;
- The assumption is made that is the only wall-proximity effect parameter for a given probe orientation;
- The case with and is assumed to only exhibit the wall-proximity effect;
- For a given probe orientation, the traverse data from the case with and are subtracted from the data with larger boundary layer thicknesses.
- 1.
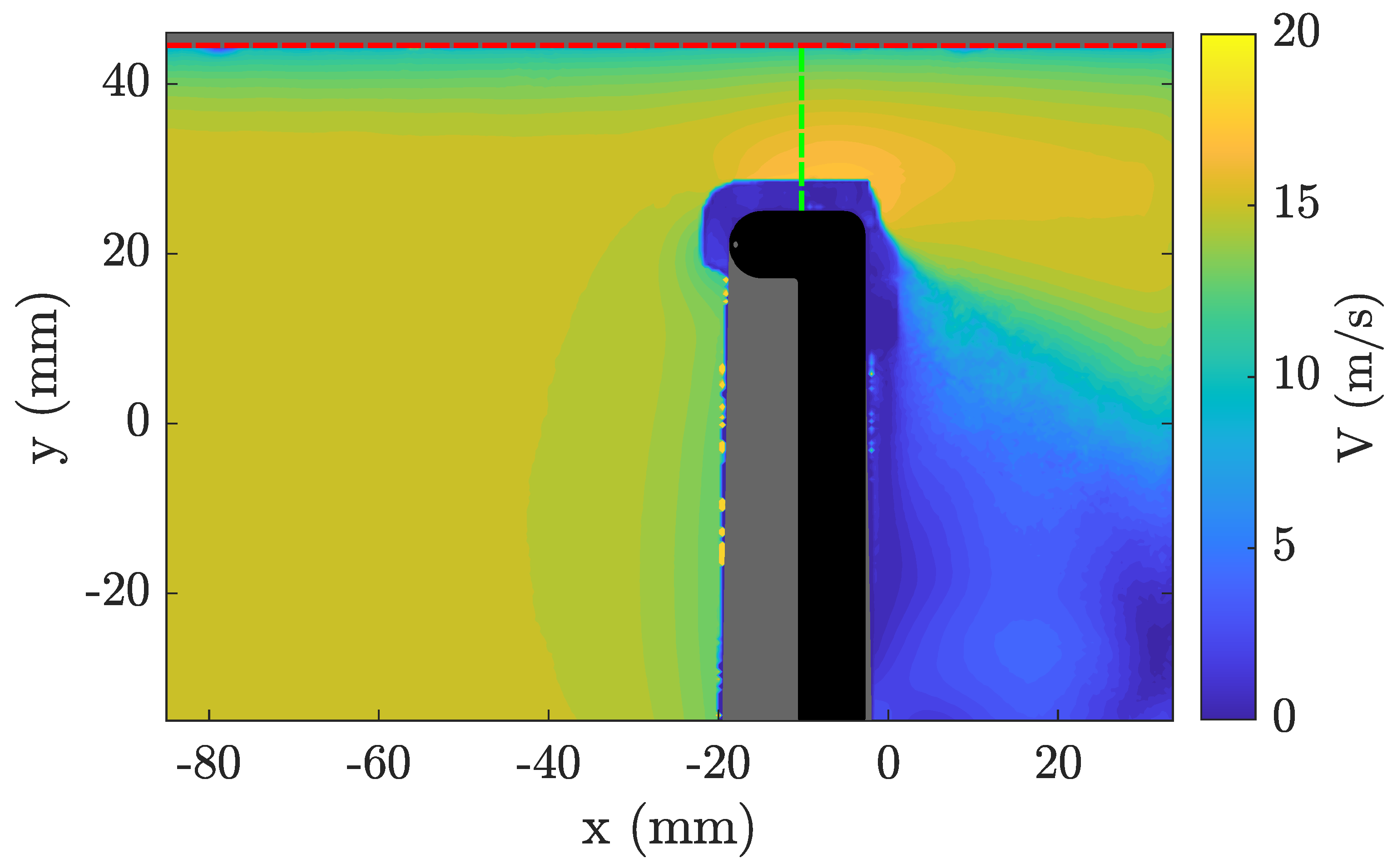
- The PIV boundary layer velocity profile was analysed thanks to the undisturbed flow PIV acquisitions;
- 2.
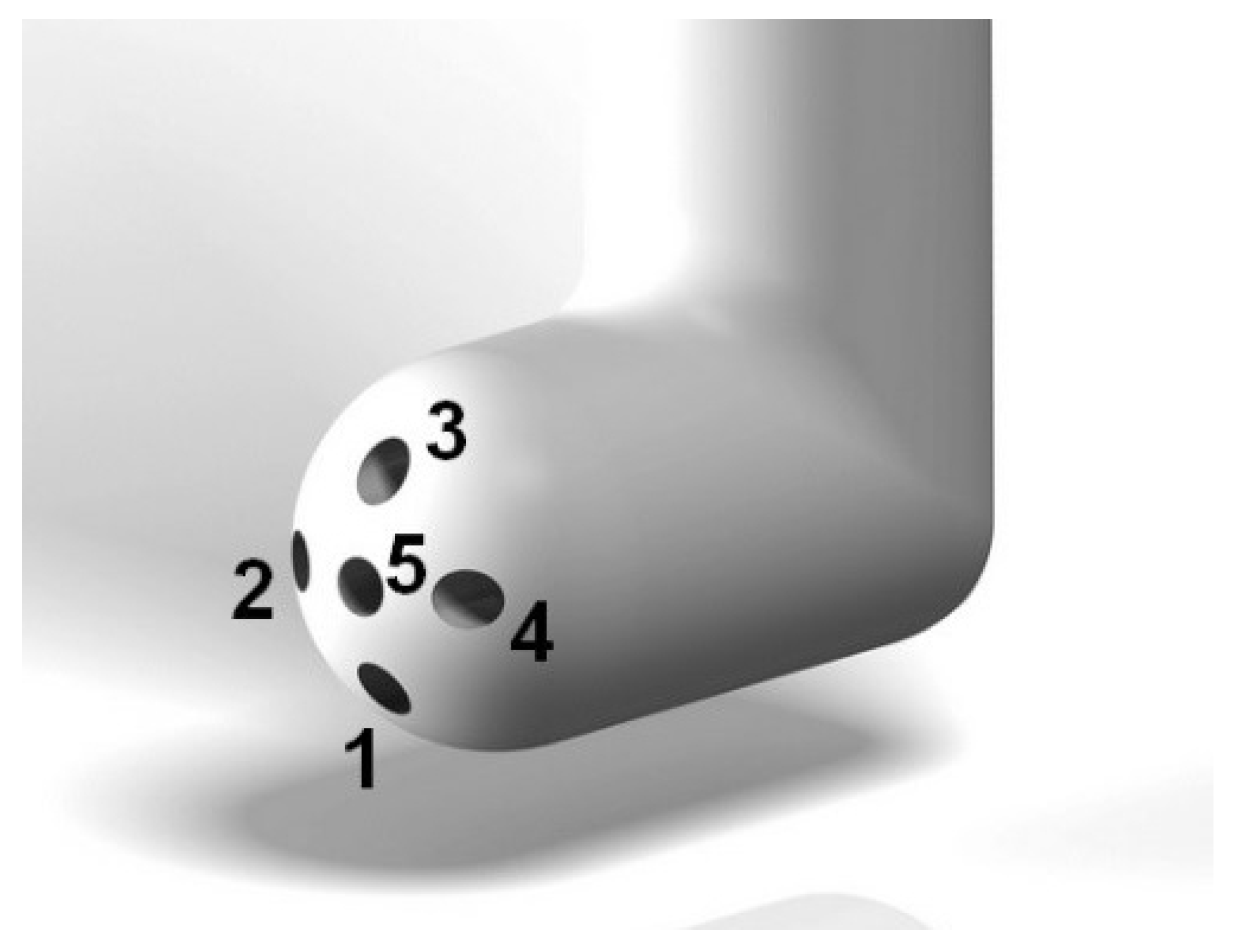
- For each probe position, the velocity facing each hole was obtained, which is illustrated in Figure 21;
- 3.
- The static pressure was assumed to be constant through the boundary layer;
- 4.
- The set of five velocity values was converted into a set of five pressure values using the calibration data;
- 5.
- The set of pressure values was converted into calibration coefficients.
- a yaw coefficient underestimation for positive pitch positions;
- a yaw coefficient overestimation for negative pitch positions;
- a shift of the map towards higher values.
3.4. Coupling between the Wall and the Boundary Layer Effects
4. Discussion
- -
- Lee’s results suggest that the further the mast is from the probe head, the closer the coefficient evolution is to the reference shape. A CFD or potential flow study of a conceptual spherical probe, free from any mast influence, could help test this hypothesis. The available dataset was not sufficient to assess whether the base shape deformation follows a specific function of the probe orientation. This obstacle could be overcome with finer calibration grids. If a model for this function is found, then the precision of the measurements can be improved by using the calibration data to set up the model and use it during measurement campaigns. The differences in the results for Lee’s work and this work in Table 5 show that this function would be geometry-dependent and suggest performing a calibration close to a wall for each probe geometry.
- -
- The magnitude of the wall-proximity and boundary layer effects varies greatly between situations, and so does the balance between the two effects. Two separate corrections specific to the potential effect and the boundary layer itself are probably required. Such corrections could help overcome the two-diameter limit when exploring a flow close to a wall. The first step is to define the wall distance from which the corrections should be triggered. The position where the probe’s tip reaches the theoretical boundary layer is a natural candidate as an indicator. However, the correlation is not good in all cases. A better indicator could consider the probe boundary layer thickness, probe diameter, and wall boundary layer thickness. It is also possible that the local acceleration around the probe affects the wall boundary layer thickness when the probe comes closer to the wall. CFD simulations would help identify those quantities.
- -
- A significant feature of the interaction between the boundary layer and the wall-proximity effects is the yaw coefficient’s weak evolution for a positive probe pitch, as highlighted in Figure 23 (the diagram’s lower part looks insensitive to the wall distance). A hypothesis for this observation is that the elbow in the probe, which is closer to the wall than the probe’s head, protects it from the most significant changes in the local velocity distribution. PIV measurements in the horizontal plane could help investigate this hypothesis. Also, the probe’s bend is above its head in these positions. The head cannot be as close to the wall as in the rest of the map. This prevents the boundary layer or the wall proximity from affecting the coefficients as much as in the prediction shown in Figure 22, for which the head is brought into contact with the wall, even if this is not physically possible.
- -
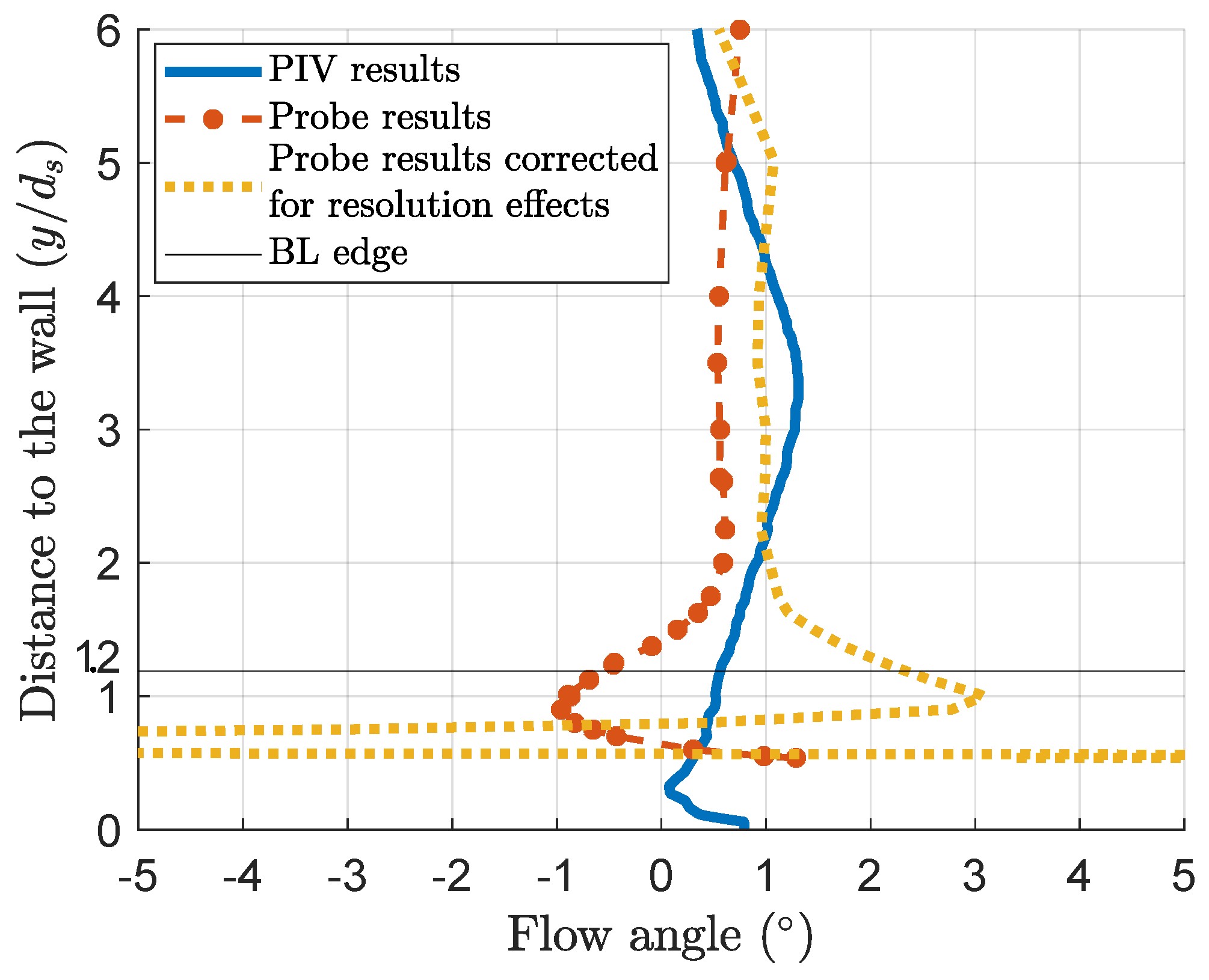
- Section 3.3 shows that the resolution problem is the main issue responsible for the boundary layer effect on 5HP measurement errors near a wall. A correction of the error due to the distance between the probe holes, as described in an article by Vinnemeier [10], is hard to enforce in the wall-proximity case. The strongest gradients happen in regions without data, requiring interpolation for the hole furthest from the wall. The extrapolation can lead to aberrant results, as shown in Figure 29. The correction helps the probe measurements better fit the PIV results between two and six probe diameters where there is enough data to perform the interpolations. Models of the boundary layer and wall-proximity effects could help extrapolate the data missing for this correction. CFD could help to separate the two error sources to design the corrections.
- -
- During a traverse in a real test bench, the probe can come close to at least two walls: the one in which it is inserted and the one at the other traverse end. Only the proximity of the wall opposite to the probe insertion hole is considered here. Another simplification in this work is that the turbomachine’s walls’ curvature is disregarded, and the flow is often not axial. The experimental conditions are also far from engine conditions, being incompressible when the flow can reach transonic velocity in the high-pressure turbine region.
- -
- The usual Reynolds number in 5HP turbomachines studies ranges from to [19], whereas it spans from to in this study. In the Reynolds region not explored in this work, above , in incompressible flows, the boundary layers would be thin compared to the probe diameter. The authors would expect the angle calibration coefficients to behave similarly to the results from Section 3.1. Mach numbers can approach 1 in turbomachines, whereas this work focuses on incompressible flows. A complementary study would be necessary to extend the results to high Reynolds numbers in compressible flow, as they might change the way the probe interacts with the wall.
- -
- Mach and Reynolds number changes have been shown to be able to adversely affect 5HP measurements [9,20,21,22,23,24]. Decoupling Mach and Reynolds number effects was not possible in this work because the quantity , which is very significant here, adds constraints to the problem. However, this work’s probe’s calibrations in the Mach and Reynolds number range considered here showed no Mach or Reynolds number effect on the yaw and pitch calibration coefficients. The errors when measuring close to the wall in the Mach and Reynolds number range considered here for this work’s probe are then not expected to come from changes in the free-stream calibration due to Mach and Reynolds number changes.
- -
- A deeper look into the evolution of each probe hole pressure shows that the hole closest to the wall is very sensitive to the wall proximity and the main hole responsible for the pitch angle coefficient drift. As 5HPs can perform measurements using solely the centre and three side holes [5], an algorithm that predicts a value for the sensible pressure hole from the four other pressures and compares it to the measured value can be designed. A significant difference between the predicted and the measured value could serve as a signal, for example, that the post-processing should be performed using a zonal calibration or that measurements are less reliable.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bidan, G.; Champion, J.L. Development of ultra high temperature multi-hole probes. In Proceedings of the XXIV Biennial Symposium on Measuring Techniques in Turbomachinery, Prague, Czech Republic, 29–31 August 2018; pp. 105–111. [Google Scholar]
- Georgiou, D.P.; Milidonis, K.F. Fabrication and calibration of a sub-miniature 5-hole probe with embedded pressure sensors for use in extremely confined and complex flow areas in turbomachinery research facilities. Flow Meas. Instrum. 2014, 39, 54–63. [Google Scholar] [CrossRef]
- Ligrani, P.M.; Singer, B.A.; Baun, L.R. Miniature five-hole pressure probe for measurement of three mean velocity components in low-speed flows. J. Phys. E Sci. Instruments 1989, 22, 868–876. [Google Scholar] [CrossRef]
- Hall, B.F.; Povey, T. The Oxford Probe: An open access five-hole probe for aerodynamic measurements. Meas. Sci. Technol. 2017, 28, 035004. [Google Scholar] [CrossRef]
- Paul, A.; Upadhyay, R.; Jain, A. A novel calibration algorithm for five-hole pressure probe. Int. J. Eng. Sci. Technol. 2011, 3, 89–95. [Google Scholar] [CrossRef]
- Ma, S.; Hu, J.; Wang, X.; Ji, J. The Application of a Laser-Printed Miniature Five-Hole Probe in the End-Wall Flow Measurement of a Multistage Axial Compressor. Aerospace 2023, 10, 1020. [Google Scholar] [CrossRef]
- Gaetani, P.; Persico, G. Technology Development of Fast-Response Aerodynamic Pressure Probes. Int. J. Turbomach. Propuls. Power 2020, 5, 6. [Google Scholar] [CrossRef]
- Bartsch, C.; Hölle, M.; Jeschke, P.; Metzler, T. 1D Adaptive Measurement Grid for Improved Pneumatic Probe Measurements. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Montreal, QC, Canada, 15–19 June 2015; p. V006T05A005. [Google Scholar] [CrossRef]
- Bailey, S.C.C.; Hultmark, M.; Monty, J.P.; Alfredsson, P.H.; Chong, M.S.; Duncan, R.D.; Fransson, J.H.M.; Hutchins, N.; Marusic, I.; McKeon, B.J.; et al. Obtaining accurate mean velocity measurements in high Reynolds number turbulent boundary layers using Pitot tubes. J. Fluid Mech. 2013, 715, 642–670. [Google Scholar] [CrossRef]
- Vinnemeier, F.; Simon, L.; Koschel, W. Korrektur des Kopfgeometrieeinflusses einer Fünfloch- Drucksonde auf die Meßergebnisse / Correction method for the head geometry influence of a five-hole pressure probe on the measurement results. Tech. Mess. 1990, 57, 296–303. [Google Scholar] [CrossRef]
- MacMillan, F.A. Experiments on Pitot-Tubes in Shear Flow. In Aeronautical Research Council Reports & Memoranda; Cranfield University: Bedford, UK, 1957. [Google Scholar]
- Treaster, A.L.; Yocum, A. The Calibration and Application of Five-Hole Probes; Technical Report; Pennsylvania State University Park Applied Research Lab: State College, PA, USA, 1978. [Google Scholar]
- Jangir, R.; Sitaram, N.; Gajanan, C. A Miniature Four-Hole Probe for Measurement of Three-Dimensional Flow with Large Gradients. Int. J. Rotating Mach. 2014, 2014, 297861. [Google Scholar] [CrossRef][Green Version]
- Smout, P.D.; Ivey, P.C. Investigation of Wedge Probe Wall Proximity Effects: Part 1—Experimental Study; American Society of Mechanical Engineers: New York, NY, USA, 1996; Volume 78767. [Google Scholar]
- Lee, S.W.; Yoon, T.J. An investigation of wall-proximity effect using a typical large-scale five-hole probe. KSME Int. J. 1999, 13, 273–285. [Google Scholar] [CrossRef]
- Grimshaw, S.D.; Taylor, J.V. Fast Settling Millimetre-Scale Five-Hole Probes. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Republic of Korea, 13–17 June 2016. [Google Scholar] [CrossRef]
- Appukuttan, R.J.A.; Miller, H.P.H. Probe Measurement Errors Caused by Shear Flows. In Proceedings of the The 17th Symposium on Measuring Techniques in Transonic and Supersonic Flow in Cascades and Turbomachines, Stockholm, Sweden, 9–10 September 2004; pp. 105–111. [Google Scholar]
- Sitaram, N.; Lakshminarayana, B.; Ravindranath, A. Conventional probes for the relative flow measurement in a turbomachinery rotor blade passage. J. Eng. Power-Trans. ASME 1981, 103, 406–414. [Google Scholar] [CrossRef]
- Lee, S.W.; Jun, S.B. Reynolds number effects on the non-nulling calibration of a cone-type five-hole probe for turbomachinery applications. J. Mech. Sci. Technol. 2005, 19, 1632–1648. [Google Scholar] [CrossRef]
- Boerner, M.; Bitter, M.; Niehuis, R. On the challenge of five-hole-probe measurements at high subsonic Mach numbers in the wake of transonic turbine cascades. J. Glob. Power Propuls. Soc. 2018, 2, 453–464. [Google Scholar] [CrossRef]
- Kost, F. The Behaviour of Probes in Transonic Flowfields of Turbomachinery. In Proceedings of the 8th European Conference on Turbomachinery—Fluid Dynamics and Thermodynamics, Graz, Austria, 23–27 March 2009. [Google Scholar]
- Sitaram, N.; Kumar, V.; Pillala, V.; Purushothama, B.; Prasad, B. Calibration of Multi Hole Pressure Probes for Three Dimensional Flow Measurements at High Mach Numbers. In Proceedings of the 12th International Symposium on Experimental Computational Aerothermodynamics of Internal Flows, Genova, Italy, 13–16 July 2015; pp. 1–9. [Google Scholar]
- Houtman, E.M.; Bannink, W.J. The Calibration and Measuring Procedure of a Five-Hole Hemispherical Head Probe in Compressible Flow; Recon Technical Report N; NASA STI: Hampton, VI, USA, 1989. [Google Scholar]
- Dominy, R.G.; Hodson, H.P. An Investigation of Factors Influencing the Calibration of 5-Hole Probes for 3-D Flow Measurements. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air. American Society of Mechanical Engineers, Cologne, Germany, 1–4 June 1992; Volume 78934, p. V001T01A077. [Google Scholar] [CrossRef]
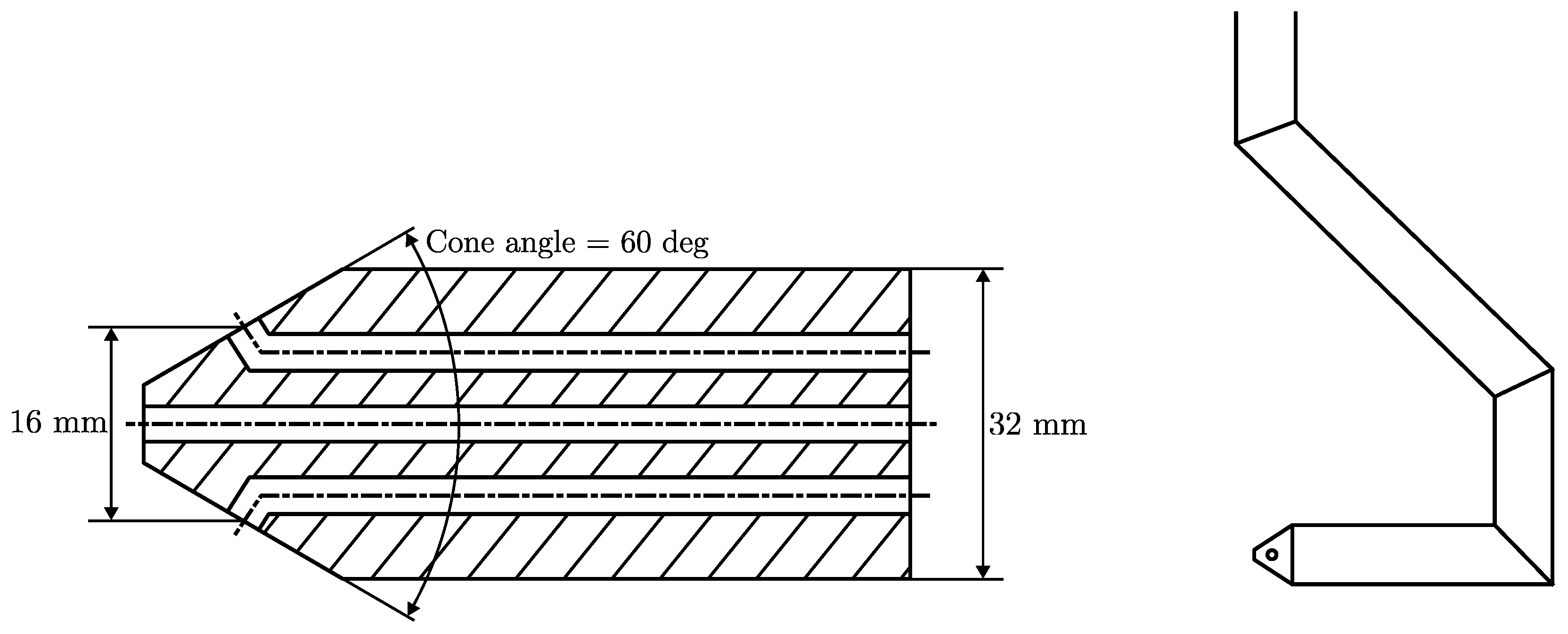
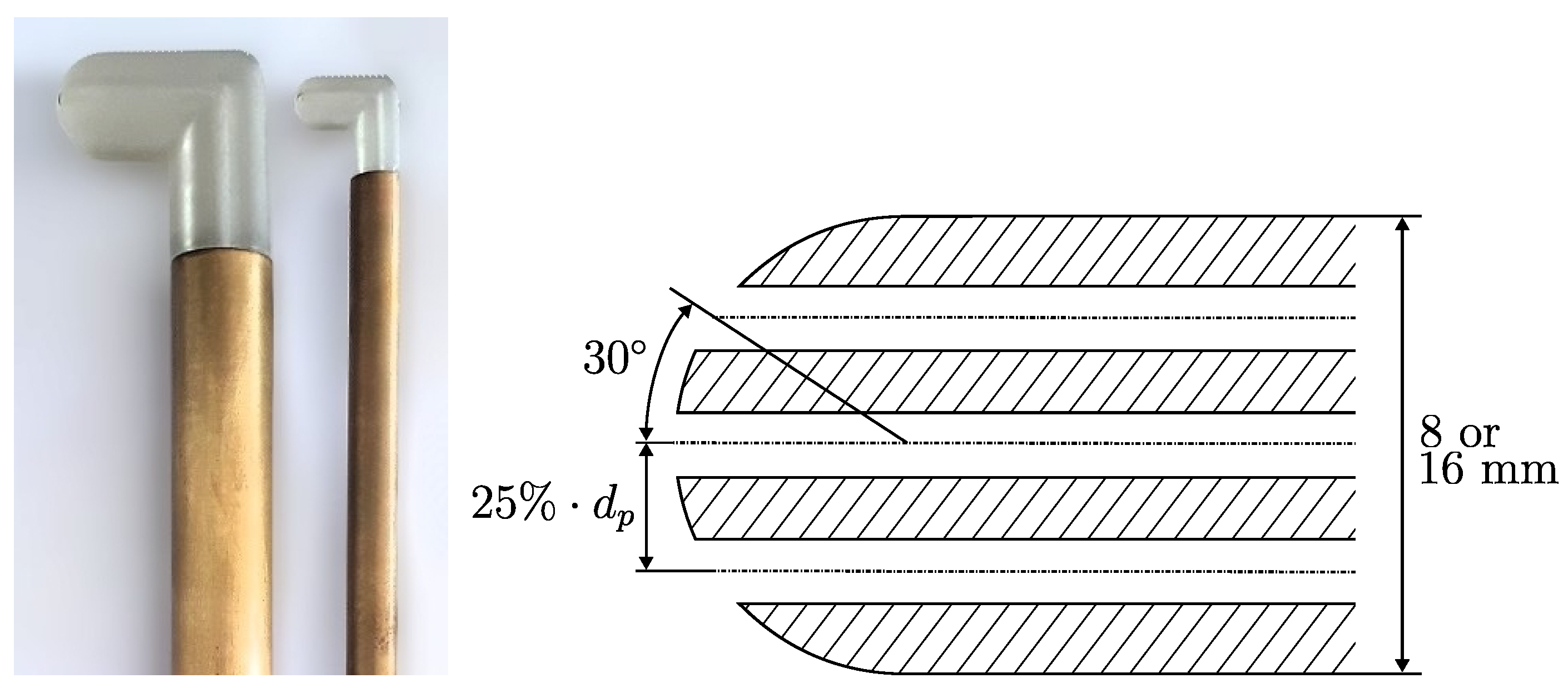








| Probe | Flow Speed (m/s) | (mm) | Reynolds Number | |
|---|---|---|---|---|
| Lee [15] | N/A | 32 | 0.028 | |
| Large probe | 16 | 16 | Up: 0.16 Down: 0.34 | |
| Large probe | 8 | 16 | Up: 0.18 Down: 0.38 | |
| Medium probe | 16 | 8 | Up: 0.33 Down: 0.69 | |
| Medium probe | 8 | 8 | Up: 0.36 Down: 0.76 |
| Traverse | Pitch | Yaw |
|---|---|---|
| 1 | 0° | 0° |
| 2 | 0° | 10° |
| 3 | 10° | 0° |
| 4 | 10° | 10° |
| 5 | −10° | 0° |
| 6 | −10° | 10° |
| Source | Uncertainty | Origin |
|---|---|---|
| Probe’s sensors | 0.12%FS + 0.5% of the result | Calibrations |
| Total pressure sensor | 0.1%FS + 1% of the result | Calibrations |
| Static pressure sensor | 0.5%FS | Data sheet |
| Probe mount | 0.2° in pitch and yaw setting 0.1 mm in height 1 mm in stream-wise position | Graduations on the gear |
| Data reduction method | 0.2° in pitch and yaw measurement | Statistics |
| PIV post-processing | 95% confidence interval | Normal sampling distribution |
| Taylor series expansion | ||
| Taylor series expansion | ||
| Room temperature | 0.5 °C | Precision of the display |
| Atmospheric pressure | 0.01%FS + 1 digit | Calibration sheet |
| Angle Reading Error | P = 0° | P = −10° |
|---|---|---|
| Y = 0° | 3.3° | 6.7° |
| Y = 10° | 3.4° | 6.2° |
| Experiment | Probe Orientation | Horizontal Scaling | Vertical Scaling | Minimal Distance |
|---|---|---|---|---|
| Constant | / | 1 | 1 | 2.3 |
| This work (ref) | P = −10°, Y = 0° | 1 | 1 | 0% |
| This work | P = −10°, Y = 10° | 0.95 | 0.99 | 0.8% |
| This work | P = 0°, Y = 0° | 0.66 | 0.93 | 0.53% |
| This work | P = 0°, Y = 10° | 0.49 | 0.87 | 0.6% |
| This work | P = 10°, Y = 0° | 0.79 | 0.99 | 0.8% |
| This work | P = 10°, Y = 10° | 0.69 | 0.96 | 0.9% |
| Lee | P = −10°, Y = 0° | 1.7 | 0.97 | 2.2% |
| Lee | P = 0°, Y = 0° | 1.5 | 1.0 | 1.7% |
| Lee | P = 10°, Y = 0° | 0.14 | 0.6 | 13% |
| Experiment | Probe Orientation | Horizontal Deformation | Vertical Deformation | Minimal Distance |
|---|---|---|---|---|
| This work | P = −10°, Y = 10° | 1.7 | 1 | 4.8% |
| This work | P = 0°, Y = 10° | 2.5 | 1.0 | 2.1% |
| This work | P = 10°, Y = 10° | 2.14 | 0.97 | 2.3% |
| Lee | P = −10°, Y = 10° | 7.2 | 0.98 | 16% |
| Lee | P = −10°, Y = −10° | −9.5 | 0.98 | 11% |
| Lee | P = 0°, Y = 10° | 3.8 | 1.0 | 4% |
| Lee | P = 0°, Y = −10° | −7.1 | 1.0 | 9% |
| Probe Distanceto the Wall () | Max Velocity () |
|---|---|
| 4 | 1.10 |
| 3 | 1.13 |
| 2 | 1.08 |
| 1.5 | 0.99 |
| 1.25 | 1.01 |
| 1 | 0.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Vasseur, A.; Binder, N.; Fontaneto, F.; Champion, J.-L. Wall-Proximity Effects on Five-Hole Probe Measurements. Int. J. Turbomach. Propuls. Power 2024, 9, 16. https://doi.org/10.3390/ijtpp9020016
Vasseur A, Binder N, Fontaneto F, Champion J-L. Wall-Proximity Effects on Five-Hole Probe Measurements. International Journal of Turbomachinery, Propulsion and Power. 2024; 9(2):16. https://doi.org/10.3390/ijtpp9020016
Chicago/Turabian StyleVasseur, Adrien, Nicolas Binder, Fabrizio Fontaneto, and Jean-Louis Champion. 2024. "Wall-Proximity Effects on Five-Hole Probe Measurements" International Journal of Turbomachinery, Propulsion and Power 9, no. 2: 16. https://doi.org/10.3390/ijtpp9020016
APA StyleVasseur, A., Binder, N., Fontaneto, F., & Champion, J.-L. (2024). Wall-Proximity Effects on Five-Hole Probe Measurements. International Journal of Turbomachinery, Propulsion and Power, 9(2), 16. https://doi.org/10.3390/ijtpp9020016








