Steady and Unsteady Numerical Characterization of the Secondary Flow Structures of a Highly Loaded Low-Pressure Compressor Stage ^†

Abstract

This paper presents the numerical characterization of a highly loaded compressor by means of 3D unsteady RANS simulations. The focus is on critical flow structures and their evolution at different operating points of the machine. First, the numerical setup and mesh quality are presented to support the reliability of the provided results. The comparison against experiments is then described for this purpose. Later, a full description of the unsteady behavior of the machine is provided, giving special attention to the two regions where the most critical features are expected: the rotor hub wall and the casing. Rotor–stator interactions are then investigated and the role of the inlet guide vane (IGV) is finally discussed. Results are analyzed at design and near-stall conditions, with a focus on the behavior close to the stability limit at 100% speed.

1. Introduction

Secondary flow structures are one of the main sources of performance and stability loss in axial compressors. They are inherently three-dimensional, unsteady, and strongly coupled with a variety of other phenomena within the blade passage and its design characteristics. Because of their effect on performance, stability, and lifetime, research is devoting significant efforts to understanding the evolution of these mechanisms. Many attempts have been made in the last few years to investigate secondary flow structures experimentally and numerically in axial compressors. The focus has been on three unsteady phenomena identified as the main sources of losses: (1) hub corner separations; (2) tip leakage flows; and (3) their interaction with rotor–stator wakes with consequent induced clocking effects in multistage configurations. The impact of the hub separation and its role in the development of a corner stall has been widely investigated in the past [1,2,3]. The authors introduced the role of the traverse pressure gradient on the development of an open separation and proposed new flow parameters to quantify the margin to stall. In this context, they classified the hub corner separation as a critical secondary structure that could possibly lead to aerodynamic stall, especially in highly loaded machines like the one presented in this paper. A similar analysis was proposed for the unsteady characterization of the tip clearance flow [4,5,6,7]. The flow redistribution observable at the casing prior to the stall and its impact on the development of spike-type stall inception mechanisms was proposed, together with suggestions for stability enhancement. Moreover, multiple studies are available in the literature concerning rotor–stator wake interactions and the consequent impact from clocking [8,9,10]. The authors proposed an overview of the main interaction mechanisms in axial compressors and described their impact on other flow phenomena, such as the tip leakage flow.

The present paper is aimed at characterizing the main secondary flow structures in a highly loaded low-pressure compressor, along with the rotor–stator wake interactions. The intent is to track their unsteady evolution and contribution to the performance deterioration, and to provide a global picture of the critical flow phenomena for the considered stage. The role of the clocking between the IGV and outlet stator is also investigated as a driving parameter for the incidence variation at the stator inlet. This prior knowledge is of fundamental interest for design.

This manuscript corresponds to the paper published in the proceedings of the 15th European Turbomachinery Conference [11].

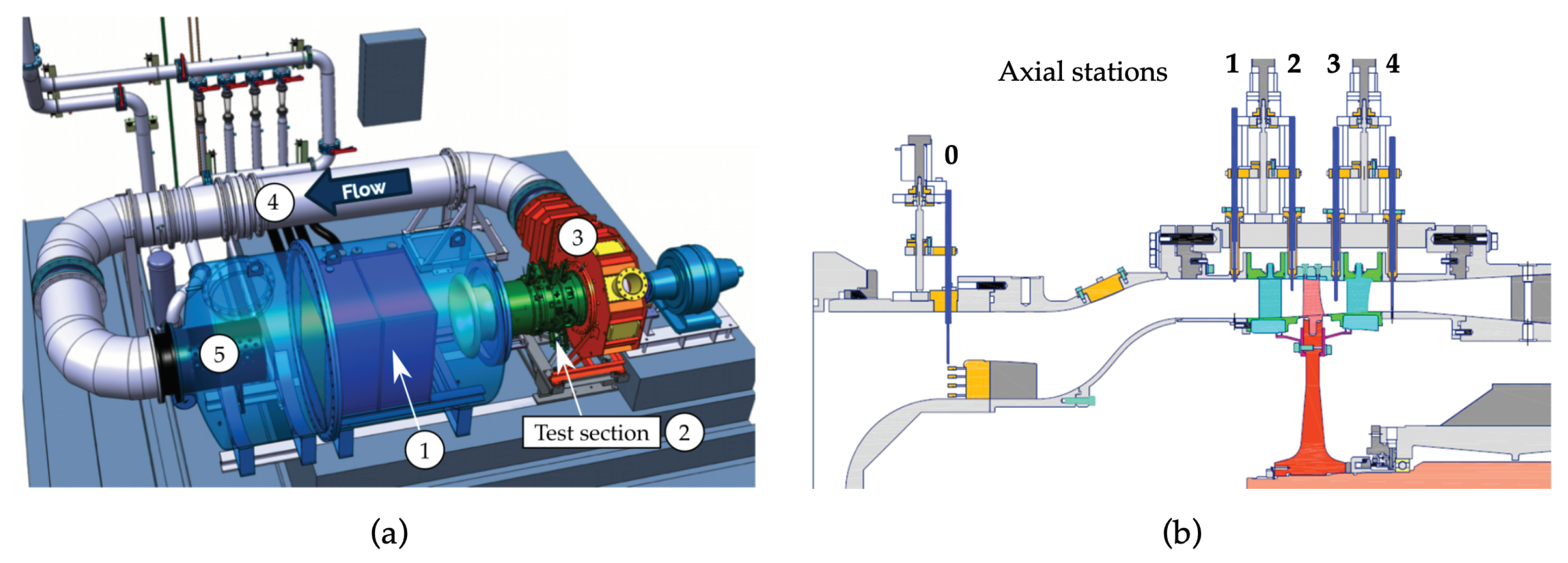
2. Compressor Test Section and Rig

The von Karman Institute high-speed compressor test rig R4 (Figure 1a) was employed for the experimental characterization of the stage. It is composed by a tank used as settling chamber (1); the test section (2); a discharging collector at the compressor outlet (3); a return channel to guide the air back to the reservoir (4); and a throttling valve (5). The heat exchanger installed in the tank and the closed-loop configuration allow to set the temperature and pressure at the test section inlet independently, so that cruise and take-off conditions can be simulated. The throttle valve is employed to modify the operating point of the compressor. The tested machine is a low-pressure compressor fully characterized in clean conditions under the EU FP7 DREAM project (valiDation of Radical Engine Architecture systeMs, GA: 211861). Figure 1b shows the meridional view of the compressor with the axial measurement planes available. It has 100, 76, and 100 blades for the IGV, rotor, and stator, respectively, and it is representative of the first stage of a modern low-pressure compressor.

3. Numerical Method

3.1. Numerical Setup

The structured, cell-centered finite-volume solver FineTurbo of Cadence was employed for the simulations. Fully turbulent compressible unsteady RANS equations were considered for the study, and experimentally obtained profiles of the total pressure, total temperature, and flow angle were imposed at the inlet for the main equations, along with the turbulence intensity and viscosity ratio for the turbulence model. Obviously, no experimental value was available for the viscosity ratio. Since values ranging between 10 and 100 are suggested for internal flows (e.g., turbomachinery) [12], it was set to an averaged value equal to 50. The outlet boundary condition was set to the experimental mass flow. The air was considered as a calorically perfect gas and the walls were considered adiabatic. The validity and robustness of different turbulence models were tested against the experimental results, and the Chien $k-\epsilon$ model was finally considered. Further details can be found in Toracchio et al. [13]. Moreover, the mixing-plane approach was used at the rotor–stator interfaces for the steady RANS simulations.

Concerning the unsteady numerical setup, a domain scaling approach with a sliding mesh for the rotor–stator interfaces was employed. To do so, one rotor blade was removed, leading to a common periodicity of 4/3/4 for the IGV, rotor, and stator, respectively. To assess the impact of a reduced domain on the computed results, the span-wise distribution of the rotor diffusion factor (as defined in [2]) and the frequency spectra at the rotor outlet were computed. It was found that a maximum absolute variation of 0.004 in the diffusion factor appeared due to scaling of the domain. Moreover, as also shown later in the paper, the dominant fluctuations visible in the flow field were due to the rotor–stator interactions, meaning that the frequency shift was only driven by the reduction of the rotor blades. Since only one rotor blade was removed for the scaling, the frequency shift computed was 1.31% of the rotor BPF. The small value of these parameters motivated therefore the use of a domain scaling approach, which was not expected to alter the findings of the present study. In total, 120 time steps per blade passing period were considered for a good reconstruction up to the 4th harmonic of the blade-passing frequency (BPF) and to allow the proper description of every relevant physical phenomenon. To motivate the number of time steps employed, the range of expected frequencies in the compressor was first estimated on the basis of the literature [14,15,16,17,18]. Moreover, following common practice [19,20,21], 30 time steps per resolved harmonic were used. Consequently, a total of 120 steps per period were used for the present study.

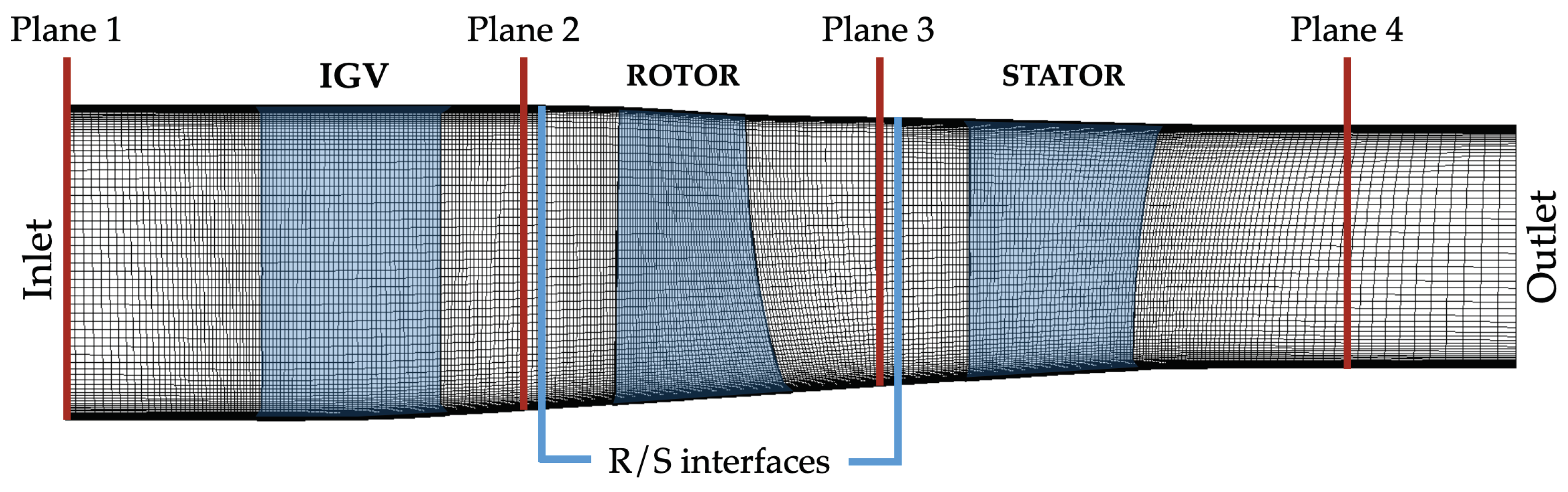
3.2. Computational Domain

The numerical domain, shown in Figure 2 (meridional view), is representative of the 1.5 stage compressor analyzed in this paper. The fillets were considered given their impact on the evolution of the secondary flows. The impact of closed cavities was assessed against a numerical domain where the cavities were removed. A block with matching connections was added at the cavity interface to connect the cavity geometry to the rotor hub. The same mesh topology was kept in the blade passage between the two configurations to avoid any possible impact of a different mesh on the obtained results. It was found that the interaction of the cavity introduced a variation in incidence at the rotor inlet by 0.3°. Such variation in incidence induced an increase in the hub corner separation size in the span-wise direction of 1.9%, with a consequent impact on the pressure ratio of the compressor of 0.16% at DE conditions. To further understand the influence of closed cavities, their small impact on the main channel flow was numerically and experimentally confirmed by the literature [22,23]. Given, therefore, the negligible impact of cavities on the flow features of the compressor and the increased computational time required (2.5 million cells added), cavities were not included in the final configuration of the numerical domain. Moreover, hot geometries, which consider the centrifugal force and the temperature effects at the nominal speed of the machine under operation, were considered with the rotor tip gap set to its averaged measured value. The 100% speed line was considered in the present study. To conclude, the outlet section was located relatively far downstream of experimental plane 4 to reduce the influence of the outlet boundary condition.

3.3. Grid Quality Assessment

Every blade row was meshed using a O4H topology, combined with an OH mesh to cover the extension of the rotor in the tip gap region. The finest mesh (later shown in the grid refinement study) was characterized by 161, 241, and 161 cells with a 20% constant size over the blade span for the IGV, rotor, and stator, respectively, with 81 cells in the tip gap region. The B2B section offset with a 25° minimum dihedral angle was used to mesh the hub and shroud fillets to guarantee acceptable skewness and resolution. Moreover, 35 points were considered along the fillet for a good resolution at the hub wall region, where most of the secondary flow phenomena take place. Everywhere, the non-dimensional wall normal resolution $y^{+}$ and the maximum expansion ratio at the wall were both smaller than 1.2. The multi-block structured grid was generated using Autogrid5 and IGG (Cadence/Numeca).

A grid convergence study was performed at DE conditions on a single passage to retrieve the optimal compromise between cost and the quality of the computation. Three levels were considered with refinement in every direction equal to 2 at each step, and with 1.2, 9.2, and 73.8 million cells for the coarse, medium, and fine mesh levels, respectively. Figure 3a,b show the evolution of the pressure ratio and skin friction lines on the rotor suction side, where the most important secondary flow phenomena occur, with the mesh resolution.

The medium and fine mesh provided results that were very close, with a percentage difference of 0.32% in the pressure ratio. The differences in the separation length and height on the rotor suction side were considered negligible, especially in view of the qualitative analysis of the critical flow features for the compressor. The latter, like the hub corner separation, as shown later in the paper, were indeed well captured by the medium mesh. Moreover, the further improvement of the separation length prediction would require a much higher cell count on the rotor suction side, with a strong impact on the computational cost. The coarse mesh, instead, predicted a much larger separation length on the rotor suction side, which led to the drop in the pressure ratio highlighted in Figure 3a. The main flow features were well captured by the medium mesh, providing also an acceptable computational cost compared to the finest mesh. The medium mesh was therefore employed for the present study.

4. Experimental Environment

The access for the instrumentation, in the test section, is available circumferentially at 0°, 90°, 180°, and 270° at the IGV inlet (plane 1), IGV outlet (plane 2), rotor outlet (plane 3), and stator outlet (plane 4), allowing for the span-wise displacement of probes. The performance (both pressure ratio and efficiency) was computed through area-averaged total pressures and temperatures retrieved from rakes installed in plane 0 (stage inlet) and plane 4. In plane 0, the rakes were distributed uniformly at 90°, while, in plane 4, they were located at 90° from each other but slightly shifted to have a representative description of the flow quantities over an entire stator pitch. The uncertainties associated with the pressure ratio, efficiency, and mass flow, respectively, were ±0.00053, ±2%, and ±0.04 kg/s, expressed through the ASME method [24] in a 95% confidence interval. The unsteady acquisition, used to retrieve phase-locked-averaged total pressure maps, was performed with a fast-response pressure probe located at the rotor outlet and characterized by a bandwidth of 40 kHz with ±1.8 mbar uncertainty. Among the possible uses of the present instrumentation, only performance and phase-locked-average maps at rotor outlet were used in the present study for the validation of the CFD results. We refer to Dell’Era et al. [25] for further details about the experimental setup.

5. Results

The validation against experiments is first introduced to demonstrate the reliability of the numerical results in correctly reproducing the flow phenomena of interest. Global performance and rotor outlet maps are used for such purposes. The most critical flow phenomena and their unsteady evolution is then described: hub-corner separation, tip leakage flow, and rotor–stator interactions with induced clocking effects.

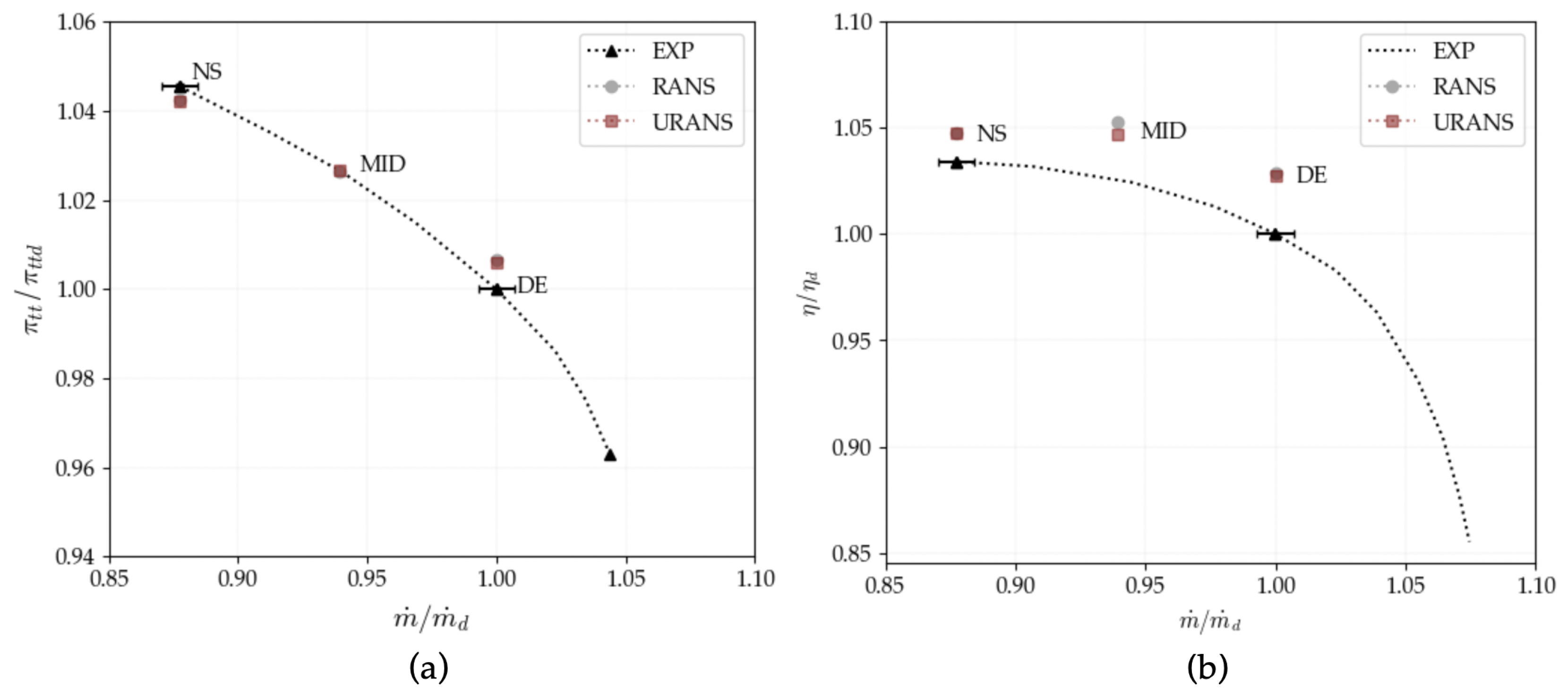
5.1. Validation against Experimental Results

5.1.1. Global Performance

Figure 4 compares the compressor performance obtained by steady and unsteady RANS simulations at three different operating points (DE, MID, and NS) to the experimental values. The total pressure ratio, efficiency, and mass flow are normalized with the experimental values at design conditions. Although the full map is presented, a more detailed experimental characterization is only available at design and near-stall operating points.

Both RANS and averaged URANS provide similar results throughout the operating range of the machine, with a maximum difference of 0.12% and 0.57% for the pressure ratio and efficiency at mid-mass-flow operating conditions. The maximum discrepancy against the experimental results arises at the design point, where a difference of 0.65% and 2.7% for pressure ratio and efficiency is present. However, the URANS simulations provide results slightly closer to the experiments compared to RANS. In Figure 4, only the mass flow uncertainty is reported.

5.1.2. Rotor Outlet Flow Field

The large rotor hub loading and degree of reaction of the present stage make the rotor corner region the primary location for the generation of critical flow structures in terms of loss and stability. For this reason, the rotor outlet total pressure map, non-dimensionalized with respect to the averaged total pressure in plane 0 (stage inlet), was chosen for comparison with experiments at the DE and NS operating points (Figure 5).

The averaged maps were computed as time mean for the URANS simulations, while a phase-locked-average approach was used for the experiments. The latter was employed since the probes did not rotate with the rotor and were fixed through the casing of the test section (fixed frame of reference). Although this could possibly lead to small differences due to the clocking of the probes with the IGV, the comparison with the simulations was still considered reliable and valid. Figure 5 shows that the CFD underestimates the size and intensity of the hub corner separation, along with the wake thickness and depth, at both operating points. Moreover, the size of the tip leakage flow is smaller, especially in the span-wise direction, compared to the experiments. This justifies why the pressure ratio and the efficiency computed through the simulations, especially at DE conditions, are larger with respect to the experiments.

Concerning the root mean square (RMS) of the fluctuations, there is qualitative agreement with the experiments. The comparison in this case cannot be quantitative since, for the simulations only, the deterministic part is represented but not the turbulent fluctuations, therefore reducing the amplitude of the RMS with respect to measurements. To improve the visualization in the regions of large fluctuation, the RMS of the simulations and experiments are reported with a different scale. However, from a qualitative point of view, the regions close to the hub and casing present large fluctuations linked to the development of the corner separation and the tip leakage flow, respectively. In particular, the presence of the hub corner separation is characterized by large periodic fluctuations due to the propagation of the IGV wakes coming upstream of the rotor row. The size and the intensity of this separation, together with its unsteadiness, further intensify at NS conditions, as predicted from the experiments. The phenomena of interest seem therefore qualitatively well captured.

An additional comparison between the CFD and experiments is shown in Figure 6, where the results of RANS and averaged URANS are compared with the phase-locked average of the experiments at the DE and NS operating points. As can be noticed in the total pressure percentage difference at design conditions (Figure 6b), the prediction of the casing region between RANS and URANS is very similar. At the hub, instead, URANS simulations show a 1.39% improvement in the total pressure prediction in the core of the corner separation, which justifies the better performance computed by the URANS approach at DE conditions (visible in Figure 4). Overall, better matching between the CFD and experiments is present at NS (Figure 6d). Again, the URANS simulation provides a 0.84% improvement in total pressure with respect to RANS close to the hub wall.

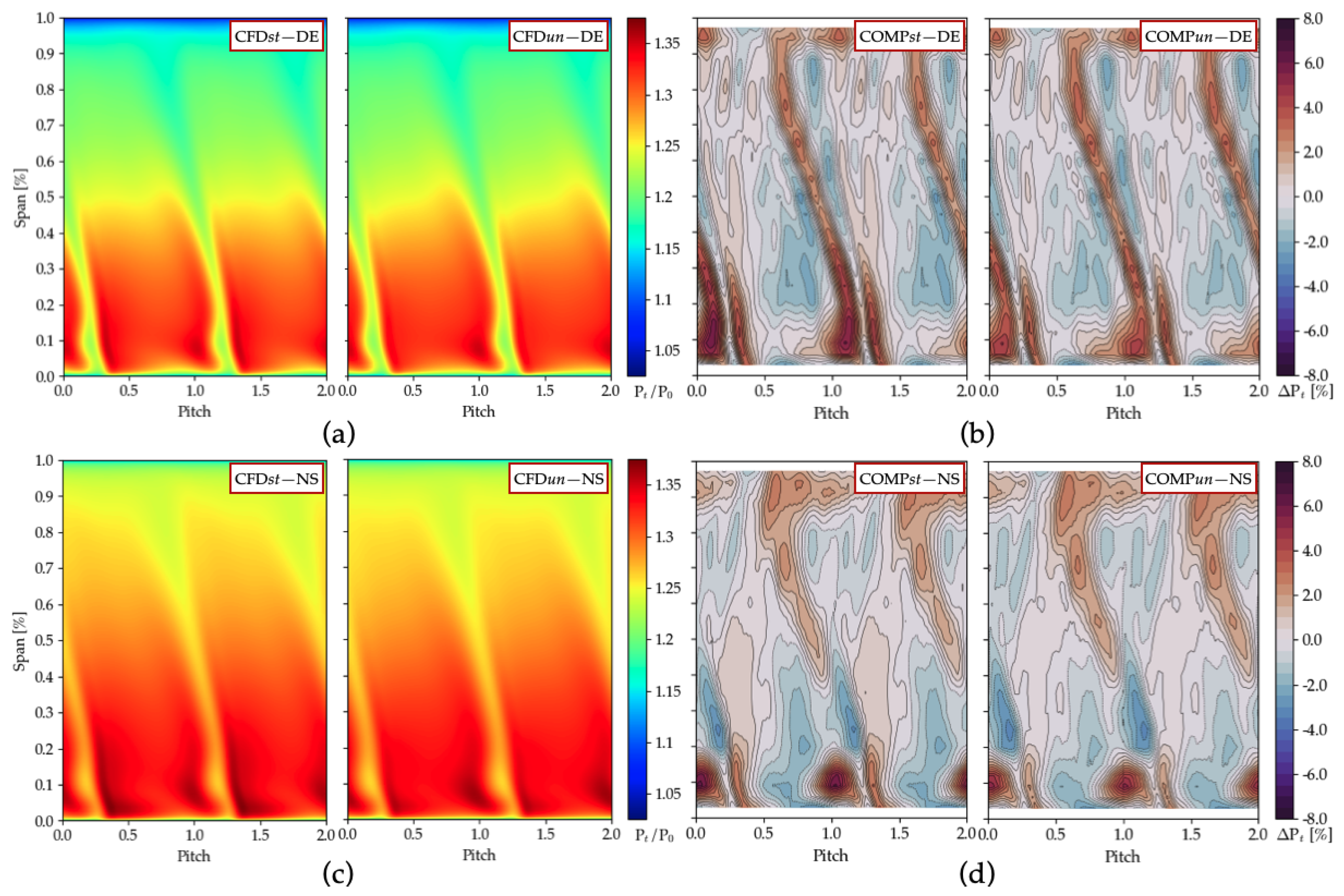
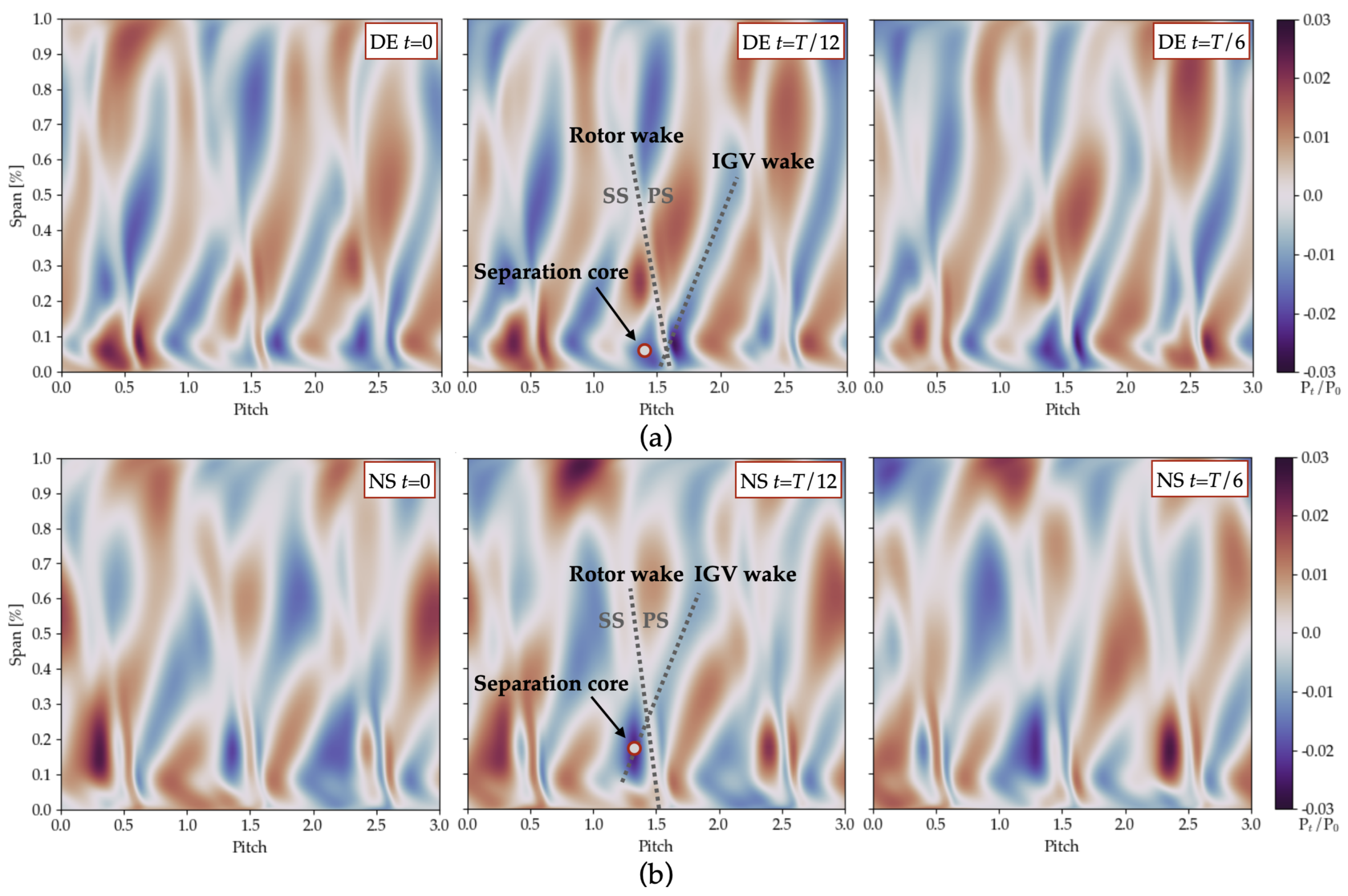
5.2. Critical Flow Structures

5.2.1. Hub Corner Separation

To describe the unsteady evolution of the hub corner separation and its interaction with the propagation of wakes, Figure 7 reports the instantaneous fluctuation of the rotor outlet total pressure with respect to the time mean ($p_t-\overline{p_t}$). Considering T as the rotor passing period, every $T/4$, the same pressure distribution shifted by one rotor pitch is expected due to the dominant contribution of the IGV wakes. To avoid the repetition of the same pattern but just shifted by one rotor passage, Figure 7 shows three time frames at $T/12$ time intervals. The results are reported in the relative frame of reference of the rotor. In Figure 7, the rotor wakes, the IGV wakes, and the core of the hub corner separation, visible in the first 30% of the blade span, are highlighted as regions of total pressure deficit compared to the averaged map. The size and the intensity of the hub corner separation seem enhanced at every interaction with the upstream IGV wakes. This is again a major effect possibly affecting the pressure ratio and efficiency of the URANS with respect to the RANS simulations, where the mutual interaction between rows is filtered out by the mixing plane. A wide total pressure reduction appears at mid-span and close to the tip region of the compressor, whose origin will be better explained in the next section. It is therefore possible to conclude that (1) the rotor hub corner separation features the largest unsteadiness, and it is therefore considered critical for the compressor; (2) the propagation of the IGV wakes is a dominant effect that drives most of the unsteady flow phenomena.

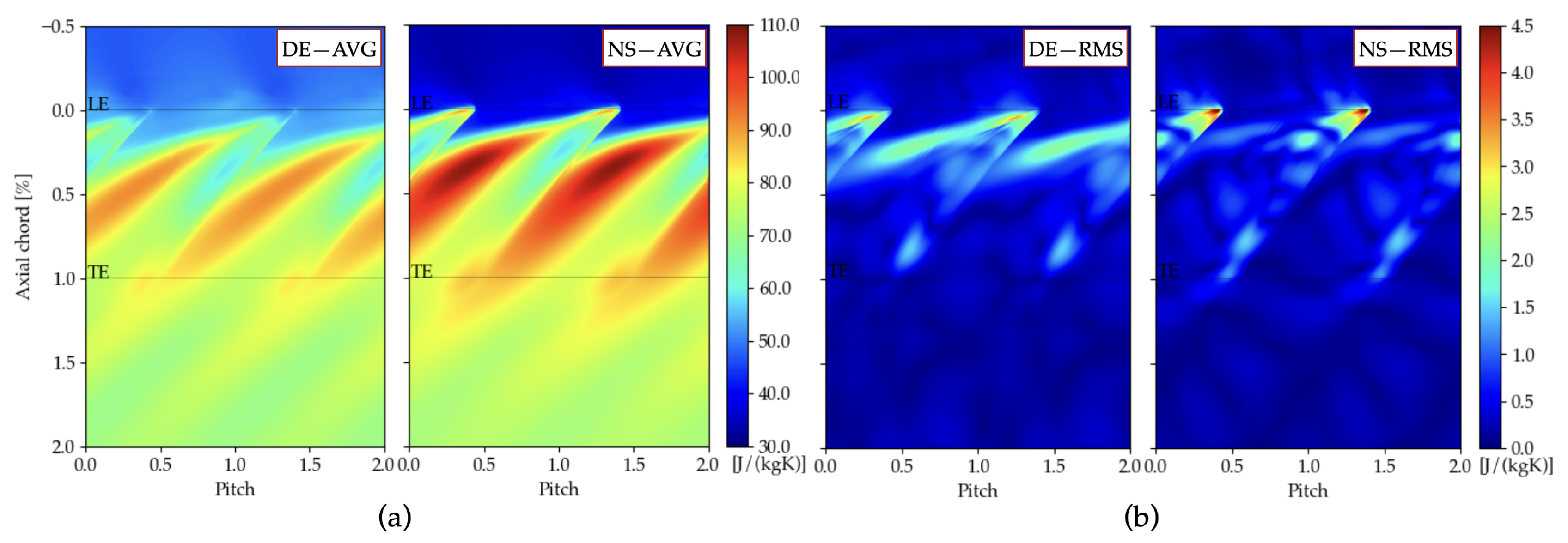
5.2.2. Tip Leakage Flow

The averaged entropy distribution at the casing and the RMS of the fluctuation at the DE and NS operating points are reported in Figure 8.

As expected, the tip leakage/main flow interface becomes more tangential closer to the stability limit of the machine and more entropy is generated. The same can be observed at the end of the blade trailing edge, where a second recirculating region appears. The tip leakage flow interface is characterized by a large value of the RMS, especially at the leading edge, where the interaction with the main flow increases the value of the entropy and the flow unsteadiness. The unsteady behavior of the flow at the casing can also be better visualized by Figure 9, reporting the instantaneous entropy fluctuation with respect to the mean flow. As for the rotor outlet map, three time frames of $T/12$ are considered on a time interval equal to the rotor passage.

As expected, the tip leakage flow fluctuation is mainly dominated by the interaction with the upstream IGV wakes, which are represented by alternation of high and low entropy regions. This alternation induced by the interaction of the upstream wakes with the tip leakage vortex was also investigated in Mailach et al. [10]. Contrarily to the DE conditions, where the large unsteadiness involved the entire core of the tip clearance flow, at NS, the value of the unsteadiness was mainly intensified at the interface and on the rotor suction side.

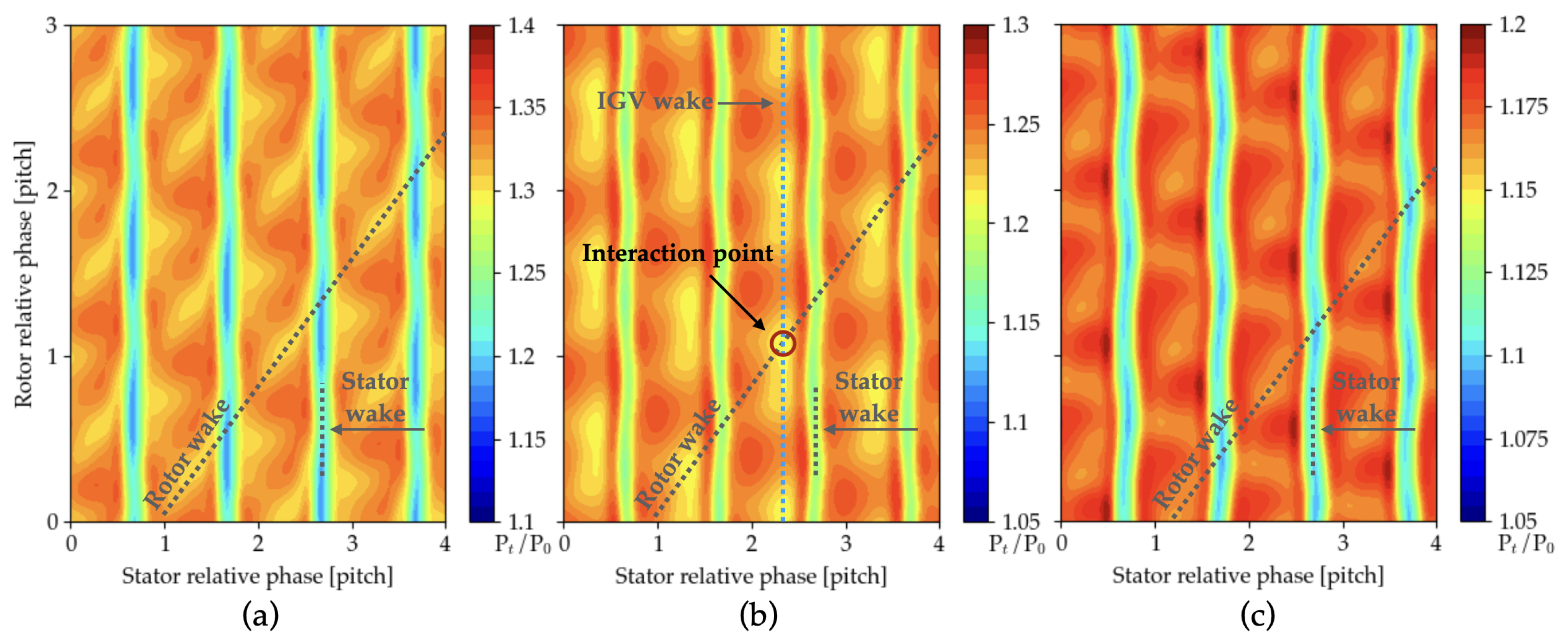
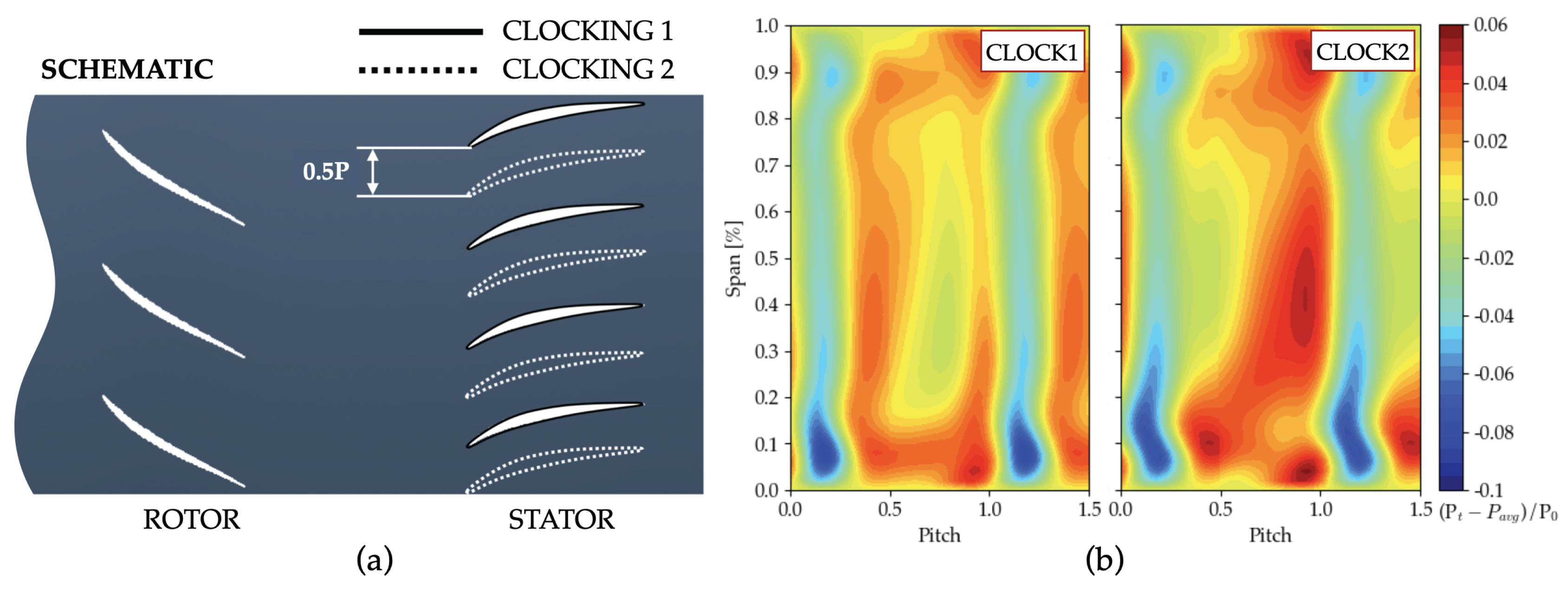
5.2.3. Rotor–Stator Interactions

The previous sections introduced the rotor–stator interactions as dominant effects driving the unsteady behavior of the hub and tip leakage flows in the rotor. However, the impact of the IGV wakes is not limited to the rotor row, as they propagate downstream with major effects also in the downstream stator of the stage. Figure 10 reports the stage outlet total pressure map, obtained by removing the pitch-averaged value at each span.

As can be observed, a low total pressure region appears in the middle of the passage (C marker) at DE conditions, which moves toward the stator suction side, and, at higher span, at NS conditions. The W marker identifies the location of the stator wake. The presence of reduced pressure, and therefore axial velocity, in the IGV wake results in an incidence variation at the stator inlet, with a detrimental impact, especially close to the stability limit of the machine.

To understand the origin of this reduced total pressure at the outlet of the stage, the phase–phase diagram of the stator outlet total pressure, at 10%, 50%, and 90% span, is reported in Figure 11 only for DE conditions. However, the same conclusions are valid for the NS operating point. The present plot was obtained extracting, at a specific span-wise location, the stage outlet total pressure over the entire stator pitch (characterized by four passages) for a time window equal to the full time period of the domain (corresponding to the time needed by the rotor to cover three passages). For this reason, the stator and rotor relative phases reported in the axes correspond, respectively, to four stator and three rotor passages. Given the large span-wise gradient of the total pressure, which corresponds in absolute terms to 16% of the experimental mass-averaged inlet total pressure in plane 0 ($P_0$), Figure 11a–c are reported with a different color map scale to improve the visualization of the results.

From Figure 11, the following dominant phenomena are visible: (1) the rotor wake (grey dotted line); (2) the IGV wake, mainly visible at the mid-span (blue). The latter is represented by a vertical line and it is therefore clocked with the outlet stator. Its propagation is more visible at mid-span and seems intensified by the interaction with the rotor wake, with a local reduction in the total pressure. Moreover, the pitch-wise location of the IGV wake seems in agreement with the position of the reduced total pressure region visible in Figure 10. To validate the hypothesis that the IGV wake is responsible for the total pressure reduction under investigation, Figure 12 reports the stage outlet total pressure map in two different configurations: (1) original clocking between the IGV and stator; (2) IGV–stator clocking modified by half stator pitch. It is important to remember that the IGV and the outlet stator are characterized by the same number of blades (100 for both rows) and that, in the CLOCKING 1 configuration (original configuration), the mechanical leading edge of the stator is aligned with the IGV trailing edge. This means that by moving the outlet stator by half pitch (to obtain the CLOCKING 2 configuration), its mechanical leading edge will be located in the middle of the IGV passage. These represent therefore two limiting conditions for the clocking, where IGV and stator are, respectively, aligned and misaligned by half the IGV/stator pitch, which is considered enough to track the IGV wake location at the outlet of the stage. For this reason, no further clocking positions are considered in the present study.

The variation in the IGV–stator clocking modifies the position of the low total pressure region, confirming that it comes from the propagation of the IGV wake (Figure 12). At the NS operating point, the location of the low total pressure region is modified, but the same conclusions obtained at DE conditions are valid. For this reason, off-design conditions are not reported in the paper. This study supports the idea that the IGV, which was installed in the present machine only to provide realistic inlet radial gradients, could be at the origin of several detrimental phenomena of the compressor. For design purposes, a different clocking, or the removal of the IGV row, could therefore reduce the risk of secondary flow structures and separations.

6. Conclusions

In this paper, the main sources of unsteadiness arising in a highly loaded axial compressor have been presented. The results of a URANS simulation have been employed to support the experimental observations and to provide an overall description of the critical flow structures. The main outcomes of the present work are as follows.

• The rotor hub corner separation is the flow phenomenon with the largest unsteadiness. Its periodic fluctuation is mainly dominated by the IGV wake propagation.
• The propagation of the IGV wakes is responsible for a reduced total pressure region located in the middle of the stator passage. In specific conditions, especially close to the stability limit of the machine, this pressure reduction could possibly lead to an increase in incidence at the stator inlet with the consequent intensification of the secondary flow structures and separations.
• In academic test stages, a very specific low-loading IGV can be used to provide realistic inlet profiles, representative of engine conditions. However, the IGV–stator clocking is shown here to potentially have a profound impact on the flow in the rotor and stator. Its role and the implications of its use should be questioned prior to the design of the test rig.