Surrogate Modeling of the Aeroacoustics of an NM80 Wind Turbine †
Abstract
:1. Introduction
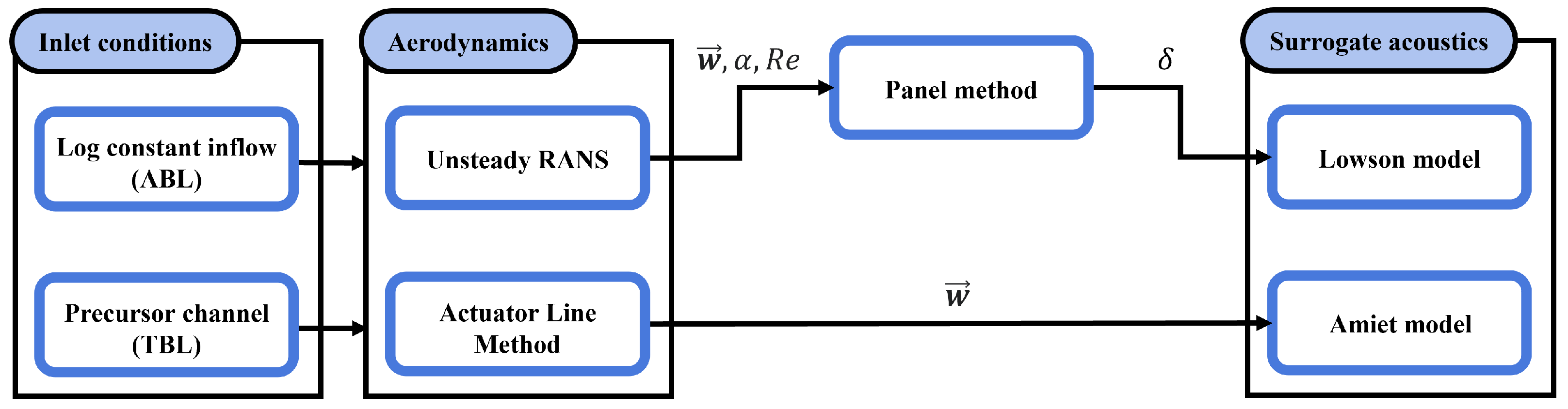
2. Surrogate Models
2.1. Aerodynamics: Actuator Line Method
2.2. Aeroacoustics: Amiet and Lowson Models
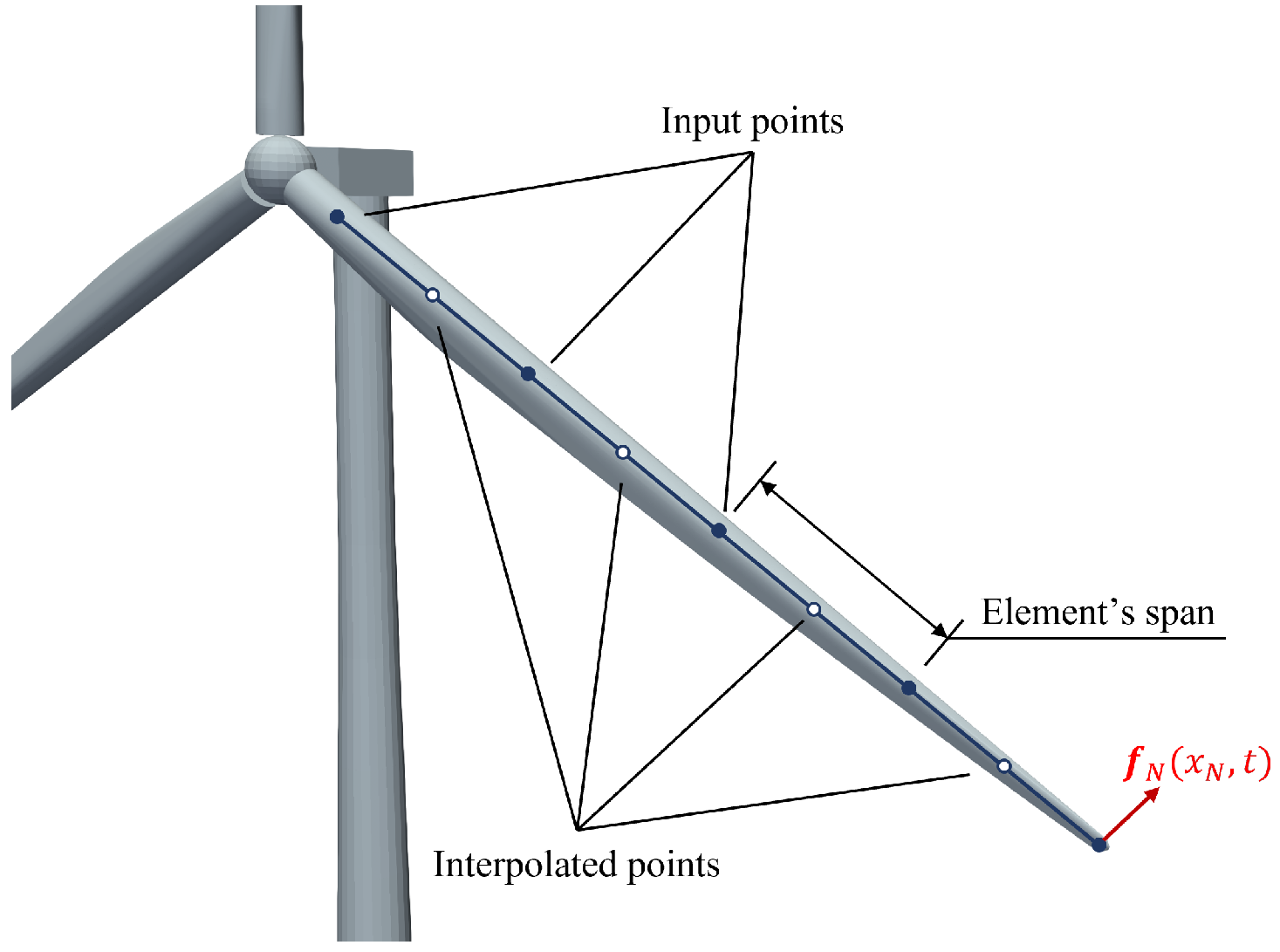
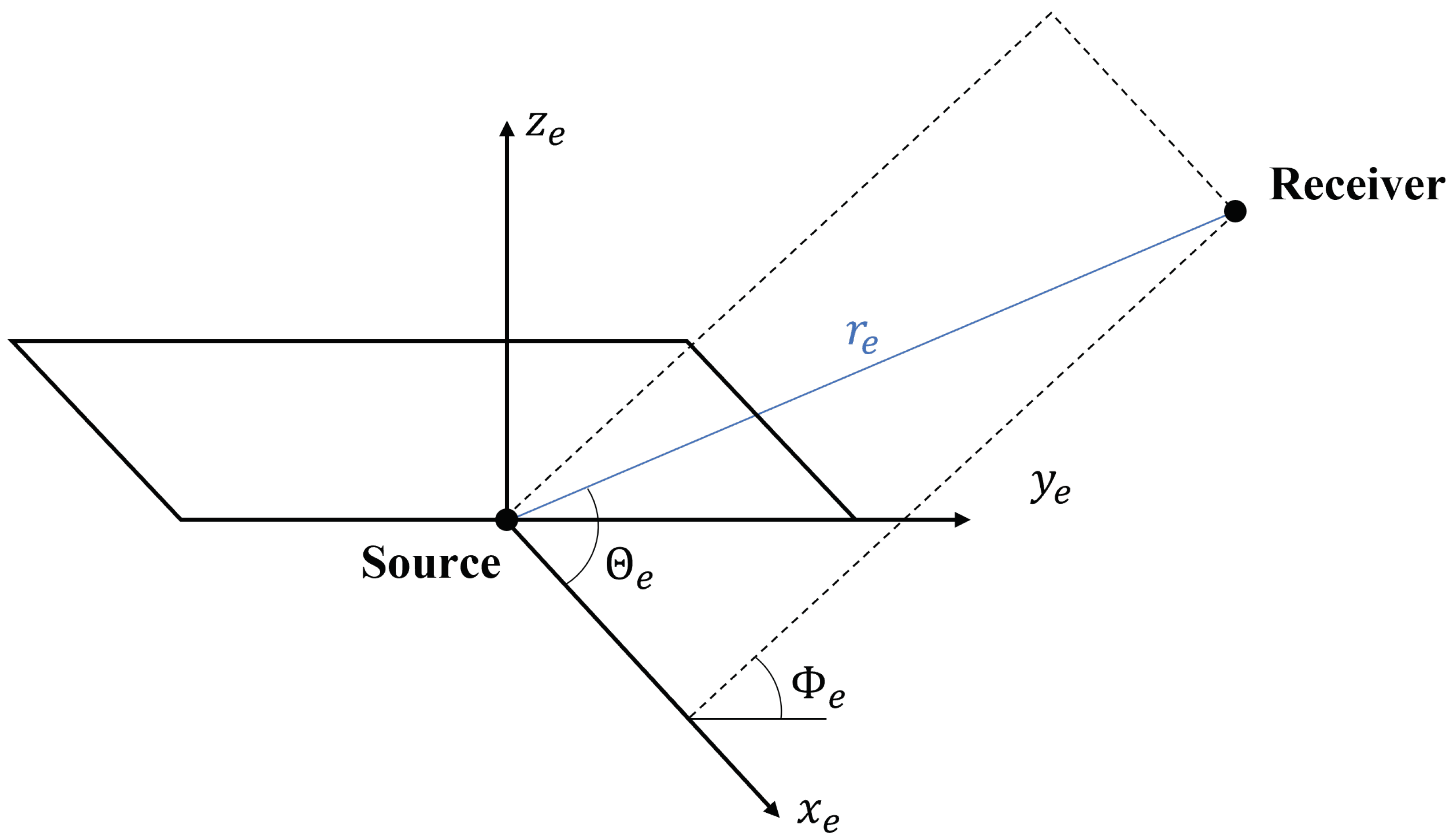
2.2.1. Amiet Model for Turbulent Inflow Noise
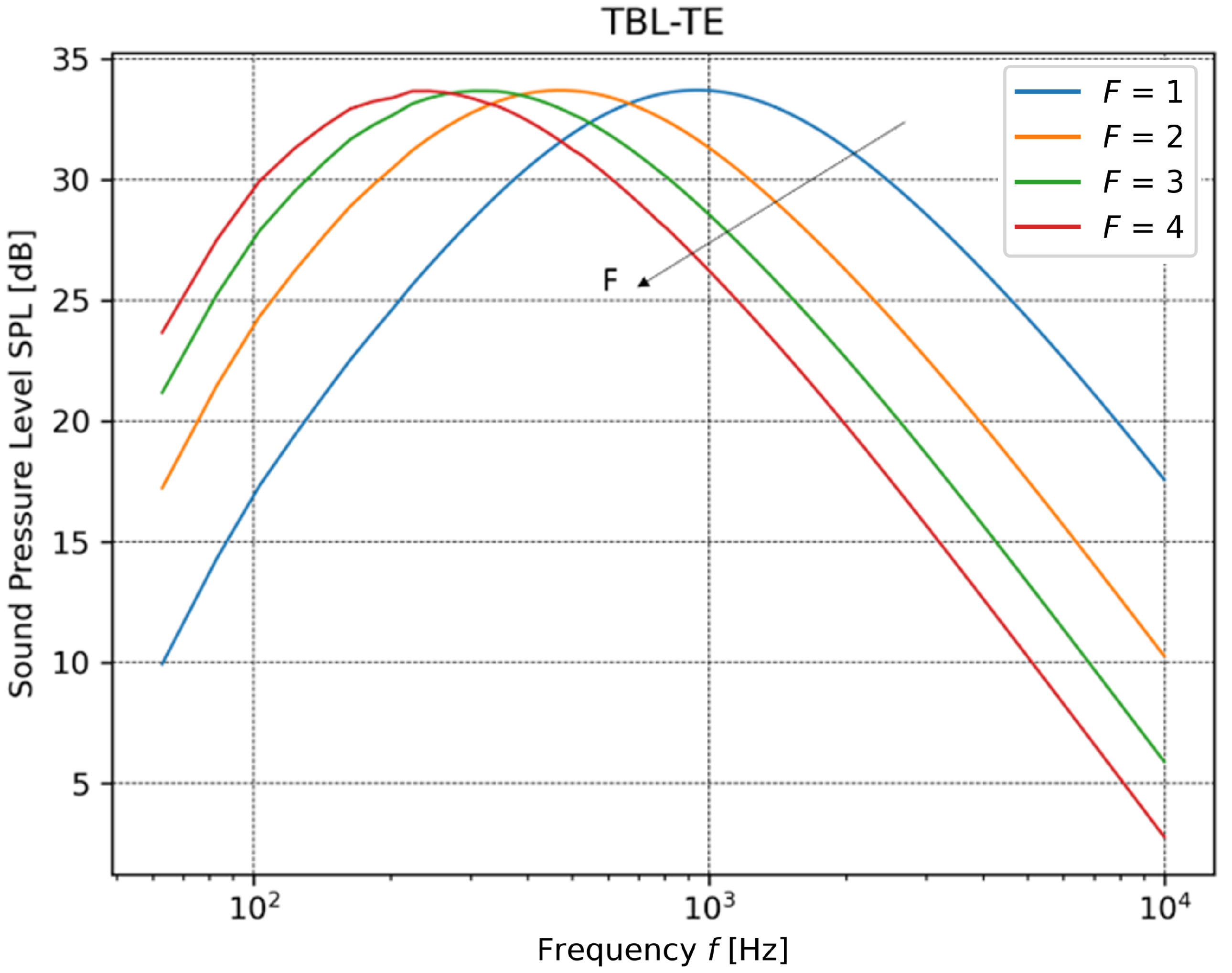
2.2.2. Lowson Model for Turbulent Boundary Layer to Trailing Edge Noise
3. Numerical Methodology
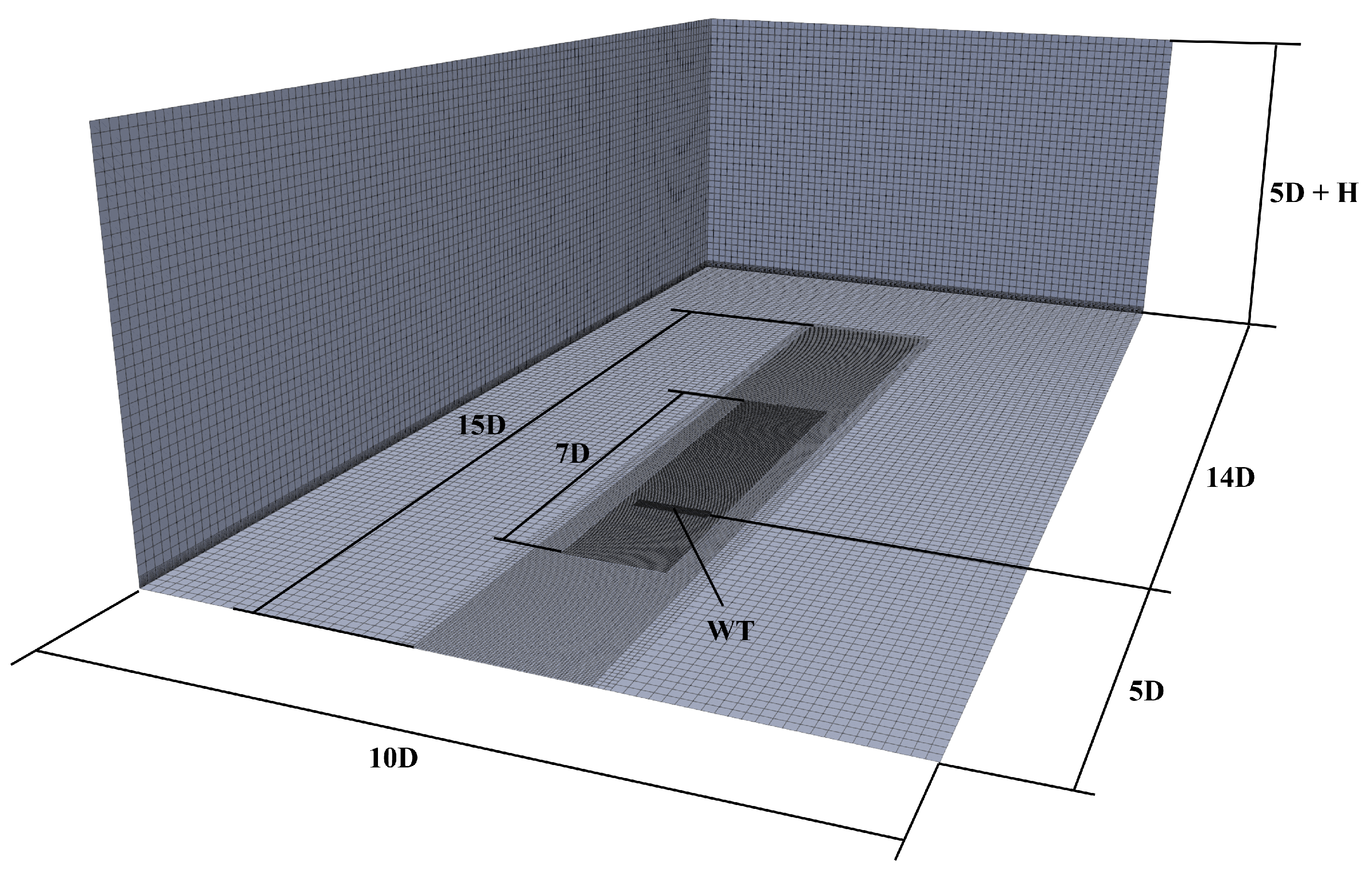
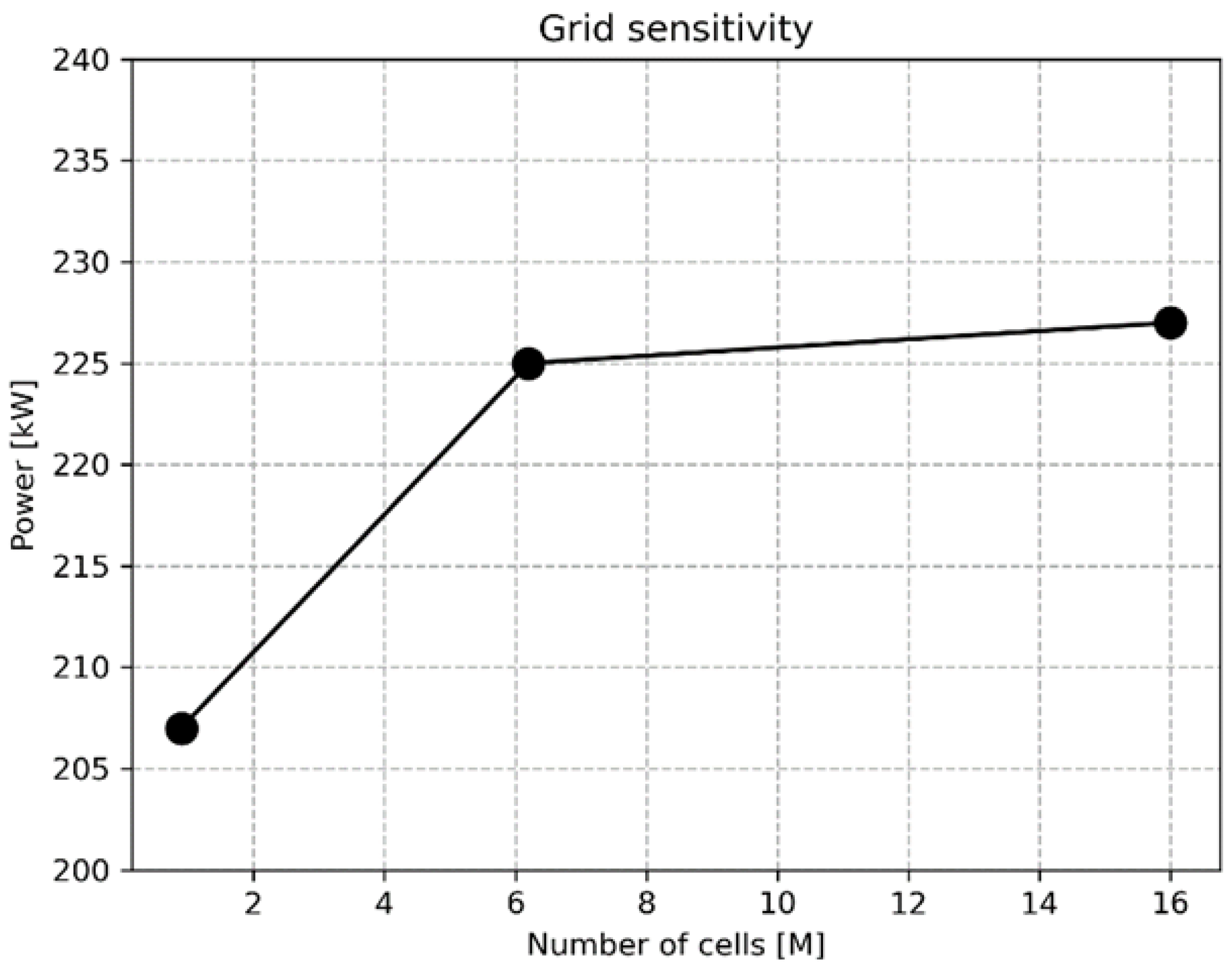
3.1. Computational Domain and Grid
3.2. Boundary Conditions
3.3. Numerical Schemes
3.4. Aerodynamics and Surrogate Acoustics Coupling
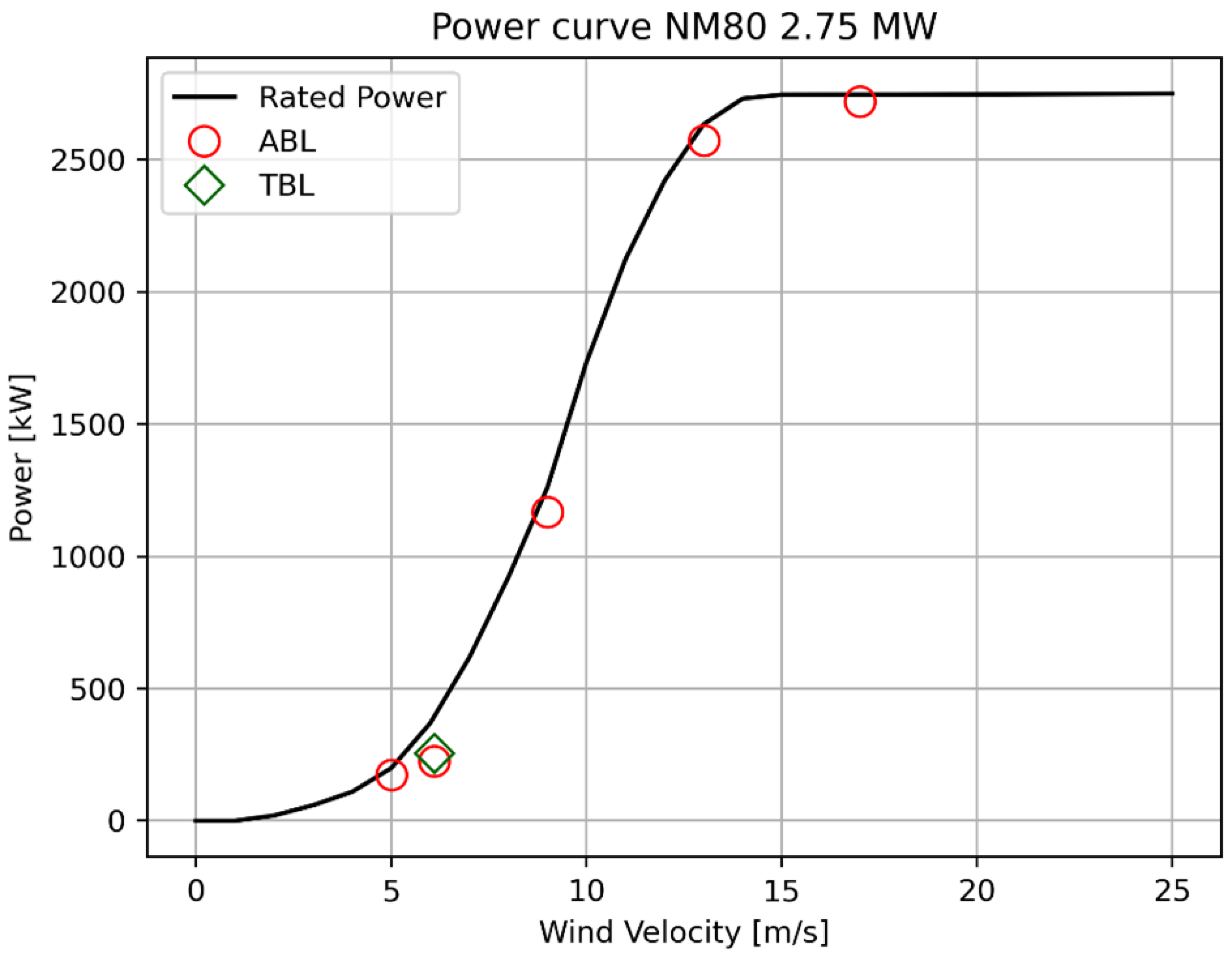
3.5. Description of the Test Case
4. Validation of the Actuator Line Setup
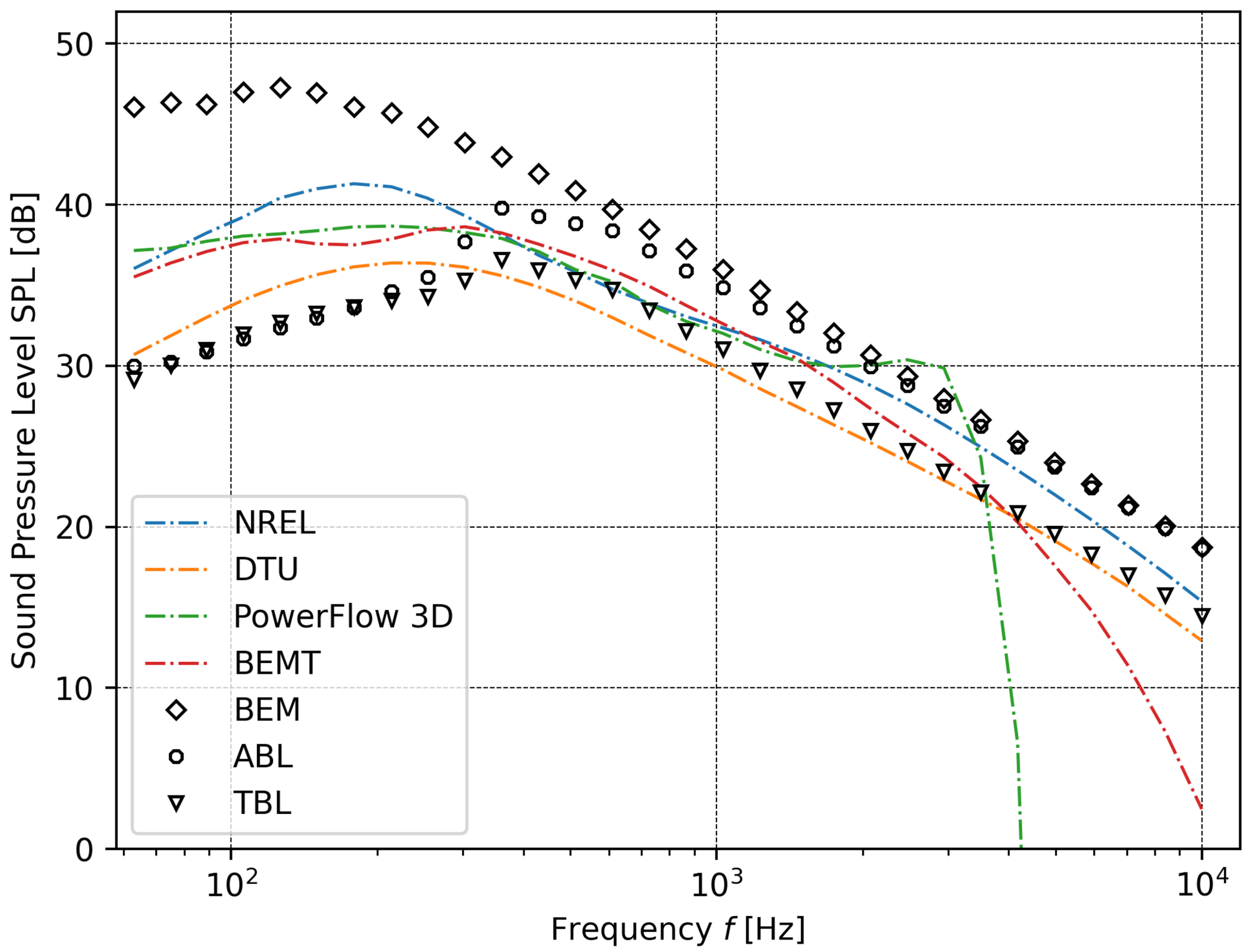
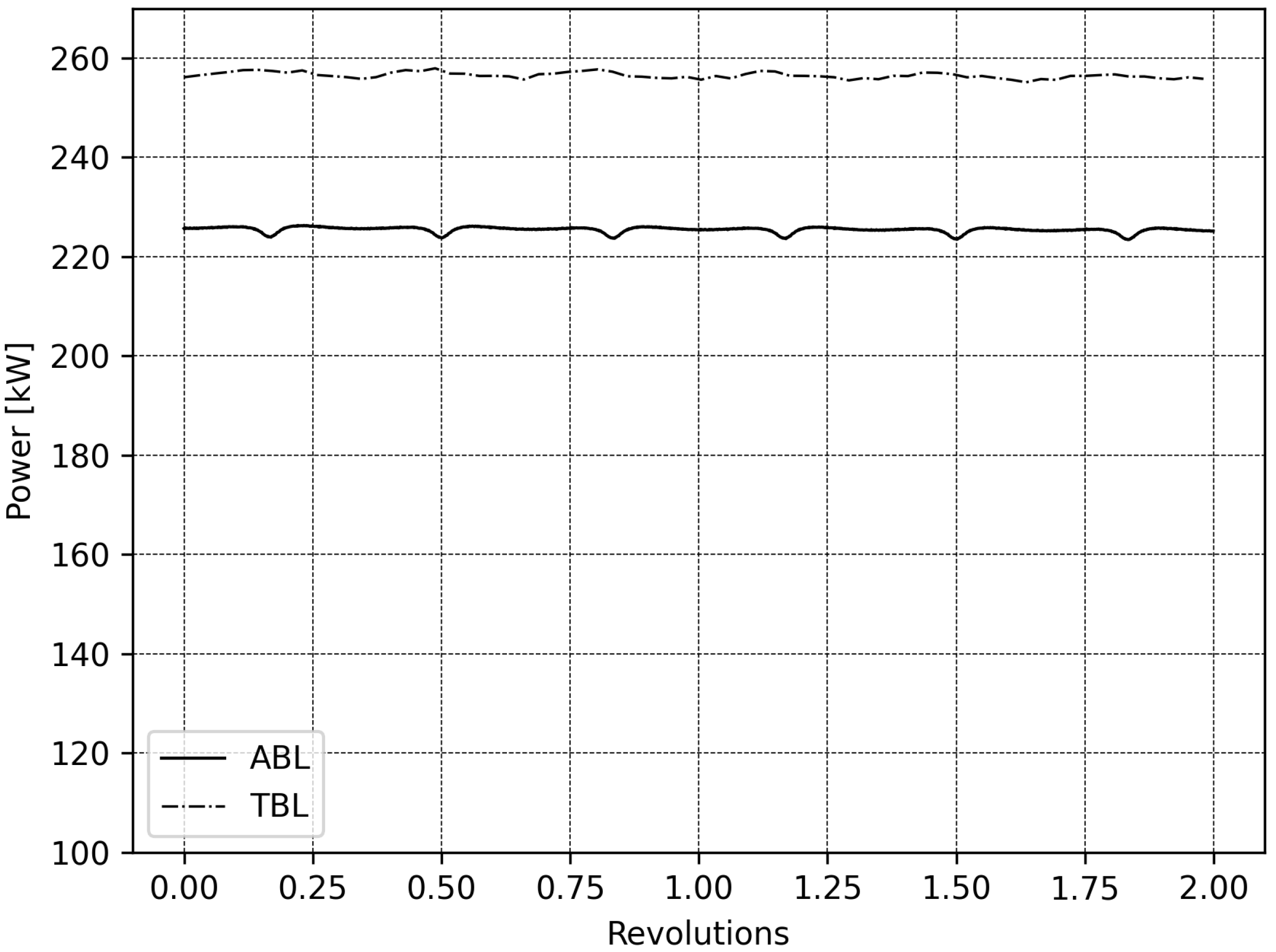
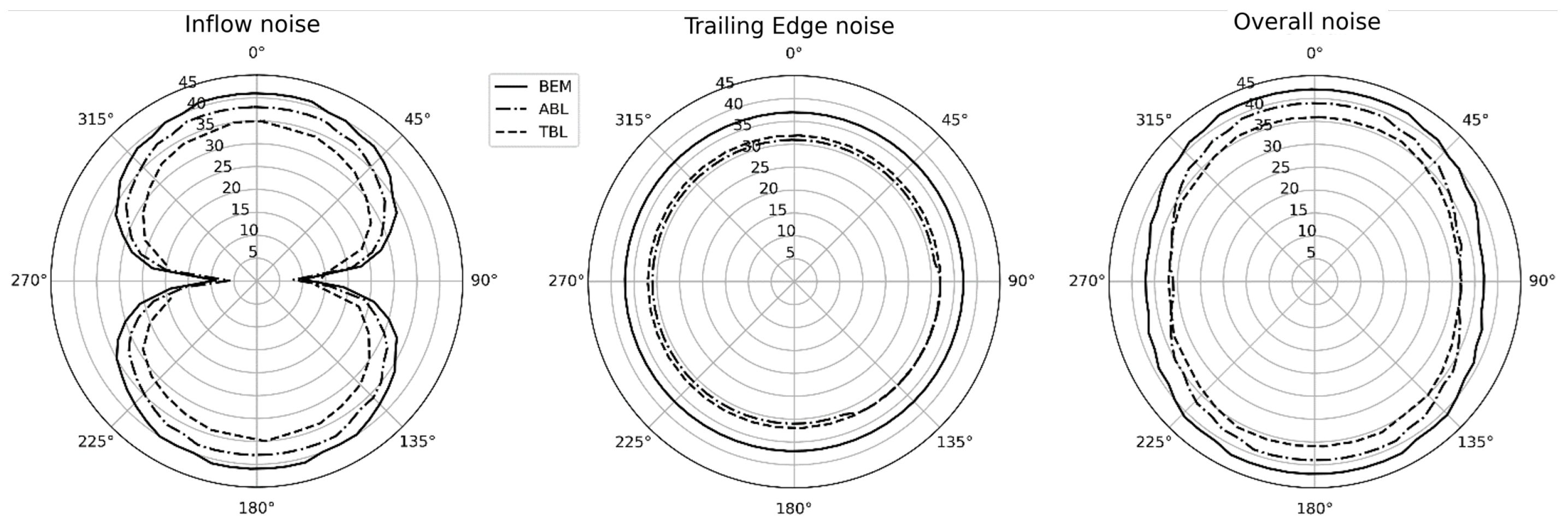
5. Results
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Buchheit, M.; Vandendriessche, T. A European Strategy for Offshore Renewable Energy; European Parliament: Brussels, Belgium, 2022.
- Qu, F.; Tsuchiya, A. Perceptions of wind turbine noise and self-reported health in suburban residential areas. Front. Psychol. 2021, 12, 736231. [Google Scholar] [CrossRef]
- Zhu, W.J.; Shen, W.Z.; Barlas, E.; Bertagnolio, F.; Sørensen, J.N. Wind turbine noise generation and propagation modeling at DTU Wind Energy: A review. Renew. Sustain. Energy Rev. 2018, 88, 133–150. [Google Scholar] [CrossRef]
- De Girolamo, F.; Tieghi, L.; Delibra, G.; Barnabei, V.F.; Corsini, C. Surrogate modeling of the aeroacoustics of an NM80 wind turbine. In Proceedings of the 15th European Turbomachinery Confeerence, Paper n. ETC2023-182, Budapest, Hungary, 24–28 April 2023; p. 900. Available online: https://www.euroturbo.eu/publications/conference-proceedings-repository/ (accessed on 30 May 2023).
- Wagner, S.; Bareiss, R.; Guidati, G. Wind Turbine Noise; Springer Science & Business Media: New York, NY, USA, 1996. [Google Scholar]
- Lowson, M. Applications of aero-acoustics to wind turbine noise prediction and control. In Proceedings of the 31st Aerospace Sciences Meeting, Reno, NV, USA, 11–14 January 1993; p. 135. [Google Scholar]
- Colonius, T.; Lele, S.K. Computational aeroacoustics: Progress on nonlinear problems of sound generation. Prog. Aerosp. Sci. 2004, 40, 345–416. [Google Scholar] [CrossRef]
- Hardin, J.C.; Hussaini, M.Y. Computational Aeroacoustics; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Tieghi, L.; Becker, S.; Corsini, A.; Delibra, G.; Schoder, S.; Czwielong, F. Machine-learning clustering methods applied to detection of noise sources in low-speed axial fan. J. Eng. Gas Turbines Power 2023, 145, 031020. [Google Scholar] [CrossRef]
- Martinez, L.; Leonardi, S.; Churchfield, M.; Moriarty, P. A comparison of actuator disk and actuator line wind turbine models and best practices for their use. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012; p. 900. [Google Scholar]
- Ravensbergen, M.; Mohamed, A.B.; Korobenko, A. The actuator line method for wind turbine modelling applied in a variational multiscale framework. Comput. Fluids 2020, 201, 104465. [Google Scholar] [CrossRef]
- Ouro, P.; Harrold, M.; Ramirez, L.; Stoesser, T. Prediction of the wake behind a horizontal axis tidal turbine using a LES-ALM. In Recent Advances in CFD for Wind and Tidal Offshore Turbines; Springer: New York, NY, USA, 2019; pp. 25–35. [Google Scholar]
- Baba-Ahmadi, M.H.; Dong, P. Numerical simulations of wake characteristics of a horizontal axis tidal stream turbine using actuator line model. Renew. Energy 2017, 113, 669–678. [Google Scholar] [CrossRef]
- Lin, X.F.; Zhang, J.S.; Zhang, Y.Q.; Zhang, J.; Liu, S. Comparison of actuator line method and full rotor geometry simulations of the wake field of a tidal stream turbine. Water 2019, 11, 560. [Google Scholar] [CrossRef]
- Castorrini, A.; Tieghi, L.; Barnabei, V.; Gentile, S.; Bonfiglioli, A.; Corsini, A.; Rispoli, F. Wake interaction in offshore wind farms with mesoscale derived inflow condition and sea waves. Proc. Iop Conf. Ser. Earth Environ. Sci. 2022, 1073, 012009. [Google Scholar] [CrossRef]
- Mikkelsen, R.; Sørensen, J.N.; Øye, S.; Troldborg, N. Analysis of power enhancement for a row of wind turbines using the actuator line technique. Proc. Iop Conf. Ser. Earth Environ. Sci. 2007, 75, 012044. [Google Scholar] [CrossRef]
- Troldborg, N.; Larsen, G.C.; Madsen, H.A.; Hansen, K.S.; Sørensen, J.N.; Mikkelsen, R. Numerical simulations of wake interaction between two wind turbines at various inflow conditions. Wind Energy 2011, 14, 859–876. [Google Scholar] [CrossRef]
- Breton, S.P.; Shen, W.Z.; Ivanell, S. Validation of the actuator disc and actuator line techniques for yawed rotor flows using the New MEXICO experimental data. Proc. Iop Conf. Ser. Earth Environ. Sci. 2017, 854, 012005. [Google Scholar] [CrossRef]
- Nilsson, K.; Shen, W.Z.; Sørensen, J.N.; Breton, S.P.; Ivanell, S. Validation of the actuator line method using near wake measurements of the MEXICO rotor. Wind Energy 2015, 18, 499–514. [Google Scholar] [CrossRef]
- Bhargava, V.; Samala, R. Acoustic emissions from wind turbine blades. J. Aerosp. Technol. Manag. 2019, 11, e4219. [Google Scholar] [CrossRef]
- Buck, S.; Oerlemans, S.; Palo, S. Experimental validation of a wind turbine turbulent inflow noise prediction code. AIAA J. 2018, 56, 1495–1506. [Google Scholar] [CrossRef]
- Oerlemans, S.; Schepers, J.G. Prediction of wind turbine noise and validation against experiment. Int. J. Aeroacoust. 2009, 8, 555–584. [Google Scholar] [CrossRef]
- Barlas, E.; Zhu, W.J.; Shen, W.Z.; Dag, K.O.; Moriarty, P. Consistent modelling of wind turbine noise propagation from source to receiver. J. Acoust. Soc. Am. 2017, 142, 3297–3310. [Google Scholar] [CrossRef]
- Moriarty, P.; Guidati, G.; Migliore, P. Prediction of turbulent inflow and trailing-edge noise for wind turbines. In Proceedings of the 11th AIAA/CEAS Aeroacoustics Conference, Monterey, CA, USA, 23–25 May 2005; p. 2881. [Google Scholar]
- Sorensen, J.N.; Shen, W.Z. Numerical modeling of wind turbine wakes. J. Fluids Eng. 2002, 124, 393–399. [Google Scholar] [CrossRef]
- Brooks, T.F.; Pope, D.S.; Marcolini, M.A. Airfoil Self-Noise and Prediction; Technical Report No. L-16528; CreateSpace Independent Publishing Platform: Scotts Valley, CA, USA, 1989. [Google Scholar]
- Grosveld, F.W. Prediction of broadband noise from horizontal axis wind turbines. J. Propuls. Power 1985, 1, 292–299. [Google Scholar] [CrossRef]
- Oerlemans, S. Wind Turbine Noise: Primary Noise Sources; National Aerospace Laboratory NLRL: Amsterdam, The Netherlands, 2011.
- Moriarty, P.; Migliore, P. Semi-Empirical Aeroacoustic Noise Prediction Code for Wind Turbines; Technical Report No. NREL/TP-500-34478; National Renewable Energy Lab.: Golden, CO, USA, 2003.
- Amiet, R.K. Acoustic radiation from an airfoil in a turbulent stream. J. Sound Vib. 1975, 41, 407–420. [Google Scholar] [CrossRef]
- Bortolotti, P.; Branlard, E.; Platt, A.; Moriarty, P.; Sucameli, C.; Bottasso, C.L. Aeroacoustics Noise Model of OpenFAST; Technical Report No. NREL/TP-5000-75731; National Renewable Energy Lab.: Golden, CO, USA, 2020.
- Guidati, G.; Bareiss, R.; Wagner, S.; Parchen, R.; Guidati, G.; Bareiss, R.; Wagner, S.; Parchen, R. Simulation and measurement of inflow-turbulence noise on airfoils. In Proceedings of the 3rd AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 12–14 May 1997; p. 1698. [Google Scholar]
- Moriarty, P. NAFNoise User’s Guide; National Wind Technology Center, National Renewable Energy Laboratory: Golden, CO, USA, 2005.
- Schlichting, H.; Kestin, J. Boundary Layer Theory; Springer: New York, NY, USA, 1961; Volume 121. [Google Scholar]
- Strelets, M. Detached eddy simulation of massively separated flows. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001; p. 879. [Google Scholar]
- Bachant, P.; Goude, A.; Wosnik, M. Zenoodo. Turbinesfoam: v0. 0.7. 2016. Available online: https://zenodo.org/record/49422 (accessed on 31 March 2018).
- Troldborg, N. APA. Actuator Line Modeling of Wind Turbine Wakes; APA: Washington, DC, USA, 2009. [Google Scholar]
- Richards, P.; Hoxey, R. Appropriate boundary conditions for computational wind engineering models using the k-ϵ turbulence model. J. Wind. Eng. Ind. Aerodyn. 1993, 46, 145–153. [Google Scholar] [CrossRef]
- Yang, Y.; Gu, M.; Jin, X. New inflow boundary conditions for modeling the neutral equilibrium atmospheric boundary layer in SST k-ω model. J. Wind Eng. Ind. Aerod 2012, 97, 88–95. [Google Scholar] [CrossRef]
- Drela, M. XFOIL: An analysis and design system for low Reynolds number airfoils. In Proceedings of the Low Reynolds Number Aerodynamics, Notre Dame, IN, USA, 5–7 June 1989; Springer: New York, NY, USA, 1989; pp. 1–12. [Google Scholar]
- Schepers, J.; Boorsma, K.; Madsen, H.A.; Pirrung, G.; Bangga, G.; Guma, G.; Lutz, T.; Potentier, T.; Braud, C.; Guilmineau, E.; et al. IEA Wind TCP Task 29, Phase IV: Detailed Aerodynamics of Wind Turbines. 2021. Available online: https://zenodo.org/record/4813068 (accessed on 26 May 2021).
- Bertagnolio, F.; Dtu, A.F.; Seel, F.; Lutz, T.; Iag, C.H.; Balterria, G.U.; Boorsma, K.; Appel, C.; Bortolotti, P. IEA Wind TCP-Task 29 T3. 7 & Task 39 Wind Turbine Noise Code Benchmark-Preliminary Results. 2021. Available online: https://iea-wind.org/wp-content/uploads/2021/05/report_WTNCBenchmark.pdf (accessed on 24 February 2021).
- Casalino, D.; van der Velden, W.C.; Romani, G. A framework for multi-fidelity wind-turbine aeroacoustic simulations. In Proceedings of the 28th AIAA/CEAS Aeroacoustics 2022 Conference, Southampton, UK, 14–17 June 2022; p. 2892. [Google Scholar]
| Blade Span [%] | BEM | ABL | TBL (Median) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
[] | [°] | [mm] | [mm] | [] | [°] | [mm] | [mm] | [] | [°] | [mm] | [mm] | |
| 34 | 3.83 | 14.7 | 27.9 | 55.9 | 3.88 | 15.03 | 0.71 | 3.1 | 3.3 | 20.82 | 1.22 | 4.6 |
| 50 | 4.5 | 7.59 | 21.1 | 43.3 | 4.41 | 8.15 | 0.475 | 2 | 4.45 | 8.87 | 0.5 | 2.17 |
| 77 | 4.61 | 4.3 | 14.5 | 29.1 | 4.52 | 4.77 | 0.32 | 0.5 | 4.53 | 5.33 | 0.31 | 0.54 |
| 99 | 13.6 | 8.11 | 4.3 | 8.7 | 11.1 | 8.25 | 0.625 | 2.2 | 11.1 | 7.95 | 0.59 | 2.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
De Girolamo, F.; Tieghi, L.; Delibra, G.; Barnabei, V.F.; Corsini, A. Surrogate Modeling of the Aeroacoustics of an NM80 Wind Turbine. Int. J. Turbomach. Propuls. Power 2023, 8, 43. https://doi.org/10.3390/ijtpp8040043
De Girolamo F, Tieghi L, Delibra G, Barnabei VF, Corsini A. Surrogate Modeling of the Aeroacoustics of an NM80 Wind Turbine. International Journal of Turbomachinery, Propulsion and Power. 2023; 8(4):43. https://doi.org/10.3390/ijtpp8040043
Chicago/Turabian StyleDe Girolamo, Filippo, Lorenzo Tieghi, Giovanni Delibra, Valerio Francesco Barnabei, and Alessandro Corsini. 2023. "Surrogate Modeling of the Aeroacoustics of an NM80 Wind Turbine" International Journal of Turbomachinery, Propulsion and Power 8, no. 4: 43. https://doi.org/10.3390/ijtpp8040043
APA StyleDe Girolamo, F., Tieghi, L., Delibra, G., Barnabei, V. F., & Corsini, A. (2023). Surrogate Modeling of the Aeroacoustics of an NM80 Wind Turbine. International Journal of Turbomachinery, Propulsion and Power, 8(4), 43. https://doi.org/10.3390/ijtpp8040043







