Abstract
Presented herein is a comparative performance analysis of a novel turbofan engine with an auxiliary combustion chamber, nicknamed the TurboAux engine, against a turbojet engine, and a low bypass ratio turbofan engine with an afterburner is presented. The TurboAux engine is an adaption of the low-bypass ratio turbofan engine, but with secondary combustion in an auxiliary bypass annular combustion chamber for thrust augmentation. The TurboAux engine is envisioned with the desire to facilitate clean secondary burning of fuel at temperatures higher than in the main combustion chamber with air exiting the low-pressure compressor. The comparative study starts by analyzing the turbojet engine and its performance with and without an afterburner segment attached. In parallel, the conventional turbofan and its mixing counterpart are analyzed, also with and without an afterburner segment. A simple optimization analysis of a conventional turbofan is performed to identify optimal ‘fan’ pressure ratios for a series of low-bypass ratios (0.1 to 1.5). The optimal fan pressure ratios and their corresponding bypass ratios are adapted to demonstrate the comparative performance of the varying configurations of the TurboAux engine. The formulation and results are an attempt to make a case for charter aircrafts and efficient close-air-support aircrafts. The results yielded increased performance in thrust augmentation, but at the cost of a spike in fuel consumption. This trade-off requires more in-depth investigation to further ascertain the TurboAux’s utility.
1. Introduction
The implementation of an afterburner, while significantly increasing thrust production, comes at a high cost in fuel consumption [1]. The process of afterburning itself is inefficient in comparison to combustion occurring in the main combustion chamber as the reactants of the combustion process in the afterburner are gases drastically depleted of oxygen from the main combustion process or more commonly referred to as a reheat cycle [1]. A novel approach to mitigate these issues experienced by afterburning engines is proposed by Asundi and Ali [2]. The authors conceived the idea of having a secondary burner in the bypass stream of a turbofan engine to utilize oxygen-rich air for a more efficient combustion process [2]. The study presented in this paper is focused on the performance comparison of the novel TurboAux engine with that of a turbojet engine and a turbofan engine both with afterburner segments, and in doing so, evaluates parameters which facilitate identification of its potential utility as a novel engine. The analysis is conducted under the assumption that the engines are operated isentropically. It takes into consideration the mixing of the two exhaust streams and the incorporation of realistic component efficiencies for the compressors and the turbines, and accounts for small frictional losses during combustion and mixing of the core and auxiliary streams. An optimization analysis is also performed to advance the TurboAux engine concept into an engineering design, so it may further highlight key expansions in the research to further understand the TurboAux. Incorporating this auxiliary combustion chamber in the bypass stream allows for much higher combustion temperatures (~2500 K) than the core stream of the engine would allow. The reason being that the hot gases exiting the auxiliary combustion chamber will not interact with the turbine blades, averting deformation and damage that could prove to be potentially catastrophic. With current material science technology, turbine blades cannot withstand temperatures greater than ~1950 K [3,4]. However, it is important to mention that advancements in ceramic composite materials for use in turbine blades could allow for much higher temperatures exiting the main combustion chamber [5]. The premise for the comparative study is to identify parameters, which would facilitate a niche utility for the TurboAux engine. The analysis of these engines is performed with the use of a computer program, MATLAB, to accurately model the thermodynamics under realistic parameters and component efficiencies. The analysis is conducted on a per-unit-mass-flow basis meaning that some of the parameters, aside from stagnation temperature, pressure, and other such flow properties, are calculated as specific quantities (for example the specific work required to run the compressors and the specific thrust output of the engine). The per-unit-mass-flow analysis allows the results to be compared for engines of similar configuration.
2. Optimization Analysis
In this chapter, the results and the findings of the optimization analysis are presented. To avoid confusion, we have elected to refer to turbofan engines that exhaust their two streams separately as a “conventional” turbofan, in reference to commercial turbofan engines, and turbofan engines that incorporate mixing of the two streams into one prior to exiting the exhaust as a “low-bypass” or “military-style” turbofan. Furthermore, the performance of a low-bypass turbofan, was analyzed to find an optimum engine configuration that would be used to model the TurboAux engine. When optimizing turbojet and turbofan engines, the turbojet has two thermodynamic properties that can be varied to study its changes in performance: overall pressure ratio (OPR) and turbine inlet temperature (TINT), while the turbofan engine has four thermodynamic properties which can be manipulated to study engine performance: OPR, TINT, bypass ratio (BPR), and fan pressure ratio (FPR) [1]. When studying these engines, OPR and TINT were fixed for both the turbojet and turbofan engines while FPR, for both engines, and BPR, for the turbofan only, were varied to see their effects on various performance parameters. To clarify, the turbojet does not operate with a bypass stream, hence its exclusion from consideration in its effects on the turbojet. The full mathematical formulation will be presented in the chapters to follow.
2.1. Low-Bypass Turbofan as a Baseline for the TurboAux Engine
Prior to conducting the optimization analysis of a low-bypass turbofan engine, the differences in performance between a turbojet engine and a conventional turbofan engine were investigated. All engine comparisons were conducted under the design points which are shown in Table 1. An altitude of 5 km was selected and the corresponding ambient conditions were adopted from International Standard Atmosphere (ISA) standards. Most close-air-support aircraft fly near this altitude thus the reasoning behind its selection. Future analysis will be conducted at higher altitudes ~10 km to compare to higher performance military aircraft. Table 1 below presents the design points for all the engines in this parametric analysis.

Table 1.
Design Points.
Fixing fuel properties and flight conditions, as well as component efficiencies adopted from Gas Turbine Theory [1] for both engines, the effect of a varying FPR (while fixing the bypass ratio for the turbofan at 1.5) on Fs and TSFC was studied. The results indicated the turbojet engine produced significantly higher Fs than the conventional turbofan engine, while the turbofan engine exhibited lower TSFC than that of the turbojet engine. The FPR values were varied from 1.3 to 7 and the turbojet and turbofan showed contrasting trends for Fs. As FPR increased, Fs values for the turbojet decreased, but for the turbofan, the Fs values increased across this same range. In both engines, however, TSFC decreased as FPR increased. These trends are illustrated in Figure 1.
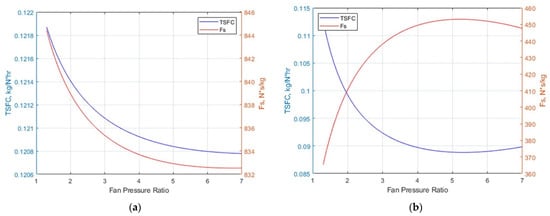
Figure 1.
Plots of performance vs. FPR for [6] (a) turbojet and (b) turbofan.
In subsequent analyses of the turbofan, as BPR decreased from 1.5 to 0.1, both Fs and TSFC increased, and the turbofan exhibited increasingly similar trends to that of the turbojet. This served as evidence as to why low-bypass turbofans are used in military aircraft applications as they perform comparatively while still improving on some of the issues faced by turbojet engines such as high fuel consumption in comparison to their turbofan counterparts. The next step in this analysis was to investigate the differences between two similar turbofans: the conventional turbofan and the military-style turbofan. To reiterate, both configurations were studied with the same design points, component efficiencies, ambient conditions, and fuel characteristics. For every BPR investigated, ranging from 0.1 to 1.5, the military-style turbofan outperformed the conventional turbofan with respect to both Fs and TSFC as well as propulsive, thermal, and overall efficiencies. This increase in performance with respect to Fs and TSFC is due to the fundamental thrust gain that occurs when the hot and cold streams mix to produce a stream of intermediate temperature. Table 2, Table 3 and Table 4 show some of the comparisons in their performance.

Table 2.
Performance with Bypass Ratio Fixed at 0.1.

Table 3.
Performance with Bypass Ratio Fixed at 0.5.

Table 4.
Performance with Bypass Ratio Fixed at 1.5.
These simulation results provide justification for the selection of a low-bypass or military-style turbofan over a conventional turbofan as the base configuration being optimized and later augmented with an auxiliary combustion chamber in the bypass stream. As illustrated in Table 2, Table 3 and Table 4 above, the military-style turbofan outperformed the conventional turbofan in all parameters. The optimization process is an attempt to close the gap between the two engines.
2.2. Low-Bypass Turbofan Engine Optimization–Engineering the TurboAux Engine
When optimizing the turbofan, there are four thermodynamic parameters that can be manipulated to investigate their effects on performance [1]. As aforementioned, these parameters are OPR, TINT, FPR, and BPR. OPR and TINT are thought to determine the “quality” of the engine cycle, while FPR and BPR characterize the effectiveness with which the available energy is converted to thrust [1]. For a given BPR, as FPR is increased, the thrust produced by the bypass stream will increase but this requires more and more energy to be extracted from the core stream thus decreasing the core stream thrust output [1]. Conversely, for low values of FPR at a fixed BPR, the thrust produced by the core stream will be high and little energy will be extracted from the core stream to drive the fan [1]. If OPR and BPR are fixed and a value for TINT is selected, then the energy input for the engine is fixed since the combustion chamber air flow and entry temperature are determined by those operating conditions [1]. This means that the optimum FPR values for maximizing Fs and minimizing TSFC coincide. From this understanding, when analyzing the low-bypass turbofan, OPR was fixed at 50, and TINT was fixed at 1922 K. Then, a BPR of 0.1 was selected as FPR varied from 1.3 to 7 to find the optimal configuration. This cycle was repeated for several BPRs ranging from 0.1 to 1.5 and yielded a set of optimal designs; designs in which with OPR and TINT fixed, every BPR had a coinciding FPR that maximized Fs and minimized TSFC simultaneously. This optimization was first performed for a low-bypass turbofan with two separate streams exhausting from separate nozzles and from previous understanding, it seemed a reasonable assumption that this optimal configuration would hold true as well for a military-style low-bypass turbofan with mixing of the hot and cold streams, as mixing only further improved the performance of the engine with respect to Fs, TSFC, and engine efficiency. The optimal FPR value found for each BPR is tabulated below in Table 5.

Table 5.
Optimal FPR Values.
It is interesting to note however that from a BPR of 1 to 1.5, some of the optimum FPR values for maximizing Fs and minimizing TSFC do not exactly coincide. Although this requires further investigation, the discrepancies in the optimum values are minuscule and as an effort to minimize fuel consumption, the optimum FPR values that minimized TSFC were selected for the final optimal design. In their investigation of the two-combustor engines, Lee et al. found that the optimal FPR for maximizing Fs and minimizing TSFC did not coincide, noting that the optimum FPR for maximizing Fs was less than the optimum FPR for minimizing TSFC [7]. This was confirmed in our optimization analysis. Figure 2 shows the graphical representation of the effects of FPR on Fs and TSFC while OPR and TINT are fixed for a fixed BPR. For each fixed BPR, the corresponding optimum values are found on their respective lines for TSFC and Fs. It can be noted that as the bypass ratio increases, the curves for Fs and TSFC transition from trending linearly to trending logarithmic and parabolically, making the optimal points increasingly easy to identify graphically.
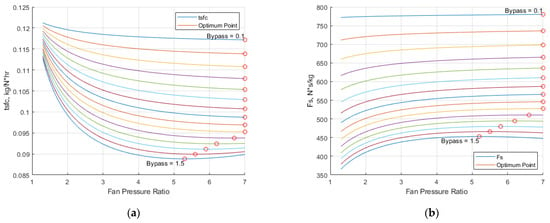
Figure 2.
Plots of the optimum FPR with BPR increasing with each line for (a) minimizing TSFC and (b) maximizing Fs.
An interesting trend to note is that the optimum FPR values for both maximizing Fs and minimizing TSFC for BPRs from 0.1 to 1.0 were all found to be the upper limit set at 7. BPR is defined as the ratio of the mass flow of air entering the bypass stream to the mass flow of air entering the core stream which diverges upon exiting the fan segment. For BPR values between 0.1 to 1.0, the bulk of the mass flow entering the inlet is passing through the core of the engine, therefore, compressing the air as much as possible in the fan or low-pressure compressor before entering the high-pressure compressor and the main combustion chamber allows for a more efficient extraction of energy and higher specific thrust output. With BPR values greater than 1.0, the bulk of the mass flow entering the inlet is passing through the bypass stream where no combustion occurs. This will also be further investigated in the research to follow.
3. High-Fidelity Formulation of the TurboAux, Turbojet, and Turbofan Engines
This chapter discusses the high-fidelity mathematical formulations, calculation of the TurboAux, turbojet, and turbofan engines to facilitate the simulation of the results presented in the next chapter. The engines that are presented in this chapter are the TurboAux, the turbojet with an afterburner segment, and the military-style turbofan with an afterburner segment. Flight conditions and simulation parameters were selected to be similar to the flight conditions of similar engines and are summarized in Table 1. When modeling the thermodynamics of these engines, a few assumptions were made:
- All component efficiencies and specific heat capacities are constant.
- Combustion chambers are adiabatic but account for frictional losses.
- The streams will mix fully in the constant-area mixing duct.
- The is no dissociation occurring in the products of combustion.
3.1. TurboAux
The optimized low-bypass turbofan engine, discussed in the previous chapter, is adopted as a basis for comparison with the TurboAux and other engines. The configuration of the TurboAux engine, which may be identical to that of the military-style turbofan engine with an auxiliary combustion chamber augmented into the bypass stream, is illustrated in Figure 3.
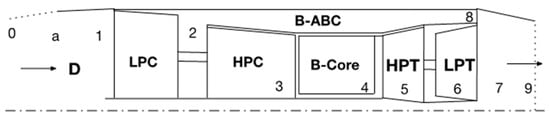
Figure 3.
TurboAux Configuration.
The TurboAux configuration is similar to that of a regular turbofan engine. Station 0 represents the far-field conditions, and station a represents the ambient conditions entering the diffuser inlet. Station 1 represents the outlet of the diffuser and the inlet of the LPC (low-pressure compressor). The stream is compressed by the LPC and exits at station 2. At station 2 the stream splits into the core and the bypass stream. Upon splitting, the bypass stream enters station B-ABC which represents the auxiliary combustion chamber and is mixed with fuel to be burned upon exiting at station 8. The core stream enters the HPC (high-pressure compressor) at station 3 where the air is compressed before entering the main combustion chamber at station 4 and is mixed with fuel for combustion. The core stream then proceeds to stations 5 and 6 which are the high-pressure and low-pressure turbines (HPT & LPT) for energy extraction to power the compressors. At station 7, the bypass and core stream mix fully in the mixing duct before being propelled out of a common nozzle at station 9.
It is important to note that these engines are of similar design thus sharing many equations. The high-fidelity formulation for the TurboAux is presented below and the subsequent sections will discuss the formulations for the other engines. The formulation for the TurboAux up until stations 6 and 8 is presented in [6] and can be found in full detail in Appendix A. As shown in Figure 4, the core and the auxiliary streams fully mix at station 7 and exhaust from a common nozzle at station 9.
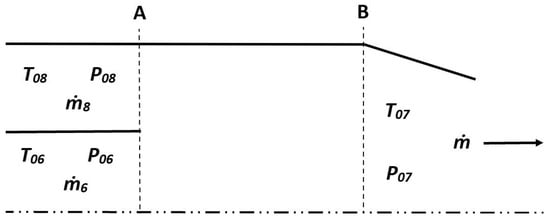
Figure 4.
TurboAux Constant-Area Mixing Duct.
Figure 4 represents the mixing duct where the two streams will fully mix before exiting as one stream. Station A is the inlet to the mixing duct where the bypass stream coming from the auxiliary combustion chamber and the core stream coming from the LPT. Station B is the outlet of the mixing duct where the combined stream will enter the nozzle.
The formulation of the mixing of the two streams was an iterative and ad hoc process, which required defining certain parameters involving the mixing duct. The ad hoc formulation of the mixing of the two streams discussed below is an adequate approximation of the solution. The stagnation temperature of the mixed streams is calculated by manipulating the conservation of energy, conservation of mass, and the first law of thermodynamics. In a similar process, the stagnation pressure is a mass-weighted average of the two streams mixing. The conservation of energy balance is shown in Equation (1) and the conservation of mass in Equation (2), states that the mass flow at station B is the sum of the individual mass flow rates at plane A. The individual mass flow rates are defined in Equations (3) and (4).
Taking Equations (2) and (3) and factoring out their respective air mass flow rates yields Equations (5) and (6). Substituting Equation (2) into Equation (1) yields Equation (7) and after subtracting the right-hand side over and simplifying, Equation (8) is the result.
Next, Equations (5) and (6) are substituted into Equation (8) to obtain Equation (9). Then, Equation (9) is divided by the mass flow of the core stream to yield Equation (10). After substituting the stagnation enthalpies with the specific heat capacity at constant pressure of the gaseous mixture into Equation (10), divide out Cp0g from (11) and distribute to arrive at Equation (12).
The next steps are to isolate T07 to one side, factor out T07, then divide everything else over to yield Equations (13)–(15) respectively.
The derivation of P07 follows in a similar fashion. Equation (16) represents the mass-weighted average of resulting stagnation pressure that will be present once the streams are mixed completely. Isolating P07 to one side yields Equation (17), where and are defined as follows in Equations (18) and (19) respectively.
The next step is to divide both the numerators and the denominators of Equations (18) and (19) by to yield Equations (20) and (21). Then, plug (20) and (21) into (17) to yield (22). Finally, simplify (22) to yield mass-weighted average stagnation pressure of the mixed stream in Equation (23).
Once the two streams have mixed into one, the new stream will exit through a converging nozzle and this formulation can also be found in [6] and is presented in Appendix A. In the subsequent subsections, the formulation for the afterburners of both the turbojet and turbofan is presented.
3.2. Turbojet Engine with Afterburner
Equation (24) calculates the work required to operate the fan or the LPC.
To compare this afterburner to the auxiliary combustion chamber in the TurboAux, the same combustion temperature of 2516 K has been adopted for the products of the reaction. The combustion process is also modeled in the same fashion using the same fuel and equations for calculating the specific enthalpies. Equation (25) is defined as the inverse of the kilomoles of fuel burned in the main combustion chamber per 1 kilomole of O2 ingested. Equation (26) represents the number of additional kilomoles of fuel burned per 1 kilomole of O2 ingested.
To calculate any frictional stagnation pressure losses, Equation (27) accounts for the losses due to friction caused by aerodynamic resistance, and momentum changes produced by the exothermic reaction. Equation (28) is used to calculate the overall fuel to air ratio of the engine which will be used in the calculations of Fs and TSFC.
The equations to check the flow at the nozzle and to calculate the flow characteristics at the exit are the same for the turbojet as seen in [6] and in the Appendix A.
3.3. Turbofan Engine with Mixing and an Afterburner
Since the TurboAux is modeled as an adaption to the turbofan, it is no surprise that nearly all of the equations modeling the turbofan are identical. Equation (29) accounts for the 2% loss in stagnation pressure in the fan chute where combustion occurs in the TurboAux similar to Equation (27). Since no combustion occurs in the fan chute and it is adiabatic, Equation (30) shows there is no change in the stagnation temperature from station 2 to 8. The combustion process, the turbine calculations, and the stream mixing calculations remain unchanged. The turbofan then adopts a similar afterburner modeling from the turbojet, but it is imperative to account for the excess oxygen entering the afterburner from the bypass stream. Equation (31) appropriately accounts for this.
The derivation of T07 and P07 follow a very similar process as presented for the TurboAux apart from having to account for the auxiliary combustion process. Equation (32) defines , and Equations (33) and (34) are the equations used to calculate those stagnation quantities. Again, Equation (35) accounts for the efficiency of the burner and calculates the change in stagnation pressure after the combustion process. Lastly, Equation (36) is used to calculate the overall fuel to air ratio to calculate Fs and TSFC as well as the engine efficiencies, and the equations to check the flow at the nozzle and to calculate the flow characteristics at the exit are again the same for the turbofan as well.
4. Results and Discussion
In this chapter, a comparison of the performance results of the various engines is presented. Table 6, Table 7 and Table 8 summarize the performance results for the various engines at BPRs of 0.1, 0.8, and 1.5, respectively.

Table 6.
Performance Results of Turbojet, Turbofan, and TurboAux at BPR of 0.1.

Table 7.
Performance Results of Turbojet, Turbofan, and TurboAux at BPR of 0.8.

Table 8.
Performance Results of Turbojet, Turbofan, and TurboAux at BPR of 1.5.
The performance efficiencies of turbofan and TurboAux engines in terms of (i) propulsive efficiency, (ii) thermal efficiency, and (iii) overall efficiency are shown in Figure 5 and Figure 6. Similarly, the performance of these engines in terms of specific thrust and TSFC is shown in Figure 7. The figures show how these performance parameters vary across each BPR-FPR configuration. It is important to note that these parameters are not only affected by BPR, but rather by the optimal BPR-FPR configuration combination that was obtained from the optimization analysis.
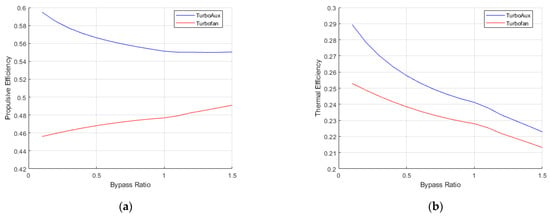
Figure 5.
Plots of efficiency vs. bypass ratio (a) propulsive and (b) thermal efficiency.
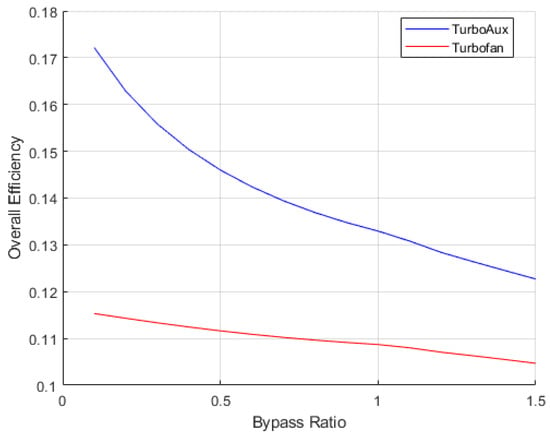
Figure 6.
Plot of overall efficiency vs. bypass ratio.
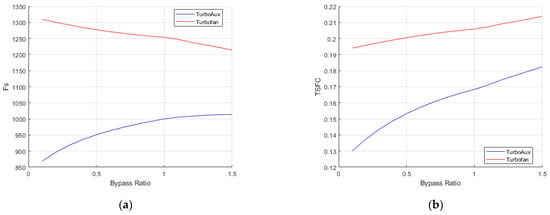
Figure 7.
Plots of performance vs. bypass ratio: (a) specific thrust and (b) thrust-specific fuel consumption.
These results illustrate many notable trends. Firstly, the tabulated results of the performance parameters for the turbojet show very little to no variation across all optimal designs. This can be attributed to FPR being the only variable in the turbojet analysis. As aforementioned, with OPR and TINT fixed, the energy input of the engine is fixed, and since a turbojet engine does not have a bypass stream and thus no BPR, the slight variation in the FPR values proved inconsequential to the performance of the engine. Secondly, the turbojet also produced the most specific thrust of the three engines, and while the turbofan outperformed the turbojet with respect to TSFC when compared without afterburner segments in either engine, the turbofan produced less Fs and exhibited an increase in TSFC when the afterburner segments were considered. While this may be an unfavorable trend at first glance, after closer investigation, it is apparent that the increase in TSFC is attributed to the increase in BPR. As BPR increases, the ratio of fresh air from the fan chute to oxygen-depleted air from the combustion chamber increases, thus lowering the stagnation temperature of the mixed stream. This means more fuel must be burned to reach a combustion temperature of 2516 K. The mixed stream exiting station 7 then enters the afterburner segment, and the difference between T07 and the afterburner combustion temperature of 2516 K is what will dictate how much more fuel must be burned to achieve this temperature. For example, at a BPR of 0.1, T07, the stagnation temperature of the mixed stream is 1224.8 K, conversely, at a BPR of 1.5, T07 is 735.7 K thus meaning more fuel is required at a BPR of 1.5 for the products of the afterburner combustion process to reach 2516 K than at a BPR of 0.1. Another trend observed in the turbofan was an increase in propulsive efficiency and a decrease in thermal efficiency. The overall efficiency, which is a product of the propulsive and thermal efficiencies showed a decrease as well. These trends were expected. Propulsive efficiency is defined as the ratio of thrust power to the rate of addition of energy to the propellant, and the rate at which thrust power decreased was less than the rate at which energy was added to the propellant with the addition of the afterburner segment. As mentioned in previous chapters, the reheat cycle proves detrimental to thermal efficiency, due to its high fuel consumption, despite augmenting a significant amount of thrust [8,9].
The TurboAux engine exhibited interesting trends as well. The TurboAux delivered much higher propulsive efficiency in comparison to the other engines. This can be attributed to the increase in BPR which also allows more mass to flow into the auxiliary combustion chamber. This is different than in the afterburning turbofan where this extra air being delivered to the bypass stream is utilized for combustion in the TurboAux rather than simply bypassing the core stream prior to mixing. However, although producing a higher thermal efficiency than the turbofan, the TurboAux exhibited a similar declining trend across the optimal design configurations. This too can be attributed to the increase in fuel consumption. In terms of Fs, the TurboAux greatly underperformed the other two engines, but drastically outperformed the other two engines with respect to TSFC. This was especially evident at lower BPRs where the fraction of the mass flow entering the auxiliary combustion chamber is much significantly less than that of the core stream.
Although these trends of the TurboAux show a promising future, it is important to compare the performance of this engine with current operational engines. This will be useful in understanding the application range of this engine and making a case for its use in specific industries. To gather a fuller understanding of this proposed engine, the TurboAux should be analyzed with computational fluid dynamics (CFD) in a future study. A CFD analysis of the TurboAux its operation and performance.
5. Conclusions and Future Work
The research presented in this paper is work conducted by Asundi and Ali [2]. The novel TurboAux engine along with the turbojet and turbofan engines (with afterburners) were modeled and analyzed in MATLAB. Upon the optimization analysis to arrive at an optimized design configuration for a range of bypass ratios from 0.1 to 1.5, the TurboAux was compared to turbojet and turbofan engines with afterburning segments. Across that range of bypass ratios, the TurboAux showed a significant increase in Fs while the turbofan exhibited a sharp decline in Fs. The TurboAux exhibited less fuel across that same BPR range as well.
To better understand the usefulness of the TurboAux, further analysis is required. This further analysis could be investigating whether the TurboAux could serve as a replacement for higher bypass ratio engines with the augmentation of a tertiary compressor or fan accompanied with an additional bypass stream and fan chute around the entire TurboAux. As a future study, the TurboAux configuration should be further analyzed with CFD to obtain a deeper understanding of the inner workings of this novel engine; more specifically, analyzing the auxiliary combustion process, as well as the mixing of the bypass and core streams using CFD, will give a more accurate physical understanding of the TurboAux and is performance capabilities in terms of thrust, fuel consumption, and efficiency. The use of numerical methods such as CFD also allows for more physically accurate models to be rendered in which many more aspects of the engine can also be studied such as the thermal loading of the components in the auxiliary stream as well as how the mixing of the two streams can affect the performance of the engine.
Author Contributions
Conceptualization, K.F.; Methodology, S.A.A. and A.C.T.; Software, K.F.; Validation, A.C.T.; Investigation, K.F.; Writing–Original Draft Preparation, K.F.; Writing–Review & Editing, K.F.; Supervision, S.A.A. and A.C.T.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| B | bypass ratio |
| C | local speed of sound |
| Cp0 | specific heat capacity at constant pressure |
| factual | actual fuel to air ratio of core stream |
| faux | actual fuel to air ratio of auxiliary stream |
| fideal | ideal fuel to air ratio |
| fo | overall actual fuel to air ratio of core and auxiliary streams |
| Fs | specific thrust |
| HrpCO2 | enthalpy of reaction of CO2 |
| Hrpf | enthalpy of reaction of fuel |
| HV | heating value of fuel |
| Ma | flight speed |
| Mair | molar mass of air |
| ṁaux | mass flow of auxiliary stream |
| ṁcore | mass flow of core stream |
| ṁf1 | mass flow of fuel into core stream |
| ṁf2 | mass flow of fuel into auxiliary stream |
| Mfuel | molar mass of fuel |
| P0 | stagnation pressure |
| Pa | ambient static pressure |
| R | specific gas constant |
| T | thrust |
| T0 | stagnation temperature |
| Ta | ambient static temperature |
| Tp | static temperature of the products of combustion |
| Tr | static temperature of the reactants of combustion |
| TSFC | thrust specific fuel consumption |
| Va | velocity of air at inlet |
| wCHP | specific work required to drive high-pressure compressor |
| wCLP | specific work required to drive low-pressure compressor |
| ΔP0b | stagnation pressure loss due to aerodynamic resistance and momentum changes from combustion |
| Ycc | moles of air required for stoichiometric combustion |
| γ | ratio of specific heat at constant pressure to specific heat at constant volume |
| ηb | burner efficiency |
| ηc | compressor efficiency |
| ηd | diffuser efficiency |
| ηf | fan chute efficiency |
| ηm | mechanical efficiency |
| ηn | nozzle efficiency |
| ηo | overall efficiency |
| ηp | propulsive efficiency |
| ηt | turbine efficiency |
| ηth | thermal efficiency |
| πc | overall pressure ratio |
| πHP | high-pressure compressor pressure ratio |
| πLP | low-pressure compressor pressure ratio |
Appendix A
Here in Appendix A are the extraneous formulations for the TurboAux that can also be found in [6]. As to keep readers engaged, I’ve elected to move the formulation here and retain the new, pertinent information in the formulation section.
The local speed of sound and the flow speed at the inlet of the diffuser are computed in Equations (A1) and (A2), respectively. Upon entering the diffuser, the stream is slowed down and the new stagnation temperature and pressure of the stream due to the reduction in velocity and diffuser efficiency are calculated in Equations (A3) and (A4), respectively.
After the diffuser, the flow is compressed by the LPC or “fan”. The stagnation pressure is simply found as the product of the pressure ratio across the fan (FPR). The optimum FPR values from the optimized design are used here in Equation (A5). The stagnation temperature is computed in Equation (A6) which accounts for the efficiency of the compressor and the specific work required to operate the LPC is computed in Equation (A7).
Following the compression of the stream in the LPC, the stream diverges into two streams: the core stream and the auxiliary stream. The bypass ratio is defined in Equation (A8). The auxiliary stream bypasses the core of the engine and enters the auxiliary combustion chamber, while the core stream is compressed further through the stages of the HPC. The combustion process of the auxiliary combustion chamber will produce products of combustion at 2516 K. The loss in stagnation pressure in this combustion process is calculated in Equation (A9).
The compression ratio of the HPC is calculated in Equation (A10) as the overall pressure ratio divided by the FPR. The stagnation pressure, stagnation temperature, and specific work required to operate the HPC are computed in a similar manner as in the LPC in Equations (A11)–(A13) respectively.
The combustion process is assumed as a complete combustion process with excess air in the products and was modeled in both the auxiliary and main combustion chambers using the enthalpy of reactions, enthalpy of combustion, and the first law of thermodynamics. Equations (A14) and (A15) are equations used to calculate the specific enthalpy, on a molar basis, of each constituent in the combustion process. The constants a, b, and c are experimental coefficients taken from literature used in the calculation of the specific enthalpy [7]. Equation (A16) calculates the change in the specific enthalpy. Due to temperature limitations of the turbine blades, the products of combustion from the main combustion chamber are exiting at 1922 K. The number of moles for stoichiometric combustion of the fuel is computed in Equation (A17), and with the fuel, the temperature of the reactants, and the temperature of the products specified, the number of moles of air required for complete combustion with excess air in the products is calculated in Equation (A18).
After the number of moles of air required for complete combustion is calculated in Equation (A18), Equation (A19) computes the ideal fuel to air ratio on a mass basis. To account for non-ideal combustion, the actual fuel-to-air ratios for both the main combustion chamber and the auxiliary combustion chamber are computed in Equations (A20) and (A21), respectively. Losses in stagnation pressure due to friction from combustion are calculated in Equation (A22). Conservation of mass states that the total mass flow rate of fuel is the sum of the separate mass flow rates in Equation (A23). Using the bypass ratio, the overall fuel to air ratio of the entire engine accounting for both combustion processes is calculated in Equation (A24).
Upon exiting the main combustion chamber, the core stream will be expanded through the high-pressure turbine and the low-pressure turbine. Equations (A25) and (A26) calculate the stagnation temperature and pressure exiting the high-pressure turbine and entering the low-pressure turbine. Similarly, Equations (A27) and (A28) calculate the stagnation temperature and pressure exiting the low-pressure turbine. Losses that occur due to the mechanical and component efficiency of the turbine are accounted for in these equations as well.
In Equation (A29), a ratio is set up to test if the nozzle is choked. If P*/P07 is greater than or equal to Pa/P07, then the nozzle is choked meaning the Mach number at the exit is 1. Subsequently, Equations (A30)–(A33) calculate the exit flow static pressure, static temperature, density, and velocity, respectively.
Conversely, if P*/P07 is less than or equal to Pa/P07, then the nozzle is not choked. This means that the exit pressure is equal to the ambient pressure. The exit flow conditions for the static temperature, density, Mach number, and velocity are calculated in Equations (A34)–(A37).
The last step of this parametric study is to calculate the performance and efficiency of this engine. Equations (A38) and (A39) calculate Fs and TSFC. In Equation (A40), the heating value of the fuel is converted from kJ/kmol to J/kg. Lastly, Equations (A41)–(A43) are used to calculate the propulsive, thermal, and overall efficiency, respectively. Conventionally, propulsive efficiency is defined as the ratio of thrust power to the rate of addition of kinetic energy, and thermal efficiency is defined as the ratio of the rate of addition of kinetic energy to the rate of total energy consumption. These are approximations that neglect to account for the rate of addition of pressure energy [8]. Since the TurboAux is utilizing a purely converging nozzle that has choked flow in every case studied, the pressure energy is not negligible. It was necessary to adjust the conventional equations for propulsive and thermal efficiency to account for the increase in pressure energy. This is outlined in Equations (A41) and (A43).
References
- Saravanamuttoo, H.I.H.; Rogers, G.F.C.; Cohen, H. Gas Turbine Theory; Pearson Education: New York, NY, USA, 2001. [Google Scholar]
- Asundi, S.A.; Ali, S.F. Parametric Study of a Turbofan Engine with an Auxiliary High-Pressure Bypass. Int. J. Turbomach. 2019, 4, 2. [Google Scholar] [CrossRef]
- Raymer, D.P. Aircraft Design: A Conceptual Approach, 5th ed.; AIAA Education Series; American Institute of Aeronautics & Astronautics: Reston, VA, USA, 2012. [Google Scholar]
- MacIsaac, B.; Langston, R. Gas Turbine Propulsion Systems, 1st ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Vaferi, K.; Vajdi, M.; Nekahi, S.; Nekahi, S.; Moghanlou, F.S.; Asl, M.S.; Mohammadi, M. Thermo-Mechanical Simulation of Ultrahigh Temperature Ceramic Composites as Alternative Materials for Gas Turbine Stator Blades. Ceram. Int. 2021, 47, 567–580. [Google Scholar] [CrossRef]
- Fetahi, K.; Asundi, S.A.; Taylor, A.C.; Ali, S.F.; Ibrahim, A.H. Parametric Study of a Turbojet Engine with Auxiliary Bypass Combustion—The TurboAux Engine. In Proceedings of the AIAA Propulsion and Energy Forum, New Orleans, LA, USA, 24 August 2020; pp. 1–11. [Google Scholar]
- Lee, A.S.; Singh, R.; Probert, S.D. Two-Combustor Engines’ Performances Under Design and Off-Design Conditions. In Proceedings of the 45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Denver, CO, USA, 2–5 August 2009. [Google Scholar] [CrossRef]
- Campbell, A.S. Thermodynamic Analysis of Combustion Engines, 1st ed.; Wiley: Hoboken, NJ, USA, 1979. [Google Scholar]
- Hill, P.; Peterson, C. Mechanics and Thermodynamics of Propulsion, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).