Experimental Investigation of a Complex System of Impinging Jets Using Infrared Thermography

Abstract

A central task in aviation technology is the development of efficient cooling techniques for thermal highly loaded engine components. For an optimal design of the cooling mechanisms, the heat transfer characteristics have to be known and need to be describable. As a cooling concept for low-pressure turbine casings, complex systems of impinging jets are used in order to reduce blade tip clearances during the flight mission. In order to improve established theoretical model approaches, this paper presents a novel method for the experimental investigation of such a complex system with 200 impinging jets using infrared thermography. The presented experimental method uses a thin electrically heated chrome-aluminum foil as target plate. Modeling the transient effects inside the foil, small structures and high gradients in the heat transfer coefficient can be reproduced with good accuracy. Experimental results of the local heat transfer characteristics are reported for jet Reynolds numbers of $\mathrm{Re}=2000$…$6000$. The influence of the jet-to-jet distance and the jet Reynolds number on the Nusselt numbers are quantified with $\mathrm{Nu}\sim {(S/D)}^{-0.47}$ and $\mathrm{Nu}\sim {\mathrm{Re}}^{0.7}$. The results indicate a dependency of the flow regime for the relatively low jet Reynolds numbers, as it is known from literature.

1. Introduction

The design of efficient aero engines at all operating points is one of the central tasks in aviation technology. An essential part of the design process is designated to the development of efficient cooling techniques for thermal highly loaded engine components. During a flight mission, the engine components are exposed to uneven expansion rates due to abrupt changes in the thermal load. Relating to turbine components, uneven expansion rates between turbine blades and turbine casing lead to a change in blade tip clearances. A reduction in these clearances is linked to an increase in the efficiency of modern aero engines [1]. Directing a controlled flow of impinging air onto the turbine casing is intended to keep these clearances constant at a desired optimum. The so-called active clearance control (ACC) system consists of several tubes surrounding the low-pressure turbine casing. The tubes are supplied with cooling air from the bypass which exits via numerous holes directed to the external side of the casing. Achieving high heat transfer rates, impingement cooling is an efficient way to counteract on locally occurring high heat loads [2]. The ACC panel system, which is investigated within this work, consists of four parallel tubes, which are supplied with cooling air from a common supply tube. The geometry of the panel system with its numerous holes is quite complex. Although the ACC panel system is successfully used in modern aero engines, associated theoretical model approaches need to be further developed to increase the accuracy. For an optimal design of the cooling mechanisms along the entire aircraft duty cycle, the heat transfer characteristics have to be known and need to be describable. For this purpose, we are investigating an ACC panel system experimentally and numerically at the Institute of Aerospace Thermodynamics (ITLR) at the University of Stuttgart. The experimental results, which will be presented within this paper, are intended to serve as a reference data set for the validation of the numerical setup. For a single impinging jet the numerical setup has already been validated using reference data from the Ercoftac database [3]. The results were presented in Wienand et al. [4].

A large number of publications exist focusing on the heat transfer characteristics of impingement cooling concepts. In comparison to a single impinging jet, flow and heat transfer characteristics of rows or arrays differ significantly due to jet interaction [5]. To this purpose, Goldstein and Seol [6] investigated a row of 16 impinging jets varying the jet Reynolds number and the distance between the jets. The dependency of the heat transfer rate from the jet Reynolds number can be described using a power law. With decreasing jet-to-jet distance, the area-averaged heat transfer is reported to increase. Huber and Viskanta [7] compared the heat transfer characteristics of an array of $3\times 3$ impinging jets to the results of a single jet. Due to jet interaction, the heat transfer in the stagnation region decreases. This effect is more apparent for higher jet-to-plate distances ($H/D=6$). Obot and Trabold [8] investigated the crossflow effect in an array of impinging jets, varying the outflow conditions of the jets after impinging onto the target plate. Due to the crossflow, the impinging jets get deflected and the heat transfer in the stagnation region decreases. This effect is more apparent for high jet-to-plate and low jet-to-jet distances. Florschuetz et al. [9] added an additional crossflow to an array of impinging jets modeling the internal cooling of a turbine blade, which leads to a further reduction in the heat transfer rates.

A common measurement technique for the experimental investigation of impinging jet configurations is the use of thermochromic liquid crystals (TLC). Geers et al. [10] and Andreini et al. [11] used wide-band TLC at an electrically heated plate predicting the heat transfer from an array [10] and rows [11] of impinging jets at steady-state conditions. For steady-state measurements, the influence of the surroundings has to be known precisely. The influence of the surrounding and the resulting uncertainty of the measurement can be reduced doing transient measurements. Instead of a heated target plate, in many transient measurement techniques the air flow of the impinging jets is heated, wheras at the target plate, one-dimensional heat conduction into a semi-infinite wall is assumed. Using narrow-band TLC, the time to reach a certain color at the target plate and therefore the heat transfer characteristics can be predicted. This method was used, e.g., by Xing et al. [12] investigating an array of impinging jets and by Ben Ahmed et al. [13] for a row of jets. Due to a wide range of heat transfer coefficients (htc), the time to reach a certain color of the TLC differs strongly over the target plate. This leads to higher uncertainties in the stagnation region with the highest htc, where the time to reach the color play tends to be too fast. For small structures with high gradients, the uncertainty in the stagnation region increases [13]. In order to reduce the uncertainty along the target plate, Schmid et al. [14] presented a method using a time varying surface heat flux for a single impinging jet. Another possibility to reduce the uncertainty for the investigation of the local heat transfer characteristics in a wide range of htc is the infrared thermography (IRT). Schreivogel and Pfitzner [15] used IRT in combination with frequency domain phosphor thermometry for a single impinging jet. For this method, it is necessary to have an optical access to the upper side of the target plate. Modak et al. [16] investigated a single impinging jet on a thin electrically heated foil, directing an IRT camera on the backside of the target plate. The results showed good agreement to data from literature.

The experimental setup of the present study is comparable to the method presented by Modak et al. [16]. As the impinging jets from the ACC panel system have a diameter of only $1 \mathrm{mm}$, small structures and high gradients have to be resolved. Compared to Modak et al. [16], lateral conduction inside the heated foil cannot be neglected, as Da Soghe et al. [17] and Cocchi et al. [18] showed for a row of impinging jets onto an electrically heated and $0.7$ mm thick target plate in a steady-state approach. The present study, which uses an electrically heated target plate with a thickness of only $50 \mathsf{\mu }\mathrm{m}$ increases the accuracy, as the temperature gradient over the plate’s thickness can be neglected and the influence of lateral conduction is reduced. The aim of this paper is the presentation of an innovative method to measure the local heat transfer characteristics of complex systems of impinging jets with good accuracy, modeling the transient effects of lateral conduction, change of internal energy, radiation and natural convection. The combination of the infrared thermography with a very thin target plate makes the method stand out against common techniques for similar applications.

2. Experimental Methods

The following section describes the experimental methods to investigate the heat transfer characteristics of an ACC panel system. The geometry of the laser-sintered panel model is shown in Figure 1. The model was designed based on an original ACC panel system from the MTU Aero Engines AG.

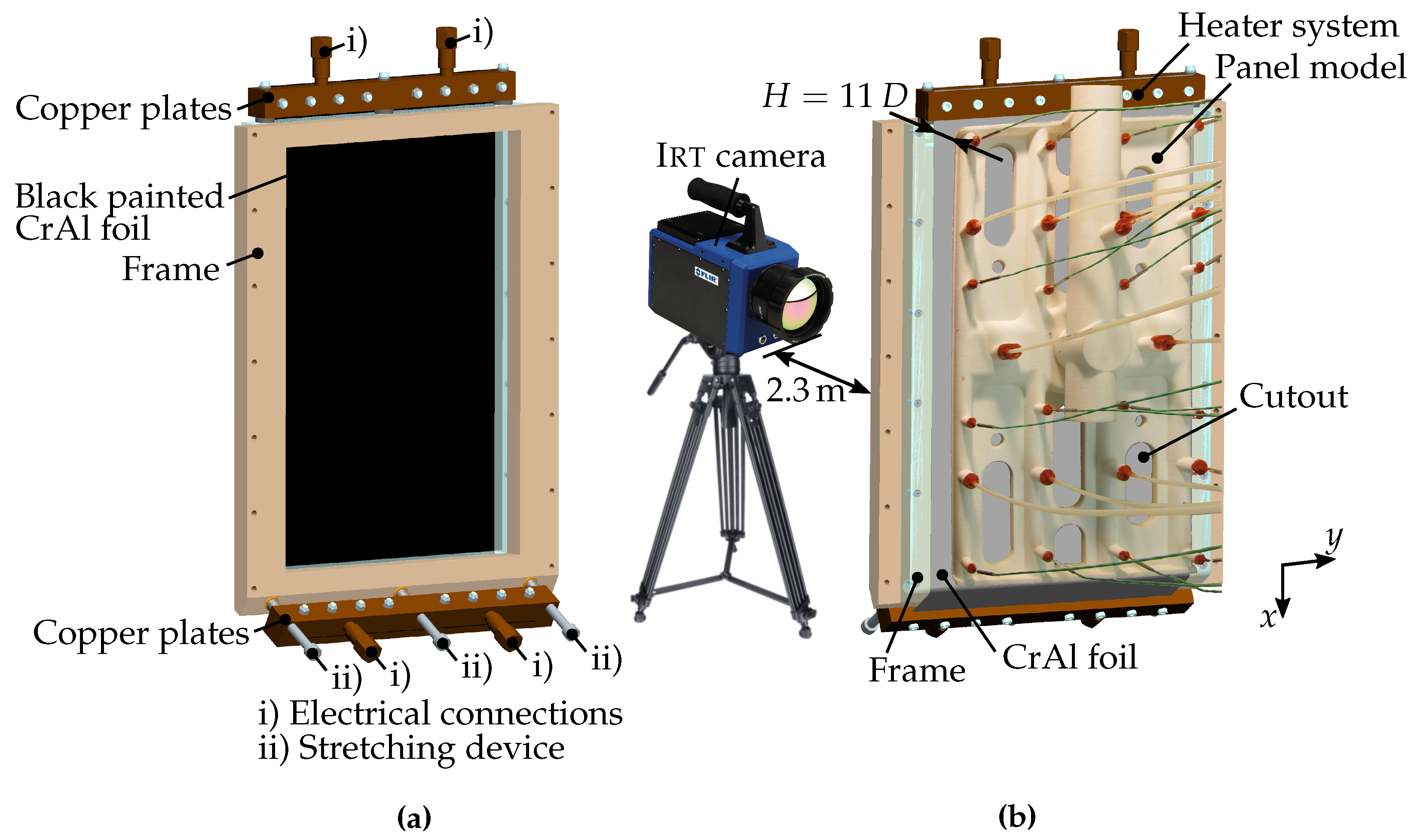
The polymer PA 2201 was used as material manufacturing the model from three individual parts on an Eosint P system (supply tube, top side and bottom side separately). To ensure the tightness of the material, the three parts were treated with a special varnish (Cramolin Plastik) before the gluing process. Silicone seal ensures tightness at the glued joints. The holes were manufactured in a second step with a molding cutter to ensure an adequate hole geometry, which was verified under a microscope.

Cooling air enters the panel from a supply tube and flows into a collector box, which is schematically illustrated in Figure 1. From the collector box, the air gets separated into four tubes with an inner diameter of $d=12.5D$, while $D=1\mathrm{mm}$ denotes the diameter of the holes on the bottom side of the tubes. The tubes are arranged in a distance of $75D$ to each other.

Table 1. Geometric parameters of the hole pattern on the panel model.

Tube	#1	#2	#3	#4
$N_{\mathrm{jet}}$	82	32	32	54
$S/D$	5.2	13	12.8	7.8

gives an overview of the number of holes N and their distance S for each tube. The air exits the panel via these holes and creates 200 impinging jets onto a flat target plate in a distance of $H/D=11$.

For the characterization of the impinging jets, the jet Reynolds number is defined based on the jet diameter

$$\mathrm{Re}=\frac{\rho \overline{u_{\mathrm{jet}}}D}{\eta }=\frac{4{\dot{m}}_{\mathrm{jet}}}{\pi D\eta }.$$

(1)

The dynamic viscosity $\eta$ of the air is modeled with Sutherland’s law [19] using the coefficients presented by White [20]. It is assumed, that the mass flow from the supply tube is separated homogeneously over the 200 impinging jets. This assumption is valid according to the results from a numerical simulation of the panel model.

The target plate is a thin chrome-aluminum (CrAl) foil with a thickness of $50 \mathsf{\mu }\mathrm{m}$. For the heat transfer measurements, the target plate is heated electrically. The electrical resistance of the foil was determined at different temperatures and is nearly constant in the applied temperature range of 290 K–380 K. As shown in Figure 2, the CrAl foil is clamped on two ends between two copper blocks, which serve as anode and cathode.

The power supply unit from DeltaElektronika delivers a current of up to 200 A and a maximum voltage of 30 V. For stability reasons, the foil is mounted in a frame and tensioned with several screws. The CrAl alloy from MK Metallfolien GmbH (MKM CrAl4, 1.4725), which is also used for catalytic converts or ceran fields, possesses good high temperature stability and a small elongation $<1.5$ % in the applied temperature range. Due to this feature, a deformation of the target plate during the heating process is successfully prevented with the tension of the screws. The position of the heater system and panel model is schematically illustrated in Figure 2.

An Flir Sc 7600 infrared thermography (IRT) camera at a frame rate of 25 Hz is directed to the backside of the target plate in a distance of $2.3$ m. The camera detector is sensitive in the spectral range from $1.5$ $\mathsf{\mu }$$\mathrm{m}$ to $5.1$ $\mathsf{\mu }$$\mathrm{m}$ and has a noise equivalent temperature difference value below 20 mK. In order to achieve a high emissivity of $\epsilon =0.93$, the CrAl foil is sprayed from one side with a temperature-resistant black paint (Supertherm from Dupli Color). The paint was applied crosswise in three layers to create a homogeneous surface. The layer thickness of the paint was measured at several points with a digital micrometer to an average value of $95 \mathsf{\mu }\mathrm{m}$.

Heater system and panel model are integrated in an open wind tunnel, which gives the opportunity to add a crossflow to the impinging jets. The experimental facility is visualized in Figure 3.

With a special mechanism, the heater system and the panel model can be rotated in an angle of up to ${30}^{\circ }$ to the crossflow. The crossflow effect is not discussed within this paper. Cooling air is supplied to the panel model from a screw compressor Atlas Copco GA 22 with a thermal mass flow controller from Teledyne Hastings. Up to $10.75$ g/s, a HFC-303 controller gives an accuracy of $\pm 0.054$ g/s. Higher mass flow rates of up to 50 g/s are generated with an accuracy of $\pm 0.5$ g/s using a HFC-207 controller. After impinging onto the target plate, the cooling air can exit via both sides in y-direction and through the cutouts (see Figure 2). The impinging jets and the target plate are protected from environmental influences, as they are integrated inside the wind tunnel. The backside of the target plate, which lies outside the wind tunnel, is protected likewise by a wooden box (not shown in Figure 3). For the optical access of the IRT camera, the box is left open to one side. In order to avoid reflections, the area between the target plate and the camera is covered with a black cloth. Two K-type thermocouples measure the ambient temperature inside the cloth. The temperature of the impinging jets is also measured using K-type thermocouples at several positions inside the panel model (see Figure 1). The thermocouples are connected to a MEASURpoint DT8874-32T from DataTranslation. A calibration of the thermocouples with a dry-block calibrator Ametek RCT-159B ensures an accuracy of $\pm 0.2$ K including the uncertainty from the resulting calibration curve.

After the electrical power at the target plate is suddenly switched on, the surface temperature at the outer side of the CrAl foil is measured with the IRT camera. The accuracy of the IRT camera was investigated in a climate chamber with known thermal conditions. Maximum deviations occur for surface temperatures near the surrounding temperature ($T_{\mathrm{w}}=T_{\infty }+6$ K) with an error of $\pm 0.6$ K. At higher surface temperatures the accuracy lies within ±0.2 K. For the transient heat transfer measurements, the temperature inside the panel model is nearly constant. With the information of the jet temperature and the IRT data, the heat transfer at the target plate can be predicted. The mathematical procedure will be discussed within the next section.

2.1. Heat Transfer Prediction

For the heat transfer prediction at the target plate, the temperature gradient across the thickness of the CrAl foil is neglected. This assumption is valid according to the lumped-capacitance method [21,22], achieving a Biot number of $\mathrm{Bi}<0.006$ for the thin foil including the black paint. With this assumption, the heat transfer characteristics at the target plate can be predicted directly from the measured IRT data at the outer side of the foil. For the evaluation process, MATLAB 18 is used.

After reaching steady-state flow conditions, the IRT camera starts recording a few seconds before the heater is switched on. To reduce the thermal noise of the IRT data, the transient temperatures are smoothed over ten values. With the smoothed temperatures, the heat transfer due to forced convection from the impinging jets ${\dot{q}}_{\mathrm{fc}}$ is calculated for each pixel

$${\dot{q}}_{\mathrm{fc},i,j}\left(t\right)=\frac{UI}{A_{\mathrm{F}}}-\sum _X{\dot{q}}_{\rho \mathrm{c},i,j}\left(t\right)+\sum _X{\dot{q}}_{\mathrm{cond},i,j}\left(t\right)-{\dot{q}}_{\mathrm{rad},i,j}\left(t\right)-{\dot{q}}_{\mathrm{nc},i,j}\left(t\right).$$

(2)

The variables $i,j$ refer to the position of the pixel on the target plate. The first term on the right-hand side of Equation (2) denotes the electrical power $P=UI$ of the power supply, which is applied to the surface of the foil $A_{\mathrm{F}}$. It is assumed, that the specific heat flux from the power supply ${\dot{q}}_{\mathrm{el}}$ is constant over $A_{\mathrm{F}}$, as the electrical resistance of the foil was found to be nearly independent of the temperature in the applied range of 290 K–380 K. The second term in Equation (2) considers the change of internal energy. As the temperature gradient across the thickness of the foil ($d_{\mathrm{F}}=50 \mathsf{\mu }\mathrm{m}$) and of the black paint ($d_{\mathrm{P}}=95 \mathsf{\mu }\mathrm{m}$) is neglected, ${\dot{q}}_{\rho \mathrm{c}}$ is constant over $d_{\mathrm{F}}$ and $d_{\mathrm{P}}$. The change of internal energy over time inside the foil and inside the black paint (index variable X) is calculated for each pixel

$$\begin{array}{cc}\hfill {\dot{q}}_{\rho \mathrm{c},i,j}\left(t\right)& ={\rho }_X{c}_{\mathrm{v},X}{d}_X\frac{\partial T_{\mathrm{w},i,j}}{\partial t}\left(t\right)\hfill \\ \hfill & \approx {\rho }_X{c}_{\mathrm{v},X}{d}_X\frac{T_{\mathrm{w},i,j}\left(t_{n+1}\right)-T_{\mathrm{w},i,j}\left(t_{n-1}\right)}{t_{n+1}-t_{n-1}}.\hfill \end{array}$$

(3)

The first line in Equation (3) describes the theoretical formulation of the change of internal energy. The second line shows the implementation in MATLAB. According to the material specification, the density of the CrAl foil is given by ${\rho }_{\mathrm{F}}=7180$ kg/m³ and the specific heat capacity by $c_{\mathrm{v},\mathrm{F}}=500$ J/(kgK). The material properties can be assumed to be constant in the applied temperature range. For the black paint no material properties are specified. For this reason, the material properties from silicone resin ${\rho }_{\mathrm{P}}=1100$ kg/m³ and $c_{\mathrm{v},\mathrm{P}}=1500$ J/(kgK) are used [23], as the black paint is based on it.

With the third term in Equation (2), the heat conduction between the pixels inside the foil and inside the black paint (index variable X) are considered

$$\begin{array}{cc}\hfill {\dot{q}}_{\mathrm{cond},i,j}\left(t\right)=-k_X& \frac{\partial T_{\mathrm{w},i,j}}{\partial n}\left(t\right)\hfill \\ \hfill \approx -k_X& [\frac{2T_{\mathrm{w},i,j}\left(t\right)-T_{\mathrm{w},i-1,j}\left(t\right)-T_{\mathrm{w},i+1,j}\left(t\right)}{l_{\mathrm{pixel}}}\hfill \\ \hfill & +\frac{2T_{\mathrm{w},i,j}\left(t\right)-T_{\mathrm{w},i,j-1}\left(t\right)-T_{\mathrm{w},i,j+1}\left(t\right)}{l_{\mathrm{pixel}}}]\frac{d_X{l}_{\mathrm{pixel}}}{A_{\mathrm{pixel}}}.\hfill \end{array}$$

(4)

As described for Equation (3), the first line in Equation (4) gives the theoretical formulation of the heat conduction and the second line shows the implementation in MATLAB. The thermal conductivity of the foil is specified to $k_{\mathrm{F}}=16$ W/(mK). For the black paint again, the value for silicone resin is used $k_{\mathrm{P}}=0.15$ W/(mK) [23]. Since the lateral heat conduction in Equation (4) refers to the cross-sectional area of the pixels inside the foil and inside the black paint ($d_X{l}_{\mathrm{pixel}}$), it has to be set in relation to the area of one pixel $A_{\mathrm{pixel}}$. This ensures that all terms in Equation (2) refer to the same surface.

With the fourth term in Equation (2), the thermal radiation is considered to

$${\dot{q}}_{\mathrm{rad},i,j}\left(t\right)=\left({\epsilon }_{\mathrm{P}}+{\epsilon }_{\mathrm{F}}\right)\sigma (T_{\mathrm{w},i,j}{\left(t\right)}^4-T_{\infty }^4).$$

(5)

The emissivity of the black paint ${\epsilon }_{\mathrm{P}}=0.93$ was measured in a climate chamber with known thermal conditions. At the inner side of the CrAl foil a value of ${\epsilon }_{\mathrm{F}}=0.10$ is used, which is valid for aluminum foils and polished chrome [24].

The influence of natural convection on the outer side of the foil is considered with the fifth term in Equation (2)

$${\dot{q}}_{\mathrm{nc},i,j}\left(t\right)=h_{\mathrm{nc},\mathrm{i}}\left(t\right)(T_{\mathrm{w},i,j}\left(t\right)-T_{\infty }).$$

(6)

The transient behavior of the heat transfer due to natural convection was determined experimentally. This procedure results in a time dependent heat transfer coefficient $h_{\mathrm{nc},\mathrm{i}}\left(t\right)$, which can be described with polynomial functions. The determination of the local heat transfer coefficient due to natural convection will be explained in Section 2.2.

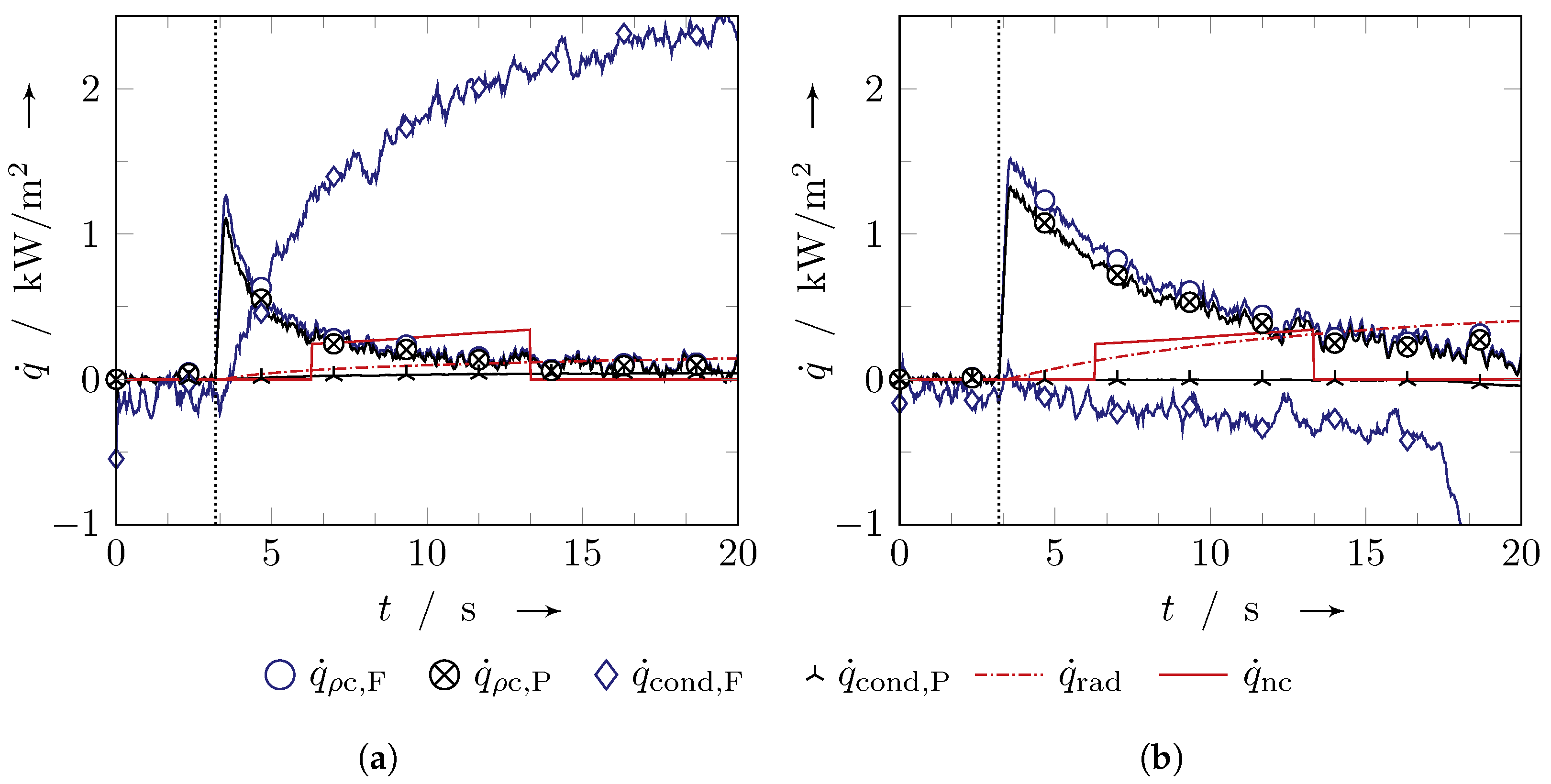
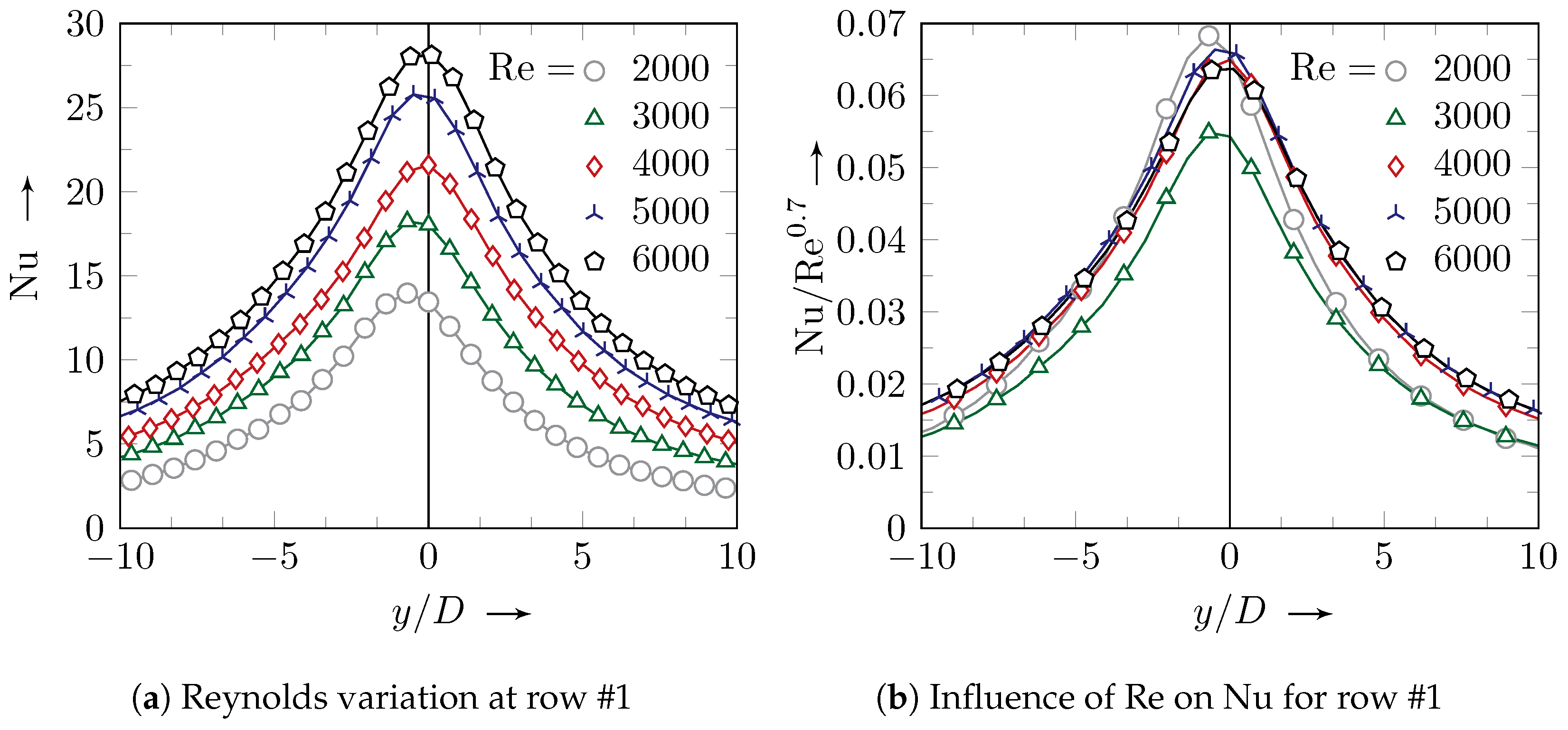
The transient results for the individual terms in Equation (2) are shown in Figure 4 exemplarily for one pixel in the stagnation point of an impinging jet and for one pixel in a distance of $7D$ from the stagnation point. The jet Reynolds number based on the jet diameter is Re = 2000.

The graphs in Figure 4 give an impression of the effect of each term on the prediction of the specific heat ${\dot{q}}_{\mathrm{fc}}$, which is transferred by forced convection. The vertical dotted line shows the starting time of the power supply. The electrical power results in a constant specific heat flux of ${\dot{q}}_{\mathrm{el}}=3.42$ kW/m² for each pixel, which is not inserted in the graphs in Figure 4. The increase in internal energy ${\dot{q}}_{\rho \mathrm{c}}$ inside the foil and inside the black paint is significant at the beginning. After about $1$ s, both terms decrease, with a steeper gradient in the stagnation point compared to the pixel $7D$ outside. Due to high temperature gradients in the stagnation region, the lateral heat conduction inside the foil in Figure 4a has a considerable effect, whereas the intensity in Figure 4b is small. At approximately $t=18$ s the term ${\dot{q}}_{\mathrm{cond},\mathrm{F}}$ decreases steeply in Figure 4b. This results from an increasing uncertainty of the IRT data, as the temperature of the pixel is outside the calibrated temperature range of the camera. The calibrated temperature range lies within 50 K to achieve higher accuracy of the IRT data. Compared to the effect inside the foil, the heat conduction inside the black paint ${\dot{q}}_{\mathrm{cond},\mathrm{P}}$ is negligible for both pixels. The term denoting the radiation ${\dot{q}}_{\mathrm{rad}}$ increases monotonically after the power supply is switched on. Due to higher heat transfer rates and therefore lower surface temperatures in the stagnation region, the effect of radiation is less apparent in Figure 4a compared to the pixel in Figure 4b. The term denoting the natural convection ${\dot{q}}_{\mathrm{nc}}$ is present only for a time interval 3 s–10 s after turning on the electrical heater. Only for this time interval, polynomial functions are defined to describe the transient behavior of natural convection. The reason for this approach will be explained in Section 2.2.

With the prediction of the individual transient terms for each pixel and the resulting specific heat flux due to forced convection ${\dot{q}}_{\mathrm{fc}}$ in Equation (2), the Nusselt number can be defined as

$${\mathrm{Nu}}_{i,j}\left(t\right)=\frac{{\dot{q}}_{\mathrm{fc},i,j}\left(t\right)D}{k(T_{\mathrm{w},i,j}\left(t\right)-T_{\mathrm{jet}})}.$$

(7)

The jet diameter D is used as a characteristic length. As a reference temperature of the fluid, the jet temperature $T_{\mathrm{jet}}$ is used. This definition is valid, as the jet temperature correlates to the surrounding air temperature and the jet Reynolds number is below 35,000 [25]. The thermal conductivity k of the air is modeled with Sutherland’s law [19] using the coefficients presented by White [20].

Figure 5 shows the transient results of the specific heat flux from Equation (2) and the Nusselt number from Equation (7) for the two pixels, which were exemplarily discussed in Figure 4.

In the stagnation point, the specific heat flux ${\dot{q}}_{\mathrm{fc}}$ rises above the specific heat flux ${\dot{q}}_{\mathrm{el}}$ from the electrical power supply. This behavior results from the high lateral heat conduction inside the foil, as shown in Figure 4a. At the pixel in a distance of $7D$ from the stagnation point, the result for the specific heat flux ${\dot{q}}_{\mathrm{fc}}$ is below ${\dot{q}}_{\mathrm{el}}$. In this region, the increase in surface temperature and therefore the effect of increasing internal energy is still dominant, as shown in Figure 4b. The fast decrease in ${\dot{q}}_{\mathrm{fc}}$ at $t=18$ s should not be considered, as it is related to the increasing uncertainty of the surface temperature $T_{\mathrm{w}}$, which increases above the calibrated range of the IRT camera.

In Figure 5b, the transient results for the Nusselt number are shown for different intensities of the electrical power supply. The blue/black colored curves belong to the specific heat flux distributions from Figure 5a with ${\dot{q}}_{\mathrm{el}}=3.42$ kW/m². The gray colored curves result from ${\dot{q}}_{\mathrm{el}}=2.80$ kW/m² and ${\dot{q}}_{\mathrm{el}}=2.21$ kW/m², respectively. The overall good agreement shows, that the results are independent of the power supply level, which is an indication, that the evaluation process characterizes the relevant effects accurately. Due to the formation of a thermal boundary layer, the Nusselt number in Figure 5b decreases rapidly, after turning on the electrical heater. However, the uncertainty in the prediction of the Nusselt number is relatively high at the beginning of the heating process, as the surface temperature is close to the surrounding air temperature, which results in a higher uncertainty of the IRT data (see Section 2.3). After a few seconds, the Nusselt number at the pixel in a distance of $7D$ from the stagnation point asymptotically approaches a constant value. At the stagnation point, the Nusselt number still decreases slightly over the entire time period. Expecting an independence of the Nusselt number from transient effects, this behavior is assumed to be related to an increasing uncertainty in the reference temperature. The air of the impinging jet is mixed with the surrounding air, which heats up during the heating process. As the jet temperature is used as a reference temperature, the error increases over time. This effect is more apparent in regions with low surface temperatures, as they occur in the stagnation region. The increasing uncertainty, as the surrounding components and the surrounding air heats up over time, demonstrates the difficulties of a steady-state technique in comparison to the transient approach, which was mentioned in Section 1.

For the final evaluation of the heat transfer characteristics, a compromise has to be performed over the described measurement uncertainties. The gray colored region in Figure 5 shows the chosen time period for the final evaluation. It starts after the steep decrease in the Nusselt number, where the uncertainty of the IRT data is more apparent. From this starting time, the results are averaged over $1.5$ s, which corresponds to 45 measured values. It is assumed, that the resulting uncertainty of the Nusselt number is smallest in this time period. 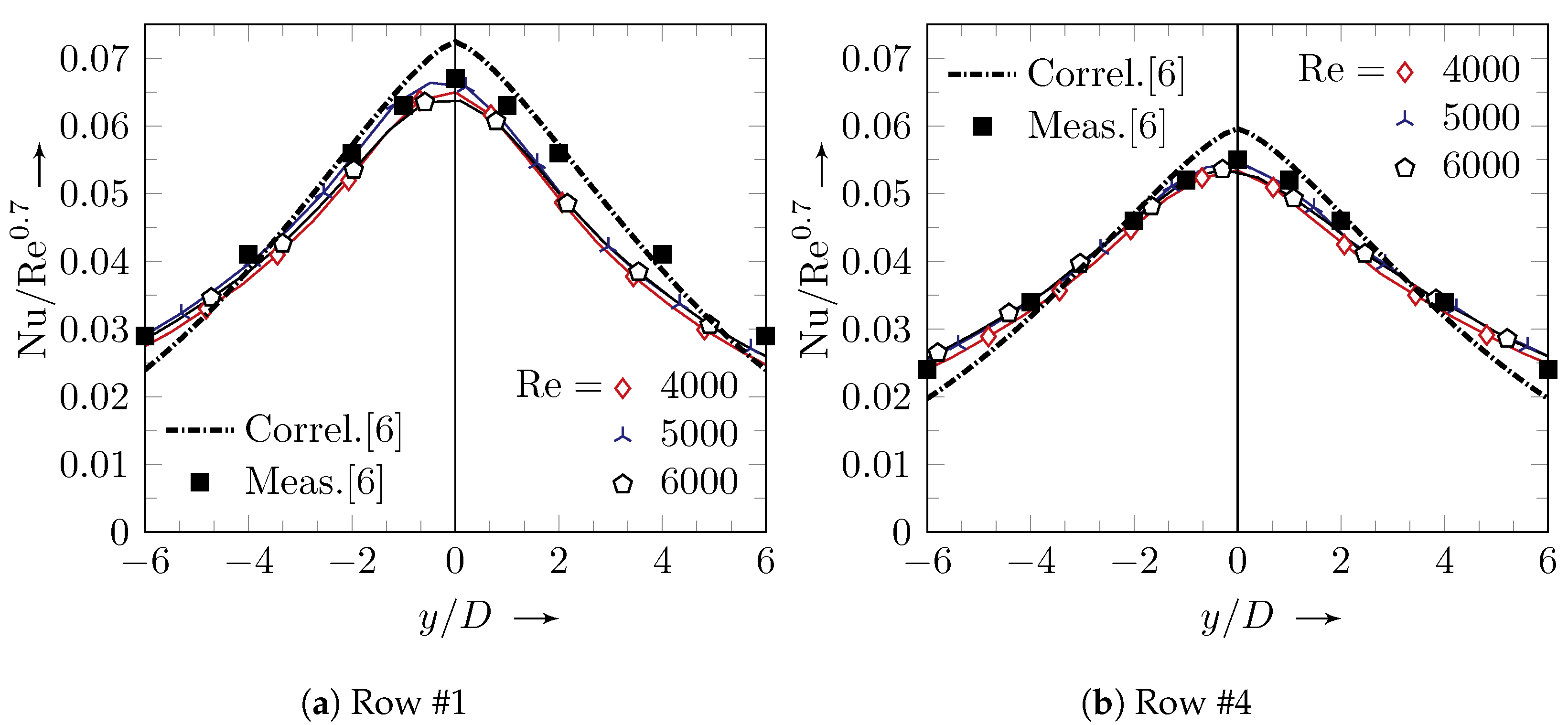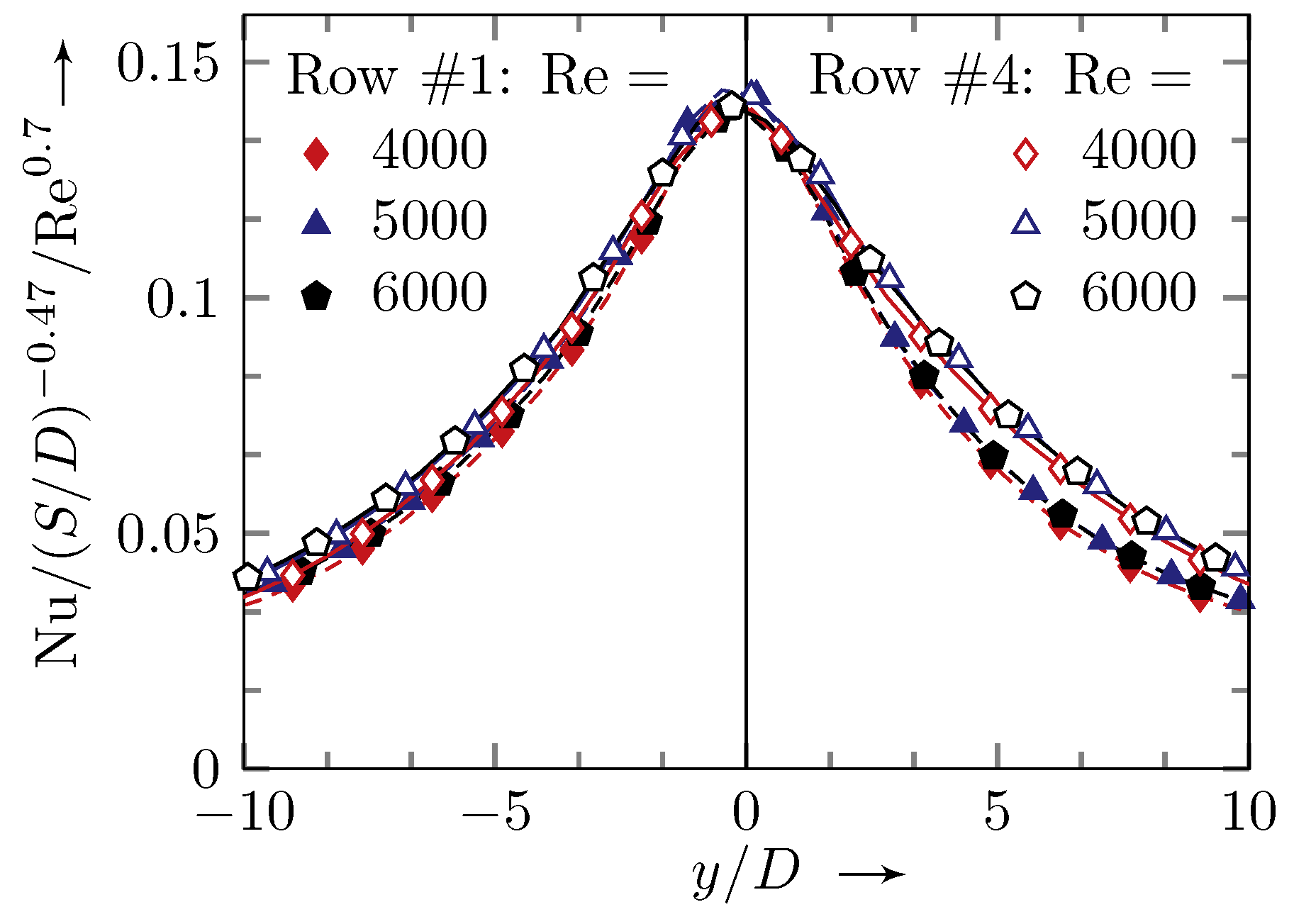For the discussion of the heat transfer characteristics in Section 3, only the averaged values will be shown.

2.2. Modeling of Natural Convection

This section describes the procedure to model the effect of natural convection at the outer side of the CrAl foil in Equation (2). The foil is similar to a vertical plate, although the plate is limited at the bottom and the top side (see Figure 2). Many research studies assume a constant value for the heat transfer coefficient due to natural convection over the complete surface [22]. A common assumption is a value of $h_{\mathrm{nc}}=5$ W/(m²K) (see, e.g., Egger et al. [26]). However, during the transient formation of a thermal boundary layer, the heat transfer coefficient can be significantly higher [27]. In order to consider the transient heat transfer characteristics of the natural convection at the CrAl foil, it was investigated experimentally. In this study, the CrAl foil was heated without an impinging jet flow. Compared to the transient measurements with impinging jets, natural convection occurs on both sides of the foil. It is assumed, that the heat transfer coefficients $h_{\mathrm{nc}}$ on both sides are identical. The transient results for the specific heat flux due to natural convection is given for each pixel by

$${\dot{q}}_{\mathrm{nc},i,j}\left(t\right)=\frac{UI}{A_{\mathrm{F}}}-\sum _X{\dot{q}}_{\rho \mathrm{c},i,j}\left(t\right)-{\dot{q}}_{\mathrm{rad},i,j}\left(t\right).$$

(8)

Compared to Equation (2), the lateral heat conduction can be neglected in Equation (8), as the temperature gradient over the surface of the foil is small. After Newton’s law of cooling, the heat transfer coefficient is defined by

$$h_{\mathrm{nc},i,j}\left(t\right)=\frac{{\dot{q}}_{\mathrm{nc},i,j}\left(t\right)}{T_{\mathrm{w},i,j}\left(t\right)-T_{\infty }}.$$

(9)

As the heat transfer coefficient for a vertical plate at steady-state conditions is a function of height [22], the transient results of Equation (9) are averaged over the width of the CrAl foil. In order to model the transient heat transfer characteristics, a polynomial function of $h_{\mathrm{nc}}$ is used for each pixel height i

$$h_{\mathrm{nc},i}\left(t\right)=h_0\left[a_i{\left(t/t_0\right)}^{b_i}+c_i\right].$$

(10)

As reference heat transfer coefficient a value of $h_0=5$ W/(m²K) is used. The reference time $t_0$ is the starting time of the electrical power supply. The results of Equations (9) and (10) are shown in Figure 6 exemplarily for three pixel heights, while $i=0$ represents the pixel at the bottom side of the foil and $i=650$ at the upper side.

Due to the formation of a thermal boundary layer, the heat transfer coefficient decreases sharply, after turning on the electrical heater and asymptotically approaches a constant value. This behavior corresponds to the findings of Goldstein and Eckert [27]. According to Goldstein and Eckert [27], the results should be independent of the pixel height at the beginning of the transient measurement. An independence of the pixel height is achieved in the upper part of the foil, which is exemplified for the pixels $i=350$ and 550. For the lower part of the foil at $i=150$, the results for $h_{\mathrm{nc}}$ are slightly higher. An explanation for this behavior is the reference temperature $T_{\infty }$ in Equation (9), which was averaged using four K-type thermocouples at different heights in a distance of $0.55$ m from the foil. The measured temperatures differ up to 2 K over height and time. Since the influence of the used reference temperature on the prediction of $h_{\mathrm{nc}}$ in Equation (9) is also apparent for the investigation of the panel model, the effect is reproduced within the modeling of natural convection with respect to Equation (2). The resulting polynomial functions of $h_{\mathrm{nc}}$ for the three positions on the foil are presented in Figure 6. The gray colored region illustrates the relevant time period for the final evaluation of the Nusselt number, as mentioned in Figure 5. In order to increase the accuracy of the polynomial functions in this time period, only the results within a time interval 3 s–10 s after turning on the electrical heater were considered. For this reason, the influence of natural convection in Figure 4 is only apparent in this time period.

2.3. Measurement Uncertainties

The uncertainty analysis of the experimental procedure is based on the GUM method (Guide to the Expression of Uncertainty in Measurement [28]), which was defined in the ISO/IEC Guide 98-3:2008. The method supports the systematic procedure in building an uncertainty analysis, as requested in the corresponding standards and guides for linear and nonlinear models according to ISO/IEC/EN 17025:2005. For the present uncertainty analysis, the results from a linear approach are compared to the results from a Monte Carlo method after ISO/IEC Guide 98-3:2008/Suppl. 1:2008 (see, e.g., Forster et al. [29]), showing negligible differences. Defining the relevant equations including the uncertainty of the contributing factors, the analysis gives the combined standard uncertainty and the impact of each contributing factor onto the result. The uncertainty of the contributing factors and their impact on the estimation of the combined standard uncertainty of the local Nusselt number are summarized in

Table 2. Measurement uncertainties of contributing factors on the estimation of the local Nusselt number; (i) Stagnation region, (ii) Assumption.

Contrib. Factor	Value of Interest	Uncertainty	Impact on Uncertainty in Nu
			Stag. Point	Between SP
$T_{\mathrm{jet}}$	292…298 K	$0.2$ K	$9.3$%	$8.4$%
$T_{\mathrm{w}}$	301…343 K	0.6…$0.2$ K	$86.9$%	$10.2$%
U	4.8…$7.7$ V	1%	$0.9$%	$16.6$%
I	77.5…$126.3$ A	0.12…$0.13$ A	$2.5$%	$49.0$%
$A_{\mathrm{F}}$	$300 \mathrm{mm}\times 558 \mathrm{mm}$	$1 \mathrm{mm}\times 1 {\mathrm{mm}}_{\left(ii\right)}$	$0.1$%	$2.3$%
${\epsilon }_{\mathrm{L}}+{\epsilon }_{\mathrm{F}}$	$0.93+0.1$	$0.1_{\left(ii\right)}$	$0.0$%	$0.6$%
${\dot{q}}_{\rho \mathrm{c}}$	$50$…$200 {\mathrm{W}/{\mathrm{m}}^2}_{\left(i\right)}$	$10{\%}_{\left(ii\right)}$	$0.03$%	$6.3$%
${\dot{q}}_{\mathrm{cond}}$	$1500$…$2000 {\mathrm{W}/{\mathrm{m}}^2}_{\left(i\right)}$	$f(\Delta T_{\mathrm{w},\mathrm{pixel}})$	$f(\Delta T_{\mathrm{w},\mathrm{pixel}})$
${\dot{q}}_{\mathrm{rad}}$	$50$…$70 {\mathrm{W}/{\mathrm{m}}^2}_{\left(i\right)}$	$f(T_{\mathrm{jet}},T_{\mathrm{w}},\epsilon )$	$f(T_{\mathrm{jet}},T_{\mathrm{w}},\epsilon )$
${\dot{q}}_{\mathrm{nc}}$	$50$…$120 {\mathrm{W}/{\mathrm{m}}^2}_{\left(i\right)}$	$13{\%}_{\left(ii\right)}$	$0.01$%	$1.3$%
$\Delta T_{\mathrm{w},\mathrm{pixel}}$	$0$…$1.5 {\mathrm{K}}_{\left(i\right)}$	$20 \mathrm{mK}$	$0.3$%	$5.3$%

. The relative contribution of each contributing factor on the estimation of the Nusselt number is calculated for each pixel. The results are given exemplarily for one pixel in a stagnation point of row #1, where the uncertainty is highest, and one pixel between two stagnation points of row #2 ($S/D=13$). Besides classical measurement uncertainties, the uncertainty of the Nusselt number depends on the accuracy of the complete modeling process. The uncertainty of ${\dot{q}}_{\rho \mathrm{c}}$ and ${\epsilon }_{\mathrm{L}}$ had to be assumed, as the exact material properties of the black paint were not known. The assumption of the uncertainty in ${\dot{q}}_{\mathrm{nc}}$ results from the modeling of natural convection (see Section 2.2), where a variation of the power supply level showed slightly different results for ${\dot{q}}_{\mathrm{nc}}$, which lie within $\pm 13\%$.

The consideration of all terms in Equation (2) results in a maximum combined standard uncertainty in the Nusselt number of up to ±9% in a pixel in the stagnation region of row #1, where the highest temperature gradients and the maximum Nusselt number occurs. In the stagnation region, the uncertainty of the IRT data is more apparent (up to $0.6$ K) as $T_{\mathrm{w}}$ is closer to the ambient temperature. This results in the higher impact of $T_{\mathrm{w}}$ on the combined standard uncertainty compared to the pixel between two stagnation points (see Table 2). The pixel between two stagnation points in row #3, that is exemplarily given in Table 2, shows a combined standard uncertainty of ±3.2%. For the averaged Nusselt number over the four rows of impinging jets, which will be discussed in the next section, the combined standard uncertainty lies within ±5%. Taking into consideration that the experimental method includes the terms of radiation, natural convection, change of internal energy and lateral conduction, the accuracy of the complete model is satisfying. A fundamental requirement to achieve a good accuracy of this method is dedicated to the IRT camera. A high quality concerning the noise equivalent temperature level is necessary to correctly describe the effect of lateral conduction. In the uncertainty analysis, the thermal noise is captured with $\Delta T_{\mathrm{w},\mathrm{pixel}}$ in Table 2. Furthermore, it is of great importance to precisely know the emissivity of the surface of interest, in order to obtain high quality temperature data from the IRT camera. If the local effects are of special interest, the IRT camera should also have a high spatial resolution. The Flir Sc 7600, which was used for the present study, has a resolution of $512\times 640$ pixels. This results in a relatively poor resolution of the impinging jets with $0.7D/\mathrm{pixel}$, as the complete panel model is measured in one experiment. For the present investigations, the spatial resolution is still sufficient, as the focus is set on the averaged heat transfer characteristics. The comparison of the transient results of the Nusselt number for different power supply levels in Figure 5b is an indication, that the experimental method captures the relevant effects with good accuracy.

Regarding the uncertainty of the jet Reynolds number, the mass flow controller HFC-303 with an accuracy of $\pm 0.054$ g/s, which was used for $\mathrm{Re}\le$ 3000, results in a combined standard uncertainty of ±1%. For $\mathrm{Re}\ge$ 4000, the HFC-207 controller with an accuracy of $\pm 0.5$ g/s results in a combined standard uncertainty of ±4%.

3. Results and Discussion

For the experimental investigation of the heat transfer characteristics of an ACC panel system, the jet Reynolds number was varied between $\mathrm{Re}=2000$…$6000$, which is the typical range for such applications in modern aero engines. The experimental settings are summarized in

Table 3. Overview of experimental conditions.

Re	$\dot{\mathit{m}}/\mathbf{g}/\mathbf{s}$	${\mathit{T}}_{\mathbf{jet}}={\mathit{T}}_{\mathit{\infty }}/\mathbf{K}$	${\mathit{p}}_{\mathit{\infty }}/\mathbf{Pa}$	${\dot{\mathit{q}}}_{\mathbf{el}}/{\mathbf{W}/\mathbf{m}}^2$
2000	5.75	297.5	96,860	3417
3000	8.59	296.4	96,400	4157
4000	11.34	293.3	96,810	4911
5000	14.14	293.2	94,700	5583
6000	16.85	291.8	97,270	5779

. A detailed description of the heat transfer at the target plate will be performed for $\mathrm{Re}=$ 4000, before comparing the results of the Reynolds number variation.

Figure 7 shows the local Nusselt number for $\mathrm{Re}=4000$. For the visualization of the geometry, the wireframe of the panel model is inserted into the results. Due to the manufacturing process, two holes in tube $\#2$ were blocked. The influence is negligible for the averaged heat transfer characteristics, which will be discussed within this section. The highest Nusselt numbers occur in the stagnation region of the impinging jets. As the jet-to-jet distance is smaller at the outer rows of impinging jets $\#1$ and $\#4$ (see Table 1), the maxima in the Nusselt number are closer.

At the lowest jet-to-jet distance in row $\#1$, the maxima partially seem to merge. Comparing the results at the outer rows to the inner rows $\#2$ and $\#3$, the heat transfer in the stagnation region increases with decreasing jet-to-jet distance. This behavior is also known from literature (see, e.g., Goldstein and Seol [6]). From the stagnation region, the cooling air gets deflected to the sides. The momentum inside the tubes in $\pm x$-direction is still apparent after impinging onto the target plate. Only for the last jets of each row at $|x/D|>170$, is the deflection in $\pm x$-direction negligible. Although the inflow conditions of the panel model are asymmetric (see Figure 1), the heat transfer at the target plate is symmetric to $x/D=0$.

For a better quantification of the local Nusselt number, in Figure 8 the results along the centerlines of row $\#1$ and $\#3$ are given exemplarily to one side at $0\le x/D\le 200$. Each value corresponds to an average over 3 pixel in y-direction (≈2.1 D).

Despite the relatively poor spatial resolution of the IRT data with $0.7D/\mathrm{pixel}$, the maxima of the impinging jets are clearly separated from each other even for the lowest jet-to-jet distance at row $\#1$, showing the highest gradients in the heat transfer coefficient. Still, the relatively poor resolution is visible within the sharp peaks. At row #3 the peaks are slightly smoother, as the gradients are smaller. For the present investigation, the exact values of the maxima are less relevant, as the focus is set on averaged values, which will be discussed in the next section. Nevertheless, the results in Figure 8 show that the experimental method is capable to resolve high gradients and small structures precisely within the respective spatial resolution. The increase in the maxima of row $\#1$ over x is related to the decreasing momentum of the air flow inside the tube. Apart from the first three jets, the maxima of row $\#3$ are nearly constant as the mass flow rate and therefore the momentum inside the tube is lower compared to tube $\#1$.

For the theoretical model approaches used during the design process of modern aero engines, the cooling mechanisms are described by averaged values and thus, the local heat transfer characteristics are less relevant. For this reason, the experimental results of the local Nusselt number are averaged in x-direction. The line-averaged Nusselt numbers for the four rows of impinging jets are shown in Figure 9a including the error bars gained from the uncertainty analysis from Section 2.3.

The results at the inner rows $\#2$ and $\#3$ with similar jet-to-jet distance are nearly identical. With decreasing jet-to-jet distance at the outer rows $\#1$ and $\#4$, the line-averaged heat transfer increases. In order to quantify the influence of the jet-to-jet distance S on the Nusselt number, the results are scaled by ${(S/D)}^a$. No exponent could be found merging the results of all rows of impinging jets. With an exponent of $a=-0.47$, the results at the outer rows merge, as shown in Figure 9b. The curves at the inner rows merge only outside the stagnation region at $|y/D|>5$. It is assumed that the different behavior between the outer and the inner rows is related to the high variation in $S/D$. The impinging jets at the outer rows are highly influenced due to jet interaction, whereas this effect is small for the relatively high $S/D$ at the inner rows. In the wall jet region of the impinging jets at $|y/D|>5$, the effect of jet interaction is not relevant regardless of $S/D$ and all curves in Figure 9b merge. For the theoretical modeling of the heat transfer characteristics in modern aero engines, the different behavior of the impinging jets depending on the level of $S/D$ should be considered to increase the accuracy of the Nusselt number approaches.

After the detailed description of the heat transfer characteristics for $\mathrm{Re}=$ 4000, the line-averaged Nusselt numbers from the jet Reynolds number variation will be discussed. Figure 10 presents the results for the different rows of impinging jets with $\mathrm{Re}=2000$…$6000$. The results of row $\#2$ are omitted, as they are close to row $\#3$.

The line-averaged Nusselt numbers increase with increasing Reynolds number, as it is also known from literature (see, e.g., Livingood and Hrycak [30]). In order to quantify the influence of the jet Reynolds number on the Nusselt number, the results on the left-hand side of Figure 10 are scaled by ${\mathrm{Re}}^b$. Using an exponent of $b=0.7$, the results of $\mathrm{Re}\ge 4000$ merge for all rows of impinging jets, as shown in the graphs on the right-hand side of Figure 10. For the lower jet Reynolds numbers, no agreement could be achieved. It is assumed, that the different behavior is related to the flow regime of the impinging jets. According to Gauntner et al. [31] impinging jets are laminar for $\mathrm{Re}<1000$, transition or semiturbulent for $1000<\mathrm{Re}<3000$ and fully turbulent for $\mathrm{Re}>3000$. Therefore, the results of the investigated range of jet Reynolds numbers are not transferable. For the lower Reynolds numbers $\mathrm{Re}=2000$ and $\mathrm{Re}=3000$, better results are achieved with an exponent of $b=0.5$, as it is typically used for laminar flows [32]. The different results of $b=0.5$ and $b=0.7$ are within the typical range of $0.5<b<0.8$ from literature (overview given in Zuckerman and Lior [33]). The different behavior of the impinging jets depending on the flow regime for the relatively low jet Reynolds numbers should also be considered with respect to accurate theoretical model approaches of real applications, as it was already mentioned for the jet-to-jet distance.

In order to verify the quality of the experimental methodology, the results are compared to data from literature. A correlation, which is often used as reference for rows of impinging jets was defined by Goldstein and Seol [6]. The correlation is of the form

$$\frac{\overline{\mathrm{Nu}}}{{\mathrm{Re}}^{0.7}}={\displaystyle \frac{2.9}{22.8+S/D\sqrt{Z/D}}}{e}^{-0.09{(y/D)}^{1.4}}.$$

(11)

With the defined limits ($2\le Z/D\le 6$; $4\le S/D\le 8$; $0\le y/D\le 6$; $10,000\le \mathrm{Re}\le$ 40,000) of the correlation, the conditions of the present study lie partly out of the validity range with a jet-to-plate distance of $Z/D=11$, a jet-to-jet distance of $5.2\le S/D\le 13$ and a jet Reynolds number of $2000\le \mathrm{Re}\le 6000$. As there is a lack of validated correlations for rows of impinging jets, which cover the limits of the present investigation, the results from Goldstein and Seol [6] seem to be the best compromise considering the effect of jet-to-plate distance, jet-to-jet distance and Reynolds number. In order to comply with the specified limits as far as possible, only the results of the fully turbulent jets ($\mathrm{Re}\ge$ 4000) at the outer rows $\#1$ and $\#4$ ($S/D=5.2$ and 7.8) are considered in Figure 11. Regarding the results from Goldstein and Seol [6], the reported deviations of the measured Nusselt numbers for the case with $Z/D=6$, $S/D=8$ and $\mathrm{Re}=10,000$ from the defined correlation are added to the graphs. These deviations do not result from an uncertainty of their measurement technique, but from the definition of a correlation which results from a great data set and which is therefore valid in a wide range of geometrical and fluid flow conditions. The conditions of this specific case from Goldstein and Seol [6] define the limit of the validity range of Equation (11), whereby the conditions are closest to the present setup and the comparison is the fairest. While in Figure 11, the correlation predicts higher maxima in the stagnation region compared to the experimental results from the present investigation, the Nusselt number is slightly lower at $y/D=6$ due to a steeper gradient over $y/D$. Considering the deviations of the exact measured results from Goldstein and Seol [6] for $Z/D=6$, $S/D=8$ and $\mathrm{Re}=10,000$ from their correlation, an overall good agreement with the present data is achieved. Especially at row $\#4$, the measured results match the data from Goldstein and Seol [6].

A combination of the discussed dependencies of the Nusselt number from the jet-to-jet distance and from the jet Reynolds number is given in Figure 12 for the outer rows $\#1$ and $\#4$. The influence of the jet-to-jet distance $S/D$, which was discussed in Figure 9b for a jet Reynolds number of $\mathrm{Re}=4000$, is also valid for the higher Reynolds numbers using an exponent of $a=-0.47$. The good agreement of the combined dependencies in Figure 12 shows, that the heat transfer characteristics of the panel model can be described accurately using the developed theoretical model approaches in consideration of the investigated limits of $S/D$ and Re.

4. Conclusions

We presented a novel method for the experimental investigation of a complex system of 200 impinging jets using infrared thermography. The experimental method uses a thin electrically heated chrome-aluminum foil as target plate. The temperature of the target plate was measured at the outer side with an IRT camera, while the temperature difference over the thickness of the thin plate of only $50 \mathsf{\mu }\mathrm{m}$ can be neglected. This option increases the accuracy in comparison to similar applications in literature investigating complex systems of impinging jets, where an optical access from the top side is not feasible. The transient effects of internal energy, lateral conduction, radiation and natural convection were considered for the heat transfer prediction from the impinging jets. Due to high gradients in the stagnation region, the effect of lateral conduction is significant. With the presented method, small structures and high gradients in the heat transfer coefficient can be reproduced with good accuracy. Experimental results of the local heat transfer characteristics were reported for jet Reynolds numbers of $\mathrm{Re}=2000$…$6000$. In order to improve established theoretical model approaches, the influence of the jet-to-jet distance and the jet Reynolds number on the Nusselt numbers were discussed. Regarding the jet-to-jet distance, a dependency on the level of $S/D$ was found due to the effect of jet interaction. For low $S/D\le 7.8$, the impinging jets are highly influenced by jet interaction, whereas this effect is low for $S/D\ge 12.8$. Therefore, the line-averaged Nusselt numbers for the rows of impinging jets showed a different behavior in the stagnation region. For the low jet-to-jet distances of $S/D=5.2$ and $S/D=7.8$, the influence of $S/D$ was quantified with $\mathrm{Nu}\sim {(S/D)}^{-0.47}$. For the higher jet-to-jet distances, no exponent could be found, as they are too close for comparison with $S/D=12.8$ and $S/D=13$. Outside the stagnation region at $|y/D|>5$, where the influence of jet interaction is negligible, all results merge with a scaling of ${(S/D)}^{-0.47}$. An investigation of the influence of the jet Reynolds number on the line-averaged Nusselt numbers indicated a dependency of the flow regime for the relatively low jet Reynolds numbers. For the fully turbulent jets at $\mathrm{Re}\ge 4000$, the dependency of the jet Reynolds number was quantified with $\mathrm{Nu}\sim {\mathrm{Re}}^{0.7}$. For the transition jets at $\mathrm{Re}\le 3000$, an exponent of $b=0.5$ showed better results. In terms of the theoretical modeling of the heat transfer characteristics in modern aero engines, the different behavior of the impinging jets depending on the level of jet-to-jet distance and jet Reynolds number should be considered to increase the accuracy of the Nusselt number approaches. While for the present investigation, the focus was set on averaged heat transfer characteristics, the presented method is able to adequately resolve local heat transfer characteristics. The requirements of the experimental application to achieve high quality data of local and averaged heat transfer characteristics is defined within the paper.