1. Introduction
The accurate prediction of aeroelastic phenomena is important to prevent costly problems arising during engine testing and certification. Since the source of all aeroelastic phenomena is the unsteady response of the blade aerodynamics to vibrations or variations in the flow conditions, the accuracy of predictions crucially depends on the ability to correctly capture this. Often the unsteady aerodynamic response is characterised by non-linear effects, three-dimensionality, shocks and flow separations.
In external aerodynamics, such unsteady aerodynamic responses have been studied extensively in the context of aerofoil dynamic stall. Dynamic stall is an aerodynamic phenomenon characterised by a delay in flow separation under the influence of time-varying incidence conditions as caused by transient manoeuvres, aerofoil oscillations or gusts in the free stream. From this, it is known that the unsteady motion of an aerofoil results in a large hysteresis of the aerodynamic force coefficients and can delay stall beyond the static stall angle. Dynamic stall research is of interest in the context of turbomachinery aeroeleasticity because the shape of the hysteresis curves, i.e., the amplitude and phase of the aerodynamic force coefficient, determines aerodynamic damping.
The principal parameters influencing the dynamic process are Reynolds number, state of the boundary layer (laminar vs. turbulent), leading edge shape, reduced frequency and amplitude [
1]. Many existing dynamic stall studies were performed on two-dimensional geometries and aerofoil sections of wings and helicopter blades. A summary of common dynamic stall parameters is given in [
2], and in-depth reviews of dynamic stall research can be found in [
3,
4,
5,
6]. Recently, significant progress on the characterisation of the aerodynamic response has been made using high-fidelity computational fluid dynamics (CFD) such as the large eddy simulations (LES) by Visbal and Garmann [
7]. These have significantly advanced the understanding of unsteady aerodynamics but the results are unlikely to be quantitatively applicable to compressors. Compressor blades have much thinner aerofoil sections, oscillate at higher frequencies, are influenced by neighbouring blades, and exhibit highly three-dimensional features, such as corner separations and tip leakage flows.
Although the term
dynamic stall is not commonly used in compressor aerodynamic research, the unsteady conditions near the stall boundary bear some similarities with those investigated in the field of dynamic stall. In addition to the intrinsic unsteadiness of flow separations, ‘external’ fluctuations in incidence at near-stall conditions occur when the rotor is vibrating or rotating through distorted inflow conditions. When the compressor is operating close to stall in such conditions, the unsteady aerodynamics are known to alter both its stall behaviour, as reported in numerous publications on inlet distortions [
8,
9,
10], and its aeromechanical behaviour [
11,
12,
13,
14]. Even before compressor stall, pre-stall disturbances travel around the circumference, result in asymmetric time-varying loads and can trigger or exacerbate vibrations [
15,
16]. In addition, vibrations caused by aeroelastic instabilities (flutter) often occur close to the stall boundary. A comprehensive review of compressor stall research is given in [
17].
One of the main challenges of characterising unsteady aerodynamics in compressors is the complexity of the flow (three-dimensional, unsteady, multi-row). In rotating environments it is also extremely difficult to accurately measure local flow structures and blade surface pressures. Studying an isolated blade hence offers benefits in terms of experimental and numerical setup. The environment is controlled and experimental conditions can easily be replicated in the numerical simulations. Furthermore, it has been shown, that for the dominant aeroelastic problem of modern fans and compressors (Non-Synchronous Vibration), aeroelastic forcing on the blades can be separated into self-forcing and forcing due to convective and acoustic disturbances originating from neighbouring blades [
16]. The latter must be investigated in full-annulus or cascade arrangements, but self-forcing can be studied with isolated configurations.
This paper will use a simplified test case, an isolated blade in pitching motion, to demonstrate some of the challenges associated with correctly predicting unsteady aerodynamic response on compressor blade geometries. The aim is to provide an illustrative example to outline the strengths and limitations of established aeroelastic modelling techniques. Although heavily simplified, the test case maintains some important features of compressors, namely a sharp leading edge, tip leakage and compressible flow conditions. The aim is not to draw physical conclusions which are directly applicable to compressors but to demonstrate the need for more thorough validation of modelling tools in turbomachinery environments and a deeper understanding of compressor unsteady aerodynamics in the presence of blade vibrations. For non-vibrating airfoils, advanced state-of-the-art methods are established and described in the literature, but are currently not applicable to turbomachinery environments. Properly resolved LES-Simulation is still too costly for aeroelastic studies, as timescales of blade vibration (
–
s) differ vastly from relevant turbulent scales (
–
s). Application of LES in turbomachinery is hence still limited to non-vibrating configurations [
18,
19,
20,
21]. Using unsteady Reynolds-averaged Navier–Stokes (URANS) and coarse large eddy simulations (LES), the flow is analysed and predictions are compared to experimental measurements. In addition, the paper demonstrates the influence of tip leakage flow on unsteady aerodynamic response and tests the sensitivity of the aerodynamic response to reduced frequency and time-averaged incidence.
2. Test Case
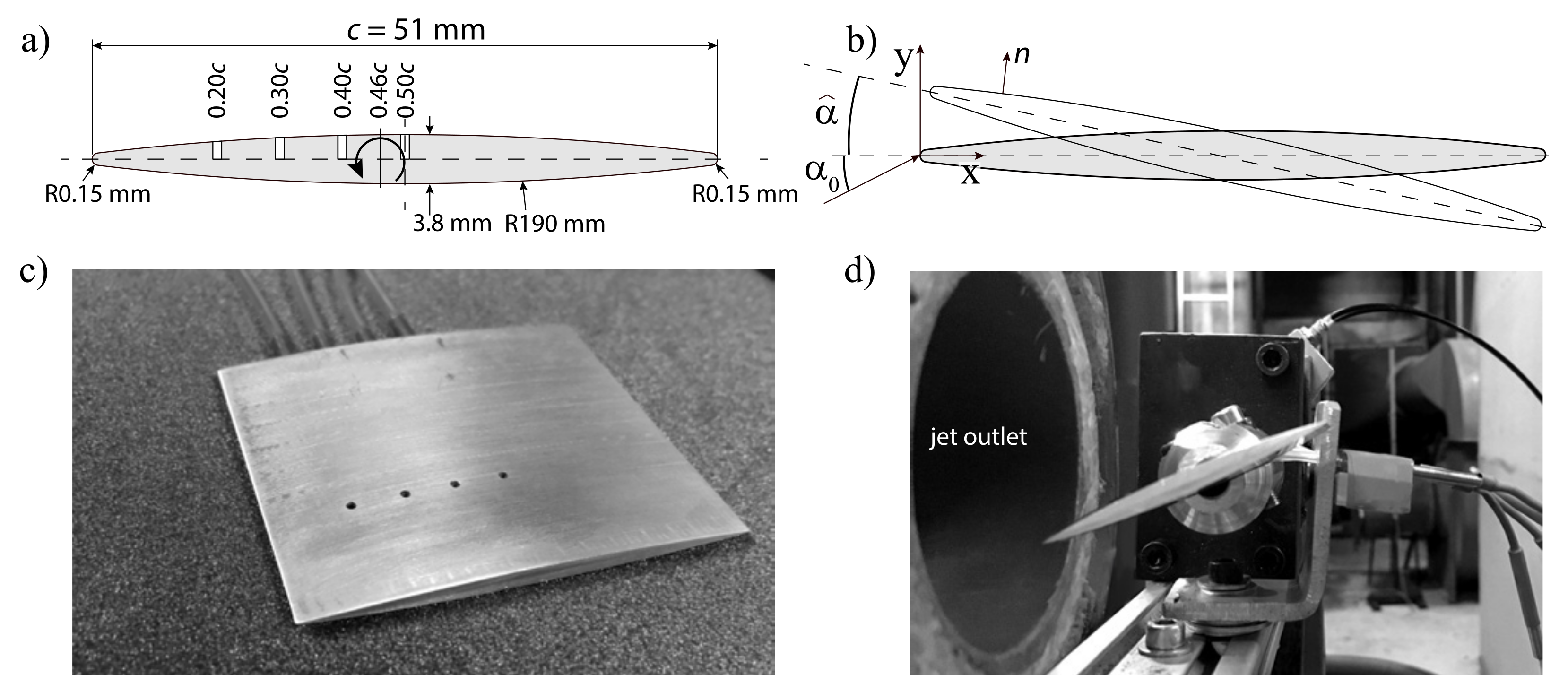
The blade geometry is quasi-two-dimensional with a symmetric double-circular arc (SDCA) aerofoil cross section and sharp leading edge (radius 4% of maximum blade thickness) as shown in
Figure 1. Its aspect ratio is approximately 1. The blade is instrumented with unsteady pressure taps at four chord-wise positions (20%, 30%, 40% and 50% chord) in the reference plane located 24% chord inboard of the blade tip (
). The blade is placed in a jet generated by a circular nozzle with one side (‘the hub’) mounted and one side open to the freestream, resulting in flow over the tip and three-dimensional flow over the blade. A turbulence grid in the jet nozzle exit can be used to raise turbulence intensity.
The blade pitching axis is located at
as indicated in
Figure 1. The time-averaged or steady incidence angle
, oscillation frequency (
) and amplitude (
) are adjustable. The pitching motion and instantaneous incidence angle are defined as:
For the numerical simulations, the displacement is linearised and modelled as a modal deformation with the mode shape defined as , modal displacement q and the physical displacement . The mode shape vector defines the blade deflection and is not mass normalised in this case.
For the results reported in this paper, the oscillation amplitude is kept constant and the mean incidence angle, , and oscillation frequency are varied.
The experimental freestream Mach number can be varied between M = 0.30 to M = 0.75, creating Reynolds numbers from 300,000 to 750,000 based on blade chord. The results in this paper focus on M = 0.50.
For the numerical simulations, two configurations are used. The nominal finite span configuration which includes tip clearance flow and an infinite span configuration with periodic boundary conditions, where the flow is quasi-two-dimensional. These will be referred to as the finite span, and infinite span configurations.
2.1. Instrumentation
As the blade is symmetric, the same instrumentation is used for pressure- and suction-side measurements by flipping the blade orientation, both for steady and phase-locked vibrating studies. The pressure sensors are Kulite XCS-062 (0.7 bar differential), which are calibrated in situ for offset and frequency response using impulse excitation. For the measurements at free-stream Mach Number of 0.5 the maximum measurement error for static pressure is estimated to 2% of , approximating 10% of the unsteady pressure amplitude for the measurements at incidence. The resonance frequency of the measurement chain due to the cavities in the blade is above 5 kHz, which is significantly higher than the maximum oscillation frequency of 250 Hz performed in this study. Data acquisition of all sensors, including oscillation encoder (resolution ), microphones and hot-wire was conducted synchronously at 50 kHz.
In addition to unsteady pressure measurements, hot wire measurements are performed to characterise the boundary layer. The used probes are TSI 1212-T1.5, in situ calibrated in the free-stream jet with an accuracy of 2% according to the manufacturer assuming isotropic turbulence. The probes are mounted vertically on a positioning device which allows traversals with an accuracy of 0.05mm with the wire oriented perpendicular to the mean flow. To calibrate zero blade distance, electric shortage with the blade was realized for each boundary layer traverse and investigated incidence to eliminate static blade deflection. Boundary layer traversals on the suction side have been taken at each 20% chord and for different span positions.
2.2. Influence of the Experimental Jet and Mounting Hub
The jet is relatively small compared to the blade (jet diameter 1.5c), allowing high relative Mach-numbers but limiting the maximum blade incidence angle to approximately . For a free-stream speed of Mach 0.4 and average incidence angles below , independence of the results at the measurement location has been validated with a significantly larger jet and sideboards at the hub for the non-vibrating case. Furthermore, simulations with the small jet have been conducted and shown minor influence on the static pressure profiles at for static incidence angles up to for the first 30% of the chord. At midchord, the difference between small jet and homogeneous inflow amount to 10% of at incidence at . The supporting hub, which is outside of the jet section in the experiment, was simulated in numerical pre-studies and has shown negligible influence on the measurement section at for the presented incidence angles.
To reduce complexity, both hub and jet have not been included in the presented coupled URANS and LES simulations.
3. Computational Approach
3.1. (U)RANS Simulations
(U)RANS simulations are performed with an in-house unsteady Reynolds-Averaged Navier–Stokes (URANS) solver, AU3D, which is a non-linear time-accurate solver, second order accurate in space and time. Details of the numerical scheme are given in [
22]. The current simulations use a Spalart–Allmaras model with the wall function. The solver has been extensively validated for unsteady aerodynamic and aeroelastic applications in turbomachinery, e.g., [
23,
24].
The computational domain extends 10 chords, symmetrically upstream and downstream of the blade. The total pressure, total temperature and flow angle boundary conditions are imposed at the far field inlet boundaries, while static pressure is prescribed at the outlet boundaries. Inlet turbulence was set to 0% and no transition models were applied. In the experiment the measured turbulence-degree directly upstream of the blade leading edge is below 0.2%. The mesh is structured in the spanwise direction and unstructured in the cross-sectional plane. Two different meshes were used for the results presented in this paper. To reduce the cost of the coupled URANS simulations, a coarse mesh with and a total of approximately 1.2 million cell nodes () was created. This follows the common practice for aeroelastic analysis of turbomachinery blades. As will be seen later, the steady pressure profile, particularly a leading edge separation bubble, is not corrected or captured by the RANS simulations. To test the influence of mesh size and wall resolution on this, a much finer mesh with a total of 15 million mesh nodes and boundary layer resolution was also tested, but it was not found to improve the steady pressure predictions significantly. Hence, the coarse mesh was used for the coupled URANS analysis. For the unsteady simulations with oscillating blades, a time step convergence study was carried out. The final time resolutions were 1000 time steps per oscillation cycle for the URANS.
3.2. LES Simulations
At selected conditions, time-resolved static and oscillating simulations using the ANSYS LES/WALE-model, with a central differencing advection and second-order backward Euler transient scheme, were performed. The inlet turbulence is set to zero. The current LES simulations with blade vibration employ the same mesh as the fine RANS simulations (
15 M), and hence the mesh does not meet LES resolution requirements. Characteristic values such as
and
are out of optimum range (order 100), and grid convergence is not assured. The time-resolution was set to 8000 physical time steps per vibration cycle following a time convergence study. For three different meshes (
15 M, 30 M, 40 M) LES simulations with the static blade have been carried out and showed minor influence on blade pressure profiles. The domain and mesh topology are presented in
Figure 2. This choice of using an under-resolved LES was necessary for computational costs. Coupled simulations over at least 10 periods of vibration for each incidence consume approximately 50,000 CPUh. This is a compromise and the LES results should be interpreted as preliminary. However, as will be seen they still deliver improvements compared to URANS for high incidence levels. The coupled LES and URANS simulations were deemed periodically converged, when the ensemble-averaged modulus and phase over oscillation cycles converged to variations below 1%, both for local values at
and for global lift and modal force.
3.3. Relationship between Unsteady Pressure and Stability
The quantities of interest for aeroelastic analysis are the amplitude and phase of the static pressure perturbation which occurs at the frequency of oscillation. This will also be referred to as the
unsteady pressure and expressed as an unsteady pressure coefficient
, where
is the freestream dynamic head. The phase
is defined relative to the displacement in Equation (
1) as:
where
is the oscillation frequency and
is the amplitude of the unsteady pressure. We write the local unsteady force vector
in the direction normal to the blade surface as:
where
is the local area normal (pointing outward as seen in
Figure 1) and its time-dependency is ignored for simplicity. The local work done by the fluid on the blade during one oscillation cycle in the direction normal to the blade surface is then given by:
which is directly proportional to aerodynamic damping. When the work input is positive, the structure absorbs energy from the fluid and the system is unstable. When the force and displacement are exactly in phase (
) or anti-phase
, the work is zero. The following will analyse
as predicted by the URANS and LES simulations. It will focus on the suction side, since the flow over the pressure side is more uniform and shows negligible differences between simulations.
Referring to
Figure 1b, the suction side normal
and blade displacement vector
have the same sign (in the dominant y-component) upstream and opposite signs downstream of the pitching axis during the first half of the oscillation cycle. Therefore, following from Equation (
4), a perturbation in static pressure with a phase
will be destabilising over the first half of the chord, and stabilising over the second half of the chord. The stability criteria are summarised in
Table 1.
4. Steady Flow Field
To validate the numerical predictions, blade surface pressure and boundary layer profiles are compared against the measurements on the static blade.
4.1. Finite Span (with Tip Clearance Flow)
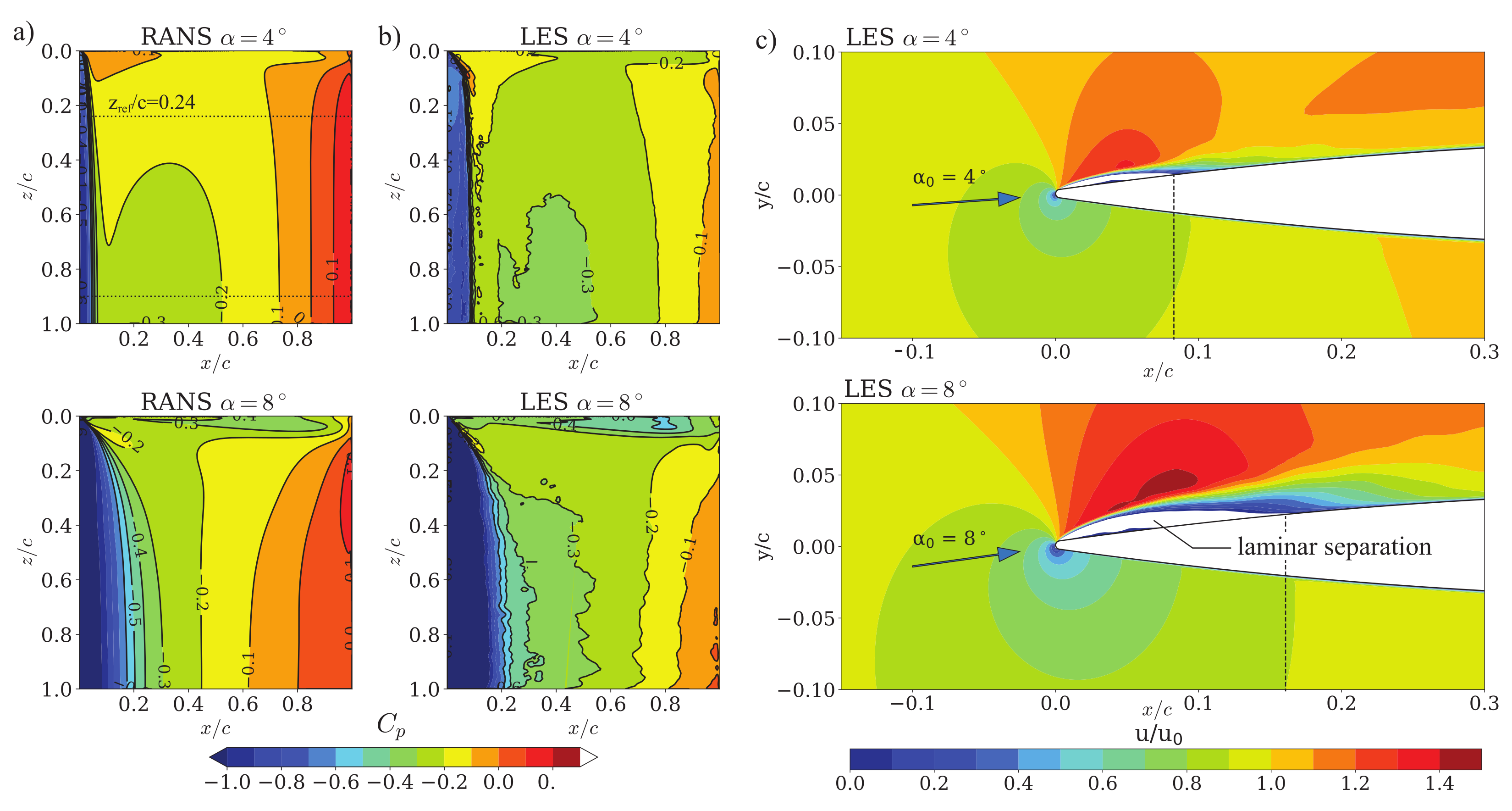
Figure 3 compares the RANS (a) and time-averaged LES (b) surface pressures on the suction side for 4
and 8
incidence for the nominal finite span configuration. It will be seen later that the flow separates during part of the vibration cycle for 8
. These two incidences were hence chosen to represent an unstalled case and one close to the stall boundary.
From
Figure 3 it is evident that the effects of the tip clearance flow reach inwards and a two-dimensional profile is not reached until about 80% span (as measured from the tip). The reference measurement location at
is hence well within the three-dimensional region, but outside of the direct influence of the tip leakage flow, as shown in the vortex structures presented in
Figure 4. Time-averaged velocity contours around the leading edge at
in
Figure 3c indicate the presence of a separation bubble. The pressure profiles at this location are compared against measurements in
Figure 5a for the same mesh with
and 15 M cells.
Experiments and predictions share the same qualitative features; the blade is foreloaded and the rise in pressure on the pressure side levels off as incidence is increased beyond 8
. Peak suction occurs in the first 10% chord. For a 4
and 8
incidence, both URANS and LES simulation quantitatively predict the suction side pressure within 3% of the freestream dynamic head at 20% and 30% chord. Further downstream, the experimental values deviate further from the simulations. This is attributed to differences in the inflow conditions. The simulations model a uniform stream but the experiment uses a circular jet. CFD simulations, which are not shown here for the sake of brevity, indicate that this has a noticeable influence on the static pressure towards mid-chord. Compared to URANS, the time-averaged LES shows a larger peak-suction zone and lower trailing edge pressure. This was found to be due to local recirculation around the trailing edge. On the pressure side, URANS consistently predicts higher
values than the experiment and LES simulations match better. Variation of the mesh resolution is shown in
Figure 5b, comparing the URANS meshes with
and the wall-function URANS mesh with
at 8
incidence. Near the leading edge, the profile gradient is affected but at the measurement locations and the pressure side, negligible influence is observed. For a 4
incidence, the difference between the meshes is further reduced. Variation of the LES resolution was performed towards higher chord- and spanwise resolution, with constant (
) towards a mesh with 40M cells. Here, differences are also limited to the leading edge region upstream of the first measurement location and of the same order of magnitude as the mesh variation of the URANS case. It must be emphasized, that even the 40M cell mesh is still coarse for LES and not capable to resolve natural transition. For 8
incidence, the transition is caused by flow separation and mesh refinement has a minor influence on the chord profiles at the measurement location.
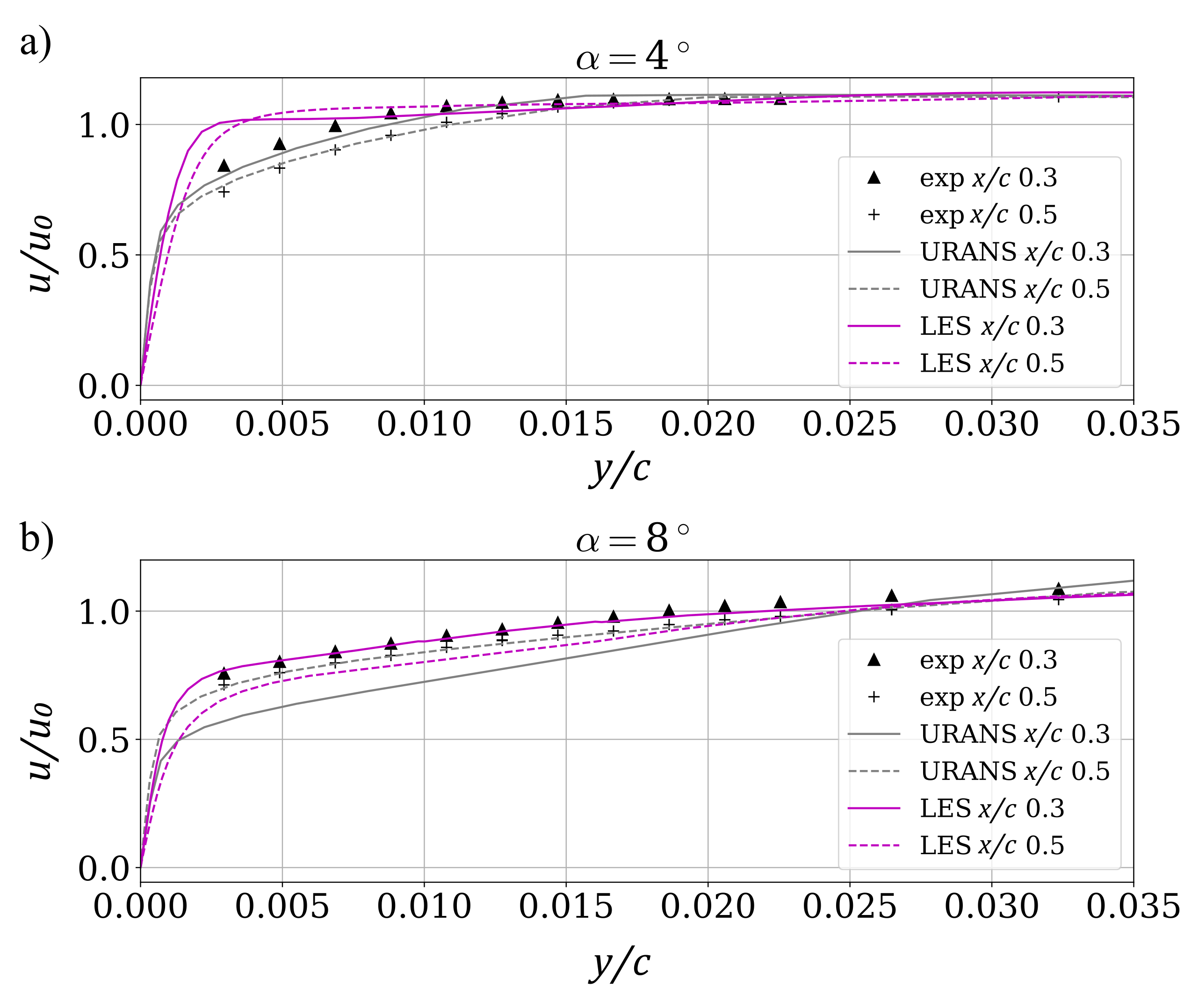
Boundary layer profiles are compared in
Figure 6 with experiments at 30% and 50% span. As expected, RANS simulations agree well at 4
with measurements, since turbulence models are well tuned and validated for this type of flow. Here, LES falls short due to the coarse meshing, and assumption of zero inflow-turbulence. To improve this, the mesh needs to be grossly refined, currently impeding feasibility of the anticipated turbomachinery application with mesh deformation. However, for 8
incidence, the RANS deviates from the experiments and LES accurately predicts the boundary layer profiles at the measurement locations. This is attributed to the separation-induced transition which is well captured by the used LES-meshes. The used (U)RANS setup falls short as no transition model was applied, which is the typical practice in high-speed turbomachinery applications.
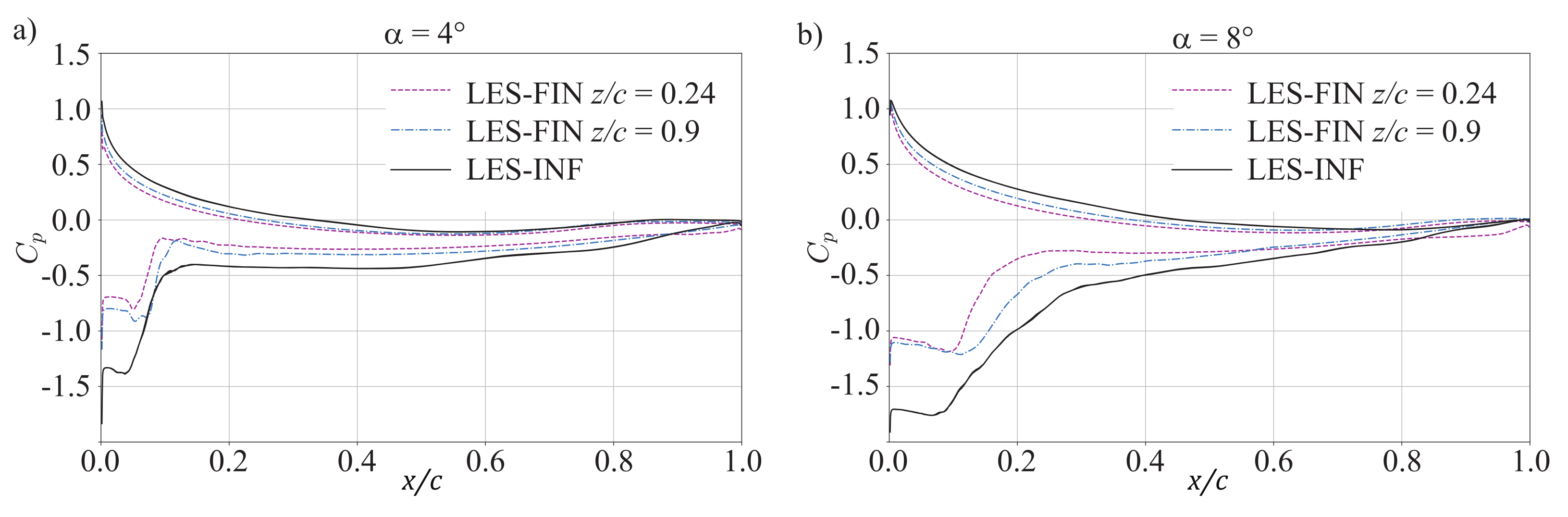
4.2. Infinite Span (without Tip Clearance)
Figure 7 compares the pressure profile of the finite span configuration at two spanwise positions against the results for equivalent simulations for the infinite span configuration. For conciseness, only the time-averaged LES results are shown. As already indicated by the finite span results, there is a notable difference in the steady state loading. The finite span results at
are still closer to the results at
than to the infinite case.
5. Unsteady Flow Field
5.1. Characterisation of the Unsteady Flow (Finite Span)
Before the sensitivity of unsteady aerodynamics to test case parameters and tip vortex is discussed, this section will describe the unsteady flow field of the oscillating blade and validate the numerical simulations for the finite span configuration. In all the results shown in this section, the blade is oscillating with a frequency of and amplitude . Results for two mean (time-averaged) incidence angles are shown: , where the flow remains attached during the whole oscillation cycle, and , where the flow separates over part of the cycle.
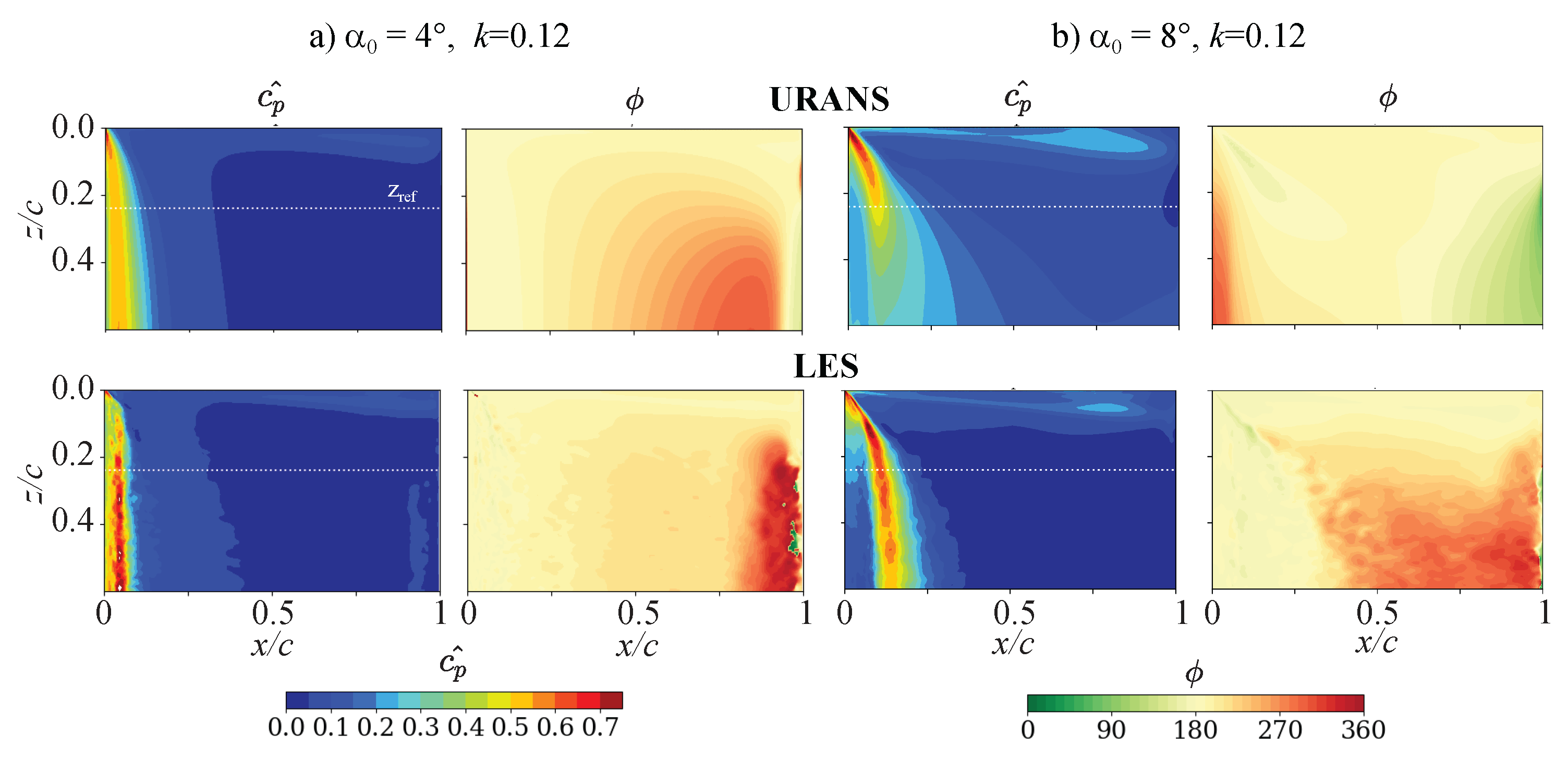
5.1.1. Comparison of URANS and LES
To analyse the unsteady aerodynamic response, the static pressure on the blade surface is Fourier-decomposed and the amplitude and phase of the unsteady surface pressure in the oscillation frequency are shown. The phase is measured relative to displacement as defined in Equation (
2). The analysis focuses on the suction side since the pressure side is comparatively uniform.
Figure 8 compares the amplitude and phases of the suction side pressure for 4
and 8
mean incidence. Both simulations show features that mirror the time-averaged pressure distribution (
Figure 3). The largest response occurs close to the leading edge and extends further aft for high incidences, and influences of the tip clearance flow is clearly identifiable and more pronounced for 8
.
URANS and LES share similar features in the distribution of unsteady pressure amplitude but differ quantitatively. The peak response near the leading edge is lower in URANS than in LES. For 4, the phase at the first 50% chord is also similar between URANS and LES. After mid-span, the amplitudes are negligible and interpretation of phase is meaningless. Closer to stall (8), however, the phase differs noticeably near the leading edge. LES predicts an unsteady pressure which is 180 out of phase with the blade displacement, whereas URANS is just under 270. This has significant implications for aeroelastic stability: the URANS phase is close to maximum stability at the point of maximum amplitude, whereas LES is neutral.
Figure 9 quantitatively compares the amplitude of the two simulations against experiments at the reference span (
). URANS and LES agree well with the experiment for low incidence. As expected, LES matches the experiment significantly better than URANS close to stalling. URANS overpredict the amplitude by more than 100% over the last 70% of the chord.
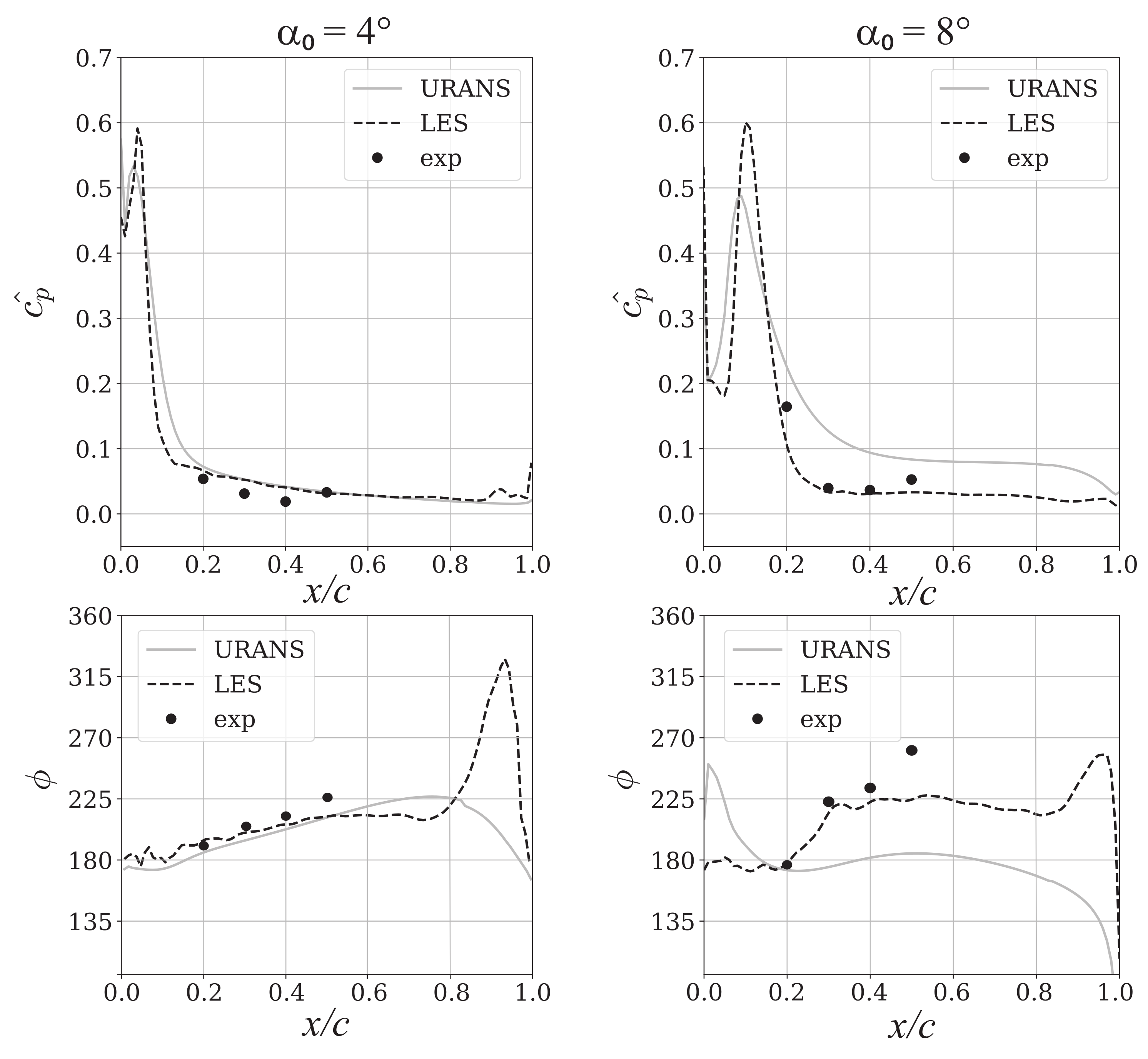
5.1.2. Hysteresis Curves
In the following, the local unsteady pressure will be analysed in more detail to highlight some differences and discuss the implications for aeroelastic predictions using URANS.
Figure 10 shows the hysteresis curves for unsteady pressure measured at 20% chord against incidence for
for two mean incidence angles,
and
. This chordwise location was chosen because of the good match between measurements and CFD results in the time-averaged pressure.
For , URANS and experiment follow similar trajectories as the instantaneous incidence changes. There is a small offset in the mean but both loops are narrow, i.e., the hysteresis is small. At higher mean incidence (), the experiment and CFD deviate. The experimental pressure rises beyond the equivalent static pressure during the upward pitching part of the cycle and then drops suddenly near the point of maximum deflection (10.5). It remains at the low pressure during the down-pitch and then recovers. The URANS response on the other hand is smoother and the pressures generated during the down- and upward pitching motion are more symmetrical. In summary, the URANS is not capturing the hysteresis and unsteady aerodynamic response correctly.
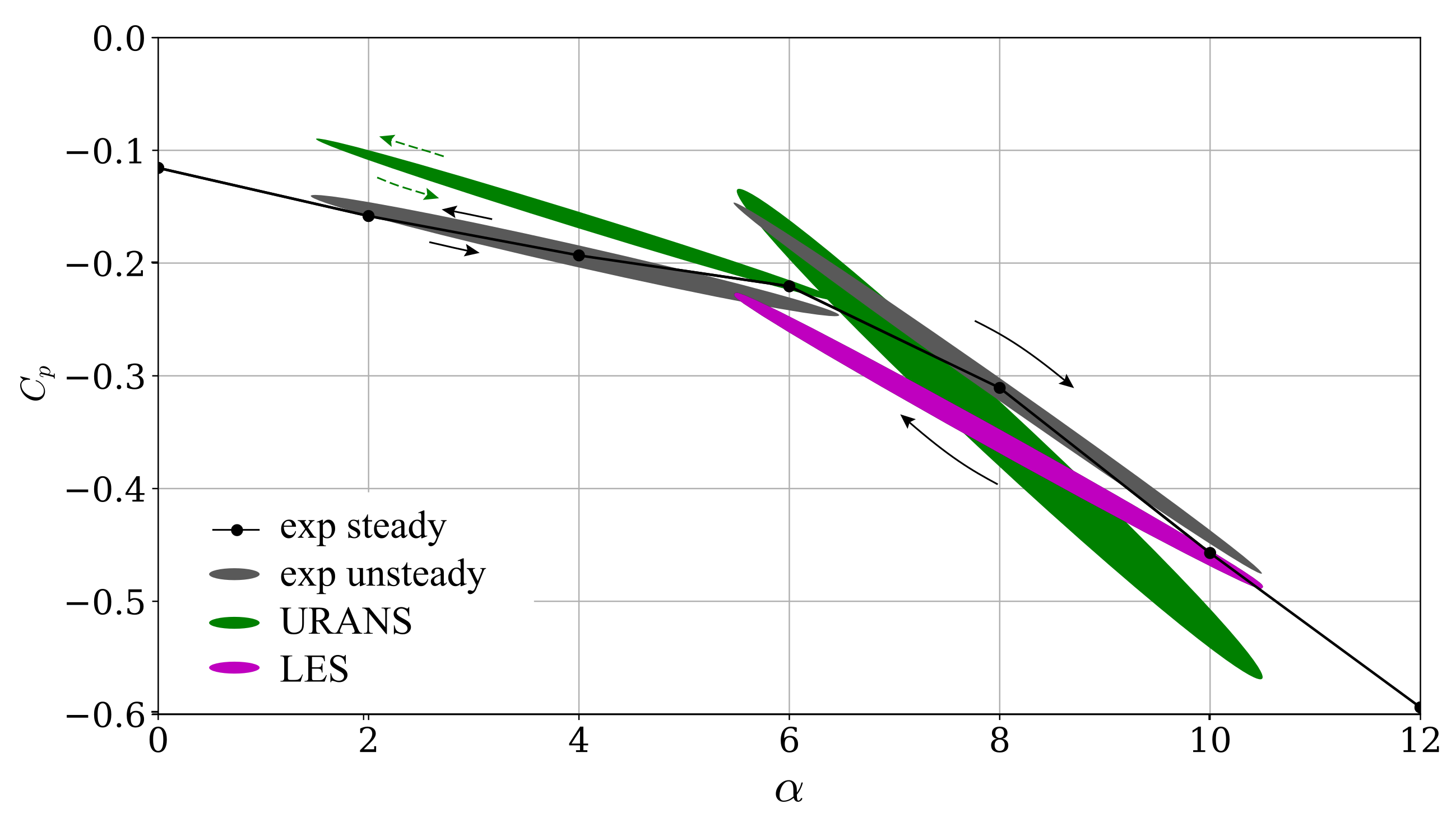
For aeroelastic stability, mainly the frequency component which corresponds to the oscillation frequency (or eigenmode in a real engine) is of interest. The hysteresis curves for this component are shown in
Figure 11. The ellipses have been filled for visualisation purposes. To place the unsteady pressures into context, the experimental steady (time-averaged) pressure coefficients are also shown. The black line connecting the steady values can be considered as the local equivalent of a lift curve slope, while the unsteady coefficients represent the unsteady lift. Results for both mean incidence angles (4 and 8
) are shown on the same plot to facilitate the comparison to the steady behaviour.
For 4
, the harmonic response is very similar to the total response shown in
Figure 10. Furthermore, the experimental unsteady pressure coefficients follow the slope of the steady curve very closely. The narrow and long hysteresis loops along the steady curve indicate that the phase lag between the blade displacement and aerodynamic response is small, and that the magnitude of the unsteady response is similar to that of the quasi-steady response.
At 8
, on the other hand, the harmonic response differs considerably from the total response shown in
Figure 10. It was already shown that the URANS overestimates the local amplitude by approximately 25% (see
Figure 9 at
). In combination with the phase shift, this creates the different URANS and experimental hysteresis curves. The LES mean value differs from the experiment but the unsteady response is much closer to the experimental than the URANS, as already seen above in
Figure 9. The experimental unsteady response still follows the steady curve. This suggests that a quasi-steady approximation may be relevant despite the more complicated flow physics close to stall, which manifests as non-linearities or the presence of multiple frequencies in the local response.
In terms of aerodynamic stability, a larger area under the hysteresis curve indicates higher energy input (positive or negative) into the blade vibration, i.e., it determines the aerodynamic damping amplitude. Whether or not this is stable depends on the direction of the hysteresis loop. A clockwise trajectory represents a destabilising phase lag, , between 0 and 180, while an anti-clockwise trajectory is stabilising. Both experiment and URANS predict instability (positive work input) at 8 for the analyzed location at 20% chord.
The results presented in the previous two sections suggest that there is a good correlation between the quasi-steady and unsteady lift curve slopes even as the flow separates. Furthermore, there are clear discrepancies between the local unsteady surface pressures as predicted by URANS and observed in the experiment and these worsen as a stall is approached. As expected, the LES compares better to experiments. The URANS predicts a very stable region near the leading edge, where LES is neutrally stable. Further downstream URANS predicts destabilizing regions where LES and experiments show negligible amplitude. This would have significant implications for the aeroelastic stability of this torsion mode but this finding should not be generalised to all modes.
5.2. Influence of Reduced Frequency and Time-Averaged Incidence
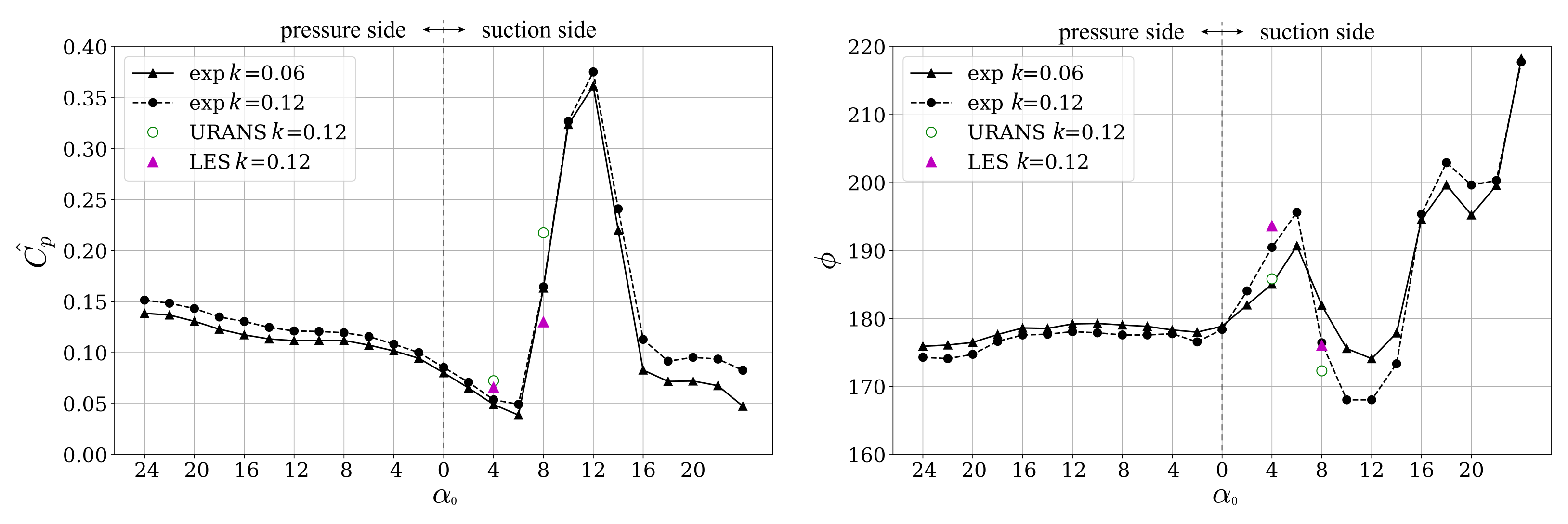
Using experimental results, the dependency of the unsteady amplitude and phase on the reduced frequency and static incidence angle is compared.
Figure 12 plots the unsteady pressure components at 20% chord against incidence. The phase along the pressure side is in anti-phase with blade displacement (
), i.e., the pressure drops as the blade pitches up. The amplitude rises as the mean incidence angle increases. The suction side behaviour is more interesting. The phase increases by 20
between 0 and 4
and then drops suddenly as amplitudes soar closer to stall. This sensitivity of unsteady pressure to steady incidence near stall demonstrates one of the big challenges in turbomachinery aeroelastic modelling. An inaccuracy in mean conditions by as little as one degree can result in a measurable miscalculation of the local phase-lag (up to 10
in this case) and amplitude (up to 60% in this case).
From
Figure 12 there is no notable difference in behaviour when the frequency is increased from
to
. In other words, it is quasi-steady and inertia is playing at most a small part. However, looking at a wider frequency range and plotting amplitude and phase against frequency (
Figure 13), differences become apparent. The local phase lag is approximately 180
at small incidences and then rises for
. Closer to stall at
; however, the phase lag initially falls until about
. The amplitudes vary less than 20% and 34% over the entire frequency range for the small and high incidence, respectively.
As already shown above for , the LES prediction perform better than URANS at high incidences and high frequencies.
5.3. Influence of Tip Clearance Flow
To demonstrate the influence of the tip clearance flow on unsteady response,
Figure 14 shows the total lift hysteresis curves as predicted from the finite (with tip clearance) and infinite (without tip clearance) URANS simulations. There is a significant difference between the two for both incidence angles. The finite blade produces a lower lift coefficient and smaller unsteady response, while the lift increases up to 10.5
incidence for the finite span case, the infinite blade stalls abruptly at an instantaneous incidence angle of approximately 9.5
. Furthermore, visualisations of the unsteady pressure evolution over the finite blade surface show evidence of pressure waves propagating in the spanwise direction which are not present on the infinite blade. This result is not surprising but highlights the importance of including endwalls and three-dimensional flow features for aeroelastic analysis. Infinite span approaches, which are not uncommon in dynamic-stall studies are inaccurate in mean loading, unsteady amplitude and phase and stall onset and behaviour. The finite case presents a smooth transition into a stall with increasing hysteresis loops, while the infinite case stalls abruptly after following a much steeper lift curve.
6. Discussion
The study on this simple test case has illustrated two commonly accepted challenges of aeroelastic modelling in turbomachinery, namely the inaccuracy of URANS simulations and the importance of modelling tip clearance flows. In addition, the analysis of the unsteady aerodynamic response over a range of operating conditions has shown parallels between the steady and unsteady aerodynamic coefficients (
Figure 11), which may prove useful for CFD-calibrated low fidelity flutter models. The implications of these findings for aeroelastic predictions will now be discussed.
Since the present study was limited to a single blade, the following points apply to the prediction of aerodynamic damping of one blade due to its own vibration and do not account for blade-to-blade coupling due to acoustic, entropic or vortical disturbances. In other words, they will affect the mean aerodynamic damping. Variations in aerodynamic damping with nodal diameter are created by blade-to-blade coupling and this is likely to be less affected by inaccuracies in local flow conditions.
6.1. Limitations of URANS Modelling
The prevalent methods in academic and industrial turbomachinery aeroelastic analysis are based on URANS simulations with one- or two-equation turbulence models, often assuming a fully turbulent boundary layer. This is the only practically feasible modelling method for large domain simulations, such as fans and intakes or multi-stage compressors. However, it is well known that the nature of turbomachinery flows, especially at off-design conditions, is not conducive to simple turbulence modelling approaches. The flow is highly three-dimensional, unsteady and transonic, causing complex strain fields and high rates of change for the flow and turbulence fields. A detailed explanation for this can be found in [
25].
The test case exhibited a laminar separation bubble near the leading edge. This is known to influence aerodynamic damping [
26] and this may be responsible for the comparatively poor performance of the present URANS model, which assumed a fully turbulent flow. This is standard practice in high-speed turbomachinery aeroelastic research and industry but a transition model or more sophisticated turbulence model might have improved the URANS predictions.
The results illustrated that LES performs significantly better, especially with respect to the unsteady quantities at high incidence angles where URANS overpredicts unsteady pressure coefficients by over 100% for large parts of the suction side (
Figure 9). Since it is precisely the unsteady response at off-design conditions which is relevant for aeroelastic stability, this presents a strong argument for trying to integrate high-fidelity simulations in aeroelastic analysis. This is attractive in an academic context but not practical for large cases or routine analysis. Even on this small test case, one vibration cycle took approximately 5000 CPU-hours for (under-resolved) LES, compared to ≈15 CPU-hours for the URANS. The simulations presented here were performed on different hardware using different codes, and the computational times can therefore not be used for rigorous performance comparison, but it demonstrates an important advantage of URANS over LES.
6.2. Importance of Tip Clearance Flow
Similarly, the huge differences in response and consequent aeroelastic stability for the finite and infinite span configurations illustrate the need for an accurate prediction of the underlying flow field. This is not surprising, it is well known that compressor aerodynamic damping is sensitive to tip clearance height for example [
27,
28], but it furthermore demonstrates the importance of correct operating conditions and geometry for reliable aeroelastic predictions. In addition, since tip leakage flows are very sensitive to turbulence models, it also supports calls for improved fidelity CFD simulations in aeroelasticity. Since the latter is difficult to achieve in rig and engine tests, this may present an argument for simplified setups such as the one presented in this study to understand fundamental principles and further develop numerical methods.
6.3. Relevance to Modern UHBR Fans
The findings of this study regarding numerical modelling are relevant to modern ultra high bypass ratio (UHBR) fans such as the composite low-speed fan developed at Ecole Centrale de Lyon [
29]. This geometry is known to have a laminar separation bubble at part-speed conditions [
21], which is not captured by the URANS methods used for stability analysis [
29]. The results presented in this paper indicate that coupled LES simulations or at least validation of transition models in aeroelastic context may be required to accurately predict aerodynamic damping of this configuration.
7. Conclusions
The paper investigated the unsteady aerodynamic response of a pitching blade with a sharp leading edge using experiments and URANS and LES simulations. The influence of oscillation frequency, mean incidence angle and tip clearance flow were investigated. The main conclusions are:
URANS and LES agreed well at low incidence angles but differed considerably near stall at incidence, which is still relevant for off design in compressors and fans. URANS overpredicted local pressure amplitudes by over 100%. The phase near the leading edge was also found to differ by almost 90 between LES and URANS, which has significant implications for aerodynamic damping.
A comparison of the finite and an infinite span configuration using URANS demonstrated that neglecting tip flows can lead to vastly different unsteady responses.
The steady incidence angle has a large influence on the phase-lag between the blade motion and pressure perturbation. Varying incidence from 0 to 12 changed the phase lag between 170 and 200. The influence of frequency on unsteady aerodynamic response was less pronounced. A four-fold increase in reduced frequency () only produced phase variations less than 10.
The experimental results also showed a correlation between the slope of the steady local pressure coefficients and the unsteady response. Although this correlation weakens as the mean incidence increases, it is still visible close to stalling.
The study hence provided a very simple test case to experimentally and numerically demonstrate (a) why high fidelity methods and accurate capturing of three-dimensional flow features are important for aeroelastic assessments of compressors, (b) that the steady operating point is one of the main drivers of instability, and (c) that a correlation exists between steady aerodynamics and unsteady aerodynamic response which can be exploited for low fidelity models. The presented studies must be significantly extended using highly-resolved experiments, particularly near the leading edge. The flow conditions in the experiment are not optimal, as only a circular jet was used and flow gradients across the blade prevail towards the hub. It is necessary to develop a robust benchmark case with controlled vibration and flow conditions which justifies also highly-resolved LES modelling efforts.
Author Contributions
C.B.: conceptualization, methodology, investigation, writing-original draft preparation, review and editing, visualization, supervision, project administration/funding acquisition: CleanSky No. 864719. S.S.: conceptualization, methodology, investigation, writing-original draft preparation, review and editing, visualization, supervision, project administration/funding acquisition: MEDY G46041. All authors have read and agreed to the published version of the manuscript.
Funding
The authors gratefully acknowledge the support of the Imperial College European Partners Fund 2019 (MEDY G46041) for the research. The presented research was supported through Clean Sky 2 Joint Undertaking (JU), project CATANA under grant agreement No. 864719. The JU receives support from the European Union’s Horizon 2020 research and innovation programme and the Clean Sky 2 JU members other than the Union. This publication reflects only the author’s view and the JU is not responsible for any use that may be made of the information it contains.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The reference data on the test case is available upon request to the corresponding author.
Acknowledgments
The authors are particularly grateful for the technical contributions of Gilbert Halter, Benoit Paoletti and Xavier Ottavy. They would also like to thank Nick Cumpsty for their advice on the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Unsteady pressure coefficient [-] |
| Unsteady pressure coefficient amplitude [-] |
| c | blade profile chord [m] |
| Unsteady force normal to the blade [kgms] |
| Reduced frequency [-] |
| LES | Large Eddy Simuation |
| M | Freestream Mach Number |
| Area normal [m] |
| number of cells in blade mesh |
| Local unsteady pressure [kgms] |
| q | Modal displacement [-] |
| Free stream dynamic head [kgms] |
| SDCA | Symmetric Double Circular Arc |
| t | Time [s] |
| Free stream velocity [m/s] |
| (U)RANS | (Unsteady) Reynolds Averaged Navier–Stokes |
| W | Local work done on the blade surface [kgms] |
| x | Axial coordinate |
| Pitching axis coordinate |
| Static incidence angle [rad] |
| Oscillation amplitude [rad] |
| Physical displacement vector [m] |
| Mode shape vector [m] |
| Phase of unsteady pressure [rad or deg] |
| Oscillation frequency [rad/s] |
| reference span position |
References
- McCroskey, W.J.; Carr, L.W.; McAlister, K.W. Dynamic stall experiments on oscillating airfoils. AIAA J. 1976, 14, 57–63. [Google Scholar] [CrossRef]
- Kim, Y.; Xie, Z.T. Modelling the effect of freestream turbulence on dynamic stall of wind turbine blades. Comput. Fluids 2016, 129, 53–66. [Google Scholar] [CrossRef]
- McCroskey, W.J. The Phenomenon of Dynamic Stall; Technical Report, NASA Technical Memorandum 81264; NASA: Washington, DC, USA, 1981. [Google Scholar]
- Carr, L.W. Progress in analysis and prediction of dynamic stall. J. Aircr. 1988, 25, 6–17. [Google Scholar] [CrossRef]
- Carr, L.W.; McCroskey, W.J. A Review of Recent Advances in Computational and Experimental Analysis of Dynamic Stall. In Fluid Dynamics of High Angle of Attack; Kawamura, R., Aihara, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 1993; pp. 3–33. [Google Scholar]
- Carr, L.W.; Chandrasekhara, M. Compressibility effects on dynamic stall. Prog. Aerosp. Sci. 1996, 32, 523–573. [Google Scholar] [CrossRef]
- Visbal, M.R.; Garmann, D.J. Analysis of dynamic stall on a pitching airfoil using high-fidelity large-eddy simulations. AIAA J. 2018, 56, 46–63. [Google Scholar] [CrossRef]
- Perovic, D.; Hall, C.; Gunn, E. Stall inception in a boundary layer ingesting fan. J. Turbomach. 2019, 141, 091007. [Google Scholar] [CrossRef]
- Zhang, W.; Stapelfeldt, S.; Vahdati, M. Influence of the inlet distortion on fan stall margin at different rotational speeds. Aerosp. Sci. Technol. 2020, 98, 105668. [Google Scholar] [CrossRef]
- Williams, T.S.; Hall, C.A.; Wilson, M. Low pressure ratio transonic fan stall with radial distortion. J. Glob. Power Propuls. Soc. 2020, 4, 226–237. [Google Scholar] [CrossRef]
- Dodds, J.; Vahdati, M. Rotating Stall Observations in a High Speed Compressor—Part I: Experimental Study. J. Turbomach. 2015, 137, 051002. [Google Scholar] [CrossRef]
- Zhao, F.; Dodds, J.; Vahdati, M. Influence of blade vibration on part-span rotating stall. Int. J. Gas Turbine Propuls. Power Syst. 2020, 12, 1–7. [Google Scholar] [CrossRef]
- Kielb, R.E.; Hall, K.C.; Spiker, M.; Thomas, J.P.; Pratt, E.T., Jr.; Jeffries, R. Non-Synchronous Vibration of Turbomachinery Airfoils; Technical Report; Duke University: Durham, NC, USA, 2006. [Google Scholar]
- Baumgartner, M.; Kameier, F.; Hourmouziadis, J. Non-engine order blade vibration in a high pressure compressor. In Proceedings of the Twelfth International Symposium on Airbreathing Engines, Melbourne, Australia, 10–15 September 1995. [Google Scholar]
- Brandstetter, C.; Juengst, M.; Schiffer, H.P. Measurements of Radial Vortices, Spill Forward, and Vortex Breakdown in a Transonic Compressor. J. Turbomach. 2018, 140, 061004. [Google Scholar] [CrossRef]
- Stapelfeldt, S.; Brandstetter, C. Non-synchronous Vibration in Axial Compressors: Lock-in Mechanism and Semi-Analytical Model. J. Sound Vib. 2020, 488, 115649. [Google Scholar] [CrossRef]
- Day, I.J. Stall, Surge, and 75 Years of Research. J. Turbomach 2015, 138, 011001. [Google Scholar] [CrossRef]
- Tucker, P. Computation of unsteady turbomachinery flows: Part 2—LES and hybrids. Prog. Aerosp. Sci. 2011, 47, 546–569. [Google Scholar] [CrossRef]
- Gao, F.; Zambonini, G.; Boudet, J.; Ottavy, X.; Lu, L.; Shao, L. Unsteady behavior of corner separation in a compressor cascade: Large eddy simulation and experimental study. Proc. Inst. Mech. Eng. Part A J. Power Energy 2015, 229, 508–519. [Google Scholar] [CrossRef]
- Pérez Arroyo, C.; Leonard, T.; Sanjosé, M.; Moreau, S.; Duchaine, F. Large Eddy Simulation of a scale-model turbofan for fan noise source diagnostic. J. Sound Vib. 2019, 445, 64–76. [Google Scholar] [CrossRef]
- Al Am, J.; Clair, V.; Giauque, A.; Boudet, J.; Gea-Aguilera, F. Direct noise predictions of fan broadband noise using LES and analytical models. In Proceedings of the 28th AIAA/CEAS Aeroacoustics 2022 Conference, Southampton, UK, 14–17 June 2022; American Institute of Aeronautics and Astronautics: Southampton, UK, 2022. Number 2022-2882 in AIAA. [Google Scholar] [CrossRef]
- Sayma, A. An Integrated Nonlinear Approach for Turbomachinery Forced Response Prediction. Part I: Formulation. J. Fluids Struct. 2000, 14, 87–101. [Google Scholar] [CrossRef]
- Stapelfeldt, S.; Parry, T.; Vahdati, M. Validation of time-domain single-passage methods for the unsteady simulation of a contra-rotating open rotor. Proc. Inst. Mech. Eng. Part A J. Power Energy 2015, 229, 443–453. [Google Scholar] [CrossRef]
- Dodds, J.; Vahdati, M. Rotating Stall Observations in a High Speed Compressor—Part II: Numerical Study. J. Turbomach. 2015, 137, 51003. [Google Scholar] [CrossRef]
- Leschziner, M.; Drikakis, D. Turbulence modelling and turbulent-flow computation in aeronautics. Aeronaut. J. 2002, 106, 349–384. [Google Scholar]
- Barnes, C.J.; Visbal, M.R. On the role of flow transition in laminar separation flutter. J. Fluids Struct. 2018, 77, 213–230. [Google Scholar] [CrossRef]
- Möller, D.; Jüngst, M.; Holzinger, F.; Brandstetter, C.; Schiffer, H.P.; Leichtfuß, S. Mechanism of Nonsynchronous Blade Vibration in a Transonic Compressor Rig. J. Turbomach. 2016, 139, 011002. [Google Scholar] [CrossRef]
- Dong, X.; Zhang, Y.; Zhang, Z.; Lu, X.; Zhang, Y. Effect of Tip Clearance on the Aeroelastic Stability of a Wide-Chord Fan Rotor. J. Eng. Gas Turbines Power 2020, 142, 091010. [Google Scholar] [CrossRef]
- Pagès, V.; Duquesne, P.; Aubert, S.; Blanc, L.; Ferrand, P.; Ottavy, X.; Brandstetter, C. UHBR Open-Test-Case Fan ECL5/CATANA. Int. J. Turbomach. Propuls. Power 2022, 7, 17. [Google Scholar] [CrossRef]
Figure 1.
Schematic of blade profile and test setup. (a) sketch of geometry, (b) coordinate convention, (c) image of instrumented blade, (d) installation on oscillation mechanism.
Figure 1.
Schematic of blade profile and test setup. (a) sketch of geometry, (b) coordinate convention, (c) image of instrumented blade, (d) installation on oscillation mechanism.
Figure 2.
Visualization of numerical domain and mesh topology.
Figure 2.
Visualization of numerical domain and mesh topology.
Figure 3.
Comparison of RANS and time-averaged LES simulations for and : (a) Surface pressure contours of RANS and (b) time averaged LES; (c) Leading edge velocity contours of time averaged LES.
Figure 3.
Comparison of RANS and time-averaged LES simulations for and : (a) Surface pressure contours of RANS and (b) time averaged LES; (c) Leading edge velocity contours of time averaged LES.
Figure 4.
Comparison of instantaneous iso-surface of constant Q-criterion for URANS and LES simulation at .
Figure 4.
Comparison of instantaneous iso-surface of constant Q-criterion for URANS and LES simulation at .
Figure 5.
Comparison of surface pressure contours between RANS, time averaged LES and steady experiment. and at ; (a) Mesh , (b) mesh variation for .
Figure 5.
Comparison of surface pressure contours between RANS, time averaged LES and steady experiment. and at ; (a) Mesh , (b) mesh variation for .
Figure 6.
RANS, LES and experimental boundary layer profiles: (a) and (b) at ; Mesh M.
Figure 6.
RANS, LES and experimental boundary layer profiles: (a) and (b) at ; Mesh M.
Figure 7.
Comparison of infinite blade (LES-INF) and finite blade (LES-FIN) time-averaged pressure profiles at two spanwise positions for: (a) and (b) .
Figure 7.
Comparison of infinite blade (LES-INF) and finite blade (LES-FIN) time-averaged pressure profiles at two spanwise positions for: (a) and (b) .
Figure 8.
Unsteady surface pressure amplitude and phase as predicted by URANS and LES on the suction side. Oscillation frequency: . Pitching axis at ; (a) , (b) .
Figure 8.
Unsteady surface pressure amplitude and phase as predicted by URANS and LES on the suction side. Oscillation frequency: . Pitching axis at ; (a) , (b) .
Figure 9.
Unsteady surface pressure amplitude and phase as predicted by URANS and LES on the suction side at . Oscillation frequency: .
Figure 9.
Unsteady surface pressure amplitude and phase as predicted by URANS and LES on the suction side at . Oscillation frequency: .
Figure 10.
Hysteresis of unsteady pressure at 20% chord for pitching amplitude around mean incidence and for .
Figure 10.
Hysteresis of unsteady pressure at 20% chord for pitching amplitude around mean incidence and for .
Figure 11.
Comparison of steady and unsteady pressure coefficients measured at and filtered at for difference incidence angles.
Figure 11.
Comparison of steady and unsteady pressure coefficients measured at and filtered at for difference incidence angles.
Figure 12.
Variation of unsteady pressure amplitude and phase with incidence angle measured at 20% chord. Oscillation frequency and .
Figure 12.
Variation of unsteady pressure amplitude and phase with incidence angle measured at 20% chord. Oscillation frequency and .
Figure 13.
Variation of unsteady pressure amplitude and phase with reduced frequency.
Figure 13.
Variation of unsteady pressure amplitude and phase with reduced frequency.
Figure 14.
Comparison of unsteady lift coefficients for finite and infinite span configuration. (a) , (b) .
Figure 14.
Comparison of unsteady lift coefficients for finite and infinite span configuration. (a) , (b) .
Table 1.
Relationship between phase of the unsteady pressure on the suction side and work input. is the axial coordinate of the pitching axis. Positive work input is destabilising.
Table 1.
Relationship between phase of the unsteady pressure on the suction side and work input. is the axial coordinate of the pitching axis. Positive work input is destabilising.
| Axial Position | | |
|---|
| Positive | Negative |
| Negative | Positive |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).