Dimensionless Numbers Relationships for Outer Air Seal of Low Pressure Turbine †
Abstract
:1. Introduction
1.1. Previous Work
1.2. Objectives of the Current Work
2. Methodology
2.1. Dimensional Analysis
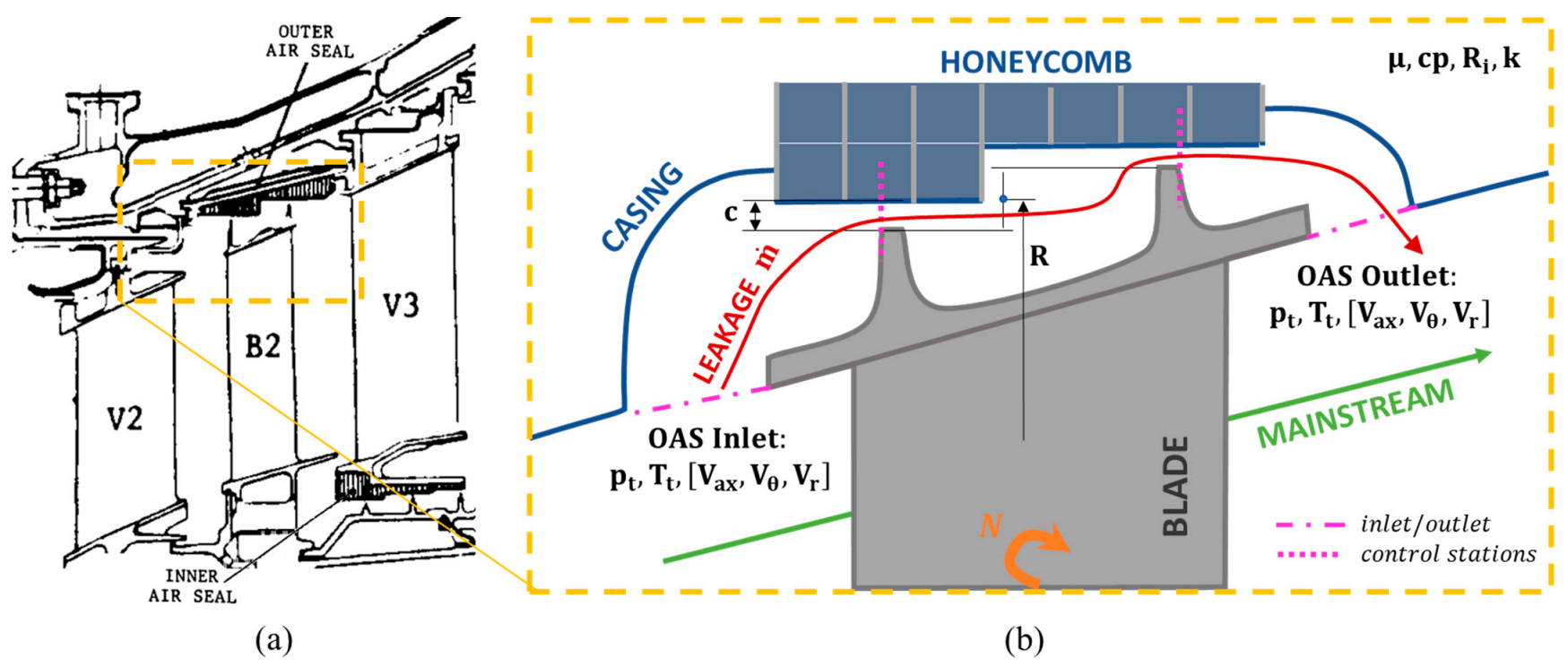
2.2. Numerical Setup
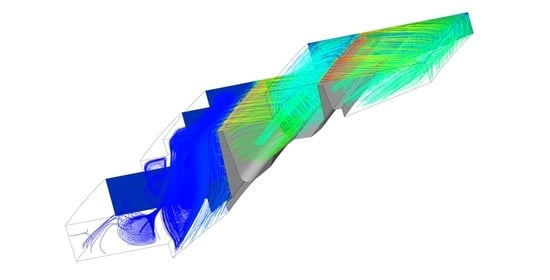
2.2.1. Geometry
2.2.2. Mesh
2.2.3. Boundary Conditions
2.2.4. Solver
3. Results and Discussion
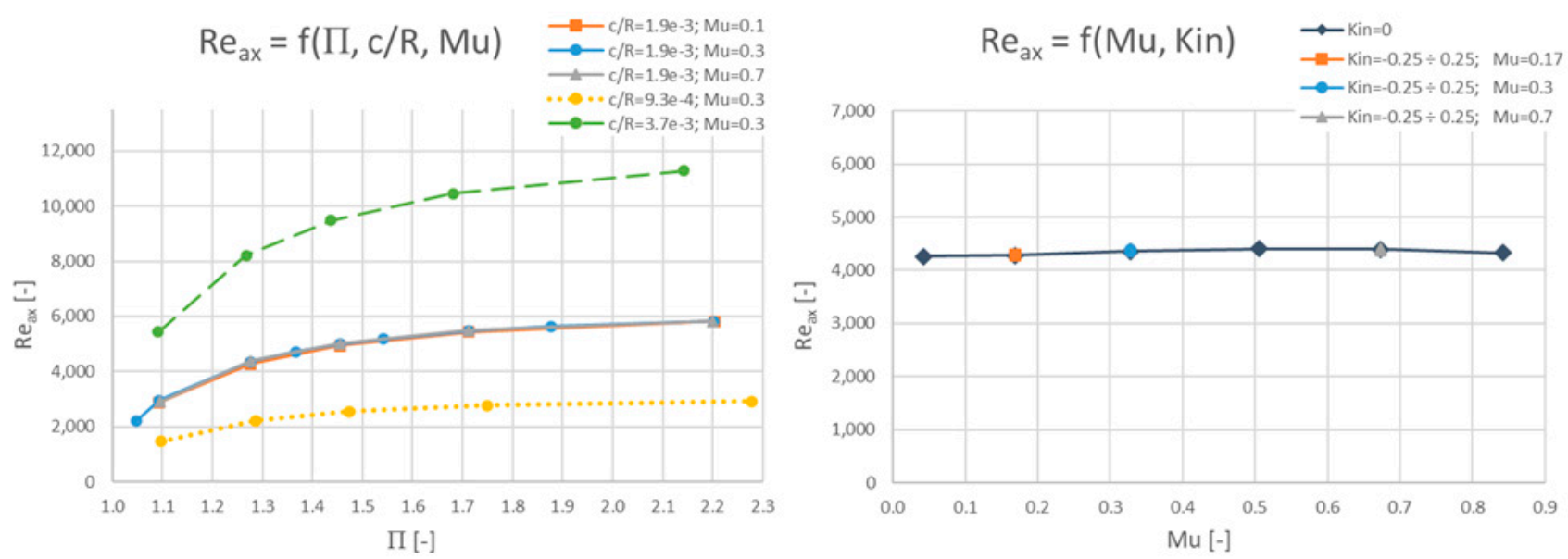
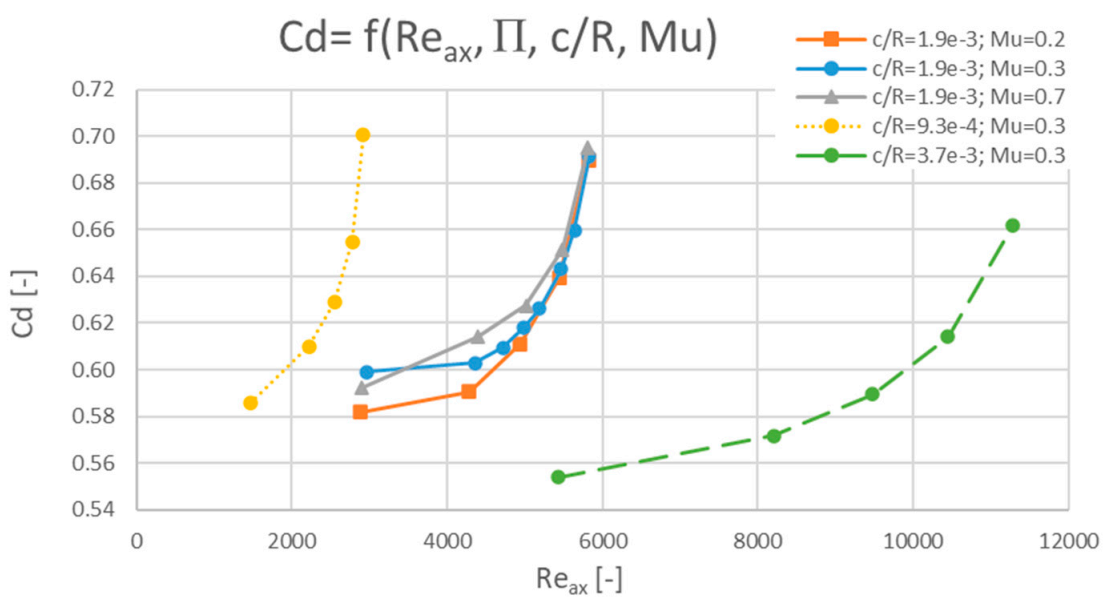
3.1. Axial Reynolds Number
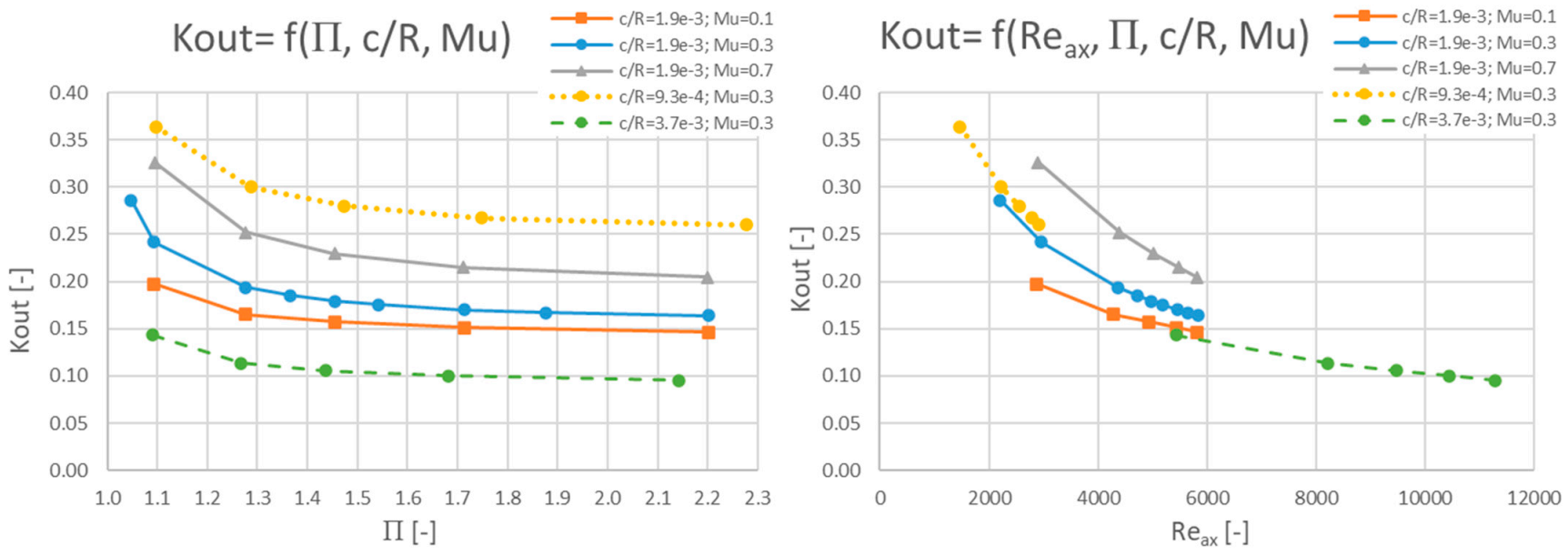
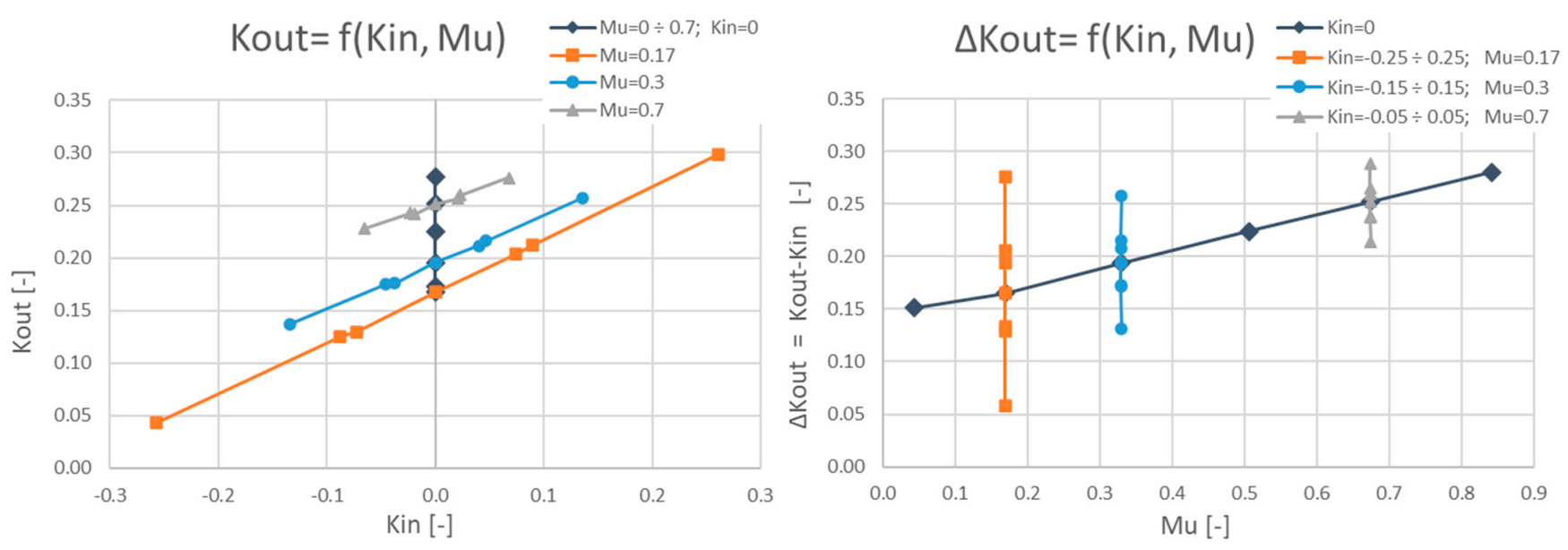
3.2. Leakage Exit Swirl Ratio
3.3. Windage Heating
3.4. Other Parameters Resulting from Dimensional Analysis
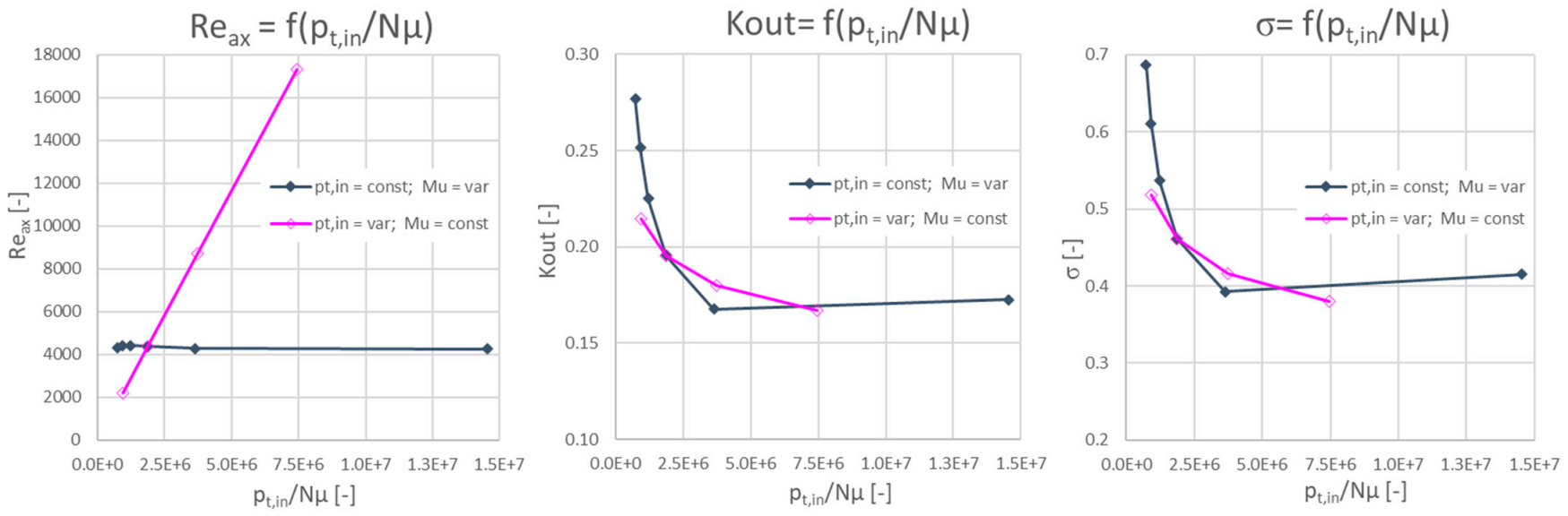
3.5. Unsteady Effects at OAS in Dimensionless Numbers
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Local speed of sound | |
| any dimensional quantity Clearance size | |
| Specific heat capacity | |
| Relative clearance | |
| Ratio of specific heats | |
| Leakage mass flow | |
| Pressure | |
| Cross-sectional area at fin | |
| Discharge coefficient | |
| Swirl ratio | |
| Circumferential Mach number | |
| Rotational speed | |
| Pr | Prandtl number |
| Average radius of fins | |
| Individual gas constant | |
| Axial Reynolds number | |
| Temperature | |
| Tu | Turbulence intensity |
| Rotor fins circumferential velocity | |
| Axial velocity component | |
| Radial velocity component | |
| Circumferential velocity component | |
| any exponents | |
| Viscosity | |
| Density | |
| Pressure Ratio | |
| any dimensionless quantity Windage heating | |
| Subscripts: | |
| t | Total quantities |
| in, out | Inlet, Outlet |
| Acronyms: | |
| CFD | Computational Fluid Dynamics |
| DA | Dimensional Analysis |
| IAS/OAS | Inner/Outer Air Seal |
| LES | Large Eddy Simulations |
| LPT | Low Pressure Turbine(s) |
| PIV | Particle Image Velocimetry |
| PVT | Particle Velocimetry Tracking |
| (U)RANS | (Unsteady) Reynolds-Averaged Navier-Stokes |
Appendix A. Main Steps of the Dimensional Analysis
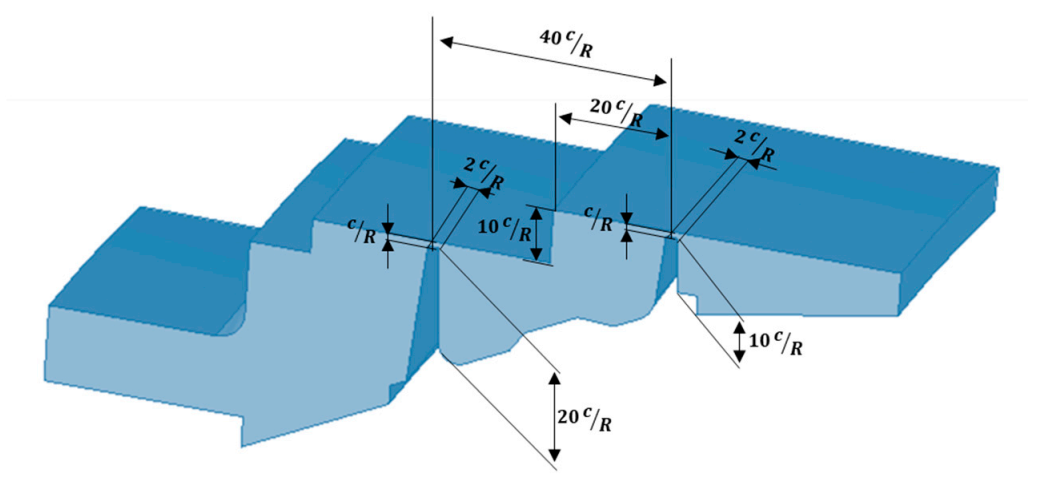
Appendix B. Details of the Investigated Seal Geometry
| Clearance Size, | 0.001 [m] |
|---|---|
| Average radius of the fins, | 0.538 [m] |
| 1st fin height | |
| 2nd fin height | |
| Width of the fins | |
| Distance between the fins | |
| Step height | |
| Distance from the step to the 2nd fin | |
| Corner radii of the fins | 0 (sharp fins) |
References
- Dinc, S.; Demiroglu, M.; Turnquist, N.; Mortzheim, J.; Goetze, G.; Maupin, J.; Hopkins, J.; Wolfe, C.; Florin, M. Fundamental Design Issues of Brush Seals for Industrial Applications. J. Turbomach. 2002, 124, 293–300. [Google Scholar] [CrossRef]
- Mahle, I. Improving the Interaction Between Leakage Flows and Main Flow in a Low Pressure Turbine. ASME J. Turbomach. 2010, 7, 1177–1186. [Google Scholar] [CrossRef]
- Wittig, S.L.K.; Dorr, L.; Kim, S. Scaling Effects on Leakage Losses in Labyrinth Seals. J. Eng. Power 1983, 105, 305–309. [Google Scholar] [CrossRef]
- Waschka, W.; Wittig, S.; Kim, S. Influence of High Rotational Speeds on the Heat Transfer and Discharge Coefficients in Labyrinth Seals. J. Turbomach. 1992, 114, 462–468. [Google Scholar] [CrossRef]
- Denecke, J.; Farber, J.; Dullenkopf, F.; Bauer, H.J. Dimensional Analysis and scaling of rotating seals. ASME J. Turbomach. 2005, 47268, 1149–1160. [Google Scholar] [CrossRef]
- Denecke, J.; Dullenkopf, K.; Wittig, S.; Bauer, H.-J. Experimental Investigation of the Total Temperature Increase and Swirl Development in Rotating Labyrinth Seals. ASME J. Turbomach. 2005, 3, 1161–1171. [Google Scholar] [CrossRef]
- Yan, X.; Li, J.; Song, L.; Feng, Z. Investigations on the Discharge and Total Temperature Increase Characteristics of the Labyrinth Seals with Honeycomb and Smooth Lands. J. Turbomach. 2009, 131, 041009. [Google Scholar] [CrossRef]
- Zimmermann, H.; Wolff, K.H. Air System Correlations: Part 1—Labyrinth Seals; ASME Paper 98-GT-206; ASME: New York, NY, USA, 1998. [Google Scholar]
- Szymanski, A.; Wroblewski, W.; Dykas, S. Flow Analysis of the Turbine Rotor Tip Seal on a Highly Rotary Test Rig. In Proceedings of the 11th European Conference on Turbomachinery Fluid dynamics & Thermodynamics, ETC11, Madrid, Spain, 23–27 March 2015; pp. 23–27. [Google Scholar]
- Szymanski, A.; Dykas, S.; Wroblewski, W.; Fraczek, D. Experimental and Numerical Validation Study of the Labyrinth Seal Configurations. In Proceedings of the 12th European Conference on Turbomachinery Fluid Dynamics & Thermodynamics ETC12, Stockholm, Sweden, 3–7 April 2017. [Google Scholar] [CrossRef] [Green Version]
- Fraczek, D.; Wroblewski, W.; Chmielniak, T. Influence of Honeycomb Rubbing on Tip Seal Performance of Turbine Rotor. In Proceedings of the 11th European Conference on Turbomachinery Fluid Dynamics & Thermodynamics, Madrid, Spain, 23–27 March 2015. [Google Scholar] [CrossRef]
- Kluge, T.; Wein, L.; Schmierer, R.; Seume, J.R. Sensitivity analysis, instrumentation and design, and experimental validation of a novel labyrinth seal rig. In Proceedings of the 13th European Conference on Turbomachinery Fluid dynamics & Thermodynamics ETC13, Lausanne, Switzerland, 8–12 April 2019. [Google Scholar] [CrossRef]
- Wein, L.; Kluge, T.; Seume, J.R.; Hain, R.; Fuchs, T.; Kähler, C.; Schmierer, R.; Herbst, F. Validation of RANS Turbulence Models for Labyrinth Seal Flows by Means of Particle Image Velocimetry. In Proceedings of the ASME Turbo Expo 2020: Turbomachinery Technical Conference and Exposition, London, UK, 21–25 September 2020. [Google Scholar] [CrossRef]
- Gao, F.; Chew, J.W.; Beard, P.; Amirante, D. Numerical Studies of Turbine Rim Sealing Flows on a Chute Seal Configuration. In Proceedings of the 12th European Conference on Turbomachinery Fluid dynamics & Thermodynamics ETC12, Stockholm, Sweden, 3–7 April 2017. [Google Scholar] [CrossRef] [Green Version]
- Kluge, T.; Lettmann, I.S.; Oettinger, M.; Wein, L.; Seume, J.R. Unsteady Flow Phenomena in Turbine Shroud Cavities. In Proceedings of the Global Power and Propulsion Society, Chania, Greece, 7–9 September 2020. [Google Scholar] [CrossRef]
- Leach, K.; Thulin, R.; Howe, D. Energy Efficient Engine. In Tubrine Indermediate Case ad Low Pressure Turbine Component Test Hardware Detailed Design Report; NASA CR-167973; PWA-5594-191; NASA Lewis Research Center: Cleveland, OH, USA, 1982; p. 44135. [Google Scholar]
- Qing-Ming, T. Dimensional Analysis with Case Studies in Mechanics; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1–41. [Google Scholar]
- Willenborg, K.; Kim, S.; Wittig, S. Effects of Reynolds Number and Pressure Ratio on Leakage Loss and Heat Transfer in a Stepped Labyrinth Seal. J. Turbomach. 2001, 123, 815–822. [Google Scholar] [CrossRef]
- Schramm, V.; Willenborg, K.; Kim, S.; Wittig, S. Influence of a Honeycomb Facing on the Flow Through a Stepped Labyrinth Seal. J. Eng. Gas Turbines Power 2000, 124, 140–146. [Google Scholar] [CrossRef]
- Denecke, J.; Schramm, V.; Kim, S.; Wittig, S. Influence of Rub-Grooves on Labyrinth Seal Leakage. J. Turbomach. 2003, 125, 387–393. [Google Scholar] [CrossRef]



| Quantities Considered Meaningful for OAS DA | |
|---|---|
| Base units | [s], [m], [kg], [K] |
| Chosen independent variables | [m], [s−1], [kg∙m−1∙s−1], [K] |
| Chosen dependent variables |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Pałkus, K.; Strzelczyk, P. Dimensionless Numbers Relationships for Outer Air Seal of Low Pressure Turbine. Int. J. Turbomach. Propuls. Power 2021, 6, 33. https://doi.org/10.3390/ijtpp6030033
Pałkus K, Strzelczyk P. Dimensionless Numbers Relationships for Outer Air Seal of Low Pressure Turbine. International Journal of Turbomachinery, Propulsion and Power. 2021; 6(3):33. https://doi.org/10.3390/ijtpp6030033
Chicago/Turabian StylePałkus, Kacper, and Piotr Strzelczyk. 2021. "Dimensionless Numbers Relationships for Outer Air Seal of Low Pressure Turbine" International Journal of Turbomachinery, Propulsion and Power 6, no. 3: 33. https://doi.org/10.3390/ijtpp6030033
APA StylePałkus, K., & Strzelczyk, P. (2021). Dimensionless Numbers Relationships for Outer Air Seal of Low Pressure Turbine. International Journal of Turbomachinery, Propulsion and Power, 6(3), 33. https://doi.org/10.3390/ijtpp6030033