Abstract
A significant share of the conversion of thermal into electrical energy is realized by steam turbines. Formerly designed for continuous operation, today’s requirements include extended part load operation that can be accompanied by highly unstable flow conditions and vibrations within the control valve of the turbine. The prediction of the flow at part load conditions requires large computational efforts with advanced turbulence modeling in order to compute the flow at a reasonable accuracy. Due to the unsteadiness of the flow, the evaluation of the numerical results itself is a major challenge. The turbulent structures require statistical approaches, of which the use of Spectral Proper Orthogonal Decomposition (SPOD) has proven itself as a powerful method. Within this paper, the application of the method on a critical operating point with a temporal excitation of pressure oscillations observed in the experiments with dry air is presented. Using SPOD, the dominating flow phenomena were isolated and flow structures visualized.
1. Introduction
Enhanced by an increasing share of renewable energy, the overall supply of electricity to the grid is becoming more dynamic and additional regulation efforts are necessary. For the stability of the grid, short-term balancing power is crucial for a safe operation, compensating not only spikes and shortages of the electrical demand but also dynamic contribution of wind and solar power plants.
Besides the dynamic operation of gas turbines, steam turbines are nowadays experiencing extended operation at part load conditions and the number of load changes of the turbines rises. At part load conditions, the turbines are usually operated outside their design point and in some cases even outside their initial operating envelope. In these conditions, the regulation of the turbine, which is often realized by the use of control valves, is stressed and flow conditions can become extremely unstable.
To allow a dynamic operation, quasi-steady operation of the boiler along with a control valve is required due to its thermal inertia, keeping the energy level of the steam prior the turbine at a constant level. At throttled conditions, large pressure gradients across the valve cause a significant acceleration of the flow followed by a dissipation process across turbulent structures, as described by Domnick and Brillert [1]. Resulting pressure fluctuations can cause strong vortex structures [2], high acoustic noise levels [3] and, depending on the valve shape and support, severe vibrations [4]. According to Hardin et al. [5], the undesired noise, pressure fluctuations and resulting vibrations can significantly reduce the lifetime of components, possibly resulting in mechanical failures.
The prediction of these flow instabilities is difficult and, even with today’s computational capabilities and numerical progress, challenging. The reproduction of the flow requires good knowledge and understanding of the real flow as the result of the computed flow varies significantly with the choice of the numerical setup [1,6]. Higher-order turbulence modeling is required in order to account for different flow features and the validation of CFD data against test results, favorably for the same geometry, is needed for the validity of results. In return, using a validated numerical setup can help understand findings in the experiment as it allows insight into the three-dimensional flow field and its structures.
The comparison of CFD results against experimental data can be a challenge on its own. Because of the random nature of the turbulent flow, instantaneous flow conditions are difficult to compare and statistical measures are needed. While minimum and maximum values as well as the time average are rather simple to compute, evaluating the temporal behavior of the flow is challenging. Due to the grid requirements of the numerical analysis and the resulting computational effort, numerical results can usually capture only a short physical time span and low frequency effects are often not captured.
For higher frequencies, the chaotic nature of the turbulent flow makes it difficult to identify dominating and reoccurring structures in the flow field, even though they are initially captured by Fourier transformations. To evaluate the random flow, statistical methods are required to analyze the flow field with respect to the temporal and spacial evolution of reoccurring flow effects. Within this study, Spectral Proper Orthogonal Decomposition (SPOD), as published by Towne et al. [7], was used, which has proven itself to be a powerful method of isolating and visualizing reoccurring flow features. Its application on a critical operating point with temporal periodic pressure trends is assessed in this paper.
2. Test Geometry
The scope of the research is the investigation of the unsteady flow field with the aim to reproduce and analyze the Fluid–Structure Interaction (FSI) within a simplified and scaled steam turbine control valve. Instead of more complex valve designs that are usually used in larger steam turbines, a simple valve geometry using a spherical valve shape is still often used in units with a smaller power output such as industrial applications. With the aim to exaggerate the instability, this design was chosen for the experimental research, focusing on a simple setup and resulting flow instabilities. The geometry of the test valve introduced by Windemuth et al. [8] is shown in Figure 1 with valve dimensions provided in Table 1. The continuous contour of the valve head allows the flow to remain attached to the wall and favors strong flow interactions within the diffuser section.
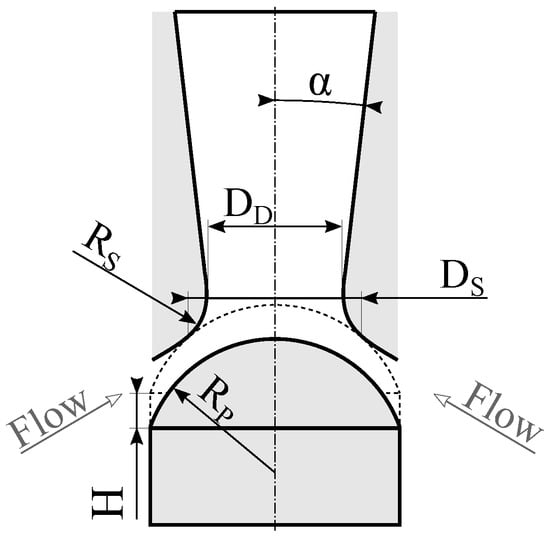
Figure 1.
Geometry of the test valve.

Table 1.
Normalized valve geometry.
2.1. Experimental Setup
Unlike field applications, the test rig at Technische Universität Dresden is driven by compressed air which is supplied by a screw compressor. The resulting operating window allows a maximum flow rate in the order of kg/s and pressure ratios (operating points are defined by = ambient pressure/inlet total pressure and = valve lift/seat diameter) down to . Exhausting into ambience, the back pressure of the valve is fixed and operating points are set by the pressure level within the valve chest.
Experimental results consist of steady measurements such as pressure and temperature probes as well as the flow rate. The time resolving pressure level can be obtained on the valve head by four circumferentially distributed pressure transducers Kulite XCQ-062-3.5bar abs. and on the diffuser wall by four Kulite XCQ-080-1.7bar abs. with variable axial and circumferential positions. For further details on the instrumentation, refer to the work of Windemuth et al. [8].
2.2. Numerical Setup
The numerical domain for the presented study is shown in Figure 2 and mirrors the experimental geometry. A partly blocked and unstructured mesh with a total of roughly 8.3 × 106 nodes was used for the transient simulations conducted with the commercial solver ANSYS© CFX© Release 19. The mesh refinement is based on a grid study using the SAS model and reflects a trade-off regarding computational cost and spacial resolution (roughly 1 week per 10,000 time steps on 240 CPUs). Consistent to the experiment the fluid is air, modeled as an ideal gas. For further details on the numerical model, refer to the work of Windemuth et al. [9].
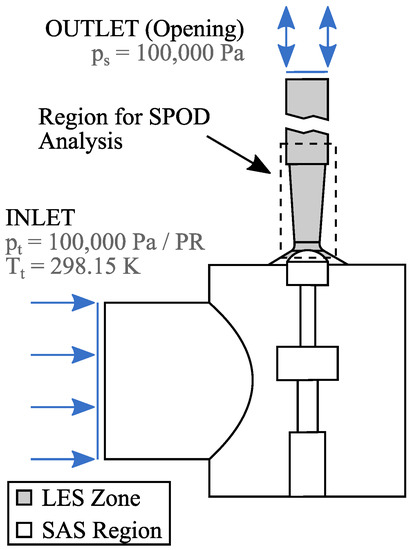
Figure 2.
Numerical domain, LES zone and region for the SPOD analysis.
Turbulence was modeled using the SAS-SST turbulence model along with a pre-specified LES zone (Zonal LES (Within the predefined LES zone, Wall Modeled LES using the Smagorinsky subgrid-scale model is applied), available as a beta feature. namely SAS-F in ANSYS© CFX©). The location of the LES zone is highlighted in Figure 2 and starts just before the throttle area, to allow a steady, nearly laminar inflow and contains all of the downstream mesh including the outlet. For the presented study, a time step of s with a minimum of eight iterations per time step was used, and the simulation captured a total of roughly s. Transient SAS simulations were used as initial solutions for all simulations.
For the investigation of time dependent flow, transient results are evaluated. Due to the size of full volume results, transient data is only captured on predefined surfaces (Diffuser XY-plane, diffuser and head surface) after each time step. The mesh used to capture the transient data is independent from the numerical grid, and results are interpolated onto the mesh after each time step before being exported. While taking interpolation errors into account, this allows a significant reduction of total grid points by neglecting refinements that are necessary for the computation. The output data includes approximately 40,000 nodes, making the evaluation of all time steps across the simulation even possible.
3. Experimental Results
While reducing the stiffness of the valve support is possible, experimental results for this study were gathered from a valve configuration considered rigid. Across the operating window, pressure signals were assessed with respect to the presence of pressure fluctuations. As already discussed in [8,9], using the standard deviation of pressure signals as a measure of flow instability, regions of increased instability were identified consistent to literature data [4,10]. For a diffuser wall pressure sensor (corresponding sensor position for experimental results in Figure 3 is Diffuser 3/3, third position on the diffuser wall in streamwise direction in Figure 4 (sensors marked as ∘)), the normalized distribution of average pressure fluctuations is shown in Figure 3a. Indicated by the shade and magnitude (both normalized without specific scale), pressure fluctuations increase as the opening and pressure ratio are decreased and reach maximum values around .
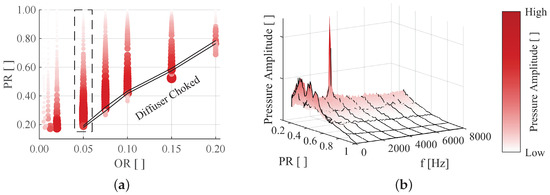
Figure 3.
Overview of diffuser wall pressure fluctuations across the operating window and frequency analysis for OR = 0.05 (Experiment): (a) average standard deviation (normalized); and (b) frequency spectra for OR = 0.05.
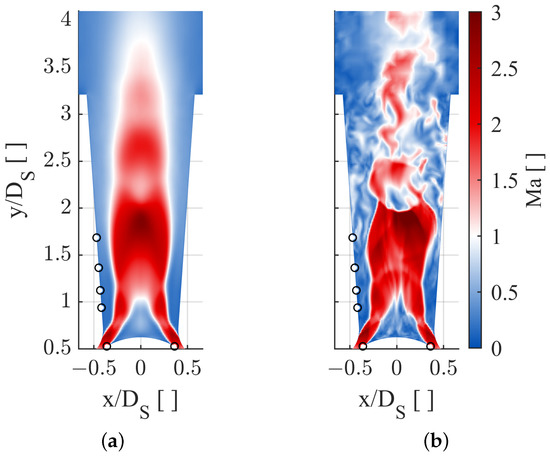
Figure 4.
Flow field at OR = 0.05, PR = 0.20 (CFD, sensor positions: ∘): (a) time averaged; and (b) instantaneous.
The pressure ratio at which maximum pressure fluctuations are observed decreases as the valve is closed. For a reduction of the pressure ratio for a given valve opening, a sudden reduction of pressure fluctuations can be observed for opening ratios . Based on experimental data and numerical simulations, the diffuser becomes choked and a strong shock evolves within the diffuser section. The approximate transition region is indicated by the solid lines in Figure 3a. For choked conditions, the flow prior the shock stabilizes and pressure fluctuations are largely reduced or even disappear.
Considering the pressure fluctuations and flow conditions, the opening ratio of is investigated in detail and an overview of the frequency analysis of a diffuser wall pressure signal is provided in Figure 3b. An increase of amplitudes can be identified across all frequencies as the pressure ratio is decreased. It can be concluded that random non-periodic flow structures dominate the flow at most pressure ratios as no specific frequency is identified and only a dominance of low frequency effects is observed. While this behavior is similar for most other sensors and opening ratios, a discrete peak can be observed near for the opening ratio of at the transition to a choked diffuser. This observation in the experiment is currently unique across the operating range and the identification of the corresponding flow structure at and is the scope of the following section.
4. Numerical Assessment of Operating Point OR = 0.05/PR = 0.20
The operating point with the small opening and pressure ratio is dominated by supersonic flow structures. Consistent with the findings of Zhang et al. [10], supersonic jets detach from both the diffuser and valve head and the time averaged flow shows a supersonic core (Figure 4a). Based on the comparison of time resolving pressure trends, the numerical results obtained with the SAS-F turbulence model and experimental data show good agreement [9]. While simulations with the SST or pure SAS-SST turbulence model show a far more stable supersonic jet, the instantaneous flow field using the SAS-F model becomes highly unsteady and temporary normal shocks evolve in the diffuser, as shown in Figure 4b.
The evaluation of the unsteady flow structures is extremely difficult due to the randomness in the flow, and the identification of frequency-related phenomena from raw flow fields at different time steps across a period of interest is complicated. For a clearer view, it is desired to isolate reoccurring flow structures for a given frequency, which is the scope of the following assessment.
4.1. Spectral Proper Orthogonal Decomposition
Because the duration of experimental measurements often greatly exceeds the elapsed time of CFD simulations, the assessment of repeating structures is of major importance. Due to the unsteadiness of the flow, statistical methods are essential, of which Proper Orthogonal Decomposition (POD) has become an established method for many CFD applications over the last decades. Because the pure POD only compares a set of snapshots, the resulting POD modes are only representations of dominating flow patterns within the dataset. For non-periodic but repeating structures, Spectral Proper Orthogonal Decomposition (SPOD) proposed by Towne et al. [7] combines the power of POD with the frequency analysis. While a pure Fourier Transformation often leads to insufficient results for turbulent flows due to changing amplitudes and frequencies, temporal extinctions and excitations or variations in the direction of propagation, SPOD has shown to be a powerful tool for the reconstruction of dominant structures.
The SPOD methodology was described in details by Towne et al. [7]. As a brief summary, the algorithm processes a dataset of arbitrary dimensions which in the presented study is the spacial pressure or flow field and transforms it into the frequency space with dominant amplitudes and phase angles. At first, the dataset is reorganized into multiple (time) segments which may overlap. Window functions can be applied to the (time) segments and good results were obtained using the Hamming-Window (default). In the second step, frequency spectra are computed for all spacial points within each (time) segment. As a result, the flow is transformed from the time into frequency space for each segment. Finally, a POD algorithm is applied onto the frequency spectra, which are now treated as snapshots for the POD. The resulting number of SPOD modes therefore equals the number of segments while the frequency resolution depends on the time step between two results of the initial dataset and the duration over which each segment extends. Compared to a pure Fourier Transformation, the frequency resolution is therefore reduced by the division into (time) segments.
The result of the SPOD is a set of SPOD modes which each represent a spacial distribution of amplitudes and phase angles for all discrete frequencies. Using the SPOD modes, key features of the flow can be reconstructed.
Due to the computational costs, a trade-off between frequency resolution (length of the individual segments) and number of SPOD modes (number of segments) is necessary. Taking into account the frequencies of interest, a block length of 10 ms was used covering 5 periods at 500 Hz and 30 at 3000 Hz.
The whole algorithm was published by Schmidt [11] as a MATLAB-Code, which was used for the presented study.
4.2. Visualization of Dominant Flow Structures Using SPOD
Following the experimental observations in Figure 3b, numerical simulations were conducted and transient wall pressures on the valve head and diffuser as well as the pressure field on a cross section of the diffuser were recorded. Afterwards a SPOD analysis was performed for the transient surface data in case of the CFD and for the data from eight pressure transducers (sensor positions indicated in Figure 4: four sensors on valve head surface (circumferential distribution declared Heads 1–4; Head 1 bottom right/Head 3 bottom left) and four sensors in the lower half of the diffuser downstream of Head 3 (declared Diffuser 3/1–3/4; axial distribution in streamwise direction)) in case of the experiment. To be consistent, the 10 ms window size of the (time) segments and the overlap of 5 ms were used for both CFD and experimental datasets to obtain the same frequency resolution. As a result, each CFD segment covers 2000 samples (time step of s) while the experiment covers only 640 samples (sample rate of 64 kHz). In both cases, the default window function (Hamming-Window) was applied. The resulting spectra of SPOD eigenvalues are shown in Figure 5 as a fraction of the overall modal energy.
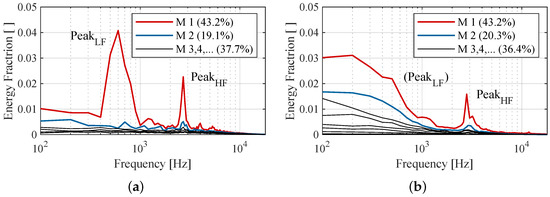
Figure 5.
Normalized eigenvalues of SPOD modes for OR = 0.05/PR = 0.2: (a) CFD (approximately 40,000 grid points); and (b) experiment (eight pressure sensors).
Two peaks appear in the energy spectrum of the CFD data in Figure 5a for frequencies at 500 Hz to 700 Hz (declared as Peak for low frequency) and 2500 Hz to 2900 Hz (declared as Peak for high frequency). For the experimental analysis, only the second peak is clearly visible in Figure 5b while the first peak cannot be clearly gathered due to the limited sensor positions. At the discussed operating point, the position of the four head sensors Heads 1–4 is within the region of detachment (visible in Figure 4) leading to partly non-periodic low frequency effects. Taking into account that the experimental SPOD uses only eight discrete positions while the transient data of the CFD are captured at about 40,000 positions, the energy spectra compare well. The first mode () of the SPOD analysis of both CFD and experiment captures already about 40% and together with the second SPOD mode, which contributes a significant amount to the second peak in both cases, roughly of the overall modal energy are represented. Concluding that a majority of the pressure oscillation can be represented by the first two modes, the sum of and is used for the following reconstructions.
For a validation that the overall pressure characteristic is captured by the two frequency bands at Peak and Peak, exemplary pressure signals corresponding to sensor Diffuser 3/3 are shown in Figure 6 for both CFD and experimental results. While the raw signal in both cases shows a rather chaotic trend, the application of bandpass filters according to the two peaks accurately captures the essential pressure trend. Throughout the illustrated time period in Figure 6a,b, a continuous oscillation at Peak and a superposition of amplitudes associated with Peak can be identified by the two bandpass filters. For both frequencies, temporal excitations and extinctions are observed. Based on the good agreement, the two dominating frequency bands are used to visualize the reoccurring pressure oscillations and their propagation in the flow field from the numerical SPOD analysis.

Figure 6.
Comparison of the raw and bandpass-filtered pressure trends for sensor location Diffuser 3/3: (a) CFD; and (b) experiment.
4.3. Axial Pressure Excitation at 600 Hz
Based on the discussion of Figure 5 and Figure 6, a superposition of the first two SPOD modes is used for the reconstruction of the flow field. Because temporal excitations are observed and the peaks in the energy spectrum include more than one frequency, a narrow band around the prominent frequency is analyzed to reproduce this behavior.
For Peak at 600 Hz, the reconstructed pressure field for and frequencies of 500 Hz to 700 Hz is shown in Figure 7 across one period (). The individual plots show the pressure distribution on the valve head (Cartesian plot using lateral coordinates; normal view onto the valve head against flow direction), the diffuser wall (polar plot using the axial position as the radial coordinate; Angle consistent to the valve head) as well as a cross section of the diffuser (Cartesian plot of the cross section of the diffuser pressure field. Location of the plane indicated by the horizontal solid line on the head and diffuser wall) based on the SPOD reconstruction. At first sight, the pressure amplitude at this frequency shows an almost axisymmetric oscillation of the pressure field across the whole diffuser in axial direction. The strongest pressure amplitudes occur within the supersonic core and suggest a strong vertical oscillation of the shock.
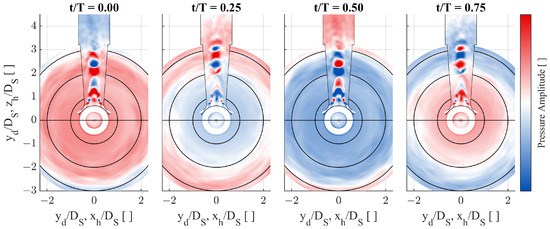
Figure 7.
Reconstructed pressure evolution at 600 Hz (CFD, M1 + 2, f = (600 ± 100) Hz, T = 1/600 s).
The comparison of the reconstructed flow field in Figure 8a supports this finding and shows a significant vertical displacement of the strong shock across half a period as marked by the dashed line. For the first time step in Figure 8a, the width of the supersonic core in the lower half is increased, and a small normal shock can be observed in the center (). The flow condition at this time is comparable to the instantaneous flow in Figure 4b. Linked to the strong oscillation of the shock, the pressure in the recirculation zone around the core flow increases periodically and interacts with the jets at the diffuser inlet. Along with the pressure oscillation in the lower half of the diffuser, reoccurring impingements on the valve head are observed and periodic axial forces are predicted at this frequency.
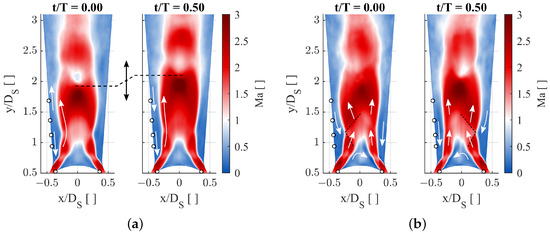
Figure 8.
Reconstructed flow field from the SPOD analysis (CFD, sensor positions: ∘): (a) M1 + 2, f = (600 ± 100) Hz, T = 1/600 s; and (b) M1 + 2, f = (2700 ± 200) Hz, T = 1/2700 s.
Following the temporal evolution of the pressure field, the recirculation zone around the supersonic jet up to the height of the strong shock seems to behave as a spring in axial direction, and an excitation across several periods with temporally changing flow directions near the wall (indicated by the arrows) can be observed due to the superposition of the different frequencies.
4.4. Lateral Pressure Excitation at 2700 Hz
For the second dominant frequency at Peak, the distribution of pressure amplitudes illustrated in Figure 9 shows a totally different pattern. Especially in the lower half of the diffuser, the reconstruction at Hz shows a pure lateral excitation, which is also visible in the corresponding flow field in Figure 8b.
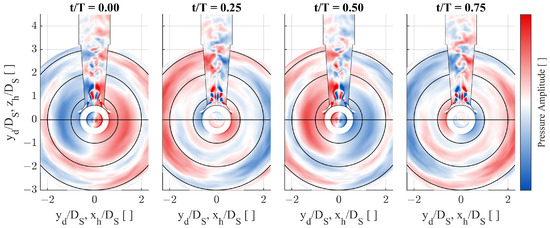
Figure 9.
Reconstructed pressure evolution at 2700 Hz (CFD, M1 + 2, f = (2700 ± 200) Hz, T = 1/2700 s).
The analysis of the temporal propagation suggests that an interaction of the first lateral pressure mode and the shock structure causes a resonance. It is expected that the lateral displacement of the strong shock causes a compression of the recirculation zone and temporally increases the downward component of the near wall velocity. Along with a local increase of the pressure, the impingement onto the incoming jet at the diffuser entry causes a stronger deflection from the wall, as indicated by the arrows in Figure 8b. As the jets are further deflected towards the contrary side, the supersonic core gets constricted by strengthened oblique shocks as indicated by black dashed lines. As the lateral component is passed downstream due to the momentum of the incoming jets, the compression of the recirculation zone on the opposite side initiates the contrary deflection.
Across multiple periods, temporal circumferential propagations of this disturbance occur as visible on the valve head in Figure 9. Similar to the axial excitation, dominating frequencies of the lateral force spectrum of the simulation match the SPOD results and may cause lateral excitations for elastic valve geometries. Even though amplitudes are small, experimental data confirm this assumption and show an increased vibration level at this frequency.
4.5. Comparison of Numerical Findings to Experimental Data
A comparison of the findings to test data is difficult as the experimental data are limited to the few wall pressure probes. Using raw numerical and experimental data, time histories, as shown in Figure 6, can be used for a first comparison of the experiment and numerical calculation. With the introduction of pure Fourier Transformations, frequency spectra similar to Figure 5 provide additional results and the occurrence of periodic phenomena can be revealed or confirmed.
Seeking for a further validation of numerical findings and motivated by the similarity in Figure 5, the SPOD algorithm is used to correlate the experimental pressure signals.
Using experimental data, SPOD modes were computed and resulting amplitudes assessed. Because the reconstruction of a full pressure field is not possible, the comparison focuses on the temporal evolution of amplitudes among the sensor positions. Using diffuser sensor Diffuser 3/1 as a reference, histograms of the phase lag between the sensors have been computed. To obtain a better resolution, the window size of the SPOD as well as the overlap were increased by a factor of 20 compared to the analysis in Figure 5b. In this case, the first mode captures roughly 55% of the overall energy and the phase lag was computed from this mode only.
While the assessment of complex amplitudes from a pure Fourier Transformation results in a far less clearer view, the SPOD results in Figure 10 show clear correlations among the different sensors. Dominant phase lags of the four circumferentially distributed valve head pressure sensors are provided in the first row and phase lags of the four diffuser wall pressure sensors downstream of valve Head Sensor 3, as indicated in Figure 4 in the second row.
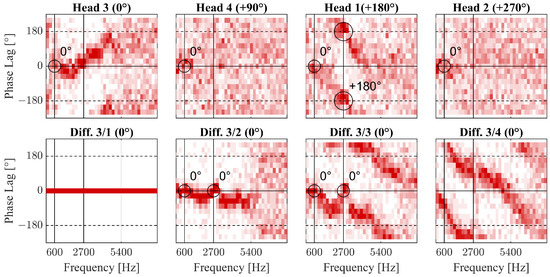
Figure 10.
Histograms of the phase lag among the pressure sensors based on the SPOD analysis of the experimental data (M1).
Focusing on the axial excitation at 600 Hz, a simultaneous pressure amplitude across the circumference is expected. Comparing the histograms of the phase lag, this numerical finding can be confirmed by the experiment. All valve head sensors as well as the two downstream diffuser sensors show a dominating phase lag of 0 at 600 Hz.
Clearly visible in the diffuser, the phase lag increases almost linearly for higher frequencies (assuming constant fluid properties and thus a constant speed of sound a, the phase lag can be estimated from the distance and the frequency f as ). At 2700 Hz, the trend is interrupted and in alignment to the numerical SPOD analysis a phase lag of 0 is observed for the first three diffuser sensors. Because the three sensors are in phase even though based on the distance a phase lag is expected, the dominant pressure propagation at this frequency must evolve in lateral direction. The valve head sensors support this thesis as sensor Head 3 shows a similar yet slightly positive phase lag and Head 1 on the opposite side confirms the lateral phase lag of 180. The experiments therefore align with the numerical findings, and the results are considered plausible.
5. Conclusions
Despite the numerical progress and the advance in turbulence modeling, the prediction of complex flow structures can still be an issue. With the requirement of higher order numerics, grid resolutions and time steps, simulations often capture only a short period of time due to the high computational cost. As a result of highly unsteady and non-periodic flows, the evaluation of numerical results can be challenging and statistical approaches have proven themselves as powerful tools in the analysis of unsteady flows.
After validation of the numerical setup, the unsteady flow of a critical operating point in a simplified steam turbine control valve is assessed. Using Spectral Proper Orthogonal Decomposition, strong temporal pressure oscillations previously observed in the experiment were isolated and corresponding flow fields were reconstructed. While the accessibility of the experiment does not allow a direct comparison of flow fields, several analogies to experimental data support the credibility of the numerical findings.
For two dominant frequencies, strong forces are predicted by the CFD as a result of temporally excited pressure oscillations and vibrations can be triggered. Experiments support this thesis as an increased lateral vibration level is observed for the lateral pressure excitation.
With the SPOD analysis, the identification and isolation of the dominant structures from the chaotic and unsteady flow was enabled and couplings with the supersonic flow are observed. The method has shown its great capabilities of isolating dominant structure which helps the understanding of fundamental phenomena. For future numerical analyses of elastic valve configurations, SPOD is expected to enhance the understanding of coupling mechanisms of fluid–structure interactions, promoting measures to increase the operational stability of the valves.
Author Contributions
Conceptualization, all; methodology, C.W., M.L. and R.M.; software, C.W.; validation, C.W. and M.L.; formal analysis, C.W.; investigation, C.W.; resources, C.W.; data curation, C.W.; writing—original draft preparation, C.W.; writing—review and editing, C.W. and M.L.; visualization, C.W.; supervision, M.L. and R.M.; project administration, R.M.; and funding acquisition, R.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), founding code MA 4922/7-1.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The authors wish to gratefully acknowledge funding and support by the Deutsche Forschungsgemeinschaft (DFG) under the founding code MA 4922/7-1. The computations were performed on the Bull HPC-cluster at the Center for Information Services and High Performance Computing (ZIH) at TU Dresden.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Abbreviations | |
| CFD | Computational Fluid Dynamics |
| LES | Large Eddy Simulation |
| Peak | Frequency Peak at ≈ 600 Hz |
| Peak | Frequency Peak at ≈ 2700 Hz |
| POD | Proper Orthogonal Decomposition |
| SAS | Scale Adaptive Simulation |
| SAS-F | SAS with zonal LES model |
| SPOD | Spectral POD |
| SST | Shear Stress Transport |
| Variables | |
| Diffuser opening angle | |
| Diffuser throat diameter | |
| Seat diameter | |
| f | Frequency |
| H | Valve Lift |
| M | SPOD Mode |
| Mach Number | |
| Opening Ratio | |
| p | Pressure (s static, t total) |
| Pressure Ratio | |
| Head radius | |
| Seat (transition) radius | |
| t | Time |
| T | Period of a given frequency |
| T | Temperature (t total) |
| Spacial coordinates |
References
- Domnick, C.B.; Brillert, D. Flow-Induced Steam Valve Vibrations—A Literature Review of Excitation Mechanisms, Preventive Measures, and Design Improvements. J. Eng. Gas Turbines Power 2019, 141, 051009. [Google Scholar] [CrossRef]
- Morita, R.; Inada, F.; Mori, M.; Tezuka, K.; Tsujimoto, Y. CFD Calculation and Experiments of Unsteady Flow on Control Valve. In Proceedings of the ASME 2004 Heat Transfer/Fluids Engineering Summer Conference, Charlotte, NC, USA, 11–15 July 2004; pp. 51–58. [Google Scholar]
- Ziada, S.; Bühlmann, E.; Bolleter, U. Flow Impingement as an Excitation Source in Control Valves. J. Fluids Struct. 1989, 3, 529–549. [Google Scholar] [CrossRef]
- Yonezawa, K.; Ogi, K.; Takino, T.; Tsujimoto, Y.; Endo, T.; Tezuka, K.; Morita, R.; Inada, F. Experimental and Numerical Investigation of Flow Induced Vibration of Steam Control Valve. In Proceedings of the ASME 2010 7th International Symposium on Fluid-Structure Interactions, Flow-Sound Interactions, and Flow-Induced Vibration and Noise, Montreal, QC, Canada, 1–5 August 2010; pp. 575–583. [Google Scholar]
- Hardin, J.; Kushner, F.; Koester, S. Elimination of Flow-Induced Instability From Steam Turbine Control Valves. In Proceedings of the Thirty-Second Turbomachinery Symposiom, Houston, TX, USA, 8–11 September 2003; Texas A&M University, Turbomachinery Laboratories: Houston, TX, USA, 2003; pp. 99–108. [Google Scholar]
- Domnick, C.B. Untersuchung Des ströMungs-Und Strukturdynamischen Verhaltens von Dampfturbineneinlassventilen im Teillastbetrieb. Ph.D. Thesis, Universität Duisburg-Essen, Duisburg, Germany, 2017. [Google Scholar]
- Towne, A.; Schmidt, O.T.; Colonius, T. Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J. Fluid Mech. 2018, 847, 821–867. [Google Scholar] [CrossRef]
- Windemuth, C.; Lange, M.; Mailach, R. Introduction of a Novel Test Rig for the Investigation of Fluid-Structure Interaction Effects in Steam Turbine Control Valves using an Elastic Model. In Proceedings of the 13th European Conference on Turbomachinery Fluid Dynamics & Thermodynamics, Lausanne, Switzerland, 8–12 April 2019. [Google Scholar]
- Windemuth, C.; Lange, M.; Mailach, R. Investigation of Unsteady Pressure Fluctuations in a Simplified Steam Turbine Control Valve. In Proceedings of the ASME Turbo Expo 2020, 21–25 September 2020. [Google Scholar]
- Zhang, D.; Engeda, A.; Hardin, J.R.; Aungier, R.H. Experimental Study of Steam Turbine Control Valves. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2004, 218, 493–507. [Google Scholar] [CrossRef]
- Schmidt, O.T. Spectral Proper Orthogonal Decomposition (SPOD). 2018. Available online: https://de.mathworks.com/matlabcentral/fileexchange/65683-spectral-proper-orthogonal-decomposition-spod (accessed on 8 February 2019).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).