Gradient-Free and Gradient-Based Optimization of a Radial Turbine †
Abstract
1. Introduction
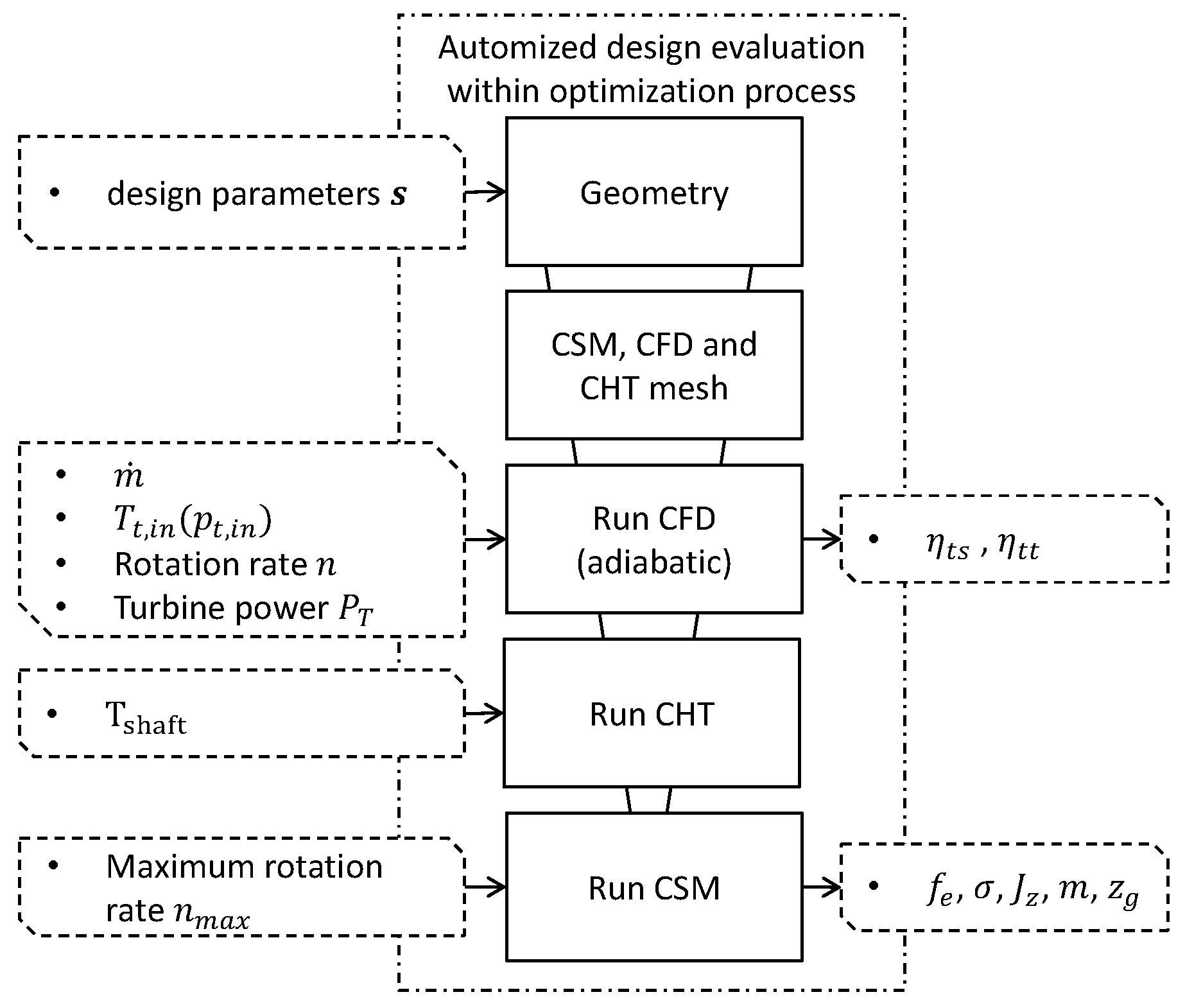
2. Gradient-Free Optimization
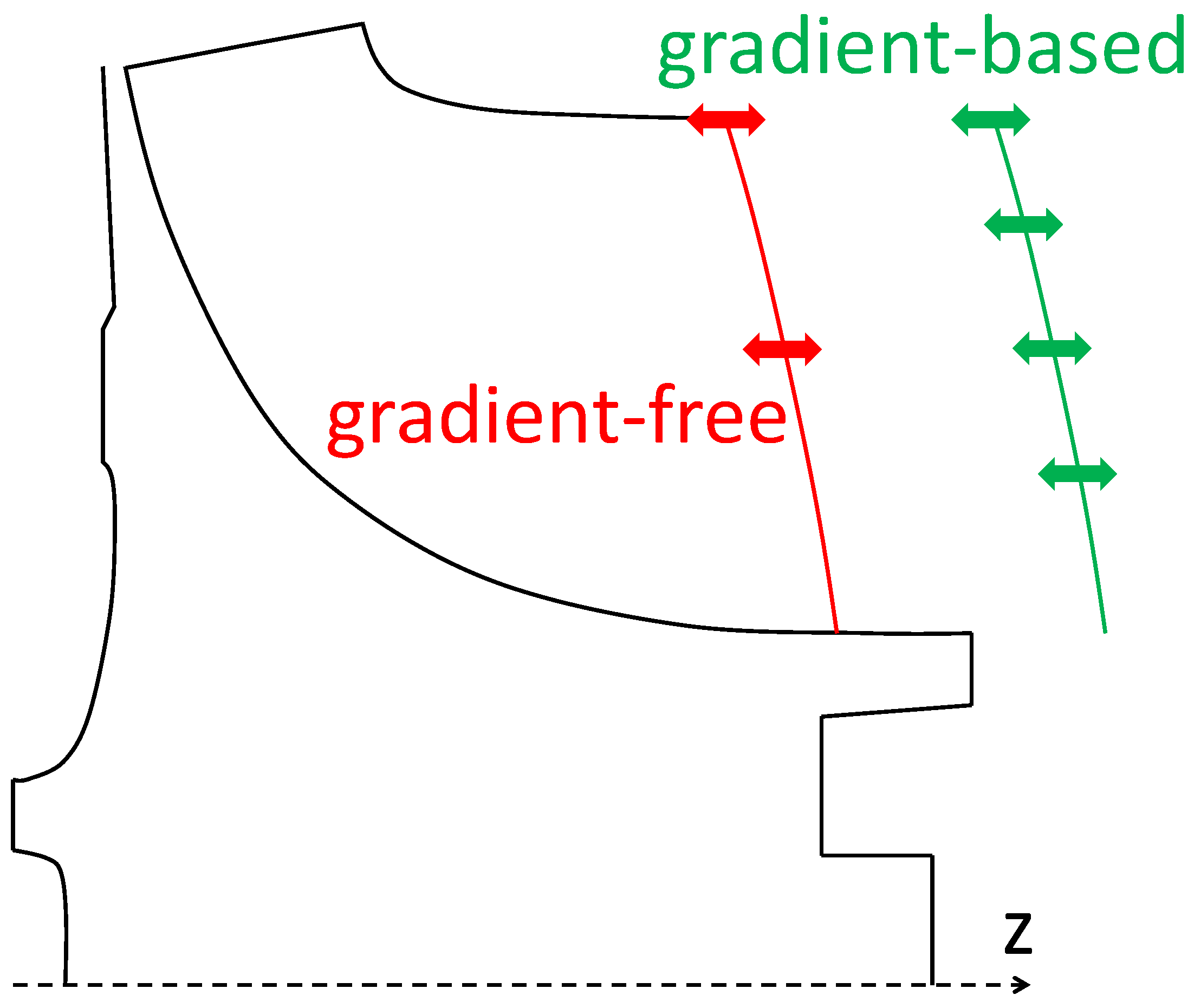
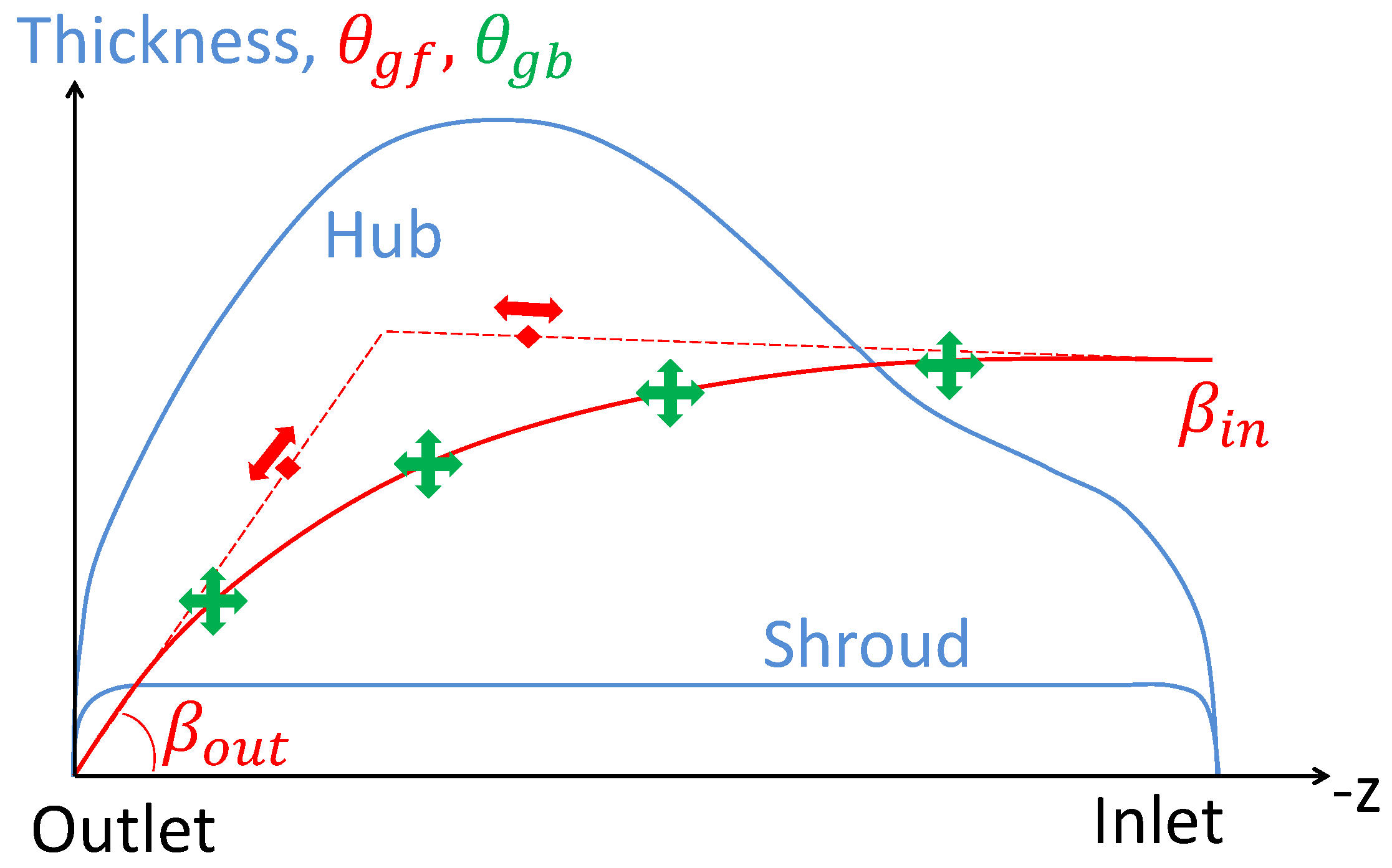
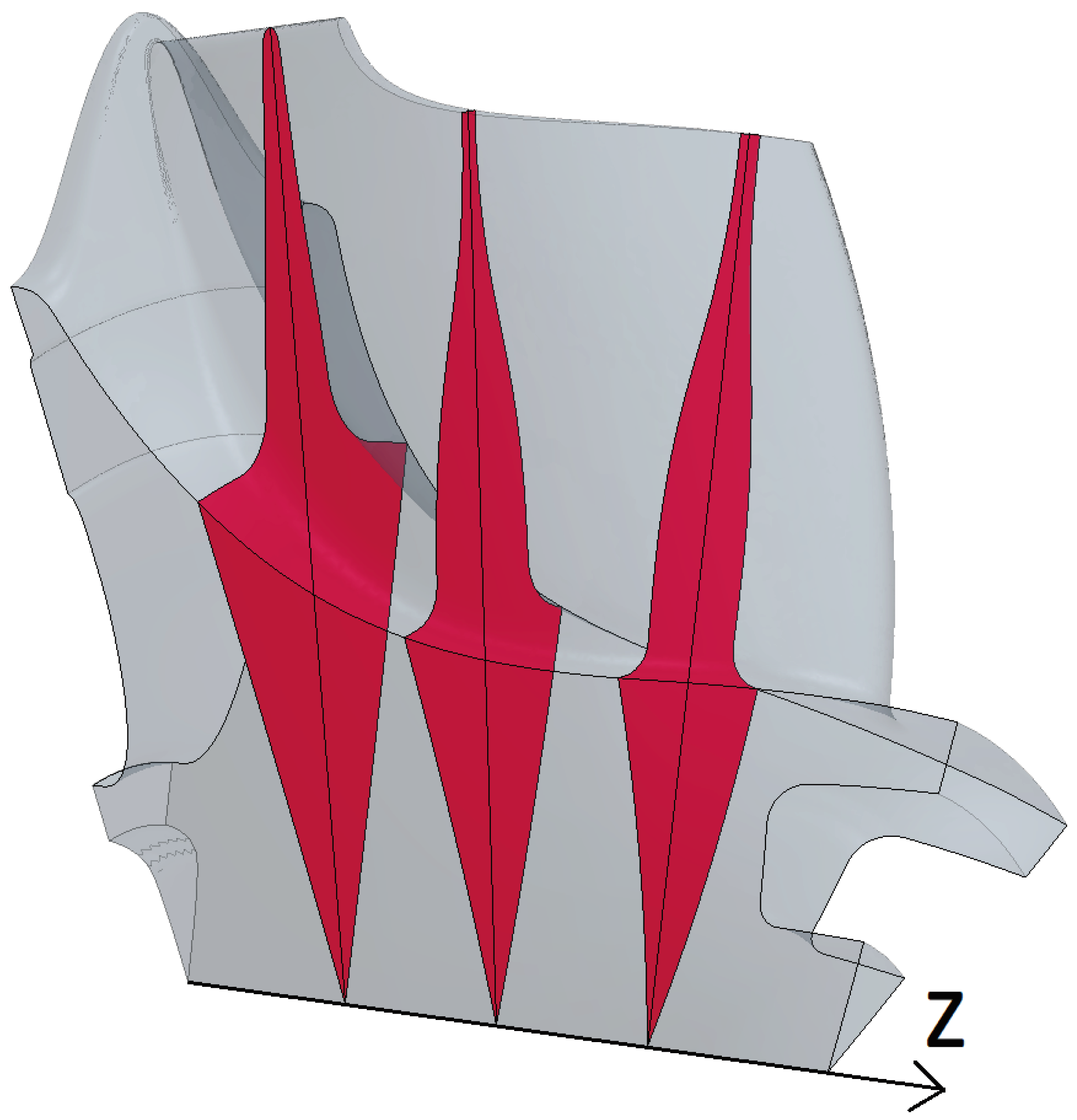
2.1. Geometry Parametrization
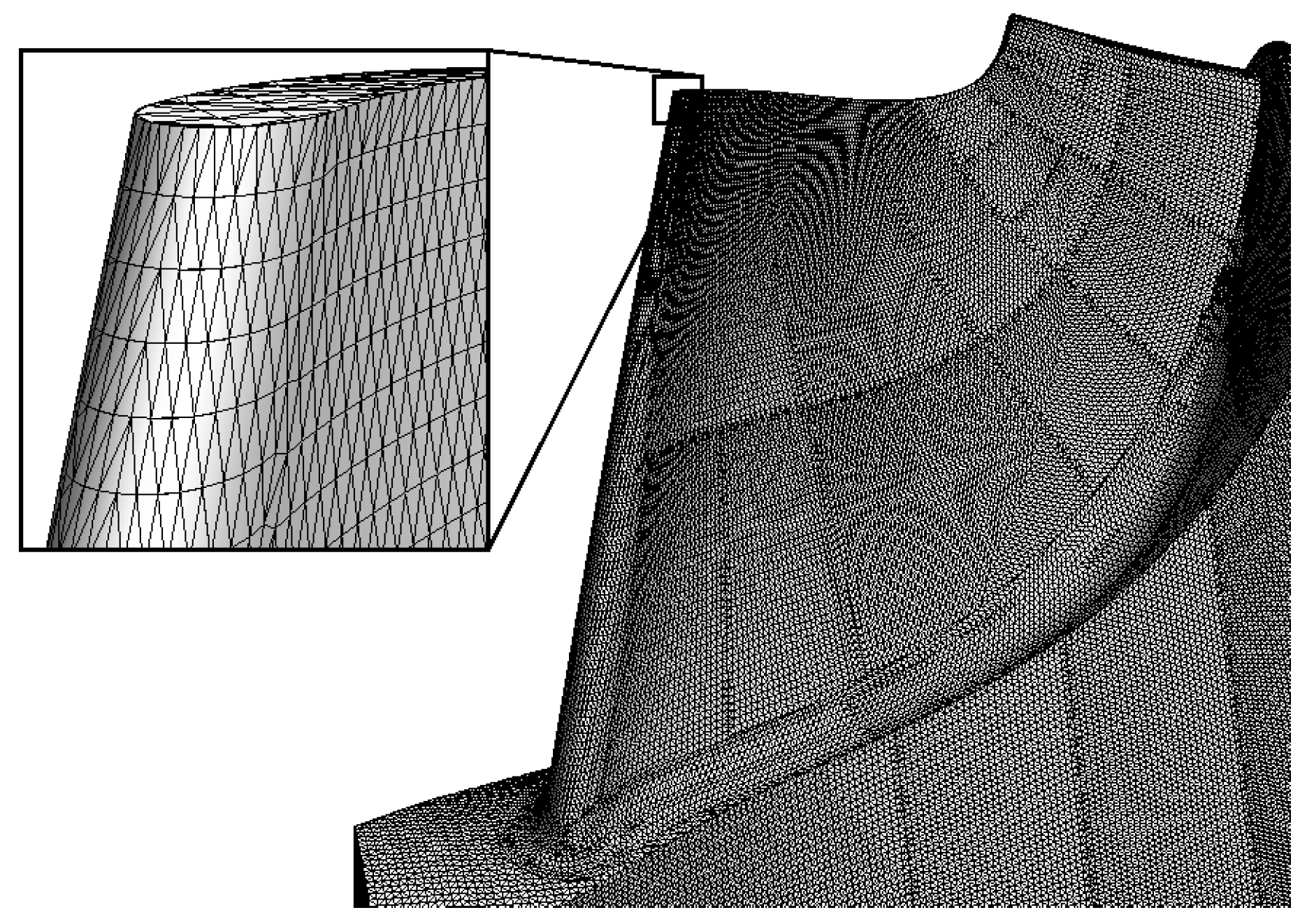
2.2. Meshes
2.3. Simulation Setup
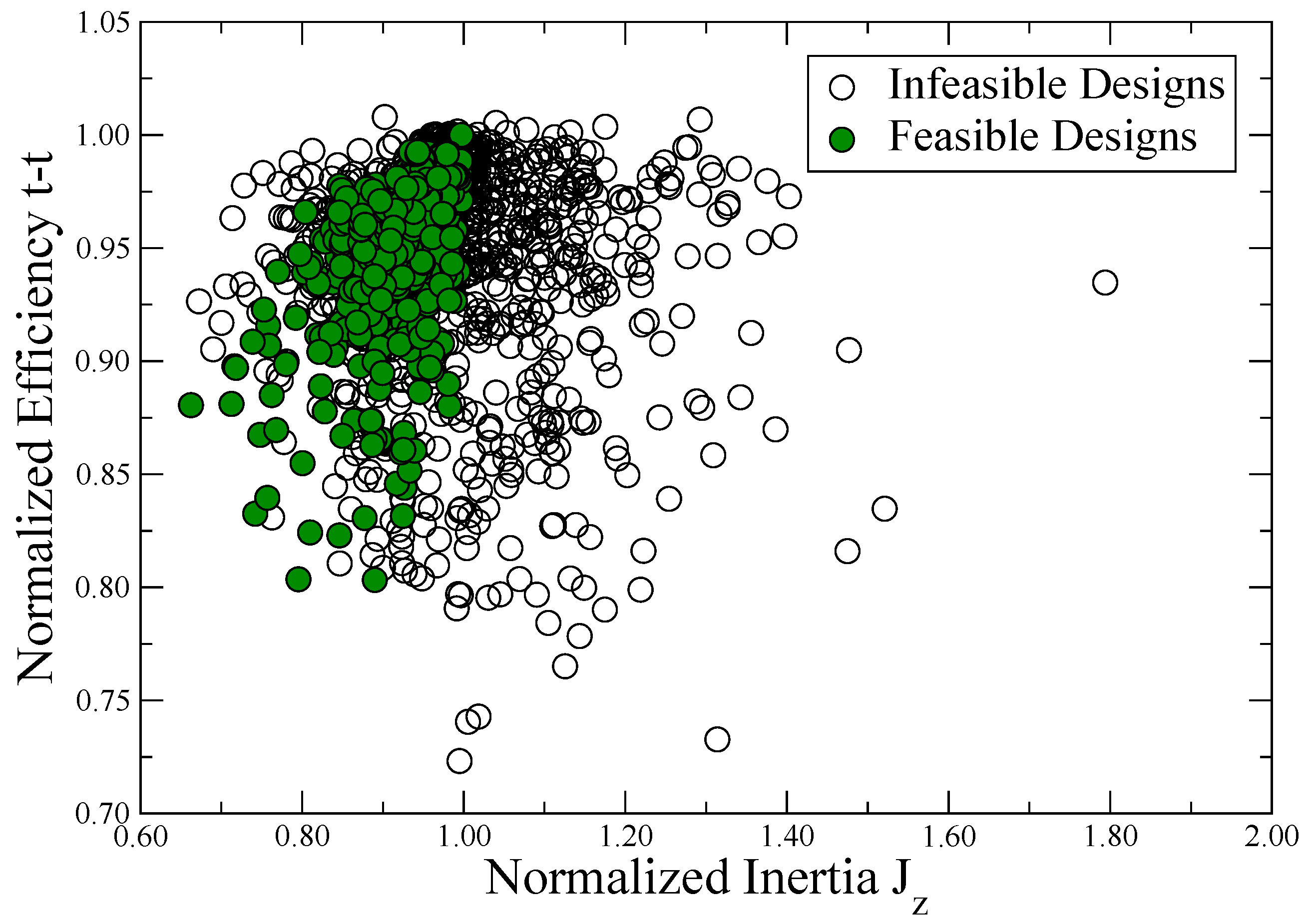
2.4. Objectives and Constraints
2.5. Optimization Results
3. Gradient-Based Optimization
3.1. Altered Geometry Parametrization and Simulation Setup
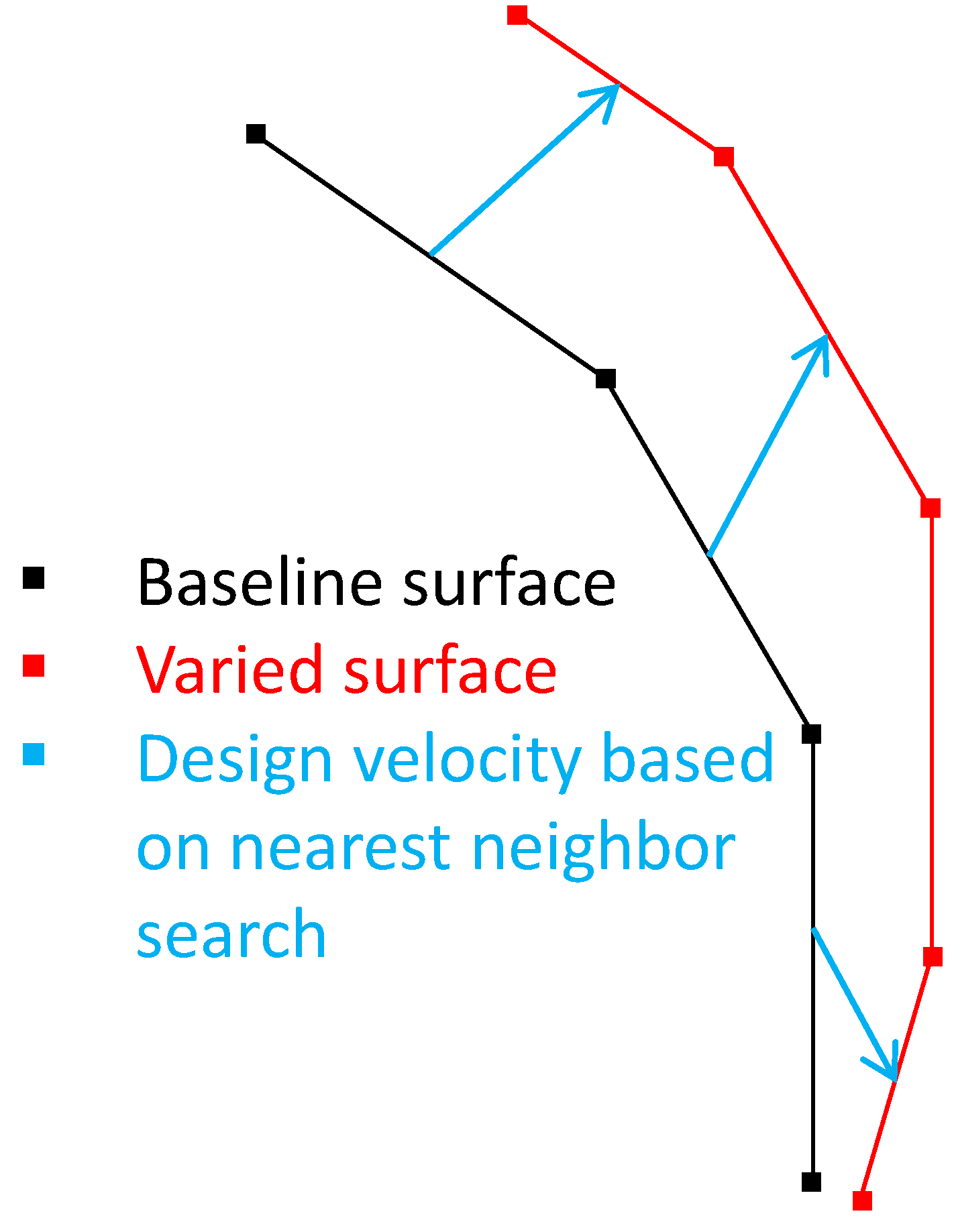
3.2. Design Velocity
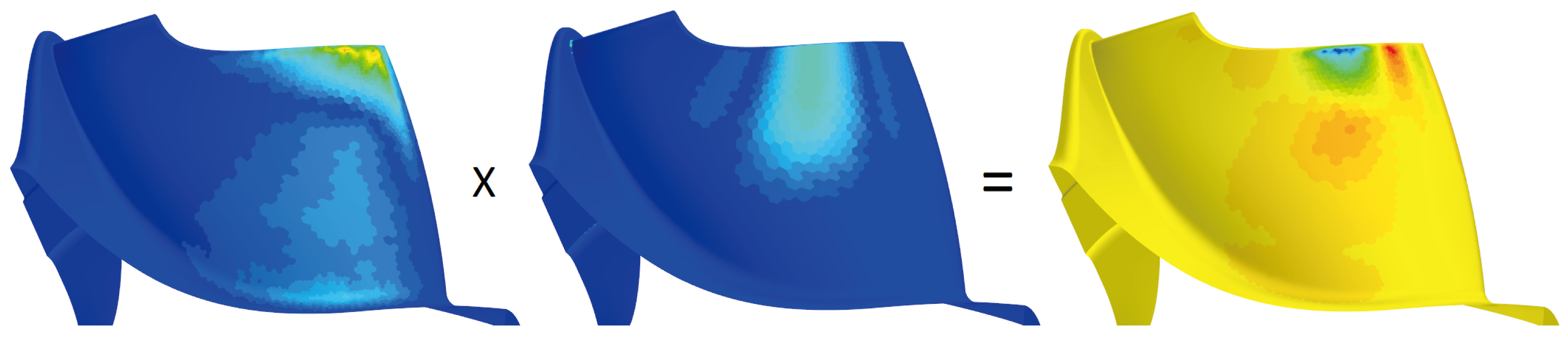
3.3. Surface Sensitivity
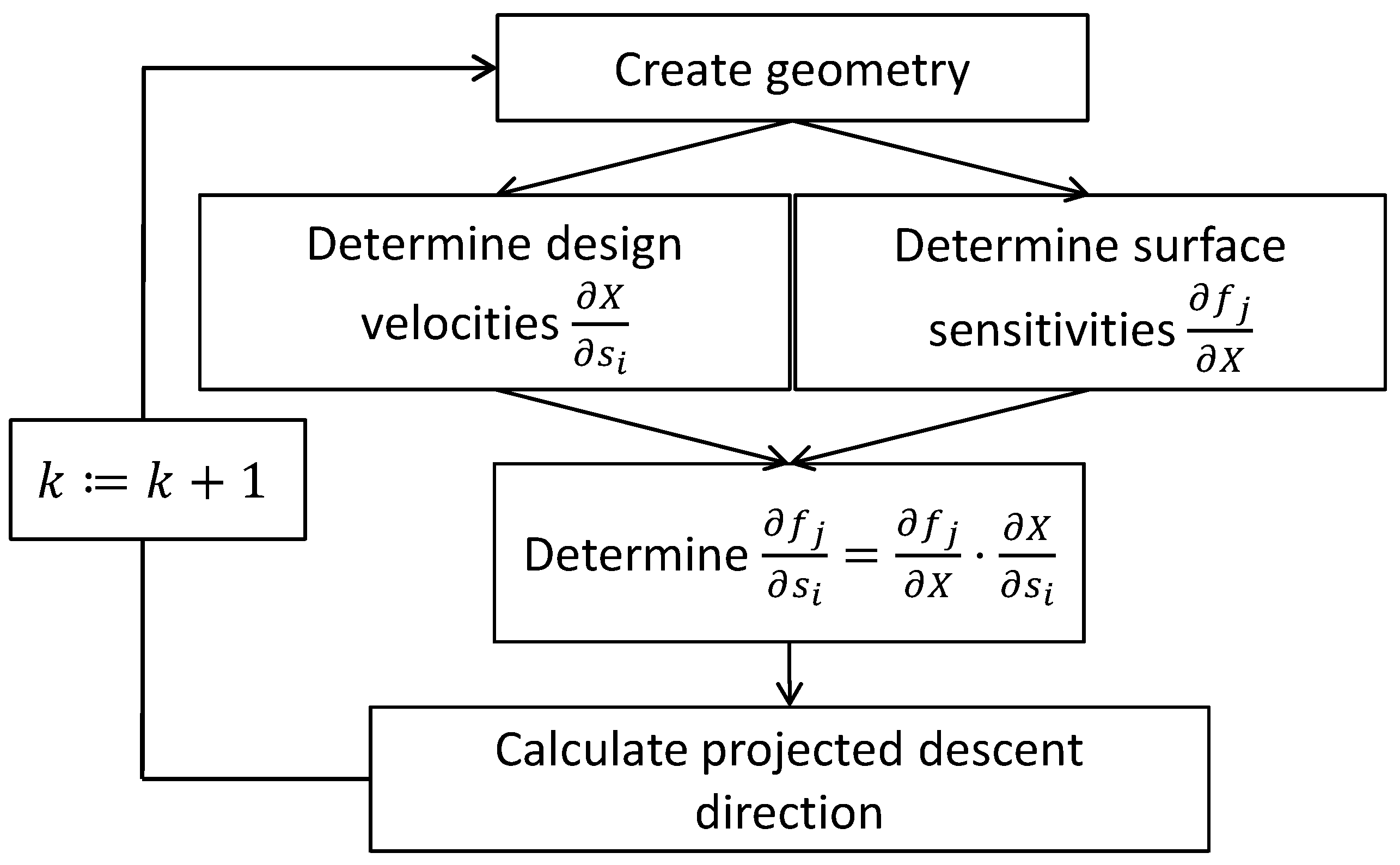
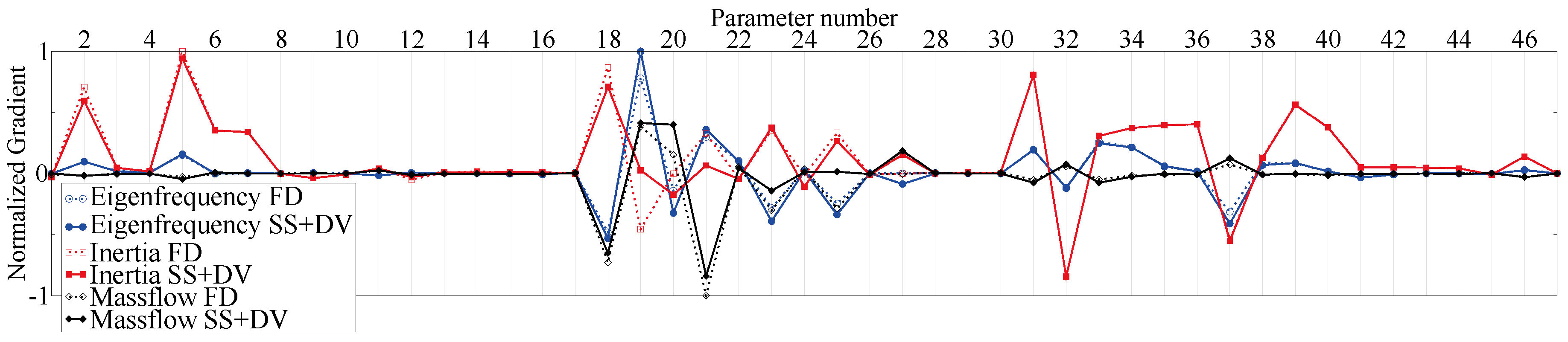
3.4. Gradient Calculation
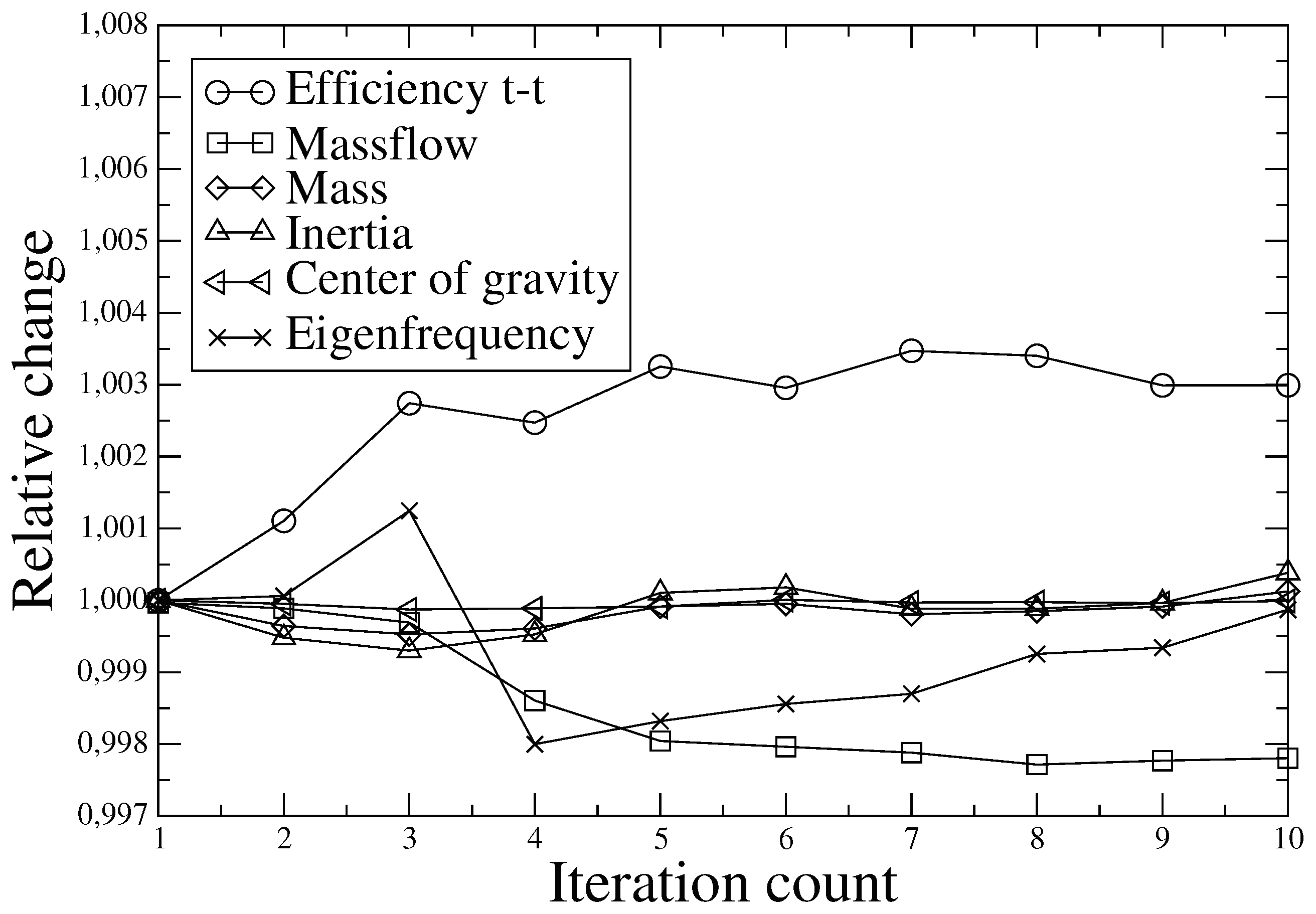
3.5. Optimization Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Latin | |
| Extrapolated relative error | |
| Eigenfrequency | |
| Cost function j | |
| h | Specific enthalpy |
| J | Inertia |
| K | Stiffness matrix |
| Mass flow | |
| m | Rotor mass |
| M | Mass matrix |
| n | Rotation rate |
| p | Pressure |
| Parameter set | |
| T | Temperature |
| v | Velocity |
| Center of gravity | |
| Greek | |
| Isentropic exponent | |
| Efficiency | |
| Stress tensor | |
| Subscripts | |
| gradient-based | |
| gradient-free | |
| s | Static quantity |
| t | Stagnation quantity |
| Abbreviations | |
| CFD | Computational Fluid Dynamics |
| CHT | Conjugate Heat Transfer |
| CSM | Computational Structural Mechanics |
| GA | Genetic algorithm |
| RANS | Reynolds-averaged Navier–Stokes |
| STL | Standard Tesselation Language |
References
- Verstraete, T. Multidisciplinary Turbomachinery Component Optimization Considering Performance, Stress, and Internal Heat Transfer. Ph.D. Thesis, von Karman Institute for Fluid Dynamics—University of Gent, Gent, Belgium, 2008. [Google Scholar]
- Müller, L.; Alsalihi, Z.; Verstraete, T. Multidisciplinary Optimization of a Turbocharger Radial Turbine. J. Turbomach. 2013, 135. [Google Scholar] [CrossRef]
- Peter, J. Numerische Untersuchung und Optimierung des Laufrades einer Pkw-Abgasturboladerturbine. Ph.D. Thesis, Leibniz Universität Hannover, Hannover, Germany, 2016. [Google Scholar]
- Khairuddin, U.B.; Costall, A.W. Aerodynamic Optimization of the High Pressure Turbine and Interstage Duct in a Two-Stage Air System for a Heavy-Duty Diesel Engine. J. Eng. Gas Turbines Power 2018, 140. [Google Scholar] [CrossRef]
- Verstraete, T.; Müller, L.; Müller, J.D. Multidisciplinary Adjoint Optimization of Turbomachinery Components Including Aerodynamic and Stress Performance. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar]
- Schwalbach, M.; Verstraete, T.; Müller, L.; Gauger, N. CAD-Based adjoint multidisciplinary optimization of a radial turbine under structural constraints. In Proceedings of the Montreal 2018 Global Power and Propulsion Forum, Zug, Switzerland, 7–9 May 2018. [Google Scholar]
- Haftka, R.T.; Gürdal, Z.; Kamat, M. Elements of Structural Optimization (Solid Mechanics and Its Applications); Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130. [Google Scholar] [CrossRef]
- Pucher, H.; Zinner, K. Aufladung von Verbrennungsmotoren: Grundlagen, Berechnungen, Ausführungen (German Edition); Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Dhondt, G.; Wittig, K. Calculix: A Free Software Three-Dimensional Structural Finite Element Program; MTU AeroEngines: Munich, Germany, 1998. [Google Scholar]
- Montrone, T.; Turco, A.; Rigoni, E. FAST Optimizers: General Description; Esteco Technical report; Esteco: Trieste, Italy, 2014. [Google Scholar]
- Verstraete, T.; Müller, L.; Müller, J.D. CAD-Based Adjoint Optimization of the Stresses in a Radial Turbine. In Proceedings of the ASME Turbo Expo 2017, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar]
- Peter, J.E.; Dwight, R.P. Numerical sensitivity analysis for aerodynamic optimization: A survey of approaches. Comput. Fluids 2010, 39, 373–391. [Google Scholar] [CrossRef]
- KRATOS-Multiphysics. Available online: https://github.com/KratosMultiphysics/Kratos (accessed on 30 September 2018).
- Firl, M. Optimal Shape Design of Shell Structures. Ph.D. Thesis, Chair of Structural Mechanics—Technical University of Munich, Munich, Germany, 2010. [Google Scholar]
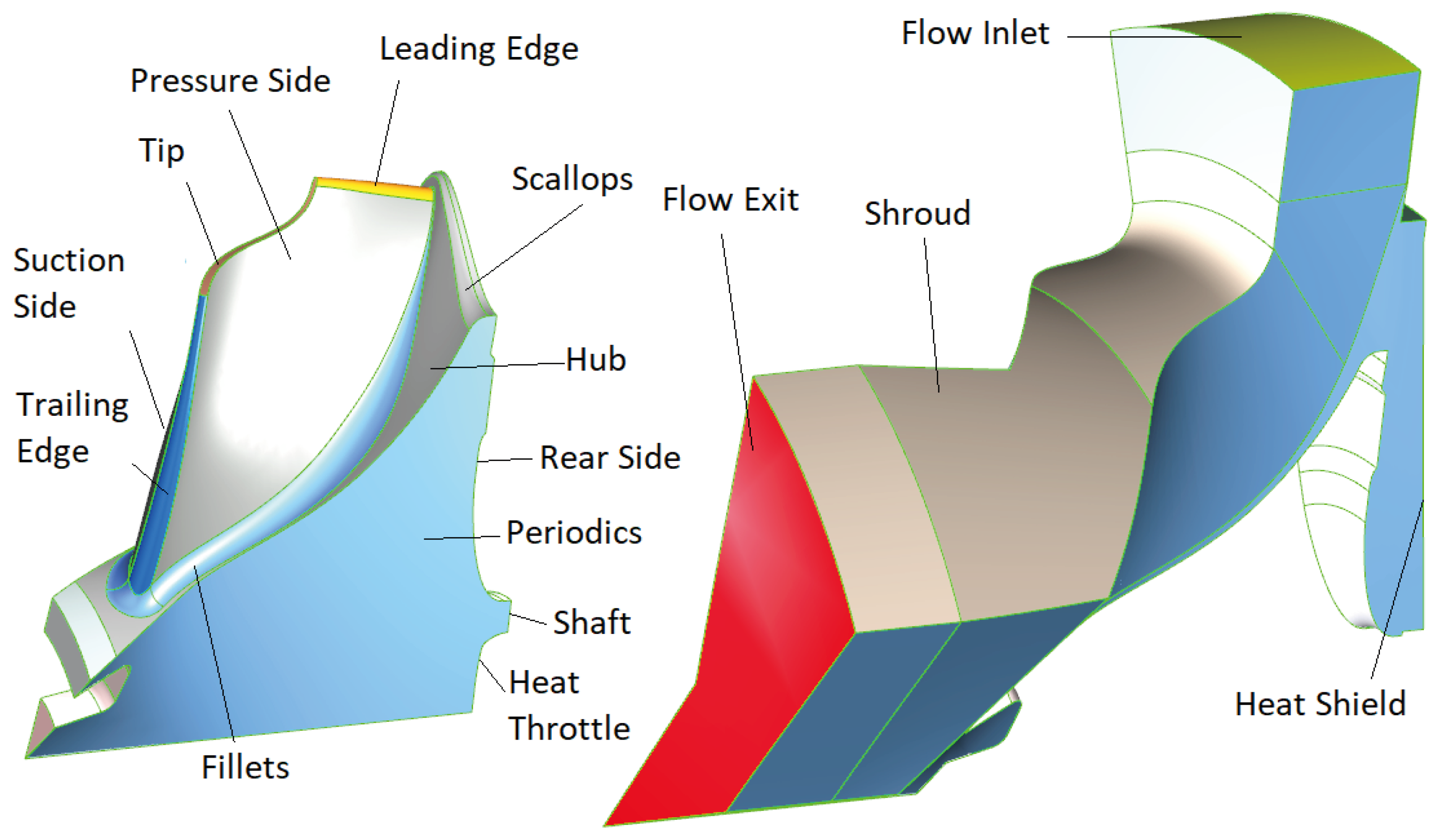
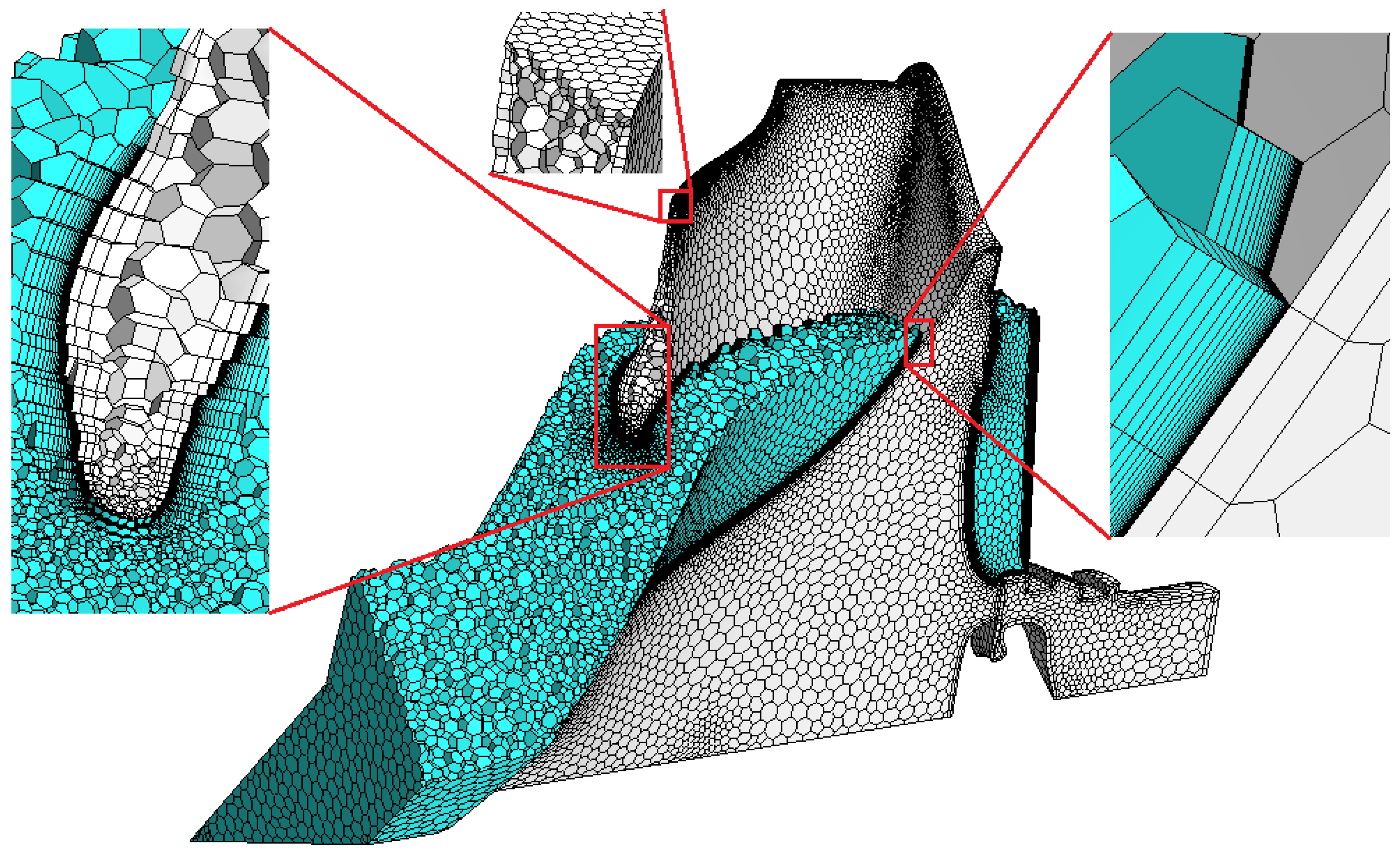
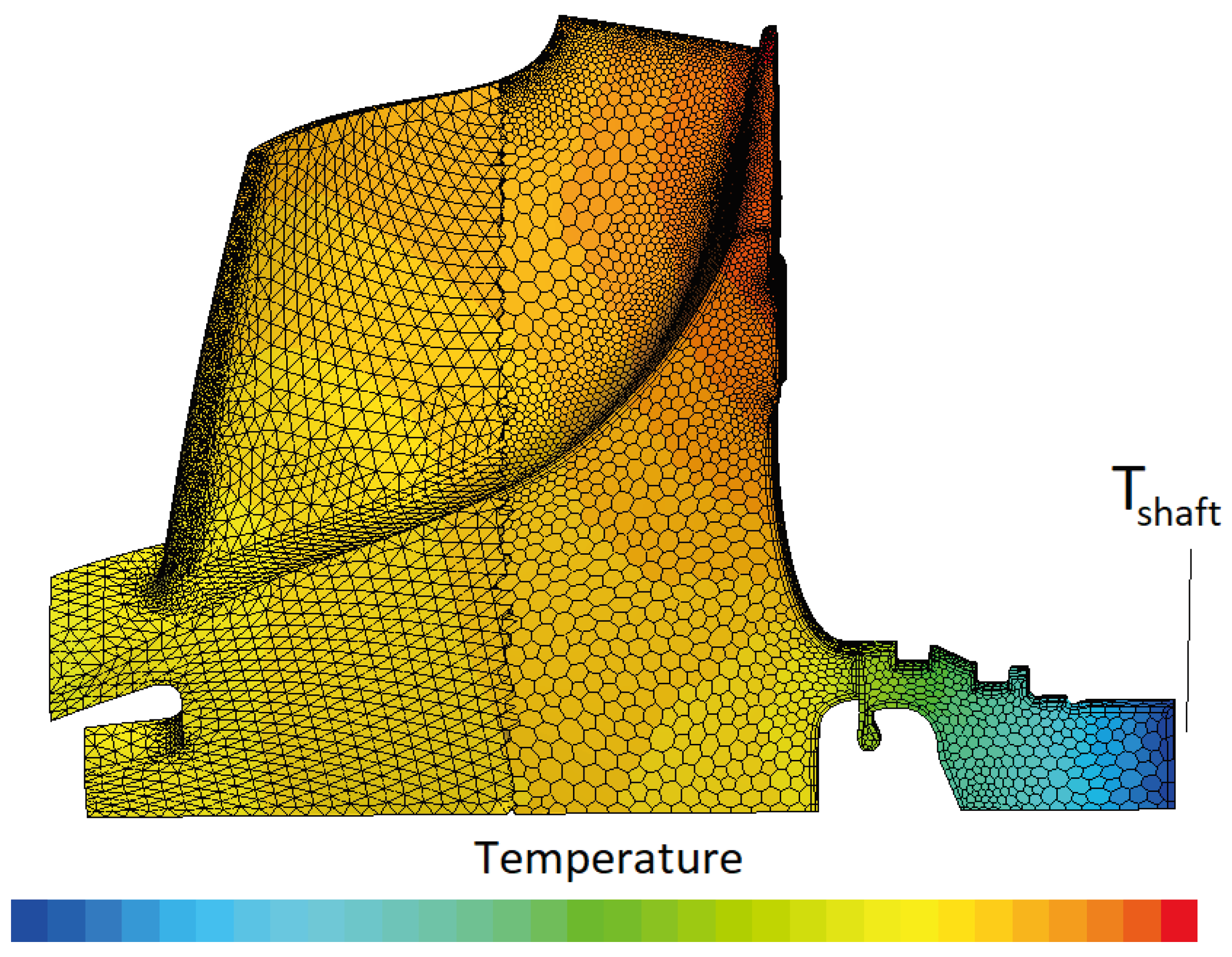
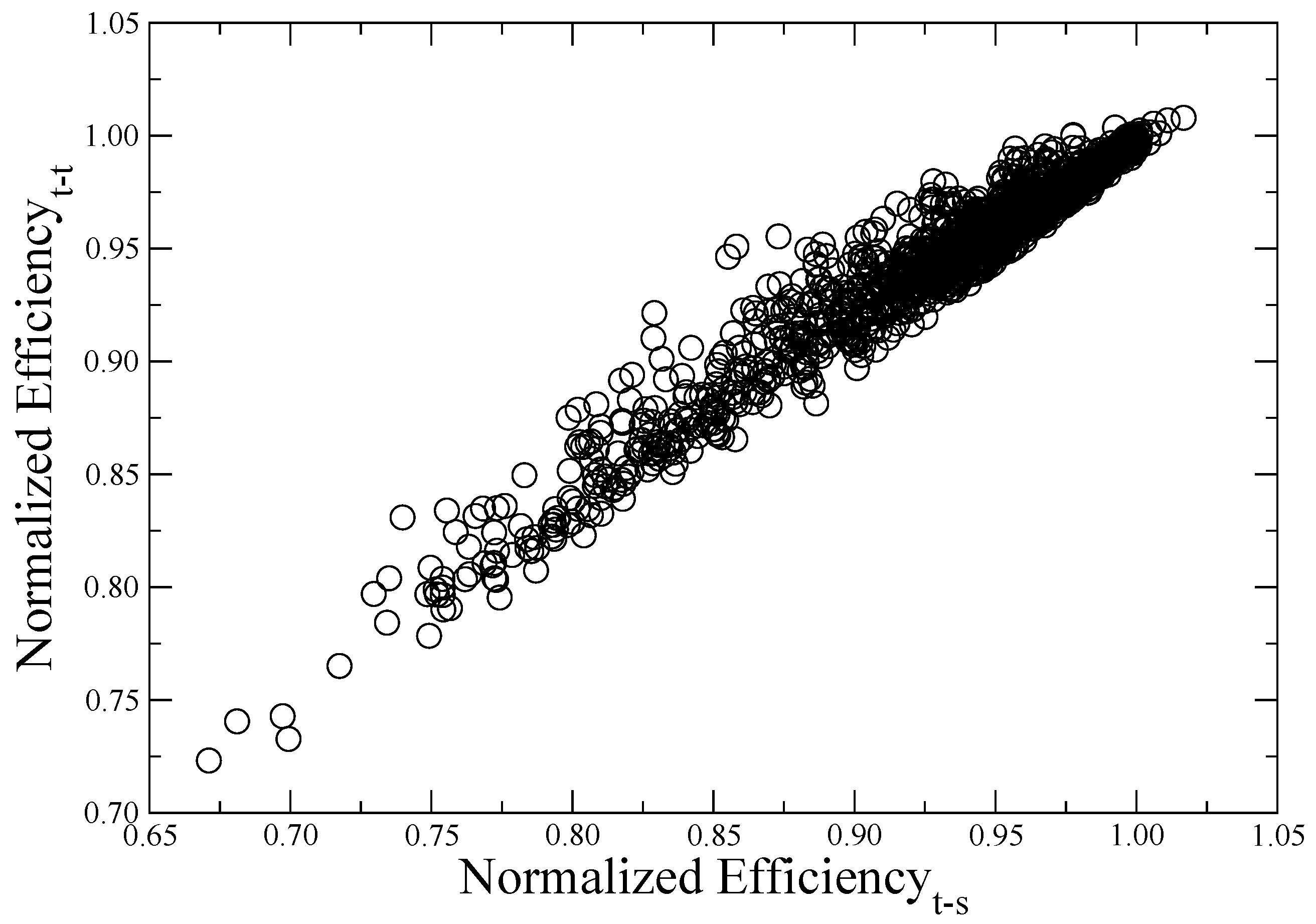

| Model Part | Parameters | Gradient-Free Setup | Gradient-Based Setup |
|---|---|---|---|
| Leading edge | 3 | 3 | |
| Trailing edge | 2 | 4 | |
| Meridional contour | Shroud contour | 4 | 4 |
| Hub contour | 4 | 4 | |
| Axial length | 1 | 1 | |
| Camber | -curve | 5 | 9 |
| At hub | 8 | 8 | |
| At shroud | 4 | 4 | |
| Thickness | Hub-to-shroud distribution | 4 | 4 |
| Leading edge ellipticity | 0 | 0 | |
| Trailing edge ellipticity | 3 | 3 | |
| Scallops | 3 | 3 | |
| Number of blades | 1 | 0 | |
| Sum | 42 | 47 |
| # Elements | [Hz] | [MPa] | [MPa] |
|---|---|---|---|
| 19051 | 6179.0 | 466.1 | 458.1 |
| 36419 | 6155.4 | 478.0 | 459.2 |
| 83585 | 6141.0 | 489.2 | 462.0 |
| 6130.0 | 516.7 | 466.0 | |
| in % | 0.18 | 5.31 | 0.85 |
| # Cells | [Pa] | [K] | |
|---|---|---|---|
| 230325 | 320,590.0 | 620.1 | 0.8349 |
| 572710 | 320,475.0 | 617.9 | 0.8451 |
| 1089061 | 320,282.6 | 617.2 | 0.8460 |
| 320,194.7 | 616.3 | 0.8463 | |
| in % | 0.03 | 0.14 | 0.03 |
| Simulation Step | Relative Wall Clock Time | #CPUs |
|---|---|---|
| Geometry generation | 0.04 | 1 |
| Meshing | 0.34 | 2 |
| CFD | 0.29 | 24 |
| CHT | 0.23 | 24 |
| CSM | 0.10 | 12 |
| Total runtime | 1.00 | |
| (47 min) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lachenmaier, N.; Baumgärtner, D.; Schiffer, H.-P.; Kech, J. Gradient-Free and Gradient-Based Optimization of a Radial Turbine. Int. J. Turbomach. Propuls. Power 2020, 5, 14. https://doi.org/10.3390/ijtpp5030014
Lachenmaier N, Baumgärtner D, Schiffer H-P, Kech J. Gradient-Free and Gradient-Based Optimization of a Radial Turbine. International Journal of Turbomachinery, Propulsion and Power. 2020; 5(3):14. https://doi.org/10.3390/ijtpp5030014
Chicago/Turabian StyleLachenmaier, Nicolas, Daniel Baumgärtner, Heinz-Peter Schiffer, and Johannes Kech. 2020. "Gradient-Free and Gradient-Based Optimization of a Radial Turbine" International Journal of Turbomachinery, Propulsion and Power 5, no. 3: 14. https://doi.org/10.3390/ijtpp5030014
APA StyleLachenmaier, N., Baumgärtner, D., Schiffer, H.-P., & Kech, J. (2020). Gradient-Free and Gradient-Based Optimization of a Radial Turbine. International Journal of Turbomachinery, Propulsion and Power, 5(3), 14. https://doi.org/10.3390/ijtpp5030014





